Exploring Relaxation Phenomenon in Cu-Substituted Ba2NiWO6 Double Perovskites
Abstract
1. Introduction
2. Synthesis Method and Characterization Techniques
3. Result and Discussion
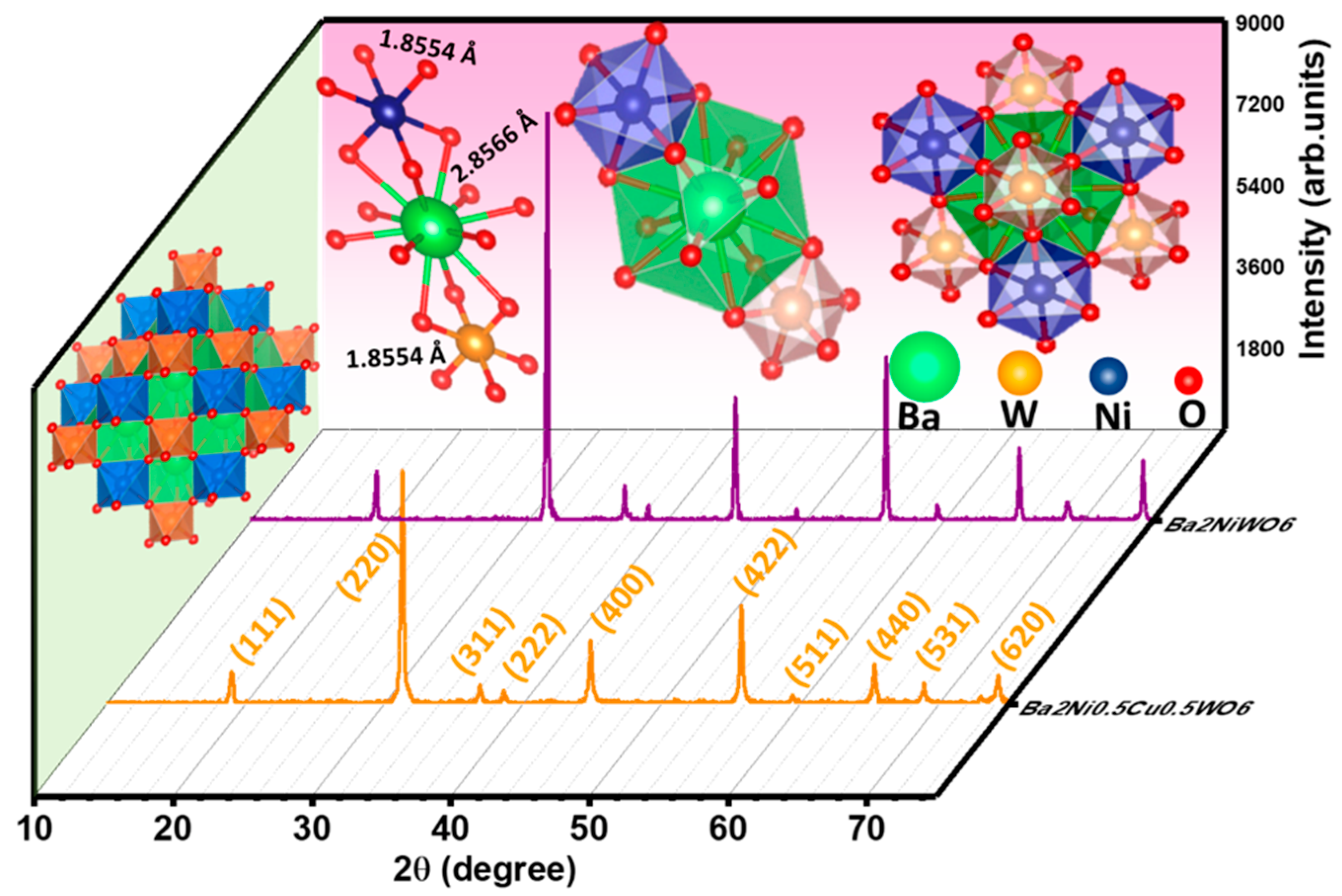
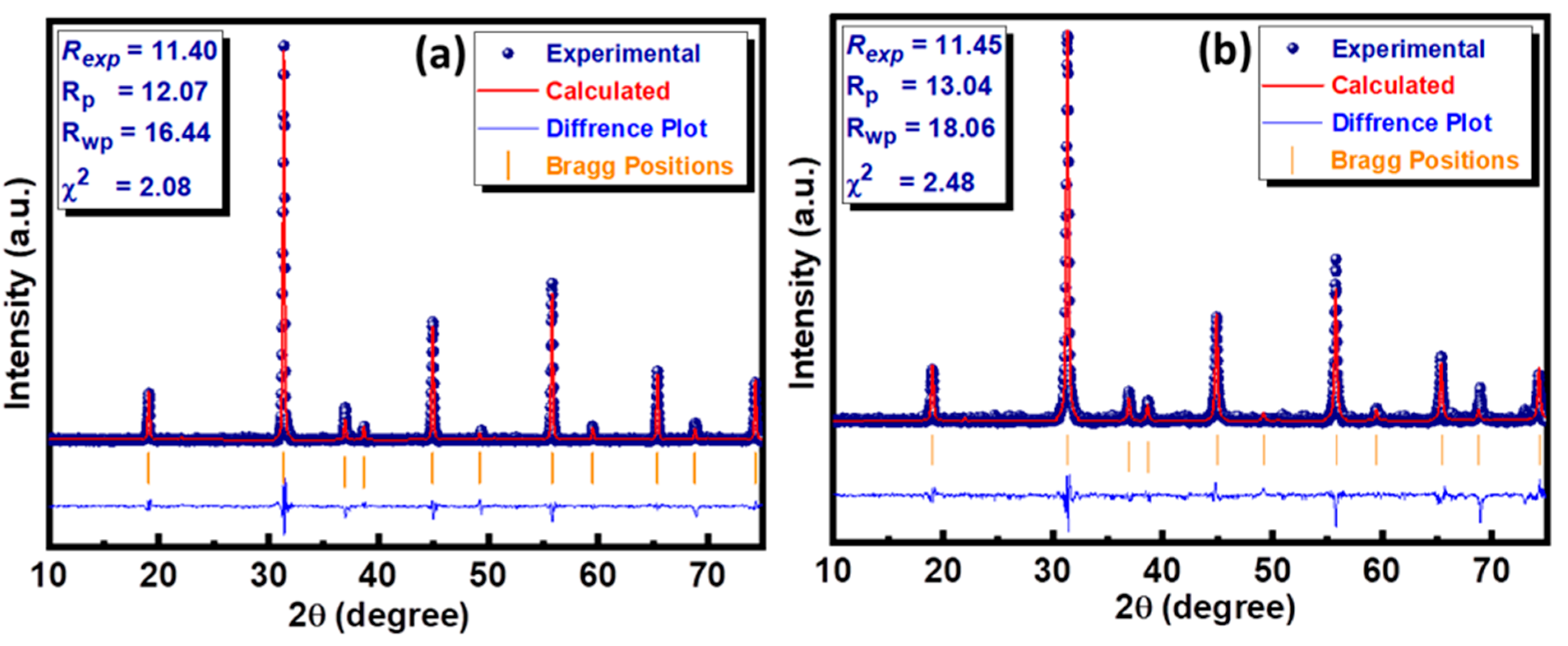
3.1. Structural Analysis
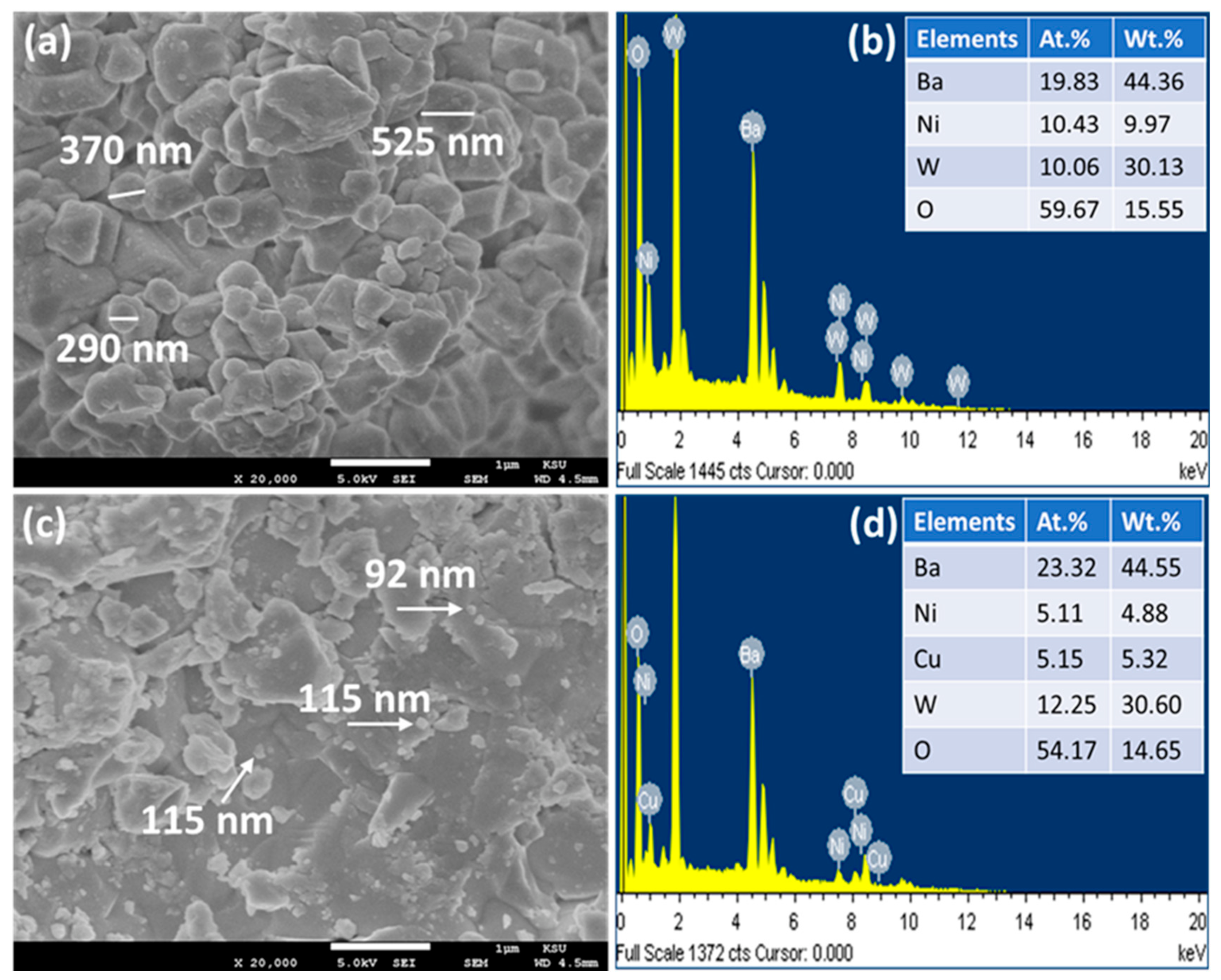
3.2. Morphological and Elemental Analysis
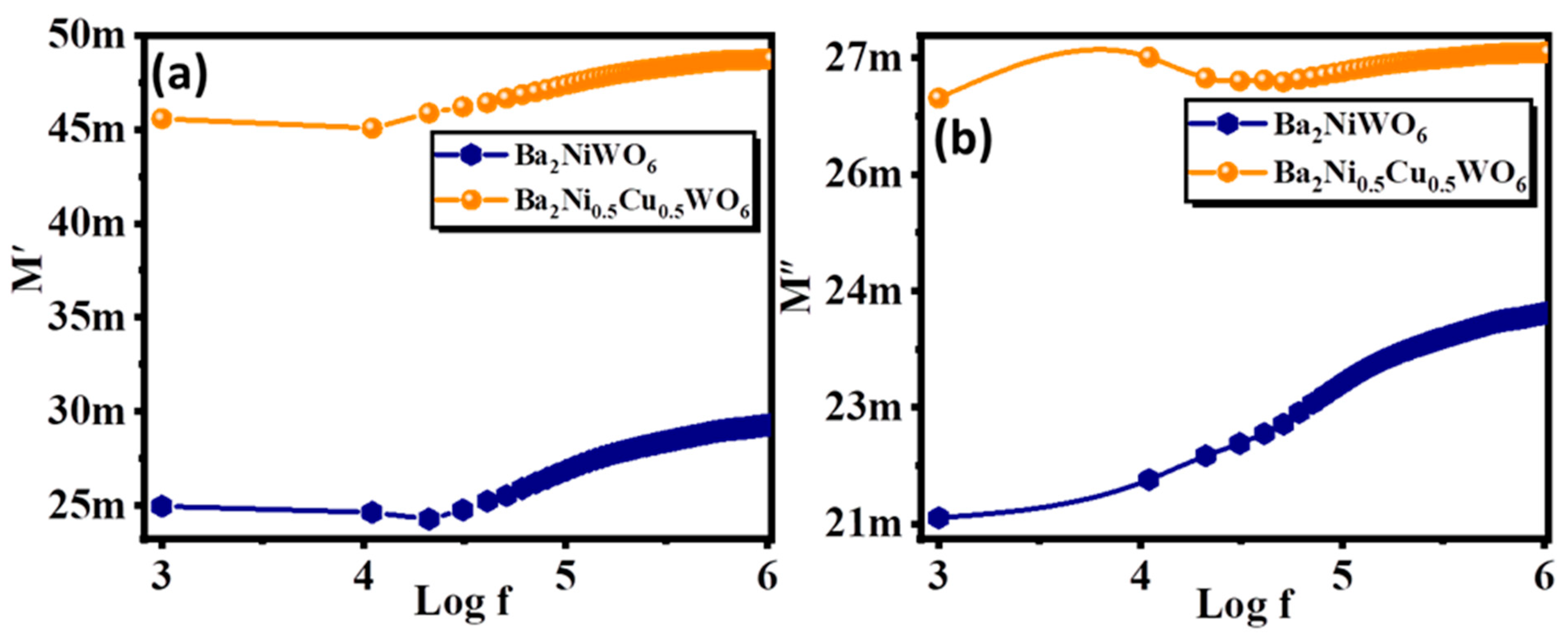
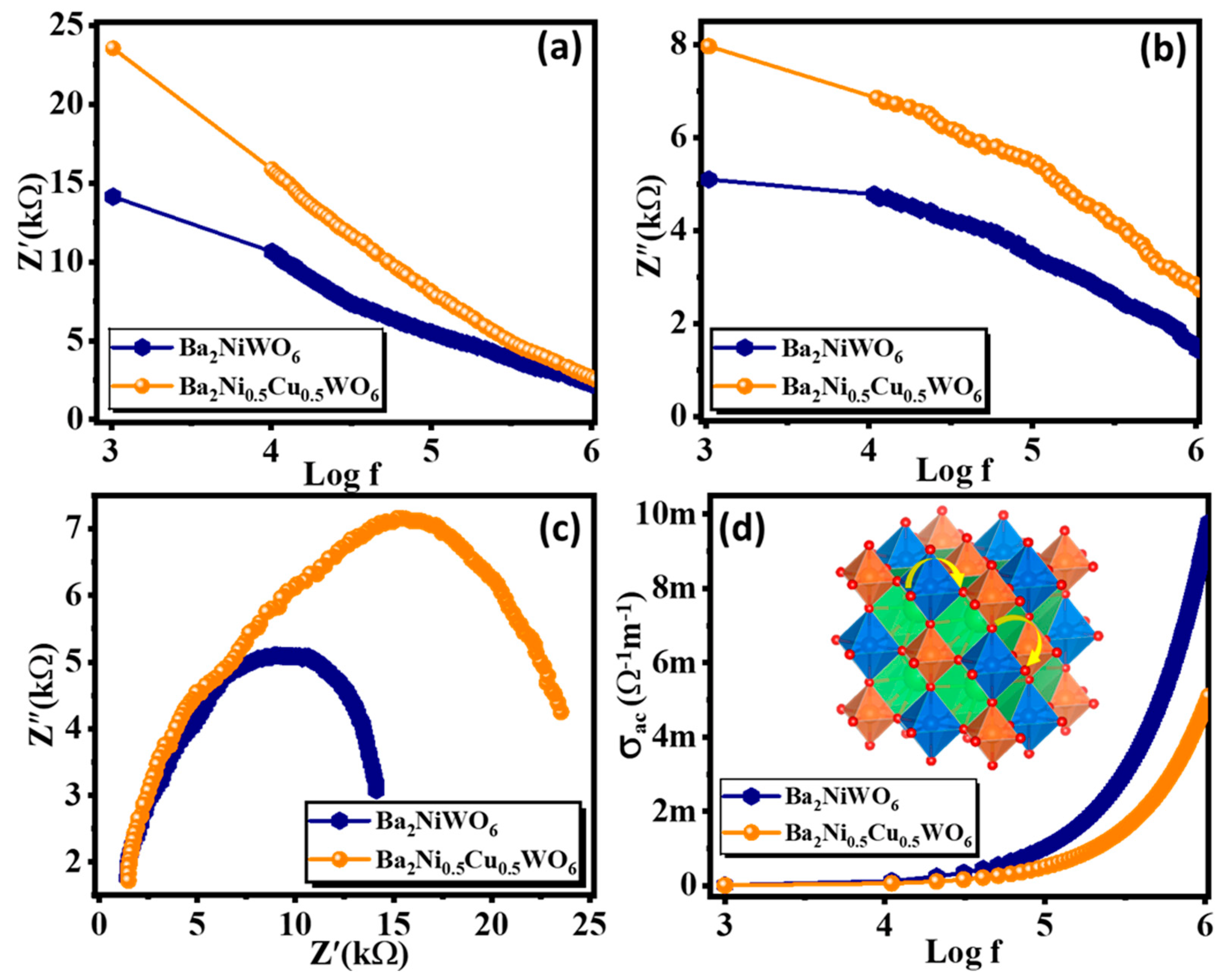
3.3. Dielectric Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Albalawi, H.; Mustafa, G.M.; Saba, S.; Kattan, N.A.; Mahmood, Q.; Somaily, H.H.; Amin, M.A. Study of optical and thermoelectric properties of double perovskites Cs2KTlX6 (X= Cl, Br, I) for solar cell and energy harvesting. Mater. Today Commun. 2022, 32, 104083. [Google Scholar] [CrossRef]
- Najar, F.A.; Abass, S.; Sultan, K.; Kharadi, M.A.; Malik, G.F.A.; Samad, R. Comparative study of optical properties of substitutionally doped La2NiMnO6 double perovskite ceramic: A potential candidate for solar cells and dielectrics. Phys. B Condens. Matter 2021, 621, 413311. [Google Scholar] [CrossRef]
- Winiarski, M.J.; Kozieł, K.; Sadecka, K.; Dereń, P.J. The substitution effects on electronic structure of Ba2MgWO6 double perovskite oxide. Solid State Commun. 2020, 314, 113936. [Google Scholar] [CrossRef]
- Chen, J.W.; Chiou, K.R.; Hsueh, A.C.; Chang, C.R. Dielectric relaxation of the double perovskite oxide Ba2PrRuO6. RSC Adv. 2019, 9, 12319–12324. [Google Scholar] [CrossRef] [PubMed]
- Miniajluk, N.; Bondzior, B.; Stefańska, D.; Dereń, P.J. Eu3+ ions in the highly symmetrical octahedral site in Ba2MgWO6 double perovskite. J. Alloy. Compd. 2019, 802, 190–195. [Google Scholar] [CrossRef]
- Bugaris, D.E.; Hodges, J.P.; Huq, A.; Zur Loye, H.C. Crystal growth, structures, and optical properties of the cubic double perovskites Ba2MgWO6 and Ba2ZnWO6. J. Solid State Chem. 2011, 184, 2293–2298. [Google Scholar] [CrossRef]
- Hanif, A.; Aldaghfag, S.A.; Aziz, A.; Yaseen, M.; Murtaza, A. Theoretical investigation of physical properties of Sr2XNbO6 (X = La, Lu) double perovskite oxides for optoelectronic and thermoelectric applications. Int. J. Energy Res. 2022, 46, 10633–10643. [Google Scholar] [CrossRef]
- Diao, C.L.; Wang, C.H.; Luo, N.N.; Qi, Z.M.; Shao, T.; Wang, Y.Y.; Jing, X.P.; Lu, J.; Shi, F.; Jing, X.-P. First-Principle Calculation and Assignment for Vibrational Spectra of Ba(Mg1/2W1/2)O3 Microwave Dielectric Ceramic. J. Am. Ceram. Soc. 2013, 96, 2898–2905. [Google Scholar] [CrossRef]
- Dehury, S.K.; Achary, P.; Choudhary RN, P. Electrical and dielectric properties of bismuth holmium cobalt titanate (BiHoCoTiO6): A complex double perovskite. J. Mater. Sci. Mater. Electron. 2018, 29, 3682–3689. [Google Scholar] [CrossRef]
- Das, N.; Singh, R.; Das, A.; Gupta, L.C.; Ganguli, A.K. Structural, magnetic and dielectric properties of a new double perovskite Pr2CoTiO6. J. Solid State Chem. 2017, 253, 355–359. [Google Scholar] [CrossRef]
- Vilesh, V.L.; Subodh, G. Crystal structure, phonon modes and dielectric properties of B site ordered ABiLiTeO6 (A= Ba, Sr) double perovskites. Ceram. Int. 2018, 44, 12036–12041. [Google Scholar] [CrossRef]
- Coşkun, M.; Polat, Ö.; Coşkun, F.M.; Durmuş, Z.; Çağlar, M.; Türüt, A. Frequency and temperature dependent electrical and dielectric properties of LaCrO3 and Ir doped LaCrO3 perovskite compounds. J. Alloy. Compd. 2018, 740, 1012–1023. [Google Scholar] [CrossRef]
- Stefańska, D.; Bondzior, B.; Vu, T.H.Q.; Miniajluk-Gaweł, N.; Dereń, P.J. The influence of morphology and Eu3+ concentration on luminescence and temperature sensing behavior of Ba2MgWO6 double perovskite as a potential optical thermometer. J. Alloy. Compd. 2020, 842, 155742. [Google Scholar] [CrossRef]
- Alsabah, Y.A.; Elden, A.T.; AlSalhi, M.S.; Elbadawi, A.A.; Siddig, M.A. Structural and optical properties of A2YVO6 (A= Mg, Sr) double perovskite oxides. Results Phys. 2019, 15, 102589. [Google Scholar] [CrossRef]
- Bharti, C.; Sinha, T.P. Dielectric properties of rare earth double perovskite oxide Sr2CeSbO6. Solid State Sci. 2010, 12, 498–502. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.; Xu, Y.; Luo, F.; Du, Y. Rare earth double perovskites: A fertile soil in the field of perovskite oxides. Inorg. Chem. Front. 2019, 6, 2226–2238. [Google Scholar] [CrossRef]
- Bharti, C.; Das, M.K.; Sen, A.; Chanda, S.; Sinha, T.P. Rietveld refinement and dielectric relaxation of a new rare earth based double perovskite oxide: BaPrCoNbO6. J. Solid State Chem. 2014, 210, 219–223. [Google Scholar] [CrossRef]
- Huyen, N.T.; Van Minh, N. Properties of (x)CoFe2O4-(1-x)BiFeO3 multiferroic composites. VNU J. Sci. Math. Phys. 2011, 27, 212–218. [Google Scholar]
- Baloch, A.A.; Alqahtani, S.M.; Mumtaz, F.; Muqaibel, A.H.; Rashkeev, S.N.; Alharbi, F.H. Extending Shannon’s ionic radii database using machine learning. Phys. Rev. Mater. 2021, 5, 043804. [Google Scholar] [CrossRef]
- Das, A.; De, S.; Bandyopadhyay, S.; Chatterjee, S.; Das, D. Magnetic, dielectric and magnetoelectric properties of BiFeO3-CoFe2O4 nanocomposites. J. Alloy. Compd. 2017, 697, 353–360. [Google Scholar] [CrossRef]
- Suresh, P.; Babu, P.D.; Srinath, S. Role of (La, Gd) co-doping on the enhanced dielectric and magnetic properties of BiFeO3 ceramics. Ceram. Int. 2016, 42, 4176–4184. [Google Scholar] [CrossRef]
- Gaikwad, V.M.; Acharya, S.A. Exploration of magnetically stable BiFeO3-CoFe2O4 composites with significant dielectric ordering at room temperature. J. Alloy. Compd. 2018, 755, 168–176. [Google Scholar] [CrossRef]
- Rawat, M.; Yadav, K.L. Structural, dielectric, ferroelectric and magnetic properties of (x)CoFe2O4-(1-x)BaTiO3 composite. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1462–1469. [Google Scholar]
- Balmuchu, S.P.; Dobbidi, P. The effect of La doping on multiferroic BiFeO3 ceramic through structural, dielectric, magnetic, ferroelectric, and optical studies. Phys. B Condens. Matter 2022, 638, 413937. [Google Scholar] [CrossRef]
- Rhaman, M.M.; Matin, M.A.; Hakim, M.A.; Islam, M.F. Dielectric, ferroelectric and ferromagnetic properties of samarium doped multiferroic bismuth ferrite. Mater. Res. Express 2019, 6, 125080. [Google Scholar] [CrossRef]
- Dash, S.; Choudhary RN, P.; Das, P.R.; Kumar, A. Structural, dielectric, and multiferroic properties of (Bi0.5K0.5)(Fe0.5Nb0.5)O3. Can. J. Phys. 2015, 93, 738–744. [Google Scholar] [CrossRef]
- Abbas, S.K.; Mustafa, G.M.; Saleem, M.; Mahmood, A.; Ramay, S.M.; Atiq, S.; Naseem, S. Morphologically controlled dielectric dispersion and energy density optimization in Co/Ni spinel ferrites. Ceram. Int. 2020, 46, 9765–9772. [Google Scholar] [CrossRef]
- Khalid, A.; Ali, M.; Mustafa, G.M.; Atiq, S.; Ramay, S.M.; Mahmood, A.; Naseem, S. Structural and dielectric properties of Sol–Gel synthesized (Mn, Cu) co-doped BiFeO3 ceramics. J. Sol Gel Sci. Technol. 2016, 80, 814–820. [Google Scholar] [CrossRef]
- Yadav, R.S.; Kuřitka, I.; Vilcakova, J.; Havlica, J.; Masilko, J.; Kalina, L.; Hajdúchová. Impact of grain size and structural changes on magnetic, dielectric, electrical, impedance and modulus spectroscopic characteristics of CoFe2O4 nanoparticles synthesized by honey mediated Sol-Gel combustion method. Adv. Nat. Sci. Nanosci. Nanotechnol. 2017, 8, 045002. [Google Scholar] [CrossRef]
- Sendhilnathan, S. Enhancement in dielectric and magnetic properties of Mg2+ substituted highly porous super paramagnetic nickel ferrite nanoparticles with Williamson-Hall plots mechanistic view. Ceram. Int. 2017, 43, 15447–15453. [Google Scholar]
- Ansar, M.T.; Ali, A.; Mustafa, G.M.; Afzal, F.; Ishaq, S.; Kanwal, F.; Atiq, S. Polypyrrole-based nanocomposites architecture as multifunctional material for futuristic energy storage applications. J. Alloy. Compd. 2021, 855, 157341. [Google Scholar] [CrossRef]
- Asandulesa, M.; Kostromin, S.; Podshivalov, A.; Tameev, A.; Bronnikov, S. Relaxation processes in a polymer composite for bulk heterojunction: A dielectric spectroscopy study. Polymer 2020, 203, 122785. [Google Scholar] [CrossRef]
- Arif, S.; Saba, S.; Mustafa, G.M.; Akhtar, M.; Saleem, M.; Riaz, S.; Atiq, S. Analysis of recoverable and energy loss density mediated by Ni/Cr co-doping in BiFeO3. J. Mater. Sci. Mater. Electron. 2020, 31, 14775–14783. [Google Scholar] [CrossRef]
- Atiq, S.; Fatima, A.; Khalid, M.; Hassan, A.; Mustafa, G.M.; Siddiqi, S.A.; Naseem, S. Multifunctionality of magnetoelectrically coupled Ni/Cr co-doped BiFeO3 multiferroics. J. Alloy. Compd. 2019, 789, 400–408. [Google Scholar] [CrossRef]
- Asandulesa, M.; Kostromin, S.; Tameev, A.; Aleksandrov, A.; Bronnikov, S. Molecular dynamics and conductivity of a PTB7: PC71BM photovoltaic polymer blend: A dielectric spectroscopy study. ACS Appl. Polym. Mater. 2021, 3, 4869–4878. [Google Scholar] [CrossRef]
- Asandulesa, M.; Chibac-Scutaru, A.L.; Culica, M.E.; Melinte, V.; Coseri, S. Cellulose-based films with enhanced load of nitrogen containing heterocycles: The impact on the surface morphology and proton conductivity. Appl. Surf. Sci. 2023, 607, 155077. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, P.; Jiang, X.; Li, L.; Zhang, J.; Peng, W. Percolation mechanism through trapping/de-trapping process at defect states for resistive switching devices with structure of Ag/SixC1− x/p-Si. J. Appl. Phys. 2014, 116, 064505. [Google Scholar] [CrossRef]
- Riaz, A.; ul Ain, Q.; Kanwal, F.; Ishaq, S.; Khan, A.R.; Mustafa, G.M.; Atiq, S. Identification of frequency regimes for short and long range mobility of charge carriers in GO/MnFe2O4/PPy nanocomposites. Synth. Met. 2020, 263, 116336. [Google Scholar] [CrossRef]
- Sheoran, N.; Kumar, V.; Kumar, A. Comparative study of structural, magnetic and dielectric properties of CoFe2O4@ BiFeO3 and BiFeO3@ CoFe2O4 core-shell nanocomposites. J. Magn. Magn. Mater. 2019, 475, 30–37. [Google Scholar] [CrossRef]
- Raja; Alexander, A.; Sathyamoorthy, B.; Chandrasekaran, G. Structural, electrical and magnetic properties of Sr doped nickel ferrite using sol-gel auto combustion route. AIP Conf. Proc. 2019, 2162, 020075. [Google Scholar]

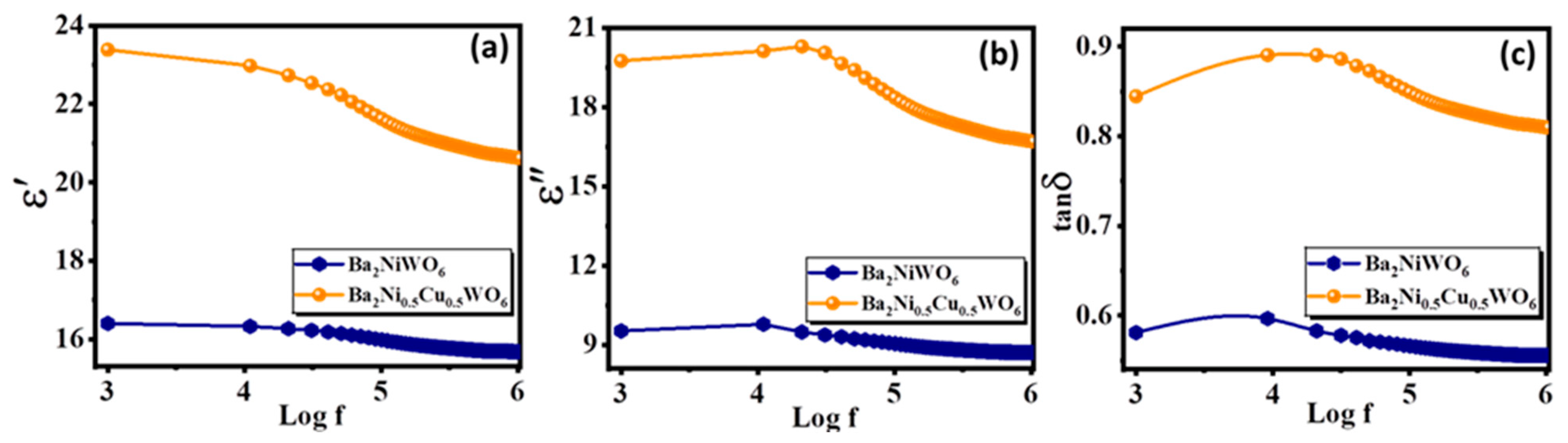
| Frequency | Ba2NiWO6 | Ba2Ni0.5Cu0.5WO6 | ||||
|---|---|---|---|---|---|---|
| ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | |
| 1 kHz | 16.40 | 9.53 | 0.58 | 23.38 | 19.75 | 0.84 |
| 10 kHz | 16.32 | 9.87 | 0.60 | 22.97 | 20.12 | 0.89 |
| 100 kHz | 15.98 | 9.05 | 0.57 | 21.62 | 18.35 | 0.85 |
| 250 kHz | 15.80 | 8.85 | 0.56 | 21.07 | 17.43 | 0.83 |
| 500 kHz | 15.72 | 8.75 | 0.55 | 20.80 | 19.99 | 0.82 |
| 750 kHz | 15.69 | 8.72 | 0.55 | 20.69 | 16.82 | 0.81 |
| 1 MHz | 15.68 | 8.71 | 0.55 | 20.62 | 16.70 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramay, S.M.; Aldosary, M.H.; Mustafa, G.M.; Saba, S.; Atiq, S.; Aftab, S.; Ebdah, M.A. Exploring Relaxation Phenomenon in Cu-Substituted Ba2NiWO6 Double Perovskites. Crystals 2023, 13, 625. https://doi.org/10.3390/cryst13040625
Ramay SM, Aldosary MH, Mustafa GM, Saba S, Atiq S, Aftab S, Ebdah MA. Exploring Relaxation Phenomenon in Cu-Substituted Ba2NiWO6 Double Perovskites. Crystals. 2023; 13(4):625. https://doi.org/10.3390/cryst13040625
Chicago/Turabian StyleRamay, Shahid M., Mohammed H. Aldosary, Ghulam M. Mustafa, Sadaf Saba, Shahid Atiq, Sikandar Aftab, and M. A. Ebdah. 2023. "Exploring Relaxation Phenomenon in Cu-Substituted Ba2NiWO6 Double Perovskites" Crystals 13, no. 4: 625. https://doi.org/10.3390/cryst13040625
APA StyleRamay, S. M., Aldosary, M. H., Mustafa, G. M., Saba, S., Atiq, S., Aftab, S., & Ebdah, M. A. (2023). Exploring Relaxation Phenomenon in Cu-Substituted Ba2NiWO6 Double Perovskites. Crystals, 13(4), 625. https://doi.org/10.3390/cryst13040625







