Effects of Crack Formation on the Mechanical Properties of Bilayer Graphene: A Comparative Analysis
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
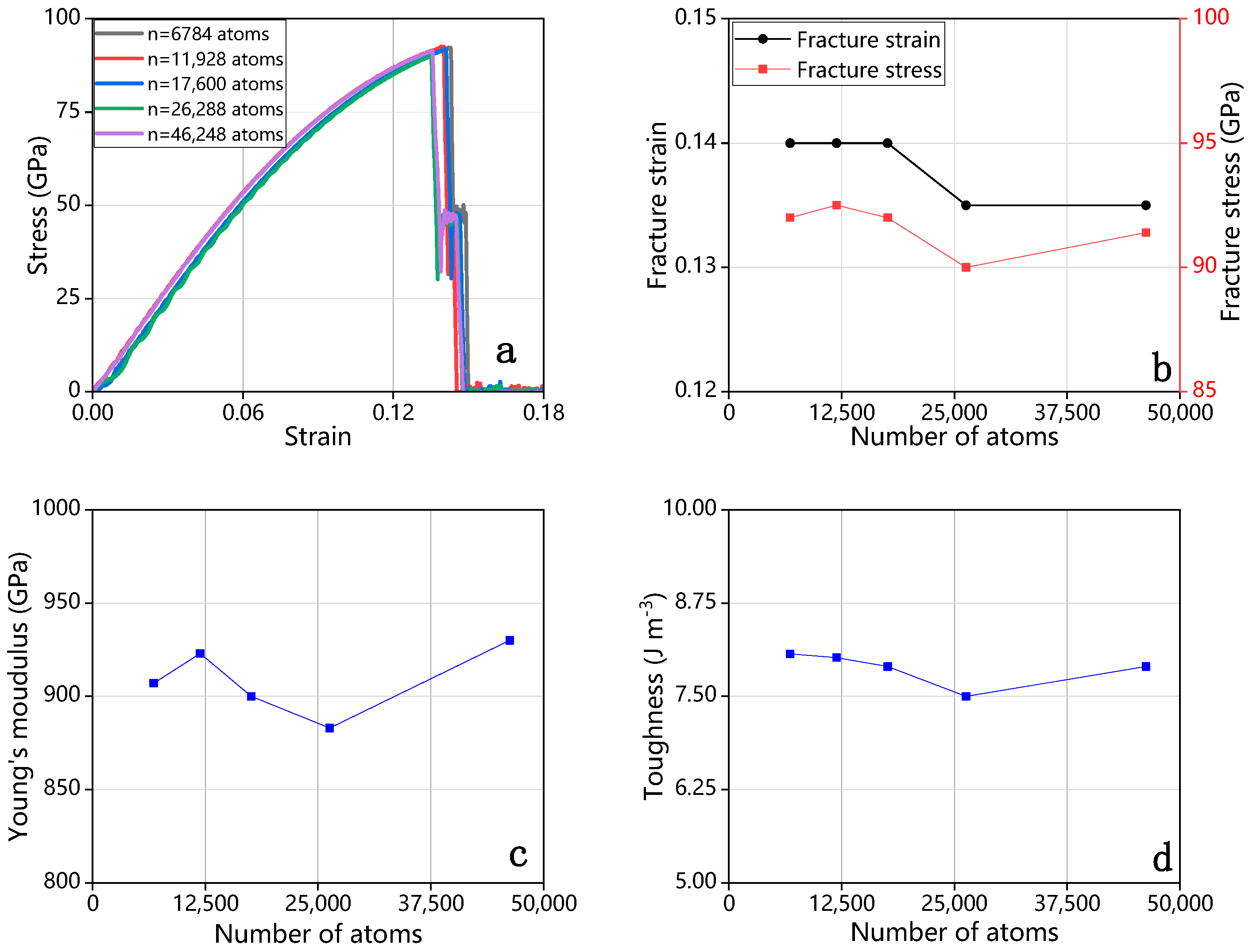
3.1. Effect of the System Size
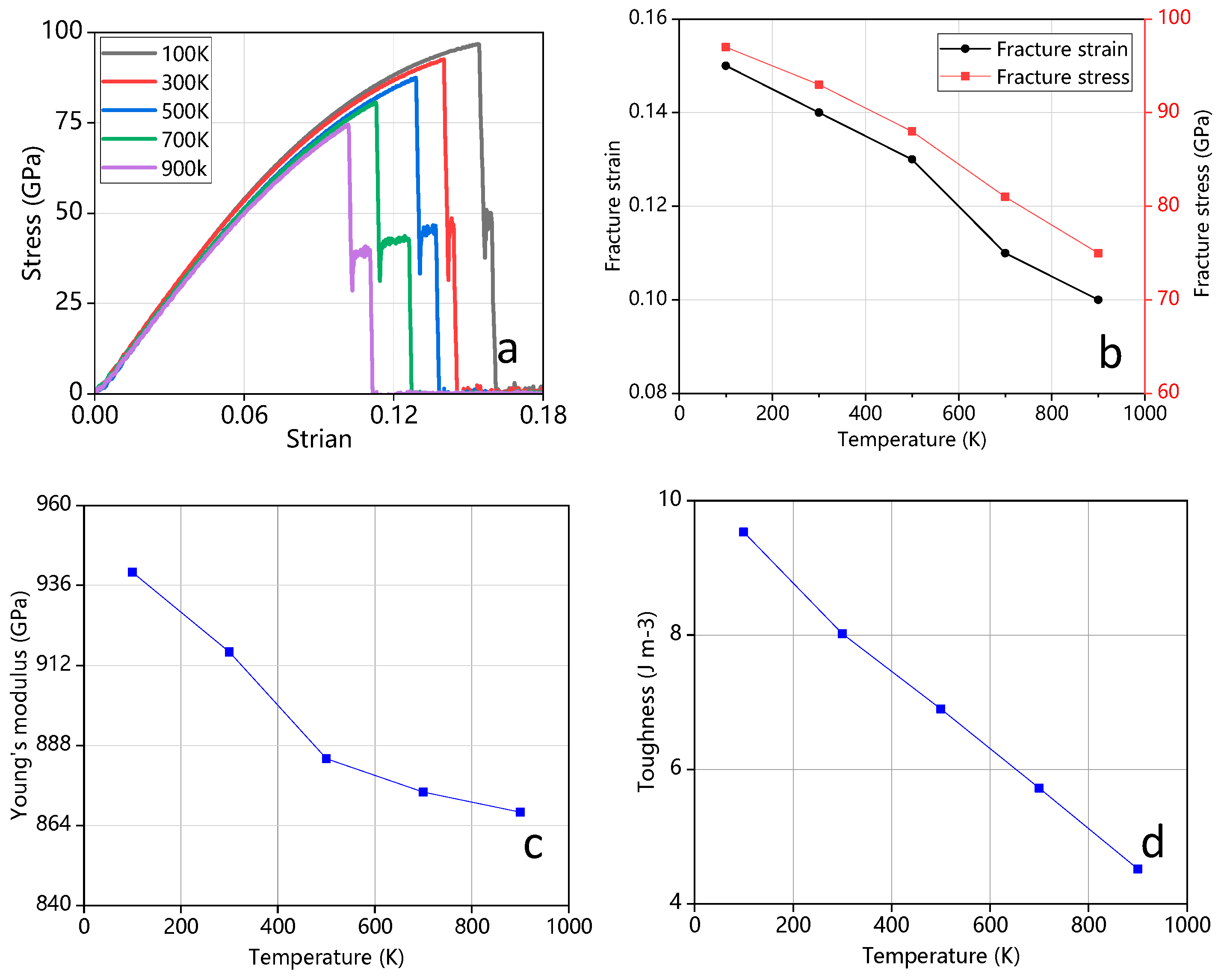
3.2. Effect of Temperature
3.3. Bilayer Graphene with Cracks on Both Layers
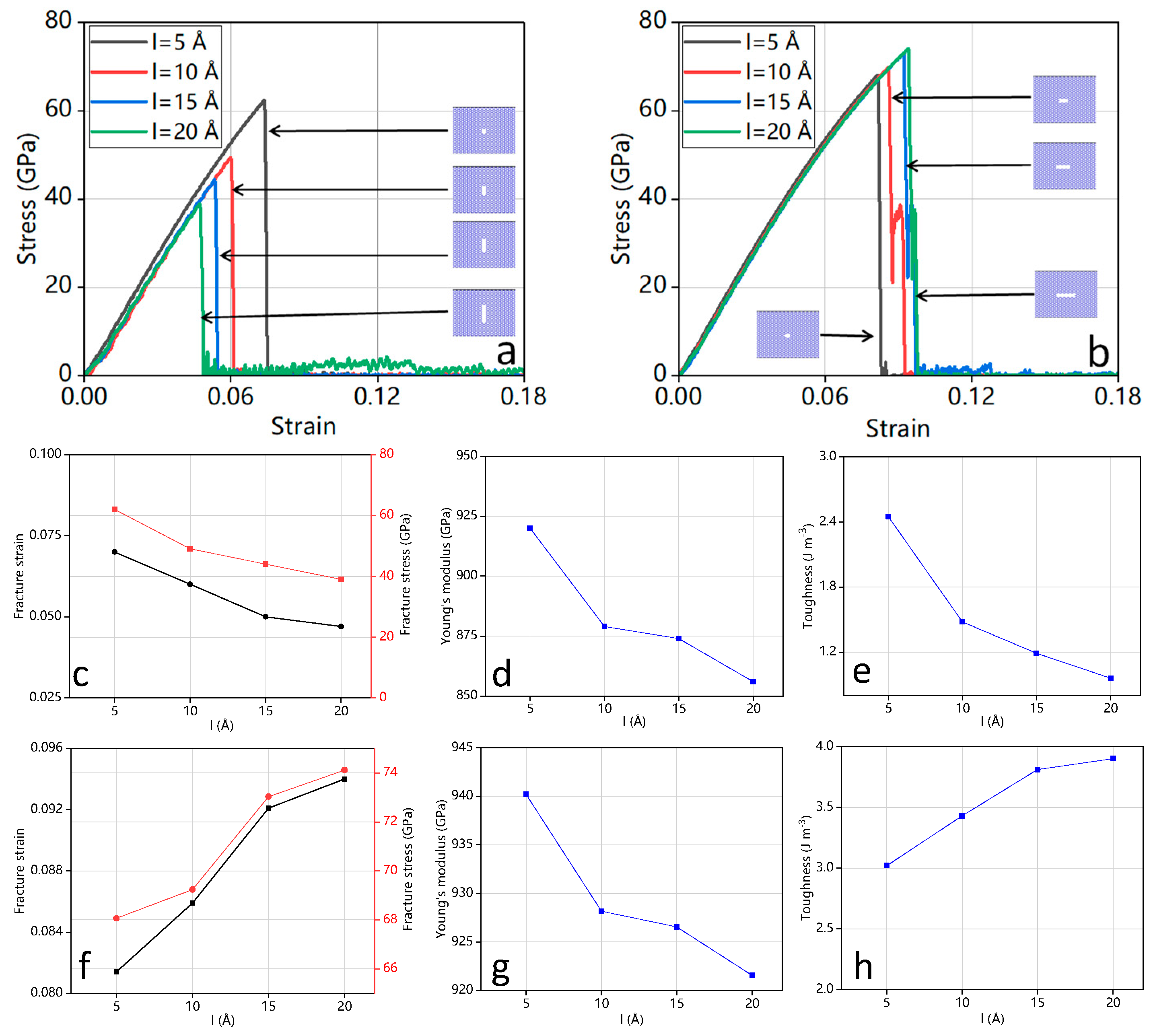
3.3.1. Rectangular Cracks
3.3.2. Circular Cracks
3.3.3. Quasi-Hexagonal Cracks and Compare with Circular Cracks
3.3.4. Comparison of Bilayer Circular Cracks and Quasi-Hexagonal Cracks
3.4. Bilayer Graphene with Cracks on Single Layer
3.4.1. Rectangular Cracks (Along y-Axis)
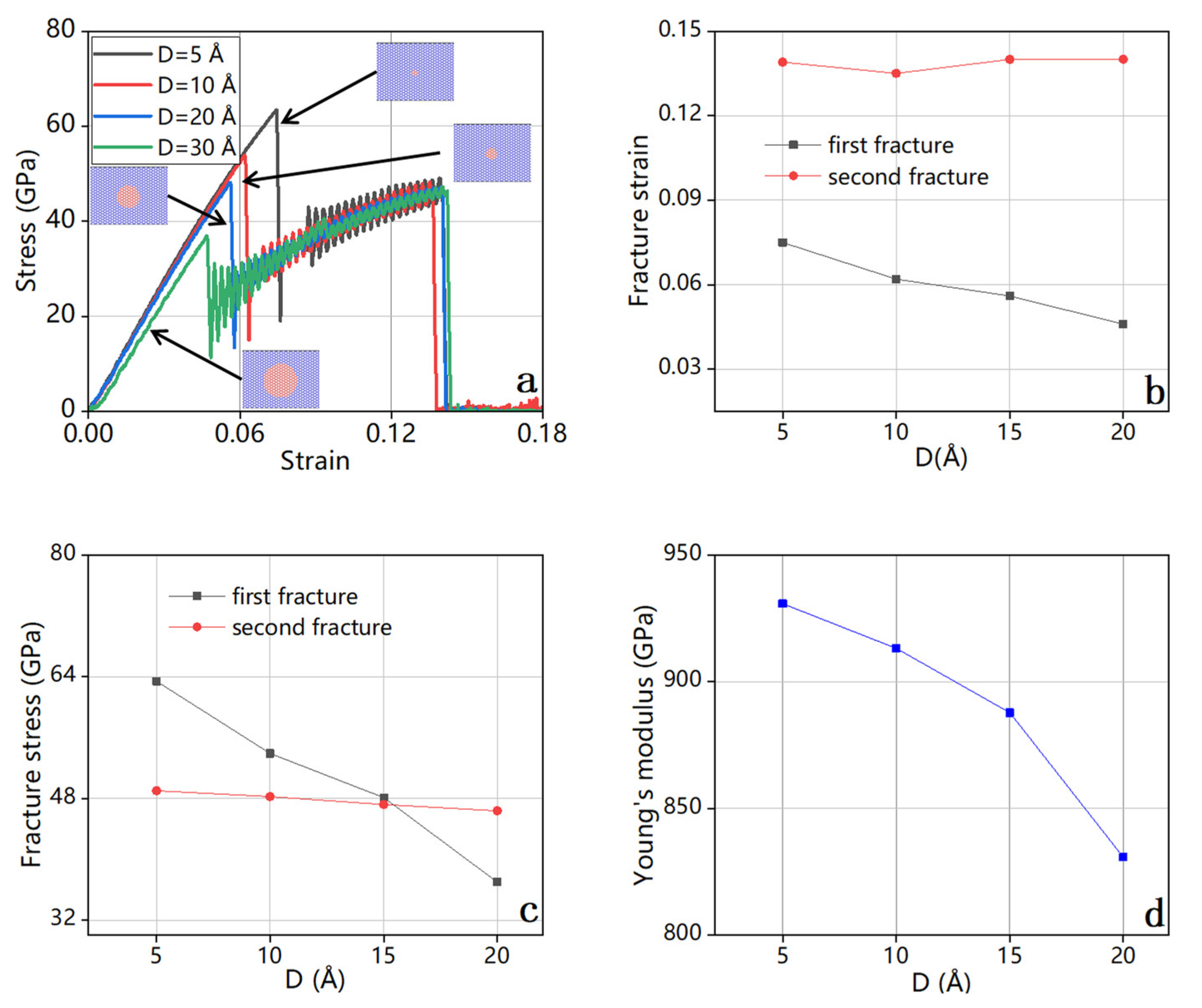
3.4.2. Circular Cracks
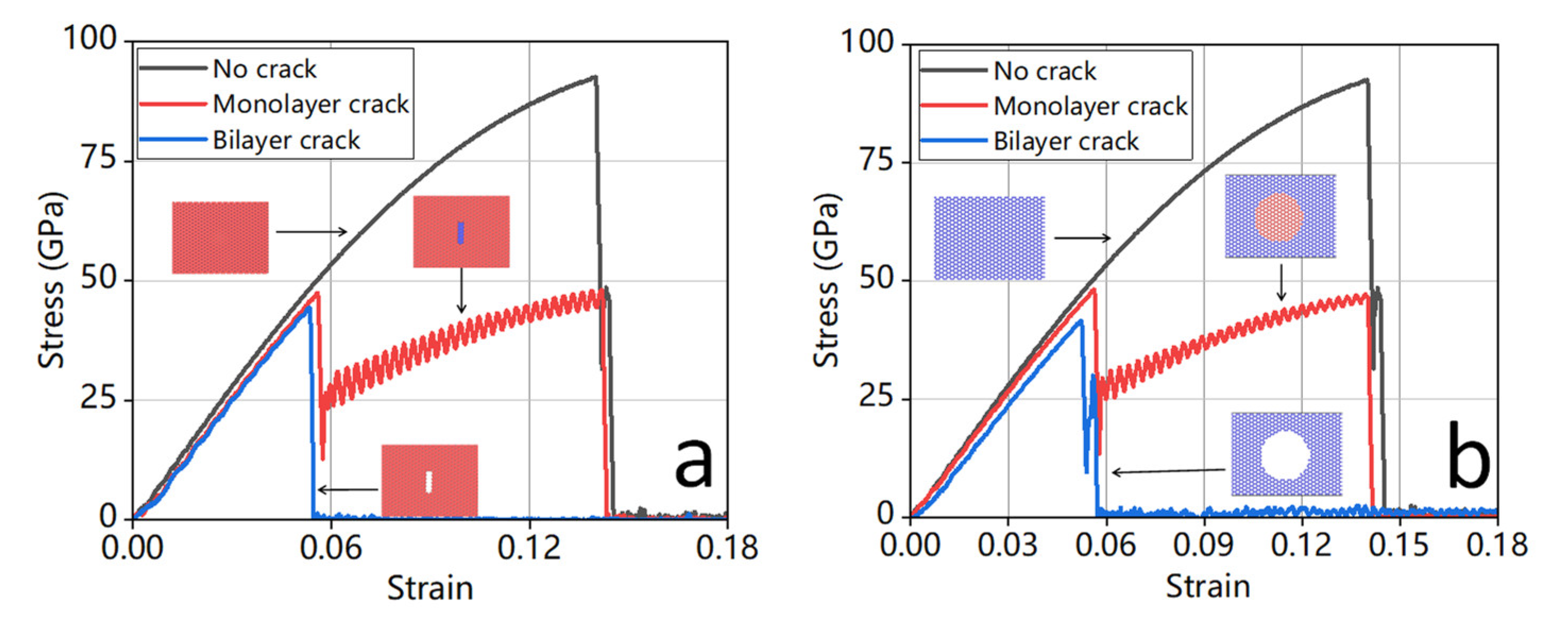
3.5. Comparison between Monolayer Cracks and Bilayer Cracks
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Aliofkhazraei, M.; Ali, N.; Milne, W.I.; Ozkan, C.S.; Mitura, S.; Gervasoni, J.L. Mechanical properties of graphene. In Graphene Science Handbook; CRC Press: Boca Raton, FL, USA, 2016; pp. 19–32. [Google Scholar]
- Anastasi, A.A.; Ritos, K.; Cassar, G.; Borg, M.K. Mechanical properties of pristine and nanoporous graphene. Mol. Simul. 2016, 42, 1502–1511. [Google Scholar] [CrossRef]
- Dewapriya, M.A.N.; Phani, A.S.; Rajapakse, R.K.N.D. Influence of temperature and free edges on the mechanical properties of graphene. Model. Simul. Mater. Sci. Eng. 2013, 21, 065017. [Google Scholar] [CrossRef]
- Zandiatashbar, A.; Lee, G.-H.; An, S.J.; Lee, S.; Mathew, N.; Terrones, M.; Hayashi, T.; Picu, C.R.; Hone, J.; Koratkar, N. Effect of defects on the intrinsic strength and stiffness of graphene. Nat. Commun. 2014, 5, 3186. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, S.; Hu, P.; Zhao, G.; Li, Y.; Zhang, X.; Han, W. Enhanced mechanical, thermal, and electric properties of graphene aerogels via supercritical ethanol drying and high-temperature thermal reduction. Sci. Rep. 2017, 7, 1439. [Google Scholar] [CrossRef] [PubMed]
- Ranjbartoreh, A.R.; Wang, B.; Shen, X.; Wang, G. Advanced mechanical properties of graphene paper. J. Appl. Phys. 2011, 109, 014306. [Google Scholar] [CrossRef]
- Li, X.; Guo, J. Numerical Investigation of the Fracture Properties of Pre-Cracked Monocrystalline/Polycrystalline Graphene Sheets. Materials 2019, 12, 263. [Google Scholar] [CrossRef] [PubMed]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.S.; Li, T.; Li, Y.; et al. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef]
- Cao, Q.; Geng, X.; Wang, H.; Wang, P.; Liu, A.; Lan, Y.; Peng, Q. A Review of Current Development of Graphene Mechanics. Crystals 2018, 8, 357. [Google Scholar] [CrossRef]
- Lee, G.-H.; Cooper, R.C.; An, S.J.; Lee, S.; van der Zande, A.; Petrone, N.; Hammerberg, A.G.; Lee, C.; Crawford, B.; Oliver, W.; et al. High-strength chemical-vapor-deposited graphene and grain boundaries. Science 2013, 340, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Zhao, Q.; Nardelli, M.B.; Bernholc, J. Ultimate strength of carbon nanotubes: A theoretical study. Phys. Rev. B 2002, 65, 144105. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef]
- McCann, E. Interlayer asymmetry gap in the electronic band structure of bilayer graphene. Phys. Status Solidi. B Basic Res. 2007, 244, 4112–4117. [Google Scholar] [CrossRef]
- McCann, E. Asymmetry gap in the electronic band structure of bilayer graphene. Phys. Review. B Condens. Matter 2006, 74, 161403. [Google Scholar] [CrossRef]
- Spirito, D.; Coquillat, D.; De Bonis, S.L.; Lombardo, A.; Bruna, M.; Ferrari, A.C.; Pellegrini, V.; Tredicucci, A.; Knap, W.; Vitiello, M.S. High performance bilayer-graphene terahertz detectors. Appl. Phys. Lett. 2014, 104, 061111. [Google Scholar] [CrossRef]
- Fiori, G.; Neumaier, D.; Szafranek, B.N.; Iannaccone, G. Bilayer Graphene Transistors for Analog Electronics. IEEE Trans. Electron Devices 2014, 61, 729–733. [Google Scholar] [CrossRef]
- Xia, F.; Farmer, D.B.; Lin, Y.-M.; Avouris, P. Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature. Nano Lett. 2010, 10, 715–718. [Google Scholar] [CrossRef]
- Zeng, L.; Xie, C.; Tao, L.; Long, H.; Tang, C.; Tsang, Y.H.; Jie, J. Bilayer graphene based surface passivation enhanced nano structured self-powered near-infrared photodetector. Opt. Express 2015, 23, 4839–4846. [Google Scholar] [CrossRef] [PubMed]
- Yan, H. Bilayer graphene: Physics and application outlook in photonics. Nanophotonics 2015, 4, 115–127. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Gu, Y.T. Mechanical properties of graphene: Effects of layer number, temperature and isotope. Comput. Mater. Sci. 2013, 71, 197–200. [Google Scholar] [CrossRef]
- Afyouni Akbari, S.; Ghafarinia, V.; Larsen, T.; Parmar, M.M.; Villanueva, L.G. Large Suspended Monolayer and Bilayer Graphene Membranes with Diameter up to 750 µm. Sci. Rep. 2020, 10, 6426. [Google Scholar] [CrossRef]
- Chen, M.-C.; Hsu, C.-L.; Hsueh, T.-J. Fabrication of Humidity Sensor Based on Bilayer Graphene. IEEE Electron Device Lett. 2014, 35, 590–592. [Google Scholar] [CrossRef]
- Nimbalkar, A.; Kim, H. Opportunities and Challenges in Twisted Bilayer Graphene: A Review. Nano-Micro Lett. 2020, 12, 126. [Google Scholar] [CrossRef] [PubMed]
- Saharudin, M.S.; Hasbi, S.; Rashidi, N.M.; Nordin, M.S.J. Effect of short-term water exposure on mechanical properties of multi-layer graphene and multi-walled carbon nanotubes-reinforced epoxy nanocomposites. J. Eng. Sci. Technol. 2018, 13, 4226–4239. [Google Scholar]
- Alahmed, I.I.; Altanany, S.M.; Abdulazeez, I.; Shoaib, H.; Alsayoud, A.Q.; Abbout, A.; Peng, Q. The Crack Angle of 60° Is the Most Vulnerable Crack Front in Graphene According to MD Simulations. Crystals 2021, 11, 1355. [Google Scholar] [CrossRef]
- Wavrunek, T.; Peng, Q.; Abu-Zahra, N. Mechanical Properties and Buckling of Kagome Graphene under Tension: A Molecular Dynamics Study. Crystals 2022, 12, 292. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Cheng, X. The effect of temperature, defect and strain rate on the mechanical property of multi-layer graphene: Coarse-grained molecular dynamics study. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 85, 97–102. [Google Scholar] [CrossRef]
- Kordkheili, S.H.; Moshrefzadeh-Sani, H. Mechanical properties of double-layered graphene sheets. Comput. Mater. Sci. 2013, 69, 335–343. [Google Scholar] [CrossRef]
- Chu, L.; Shi, J.; Braun, R. The equivalent Young’s modulus prediction for vacancy defected graphene under shear stress. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 110, 115–122. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, C. Measurements of mechanical properties and number of layers of graphene from nano-indentation. Diam. Relat. Mater. 2012, 24, 1–5. [Google Scholar] [CrossRef]
- Liu, A.; Peng, Q. A Molecular Dynamics Study of the Mechanical Properties of Twisted Bilayer Graphene. Micromachines 2018, 9, 440. [Google Scholar] [CrossRef]
- Guadagno, L.; Raimondo, M.; Vertuccio, L.; Mauro, M.; Guerra, G.; Lafdi, K.; De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. Optimization of graphene-based materials outperforming host epoxy matrices. RSC Adv. 2015, 5, 36969–36978. [Google Scholar] [CrossRef]
- Jin, X.; Adpakpang, K.; Kim, I.Y.; Oh, S.M.; Lee, N.-S.; Hwang, S.-J. An Effective Way to Optimize the Functionality of Graphene-Based Nanocomposite: Use of the Colloidal Mixture of Graphene and Inorganic Nanosheets. Sci. Rep. 2015, 5, 11057. [Google Scholar] [CrossRef] [PubMed]
- Duong, H.M.; Tran, T.Q.; Kopp, R.; Myint, S.M.; Peng, L. Chapter 1—Direct Spinning of Horizontally Aligned Carbon Nanotube Fibers and Films From the Floating Catalyst Method, 2nd ed.; Schulz, M.J., Shanov, V., Yin, Z., Cahay, M., Eds.; Nanotube Superfiber Materials; William Andrew Publishing: Norwich, NY, USA, 2019; pp. 3–29. [Google Scholar]
- Duong, H.M.; Myint, S.M.; Tran, T.Q.; Le, D.K. Post-spinning treatments to carbon nanotube fibers. In Carbon Nanotube Fibers and Yarns; Elsevier: Amsterdam, The Netherlands, 2020; pp. 103–134. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Yang, X.; Wu, S.; Xu, J.; Cao, B.; To, A.C. Spurious heat conduction behavior of finite-size graphene nanoribbon under extreme uniaxial strain caused by the AIREBO potential. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 96, 46–53. [Google Scholar] [CrossRef]
- Wang, X.; Hong, Y.; Ma, D.; Zhang, J. Molecular dynamics study of thermal transport in a nitrogenated holey graphene bilayer. J. Mater. Chem. 2017, 5, 5119–5127. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, L.; Fan, F.; Zeng, Z.; Peng, C.; Loya, P.E.; Liu, Z.; Gong, Y.; Zhang, J.; Zhang, X.; et al. Fracture toughness of graphene. Nat. Commun. 2014, 5, 3782. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhou, M.; Sun, X.; Qian, L.; Li, L.; Xie, Y.; Liu, Z.; Wu, D.; Yang, L.; Wu, T.; et al. Effects of Temperature and Strain Rate on the Fracture Behaviors of an Al-Zn-Mg-Cu Alloy. Materials 2018, 11, 1233. [Google Scholar] [CrossRef] [PubMed]
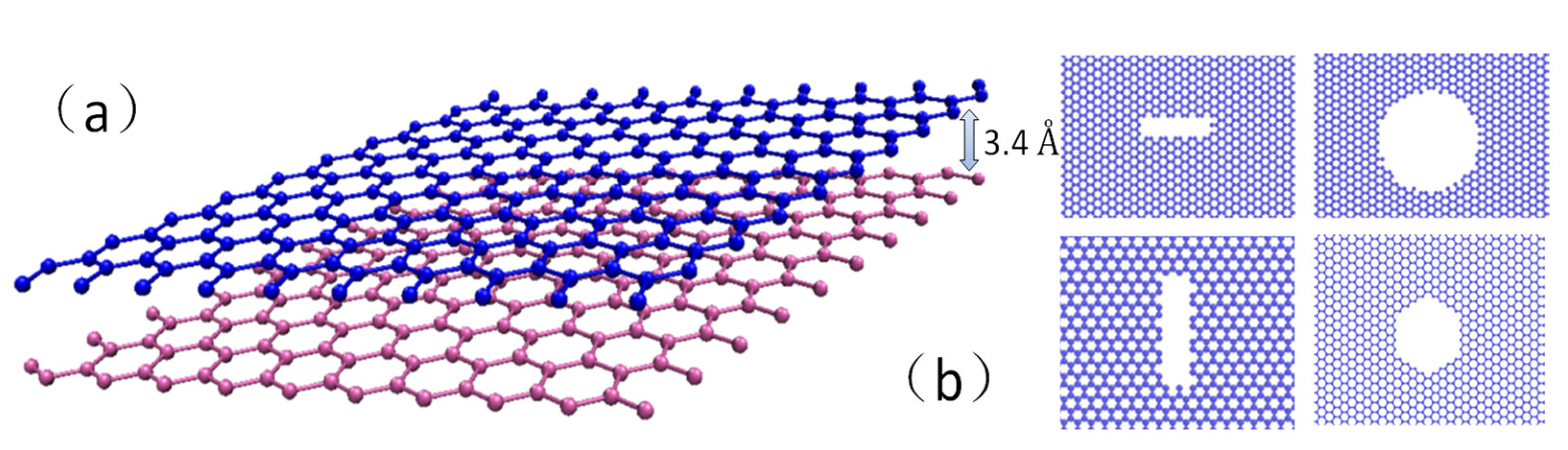
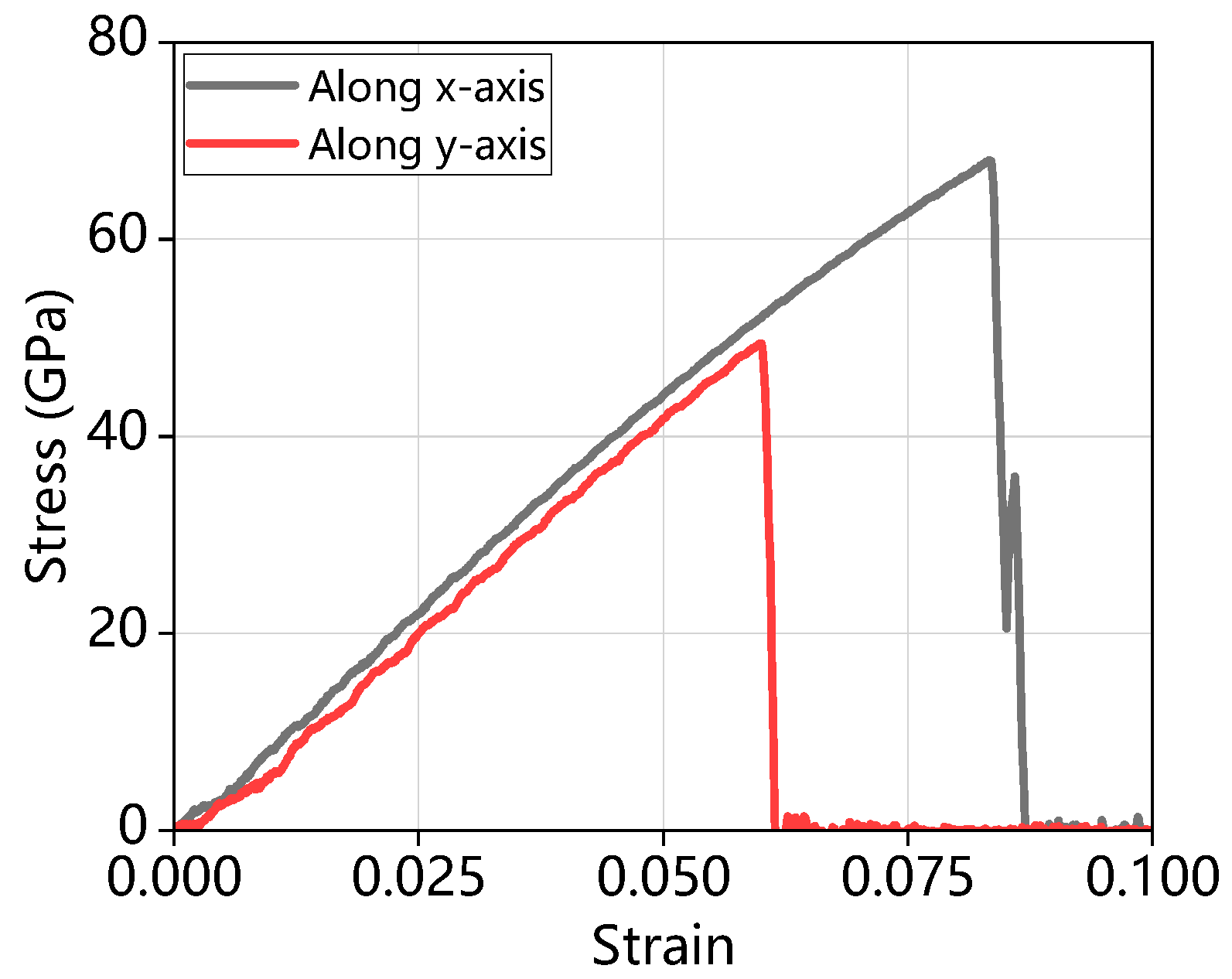
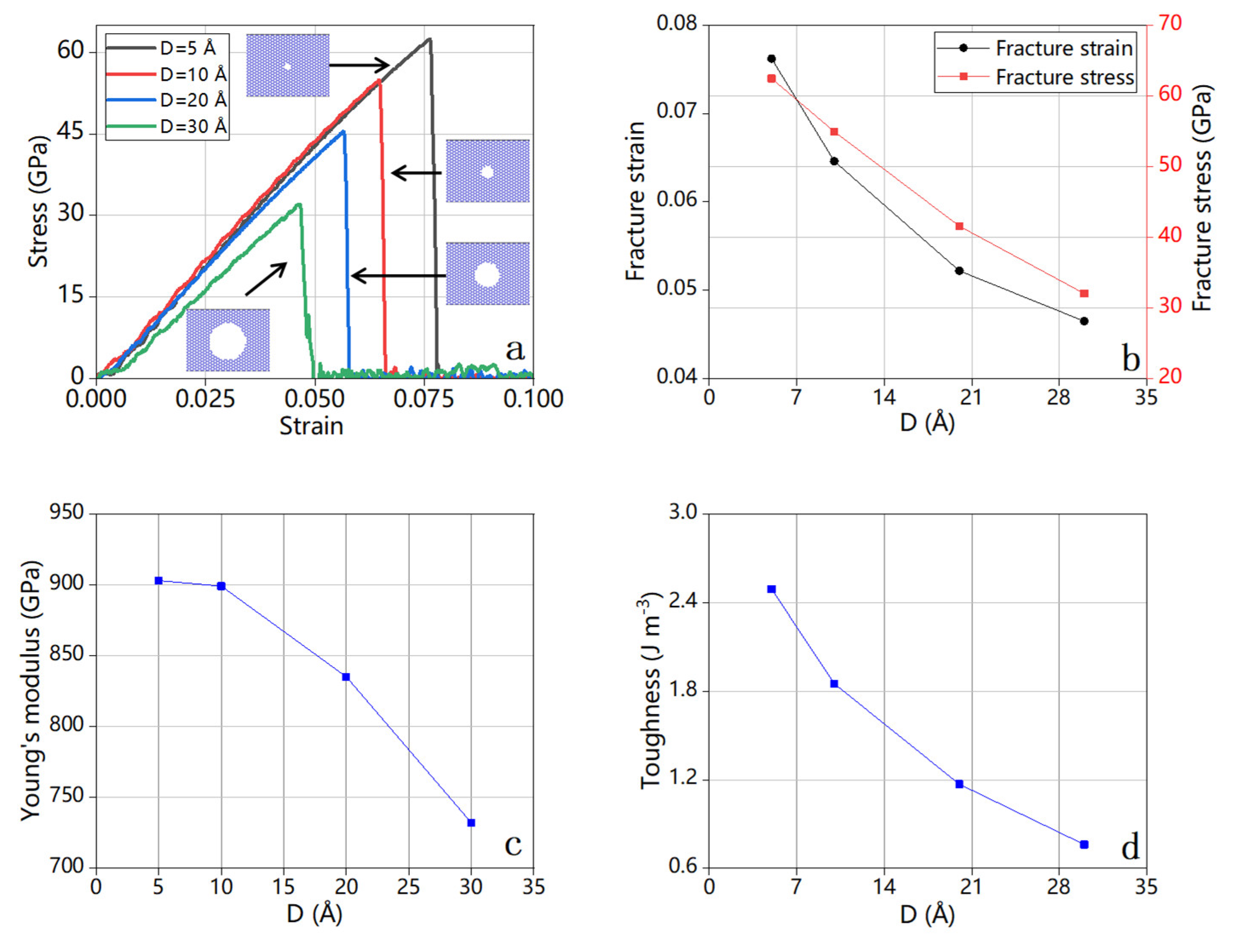
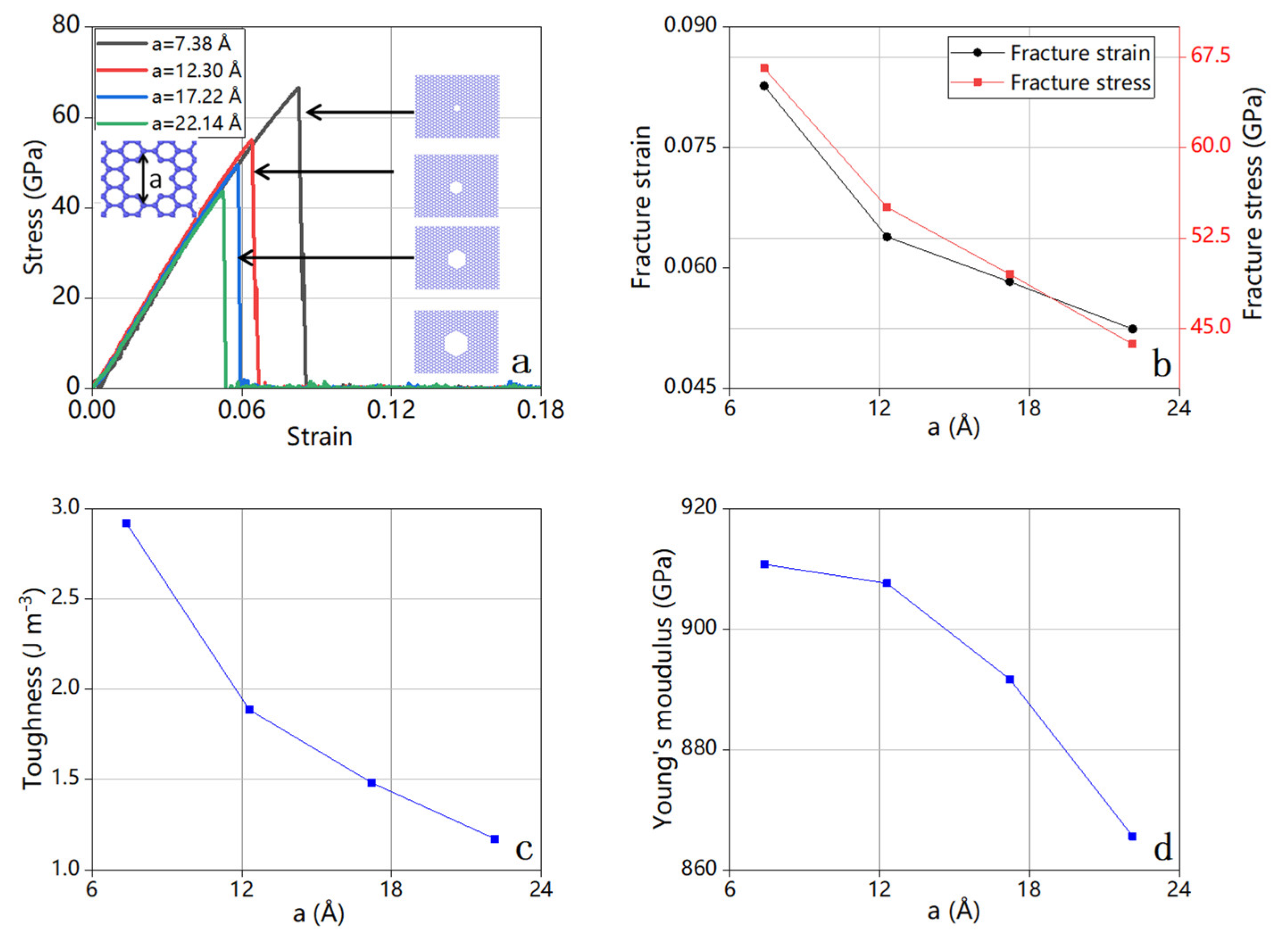
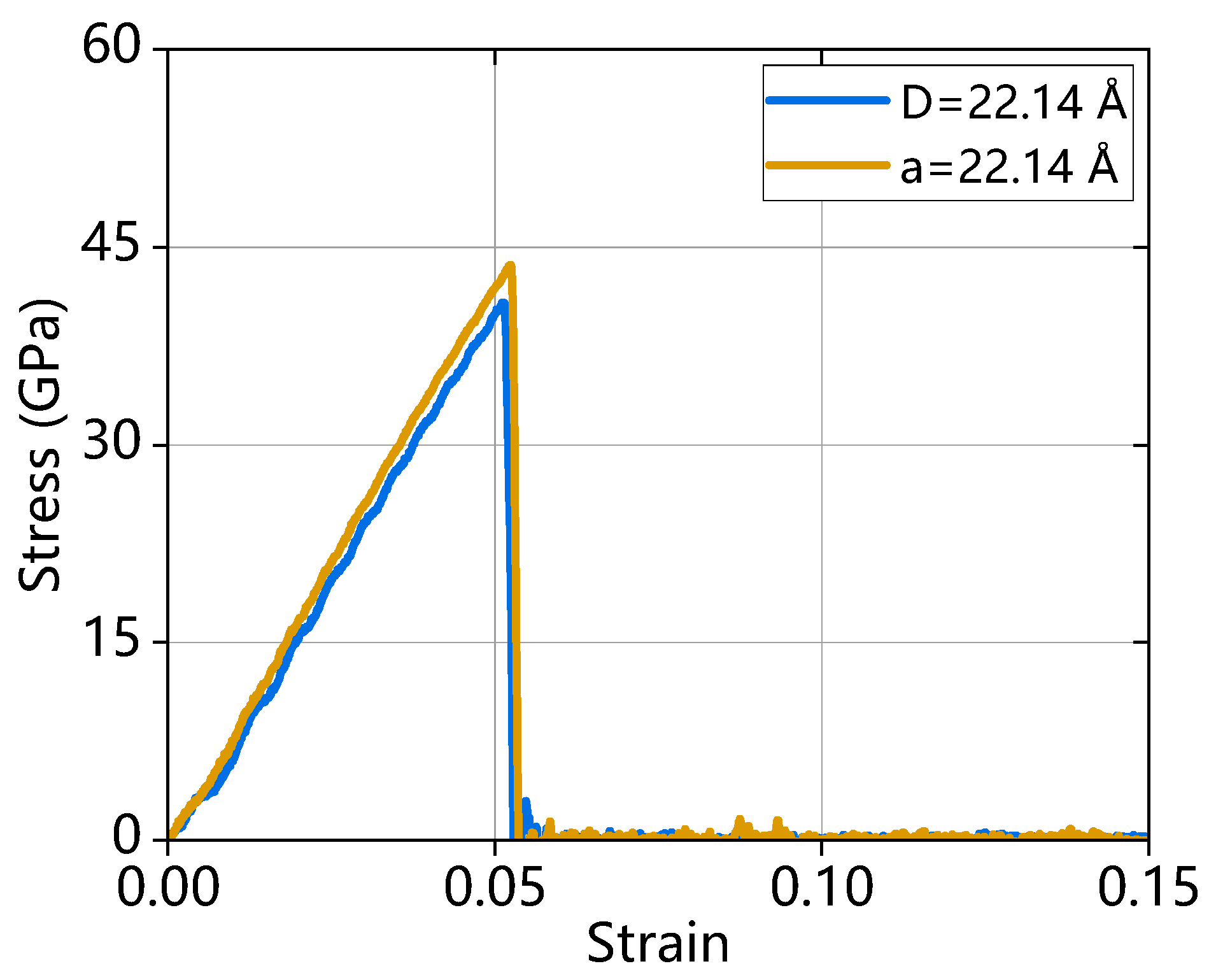
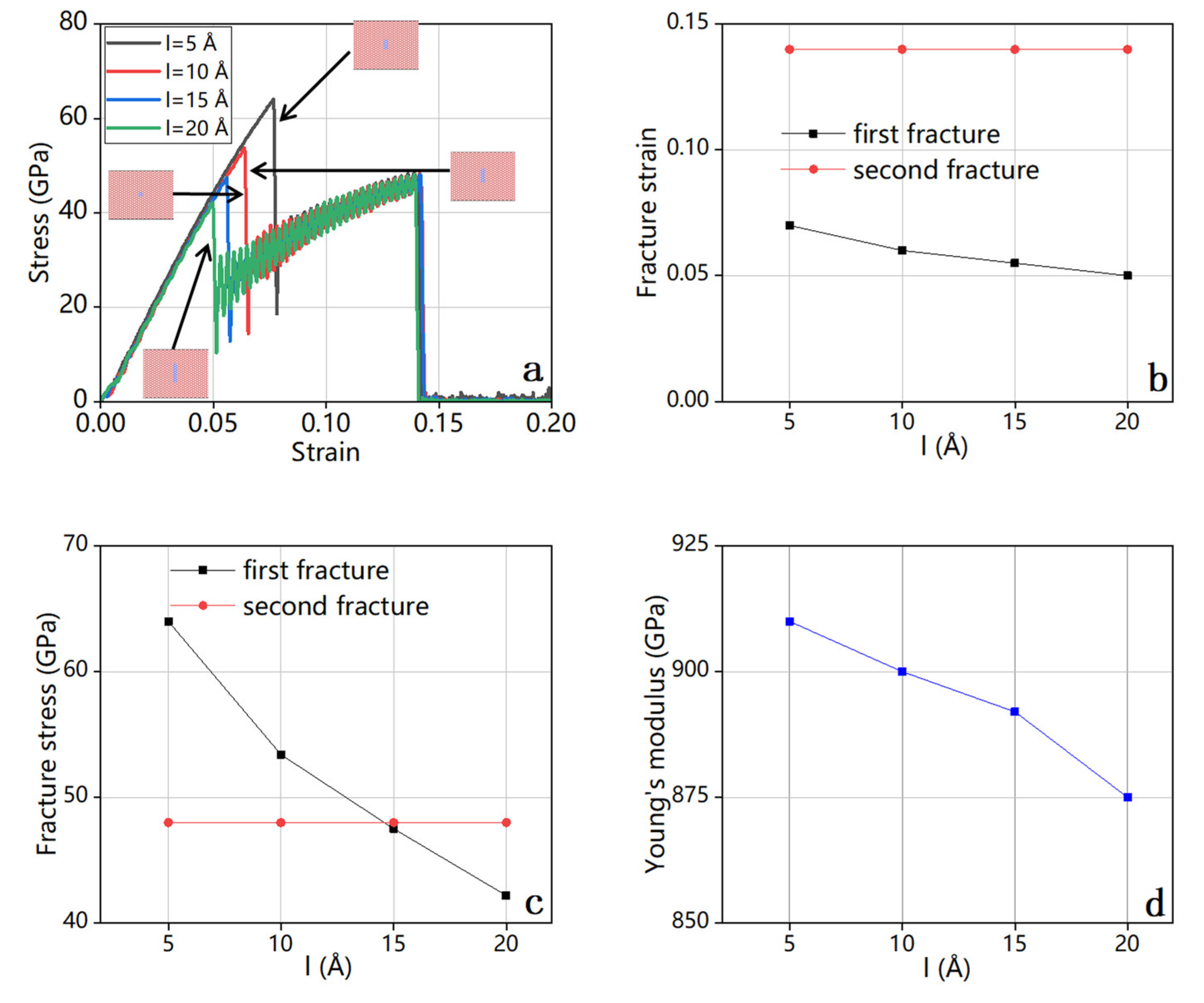
| Crack Orientation | Fracture Strain | Fracture Stress (GPa) | Young’s Modulus (GPa) | Toughness (J m−3) |
|---|---|---|---|---|
| Along x-axis | 0.08 | 67.93 | 917.16 | 3.11 |
| Along y-axis | 0.06 | 49.41 | 874.66 | 1.19 |
| D (Å) | Fracture Strain | Fracture Stress (GPa) | Young’s Modulus (GPa) | Toughness (J m−3) |
|---|---|---|---|---|
| 12.30 | 0.06 | 51.63 | 911.77 | 1.84 |
| 17.22 | 0.06 | 44.76 | 875.81 | 1.27 |
| 22.14 | 0.05 | 40.68 | 841.45 | 1.06 |
| a (Å) | Fracture Strain | Fracture Stress (GPa) | Young’s Modulus (GPa) | Toughness (J m−3) |
|---|---|---|---|---|
| 12.30 | 0.06 | 54.95 | 921.14 | 1.89 |
| 17.22 | 0.06 | 49.17 | 905.49 | 1.48 |
| 22.14 | 0.05 | 43.68 | 876.54 | 1.17 |
| Crack | Fracture Strain | Fracture Stress (GPa) | Young’s Modulus (GPa) | Toughness (J m−3) |
|---|---|---|---|---|
| No crack | 0.14 | 92.57 | 930.59 | 7.96 |
| Monolayer crack | 0.05 | 47.46 | 889.59 | 4.60 |
| Bilayer crack | 0.05 | 44.43 | 872.03 | 1.19 |
| Crack | Fracture Strain | Fracture Stress (GPa) | Young’s Modulus (GPa) | Toughness (J m−3) |
|---|---|---|---|---|
| No crack | 0.14 | 92.57 | 930.59 | 7.96 |
| Monolayer crack | 0.06 | 53.90 | 913.22 | 4.66 |
| Bilayer crack | 0.06 | 54.94 | 899.00 | 1.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Li, J.; Yang, Z.; Li, H.; Peng, Q.; Tang, H.-K. Effects of Crack Formation on the Mechanical Properties of Bilayer Graphene: A Comparative Analysis. Crystals 2023, 13, 584. https://doi.org/10.3390/cryst13040584
Yu T, Li J, Yang Z, Li H, Peng Q, Tang H-K. Effects of Crack Formation on the Mechanical Properties of Bilayer Graphene: A Comparative Analysis. Crystals. 2023; 13(4):584. https://doi.org/10.3390/cryst13040584
Chicago/Turabian StyleYu, Taotao, Jianyu Li, Ziqiang Yang, Haipeng Li, Qing Peng, and Ho-Kin Tang. 2023. "Effects of Crack Formation on the Mechanical Properties of Bilayer Graphene: A Comparative Analysis" Crystals 13, no. 4: 584. https://doi.org/10.3390/cryst13040584
APA StyleYu, T., Li, J., Yang, Z., Li, H., Peng, Q., & Tang, H.-K. (2023). Effects of Crack Formation on the Mechanical Properties of Bilayer Graphene: A Comparative Analysis. Crystals, 13(4), 584. https://doi.org/10.3390/cryst13040584







