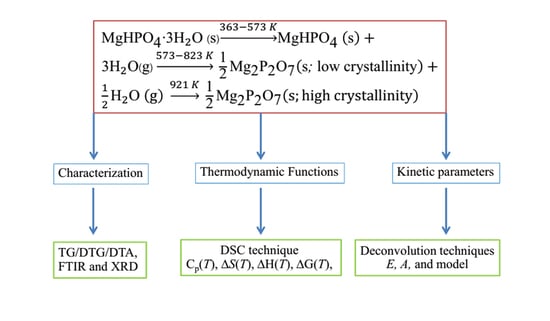
Characterization, Kinetic Using Deconvolution Techniques and Thermodynamic Study of Synthetic MgHPO4·3H2O
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis and Characterization
2.2. The Temperature Dependence of the Thermodynamic Functions
2.3. Kinetic Study of Thermal Transformation
- Gaussian Function: Ref. [25] There Are Many Versions of Gaussian Functions:
- 2.
- Amplitude Version of Weibull Peak Function
- 3.
- Fraser-Suzuki Peak Function
- (i)
- Assume h(x) = 1 to estimate the initial value of E1. The isoconversional methods stop the calculation at this step.
- (ii)
- Using E1, calculate a new value of E2 from the plot of ln [β/h(x)T2] versus 1000/T.
- (iii)
- Repeat step (ii), replacing E1 with E2. When Ei − Ei−1 < 0.1 kJ mol−1, the last value of Ei was considered to be the exact value of the activation energy of the reaction.
3. Results and Discussion
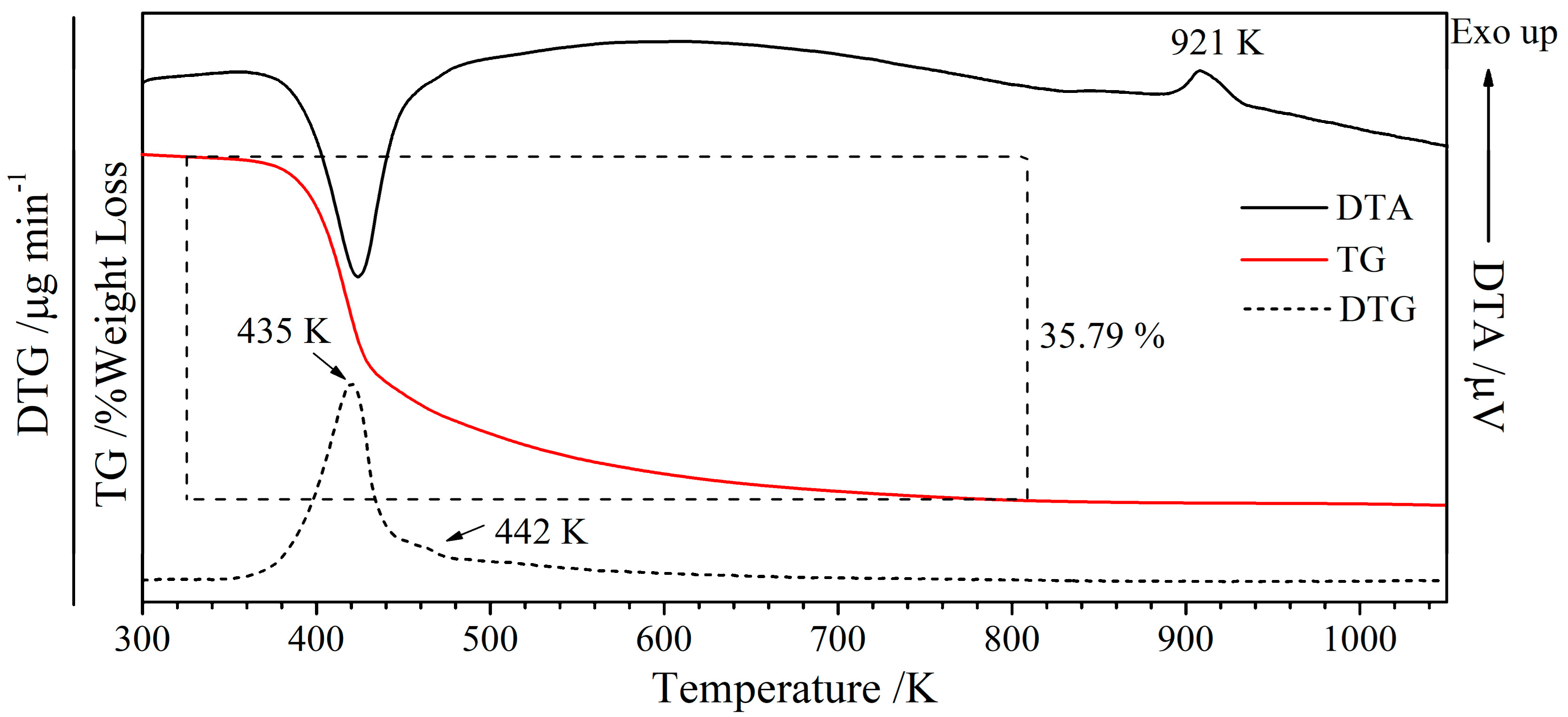
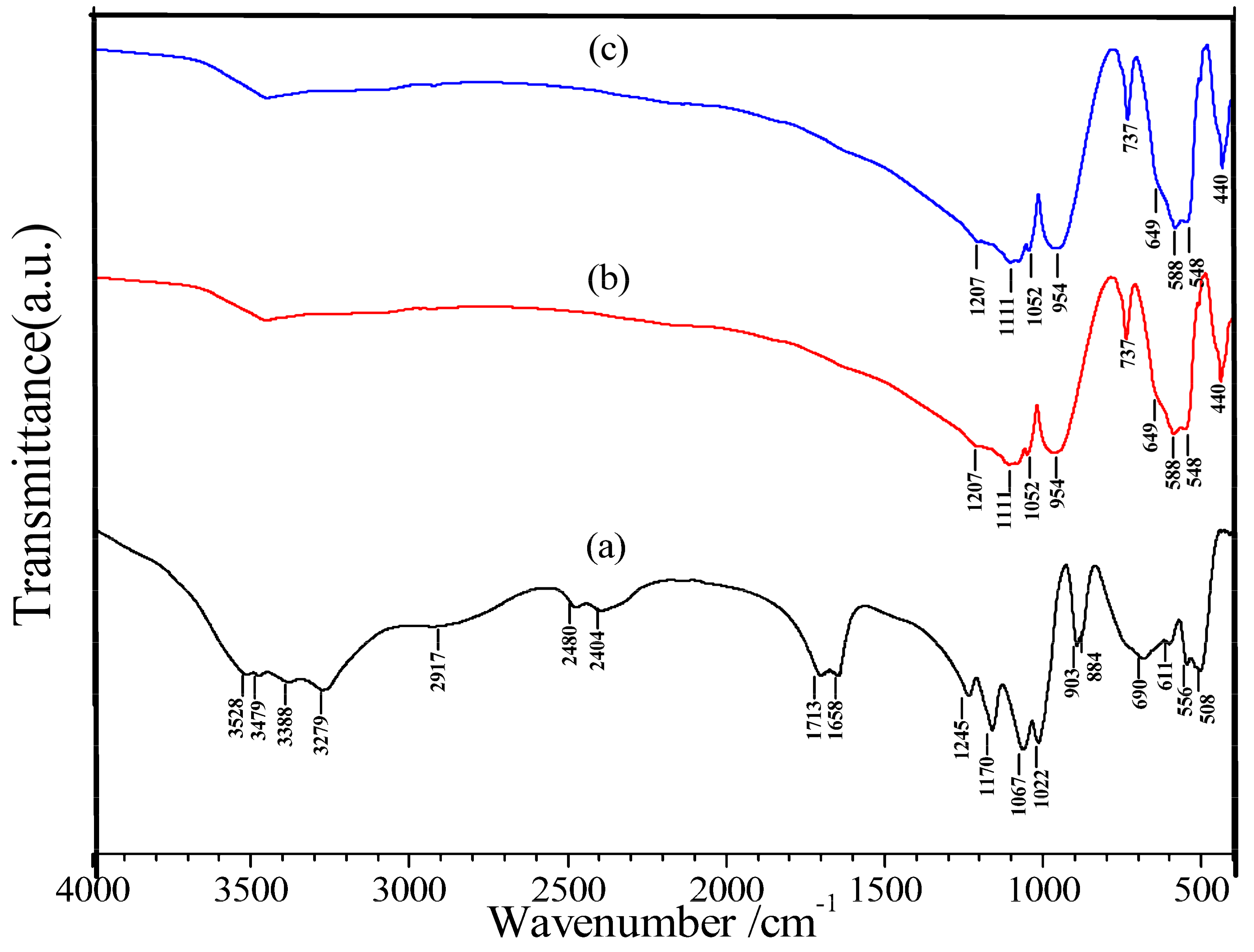
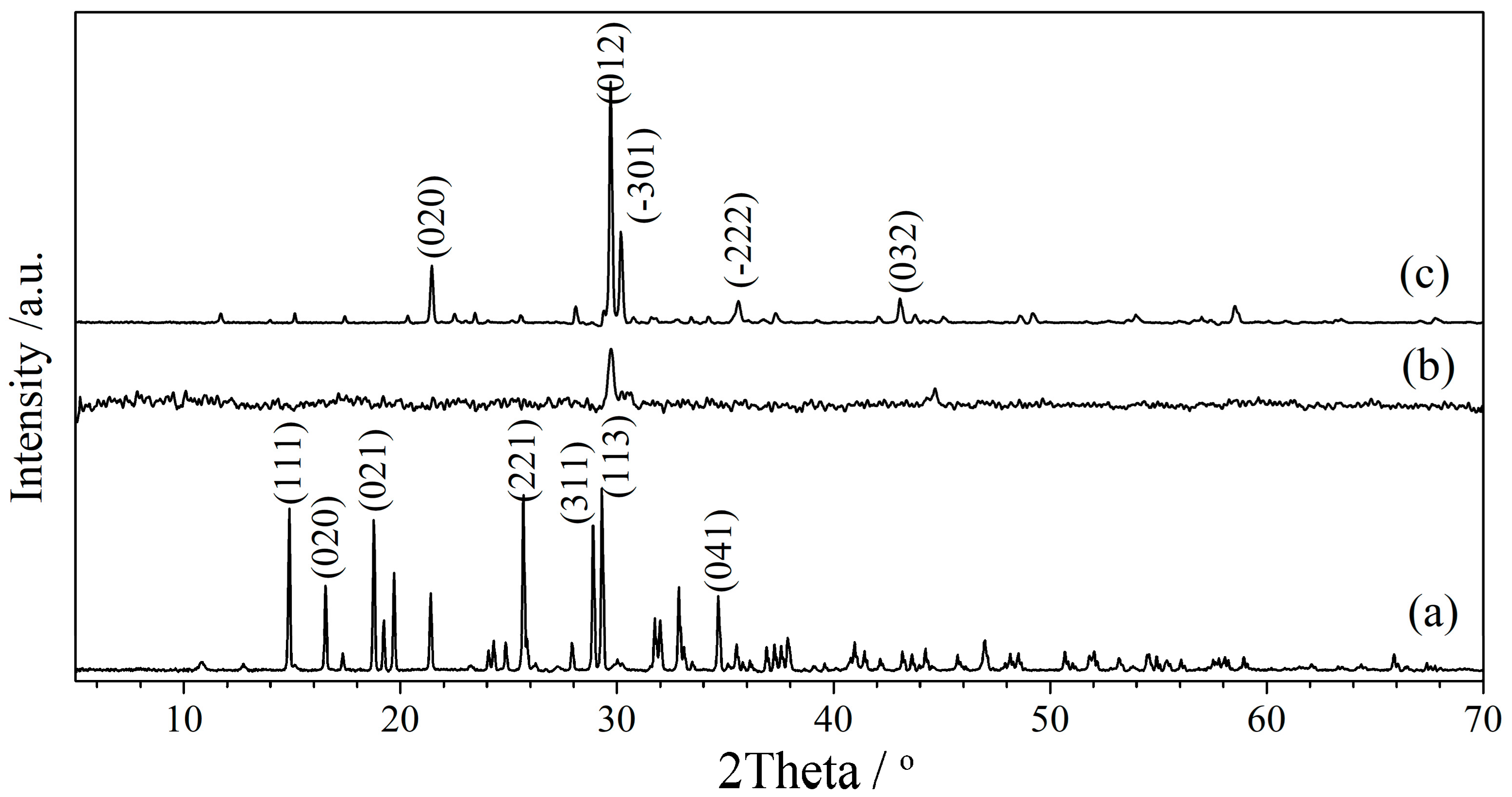
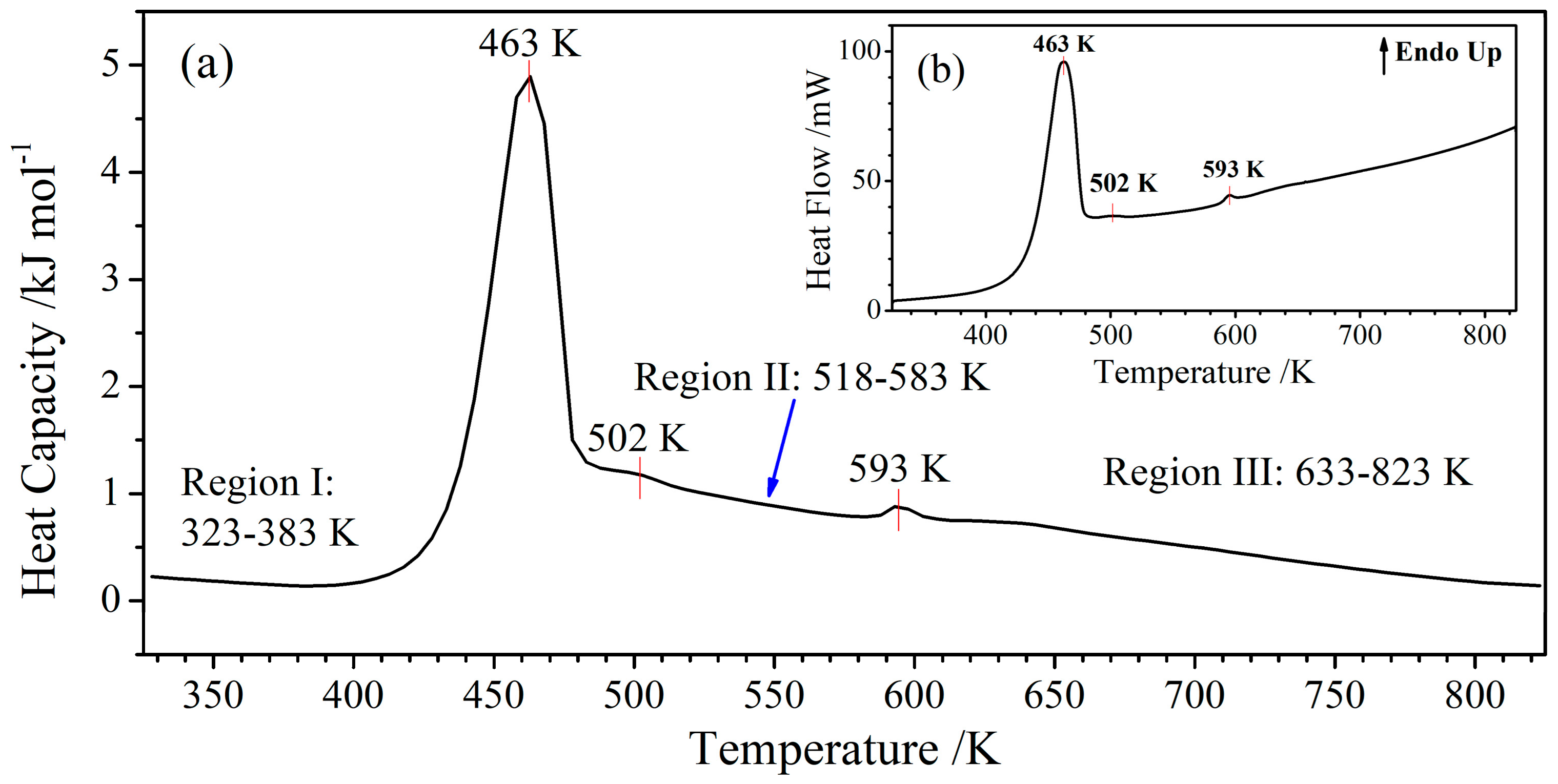
3.1. Characterization
3.2. The Temperature Dependence of the Thermodynamic Functions
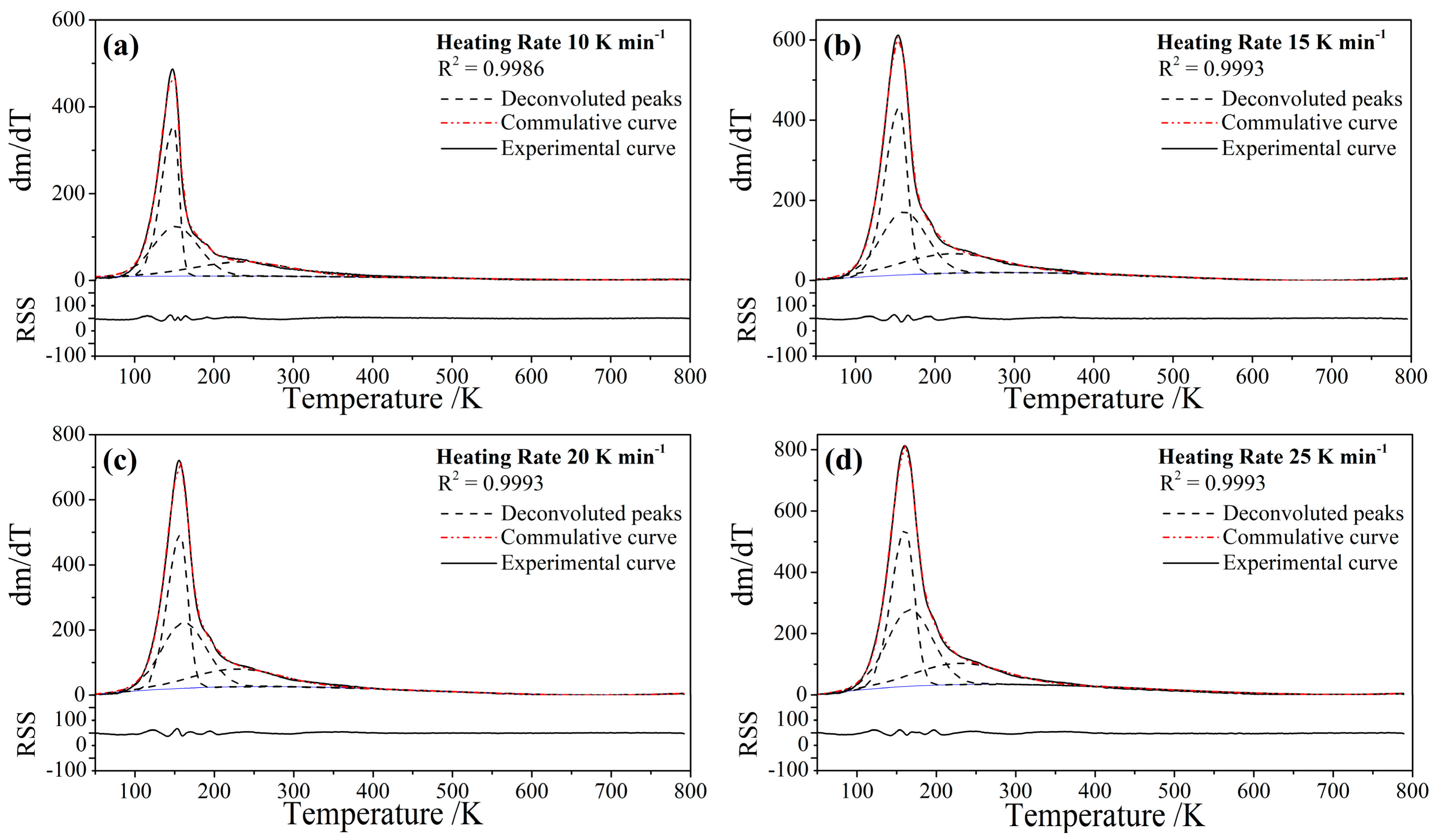
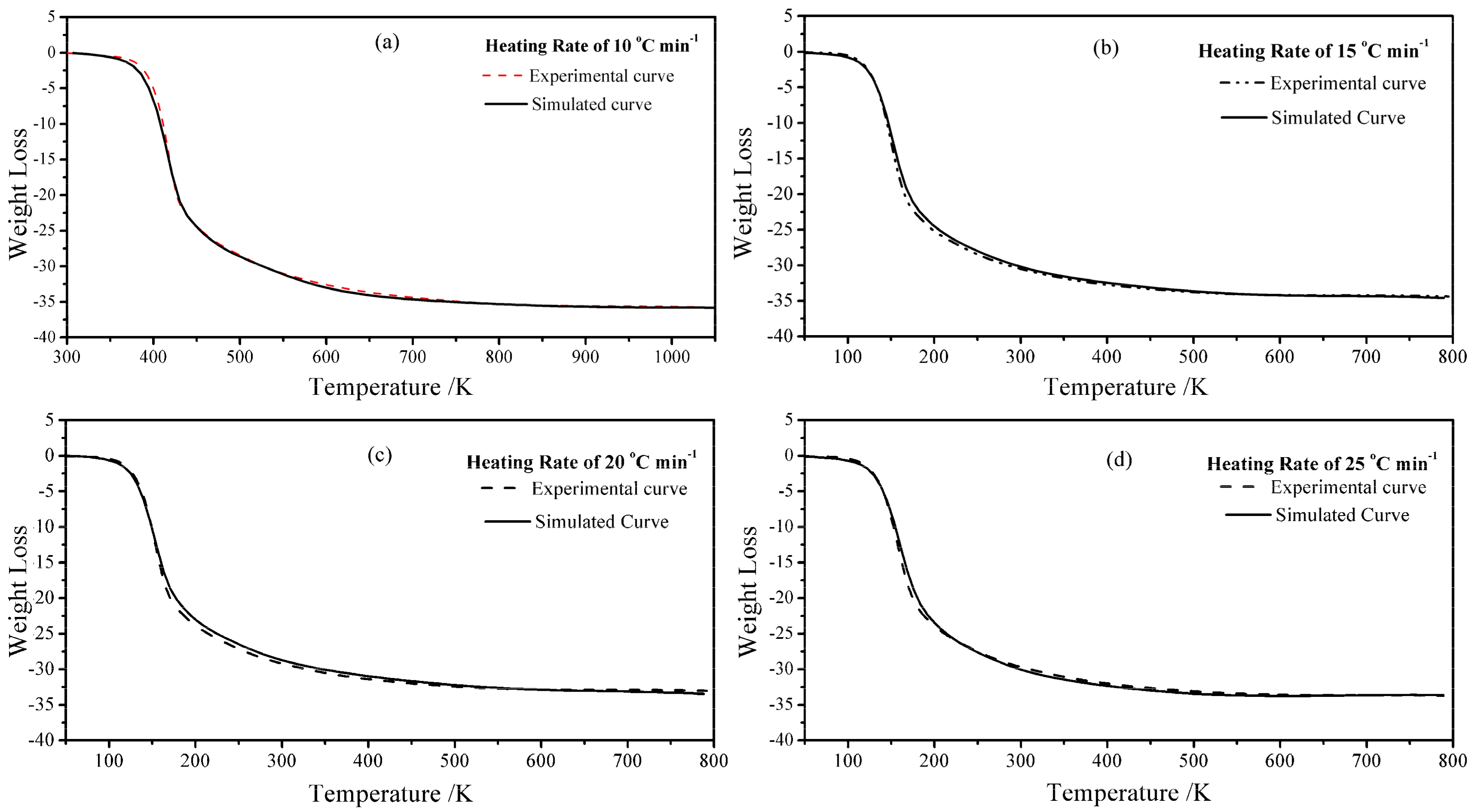
3.3. Kinetic Study
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muryanto, S. On precipitation of struvite (MgNH4PO4.6H2O). J. Sci. Sci. Educ. 2017, 1, 21–29. [Google Scholar] [CrossRef]
- Mesíková, Ž.; Šulcová, P.; Trojan, M. Synthesisand characterization of newberyite. J. Therm. Anal. Calorim. 2007, 88, 103–106. [Google Scholar] [CrossRef]
- Takagi, S.; Mathew, M.; Brown, W.E. Crystal structures of bobierrite and synthetic Mg3(PO4)2·8H2O. Am. Mineral. 1986, 71, 1229–1233. [Google Scholar]
- Frost, R.L.; Weier, M.L.; Martens, W.N.; Henry, D.A.; Mills, S.J. Raman spectroscopy of newberyite, hannayite and struvite. Spectrochim. Acta A 2005, 62, 181–188. [Google Scholar] [CrossRef]
- Tamimi, F.; Nihouannen, D.L.; Bassett, D.C.; Ibasco, S.; Gbureck, U.; Knowles, J.; Wright, A.; Flynn, A.; Komarova, S.V.; Barralet, J.E. Biocompatibility of magnesium phosphate minerals and their stability under physiological conditions. Acta Biomater. 2011, 7, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Kurtulus, G.; Tas, A.C. Transformations of neat and heated struvite (MgNH4PO4·6H2O). Mater. Lett. 2011, 65, 2883–2886. [Google Scholar] [CrossRef]
- Boonchom, B. Kinetic and thermodynamic studies of MgHPO4·3H2O by non-isothermal decomposition data. J. Therm. Anal. Calorim. 2009, 98, 863–871. [Google Scholar] [CrossRef]
- Bayuseno, A.P.; Perwitasari, D.S.; Muryanto, S.; Tauviqirrahman, M.; Jamari, J. Kinetics and morphological characteristics of struvite (MgNH4PO4.6H2O) under the influence of maleic acid. Heliyon 2020, 6, e03533. [Google Scholar] [CrossRef]
- Bhuiyan, M.I.H.; Mavinic, D.S.; Koch, F.A. Thermal decomposition of struvite and its phase transition. Chemosphere 2008, 70, 1347–1356. [Google Scholar] [CrossRef]
- Boonchom, B. Kinetics of thermal transformation of Mg3(PO4)2·8H2O to Mg3(PO4)2. Int. J. Thermophys. 2010, 31, 416–429. [Google Scholar] [CrossRef]
- Şenberber, F.T.; Derun, E.M. Thermal kinetics and thermodynamics of the dehydration reaction of Mg3(PO4)2·22H2O. Eurasian J. Biol. Chem. Sci. 2019, 2, 47–51. [Google Scholar]
- Marcu, I.-C.; Sandulescu, I.; Millet, J.-M.M. Oxidehydrogenation of n-butane over tetravalent metal phosphates based catalysts. Appl. Catal. A Gen. 2002, 227, 309–320. [Google Scholar] [CrossRef]
- Aramendıa, M.A.; Borau, V.; Jiménez, C.; Marinas, J.M.; Romero, F.J. Synthesis and characterization of magnesium phosphates and their catalytic properties in the conversion of 2-hexanol. J. Colloid Interface Sci. 1999, 217, 288–298. [Google Scholar] [CrossRef]
- Sadiq, M.; Abdennouri, M.; Barka, N.; Baâlala, M.; Lamonier, C.; Bensitel, M. Influence of the crystal phase of magnesium phosphates catalysts on the skeletal isomerization of 3,3-dimethylbut-1-ene. Can. Chem. Trans. 2015, 3, 225–233. [Google Scholar]
- Llusar, M.; Zielinska, A.; Tena, M.A.; Badenes, J.A.; Monrós, G. Blue-violet ceramic pigments based on Co and Mg Co2−xMgxP2O7 diphosphates. J. Eur. Ceram. Soc. 2010, 30, 1887–1896. [Google Scholar] [CrossRef]
- Ostrowski, N.; Roy, A.; Kumta, P.N. Magnesium phosphate cement systems for hard tissue applications: A review. ACS Biomater. Sci. Eng. 2016, 2, 1067–1083. [Google Scholar] [CrossRef] [PubMed]
- Chong, L.; Shi, C.; Yang, J.; Jia, H. Effect of limestone powder on the water stability of magnesium phosphate cement-based materials. Constr. Build. Mater. 2017, 148, 590–598. [Google Scholar] [CrossRef]
- Aramendía, M.a.A.; Borau, V.; Jiménez, C.; Marinas, J.M.a.; Romero, F.J.; Ruiz, J.R. Characterization by XRD, DRIFT, and MAS NMR spectroscopies of a Mg2P2O7 catalyst. J. Colloid Interface Sci. 1998, 202, 456–461. [Google Scholar] [CrossRef]
- Sadiq, M.; Sahibed-dine, A.; Baalala, M.; Nohair, K.; Abdennouri, M.; Bensitel, M.; Lamonier, C.; Leglise, J. Influence of acid–base properties of cobalt–molybdenum catalysts supported on magnesium orthophosphates in isomerization of 3,3-dimethylbut-1-ene. Arab. J. Chem. 2011, 4, 449–457. [Google Scholar] [CrossRef]
- Sugiyama, S.; Yokoyama, M.; Ishizuka, H.; Sotowa, K.-I.; Tomida, T.; Shigemoto, N. Removal of aqueous ammonium with magnesium phosphates obtained from the ammonium-elimination of magnesium ammonium phosphate. J. Colloid Interface Sci. 2005, 292, 133–138. [Google Scholar] [CrossRef]
- Mohammad, F.; Arfin, T.; Al-Lohedan, H.A. Sustained drug release and electrochemical performance of ethyl cellulose-magnesium hydrogen phosphate composite. Mater. Sci. Eng. C 2017, 71, 735–743. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Res. Rep. Chiba Inst. Technol. 1971, 16, 22–31. [Google Scholar]
- Kullyakool, S.; Siriwong, K.; Noisong, P.; Danvirutai, C. Kinetic triplet evaluation of a complicated dehydration of Co3(PO4)2·8H2O using the deconvolution and the simplified master plots combined with nonlinear regression. J. Therm. Anal. Calorim. 2017, 127, 1963–1974. [Google Scholar] [CrossRef]
- Perejón, A.; Sánchez-Jiménez, P.E.; Criado, J.M.; Pérez-Maqueda, L.A. Kinetic analysis of complex solid-state reactions. A new deconvolution procedure. J. Phys. Chem. B 2011, 115, 1780–1791. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Kou, K.; Jia, Q.; Xu, Y.; Liu, N.; Hu, R. Standard enthalpy of formation, thermal behavior, and specific heat capacity of 2HNIW·HMX co-crystals. J. Chem. Eng. Data 2019, 64, 42–50. [Google Scholar] [CrossRef]
- Chirico, R.D.; Steele, W.V. Thermodynamic properties of 2-methylquinoline and 8-methylquinoline. J. Chem. Eng. Data 2005, 50, 697–708. [Google Scholar] [CrossRef]
- Perwitasari, D.S.; Muryanto, S.; Schmahl, W.W.; Jamari, J.; Bayuseno, A.P. A kinetic and structural analysis of the effects of Ca- and Fe ions on struvite crystal growth. Solid State Sci. 2022, 134, 107062. [Google Scholar] [CrossRef]
- Viani, A.; Zárybnická, L.; Ševčík, R.; Mácová, P.; Machotová, J.; Veltruská, K. Struvite-K crystal growth inhibition by citric acid: Formation of complexes in solution and surface adsorption effects. J. Cryst. Growth 2022, 598, 126858. [Google Scholar] [CrossRef]
- Ambekar, A.; Yoh, J.J. Chemical kinetics of multi-component pyrotechnics and mechanistic deconvolution of variable activation energy. Proc. Combus. Inst. 2019, 37, 3193–3201. [Google Scholar] [CrossRef]
- Kullyakool, S.; Boonchom, B.; Chaiseeda, K. Simple synthesis, kinetics and thermodynamics of rod-like Cu2(OH)PO4 microparticles and rod-like Cu4O(PO4)2 nanoparticles. Mater. Chem. Physics 2020, 250, 123158. [Google Scholar] [CrossRef]
- Chaudhary, R.G.; Ali, P.; Gandhare, N.V.; Tanna, J.A.; Juneja, H.D. Thermal decomposition kinetics of some transition metal coordination polymers of fumaroyl bis (paramethoxyphenylcarbamide) using DTG/DTA techniques. Arabian J. Chem. 2019, 12, 1070–1082. [Google Scholar] [CrossRef]
- Devi, P.; Singh, K.; Kubavat, B. Synthesis, spectroscopic, quantum, thermal and kinetics, antibacterial and antifungal studies: Novel Schiff base 5-methyl-3-((5-bromosalicylidene) amino)- pyrazole and its transition metal complexes. Res. Chem. 2023, 5, 100813. [Google Scholar] [CrossRef]
- Kullyakool, S.; Siriwong, K.; Noisong, P.; Danvirutai, C. Studies of thermal decomposition kinetics and temperature dependence of thermodynamic functions of the new precursor LiNiPO4·3H2O for the synthesis of olivine LiNiPO4. J. Therm. Anal. Calorim. 2015, 122, 665–677. [Google Scholar] [CrossRef]
- Cheng, Z.; Wu, W.; Ji, P.; Zhou, X.; Liu, R.; Cai, J. Applicability of Fraser–Suzuki function in kinetic analysis of DAEM processes and lignocellulosic biomass pyrolysis processes. J. Therm. Anal. Calorim. 2015, 119, 1429–1438. [Google Scholar] [CrossRef]
- Senum, G.I.; Yang, R.T. Rational approximations of the integral of the Arrhenius function. J. Therm. Anal. 1977, 11, 445–447. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Galwey, A.K. Is the science of thermal analysis kinetics based on solid foundations? A literature appraisal. Thermochim. Acta 2004, 413, 139–183. [Google Scholar] [CrossRef]
- Gotor, F.J.; Criado, J.M.; Malek, J.; Koga, N. Kinetic analysis of solid-state reactions: the universality of master plots for analyzing isothermal and nonisothermal experiments. J. Phys. Chem. A 2000, 104, 10777–10782. [Google Scholar] [CrossRef]
- Khanwan, A.; Flanagan, D.R. Solid-state kinetic models: Basics and mathematical fundamentals. J. Phys. Chem. 2006, 110, 17315–17328. [Google Scholar]
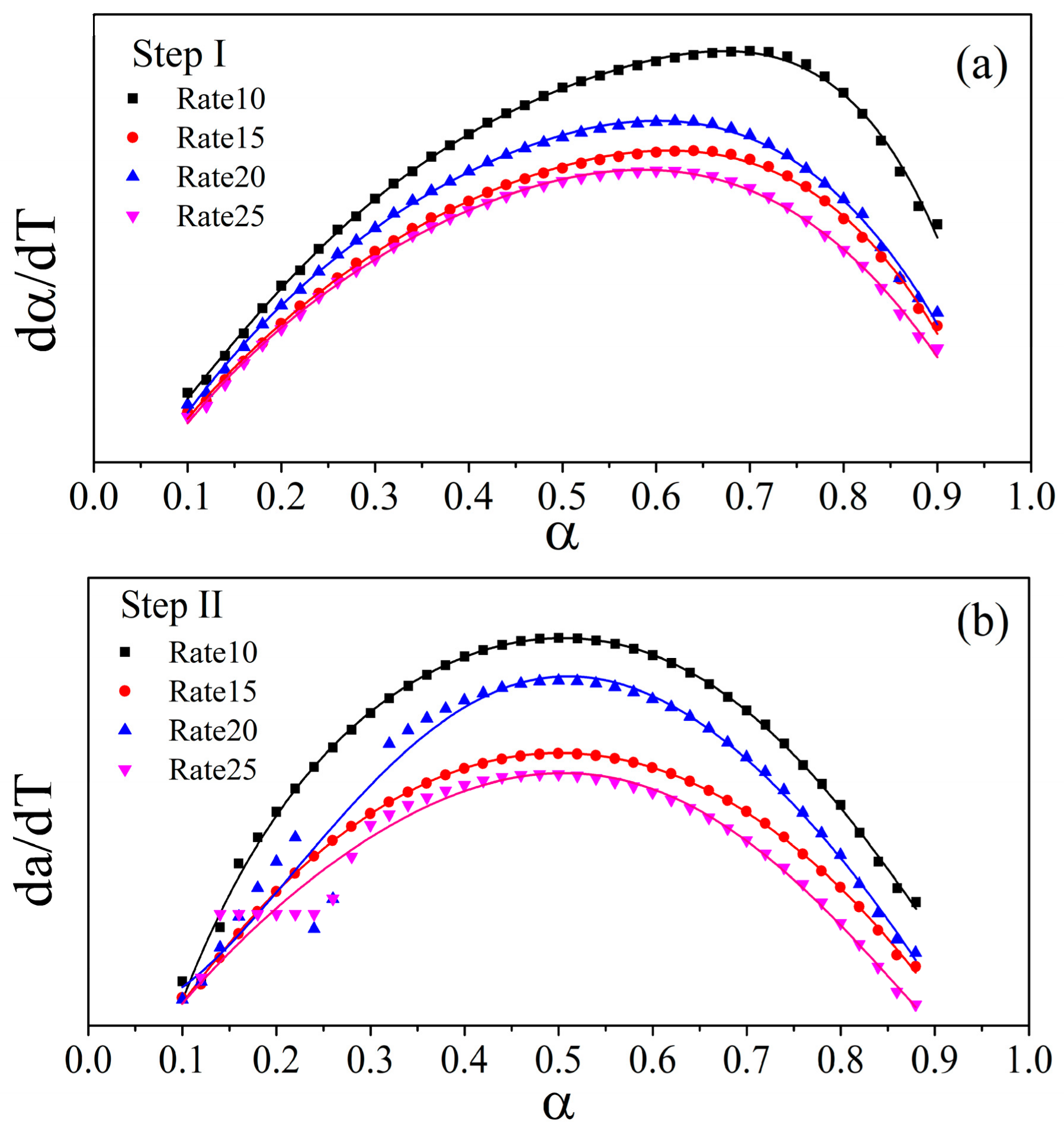
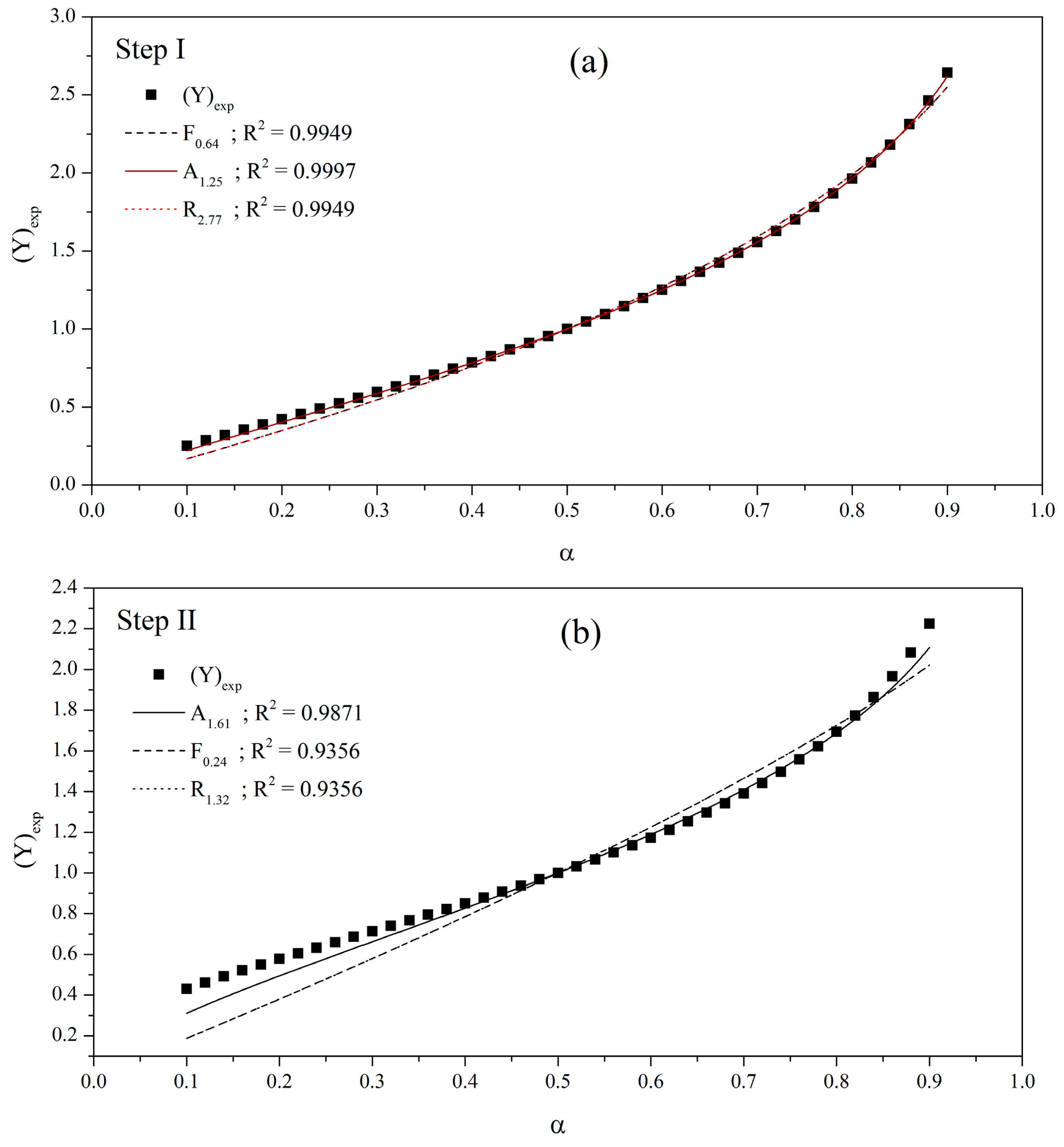
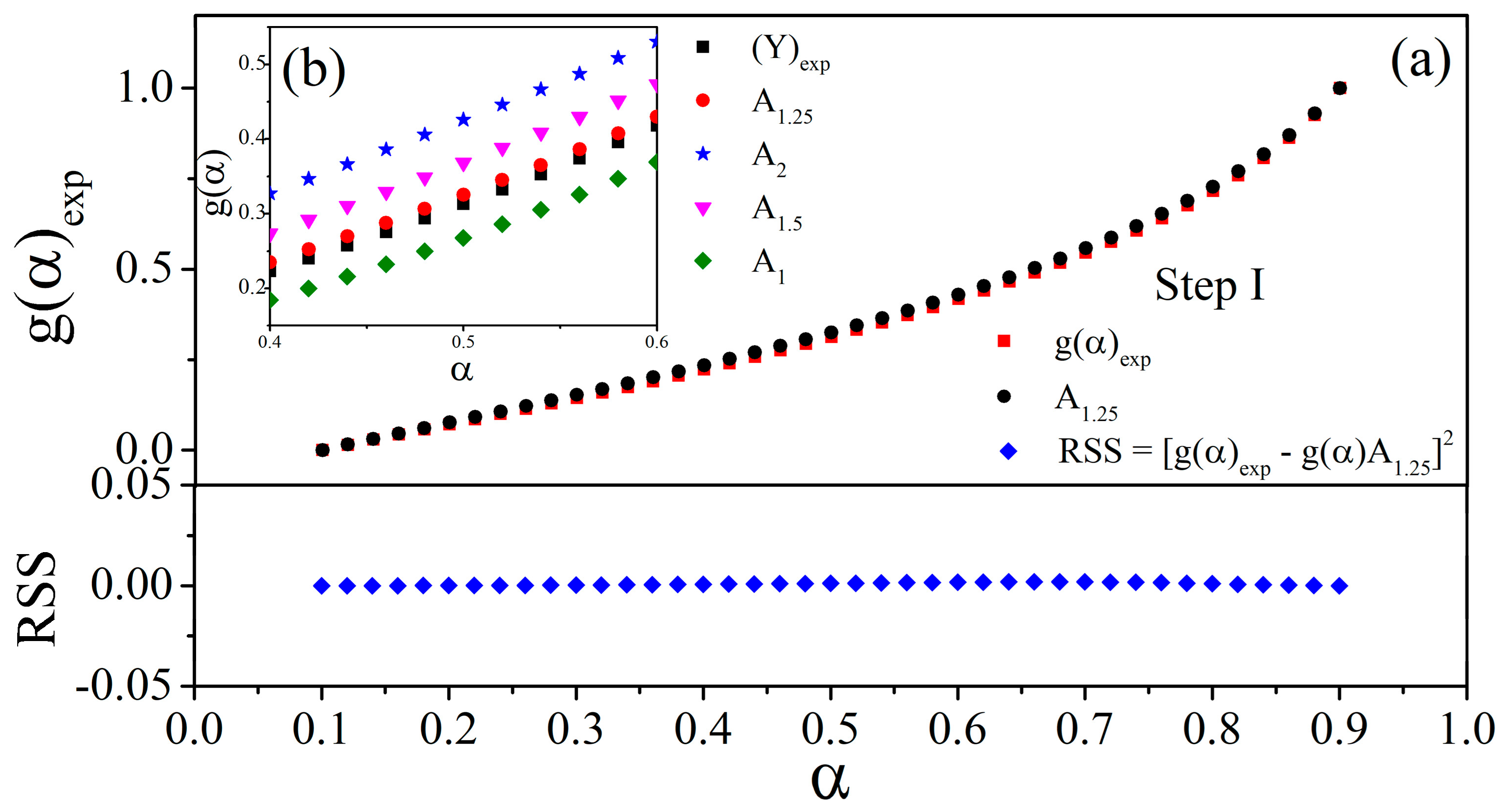
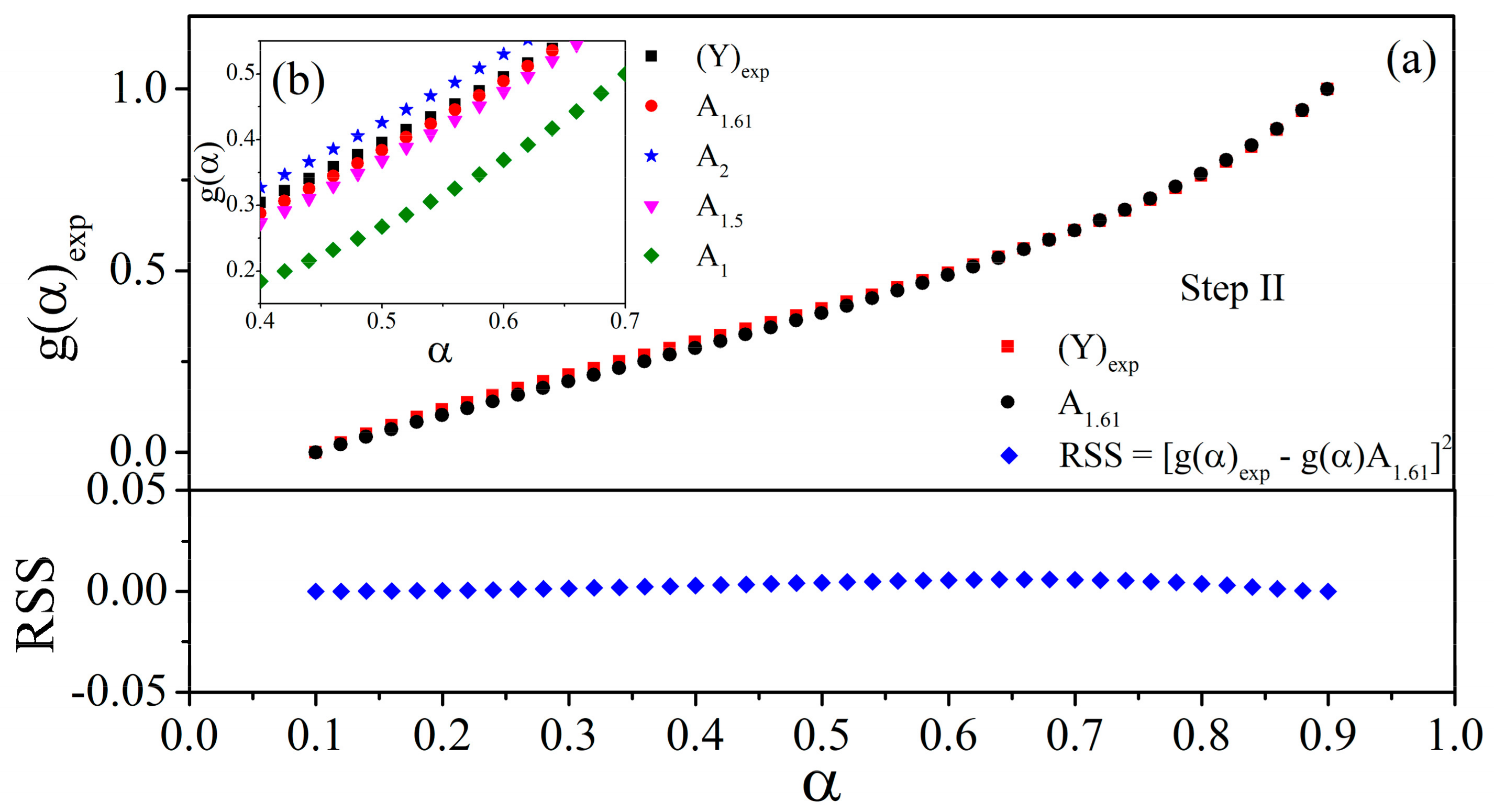
| α | Step I | Step II | Step III | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E/kJ mol−1 | %Error | R2 | A/s−1 | E/kJ mol−1 | %Error | R2 | A/s−1 | E/kJ mol−1 | %Error | R2 | A/s−1 | |
| 0.10 | 106.84 | 0.62 | 0.9947 | 8.18 × 1013 | 80.98 | 7.77 | 0.9819 | 4.97 × 1010 | 53.35 | 38.19 | 0.4372 | - |
| 0.12 | 105.88 | 0.49 | 0.9966 | 5.25 × 1013 | 81.07 | 8.75 | 0.9772 | 4.16 × 1010 | 51.90 | 38.55 | 0.4307 | - |
| 0.14 | 104.98 | 0.38 | 0.9980 | 3.51 × 1013 | 80.99 | 9.54 | 0.9730 | 3.38 × 1010 | 52.27 | 37.11 | 0.4570 | - |
| 0.16 | 104.32 | 0.28 | 0.9989 | 2.56 × 1013 | 80.84 | 10.21 | 0.9691 | 2.73 × 1010 | 51.71 | 37.29 | 0.4537 | - |
| 0.18 | 103.88 | 0.18 | 0.9996 | 2.02 × 1013 | 80.65 | 10.78 | 0.9655 | 2.22 × 1010 | 51.19 | 37.48 | 0.4502 | - |
| 0.20 | 103.08 | 0.09 | 0.9999 | 1.44 × 1013 | 80.45 | 11.26 | 0.9623 | 1.81 × 1010 | 51.08 | 36.80 | 0.4628 | - |
| 0.22 | 102.34 | 0.07 | 0.9999 | 1.06 × 1013 | 80.23 | 11.68 | 0.9593 | 1.49 × 1010 | 50.88 | 36.98 | 0.4595 | - |
| 0.24 | 101.72 | 0.13 | 0.9998 | 8.11 × 1012 | 80.01 | 12.05 | 0.9566 | 1.23 × 1010 | 50.68 | 37.18 | 0.4558 | - |
| 0.26 | 101.02 | 0.22 | 0.9993 | 6.10 × 1012 | 79.79 | 12.38 | 0.9541 | 1.03 × 1010 | 50.48 | 37.40 | 0.4517 | - |
| 0.28 | 100.40 | 0.29 | 0.9988 | 4.72 × 1012 | 79.57 | 12.67 | 0.9517 | 8.62 × 109 | 50.17 | 37.13 | 0.4568 | - |
| 0.30 | 99.76 | 0.36 | 0.9982 | 3.64 × 1012 | 79.34 | 12.94 | 0.9495 | 7.25 × 109 | 50.08 | 37.36 | 0.4524 | - |
| 0.32 | 99.02 | 0.43 | 0.9975 | 2.74 × 1012 | 79.12 | 13.19 | 0.9473 | 6.13 × 109 | 49.98 | 37.62 | 0.4477 | - |
| 0.34 | 98.44 | 0.50 | 0.9965 | 2.17 × 1012 | 78.91 | 13.44 | 0.9452 | 5.23 × 109 | 49.89 | 37.89 | 0.4427 | - |
| 0.36 | 97.79 | 0.56 | 0.9956 | 1.68 × 1012 | 78.69 | 13.65 | 0.9433 | 4.47 × 109 | 49.61 | 37.94 | 0.4419 | - |
| 0.38 | 97.12 | 0.62 | 0.9946 | 1.30 × 1012 | 78.48 | 13.85 | 0.9414 | 3.83 × 109 | 49.49 | 38.16 | 0.4377 | - |
| 0.40 | 96.47 | 0.68 | 0.9935 | 1.02 × 1012 | 78.25 | 14.03 | 0.9396 | 3.27 × 109 | 49.37 | 38.41 | 0.4333 | - |
| 0.42 | 95.81 | 0.75 | 0.9923 | 7.92 × 1011 | 78.03 | 14.21 | 0.9378 | 2.81 × 109 | 49.25 | 38.67 | 0.4286 | - |
| 0.44 | 95.14 | 0.80 | 0.9911 | 6.16 × 1011 | 77.80 | 14.38 | 0.9360 | 2.41 × 109 | 49.14 | 38.94 | 0.4238 | - |
| 0.46 | 94.48 | 0.86 | 0.9899 | 4.82 × 1011 | 77.55 | 14.54 | 0.9343 | 2.06 × 109 | 49.03 | 39.22 | 0.4187 | - |
| 0.48 | 93.82 | 0.91 | 0.9886 | 3.78 × 1011 | 77.30 | 14.69 | 0.9327 | 1.76 × 109 | 48.92 | 39.51 | 0.4135 | - |
| 0.50 | 93.12 | 0.96 | 0.9872 | 2.94 × 1011 | 77.04 | 14.83 | 0.9310 | 1.51 × 109 | 48.82 | 39.82 | 0.4081 | - |
| 0.52 | 92.43 | 1.02 | 0.9858 | 2.28 × 1011 | 76.77 | 14.97 | 0.9294 | 1.28 × 109 | 48.72 | 40.14 | 0.4026 | - |
| 0.54 | 91.73 | 1.07 | 0.9844 | 1.78 × 1011 | 76.48 | 15.09 | 0.9277 | 1.09 × 109 | 48.62 | 40.46 | 0.3969 | - |
| 0.56 | 91.02 | 1.12 | 0.9830 | 1.38 × 1011 | 76.18 | 15.22 | 0.9261 | 9.19 × 108 | 48.53 | 40.80 | 0.3911 | - |
| 0.58 | 90.30 | 1.17 | 0.9815 | 1.07 × 1011 | 75.86 | 15.34 | 0.9244 | 7.73 × 108 | 48.44 | 41.14 | 0.3852 | - |
| 0.60 | 89.57 | 1.21 | 0.9800 | 8.24 × 1010 | 75.51 | 15.43 | 0.9229 | 6.46 × 108 | 48.35 | 41.50 | 0.3791 | - |
| 0.62 | 88.82 | 1.26 | 0.9784 | 6.34 × 1010 | 75.14 | 15.54 | 0.9212 | 5.36 × 108 | 48.26 | 41.85 | 0.3731 | - |
| 0.64 | 88.05 | 1.30 | 0.9769 | 4.86 × 1010 | 74.74 | 15.63 | 0.9196 | 4.41 × 108 | 48.17 | 42.24 | 0.3666 | - |
| 0.66 | 87.25 | 1.35 | 0.9753 | 3.69 × 1010 | 74.32 | 15.72 | 0.9179 | 3.60 × 108 | 48.10 | 42.61 | 0.3605 | - |
| 0.68 | 86.41 | 1.39 | 0.9737 | 2.77 × 1010 | 73.87 | 15.79 | 0.9162 | 2.92 × 108 | 48.02 | 43.01 | 0.3539 | - |
| 0.70 | 85.51 | 1.44 | 0.9721 | 2.04 × 1010 | 73.37 | 15.88 | 0.9143 | 2.33 × 108 | 47.95 | 43.43 | 0.3471 | - |
| 0.72 | 84.53 | 1.48 | 0.9705 | 1.47 × 1010 | 72.82 | 15.96 | 0.9123 | 1.83 × 108 | 47.90 | 43.83 | 0.3407 | - |
| 0.74 | 83.49 | 1.52 | 0.9688 | 1.04 × 1010 | 72.17 | 16.02 | 0.9103 | 1.40 × 108 | 46.95 | 44.77 | 0.3257 | - |
| 0.76 | 82.37 | 1.56 | 0.9670 | 7.21 × 109 | 71.54 | 16.05 | 0.9085 | 1.07 × 108 | 45.30 | 46.35 | 0.3016 | - |
| 0.78 | 81.17 | 1.61 | 0.9653 | 4.87 × 109 | 70.86 | 16.07 | 0.9067 | 8.06 × 107 | 45.77 | 44.63 | 0.3280 | - |
| 0.80 | 79.89 | 1.65 | 0.9633 | 3.22 × 109 | 70.09 | 16.10 | 0.9045 | 5.91 × 107 | 47.41 | 44.90 | 0.3238 | - |
| 0.82 | 78.56 | 1.71 | 0.9611 | 2.09 × 109 | 69.14 | 16.15 | 0.9016 | 4.10 × 107 | 49.09 | 45.18 | 0.3194 | - |
| 0.84 | 77.21 | 1.77 | 0.9583 | 1.35 × 109 | 68.13 | 16.17 | 0.8988 | 2.80 × 107 | 50.81 | 45.48 | 0.3148 | - |
| 0.86 | 75.66 | 1.79 | 0.9573 | 8.19 × 108 | 67.07 | 16.14 | 0.8962 | 1.86 × 107 | 52.58 | 45.79 | 0.3101 | - |
| 0.88 | 74.05 | 1.83 | 0.9552 | 4.88 × 108 | 65.87 | 16.10 | 0.8933 | 1.19 × 107 | 54.38 | 46.12 | 0.3051 | - |
| 0.90 | 72.32 | 1.90 | 0.9521 | 2.79 × 108 | 64.55 | 16.07 | 0.8897 | 7.28 × 106 | 46.83 | 52.08 | 0.2233 | - |
| average | 91.86 | 1.31 | 0.9628 | 5.98 × 109 | 75.85 | 16.06 | 0.816 | 8.27 × 107 | 49.45 | 22.22 | 0.63 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kullyakool, S.; Thompho, S.; Boonchom, B.; Rungrojchaipon, P. Characterization, Kinetic Using Deconvolution Techniques and Thermodynamic Study of Synthetic MgHPO4·3H2O. Crystals 2023, 13, 567. https://doi.org/10.3390/cryst13040567
Kullyakool S, Thompho S, Boonchom B, Rungrojchaipon P. Characterization, Kinetic Using Deconvolution Techniques and Thermodynamic Study of Synthetic MgHPO4·3H2O. Crystals. 2023; 13(4):567. https://doi.org/10.3390/cryst13040567
Chicago/Turabian StyleKullyakool, Saifon, Somphob Thompho, Banjong Boonchom, and Pesak Rungrojchaipon. 2023. "Characterization, Kinetic Using Deconvolution Techniques and Thermodynamic Study of Synthetic MgHPO4·3H2O" Crystals 13, no. 4: 567. https://doi.org/10.3390/cryst13040567
APA StyleKullyakool, S., Thompho, S., Boonchom, B., & Rungrojchaipon, P. (2023). Characterization, Kinetic Using Deconvolution Techniques and Thermodynamic Study of Synthetic MgHPO4·3H2O. Crystals, 13(4), 567. https://doi.org/10.3390/cryst13040567