Constitution Method for Broadband Acoustic Metamaterials Based on the Design Theory of a One-Dimensional Distributed Transmission-Line Model

Abstract

A method for realizing broadband acoustic metasurfaces composed of a one-dimensional distributed transmission-line model is proposed. There are no design formulas for determining the structural parameters of the structure constituting acoustic metasurfaces in the conventional method, and therefore parameter extractions by means of many calculations with numerical simulations are needed to realize acoustic metasurfaces. There are also narrow band operations or impedance matching problems. On the other hand, this paper shows that we can design broadband acoustic metasurfaces by determining the structural parameters with the design formulas of the model without many calculations. An acoustic metasurface that refracts incident plane waves at an angle of 20 degrees is first designed by using one-dimensional meander acoustic waveguide structures equivalent to the model, and these structural parameters are determined by the design formulas of the model and the modifications of the error from the theory. Full-wave simulations are performed, and the broadband operations and the validity of the design theory are shown from these results. Furthermore, a broadband acoustic flat lens is designed with the proposed structures as an example of the application of the proposed method, and these operations are also demonstrated by similar full-wave simulations.

1. Introduction

Acoustic metasurfaces are sheet-type acoustic metamaterials whose thickness is much thinner than the wavelength of incident waves [1,2,3,4,5,6,7,8,9,10,11,12]. These can achieve unique wavefront manipulations and realize flat-shape acoustic devices such as lenses [3,4,5,6], reflectors [7,8,9], and absorbers [10,11,12]. For example, applications to flat reflectors for the control of reflected waves in concert halls, very thin and low-cost flat lenses for underwater cameras, and very thin absorbers for the reduction in noise from engines of cars or airplanes are considered. To realize acoustic metasurfaces, various design methods have been proposed so far, such as the method of using structures with periodically arranged unit cells, but those have some issues. For example, many numerical calculations using numerical simulators are needed to determine the structural parameters (e.g., width and length) of the structure constituting acoustic metasurfaces because there are no design formulas relating to them. Additionally, narrowband operations are an issue if we adopt periodic structures for the constitution the acoustic metasurfaces. There are also impedance matching problems of the boundary between the background medium and acoustic metasurfaces.

Recently, a method for constituting acoustic metasurfaces with a one-dimensional (1D) distributed transmission-line model was proposed to solve these problems simultaneously [13]. This method was introduced from the field of electromagnetic metasurfaces [14,15], and the transmission-line parameters are linked to the material parameters of electromagnetic or acoustic metasurfaces by their duality. It is also suggested that the line length of the structure can be uniquely calculated from the design formula of the model and that the line width for impedance matching can be specifically determined from the characteristic impedance. In addition, acoustic metasurfaces with the proposed method can achieve broadband operations due to their intrinsic nature of non-resonance. Although the validity of the theory so far has been shown by circuit simulations, the specific constitution method of structures based on this model has not yet been revealed.

In this paper, we present a method to constitute broadband acoustic metasurfaces based on the design theory of the distributed transmission-line model. In Section 2, the concept of acoustic metasurfaces for refracting incident plane waves and the design formulas of the model [13] are first presented for the completion of this paper. Secondly, four types of 1D meander acoustic waveguide structure for acoustic metasurfaces and a 2D straight acoustic waveguide structure for background media are proposed, and the waveguide length and width are calculated according to the theory of the model. In addition, the error of the waveguide length from the theoretical values is modified by eigenvalue analysis with COMSOL. Finally, a broadband acoustic flat lens [15] is designed with the proposed four types of 1D meander acoustic waveguide structure as an example of the application in order to show the usefulness of the proposed method. In Section 3, the complex sound pressure distributions are calculated by full-wave simulations with COMSOL, and the broadband operations of the acoustic metasurface and the flat lens are confirmed to verify the validity of the proposed method. In Section 4, this paper is concluded.

2. Methods

2.1. Design Theory Based on a 1D Distributed Transmission-Line Model

Figure 1 shows the concept of a broadband acoustic metasurface [13]. An acoustic metasurface is placed at the area of −∆d < x < 0 and −a/2 < y < a/2, and is composed of a 1D distributed transmission-line model. The other areas correspond to the background medium and are assumed to be composed of a 2D distributed transmission-line model. a is the aperture size of the acoustic metasurface or the number of 1D distributed transmission-line models, and ∆d is the unit cell length of each model or the thickness of the metasurface. Z₀ and Z_0b present the characteristic impedance, β and β_b represent the phase constant, and l and l_b (=∆d) represent the line length.

Let us now consider the situation shown in Figure 1 where a normal incident plane wave is refracted by an acoustic metasurface with an angle of θ. In this case, the difference of the transmission phase of the adjacent unit cells becomes β∆dsin θ, and the electrical length (βl(y)) of each cell can be calculated using the following formula:

$$\beta l\left(y\right)=\beta \Delta d+\beta \{(\frac{a}{2}-\frac{\Delta d}{2})-y\}\sin \theta ·(-\frac{a}{2}<y<\frac{a}{2})$$

(1)

Therefore, the line length (l(y)) of each cell can be determined by

$$l\left(y\right)=\Delta d+\{(\frac{a}{2}-\frac{\Delta d}{2})-y\}\sin \theta$$

(2)

From this formula, the acoustic metasurface in Figure 1 has essentially broadband characteristics since the line length is independent of the frequency. In addition, the condition for impedance matching between the background medium and the acoustic metasurface becomes

$$Z_{0\mathrm{b}}=\sqrt{2}{Z}_0$$

(3)

where $\sqrt{2}$ represents the 2D effect [13]. We propose structures with characteristics equivalent to each model comprising this acoustic metasurface in the next subsection, and these structural parameters are determined based on the theory of this subsection.

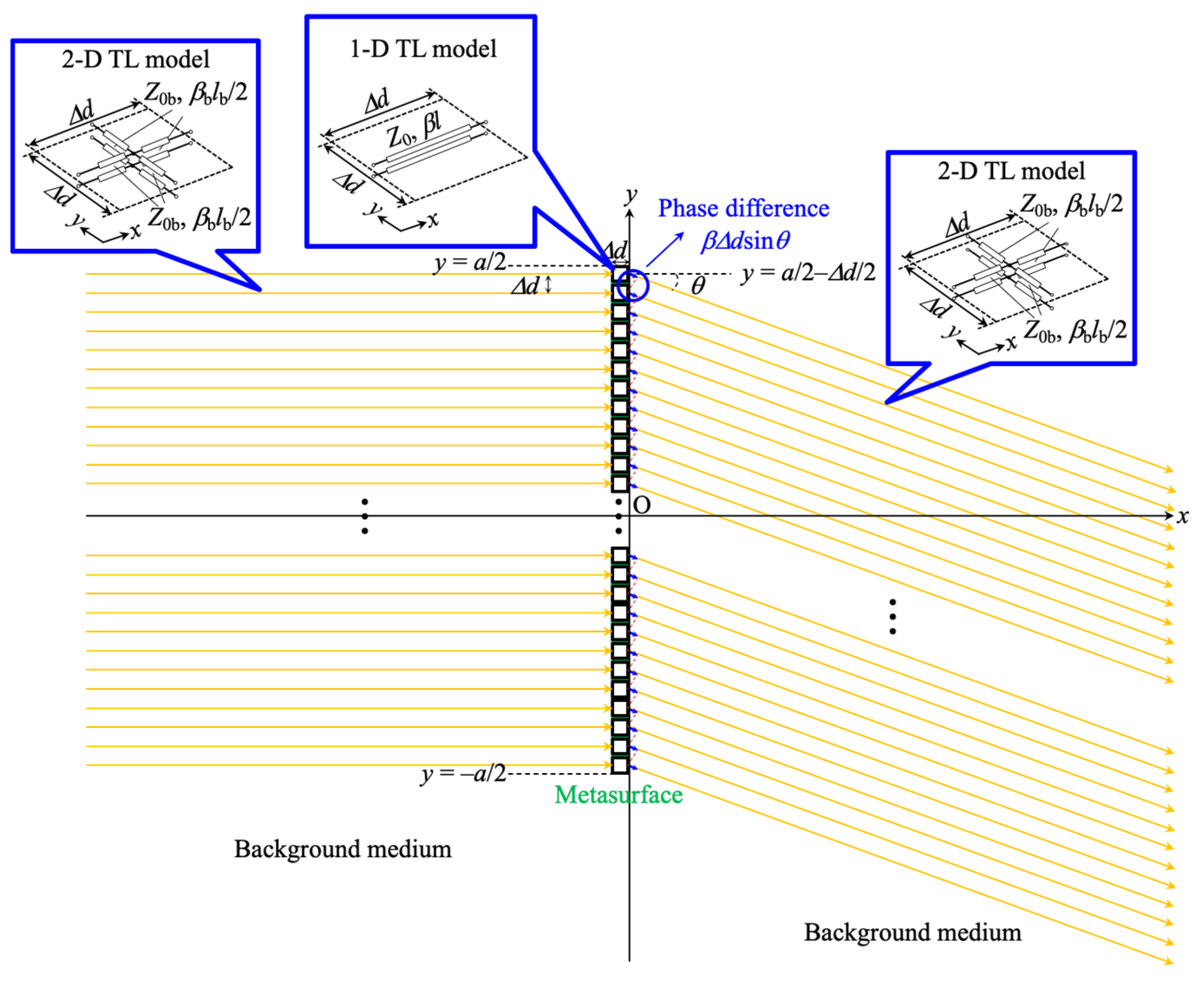
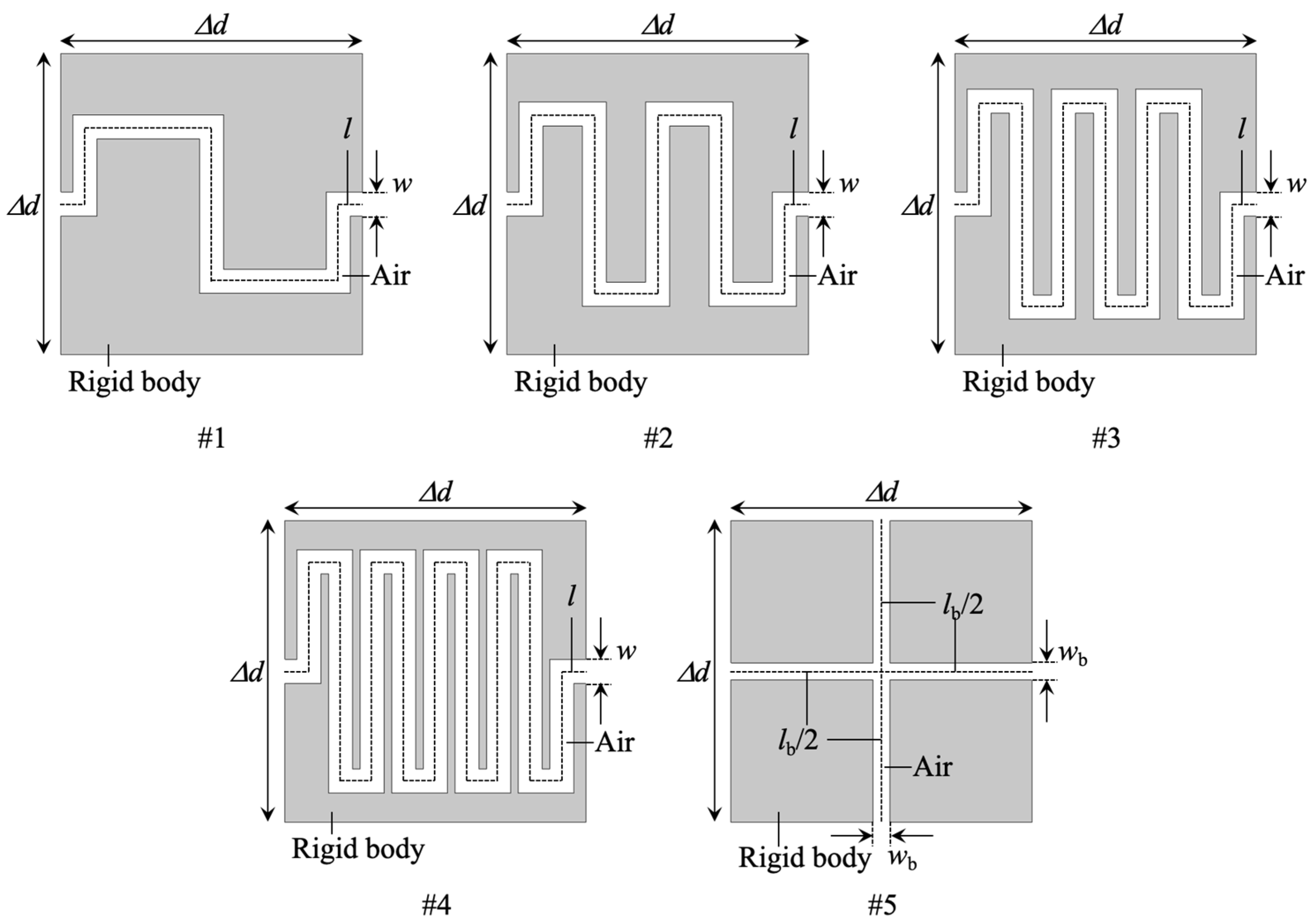
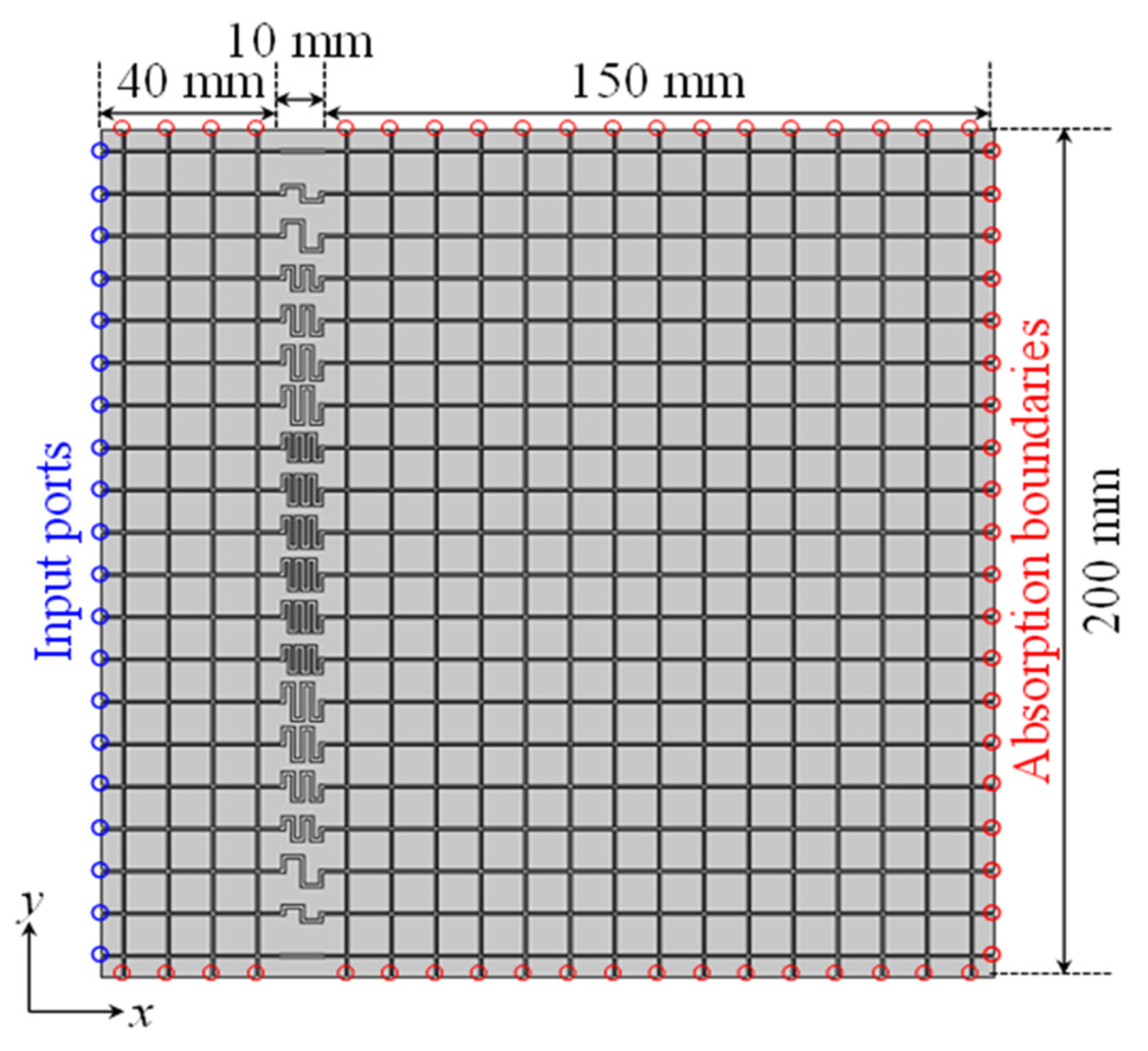
2.2. Proposal Structures and Acoustic Broadband Metasurface Design

Figure 2 shows four types of 1D meander acoustic waveguide structure (#1–#4) for the acoustic metasurface and a 2D straight acoustic waveguide structure (#5) for the background medium. These acoustic waveguides are formed in a rigid body and filled with air (β = β_b = β_air, c = c_b = c_air). For impedance matching and feasibility, the waveguide widths are set to w = 0.8 mm and w_b = w/$\sqrt{2}$ = 0.566 mm, and the unit cell length is chosen as ∆d = l_b = 10 mm. The solid line in Figure 3 represents the theoretical waveguide length for each cell obtained by using Formula (2) with θ = 20 degrees and a = 20∆d = 200 mm, and these parameters are set to feasible values. This can be basically realized by selecting the one appropriate structure from #1 to #4 in Figure 2, but the acoustical length (βl) becomes smaller than the theoretical one due to the effect of the bent waveguide if we adopt the theoretical one as it is. Therefore, we need to modify the waveguide length by calculating the frequency dispersion characteristics with eigenvalue analysis.

The dots in Figure 3 show the calculated results of the optimized waveguide length. The values #1–#4 correspond to those in Figure 2, and it is seen that these become larger than the theoretical values. Incidentally, the value at y = 95 mm (#0) agrees with the theory and a 1D straight acoustic waveguide structure with w = 0.8 mm and l = ∆d = 10 mm is used there. The designed acoustic metasurface with the optimized parameters in Figure 3 is illustrated in Figure 4, and its broadband operations are confirmed by full-wave simulations in Section 3.

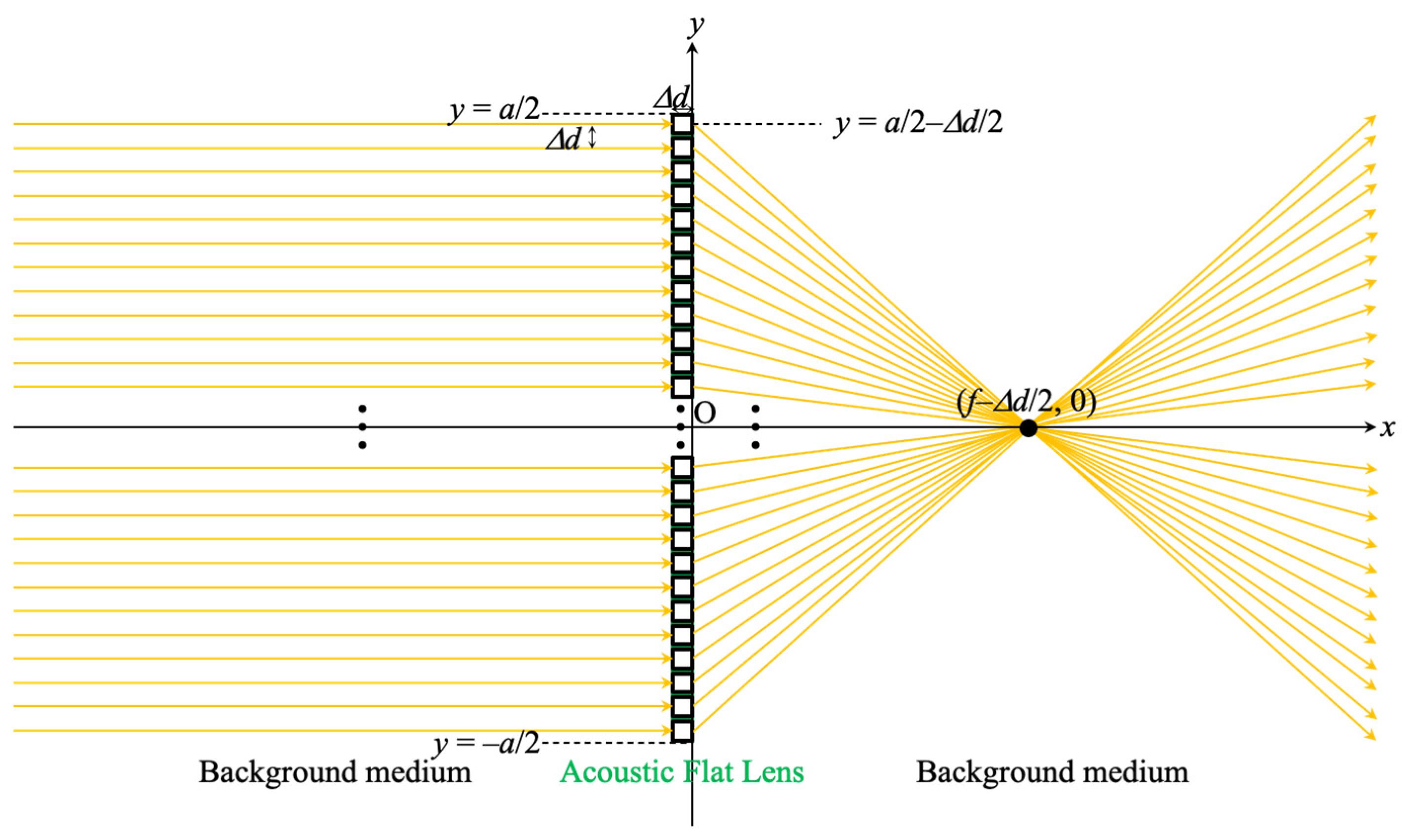
2.3. Flat Acoustic Lens Design

We also design an acoustic flat lens [15] illustrated in Figure 5 by using the proposed meander acoustic waveguide structures in Figure 2 to show an application example and the usefulness of the proposed method. a and ∆d are the aperture size and the unit cell length, respectively, and f is the focal length. Since this lens operates when the propagation paths from the left side of each cell to the focal point agree with each other, the theoretical waveguide length can be determined from the following formula [15]:

$$l\left(y\right)+\sqrt{y^2+{\left(f-\frac{\Delta d}{2}\right)}^2}=\Delta d+\sqrt{{\left(\frac{a}{2}-\frac{\Delta d}{2}\right)}^2+{\left(f-\frac{\Delta d}{2}\right)}^2}$$

(4)

Figure 6 shows the theoretical values of the waveguide length and the optimized values calculated by eigenvalue analysis with COMSOL. The values of a, ∆d, w, w_b, and f are 200, 10, 0.8, 0.566, and 105 mm, respectively, and 1D meander acoustic waveguide structures of #1–#3 in Figure 2 and a 1D straight acoustic waveguide structure (#0) are used for the design of the lens. Given these parameters and the optimized waveguide length, we constructed the lens as shown in Figure 7. In the next section, its broadband operations are investigated by full-wave simulations and the results are presented with those of the designed acoustic metasurface in the previous subsection.

3. Results and Discussion

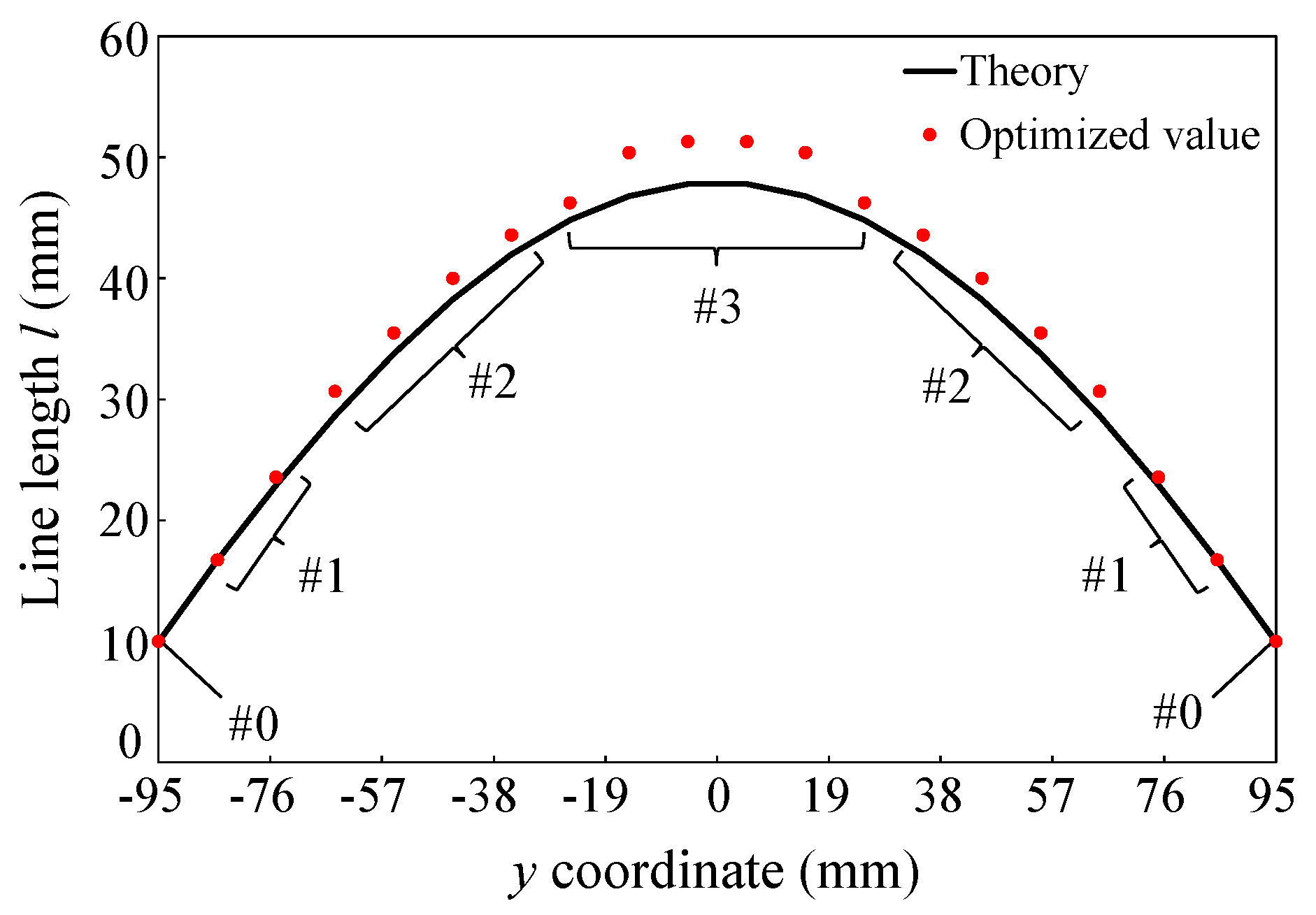
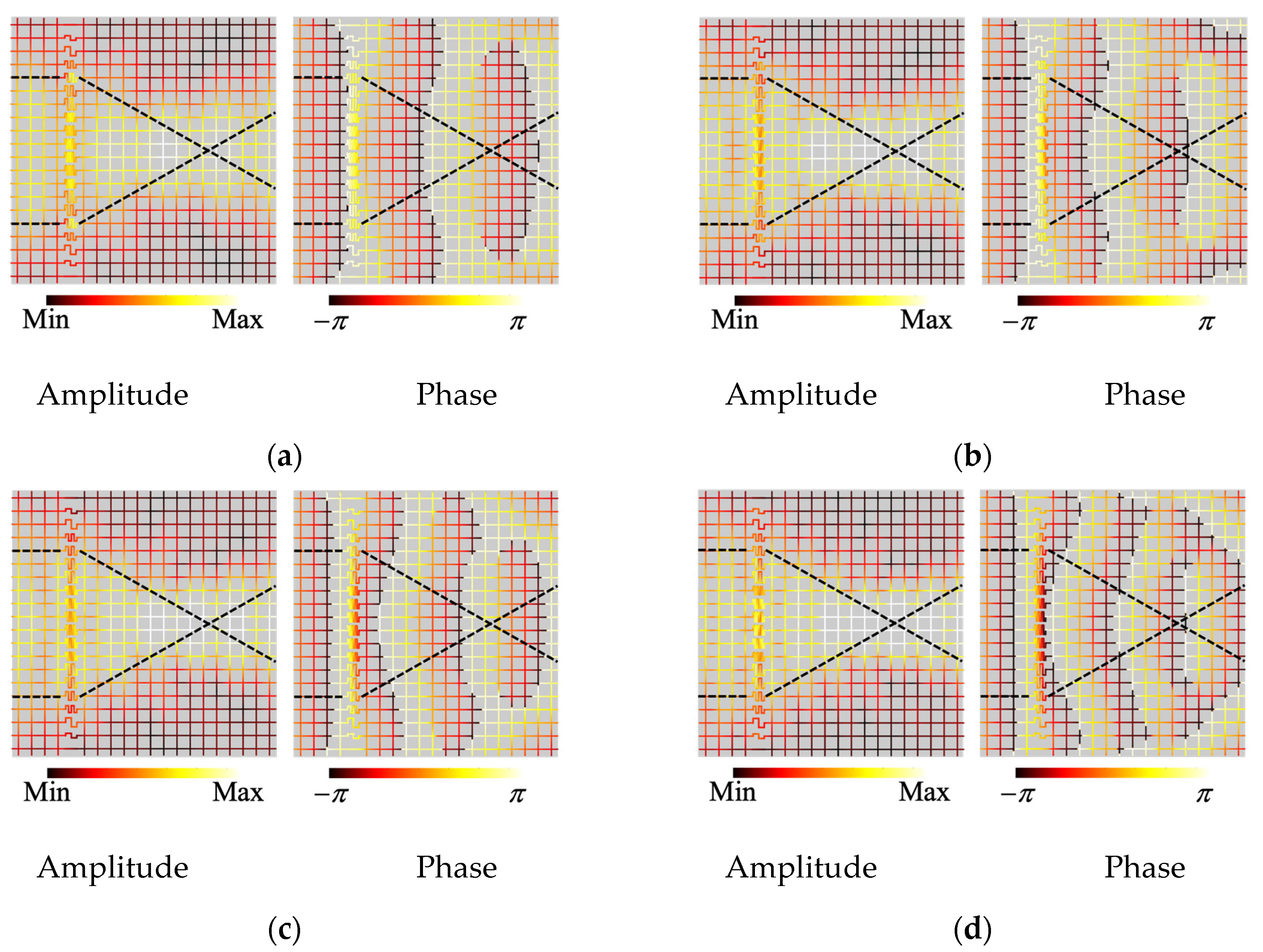
3.1. Acoustic Metasurface

The configuration of full-wave simulations for the designed acoustic metasurface is shown in Figure 8. The two background media are composed of the structure of #5 in Figure 2, and their sizes are set to 20∆d × 4∆d = 200 mm × 40 mm and 20∆d × 15∆d = 200 mm × 150 mm. The acoustic metasurface in Figure 4 is sandwiched between them. Twenty input ports are set at the boundaries of the acoustic waveguide of the left side, and a Gaussian beam with a beam waist of 80 mm is perpendicularly illuminated to the acoustic metasurface. Other boundaries are set as acoustic absorption boundaries. We performed full-wave simulations with COMSOL under these conditions and calculated the complex sound pressure distributions in the acoustic waveguide.

Figure 9a–f show the calculated amplitude and phase distributions of the sound pressure at 3.063, 3.500, 4.084, 4.900, 6.125, and 8.167 kHz. These wavelengths (λ) are 8∆d = 80, 7∆d = 70, 6∆d = 60, 5∆d = 50, 4∆d = 40, and 3∆d = 30 mm, respectively. The broken lines represent the theoretical propagation direction of incident and refracted waves, and it is seen from the results of Figure 9a–e that the propagation directions agree well with the theoretical ones. On the other hand, in the case of Figure 9f, the refracted angle becomes larger than the theoretical one since the wavelength is shorter than the other cases; however, the refraction effect can be obtained by the designed acoustic metasurface. Therefore, we can conclude that the broadband operations and the validity of the constitutive method are confirmed.

3.2. Acoustic Flat Lens

Figure 10 shows the setup of the full-wave simulations of the designed acoustic flat lens. The size of the analysis area and the boundary conditions are the same as those in Figure 8, and the acoustic metasurface in Figure 4 is replaced by the designed lens in Figure 7. The beam waist of the normal incident Gaussian beam is set to 100 mm, and the complex sound pressure distributions are calculated with COMSOL.

The calculated amplitude and phase distributions of sound pressure at 3.063, 3.500, 4.084, 4.900, 6.125, and 8.167 kHz are shown in Figure 11a–f, respectively. The broken lines represent the theoretical trajectory of the incident wave, and the results in Figure 11a–e show that the focus is generated roughly at the theoretical position. On the other hand, in the case of Figure 11f, the focus is shifted to the left from the theoretical position, but it is seen that the designed acoustic metasurface has the function of a lens. Thus, it is concluded that the broadband operations of the designed acoustic flat lens and the usefulness of the proposed design method are shown.

4. Conclusions

We have presented a method for realizing broadband acoustic metasurfaces based on the 1D distributed TL model. One-dimensional meander acoustic waveguide structures have been proposed, and an acoustic metasurface for refracting incident plane waves with an angle of 20 degrees has been designed with the structures. The waveguide length has been calculated according to the theory of the model, and the waveguide width has been chosen as the value for impedance matching. To consider the effect of the bent waveguide of the structures, the waveguide length has been modified by eigenvalue analysis with COMSOL. We have carried out full-wave simulations and have calculated complex sound pressure in the acoustic waveguide to confirm the broadband operations of the designed acoustic metasurface. The results show that the acoustic metasurface has broadband characteristics.

Furthermore, we have designed a broadband acoustic flat lens by using 1D meander acoustic waveguide structures as an example of the application in order to show the usefulness of the proposed method. It can be seen from the results of similar full-wave simulations that the designed lens has broadband characteristics similar to the designed acoustic metasurface for refracting incident plane waves.

From the results above, it can be concluded that the proposed method based on the theory of the 1D TL model can simultaneously overcome conventional issues such as the large number of calculations required for determining the structural parameters of acoustic metasurfaces as well as narrowband characteristics and impedance matching problems.