Next Article in Journal
Intermolecular Hydrogen Bonding in Alpha-Hydroxy Carboxylic Acids Crystals: Connectivity, Synthons, Supramolecular Motifs
Previous Article in Journal
Wafer-Scale Fabrication of Silicon Film on Lithium Niobate on Insulator (LNOI)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 10
10.3390/cryst12101478
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Coincident Nodal Line and Nodal Surface Phonon States in Ternary Phosphide Compound BaLiP

by
Hong Cui
1,2,*,
Yunjian Chen
1,2,
Qin Kang
1,2,
Pengyue Shan
1,2,
Tie Yang
3 and
Peng Wang
3,*
1
School of Mechanical Engineering, Shaanxi University of Technology, Hanzhong 723001, China
2
Shaanxi Key Laboratory of Industrial Automation, Shaanxi University of Technology, Hanzhong 723001, China
3
School of Physical Science and Technology, Southwest University, Chongqing 400715, China
*
Authors to whom correspondence should be addressed.
Crystals 2022, 12(10), 1478; https://doi.org/10.3390/cryst12101478
Submission received: 7 October 2022 / Accepted: 12 October 2022 / Published: 18 October 2022
Browse Figures
Versions Notes

Abstract

:
With the continuous development of topological properties in condensed matter systems, the current research focus has been expanded into phononic bosonic states. Compared with the conventional electronic fermions, topological phonons exhibit very distinct features. In this study, based on density functional calculations, we have systematically investigated the topological phonons in the ternary phosphide compound BaLiP. Coincident nodal line and nodal surface states are revealed in the middle part of the phononic spectrum and they are formed by the same two phonon bands. Detailed band structure mechanism and symmetry operation formalism are provided. More importantly, evident surface states are observed from the entire nodal line and they are all well separated from the bulk state projection, very beneficial and preferable for future experimental investigation. Lastly, the mechanical properties are also examined and several important parameters are provided, which can be very useful for the practical application. Considering the multiple advantages of the topological nodal states in this material, the corresponding experimental study can be immediately inspired.

1. Introduction

Topological states in condensed matter scale have continuously been the research focus in the field of solid state physics for tens of years since the discovery of topological insulators [1,2,3,4,5]. They have not only deepened the understanding of basic science in the crystalline materials but also opened a new scenario for the potential quantum applications. Persistent research effort and scientific attention are still being dedicated into the search of new topological states or phases from both theoretical and experimental points of view, and, especially with the successful establishment of topological band theory and the effective employment of high throughput calculation technique [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], several wonderful topological material databases have been founded, for example, Materiae [12], Topological Materials Database [10,11], Topological Materials Arsenal [20,21], Topological Magnetic Materials Database [13,14], and Topological Phononics of Materials [23,24], which, in turn, further arouse the great research interests and spark the tremendous scientific enthusiasms in this research field.
As the intrinsic physical properties of crystalline lattices, topological ordered states are produced from the inherent crystallography symmetry constraints and, more importantly, they are often accompanied with nontrivial surface states. For topological nodal point, Fermi arc states are emitted and they generally connect different nodal points; for topological nodal line, drumhead surface states are originated from the entire nodal line and, actually, they can be regard as the connection of numerous Fermi arcs from each point along the nodal line. Indeed, these exotic surface states correspond the ultimate aspects of the topological states, in particular for the final quantum applications. According to the different band crossing conditions, different topological phases can be defined, such as, nodal point [25,26,27,28,29], nodal line [30,31,32,33,34,35,36,37,38] and nodal surface [39,40,41,42,43,44,45] can be differentiated based on the band crossing dimensionality; linear, quadratic [46,47] and cubic [47,48,49,50] topological elements can be divided with respect to the compositive band dispersion; Weyl [51,52,53,54,55], triple [27,56,57,58,59,60,61], Dirac [62,63,64,65,66,67,68,69,70,71,72], sextuple [73,74,75,76,77,78] topological states can be discriminated in accordance with the band crossing degeneracy; Type-I [79], Type-II [28,36,80,81,82,83,84,85] and Type-III [86,87] topological types can be distinguished from the crossing band dispersion configuration. In specific for topological nodal lines, different spatial distributions and combinations lead to diverse topological structures or configurations, like nodal ring or loop [88,89,90,91,92], nodal link [93,94,95,96], nodal net [97,98,99], nodal chain [100,101,102,103,104], nodal knot [105], nodal box [106,107], nodal sphere [108] and nodal cage [109,110,111].
Rapid progress and great development have been witnessed within this field for the last decades and the recent research attention has also been further expanded from the original electronic fermionic states into phononic bosonic ones [112,113,114,115,116,117,118,119]. In comparison with the electronic counterpart, the topological phononic states exhibit multiple distinct properties, such as the spin orbital coupling effect is absent and the Pauli exclusion principle is not restricted [77,91,99,120,121]. These features render the superiority of phononic bosons as the energy limitation can be removed and the topological states can be accessed in an ideal manner. However, the study of topological phononics has been just started and much fewer material candidates can be found, in contract to the enormous researches and massive materials in the electronic systems. Consequently, the search for topological phononic states, especially for the ideal ones, is in great need. Besides, the current studies mainly focused on the isolated phononic nodal states or the separated phononic nodal elements, and there are very few researches with combination of different nodal states within the same band structure. Under this condition, we present an investigation of the topological phononic states in the ternary phosphide compound BaLiP. Detailed first principles calculations have been conducted and obtained results reveal that there is the coincidence of topological nodal line and nodal surface phonons in the middle part of the phononic spectrum around 8.2 THz to 9.2 THz, which leads to the formation of an exotic topological nodal structure. Note that the nodal states in BaLiP are formed by the linear band crossings, which are different from our previous study of quadratic nodal line [46], and the distinct part is that the quadratic nodal line can leads to the formation of double surface states. Systematic band formation mechanism has been provided and evident surface states are separated from the bulk band projection. These advantageous properties make the current material as an ideal platform for the examination of topological nodal line and surface states and, considering this material has been synthesized, the corresponding experimental characterization can be immediately advanced.

2. Computational Methodology

First principles calculations have been performed to study the ternary hexagonal compound BaLiP and the Vienna AB Initio Simulation Package (VASP) [122] has been applied under the basis of density functional theory [123]. The projector augmented wave method [124] and the generalized gradient approximation of the revised Perder-Burke-Ernzerhof formalism [125,126] were employed to deal with the ionic interaction and exchange correlation protentional. After the initial convergence test, a plane wave cutoff energy of 520 eV was set and a 5 × 5 × 2 Γ centered Monkhorst-Pack k mesh was selected. The ground structural state is fully relaxed until the total force per atom was less than 10−5 eV/Å and the self-consistent loop was reached when the total energy variation per atom was smaller than 10−6 eV. To examine the phononic property, a 3 × 3 × 2 supercell was employed the density functional perturbation theory [127,128] was adopted to calculation the force constant as implemented within the PHONONPY program [129]. For the topological phonon spectrum, a Wannier-type tight-binding Hamiltonian was constructed and then the surface states were obtained by the WannierTools package [130].

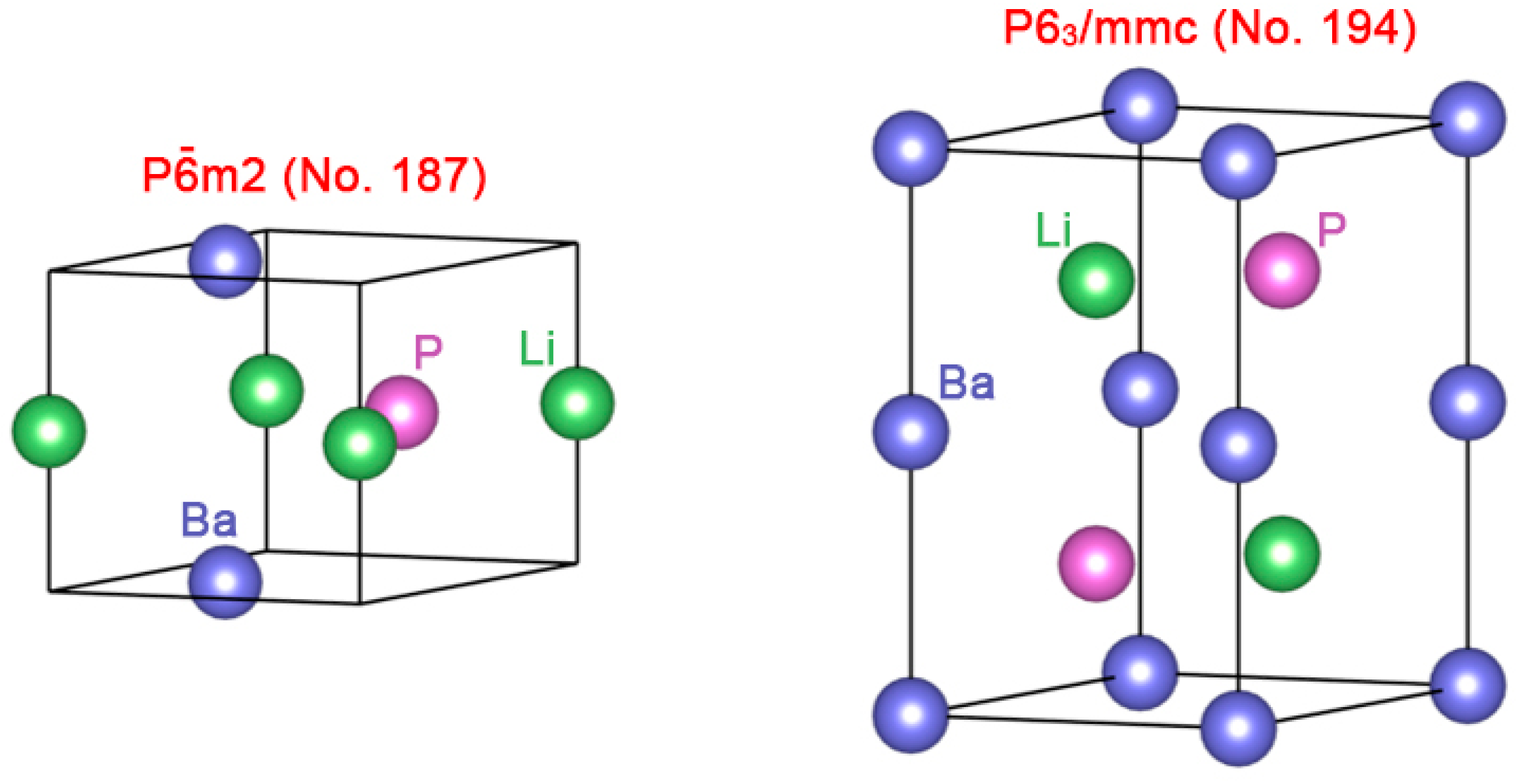
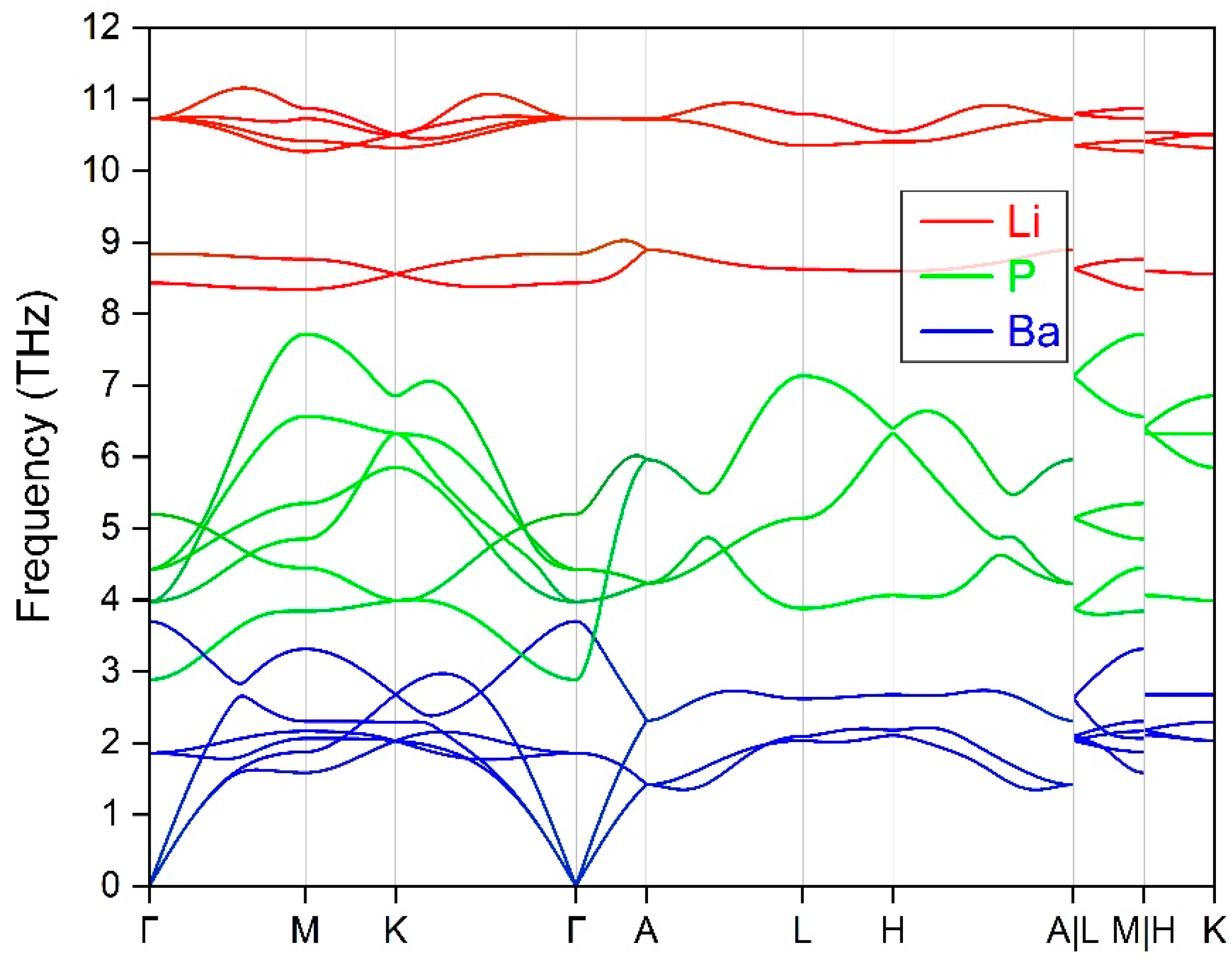
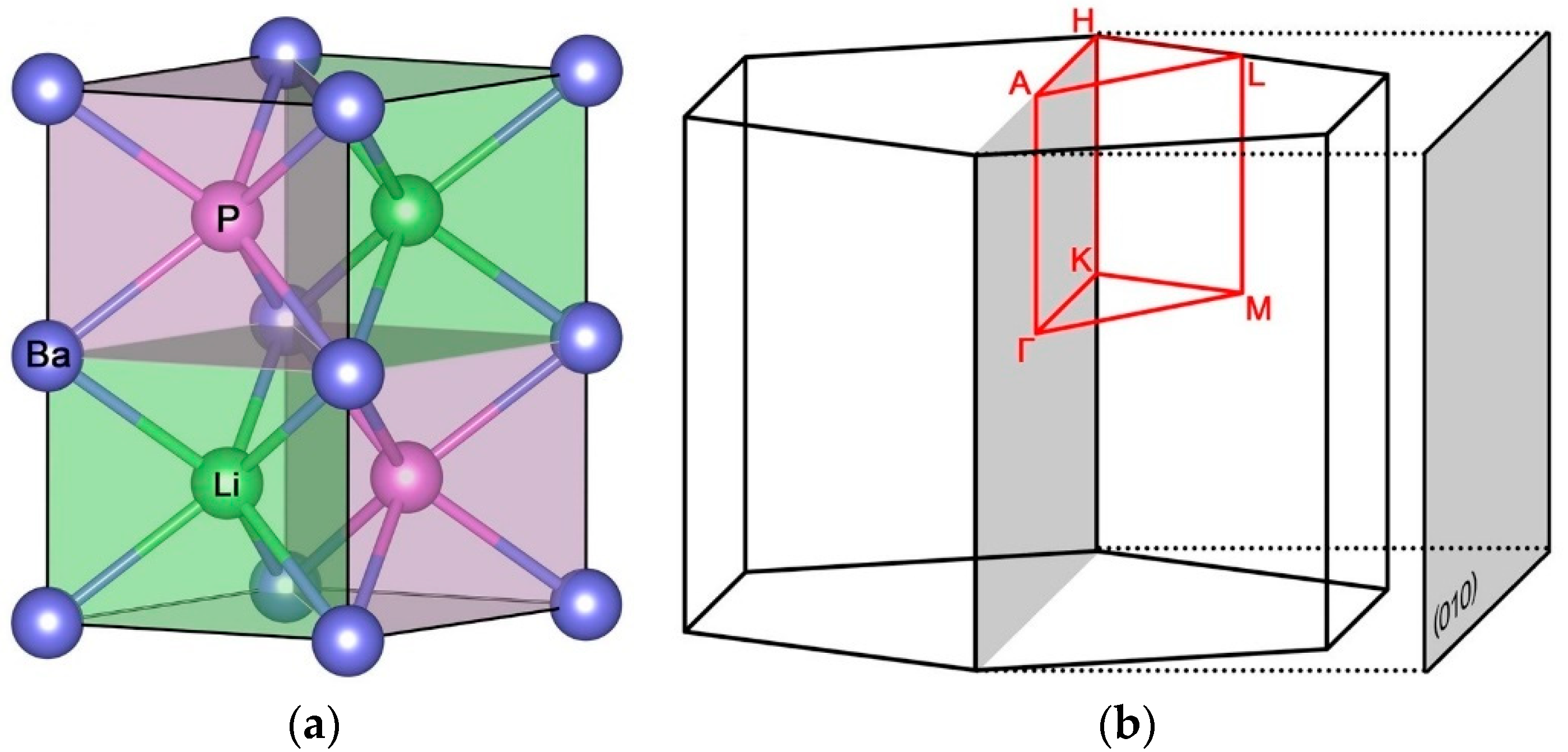
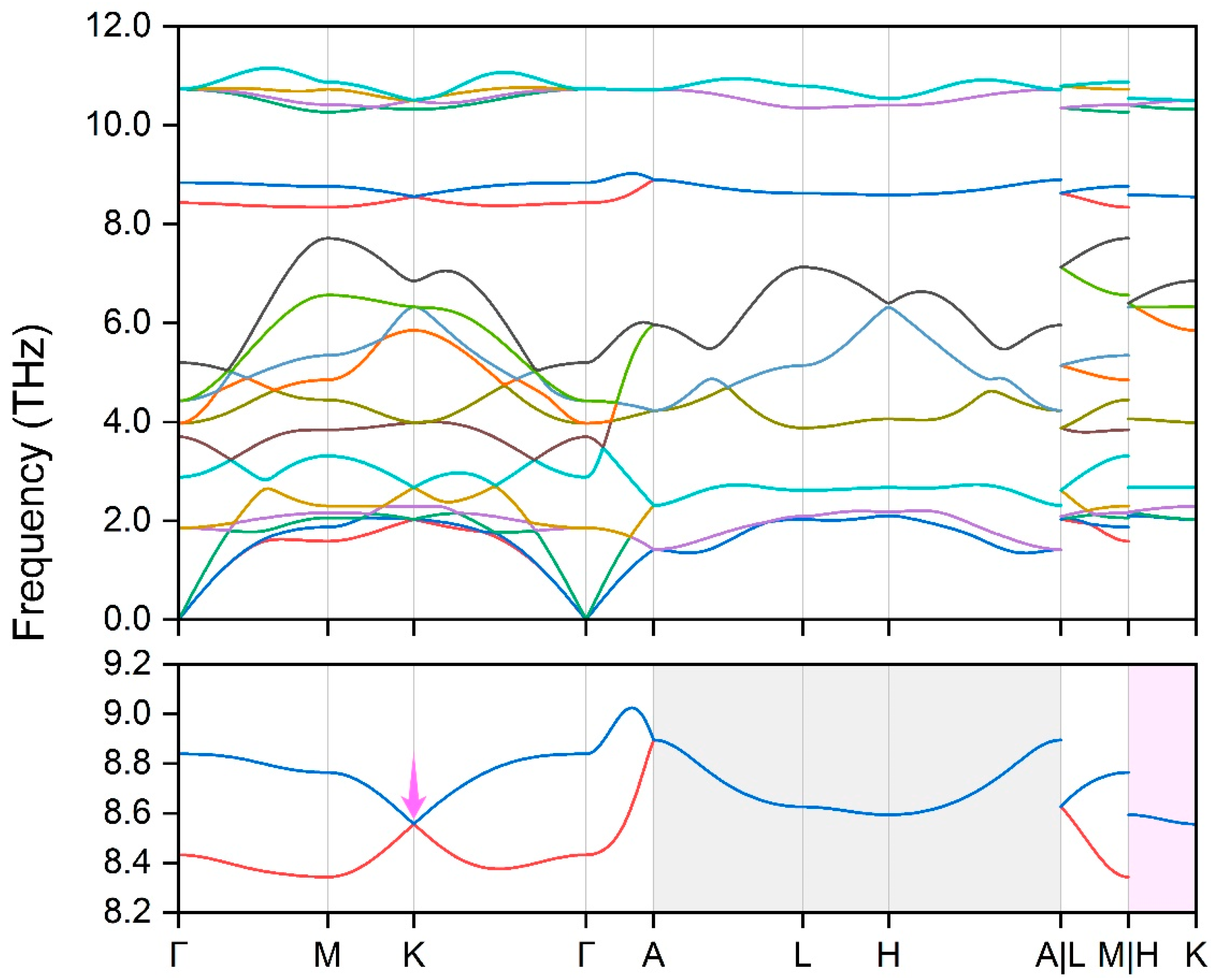
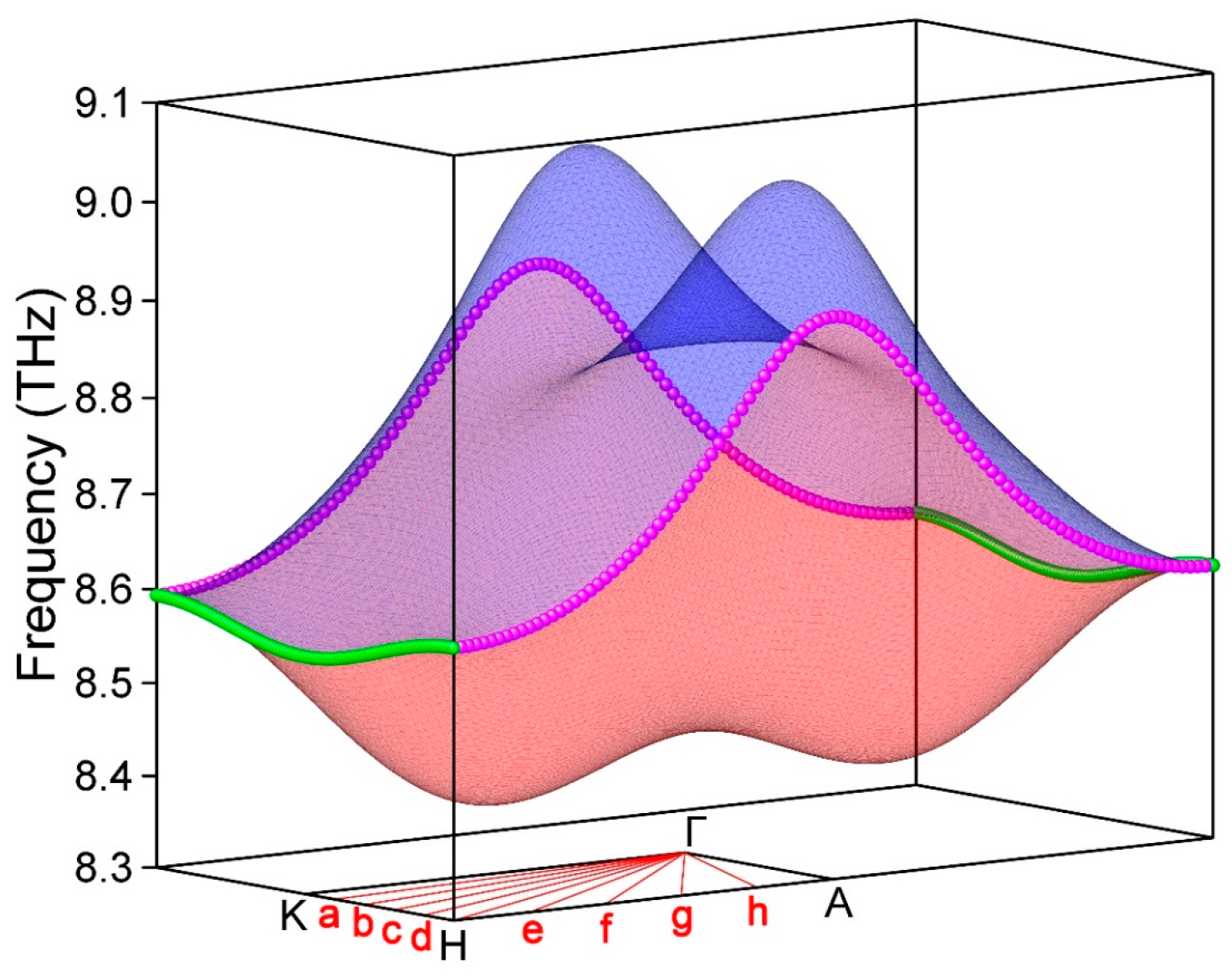
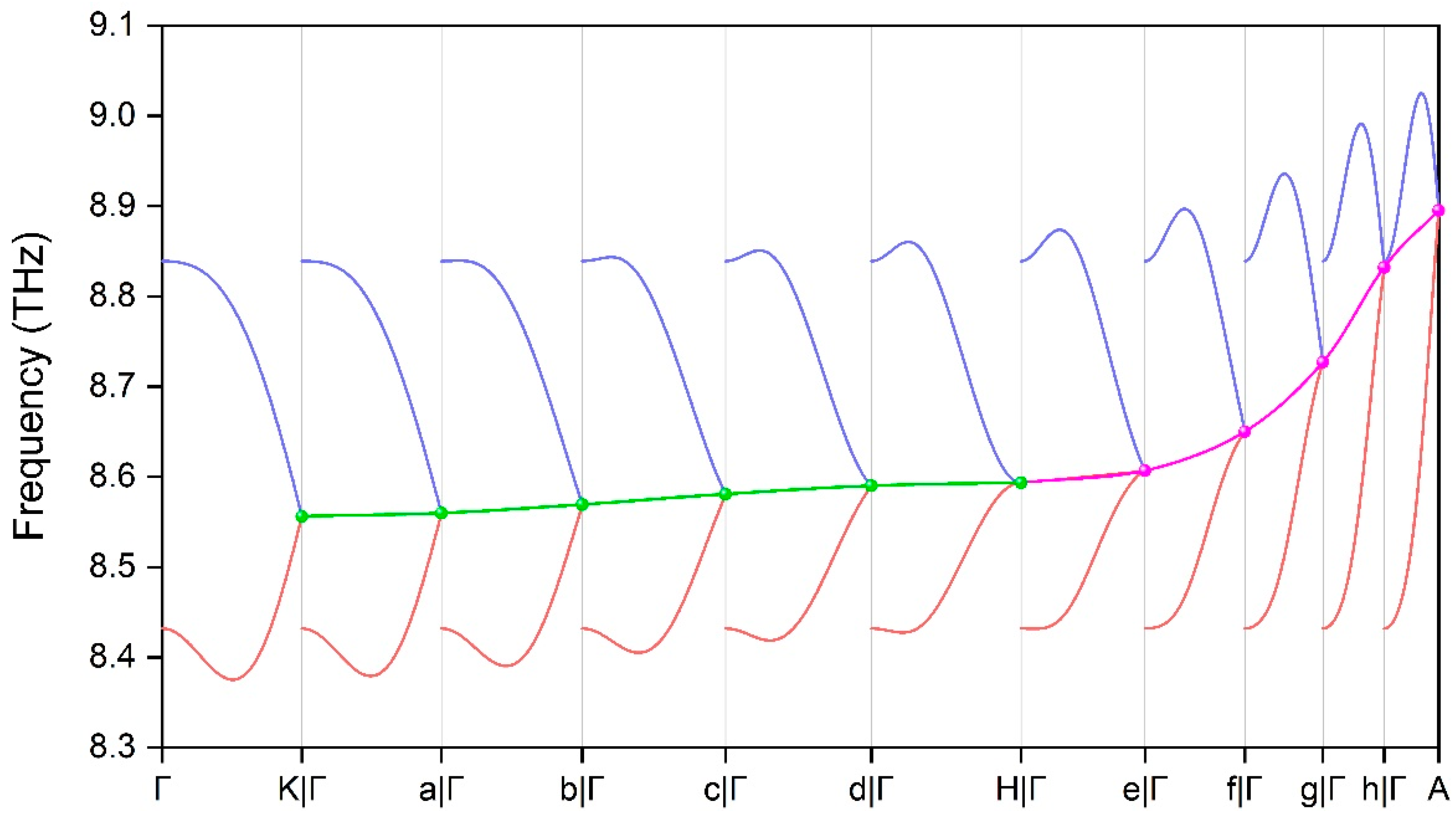
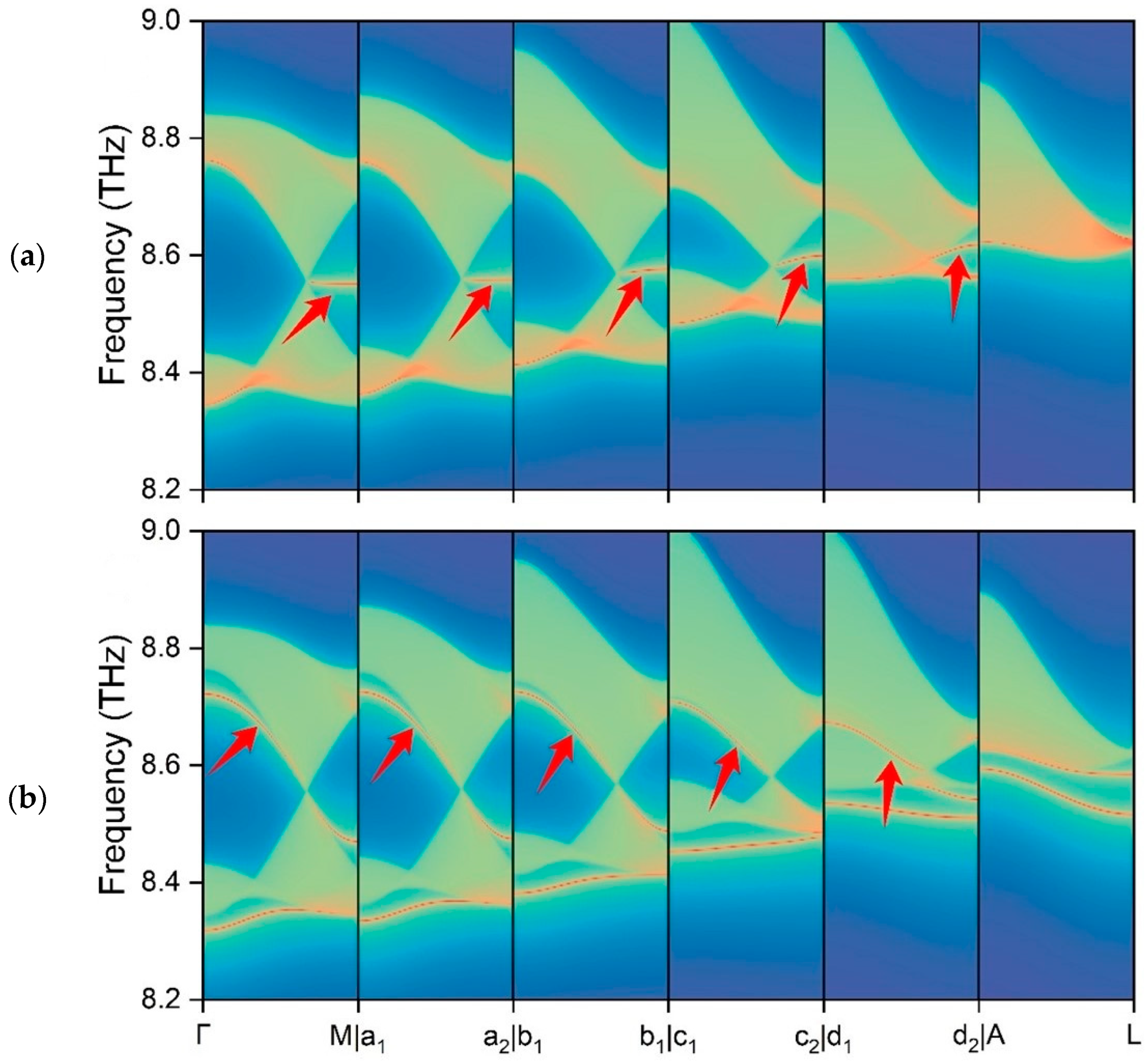
3. Results and Discussions

The single crystal of the ternary phosphide compound BaLiP has been previously synthesized by stoichiometric chemical reaction method [131] and it crystalized in the centrosymmetric hexagonal structure with space group P63/mmc, No. 194. As shown in Figure 1a, the unit cell of BaLiP contains two Ba atoms located at the 2a (0, 0, 0) Wyckoff site, two Li atoms located at the 2c (1/3, 2/3, 1/4) Wyckoff sites and two P atoms located at 2d (1/3, 2/3, 3/4) Wyckoff sites, respectively. Different atoms are represented by different colors in the figure, as indicated by the text labels, and their bonding configurations form multiple polyhdera as displayed by the color shaded areas, in which the Ba atoms are allocated at the six corners and the Li and P atoms are alternately distributed at the central position. To be specific, the BaLiP crystal also exhibits a layered structure with the coplanar Li-P layer distributed between the Ba layer rotationally in the vertical axis. The lattice constants from the fully optimized crystal structure are a = b = 4.486 Å, c = 8.588 Å, which have a very good coincidence with the corresponding experimental values [131], a = b = 4.500 Å, c = 8.605 Å. Since the deviation is less than 1%, this calculated crystal structure is further taken into use for the following calculations and discussions. Note that the currently studied material is different from the other consubstantial one in Ref. [24] because they have both different crystal structures and containing atom numbers. Detailed comparison between two materials and their different phonon spectra can be found in the Appendix A.
The phononic band structure of the ternary phosphide BaLiP has been calculated on the basis of the relaxed crystal structure by density functional perturbation theory and the results are shown in Figure 2. The high symmetry paths were chosen according to the corresponding crystallography as realized by the SeeK-path tool [132] and their spatial distribution in the first Brillouin zone can be referred to Figure 1b. From the phononic spectrum, several prominent features can be immediately observed. There are 18 phononic bands in total, as counted by the different color lines, and they represent the 3 × 6 = 18 vibrational modes for the six atoms in the unit cell. There is no soft phonon mode or imaginary frequency band present, indicating the dynamic stability of this BaLiP structure. Also, the low frequency acoustic branches are interwind with the high frequency optical branches. The phononic bands in the entire range can be separated into three discrete parts with different energy gaps distributed between them. Although all band crossings in the phonon spectrum can be accessed for the topological states, we still focus on the middle part between 8.2 THz and 9.2 THz since there are only two phononic bands, with band gaps of 1.24 THz and 0.63 THz from above and beneath bands, respectively, and their topological features are relatively simple. To further examine the corresponding phononic mode and vibrate direction of these two bands, we have decomposed the bands with element contribution and vibration, from which we found the two bands are mainly contributed from the two Li atoms in the primitive cell and they vibrate along the vertical direction but against each other. Detailed information can be found in the Appendix A. The local enlargement of this middle part from 8.2 THz to 9.2 THz is further displayed at the bottom panel of Figure 2. It can be observed that the two band constitute bands degeneracy in different positions. To be specific, the two bands form a crossing point at K point as indicated by the pink arrow and they further become doubly degenerate convergence along A-L-H-A and H-K paths as highlighted by the color shaded areas in the figure. Note that the K point is located along the H-K path, the crossing point at K actually belong to the double degeneracy along H-K path. Considering their different spatial location and configural distribution of the two paths A-L-H-A and H-K, we can divide their band crossing conditions into different topological states.
As shown in Figure 1b, the H-K path is located along one of the six vertical borders of the hexagonal Brillouin zone and it has a straight line shape. Given that the two bands form a linear crossing point at K point along M-K-Γ path, as indicated by the arrow in the bottom panel of Figure 2, and the two paths M-K and K-Γ are perpendicularly located with respect to the vertical H-K path, the double band degeneracy along H-K path should correspond to a topological nodal line state. Similarly, considering the entire path A-L-H-A is distributed completely within the kz = π plane, see Figure 1b, and the double band convergence along this path is constituent of the linear band crossing from the transverse direction, such as along Γ-A and M-L paths, the double band degeneracy along A-L-H-A path should correspond to a topological nodal surface state. This type of phononic nodal line or nodal surface state has been reported and their symmetry determined nature has also been theoretically analyzed [16]. To brief recall, the nodal line state is protected by the threefold rotation symmetry C 3 z and the combined time reversal and spatial inversion operation P T , and the nodal surface state is dictated by the combined antiunitary C ~ 2 z T symmetries, where C ~ 2 z is the twofold screw axis along the z ^ direction. However, most of the previous studies are focused on the electronic fermionic systems, in which the spin orbital coupling effect often shifts the original topological states into other phases or even destroy the topological features. Although some of the nodal line or nodal surface states can be properly maintained under the spin orbital coupling effect, special symmetry constraints or specific structural coordiations are required, which leads to the extreme limit and great restriction of the available material candidates, not to mention the future application potential. Compared with the tremendous studies in electronic systems, the research in phononic system has just been started and the current study can provide an effective platform for the examination of the phononic topological states. Furthermore, since the spin orbital coupling effect is absent in the phononic state, these nodal line and surface states can be ideally assessed.
To further examine these phononic nodal states and understand their formation mechanism, we have calculated the phononic dispersion of the same two bands in the kx = 0 plane, see the grey color shaded area within the Brillouin zone in Figure 1b, and the obtained three dimensional band surface distribution is reported in Figure 3. The same colors for the top and bottom bands are selected as the phonon spectrum in Figure 1. The local coordination system is overlaid on the bottom. It can be seen that the two bands only overlap with each other at the four rectangular borders and they are well separated elsewhere and their crossing points at the borders are highlighted with different color dots: green dots along K-H border and purple dots along H-A border. From this three dimensional band surface, we can clearly find the double band degeneracies along H-A and K-H are formed by the linear crossing of the same two bands from the transverse direction, confirming their topological nature. The nodal line state along K-H stretches through the entire Brillouin zone and its frequency variation is much smaller than that of the nodal surface along H-A. According to the reverse dispersions of the crossing two bands, the entire nodal line has a Type-I configuration. In combination with its vertical line shape, this straight Type-I phononic nodal line has been scarcely reported and it has only been found in few phononic systems with similar crystal structures.
Given the very different frequency variations along the nodal line and nodal surface, a precise band dispersion has been scanned along different path segments within the kx = 0 plane and the results are shown in Figure 4, where the spatial distribution of the various path segments can be referred to the bottom local coordinate system in Figure 3. Note the lengths of the different path segments are scaled proportionally to their authentic dimensions in the Brillouin zone. Besides, the same colors are applied for the two bands as Figure 2 and Figure 3. We can observe that the two bands form crossings at the right border of each path segments and they actually correspond to the nodal line along K-H and nodal surface along H-A. The crossing points are also highlighted by the same color dots as Figure 3 and they are also connected to review their frequency variation. We can see the crossing points along the left half segments have very small frequency variation for the nodal line, less than 0.05 THz, whereas they exhibit much larger change along the right half segments for the nodal surface, about 0.40 THz. Besides, from the band distributions we can see the two bands have approximately the same linear dispersion range along the nodal line; while, they take rapid variation in the reverse manner: shrink for the top band of blue color and expand for the bottom band of red color, leading to the extreme linear dispersion range variations, increase for the bottom band the decrease for the top band, respectively. These different conditions for the frequency variation of the topological nodal states are only related with the specific materials and they are not restricted by the crystalline symmetries.
For the symmetry determined topological states, they are often accompanied by the nontrivial surface states, Fermi arcs for nodal points and drumhead states for nodal lines, which are indeed the primary characteristics for the topological properties. However, in most cases these surface states are mixed or covered with the bulk ones, leading to the abolishment of the potential topological application. In some cases, relatively clean band structures can be present and the topological surface states can be thus well separated from the bulk ones. This special condition is quite limited around the Fermi energy level for electronic fermionic systems; yet there is no such restraint for the topological phononic states. Besides, these nontrivial surface states are generally applied to verify the corresponding topological states for both electronic and phononic systems from both theoretical and experimental points of view.
Based on the constructed Wannier-type tight-binding Hamiltonian, we have examined the surface states of the nodal line and nodal surface in the ternary phosphide BaLiP. A 30-layer slab system was cleaved along the (010) surface, on which the surface spectrum has been calculated and the results are reported in Figure 5. In consideration of the nodal line or the nodal surface with large spatial occupation in the Brillouin zone and, in particular, the nodal line stretches through the Brillouin zone border, the surface spectrum has been calculated along multiple path segments. The middle path segments a1-a2/b1-b2/c1-c2/d1-d2 are evenly distributed between Γ-M and A-L paths. Since the slab layer structure along the (010) surface has asymmetric termination condition, the surface spectra for the top and bottom surfaces exhibit different distribution, see Figure 5a for the top termination and Figure 5b for the bottom termination, respectively. The same frequency range from 8.2 THz to 9.2 THz is applied for both plots. Prominent drumhead surface states are emitted from the crossing points along the nodal line for both top and bottom termination surfaces, as indicated by the red arrows in the figures. More importantly, these surface states are all well separated from the bulk band projections along the different path segments, especially for the top termination surface of Figure 5a. This feature can be very beneficial for future experimental characterization or be very preferable for potential practical application. For the A-L path, the surface state is buried within the bulk band projection. In previous works, the phononic nodal line or nodal surface state has been reported; whereas, they are most constituted by different bands or they are not directly connected. The coincidence of nodal line and nodal surface states with the same two bands leads to the formation of exotic nodal cage state, which is very rare and can provide an exotic platform to further studied the possible correlation effect between different topological states.
Except the dynamic perspective, the mechanical property for a material also plays a crucial role regarding to its practical application. Consequently, we further assessed the mechanical parameters of this ternary phosphide BaLiP. There are five independent elastic constants for this hexagonal compound, namely, C11, C12, C13, C33 and C44, and they are estimated by the stress-strain method [133]. In addition, several other important mechanical properties can be obtained with the Voigt-Reuss-Hill approximation [134], including the Young’s modulus, shear modulus and Poisson’s ratio. All the mechanical values are reported in Table 1. Furthermore, we also examined the mechanical anisotropy by calculating the spatial dependent distribution of Young’s modulus, shear modulus and Poisson’s ratio and their results are displayed in Figure 6. We can directly observe that the Young’s modulus has its minimum value along [001] direction while shear modulus and Poisson’s ratio exhibit the maximum value along the same direction. These mechanical properties can provide a practical reference for its applied usage.

4. Conclusions

In conclusion, a systematic investigation has been conducted to examine the topological states in the ternary phosphide compound BaLiP. Theoretical calculation results show that there are ideal nodal line and nodal surface states in the phononic spectrum. The nodal line is distributed along the vertical border line of the hexagonal Brillouin zone, whereas the nodal surface is located in the top/bottom surface, which is perpendicular to the nodal line. Detailed band structure analysis and symmetry model argument are provided. Different from previous studies, the nodal line and nodal surface are constituted from the same two bands and they together form an exotic nodal cage. Based on the constructed tight-binding Hamiltonian, the surface states for the topological phononic states are examined. Evident drumhead surface states are observed and they are originated from the entire nodal line and, more importantly, all the surface states are well separated from the bulk band projection, which can be very preferable for both future experimental detection and potential practical application. Besides, the mechanical properties are further assessed and several important parameters are obtained, which can provide a useful reference for its final application. Overall, the topological phononic states found in current study exhibit multiple advantageous properties and, especially, the coincidence of two different nodal states can offer a platform to further examine their correlation effect, leading to the inspiration of the relative studies from both theoretical and experimental perspectives.

Author Contributions

Data curation, Q.K. and P.S.; Formal analysis, Y.C., Q.K., P.S. and T.Y.; Investigation, H.C., Y.C., Q.K., P.S. and T.Y.; Methodology, Y.C., Q.K. and P.W.; Project administration, H.C. and P.W.; Resources, H.C. and P.W.; Software, P.W.; Supervision, H.C. and P.W.; Validation, P.S.; Writing—original draft, Y.C., Q.K. and P.S.; Writing—review & editing, T.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (12004315), the Basic Research Plan of Natural Science in Shaanxi province (No. 2021JM-485) and the Key Scientific Research Project of Shaanxi provincial education department (No. 20JS019).

Data Availability Statement

The data that support the findings of this study are available upon reasonable request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The studied BaLiP with space group P63/mmc (No. 194) has different crystal structure with the other consubstantial one with space group P 6 - m2 (No. 187) in Ref. [24]. To be specific, we put the two structures together in the following Figure A1. We can see that the two crystal structures are very different not only in the lattice constants but also in the containing atom number.
Crystals 12 01478 g0a1 550
Figure A1. The different crystal structures for BaLiP under the two space groups. Spheres of different colors represent different atoms, as also labeled by the color text. Note the two structures contain different total number of atoms.
Figure A1. The different crystal structures for BaLiP under the two space groups. Spheres of different colors represent different atoms, as also labeled by the color text. Note the two structures contain different total number of atoms.
Crystals 12 01478 g0a1
The BaLiP in Ref. [24] has space group P 6 - m2 (No. 187) and it has three atoms in total whereas the other one with space group P63/mmc (No. 194) contains six atoms. This different atom numbers can also be reflected from the different phonon bands, as plotted in the following Figure A2. Note that the same phonon band structure is obtained for BaLiP in space group P 6 - m2 (No. 187) as Ref. [24], which can also confirm the validity of our calculation method. We can see the phonon spectrum for BaLiP with space group P63/mmc in the left panel has 18 bands, equal to 3 × 6, where 6 stands for the containing atom number in the primitive cell. For BaLiP with space group P 6 - m2 in the right panel of Figure A2, there are only 9 bands, equal to 3 × 3, where 3 stands for the containing atom number in the primitive cell. This different crystal structures and atom numbers would lead to the distinct topological properties.
Crystals 12 01478 g0a2 550
Figure A2. The phono band spectra for BaLiP materials under the two different crystal structures. The corresponding crystal space groups are located on the top with different colors. To further examine the phononic mode and vibrate direction of the studied two topological bands, we have decomposed the bands with element contribution and vibration, and their results are reported Figure A3 and Figure A4, respective. From Figure A3, we found the entire phonon band can be divided into three parts from the frequency range: low frequency bands from Ba element, middle frequency bands from P element and high frequency bands from Li element. Especially, the two bands between 8.2 THz and 9.2 THz are only contributed by the Li element.
Figure A2. The phono band spectra for BaLiP materials under the two different crystal structures. The corresponding crystal space groups are located on the top with different colors. To further examine the phononic mode and vibrate direction of the studied two topological bands, we have decomposed the bands with element contribution and vibration, and their results are reported Figure A3 and Figure A4, respective. From Figure A3, we found the entire phonon band can be divided into three parts from the frequency range: low frequency bands from Ba element, middle frequency bands from P element and high frequency bands from Li element. Especially, the two bands between 8.2 THz and 9.2 THz are only contributed by the Li element.
Crystals 12 01478 g0a2
Crystals 12 01478 g0a3 550
Figure A3. The phono band spectra with element contribution decomposition as overlaid by different color weights: red color for Li, green color for P and blue color for Ba.
Figure A3. The phono band spectra with element contribution decomposition as overlaid by different color weights: red color for Li, green color for P and blue color for Ba.
Crystals 12 01478 g0a3
Considering there are two Li atoms in the primitive cell, we further decompose the phonon spectra with vibration mode for the two Li atoms and the obtained results are displayed in Figure A4. It can be seen that the two focused bands between 8.2 THz and 9.2 THz have mostly blue colors, which correspond to the vibration mode along vertical direction. The two insets exhibit the vibration direction for the two Li atoms as indicated by the color arrows, and it is found the two Li atoms have reverse vibration mode along the vertical direction. Thus the topological feature of the two bands are mainly constituted by the Li atoms with opposite vibration mode along the vertical direction. This clean phonon band with simple vibration mode can be very beneficial for the corresponding experimental verification.
Crystals 12 01478 g0a4 550
Figure A4. The phono band spectra with vibration mode decomposition for two Li atoms in the primitive cell: Li (1/3, 2/3, 1/4) for (a) and Li (1/3, 2/3, 3/4) for (b). The two insets indicate the vibration direction of the corresponding Li atom in the primitive cell, as indicated by the color arrows.
Figure A4. The phono band spectra with vibration mode decomposition for two Li atoms in the primitive cell: Li (1/3, 2/3, 1/4) for (a) and Li (1/3, 2/3, 3/4) for (b). The two insets indicate the vibration direction of the corresponding Li atom in the primitive cell, as indicated by the color arrows.
Crystals 12 01478 g0a4

References

  1. Senthil, T. Symmetry-Protected Topological Phases of Quantum Matter. Annu. Rev. Condens. Matter Phys. 2015, 6, 299–324. [Google Scholar] [CrossRef] [Green Version]
  2. Yan, B.; Felser, C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. [Google Scholar] [CrossRef] [Green Version]
  3. Gao, H.; Venderbos, J.W.F.; Kim, Y.; Rappe, A.M. Topological Semimetals from First Principles. Annu. Rev. Mater. Res. 2019, 49, 153–183. [Google Scholar] [CrossRef] [Green Version]
  4. Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
  5. Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef] [Green Version]
  6. Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef] [Green Version]
  7. Chiu, C.-K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef] [Green Version]
  8. Cooper, N.R.; Dalibard, J.; Spielman, I.B. Topological bands for ultracold atoms. Rev. Mod. Phys. 2019, 91, 015005. [Google Scholar]
  9. Bernevig, B.A.; Felser, C.; Beidenkopf, H. Progress and prospects in magnetic topological materials. Nature 2022, 603, 41–51. [Google Scholar] [CrossRef] [PubMed]
  10. Bradlyn, B.; Elcoro, L.; Cano, J.; Vergniory, M.G.; Wang, Z.; Felser, C.; Aroyo, M.I.; Bernevig, B.A. Topological quantum chemistry. Nature 2017, 547, 298–305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  11. Vergniory, M.G.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480–485. [Google Scholar] [CrossRef] [PubMed]
  12. Zhang, T.; Jiang, Y.; Song, Z.; Huang, H.; He, Y.; Fang, Z.; Weng, H.; Fang, C. Catalogue of topological electronic materials. Nature 2019, 566, 475–479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Xu, Y.; Elcoro, L.; Song, Z.-D.; Wieder, B.J.; Vergniory, M.G.; Regnault, N.; Chen, Y.; Felser, C.; Bernevig, B.A. High-throughput calculations of magnetic topological materials. Nature 2020, 586, 702–707. [Google Scholar] [CrossRef] [PubMed]
  14. Elcoro, L.; Wieder, B.J.; Song, Z.; Xu, Y.; Bradlyn, B.; Bernevig, B.A. Magnetic topological quantum chemistry. Nat. Commun. 2021, 12, 5965. [Google Scholar] [CrossRef] [PubMed]
  15. Liu, G.-B.; Chu, M.; Zhang, Z.; Yu, Z.-M.; Yao, Y. SpaceGroupIrep: A package for irreducible representations of space group. Comput. Phys. Commun. 2021, 265, 107993. [Google Scholar] [CrossRef]
  16. Yu, Z.; Zhang, Z.; Liu, G.-B.; Wu, W.; Li, X.-P.; Zhang, R.-W.; Yang, S.; Yao, Y. Encyclopedia of emergent particles in three-dimensional crystals. Sci. Bull. 2021, 67, 375. [Google Scholar] [CrossRef]
  17. Zhang, Z.; Liu, G.-B.; Yu, Z.-M.; Yang, S.A.; Yao, Y. Encyclopedia of emergent particles in type-IV magnetic space groups. Phys. Rev. B 2022, 105, 104426. [Google Scholar] [CrossRef]
  18. Gao, J.; Wu, Q.; Persson, C.; Wang, Z. Irvsp: To obtain irreducible representations of electronic states in the VASP. Comput. Phys. Commun. 2021, 261, 107760. [Google Scholar] [CrossRef]
  19. Zhi, G.-X.; Xu, C.; Wu, S.-Q.; Ning, F.; Cao, C. WannSymm: A symmetry analysis code for Wannier orbitals. Comput. Phys. Commun. 2022, 271, 108196. [Google Scholar] [CrossRef]
  20. Tang, F.; Po, H.C.; Vishwanath, A.; Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 2019, 566, 486–489. [Google Scholar] [CrossRef] [Green Version]
  21. Tang, F.; Po, H.C.; Vishwanath, A.; Wan, X. Efficient topological materials discovery using symmetry indicators. Nat. Phys. 2019, 15, 470–476. [Google Scholar] [CrossRef]
  22. Po, H.C.; Vishwanath, A.; Watanabe, H. Complete theory of symmetry-based indicators of band topology. Nat. Commun. 2017, 8, 50. [Google Scholar] [CrossRef] [Green Version]
  23. Chen, X.-Q.; Liu, J.; Li, J. Topological phononic materials: Computation and data. Innovation 2021, 2, 100134. [Google Scholar] [CrossRef] [PubMed]
  24. Li, J.; Liu, J.; Baronett, S.A.; Liu, M.; Wang, L.; Li, R.; Chen, Y.; Li, D.; Zhu, Q.; Chen, X.-Q. Computation and data driven discovery of topological phononic materials. Nat. Commun. 2021, 12, 1204. [Google Scholar] [CrossRef]
  25. Cano, J.; Bradlyn, B.; Vergniory, M.G. Multifold nodal points in magnetic materials. Apl Mater. 2019, 7, 101125. [Google Scholar] [CrossRef]
  26. He, T.; Zhang, X.; Meng, W.; Jin, L.; Dai, X.; Liu, G. Topological nodal lines and nodal points in the antiferromagnetic material β-Fe2PO5. J. Mater. Chem. C 2019, 7, 12657–12663. [Google Scholar] [CrossRef]
  27. Jin, L.; Zhang, X.; Dai, X.; Liu, H.; Chen, G.; Liu, G. Centrosymmetric Li2NaN: A superior topological electronic material with critical-type triply degenerate nodal points. J. Mater. Chem. C 2019, 7, 1316–1320. [Google Scholar] [CrossRef] [Green Version]
  28. Zhang, T.-T.; Yu, Z.-M.; Guo, W.; Shi, D.; Zhang, G.; Yao, Y. From Type-II Triply Degenerate Nodal Points and Three-Band Nodal Rings to Type-II Dirac Points in Centrosymmetric Zirconium Oxide. J. Phys. Chem. Lett. 2017, 8, 5792–5797. [Google Scholar] [CrossRef] [Green Version]
  29. Weng, H.; Fang, C.; Fang, Z.; Dai, X. Topological semimetals with triply degenerate nodal points in theta-phase tantalum nitride. Phys. Rev. B 2016, 93, 241202. [Google Scholar] [CrossRef] [Green Version]
  30. Wang, J.-T.; Weng, H.; Chen, C. Topological nodal line semimetals in graphene network structures. Adv. Phys. X 2019, 4, 1625724. [Google Scholar] [CrossRef] [Green Version]
  31. Yang, T.; Gu, Q.; Wang, P.; Wu, Z.; Zhang, Z. Phononic quadratic nodal lines of different types in Li2NaN. Appl. Phys. Lett. 2022, 121, 053102. [Google Scholar] [CrossRef]
  32. Jin, L.; Zhang, X.; He, T.; Meng, W.; Dai, X.; Liu, G. Ferromagnetic two-dimensional metal-chlorides MCl (M = Sc, Y, and La): Candidates for Weyl nodal line semimetals with small spin-orbit coupling gaps. Appl. Surf. Sci. 2020, 520, 146376. [Google Scholar] [CrossRef]
  33. Fang, C.; Weng, H.; Dai, X.; Fang, Z. Topological nodal line semimetals. Chin. Phys. B 2016, 25, 117106. [Google Scholar] [CrossRef] [Green Version]
  34. Jin, L.; Zhang, X.; He, T.; Meng, W.; Dai, X.; Liu, G. Topological nodal line state in superconducting NaAlSi compound. J. Mater. Chem. C 2019, 7, 10694–10699. [Google Scholar] [CrossRef]
  35. Zhang, X.; Fu, B.; Jin, L.; Dai, X.; Liu, G.; Yao, Y. Topological Nodal Line Electrides: Realization of an Ideal Nodal Line State Nearly Immune from Spin-Orbit Coupling. J. Phys. Chem. C 2019, 123, 25871–25876. [Google Scholar] [CrossRef]
  36. He, J.; Kong, X.; Wang, W.; Kou, S.-P. Type-II nodal line semimetal. New J. Phys. 2018, 20, 053019. [Google Scholar] [CrossRef]
  37. Khan, M.R.; Bu, K.; Wang, J.-T. Topological nodal line semimetal in an all-sp2 monoclinic carbon. New J. Phys. 2022, 24, 043007. [Google Scholar] [CrossRef]
  38. Li, Z.H.; Wang, W.; Zhou, P.; Ma, Z.S.; Sun, L.Z. New type of hybrid nodal line semimetal in Be2Si. New J. Phys. 2019, 21, 033018. [Google Scholar] [CrossRef]
  39. Yang, T.; Zhang, X. Nearly flat nodal surface states in pseudo-one-dimensional molybdenum monochalcogenides X(MoS)3 (X = K, Rb, and Cs). J. Mater. Chem. C 2020, 8, 9046–9054. [Google Scholar] [CrossRef]
  40. Khan, M.R.; Bu, K.; Wang, J.-T.; Chen, C. Topological nodal surface semimetal states in Sr5X3 compounds (X = As, Sb, Bi). Phys. Rev. B 2022, 105, 245152. [Google Scholar] [CrossRef]
  41. Xie, C.; Yuan, H.; Liu, Y.; Wang, X. Two-nodal surface phonons in solid-state materials. Phys. Rev. B 2022, 105, 054307. [Google Scholar] [CrossRef]
  42. Zhang, X.M.; Yu, Z.M.; Zhu, Z.M.; Wu, W.K.; Wang, S.S.; Sheng, X.L.; Yang, S.A. Nodal loop and nodal surface states in the Ti3Al family of materials. Phys. Rev. B 2018, 97, 235150. [Google Scholar] [CrossRef] [Green Version]
  43. Fu, B.-B.; Yi, C.-J.; Zhang, T.-T.; Caputo, M.; Ma, J.-Z.; Gao, X.; Lv, B.Q.; Kong, L.-Y.; Huang, Y.-B.; Richard, P.; et al. Dirac nodal surfaces and nodal lines in ZrSiS. Sci. Adv. 2019, 5, eaau6459. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Xiao, M.; Ye, L.; Qiu, C.; He, H.; Liu, Z.; Fan, S. Experimental demonstration of acoustic semimetal with topologically charged nodal surface. Sci. Adv. 2020, 6, eaav2360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  45. Yang, T.; Khenata, R.; Wang, X. Predicted remarkably topological nodal surface states in P63/m type Sr3WN3 from first-principles. Results Phys. 2020, 17, 103026. [Google Scholar] [CrossRef]
  46. Kang, Q.; Chen, Y.; Shan, P.; Wang, P.; Cui, H.; Yang, T. Quadratic nodal line phonon with hybrid type in hexagonal compound SrCuSi. Results Phys. 2022, 41, 105953. [Google Scholar] [CrossRef]
  47. Yu, Z.-M.; Wu, W.; Sheng, X.-L.; Zhao, Y.X.; Yang, S.A. Quadratic and cubic nodal lines stabilized by crystalline symmetry. Phys. Rev. B 2019, 99, 121106. [Google Scholar] [CrossRef] [Green Version]
  48. Zhang, T.; Takahashi, R.; Fang, C.; Murakami, S. Twofold quadruple Weyl nodes in chiral cubic crystals. Phys. Rev. B 2020, 102, 125148. [Google Scholar] [CrossRef]
  49. Yu, W.C.; Zhou, X.; Chuang, F.-C.; Yang, S.A.; Lin, H.; Bansil, A. Nonsymmorphic cubic Dirac point and crossed nodal rings across the ferroelectric phase transition in LiOsO3. Phys. Rev. Mater. 2018, 2, 051201. [Google Scholar] [CrossRef]
  50. Liu, Q.; Zunger, A. Predicted Realization of Cubic Dirac Fermion in Quasi-One-Dimensional Transition-Metal Monochalcogenides. Phys. Rev. X 2017, 7, 021019. [Google Scholar] [CrossRef] [Green Version]
  51. Jia, S.; Xu, S.-Y.; Hasan, M.Z. Weyl semimetals, Fermi arcs and chiral anomalies. Nat. Mater. 2016, 15, 1140–1144. [Google Scholar] [CrossRef] [PubMed]
  52. Ma, Q.; Xu, S.-Y.; Chan, C.-K.; Zhang, C.-L.; Chang, G.; Lin, Y.; Xie, W.; Palacios, T.; Lin, H.; Jia, S.; et al. Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 2017, 13, 842–847. [Google Scholar] [CrossRef] [Green Version]
  53. Xu, S.-Y.; Alidoust, N.; Belopolski, I.; Yuan, Z.; Bian, G.; Chang, T.-R.; Zheng, H.; Strocov, V.N.; Sanchez, D.S.; Chang, G.; et al. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nat. Phys. 2015, 11, 748–754. [Google Scholar] [CrossRef] [Green Version]
  54. Yang, L.X.; Liu, Z.K.; Sun, Y.; Peng, H.; Yang, H.F.; Zhang, T.; Zhou, B.; Zhang, Y.; Guo, Y.F.; Rahn, M.; et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 2015, 11, 728–732. [Google Scholar] [CrossRef] [Green Version]
  55. Manna, K.; Sun, Y.; Muechler, L.; Kubler, J.; Felser, C. Heusler, Weyl and Berry. Nat. Rev. Mater. 2018, 3, 244–256. [Google Scholar] [CrossRef] [Green Version]
  56. Winkler, G.W.; Singh, S.; Soluyanov, A.A. Topology of triple-point metals. Chin. Phys B 2019, 28, 077303. [Google Scholar] [CrossRef] [Green Version]
  57. Cai, J.; Xie, Y.; Chang, P.-Y.; Kim, H.-S.; Chen, Y. Nodal-chain network, intersecting nodal rings and triple points coexisting in nonsymmorphic Ba3Si4. Phys. Chem. Chem. Phys. 2018, 20, 21177–21183. [Google Scholar] [CrossRef] [Green Version]
  58. Barman, C.K.; Mondal, C.; Pathak, B.; Alam, A. Quaternary Heusler alloy: An ideal platform to realize triple point fermions. Phys. Rev. B 2019, 99, 045144. [Google Scholar] [CrossRef] [Green Version]
  59. Yang, H.; Yu, J.; Parkin, S.S.P.; Felser, C.; Liu, C.-X.; Yan, B. Prediction of Triple Point Fermions in Simple Half-Heusler Topological Insulators. Phys. Rev. Lett. 2017, 119, 136401. [Google Scholar] [CrossRef] [Green Version]
  60. Singh, S.; Wu, Q.; Yue, C.; Romero, A.H.; Soluyanov, A.A. Topological phonons and thermoelectricity in triple-point metals. Phys. Rev. Mater. 2018, 2, 114204. [Google Scholar] [CrossRef]
  61. Zhu, Z.; Winkler, G.W.; Wu, Q.; Li, J.; Soluyanov, A.A. Triple Point Topological Metals. Phys. Rev. X 2016, 6, 031003. [Google Scholar] [CrossRef]
  62. Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. Dirac materials. Adv. Phys. 2014, 63, 1–76. [Google Scholar] [CrossRef] [Green Version]
  63. Pal, P.B. Dirac, Majorana, and Weyl fermions. Am. J. Phys. 2011, 79, 485–498. [Google Scholar] [CrossRef] [Green Version]
  64. Vafek, O.; Vishwanath, A. Dirac Fermions in Solids: From High-T-c Cuprates and Graphene to Topological Insulators and Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2014, 5, 83–112. [Google Scholar] [CrossRef] [Green Version]
  65. Xie, L.S.; Schoop, L.M.; Seibel, E.M.; Gibson, Q.D.; Xie, W.; Cava, R.J. A new form of Ca3P2 with a ring of Dirac nodes. Apl Mater. 2015, 3, 083602. [Google Scholar] [CrossRef] [Green Version]
  66. Zhang, H.; Meng, W.; Liu, Y.; Zhang, X.; Gao, J.; Dai, X.; Liu, G. Theoretical study of compounds XSb (X = La, Pr, Nd): Realization of inner nodal chains, nodal line frame, and Dirac points. Comput. Mater. Sci. 2022, 206, 111231. [Google Scholar] [CrossRef]
  67. Okamoto, Y.; Inohara, T.; Yamakage, A.; Yamakawa, Y.; Takenaka, K. Low Carrier Density Metal Realized in Candidate Line-Node Dirac Semimetals CaAgP and CaAgAs. J. Phys. Soc. Jpn. 2016, 85, 123701. [Google Scholar] [CrossRef] [Green Version]
  68. Yamakage, A.; Yamakawa, Y.; Tanaka, Y.; Okamoto, Y. Line-Node Dirac Semimetal and Topological Insulating Phase in Noncentrosymmetric Pnictides CaAgX (X = P, As). J. Phys. Soc. Jpn. 2016, 85, 013708. [Google Scholar] [CrossRef] [Green Version]
  69. Yang, T.Y.; Wan, Q.; Yan, D.Y.; Zhu, Z.; Wang, Z.W.; Peng, C.; Huang, Y.B.; Yu, R.; Hu, J.; Mao, Z.Q.; et al. Directional massless Dirac fermions in a layered van der Waals material with one-dimensional long-range order. Nat. Mater. 2019, 19, 27–33. [Google Scholar] [CrossRef] [Green Version]
  70. Tang, P.; Zhou, Q.; Xu, G.; Zhang, S.-C. Dirac fermions in an antiferromagnetic semimetal. Nat. Phys. 2016, 12, 1100–1104. [Google Scholar] [CrossRef] [Green Version]
  71. Lu, Y.; Zhou, D.; Chang, G.; Guan, S.; Chen, W.; Jiang, Y.; Jiang, J.; Wang, X.-s.; Yang, S.A.; Feng, Y.P.; et al. Multiple unpinned Dirac points in group-Va single-layers with phosphorene structure. Npj Comput. Mater. 2016, 2, 16011. [Google Scholar] [CrossRef]
  72. Du, Y.; Tang, F.; Wang, D.; Sheng, L.; Kan, E.-j.; Duan, C.-G.; Savrasov, S.Y.; Wan, X. CaTe: A new topological node-line and Dirac semimetal. Npj Quantum Mater. 2017, 2, 3. [Google Scholar] [CrossRef] [Green Version]
  73. Kumar, N.; Yao, M.; Nayak, J.; Vergniory, M.G.; Bannies, J.; Wang, Z.; Schroeter, N.B.M.; Strocov, V.N.; Muechler, L.; Shi, W.; et al. Signatures of Sixfold Degenerate Exotic Fermions in a Superconducting Metal PdSb2. Adv. Mater. 2020, 32, e1906046. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  74. Chapai, R.; Jia, Y.; Shelton, W.A.; Nepal, R.; Saghayezhian, M.; DiTusa, J.F.; Plummer, E.W.; Jin, C.; Jin, R. Fermions and bosons in nonsymmorphic PdSb2 with sixfold degeneracy. Phys. Rev. B 2019, 99, 161110. [Google Scholar] [CrossRef] [Green Version]
  75. Jin, L.; Liu, Y.; Zhang, X.; Dai, X.; Liu, G. Sixfold, fourfold, and threefold excitations in the rare-earth metal carbide R2C3. Phys. Rev. B 2021, 104, 045111. [Google Scholar] [CrossRef]
  76. Sun, Z.P.; Hua, C.Q.; Liu, X.L.; Liu, Z.T.; Ye, M.; Qiao, S.; Liu, Z.H.; Liu, J.S.; Guo, Y.F.; Lu, Y.H.; et al. Direct observation of sixfold exotic fermions in the pyrite-structured topological semimetal PdSb2. Phys. Rev. B 2020, 101, 155114. [Google Scholar] [CrossRef] [Green Version]
  77. Zhong, M.; Liu, Y.; Zhou, F.; Kuang, M.; Yang, T.; Wang, X.; Zhang, G. Coexistence of phononic sixfold, fourfold, and threefold excitations in the ternary antimonide Zr3Ni3Sb4. Phys. Rev. B 2021, 104, 085118. [Google Scholar] [CrossRef]
  78. Nie, S.; Bernevig, B.A.; Wang, Z. Sixfold excitations in electrides. Phys. Rev. Res. 2021, 3, L012028. [Google Scholar] [CrossRef]
  79. Huang, H.; Jin, K.-H.; Liu, F. Black-hole horizon in the Dirac semimetal Zn2In2S5. Phys. Rev. B 2018, 98, 121110. [Google Scholar] [CrossRef] [Green Version]
  80. Chang, T.-R.; Pletikosic, I.; Kong, T.; Bian, G.; Huang, A.; Denlinger, J.; Kushwaha, S.K.; Sinkovic, B.; Jeng, H.-T.; Valla, T.; et al. Realization of a Type-II Nodal-Line Semimetal in Mg3Bi2. Adv. Sci. 2019, 6, 1800897. [Google Scholar] [CrossRef] [Green Version]
  81. Zhang, X.; Jin, L.; Dai, X.; Liu, G. Highly anisotropic type-II nodal line state in pure titanium metal. Appl. Phys. Lett. 2018, 112, 122403. [Google Scholar] [CrossRef]
  82. Zhang, X.; Jin, L.; Dai, X.; Liu, G. Topological Type-II Nodal Line Semimetal and Dirac Semimetal State in Stable Kagome Compound Mg3Bi2. J. Phys. Chem. Lett. 2017, 8, 4814–4819. [Google Scholar] [CrossRef] [PubMed]
  83. Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  84. Li, P.; Wen, Y.; He, X.; Zhang, Q.; Xia, C.; Yu, Z.-M.; Yang, S.A.; Zhu, Z.; Alshareef, H.N.; Zhang, X.-X. Evidence for topological type-II Weyl semimetal WTe2. Nat. Commun. 2017, 8, 2150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  85. Li, S.; Yu, Z.-M.; Liu, Y.; Guan, S.; Wang, S.-S.; Zhang, X.; Yao, Y.; Yang, S.A. Type-II nodal loops: Theory and material realization. Phys. Rev. B 2017, 96, 081106. [Google Scholar] [CrossRef] [Green Version]
  86. Li, X.-P.; Deng, K.; Fu, B.; Li, Y.; Ma, D.-S.; Han, J.; Zhou, J.; Zhou, S.; Yao, Y. Type-III Weyl semimetals: (TaSe4)2I. Phys. Rev. B 2021, 103, L081402. [Google Scholar] [CrossRef]
  87. Zheng, B.; Xia, B.; Wang, R.; Chen, Z.; Zhao, J.; Zhao, Y.; Xu, H. Ideal type-III nodal-ring phonons. Phys. Rev. B 2020, 101, 100303. [Google Scholar] [CrossRef]
  88. Yang, T.; Cheng, Z.; Wang, X.; Wang, X.-L. Nodal ring spin gapless semiconductor: New member of spintronic materials. J. Adv. Res. 2021, 28, 43–49. [Google Scholar] [CrossRef]
  89. Yang, T.; Ding, G.; Cheng, Z.; Wang, X.; Zhang, G. Diverse topological states in a ternary NdAsPd compound. J. Mater. Chem. C 2020, 8, 7741–7748. [Google Scholar] [CrossRef]
  90. Yang, T.; Ding, S.; Liu, Y.; Wu, Z.; Zhang, G. An ideal Weyl nodal ring with a large drumhead surface state in the orthorhombic compound TiS2. Phys. Chem. Chem. Phys. 2022, 24, 8208–8216. [Google Scholar] [CrossRef]
  91. Yang, T.; Jin, L.; Liu, Y.; Zhang, X.; Wang, X. Spin-polarized type-II nodal loop and nodal surface states in hexagonal compounds XTiO2 (X = Li, Na, K, Rb). Phys. Rev. B 2021, 103, 235140. [Google Scholar] [CrossRef]
  92. Yang, T.; Liu, Y.; Wu, Z.; Wang, X.; Zhang, G. Coexistence of different dimensional topological states in stable ternary compound PrSbPt. Mater. Today Phys. 2021, 18, 100348. [Google Scholar] [CrossRef]
  93. Liu, Q.-B.; Fu, H.-H.; Wu, R. Topological phononic nodal hexahedron net and nodal links in the high-pressure phase of the semiconductor CuCl. Phys. Rev. B 2021, 104, 045409. [Google Scholar] [CrossRef]
  94. Yan, Z.; Bi, R.; Shen, H.; Lu, L.; Zhang, S.-C.; Wang, Z. Nodal-link semimetals. Phys. Rev. B 2017, 96, 041103. [Google Scholar] [CrossRef] [Green Version]
  95. Ahn, J.; Kim, D.; Kim, Y.; Yang, B.-J. Band Topology and Linking Structure of Nodal Line Semimetals with Z(2) Monopole Charges. Phys. Rev. Lett. 2018, 121, 106403. [Google Scholar] [CrossRef] [Green Version]
  96. Chang, G.; Xu, S.-Y.; Zhou, X.; Huang, S.-M.; Singh, B.; Wang, B.; Belopolski, I.; Yin, J.; Zhang, S.; Bansil, A.; et al. Topological Hopf and Chain Link Semimetal States and Their Application to Co2MnGa. Phys. Rev. Lett. 2017, 119, 156401. [Google Scholar] [CrossRef] [Green Version]
  97. Shao, D.-F.; Zhang, S.-H.; Dang, X.; Tsymbal, E.Y. Tunable two-dimensional Dirac nodal nets. Phys. Rev. B 2018, 98, 161104. [Google Scholar] [CrossRef] [Green Version]
  98. Zhang, H.; Zhang, X.; He, T.; Dai, X.; Liu, Y.; Liu, G.; Wang, L.; Zhang, Y. Three-dimensional Weyl hourglass networks in the nonsymmorphic half-metal Mg2VO4. Phys. Rev. B 2020, 102, 155116. [Google Scholar] [CrossRef]
  99. Wang, J.; Yuan, H.; Yu, Z.-M.; Zhang, Z.; Wang, X. Coexistence of symmetry-enforced phononic Dirac nodal-line net and three-nodal surfaces phonons in solid-state materials: Theory and materials realization. Phys. Rev. Mater. 2021, 5, 124203. [Google Scholar] [CrossRef]
  100. Chen, C.; Su, Z.; Zhang, X.; Chen, Z.; Sheng, X.-L. From Multiple Nodal Chain to Dirac/Weyl Semimetal and Topological Insulator in Ternary Hexagonal Materials. J. Phys. Chem. C 2017, 121, 28587–28593. [Google Scholar] [CrossRef] [Green Version]
  101. Yu, R.; Wu, Q.; Fang, Z.; Weng, H. From Nodal Chain Semimetal to Weyl Semimetal in HfC. Phys. Rev. Lett. 2017, 119, 036401. [Google Scholar] [CrossRef] [PubMed]
  102. Gao, Y.; Xie, Y.; Chen, Y.; Gu, J.; Chen, Z. Spindle nodal chain in three-dimensional α′ boron. Phys. Chem. Chem. Phys. 2018, 20, 23500–23506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  103. Yan, Q.; Liu, R.; Yan, Z.; Liu, B.; Chen, H.; Wang, Z.; Lu, L. Experimental discovery of nodal chains. Nat. Phys. 2018, 14, 461–464. [Google Scholar] [CrossRef] [Green Version]
  104. Yi, C.J.; Lv, B.Q.; Wu, Q.S.; Fu, B.B.; Gao, X.; Yang, M.; Peng, X.L.; Li, M.; Huang, Y.B.; Richard, P.; et al. Observation of a nodal chain with Dirac surface states in TiB2. Phys. Rev. B 2018, 97, 201107. [Google Scholar] [CrossRef] [Green Version]
  105. Bi, R.; Yan, Z.; Lu, L.; Wang, Z. Nodal-knot semimetals. Phys. Rev. B 2017, 96, 201305. [Google Scholar] [CrossRef] [Green Version]
  106. Sheng, X.-L.; Yu, Z.-M.; Yu, R.; Weng, H.; Yang, S.A. d Orbital Topological Insulator and Semimetal in the Antifluorite Cu2S Family: Contrasting Spin Helicities, Nodal Box, and Hybrid Surface States. J. Phys. Chem. Lett. 2017, 8, 3506–3511. [Google Scholar] [CrossRef] [Green Version]
  107. Zhou, F.; Chen, H.; Yu, Z.-M.; Zhang, Z.; Wang, X. Realistic cesium fluogermanate: An ideal platform to realize the topologically nodal-box and nodal-chain phonons. Phys. Rev. B 2021, 104, 214310. [Google Scholar]
  108. Wang, J.; Liu, Y.; Jin, K.-H.; Sui, X.; Zhang, L.; Duan, W.; Liu, F.; Huang, B. Pseudo Dirac nodal sphere semimetal. Phys. Rev. B 2018, 98, 201112. [Google Scholar] [CrossRef] [Green Version]
  109. Wang, M.; Wang, Y.; Yang, Z.; Fan, J.; Zheng, B.; Wang, R.; Wu, X. Symmetry-enforced nodal cage phonons in Th2BC2. Phys. Rev. B 2022, 105, 174309. [Google Scholar] [CrossRef]
  110. Ding, G.; Sun, T.; Wang, X. Ideal nodal-net, nodal-chain, and nodal-cage phonons in some realistic materials. Phys. Chem. Chem. Phys. 2022, 24, 11175–11182. [Google Scholar] [CrossRef]
  111. Zheng, B.; Zhan, F.; Wu, X.; Wang, R.; Fan, J. Hourglass phonons jointly protected by symmorphic and nonsymmorphic symmetries. Phys. Rev. B 2021, 104, L060301. [Google Scholar] [CrossRef]
  112. Liu, Y.; Xu, Y.; Duan, W. Berry phase and topological effects of phonons. Natl. Sci. Rev. 2018, 5, 314–316. [Google Scholar] [CrossRef]
  113. Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  114. Liu, Q.-B.; Qian, Y.; Fu, H.-H.; Wang, Z. Symmetry-enforced Weyl phonons. Npj Comput. Mater. 2020, 6, 95. [Google Scholar] [CrossRef]
  115. Süsstrunk, R.; Huber, S.D. Classification of topological phonons in linear mechanical metamaterials. Proc. Natl. Acad. Sci. USA 2016, 113, E4767–E4775. [Google Scholar] [CrossRef] [Green Version]
  116. Süsstrunk, R.; Huber, S.D. Observation of phononic helical edge states in a mechanical topological insulator. Science 2015, 349, 47–50. [Google Scholar] [CrossRef] [Green Version]
  117. Peng, B.; Hu, Y.; Murakami, S.; Zhang, T.; Monserrat, B. Topological phonons in oxide perovskites controlled by light. Sci. Adv. 2020, 6, eabd1618. [Google Scholar] [CrossRef]
  118. Zhang, L.; Niu, Q. Chiral Phonons at High-Symmetry Points in Monolayer Hexagonal Lattices. Phys. Rev. Lett. 2015, 115, 115502. [Google Scholar] [CrossRef] [Green Version]
  119. Liu, Y.; Chen, X.; Xu, Y. Topological Phononics: From Fundamental Models to Real Materials. Adv. Funct. Mater. 2020, 30, 1904784. [Google Scholar] [CrossRef]
  120. Wang, J.; Yuan, H.; Liu, Y.; Zhou, F.; Wang, X.; Zhang, G. Hourglass Weyl and Dirac nodal line phonons, and drumhead-like and torus phonon surface states in orthorhombic-type KCuS. Phys. Chem. Chem. Phys. 2022, 24, 2752–2757. [Google Scholar] [CrossRef]
  121. Zhou, F.; Liu, Y.; Wang, J.; Kuang, M.; Yang, T.; Chen, H.; Wang, X.; Cheng, Z. Intersecting topological nodal ring and nodal wall states in superhard superconductor FeB4. Phys. Rev. Mater. 2021, 5, 074201. [Google Scholar] [CrossRef]
  122. Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
  123. Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques forab initiototal-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef] [Green Version]
  124. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  125. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  126. Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
  127. Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
  128. Giannozzi, P.; de Gironcoli, S.; Pavone, P.; Baroni, S. Ab initio calculation of phonon dispersions in semiconductors. Phys. Rev. B 1991, 43, 7231–7242. [Google Scholar] [CrossRef]
  129. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
  130. Wu, Q.; Zhang, S.; Song, H.-F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405–416. [Google Scholar] [CrossRef] [Green Version]
  131. Dong, Y.; DiSalvo, F.J. Synthesis and single crystal structures of ternary phosphides Li4SrP2 and AAeP (A = Li, Na; Ae = Sr, Ba). J. Solid State Chem. 2007, 180, 432–439. [Google Scholar] [CrossRef]
  132. Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band structure diagram paths based on crystallography. Comput. Mater. Sci. 2017, 128, 140–184. [Google Scholar] [CrossRef]
  133. Wang, J.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B Condens Matter 1995, 52, 12627–12635. [Google Scholar] [CrossRef] [PubMed]
  134. Yip, S.; Li, J.; Tang, M.J.; Wang, J.G. Mechanistic aspects and atomic-level consequences of elastic instabilities in homogeneous crystals. Mater. Sci. Eng. A 2001, 317, 236–240. [Google Scholar] [CrossRef]
Crystals 12 01478 g001 550
Figure 1. The unit cell (a) of the ternary phosphide compound BaLiP with the centrosymmetric hexagonal structure with space group P63/mmc, No. 194. The spheres of various colors represent different atoms, as denoted by the text labels. Their bonding configurations form multiple polyhdera as displayed by the color shaded areas, in which the Ba atoms are allocated at the six corners and the Li and P atoms are alternately distributed at the central position. The corresponding bulk Brillouin zone (b) with the high symmetry points and paths, as highlighted by red color. The translucent gray color area stands for the (010) surface projection.
Figure 1. The unit cell (a) of the ternary phosphide compound BaLiP with the centrosymmetric hexagonal structure with space group P63/mmc, No. 194. The spheres of various colors represent different atoms, as denoted by the text labels. Their bonding configurations form multiple polyhdera as displayed by the color shaded areas, in which the Ba atoms are allocated at the six corners and the Li and P atoms are alternately distributed at the central position. The corresponding bulk Brillouin zone (b) with the high symmetry points and paths, as highlighted by red color. The translucent gray color area stands for the (010) surface projection.
Crystals 12 01478 g001
Crystals 12 01478 g002 550
Figure 2. The calculated phononic spectrum of the ternary phosphide compound BaLiP along high symmetry paths. The bottom panel corresponds to the local enlargement of the two band distributions at the frequency range from 8.2 to 9.2 THz. The color shaded areas along A-L-H-A and H-K highlight the doubly degenerate convergence between these two bands. The band crossing at K point is indicated by the arrow.
Figure 2. The calculated phononic spectrum of the ternary phosphide compound BaLiP along high symmetry paths. The bottom panel corresponds to the local enlargement of the two band distributions at the frequency range from 8.2 to 9.2 THz. The color shaded areas along A-L-H-A and H-K highlight the doubly degenerate convergence between these two bands. The band crossing at K point is indicated by the arrow.
Crystals 12 01478 g002
Crystals 12 01478 g003 550
Figure 3. The three-dimensional phononic dispersion surface of the two bands in the middle part for the ternary phosphide compound BaLiP in the kx = 0 plane. The band crossing points at the rectangular border are highlighted with green and purple dots and the coordinate system is shown on the bottom.
Figure 3. The three-dimensional phononic dispersion surface of the two bands in the middle part for the ternary phosphide compound BaLiP in the kx = 0 plane. The band crossing points at the rectangular border are highlighted with green and purple dots and the coordinate system is shown on the bottom.
Crystals 12 01478 g003
Crystals 12 01478 g004 550
Figure 4. The precise band dispersion scan along various path segments within the kx = 0 plane. The spatial distribution of these path segments can be referred to the bottom local coordinate system in Figure 3. The overlapping points between the two bands are highlighted by the color dots and their frequency variation range can be seen by the connected line curve.
Figure 4. The precise band dispersion scan along various path segments within the kx = 0 plane. The spatial distribution of these path segments can be referred to the bottom local coordinate system in Figure 3. The overlapping points between the two bands are highlighted by the color dots and their frequency variation range can be seen by the connected line curve.
Crystals 12 01478 g004
Crystals 12 01478 g005 550
Figure 5. The calculated surface spectrum along the (010) surface for the top (a) and bottom (b) terminations, respectively. The drumhead surface states are indicated by the red arrows.
Figure 5. The calculated surface spectrum along the (010) surface for the top (a) and bottom (b) terminations, respectively. The drumhead surface states are indicated by the red arrows.
Crystals 12 01478 g005
Crystals 12 01478 g006 550
Figure 6. The calculated spatial dependent mechanical properties for the ternary phosphide BaLiP, including Young’s modulus, Shear modulus and Poisson’s ratio. All units are in GPa, except no unit for the Poisson’s ratio.
Figure 6. The calculated spatial dependent mechanical properties for the ternary phosphide BaLiP, including Young’s modulus, Shear modulus and Poisson’s ratio. All units are in GPa, except no unit for the Poisson’s ratio.
Crystals 12 01478 g006
Table
Table 1. The calculated various elastic constants (Cij), Young’s modulus E, shear modulus G and Poisson’s ratio ν for the ternary phosphide BaLiP. All units are in GPa, except no unit for the Poisson’s ratio.
Table 1. The calculated various elastic constants (Cij), Young’s modulus E, shear modulus G and Poisson’s ratio ν for the ternary phosphide BaLiP. All units are in GPa, except no unit for the Poisson’s ratio.
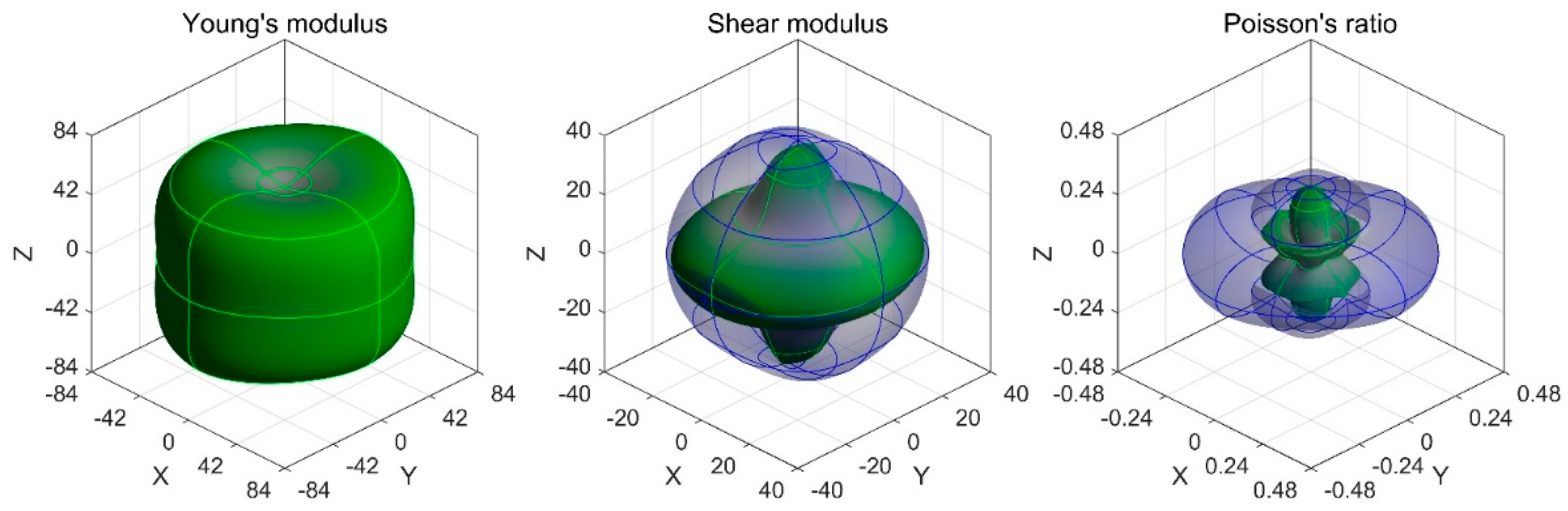
C11C12C13C33C44EGυ
99.8522.8833.1065.3038.48879.8032.520.227
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Cui, H.; Chen, Y.; Kang, Q.; Shan, P.; Yang, T.; Wang, P. Coincident Nodal Line and Nodal Surface Phonon States in Ternary Phosphide Compound BaLiP. Crystals 2022, 12, 1478. https://doi.org/10.3390/cryst12101478

AMA Style

Cui H, Chen Y, Kang Q, Shan P, Yang T, Wang P. Coincident Nodal Line and Nodal Surface Phonon States in Ternary Phosphide Compound BaLiP. Crystals. 2022; 12(10):1478. https://doi.org/10.3390/cryst12101478

Chicago/Turabian Style

Cui, Hong, Yunjian Chen, Qin Kang, Pengyue Shan, Tie Yang, and Peng Wang. 2022. "Coincident Nodal Line and Nodal Surface Phonon States in Ternary Phosphide Compound BaLiP" Crystals 12, no. 10: 1478. https://doi.org/10.3390/cryst12101478

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop