Next Article in Journal
Spin-Polarized Study of the Structural, Optoelectronic, and Thermoelectric Properties of the Melilite-Type Gd2Be2GeO7 Compound
Previous Article in Journal
A New Insight into the Role of Silicate-Type Binders on the Crushing Strength of Alumina Foams
Previous Article in Special Issue
Hematite Exsolutions in Corundum from Cenozoic Basalts in Changle, Shandong Province, China: Crystallographic Orientation Relationships and Interface Characters
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 10
10.3390/cryst12101396
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A TEM Study on a Polycrystalline Olivine Sample Deformed in a D-DIA under Mantle Conditions

by
Tao Chen
1,2,*,
Nadege Hilairet
3,† and
Yanbin Wang
3
1
Institute of Gemology, China University of Geosciences, Wuhan 430074, China
2
State Key Laboratory of Geological Processes and Mining Resources, China University of Geosciences, Wuhan 430200, China
3
Center for Advanced Radiation Sources, The University of Chicago, Chicago, IL 60637, USA
*
Author to whom correspondence should be addressed.
†
Current affiliation: UMR 8207-UMET-Unité Matériaux et Transformations, Centrale Lille, INRAE, CNRS, University Lille, F-59000 Lille, France.
Crystals 2022, 12(10), 1396; https://doi.org/10.3390/cryst12101396
Submission received: 30 August 2022 / Revised: 26 September 2022 / Accepted: 27 September 2022 / Published: 2 October 2022
(This article belongs to the Special Issue Dislocation in Minerals)
Browse Figures
Versions Notes

Abstract

We carried out an electron microscopy study on a polycrystalline olivine sample that was deformed with multiple deformation cycles under controlled differential stresses and strain rates at high pressures and high temperatures. Low-angle backscattered electron images thereof showed randomly oriented grains. Most of the grains were about 10–20 μm wide. The grains were irregular with wavy grain boundaries, indicating high grain boundary mobility during deformation. Transmission electron microscopy (TEM) images showed complex dislocation microstructure characteristics of high temperature, high pressure, and high strain. Free dislocations were predominantly either short and straight screw dislocations or curved dislocations with mixed screw and edge characters. Many of them split into partial dislocations. The differential stress estimated with the free dislocations was ~780 MPa, which was close to the value of differential stress attained in the final deformation cycle. We also observed dense dislocation tangles, which formed dislocation cell substructures under high strain. The existence of dislocation loops and jogs indicated significant climbing activity, providing evidence for high-temperature creep as the dominant deformation mechanism. All of the dislocations observed in this study were exclusively with a [001] Burgers vector. Dislocations with a [100] Burgers vector were absent, suggesting that the activity of the a-slip (i.e., (010)[100] and (001)[100] slip systems) was completely suppressed. These observations support a conclusion that was reported based on an X-ray texture analysis, which considered that a high pressure promotes the activities of the c-slip (i.e., (010)[001] and (100)[001] slip systems). It appears that the transition from the a-slip to the c-slip was complete with multiple deformation cycles at a relatively lower pressure of 5.1 GPa than previously thought, corresponding to a depth of 165 km in the mantle.

1. Introduction

Knowledge of the rheological properties of mantle materials is critical for the understanding of the dynamic processes in the Earth’s interior. Olivine, (Mg,Fe)2SiO4, which is generally regarded as the most abundant mineral in the upper mantle, is expected to dominate the rheology and seismic anisotropy of this portion of the Earth. The constitutive flow laws of olivine under mantle conditions are especially important for constraining the strength and other mechanical properties of the upper mantle [1].
The dislocation microstructures in natural olivine have been examined extensively to understand the deformation processes that are operative in the upper mantle [2,3,4,5]. However, because of the complex deformation processes of the evolving mantle, dislocation microstructures produced in early tectonic history may have been subjected to various degrees of post-tectonic modifications [6]. Many natural olivine samples in peridotites, for example, were found to possess superimposed microstructures due to complex deformation events in geological history [5,7,8,9,10], making the interpretation of the microstructures difficult.
Laboratory studies on the high-temperature creep behavior of olivine are fundamental for understanding and realistically modeling various tectonic processes [1]. Dislocation microstructures produced in laboratory deformation experiments have been used for comparisons with those produced in nature in order to help determine whether the same rate-controlling creep mechanisms also operate in natural environments [6]. Recently, a growing number of controlled deformation studies have been carried out on olivine using an apparatus known as the deformation DIA (D-DIA) [11,12,13,14,15,16]. There were some studies with the D-DIA that showed the transition from (010)[100] and (001)[100] slip systems (hereafter referred to as a-slip) at low pressures to (010)[001] and (100)[001] slip systems (hereafter referred to as c-slip) at high pressures [17,18,19,20,21,22]. A series of deformation experiments were conducted under mantle conditions (2.8–7.8 GPa, 1153–1670 K), and it was shown that the activity of a-slip began to decrease as early as 4 GPa, with a transition to c-slip occurring gradually over the entire investigated pressure range [23].
Transmission electron microscopy (TEM) is a powerful technique for directly observing and studying dislocation microstructures and slip systems that have been activated by an applied stress [24,25,26]. In recent years, the focused ion beam (FIB) technique has made it possible to prepare thin foils for TEM from precious (and often small) high-pressure and high-temperature (HP-HT) samples. This technique can damage the precious samples in a minimal area and preserve them in a maximal range relative to the former methods of TEM sample preparation. In this paper, we report the results of TEM on a nominally dry polycrystalline olivine sample that was deformed in an experimental study [23]. The deformation microstructures of the recovered specimen were characterized through scanning electron microscopy (SEM) and TEM. These new, direct microstructure data allow us to evaluate the proposed deformation mechanisms based on an X-ray texture analysis [23].

2. Sample Description and Experimental Details

A series of deformation experiments using the deformation DIA (D-DIA) were conducted at high pressures and high temperatures with final axial strains on hot-pressed samples from powders of San Carlos olivine [23]. All samples were shortened and lengthened in multiple deformation cycles. At the end of each cycle, the sample’s axial strain was carefully adjusted to be in a lengthened state in order to shorten (elongate) the sample along the vertical axis. This allowed a clear definition of the zero-differential-stress state for the following stress–strain curve. In this study, a recovered samples (D0966) was examined, and it underwent three deformation cycles (Table 1). This sample underwent the maximum changes in pressure (from 2.81 to 5.09 GPa) and a higher temperature (from 1458 to 1671 K) [23]. Therefore, it was the best choice to study the deformation of olivine under mantle conditions by using the D-DIA samples of Hilairet et al.. The microstructures were examined through SEM with a Hitachi S-4700-II SEM after coating with gold at an accelerating voltage of 10 kV at Nanoscale Materials, Argonne National Laboratory (CNM/ANL), Illinois, USA. The SEM images were taken using low-angle backscattered electrons. The sample was polished and prepared for a TEM study (Figure 1) with an FIB at the Electron Microscope Laboratory of the School of Physics, Peking University, Beijing, China. A thin foil (about 5 by 12 microns in area and <150 nanometers in thickness) was placed on a carbon-coated copper grid and loaded into a sample holder. The TEM experiments were carried out using a Philips-CM12 microscope operated at 120 kV at the State Key Laboratory of Geological Processes and Mining Resources, China University of Geosciences (Wuhan), Wuhan, China, and an FEI Tecnai F20 microscope operated at 200 kV at CNM/ANL.

3. Results

3.1. Morphology of the Recrystallized Olivine Grains

The reported sample underwent significant grain growth above 1600 K, from about 5 μm (the starting particle size of the powder) to about 10–20 μm (the particle size of D0966, Figure 2a) [23]. The variation in grain size appeared to be reproducible under X-ray diffraction when the critical temperature (1600 K) was crossed (regardless of the crossing direction). It was observed that the patterns collected below 1600 K all showed smooth and continuous diffraction rings, indicating much smaller grain sizes and a more or less random grain orientation. However, the diffraction patterns collected above 1600 K were spotty, and the diffraction spots changed locations in the detected area on a time scale of minutes, suggesting dynamic grain growth. It is important to note that the sample studied here underwent deformation cycles at progressively higher temperatures (Table 1); as discussed, the process was terminated after significant recrystallization [23].
The low-angle backscattered electron images obtained from SEM could show the orientation contrast. The different gray contrasts shown in Figure 2 indicate that the orientation of the olivine grains was random. Most of the grains were uniform at about 10–20 μm wide, as shown in Figure 2a. Occasionally, there were some very small grains inside the bigger grains, which were smaller than 1 μm and showed different orientations relative to the surrounding grains, as shown in Figure 2b. The very small particles observed on the surface in Figure 2b were gold particles that were introduced by coating. Most of the olive grains were irregular in shape with wavy grain boundaries. Microfractures or microcracks were observed at some grain boundaries, indicating brittle deformation that was most likely produced upon the release of pressure/stress at the end of the experiment. The shapes of the boundaries indicated the strong influence of grain growth during deformation, lending support for dynamic recrystallization. “Dynamic recrystallization” here is not to be taken as meaning recrystallization due to grain size reduction during deformation, but rather as a result of enhanced dynamic growth and grain boundary migration during deformation.

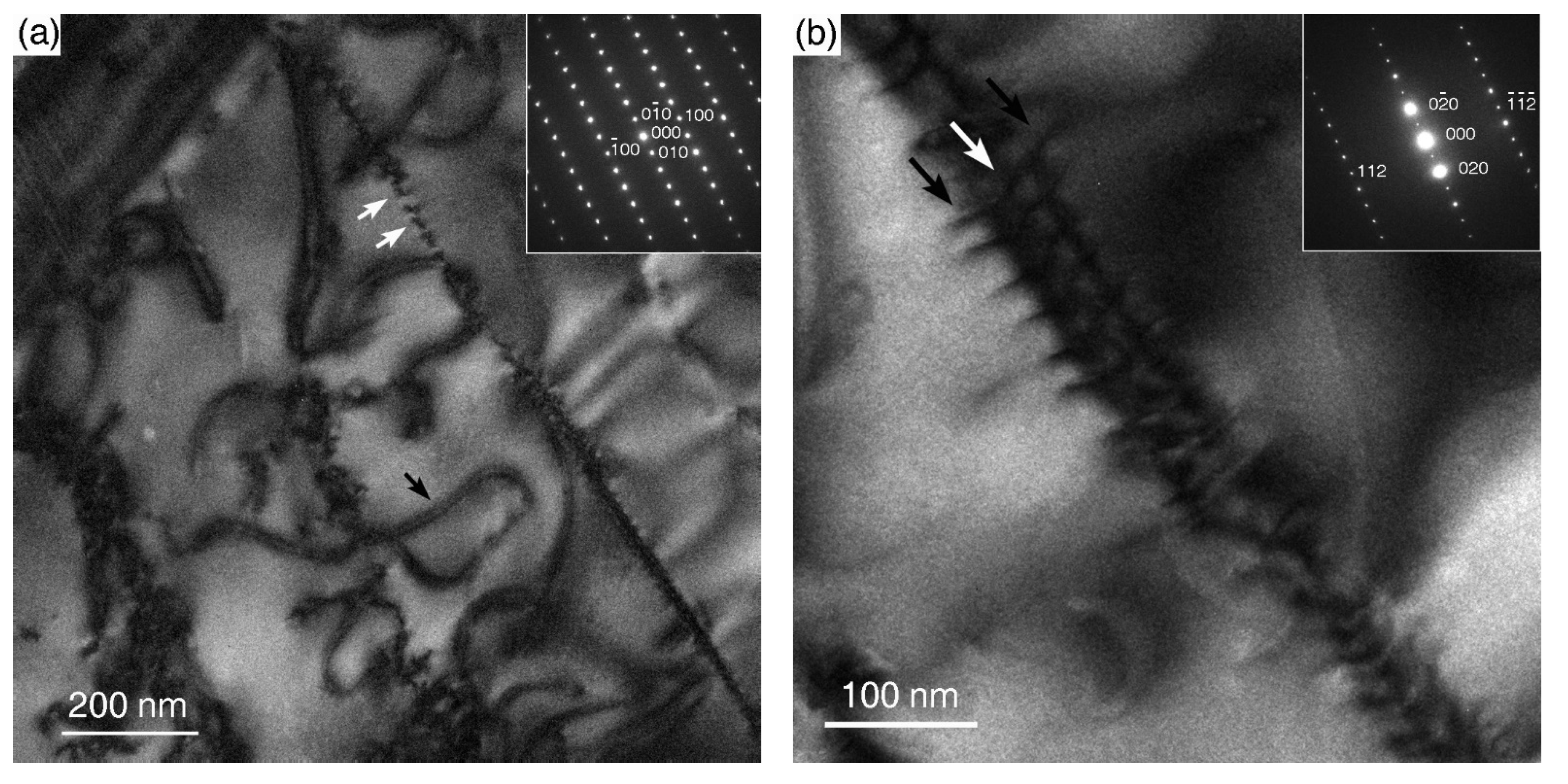
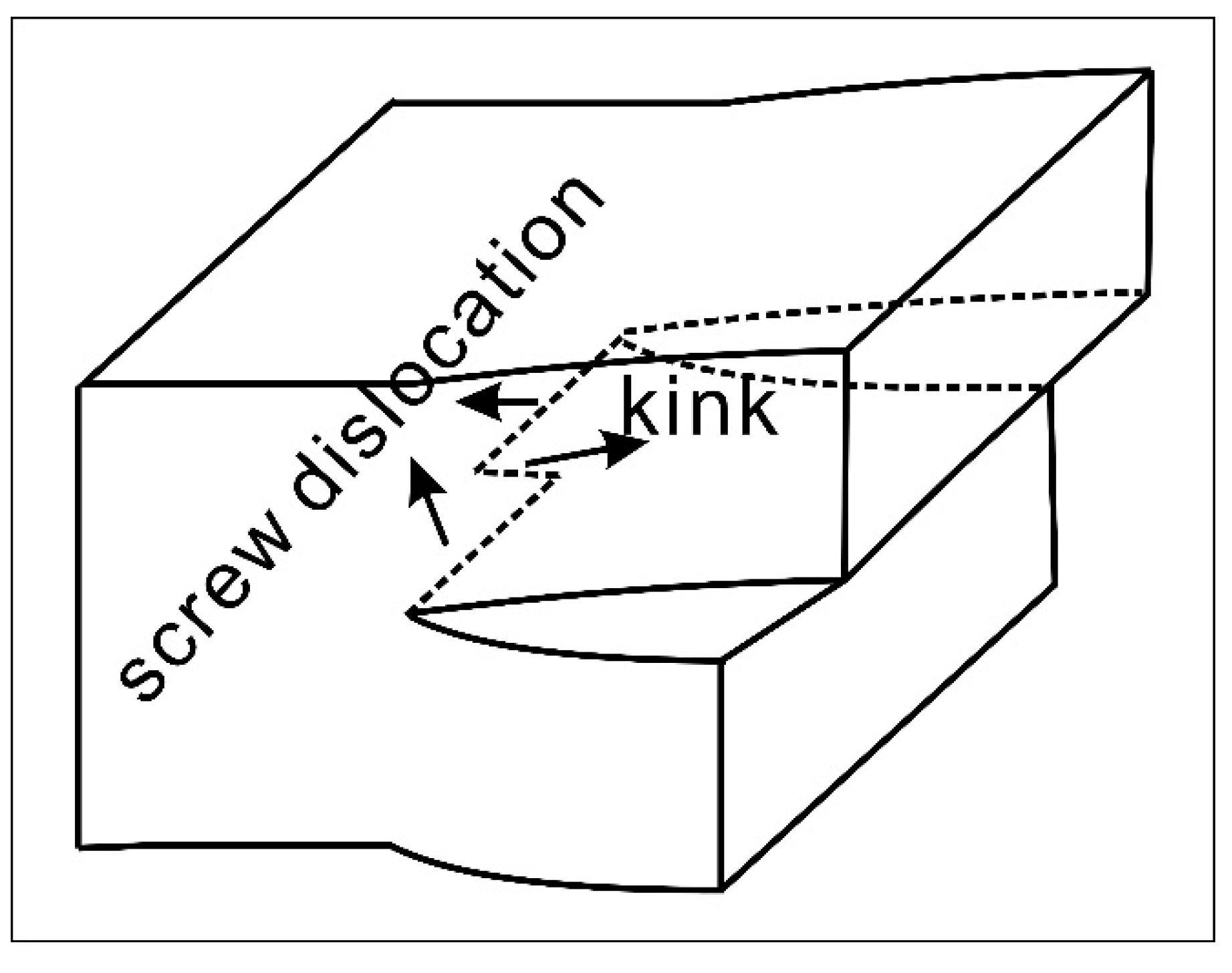
3.2. Dislocation Microstructure and Slip System

In the deformed sample, the polycrystalline olivine grains were considered to undergo consistent differential stress and strain rates in the deformation cycle, though it was difficult for the sample to undergo the same differential stress throughout. Our TEM sample prepared with the FIB was used try to contain the maximum number of grains in one foil in order to represent the intra- and intergranular deformation in the deformed D-DIA sample. In this study, the TEM foil contained three olivine grain fragments.
Figure 3a–f show dislocations in the middle grain of the foil. Short, straight dislocations were dominant. Because the D0966 sample underwent multiple deformation cycles, the “field” of its TEM image was not purely bright or dark in the bright-field (BF) or dark-field (DF) image (e.g., Figure 3a,b). The “dashed-line” appearance of the short screws was also consistent with the line segments of the inclined dislocation relative to the foil, as shown in Figure 3a. All of the dislocations in this area were simultaneously out of contrast under two-beam conditions with g = 0–20 (shown in Figure 3b) and g = 1–10, indicating that [001] was the unique Burgers vector. Here, g represents the two-beam condition in which the DF TEM images were taken. The short, straight dislocation lines were perpendicular to g1-10, g010, g100, and g120, indicating that the linear direction of these dislocations was [001]. Therefore, these were screw dislocations, and the slip system was consistent with (hk0)[001] according to the TEM analyses. We could not uniquely determine the slip plane. According to the crystallographic structure of olivine, the most possible and energetically favored slip planes are (010) and (100) [27]. Based on the texture and elasto-plastic self-consistent (EPSC) analyses [23], the dominant slip system in this sample was (010)[001] (i.e., c-slip). Therefore, we assumed that the slip planes were (010) for these [001] screw dislocations, while noting that evidence of [001] dislocations gliding on the (010) plane was also found [17].
A pair of long and curved dislocations are presented in Figure 3a. The direction of the straight dislocation segment (indicated by the broken black arrow) was [10-1] (u = g111 × g101); thus, the segment had mixed screw and edge characters. The solid black arrow in Figure 3a indicates an intermediate jog at the end of the dipole trail. The jog is almost out of contrast in this figure. A jog is a short edge element of a dislocation that links two slip planes, like a step. Jogs have the same Burgers vector as the dislocation line on which they lie [28]. The dipole trail of the pair of the dislocations was pinned by the jog, which could be observed in the dark-field image with g22-2 taken with two weak beams (Figure 3c black arrow), resulting in a sessile configuration in which the two dislocations could not glide freely. The curved portions indicate increased mobility due to climbing activity at high temperatures [28]. Many curved free dislocations with mixed screw and edge characters can be observed in Figure 3d,e. Some small loops also existed in this grain. Figure 3a shows a small prismatic loop formed by the movement of the dislocation dipole (indicated by white arrow), and Figure 3e shows some dislocation loops that formed from the vacancy (indicated by black arrows). Dislocation walls of twist boundaries composed of arrays of [001] screw dislocations are shown in Figure 3f.
Figure 4a,b show the dislocation structure of another grain. The dislocations were simultaneously out of contrast with g200 and g020, indicating again that [001] was the unique Burgers vector. Figure 4a is a bright-field image with [001] incidence. A line of end-on screw dislocations can be observed in Figure 4a (such as those indicated by the white arrows). This dislocation wall was perpendicular to g100, indicating that its slip system was (100)[001]. The screw dislocation wall was likely an original sub-grain boundary in San Carlos olivine because the sub-grains that are elongated parallel to (100) are frequently reported to exist in natural olivine samples [5,8]. Figure 4b is a bright-field image that shows this dislocation wall in another incident direction [20-1]. In this figure, all of the dislocation lines in the array were folded, indicating the formation of dislocation kinks. Figure 5 is a schematic representation of the formation mechanism of a kink. A kink is also a short element of dislocation with the same Burgers vector as the line on which it lies. However, unlike jogs, a kink is a step in the same slip plane [28]. Commonly, kinks represent a deformation mode found in crystals with few slip planes. When the compression axis is nearly parallel to the slip plane, the slip plane will bend and form sharp kink band boundaries [27]. Figure 4b shows a kink band (marked by the white arrow) in an array of screw dislocations (marked by the black arrows). These kinks are within the same slip plane (100) as the screw dislocations, and, when viewed edge-on, they appear as very short lines in Figure 4a (white arrows).
Another interesting phenomenon is that many dislocation lines are split into partial dislocations. There were two kinds of partial dislocations observed in this study. One kind was straight [001] screw dislocations that were split into partial dislocations with stacking faults, as shown in Figure 3e by the white arrows. The separations between the partials ranged from 10 to 15 nm. The other kind was dissociated curved mixed dislocations, as shown in Figure 3a (e.g., that indicated by the broken arrow), Figure 3d (e.g., those indicated by the black arrows), and Figure 4a (e.g., the black arrow). The separations of the curved partial dislocations varied from 10 to 25 nm.
Figure 6a–c are BF images that were observed with [-2-12] incidence. Figure 6a shows a small olivine grain with approximately 2 μm of its length within a larger grain. There was a micro-crack between the two grains (indicated by the white arrow). The dislocation density was very high in this small grain, and the distribution of dislocations was much more heterogeneous. Figure 6b,6c show enlarged areas of the small olivine grain shown in Figure 6a. As shown in Figure 6b, free dislocations were rare in the smaller grain, while tangles of dislocations were dominant. Figure 6c shows a nearly rectangular cell substructure. Dense tangles of dislocations were observed, and they were arranged around cells. Free dislocations were much less frequent in the cells.
The differential stresses generated in a large-volume, high-pressure apparatus can be estimated from the density of free dislocations [29]. Differential stress (σ1 − σ3) is a function of the density of dislocations for olivine single crystal [29]:
(σ1 −σ3) = αμbρ·1/2,
where α is an empirical constant (assumed to be 3 here), μ is the shear modulus of San Carlos olivine, and b is the magnitude of the Burgers vector of mobile dislocations. In Equation (1), μ is calculated to be 68 GPa under the P-T condition of the third deformation cycle by using the ambient shear modulus μ0 (77 GPa), (αμ/αρ)T (1.6), and (αμ/αT)ρ (−0.013 GPa/K) [30,31]. Figure 3 shows the same area observed along different incident directions. So, all of the free dislocations in this area could be observed. There were about 34 free dislocations in the area (1.1 × 10−8 cm2). Thus, the mean density of the free dislocations was measured to be about 3.1 × 109 cm−2, which corresponded to a differential stress of ~780 MPa according to (1). The stresses of the three cycles in the D0966 sample were 543, 445, and 897 MPa, respectively (Table 1) [23]. Considering uncertainties in the measurement of dislocation density (estimated to be 20–30%) and the semi-quantitative nature of Equation (1), this value is in broad agreement with the stress levels determined with X-rays in the third cycle [1].

4. Discussion and Conclusion

4.1. Evidence of High-Temperature Dislocation Creep

In materials deformed at high temperatures (above roughly 50% of the melting point), dislocation climbing is an important deformation mechanism. Jogs on screw dislocations provide the position for climbing to non-planar dislocation lines because climbing only exists in edge segments [27,28]. As shown in Figure 3a, the existence of an intermediate jog indicates climbing activities in high-temperature dislocation creep. Both vacancy loops and prismatic loops are also indications of high-temperature deformation. Vacancy loops are formed only at sufficiently high temperatures because of the restricted rates of elemental diffusion. Prismatic loops are formed from dislocation dipoles through dislocation climbing. Vacancy loops form only at sufficiently high temperatures because of the restricted rate of diffusion. If the temperature is sufficiently high to allow diffusion of the defects, they can collect together to form a dislocation loop [28]. Figure 3e shows some very small and individual loops, which are dislocation loops formed from a vacancy. The existence of these loops suggests the effects of high-temperature diffusion creep on the plastic deformation processes above ~1600 K.
Another dislocation microstructure that is characteristic of high-temperature flow is the existence of polygonized sub-grains: Dislocations rearrange themselves by climbing and, thus, producing walls with low angles among the different sub-grains [27]. Figure 3f shows that arrays of [001] screw dislocations produced twist boundaries and formed a sub-grain. In addition, because grain growth tends to wipe out dislocations as the crystal lattice re-organizes during grain growth, few free dislocations were present inside the sub-grain. These phenomena indicated that dynamic recrystallization and grain boundary migration mediated by diffusion were active in assisting the deformation process in our deformation experiments.

4.2. Activation of [001] Dislocations

The different activities of [100] and [001] dislocations were observed in natural olivine for the first time. The dislocation microstructures of olivine from lherzolites, spinel, or garnet peridotite xenoliths in varying geological environments have been studied through TEM. It was found that [001] screw dislocations were generated by high strain rates over a wide temperature range. Generally, [001] screws dominate in highly deformed olivines, while [100] dislocations are typically observed in weakly deformed olivines [2,3,5]. Thus, in earlier studies, the activities of [100] and [001] dislocations were considered to represent different deformation conditions [2,7,32].
In laboratory studies at P < 3 GPa, with high temperatures moderate differential stresses, and under dry conditions, it was found that the a-slip dominated the deformation microstructure [6,33]. Recent deformation experiments suggested that the c-slip is dominant at higher pressures. Although the transition from the a-slip to the c-slip was previously attributed to the presence of water in the deformation of olivine [34,35], it was pointed out that pressure alone can induce this transition in slip systems, and it was suggested that [001] glide would dominate at the lower most upper mantle according to the experimental conditions at 11 GPa [17]. This transition has been used to explain the variation of the anisotropy patterns of P and S waves with depth [1,36]. It was considered that the dominant activity of (hk0)[001] in olivine at high pressures indicates a weak anisotropy in the upper mantle below 300 km [1]. Pressure was considered to be the dominant reason for the transition from the a-slip to the c-slip as a result of a series of deformation experiments on a single olivine crystal [19,20,21,37]. The dual activity of [100](001) and [001](100) slips becomes comparable to that of the [100](010) slip at depths greater than ~65 km along a 20-Ma oceanic geotherm or ~155 km along a continental geotherm, and the (010)[001] slip becomes dominant over all other investigated slip systems at depths greater than ~240 km [37]. It was found that the contributions of the a-slip ((010)[100]) gradually decrease, while those of the c-slip ((010)[001]) increase; the transition in the slip system is not a sharp one, but is spread out over a considerable pressure range from about 3–4 GPa and up to 8 GPa [23]. Therefore, the evolution in the slip system was considered to affect the interpretation of seismic anisotropy data at depths between 120 and 300 km [23].
In our TEM study, the dislocations that we observed were exclusively with the [001] Burgers vector. Dislocations with [100] Burgers vector were, interestingly, absent. Thus, it appears that although the sample underwent deformation at low pressures in the early deformation cycles, the last high-pressure deformation cycle effectively shut down the activation of [100] dislocations. This study indicates that the activity of the a-slip was completely suppressed in the third deformation cycle (5.09 GPa and 1676 K), which is equivalent to a depth of 165 km in the upper mantle. This agrees well with the monochromatic synchrotron radiation analysis [23]. It suggests that the transition from the a-slip to c-slip can be completed at a relatively low pressure or a lower depth in the upper mantle than previously estimated [19,20,21,37]. However, the deformed sample underwent multiple deformation cycles, so the formed slip system may not only have relationship with pressure. Since both the stress levels and the strain rates in the experiments were vastly different from those in geodynamic processes, the application of this observation to the Earth’s mantle should be treated with caution.

4.3. Dissociated Dislocations in Deformed Olivine

We observed some evidence for dislocation splitting. Unfortunately, due to the small separation of the partial dislocations (about 10–25 nm), we were unable to fully characterize the dissociated dislocations. The partial separation of [001] dislocations with a distance of about 4 nm was first observed in single olivine crystals that were experimentally deformed at a temperature of 1723 K and a differential stress of 300 bars [38]. The dissociation of [001] dislocations has also been reported in natural olivines. Stacking faults were observed in the (100) plane [5]. The Burgers vector bp of the partial dislocations that bounded the stacking faults was parallel to [001], and the widths of the faults were about 100 nm. The splitting reaction of the [001] unit dislocations was involved with climbing dissociation on the (001) and {021} planes [39]. The partial dislocations were characterized by Burgers vectors that were approximately equal to 1/x<011>, and the separation between partials was reported to be as large as 230 nm under hydrous conditions. Calculations of dislocation cores and Peierls stresses were presented based on the Peierls–Nabarro model [40]. The model predicted dissociation in gliding [001] dislocations. It was found that [001] dislocations have comparable tendencies to spread into the three planes that contain the screw direction—(100), (110), and (110)—while [001] dislocations do not [40]. Grain boundary structures were considered to consist of arrays of partial edge dislocations with a Burgers vector of 1/2[001] that was associated with stacking faults through molecular dynamics simulations [41]. More relevant to this study is a work that reported widely dissociated dislocations when deformed for one hour at 11 GPa and 1673 K [17]. It was found that one of the stacking faults was parallel to (021) [17].
The unit dislocations exclusively had a [001] Burgers vector in our polycrystalline olivine sample. Figure 3e shows narrowly dissociated straight screw dislocations in nominally dry olivine, though the dissociation of the dislocations was suggested to be related to the hydration of olivine [39,42]. According to Hilairet et al. (2012), the D0966 sample showed a very broad increase in absorbance from 3025 to 3700 cm−1, which was mainly interpreted as a result of water at the grain boundaries [23]. The observation of straight screw [001] dislocations can be explained by the Peierls stress [40]. If dislocations have a dissociated core structure that is defined by a number of partial dislocations that are separated by planar defects, deformation processes, such as glide, are allowed when the fault plane lies in a glide plane [39]. Glide becomes possible when a large enough stress is applied—in conjunction with thermal agitation—to force the configuration of the core into a glissile splitting configuration on one plane [43]. In this study, the dislocations observed in Figure 3e were dissociated into Shockley partials, which should be connected by an intrinsic stacking fault [44]. We assumed that the slip planes were (010) for these [001] screw dislocations. Therefore, we consider that the stacking fault between the dissociated straight screw dislocations lies in the (010) plane, and the Burgers vector bp of the partial dislocation is parallel to [001].
In this study, Figure 3a,d, and Figure 5a show some dissociated curved mixed dislocations. The mechanism of dissociated curved mixed dislocations cannot be the same as that of dissociated screw dislocations. Mechanisms other than Peierls friction are required to explain the occurrence of mixed segments, but the occurrence of lattice friction of [001] dislocations is still possible with a non-planar core [40]. Because the geometrical structure of curved mixed dislocations in deformed olivine is still unclear, the mechanism of their dissociation needs further study.

5. Conclusions

High-temperature deformations, such as vacancy loops, prismatic loops, and polygonized sub-grains, were observed in the studied D-DIA sample; these formed because of high-temperature cycles. Tangles of dislocations were dominant in the very small grain, while free dislocations were dominant in the normal-sized grains (10–20 μm). The dislocations exclusively had a [001] Burgers vector, which was promoted by the high pressure and high strain rate has and might also have a relationship with the multiple deformation cycles.
This study also indicated that the slip system can be studied by using an X-ray texture analysis that is synchronized with D-DIA experiments or by using TEM on a recovered sample. These two methods can allow one to obtain a consistent conclusion concerning the slip system. However, TEM can provide direct and detailed observations of various dislocations and can be used to estimate differential stresses on the recovered sample.

Author Contributions

Conceptualization, Y.W. and N.H.; methodology and formal analysis, T.C.; resources, Y.W.; writing—original draft preparation, T.C.; writing—review and editing, Y.W. and N.H.; funding acquisition, T.C. and Y.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the NSF grant EAR-1361276 (to Y.W.), the National Natural Science Foundation of China (42072252, 41572033, 41172050), and the China Scholarship Council.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All supporting data and computational details are available on written request. These data are held by the main author of this article.

Acknowledgments

The authors thank Jun Xu for the help with the FIB experiments at the Electron Microscope Laboratory of the School of Physics, Peking University and the Geophysical Lab. The deformation projects were carried out at GSECARS at APS. The work performed at the Center for Nanoscale Materials using Hitachi SEM and Tecani STEM was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mainprice, D.; Tommasi, A.; Couvy, H.; Cordier, P.; Frost, D. Pressure Sensitivity of Olivine Slip Systems and Seismic Anisotropy of Earth’s Upper Mantle. Nature 2005, 433, 731–733. [Google Scholar] [CrossRef] [PubMed]
  2. Olsen, A.; Birkeland, T. Electron Microscope Study of Peridotite Xenoliths in Kimberlites. Contrib. Mineral. Petrol. 1973, 42, 147–157. [Google Scholar] [CrossRef]
  3. Toxopeus, J.B.; Boland, J. Several Types of Natural Deformation in Olivine, an Electron Microscope Study. Tectonophysics 1976, 32, 209–233. [Google Scholar] [CrossRef]
  4. Jin, Z.; Green, H.; Borch, R. Microstructures of Olivine and Stresses in the Upper Mantle Beneath Eastern China. Tectonophysics 1989, 169, 23–50. [Google Scholar] [CrossRef]
  5. Skrotzki, W.; Wedel, A.; Weber, K.; Muller, W. Microstructure and Texture in Lherzolites of the Balmuccia Massif and Their Significance Regarding the Thermomechanical History. Tectonophysics 1990, 179, 227–251. [Google Scholar] [CrossRef]
  6. Bai, Q.; Kohlstedt, D. High-temperature Creep of Olivine Single Crystals, 2. Dislocation Structures. Tectonophysics 1992, 206, 1–29. [Google Scholar] [CrossRef]
  7. Boland, J.N.; Toxopeus, J.M.A.B. Dislocation Deformation Mechanisms in Peridotite Xenoliths in Kimberlites. Contrib. Mineral. Petrol. 1977, 60, 17–30. [Google Scholar] [CrossRef]
  8. Matysiak, A.K.; Trepmann, C.A. Crystal-plastic Deformation and Recrystallization of Peridotite Controlled By the Seismic Cycle. Tectonophysics 2012, 530, 111–127. [Google Scholar] [CrossRef]
  9. Marquardt, K.; Faul, U.H. The Structure and Composition of Olivine Grain Boundaries: 40 Years of Studies, Status and Current Developments. Phys. Chem. Miner. 2018, 45, 139–172. [Google Scholar] [CrossRef]
  10. Ferreira, F.; Hansen, L.N.; Marquardt, K. The Effect of Grain Boundaries on Plastic Deformation of Olivine. J. Geophys. Res.-Solid Earth 2021, 126, e2020JB020273. [Google Scholar] [CrossRef]
  11. Wang, Y.; Rivers, M.; Sutton, S.; Eng, P.; Shen, G.; Getting, I. A Multi-anvil, High-pressure Facility for Synchrotron Radiation Research at Geosoilenvirocars at the Advanced Photon Source. Rev. High Press. Sci. Technol. 1998, 15, 1490–1495. [Google Scholar] [CrossRef]
  12. Wang, Y.; Durham, W.; Getting, I.; Weidner, D. The Deformation-dia: A New Apparatus for High Temperature Triaxial Deformation to Pressures Up to 15 Gpa. Rev. Sci. Instrum. 2003, 74, 3002–3011. [Google Scholar] [CrossRef]
  13. Bollinger, C.; Merkel, S.; Cordier, P.; Raterron, P. Deformation of Forsterite Polycrystals at Mantle Pressure: Comparison with Fe-bearing Olivine and the Effect of Iron on Its Plasticity. Phys. Earth Planet. Inter. 2015, 240, 95–104. [Google Scholar] [CrossRef]
  14. Kaboli, S.; Burnley, P.C.; Xia, G.; Green, I.H.W. Pressure Dependence of Creep in Forsterite Olivine: Comparison of Measurements From the D-dia and Griggs Apparatus. Geophys. Res. Lett. 2017, 44, 10–939. [Google Scholar] [CrossRef]
  15. Thieme, M.; Pozzi, G.; Demouchy, S.; De Paola, N.; Barou, F.; Koizumi, S.; Bowen, L. Shear Deformation of Nano- and Micro-crystalline Olivine at Seismic Slip Rates. Tectonophysics 2021, 802, 228736. [Google Scholar] [CrossRef]
  16. Bollinger, C.; Merkel, S.; Raterron, P. In Situ Quantitative Analysis of Stress and Texture Development in Forsterite Aggregates Deformed at 6 Gpa and 1373 K. J. Appl. Crystallogr. 2012, 45, 263–271. [Google Scholar] [CrossRef]
  17. Couvy, H.; Frost, D.; Heidelbach, F.; Nyilas, K.; Ungar, T.; Mackwell, S.; Cordier, P. Shear Deformation Experiments of Forsterite at 11gpa-1400 Degrees C in the Multianvil Apparatus. Eur. J. Mineral. 2004, 16, 877–889. [Google Scholar] [CrossRef]
  18. Durinck, J.; Legris, A.; Cordier, P. Pressure Sensitivity of Olivine Slip Systems: First-principle Calculations of Generalised Stacking Faults. Phys. Chem. Miner. 2005, 32, 646–654. [Google Scholar] [CrossRef]
  19. Raterron, P.; Chen, J.; Li, L.; Weidner, D.; Cordier, P. Pressure-induced Slip-system Transition in Forsterite: Single-crystal Rheological Properties at Mantle Pressure and Temperature. Am. Mineral. 2007, 92, 1436–1445. [Google Scholar] [CrossRef]
  20. Raterron, P.; Amiguet, E.; Chen, J.; Li, L.; Cordier, P. Experimental Deformation of Olivine Single Crystals at Mantle Pressures and Temperatures. Phys. Earth Planet. Inter. 2009, 172, 74–83. [Google Scholar] [CrossRef]
  21. Raterron, P.; Chen, J.; Geenen, T.; Girard, J. Pressure Effect on Forsterite Dislocation Slip Systems: Implications for Upper-mantle Lpo and Low Viscosity Zone. Phys. Earth Planet. Inter. 2011, 188, 26–36. [Google Scholar] [CrossRef]
  22. Ohuchi, T.; Kawazoe, T.; Nishihara, Y.; Nishiyama, N.; Irifune, T. High Pressure and Temperature Fabric Transitions in Olivine and Variations in Upper Mantle Seismic Anisotropy. Earth Planet. Sci. Lett. 2011, 304, 55–63. [Google Scholar] [CrossRef]
  23. Hilairet, N.; Wang, Y.; Sanehira, T.; Merkel, S.; Mei, S. Deformation of Olivine Under Mantle Conditions: An in Situ High-pressure, High-temperature Study Using Monochromatic Synchrotron Radiation. J. Geophys. Res.-Solid Earth 2012, 117, B01203. [Google Scholar] [CrossRef]
  24. Mussi, A.; Cordier, P.; Demouchy, S.; Vanmansart, C. Characterization of the Glide Planes of the [001] Screw Dislocations in Olivine Using Electron Tomography. Phys. Chem. Miner. 2014, 41, 537–545. [Google Scholar] [CrossRef]
  25. Mussi, A.; Cordier, P.; Demouchy, S.; Hue, B. Hardening Mechanisms in Olivine Single Crystal Deformed at 1090 Degrees C: An Electron Tomography Study. Philos. Mag. 2017, 97, 3172–3185. [Google Scholar] [CrossRef]
  26. Gerrits, R.; Wirth, R.; Schreiber, A.; Feldmann, I.; Knabe, N.; Schott, J.; Benning, L.G.; Gorbushina, A.A. High-resolution Imaging of Fungal Biofilm-induced Olivine Weathering. Chem. Geol. 2021, 559, 119902. [Google Scholar] [CrossRef]
  27. Nicolas, A.; Poirier, J.P. Crystalline Plasticity and Solid State Flow in Metamorphic Rocks; John Wiley & Sons Press: London, UK; New York, NY, USA, 1976; p. 444. [Google Scholar]
  28. Hull, D.; Bacon, D.J. Introduction to Dislocations, 4th ed.; Oxford Press: Oxford, UK, 2001; p. 249. [Google Scholar]
  29. Wang, Y.; Liebermann, R.C.; Boland, J.N. Olivine as an in Situ Piezometer in High Pressure Apparatus. Phys. Chem. Miner. 1988, 15, 493–497. [Google Scholar] [CrossRef]
  30. Zha, C.; Duffy, T.; Downs, R.; Mao, H.; Hemley, R. Brillouin Scattering and X-ray Diffraction of San Carlos Olivine: Direct Pressure Determination to 32 Gpa. Earth Planet. Sci. Lett. 1998, 159, 25–33. [Google Scholar] [CrossRef]
  31. Liu, W.; Kung, J.; Li, B. Elasticity of San Carlos Olivine to 8 Gpa and 1073 K. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
  32. Green, H.; Radcliffe, S. Dislocation Mechanisms in Olivine and Flow in the Upper Mantle. Earth Planet. Sci. Lett. 1972, 15, 239–247. [Google Scholar] [CrossRef]
  33. Jin, Z.; Bai, Q.; Kohlstedt, D. High-temperature Creep of Olivine Crystals From Four Localities. Phys. Earth Planet. Inter. 1994, 82, 55–64. [Google Scholar] [CrossRef]
  34. Jung, H.; Karato, S. Water-induced Fabric Transitions in Olivine. Science 2001, 293, 1460–1463. [Google Scholar] [CrossRef] [PubMed]
  35. Jung, H.; Katayama, I.; Jiang, Z.; Hiraga, T.; Karato, S. Effect of Water and Stress on the Lattice-preferred Orientation of Olivine. Tectonophysics 2006, 421, 1–22. [Google Scholar] [CrossRef]
  36. Jung, H.; Mo, W.; Green, H.W. Upper Mantle Seismic Anisotropy Resulting From Pressure-induced Slip Transition in Olivine. Nat. Geosci. 2009, 2, 73–77. [Google Scholar] [CrossRef]
  37. Raterron, P.; Girard, J.; Chen, J. Activities of Olivine Slip Systems in the Upper Mantle. Phys. Earth Planet. Inter. 2012, 200, 105–112. [Google Scholar] [CrossRef]
  38. Sande, J.B.V.; Kohlstedt, D.L. Observation of Dissociated Dislocations in Deformed Olivine. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1976, 34, 653–658. [Google Scholar] [CrossRef]
  39. Drury, M. hydration-induced Climb Dissociation of Dislocations in Naturally Deformed Mantle Olivine. Phys. Chem. Miner. 1991, 18, 106–116. [Google Scholar] [CrossRef]
  40. Durinck, J.; Carrez, P.; Cordier, P. Application of the Peierls-nabarro Model to Dislocations in Forsterite. Eur. J. Mineral. 2007, 19, 631–639. [Google Scholar] [CrossRef]
  41. Adjaoud, O.; Marquardt, K.; Jahn, S. Atomic Structures and Energies of Grain Boundaries in Mg2SiO4 Forsterite from Atomistic Modeling. Phys. Chem. Miner. 2012, 39, 749–760. [Google Scholar] [CrossRef]
  42. Kitamura, M.; Kondoh, S.; Morimoto, N.; Miller, G.; Rossman, G.; Putnis, A. Planar OH-bearing Defects in Mantle Olivine. Nature 1987, 328, 143–145. [Google Scholar] [CrossRef]
  43. Poirier, J.; Vergobbi, B. Splitting of Dislocations in Olivine, Cross-slip-controlled Creep and Mantle Rheology. Phys. Earth Planet. Inter. 1978, 16, 370–378. [Google Scholar] [CrossRef]
  44. Cai, W.; Bulatov, V.V.; Chang, J.; Li, J.; Yip, S. Dislocations in Solids. In Dislocation Core Effects on Mobility; Elsevier: Amsterdam, The Netherlands, 2004; pp. 1–80. [Google Scholar]
Crystals 12 01396 g001
Figure 1. The studied TEM foil cut with an FIB in the polycrystalline olivine sample deformed by the D-DIA (D0966). (a) An SEM image showing the foil from an edge-on point of view (middle of the image). (b) A TEM image of the foil showing mottled contrast, indicating abundant dislocations in it.
Figure 1. The studied TEM foil cut with an FIB in the polycrystalline olivine sample deformed by the D-DIA (D0966). (a) An SEM image showing the foil from an edge-on point of view (middle of the image). (b) A TEM image of the foil showing mottled contrast, indicating abundant dislocations in it.
Crystals 12 01396 g001
Crystals 12 01396 g002
Figure 2. Low-angle backscattered electron images showing the orientation contrast, grain sizes, and shapes of recrystallized olivine grains. (a) All grains are irregular with wavy grain boundaries. Microfractures and microcracking exist in the deformed olivine. (b) Very small particles (about 500 nm; the gray particle in the lower middle) existed in the sample.
Figure 2. Low-angle backscattered electron images showing the orientation contrast, grain sizes, and shapes of recrystallized olivine grains. (a) All grains are irregular with wavy grain boundaries. Microfractures and microcracking exist in the deformed olivine. (b) Very small particles (about 500 nm; the gray particle in the lower middle) existed in the sample.
Crystals 12 01396 g002
Crystals 12 01396 g003aCrystals 12 01396 g003b
Figure 3. (a) Dark-field (DF) image with g101 (long white arrow indicated) taken in g/5g conditions. Short, straight [001] screw dislocations were dominant in the area. Movement of the dislocation dipoles introduced an intermediate jog, indicated by the short black arrow. Small loops are indicated by the short gray arrows. The curved mixed dislocation was split into partial dislocations, indicated by the short white arrow. (b) DF images with g0-20 and g1-10 obtained from the same area of (a). All dislocations were simultaneously out of contrast and were imaged in g/2g and g conditions, respectively. (c) DF image with g22-2 obtained from the same area of (a), taken in g/2g conditions. An intermediate jog pinned the dipole trail in this image (indicated by the black arrow). (d) DF image with g101 (indicated by the long white arrow) taken in g/5g conditions, showing curved mixed dislocations. (e) Bright-field (BF) image with [113] incidence showing small loops (such as those indicated by the short black arrows) and dissociated screw dislocations (such as those indicated by the short white arrows). The dissociation width varied from 10 to 15 nm. (f) DF image with g20-2 taken in g/2g conditions. The dislocations’ walls were composed of arrays of screw dislocations.
Figure 3. (a) Dark-field (DF) image with g101 (long white arrow indicated) taken in g/5g conditions. Short, straight [001] screw dislocations were dominant in the area. Movement of the dislocation dipoles introduced an intermediate jog, indicated by the short black arrow. Small loops are indicated by the short gray arrows. The curved mixed dislocation was split into partial dislocations, indicated by the short white arrow. (b) DF images with g0-20 and g1-10 obtained from the same area of (a). All dislocations were simultaneously out of contrast and were imaged in g/2g and g conditions, respectively. (c) DF image with g22-2 obtained from the same area of (a), taken in g/2g conditions. An intermediate jog pinned the dipole trail in this image (indicated by the black arrow). (d) DF image with g101 (indicated by the long white arrow) taken in g/5g conditions, showing curved mixed dislocations. (e) Bright-field (BF) image with [113] incidence showing small loops (such as those indicated by the short black arrows) and dissociated screw dislocations (such as those indicated by the short white arrows). The dissociation width varied from 10 to 15 nm. (f) DF image with g20-2 taken in g/2g conditions. The dislocations’ walls were composed of arrays of screw dislocations.
Crystals 12 01396 g003aCrystals 12 01396 g003b
Crystals 12 01396 g004
Figure 4. (a) BF image with [001] incidence. A line of end-on screw dislocations is shown (such as that indicated by the white arrow). This sub-grain boundary is parallel to (100). Some curved dissociated dislocations are shown (such as that indicated by the black arrow). The dissociation width varies from 10 to 25 nm. (b) BF image with [20-1] incidence. The sub-grain boundary in (a) exhibits a kink band (indicated by the white arrow) on the screw dislocation wall (black arrows).
Figure 4. (a) BF image with [001] incidence. A line of end-on screw dislocations is shown (such as that indicated by the white arrow). This sub-grain boundary is parallel to (100). Some curved dissociated dislocations are shown (such as that indicated by the black arrow). The dissociation width varies from 10 to 25 nm. (b) BF image with [20-1] incidence. The sub-grain boundary in (a) exhibits a kink band (indicated by the white arrow) on the screw dislocation wall (black arrows).
Crystals 12 01396 g004
Crystals 12 01396 g005
Figure 5. Diagrammatic representation of a kink on a screw dislocation. A kink is a short element of dislocation with the same Burgers vector as the slip plane. It is a deformation mode that is commonly found in crystals with only a slip plane when no extensive glide on the system is geometrically possible and when bending moments are present.
Figure 5. Diagrammatic representation of a kink on a screw dislocation. A kink is a short element of dislocation with the same Burgers vector as the slip plane. It is a deformation mode that is commonly found in crystals with only a slip plane when no extensive glide on the system is geometrically possible and when bending moments are present.
Crystals 12 01396 g005
Crystals 12 01396 g006
Figure 6. BF images with [-2-12] incidence. (a) A small olivine grain with approximately 2 μm inside a larger grain. The white arrow indicates a micro-crack between the two. (b) Tangles of dislocations in this grain. (c) A dislocation cell substructure surrounded by tangles of dislocations.
Figure 6. BF images with [-2-12] incidence. (a) A small olivine grain with approximately 2 μm inside a larger grain. The white arrow indicates a micro-crack between the two. (b) Tangles of dislocations in this grain. (c) A dislocation cell substructure surrounded by tangles of dislocations.
Crystals 12 01396 g006
Table 1. Experimental conditions of the studied sample [23].
Table 1. Experimental conditions of the studied sample [23].
Deformation
Segment		P(GPa)T(K)Strain Rate
(10−5 s−1)		Stress (MPa)Maximum Strain (%)
Seg 12.811576/14581.35543−12
Seg 22.961643/16041.22445−11
Seg 35.091671/16260.98897−12
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chen, T.; Hilairet, N.; Wang, Y. A TEM Study on a Polycrystalline Olivine Sample Deformed in a D-DIA under Mantle Conditions. Crystals 2022, 12, 1396. https://doi.org/10.3390/cryst12101396

AMA Style

Chen T, Hilairet N, Wang Y. A TEM Study on a Polycrystalline Olivine Sample Deformed in a D-DIA under Mantle Conditions. Crystals. 2022; 12(10):1396. https://doi.org/10.3390/cryst12101396

Chicago/Turabian Style

Chen, Tao, Nadege Hilairet, and Yanbin Wang. 2022. "A TEM Study on a Polycrystalline Olivine Sample Deformed in a D-DIA under Mantle Conditions" Crystals 12, no. 10: 1396. https://doi.org/10.3390/cryst12101396

APA Style

Chen, T., Hilairet, N., & Wang, Y. (2022). A TEM Study on a Polycrystalline Olivine Sample Deformed in a D-DIA under Mantle Conditions. Crystals, 12(10), 1396. https://doi.org/10.3390/cryst12101396

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop