Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation
Abstract
:1. Introduction
2. Methods
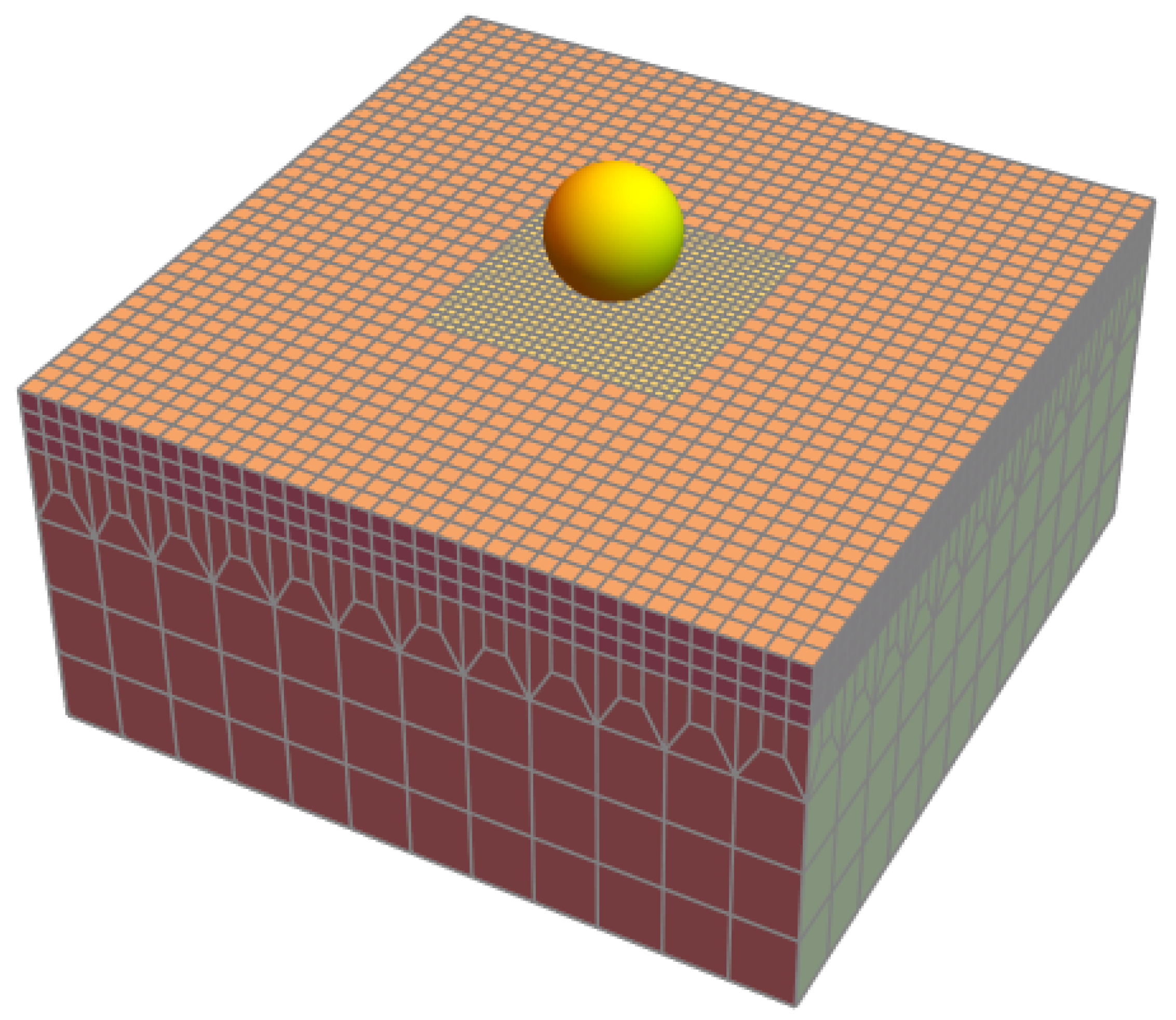
2.1. Crystal Plasticity Finite Element Method
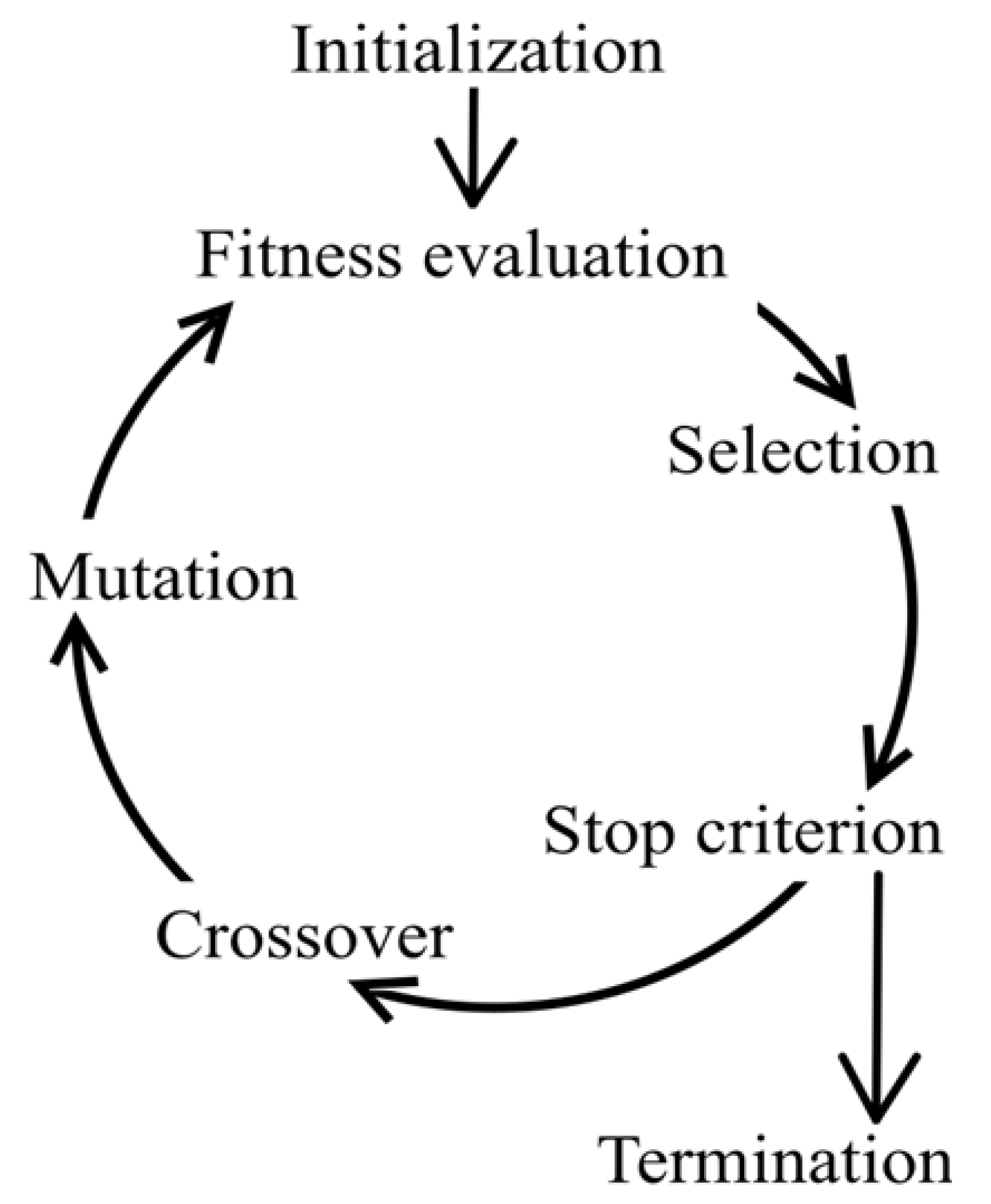
2.2. Optimization
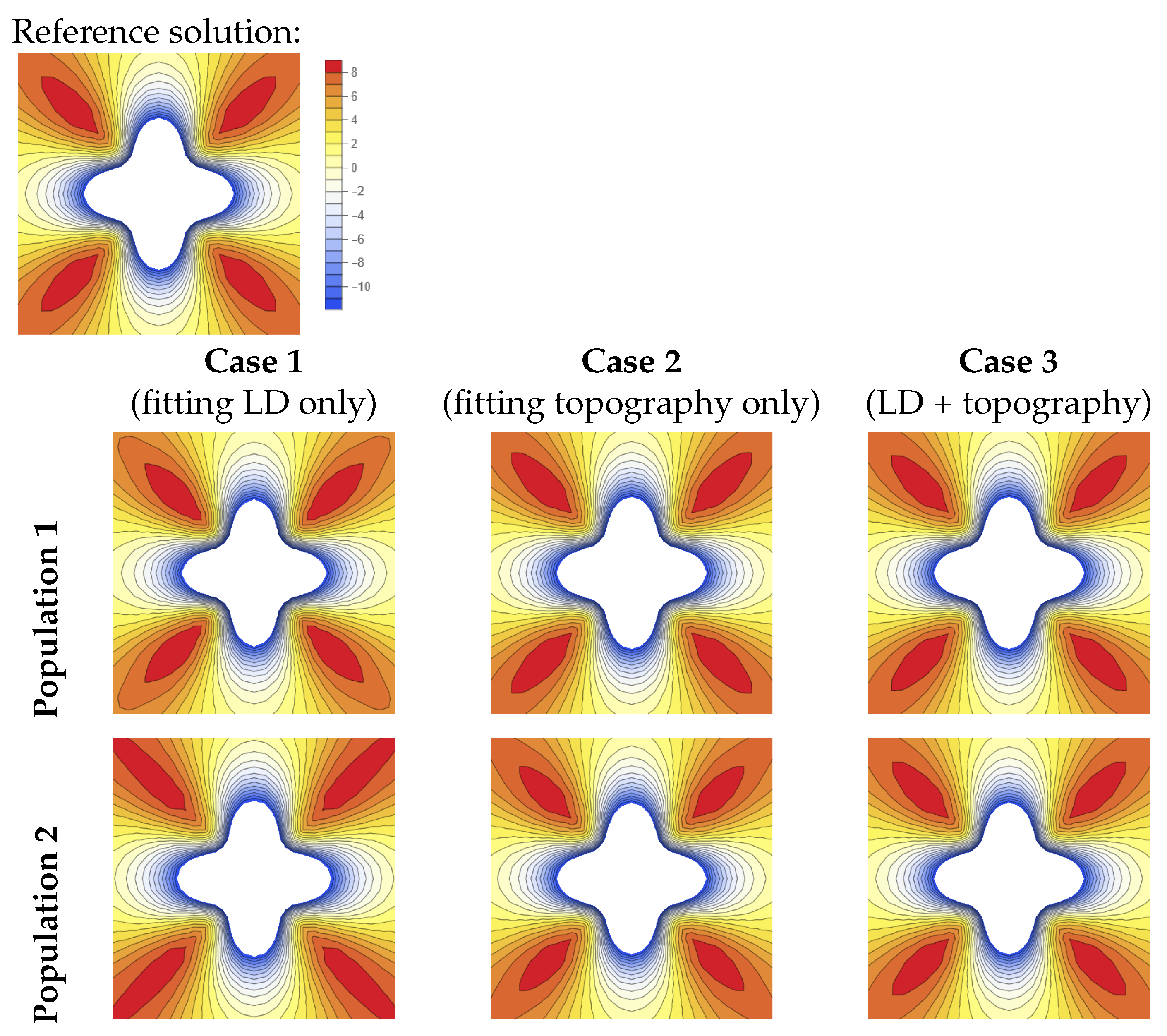
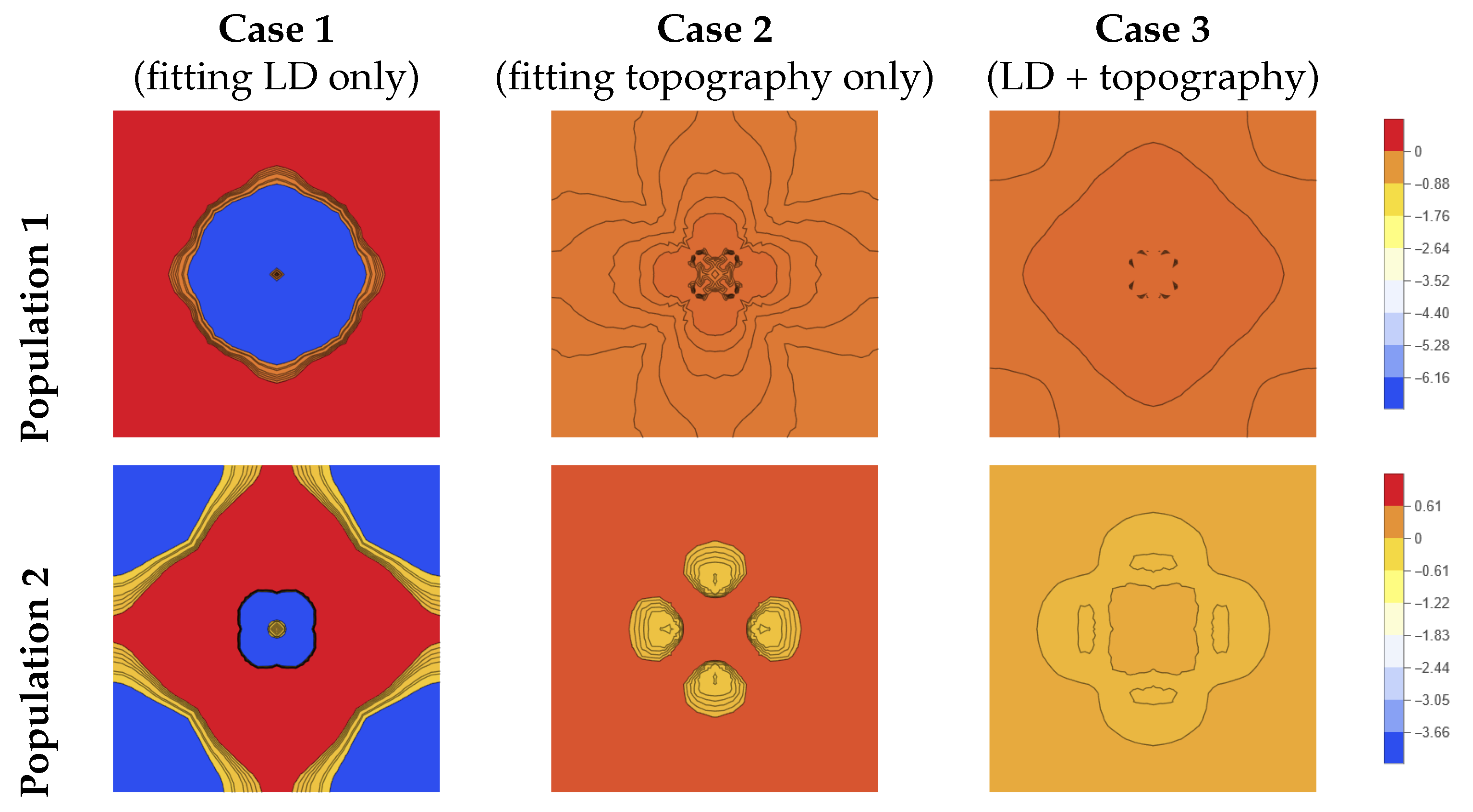
3. Results and Discussion
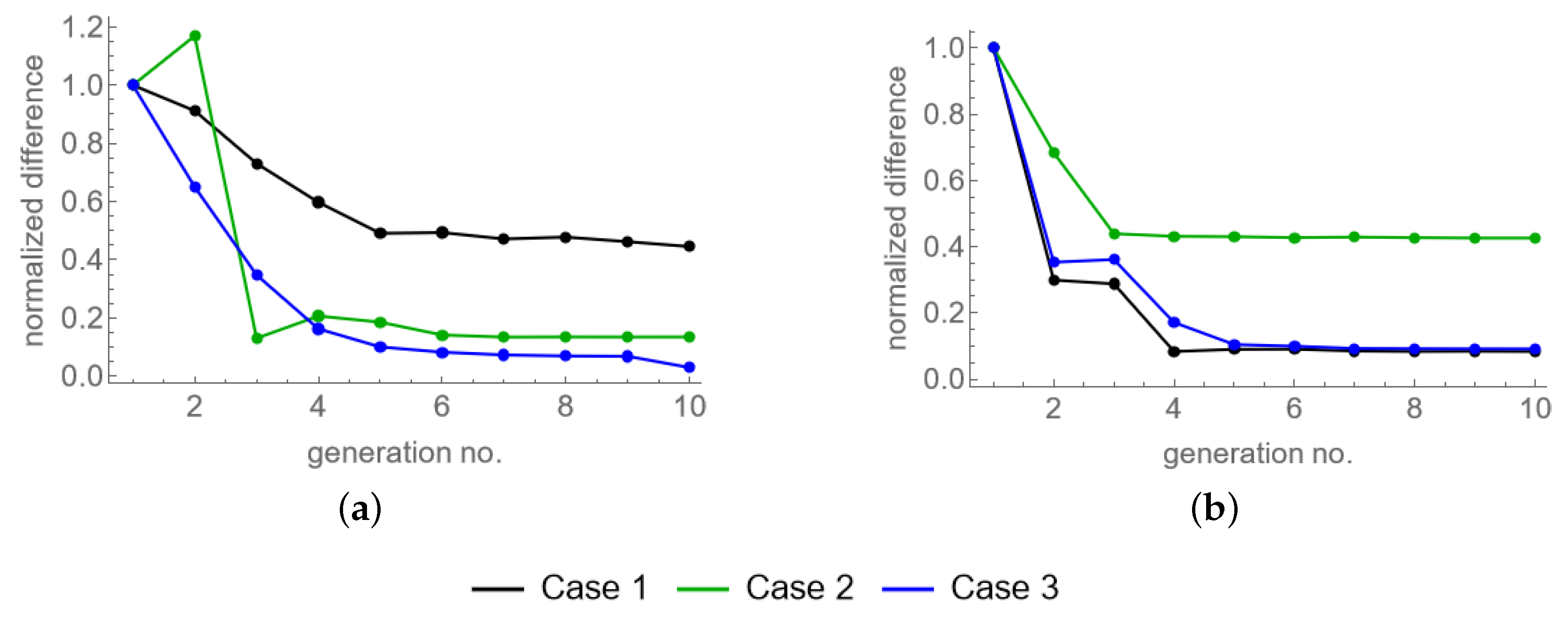
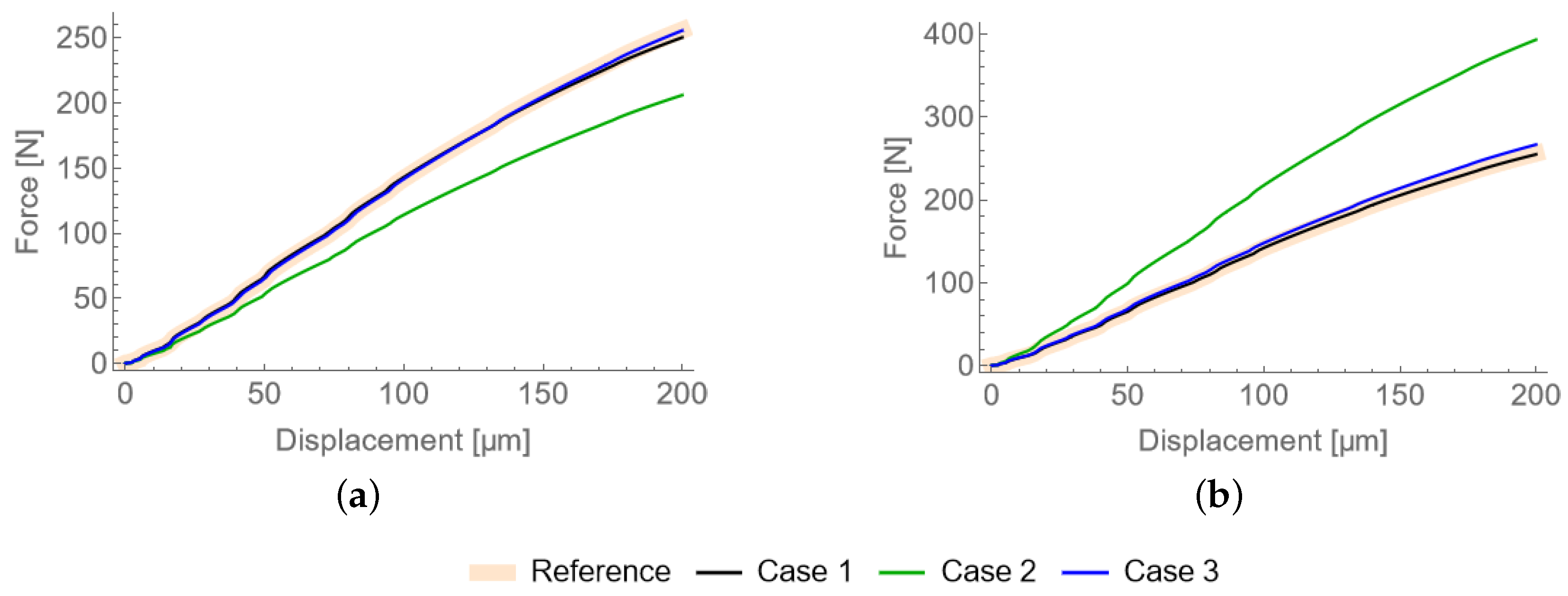
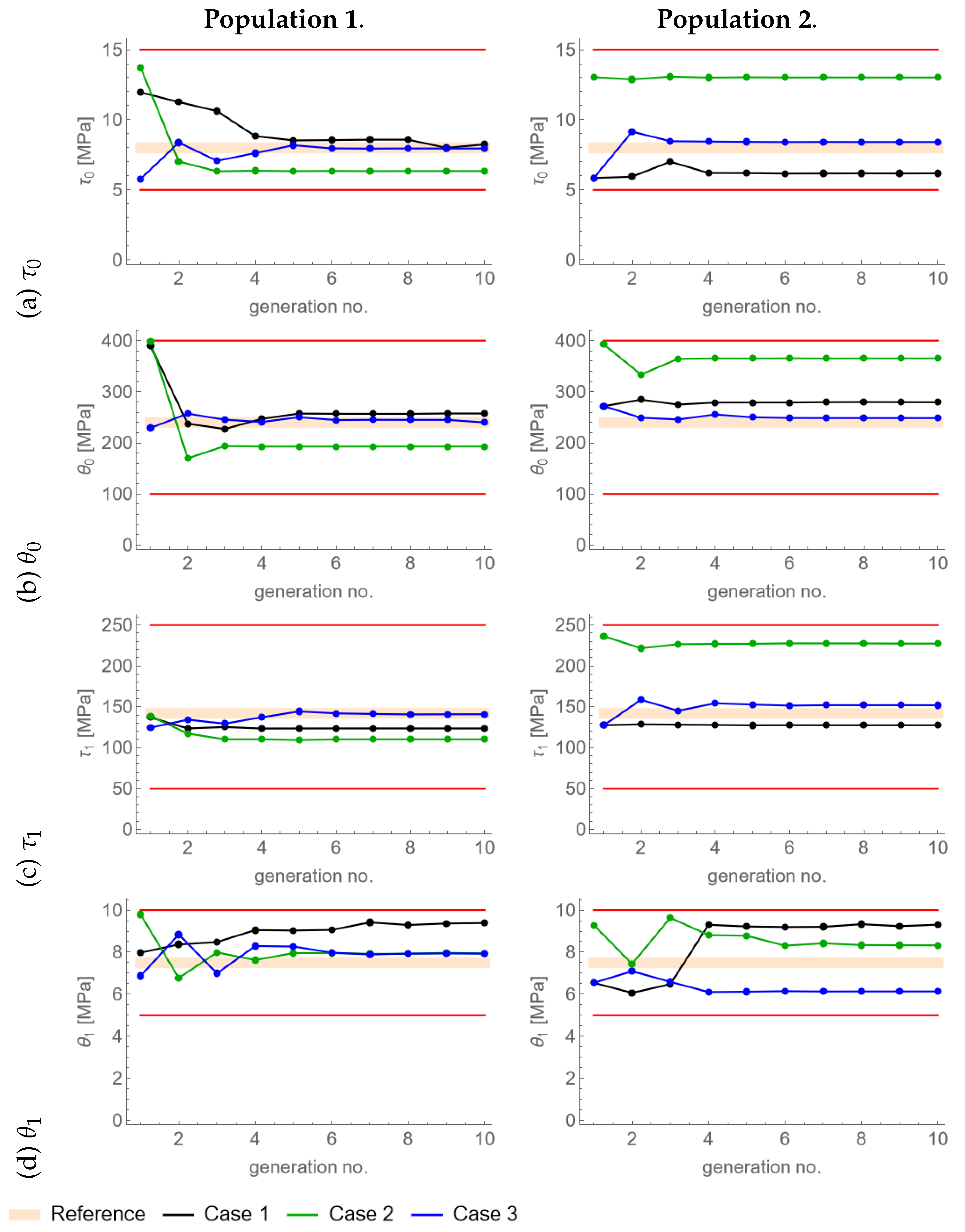
3.1. Parameter Optimization
- Case 1: fitting only LD curve,
- Case 2: fitting only surface topography,
- Case 3: fitting LD curve and surface topography.
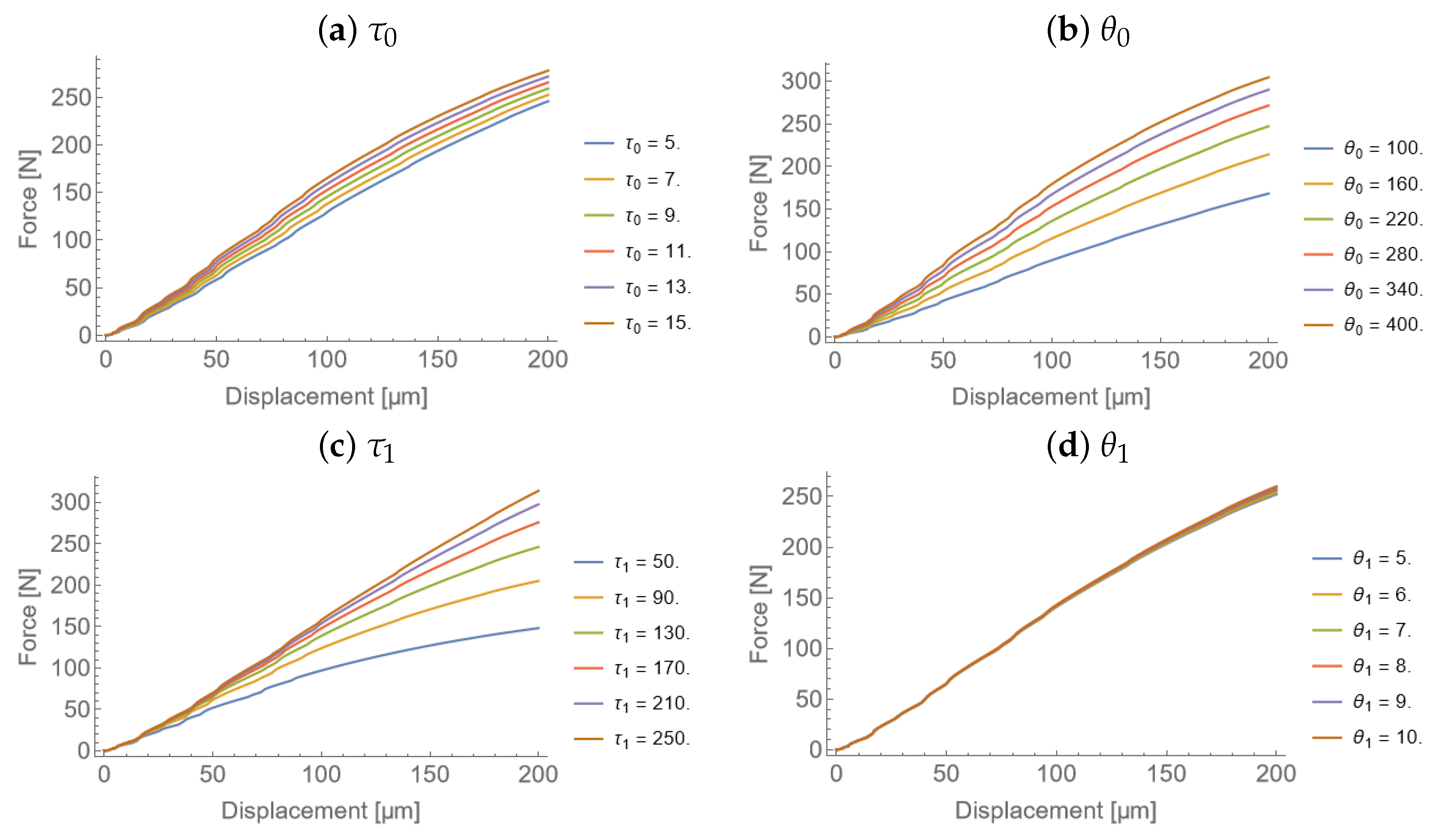
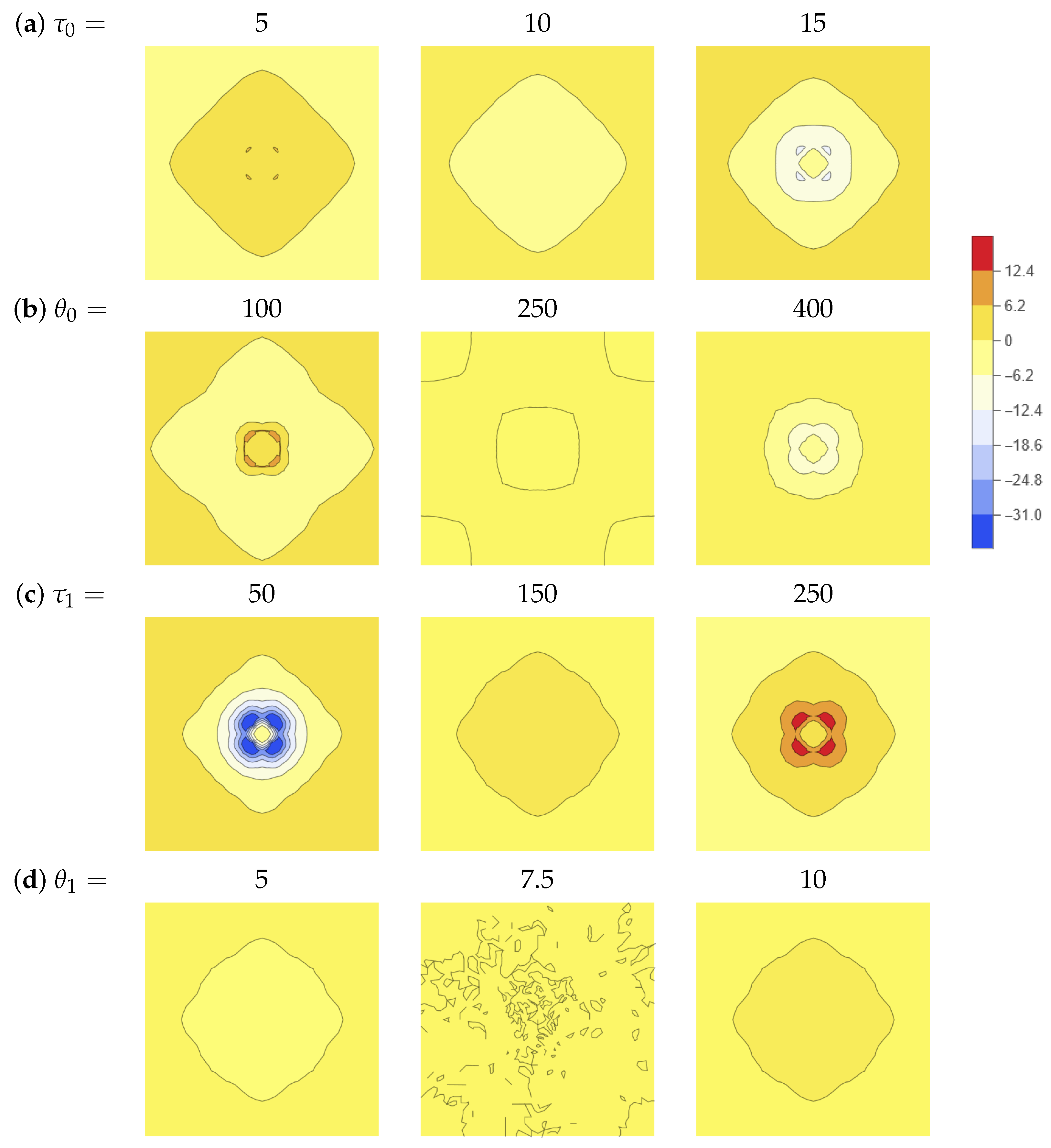
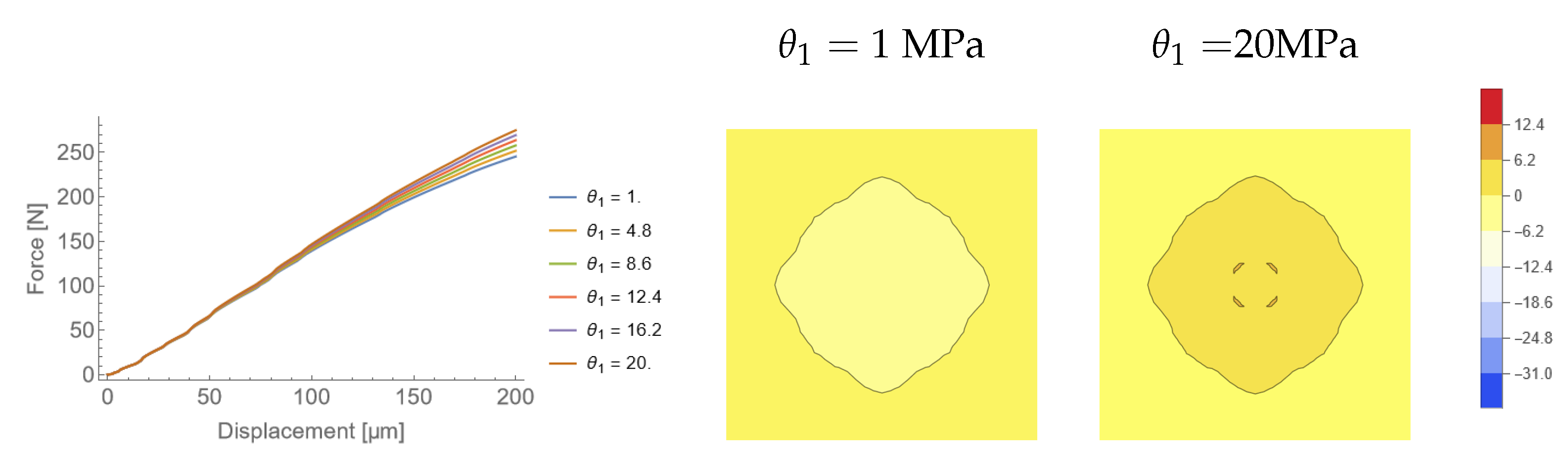
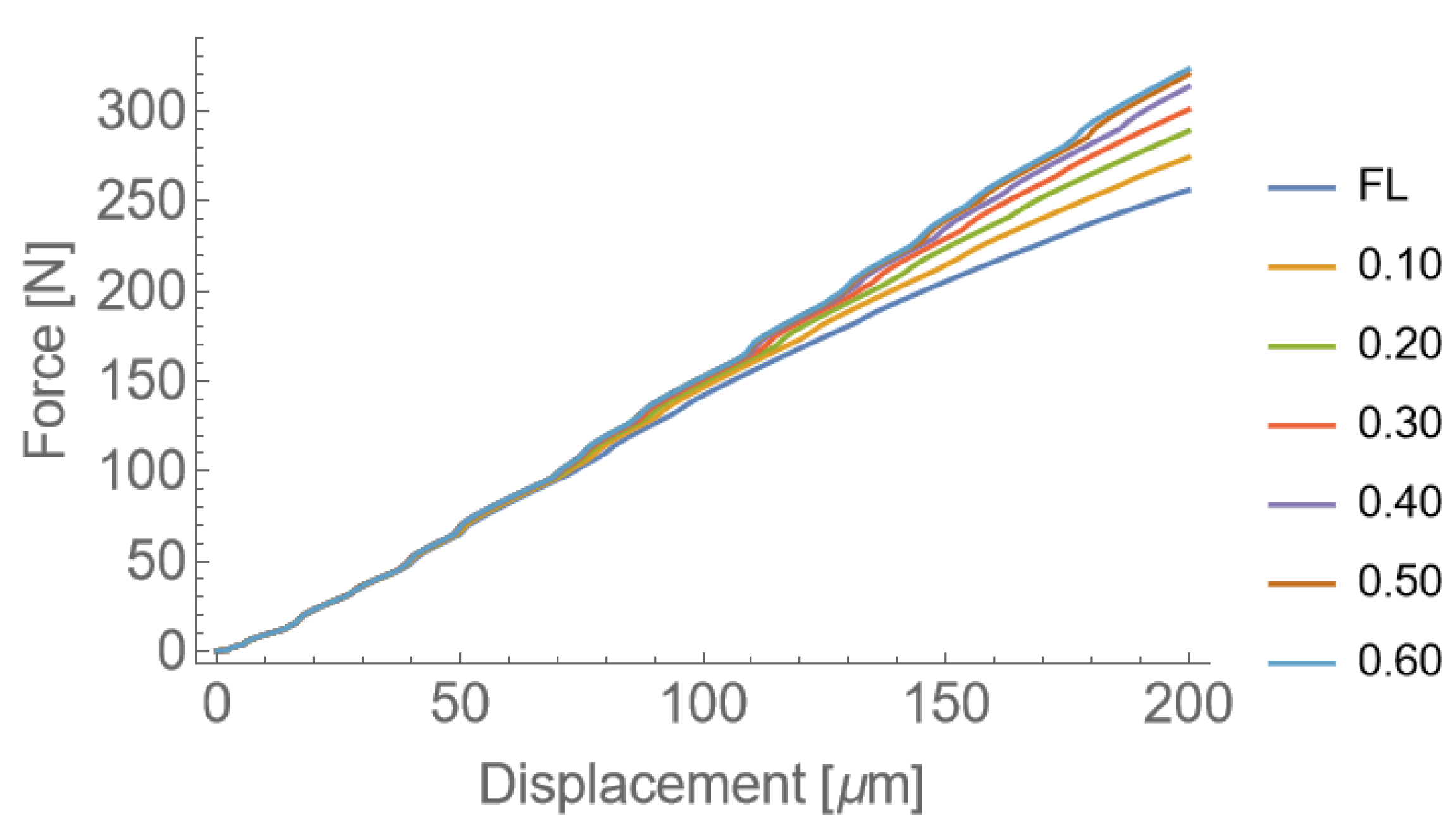
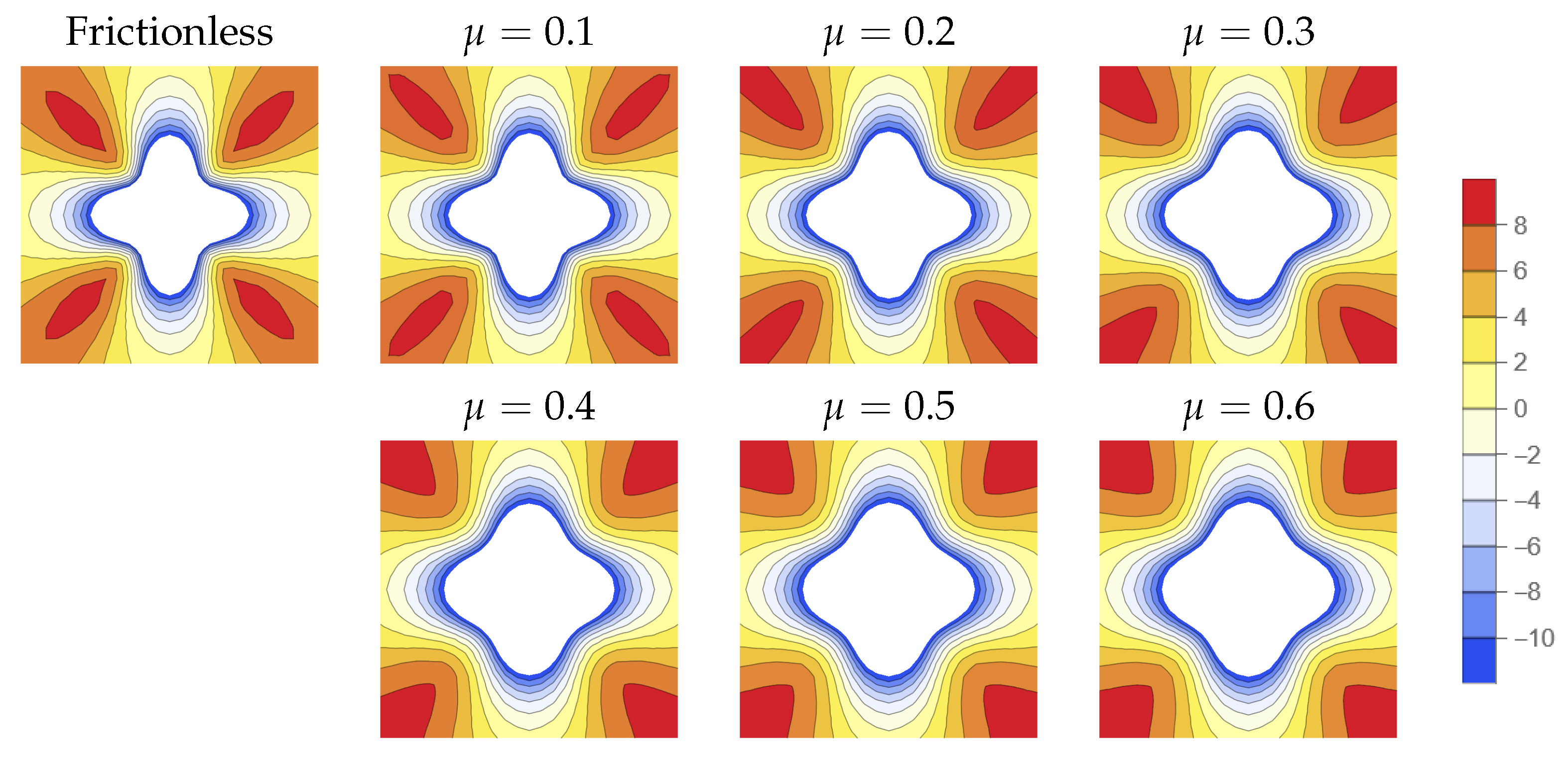
3.2. Sensitivity Analysis
3.3. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.Z.; Lawn, B.R. A simple indentation stress–strain relation for contacts with spheres on bilayer structures. Thin Solid Films 1998, 322, 225–232. [Google Scholar] [CrossRef]
- Moharrami, N.; Bull, S. A comparison of nanoindentation pile-up in bulk materials and thin films. Thin Solid Films 2014, 572, 189–199. [Google Scholar]
- Nayebi, A.; Bartier, O.; Mauvoisin, G.; El Abdi, R. New method to determine the mechanical properties of heat treated steels. Int. J. Mech. Sci. 2001, 43, 2679–2697. [Google Scholar] [CrossRef]
- Elghazal, H.; Lormand, G.; Hamel, A.; Girodin, D.; Vincent, A. Microplasticity characteristics obtained through nano-indentation measurements: Application to surface hardened steels. Mater. Sci. Eng. A 2001, 303, 110–119. [Google Scholar] [CrossRef]
- Hosemann, P.; Vieh, C.; Greco, R.; Kabra, S.; Valdez, J.; Cappiello, M.; Maloy, S. Nanoindentation on ion irradiated steels. J. Nucl. Mater. 2009, 389, 239–247. [Google Scholar] [CrossRef]
- Hosemann, P.; Kiener, D.; Wang, Y.; Maloy, S.A. Issues to consider using nano indentation on shallow ion beam irradiated materials. J. Nucl. Mater. 2012, 425, 136–139. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method for Solid and Structural Mechanics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Stupkiewicz, S. Micromechanics of Contact and Interphase Layers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 30. [Google Scholar]
- Korelc, J. Multi-language and multi-environment generation of nonlinear finite element codes. Eng. Comput. 2002, 18, 312–327. [Google Scholar] [CrossRef]
- Korelc, J.; Wriggers, P. Automation of Finite Element Methods; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Helfer, T.; Michel, B.; Proix, J.M.; Salvo, M.; Sercombe, J.; Casella, M. Introducing the open-source mfront code generator: Application to mechanical behaviours and material knowledge management within the PLEIADES fuel element modelling platform. Comput. Math. Appl. 2015, 70, 994–1023. [Google Scholar] [CrossRef]
- Zambaldi, C.; Raabe, D. Plastic anisotropy of γ-TiAl revealed by axisymmetric indentation. Acta Mater. 2010, 58, 3516–3530. [Google Scholar] [CrossRef]
- Kucharski, S.; Stupkiewicz, S.; Petryk, H. Surface Pile-Up Patterns in Indentation Testing of Cu Single Crystals. Exp. Mech. 2014, 54, 957–969. [Google Scholar] [CrossRef]
- Frydrych, K. Crystal plasticity finite element simulations of the indentation test. Comput. Methods Mater. Sci. 2019, 19, 41–49. [Google Scholar] [CrossRef]
- Ganesan, S.; Yaghoobi, M.; Githens, A.; Chen, Z.; Daly, S.; Allison, J.E.; Sundararaghavan, V. The effects of heat treatment on the response of WE43 Mg alloy: Crystal plasticity finite element simulation and SEM-DIC experiment. Int. J. Plast. 2021, 137, 102917. [Google Scholar] [CrossRef]
- Guery, A.; Hild, F.; Latourte, F.; Roux, S. Identification of crystal plasticity parameters using DIC measurements and weighted FEMU. Mech. Mater. 2016, 100, 55–71. [Google Scholar] [CrossRef]
- Cruzado, A.; LLorca, J.; Segurado, J. Modeling cyclic deformation of inconel 718 superalloy by means of crystal plasticity and computational homogenization. Int. J. Solids Struct. 2017, 122, 148–161. [Google Scholar] [CrossRef]
- Kuhn, J.; Spitz, J.; Sonnweber-Ribic, P.; Schneider, M.; Böhlke, T. Identifying material parameters in crystal plasticity by Bayesian optimization. Optim. Eng. 2022, 23, 1489–1523. [Google Scholar] [CrossRef]
- Hu, L.; Jiang, S.y.; Zhang, Y.q.; Zhu, X.m.; Sun, D. Texture evolution and inhomogeneous deformation of polycrystalline Cu based on crystal plasticity finite element method and particle swarm optimization algorithm. J. Cent. South Univ. 2017, 24, 2747–2756. [Google Scholar] [CrossRef]
- Sedighiani, K.; Diehl, M.; Traka, K.; Roters, F.; Sietsma, J.; Raabe, D. An efficient and robust approach to determine material parameters of crystal plasticity constitutive laws from macro-scale stress–strain curves. Int. J. Plast. 2020, 134, 102779. [Google Scholar] [CrossRef]
- Girard, G.; Frydrych, K.; Kowalczyk-Gajewska, K.; Martiny, M.; Mercier, S. Cyclic response of electrodeposited copper films. Experiments versus elastic-viscoplastic mean-field approach predictions. Mech. Mater. 2021, 153, 103685. [Google Scholar] [CrossRef]
- Sajjad, H.M.; Hanke, S.; Güler, S.; ul Hassan, H.; Fischer, A.; Hartmaier, A. Modelling cyclic behaviour of martensitic steel with J2 plasticity and crystal plasticity. Materials 2019, 12, 1767. [Google Scholar] [CrossRef]
- Savage, D.J.; Feng, Z.; Knezevic, M. Identification of crystal plasticity model parameters by multi-objective optimization integrating microstructural evolution and mechanical data. Comput. Methods Appl. Mech. Eng. 2021, 379, 113747. [Google Scholar] [CrossRef]
- Skippon, T.; Mareau, C.; Daymond, M.R. On the determination of single-crystal plasticity parameters by diffraction: Optimization of a polycrystalline plasticity model using a genetic algorithm. J. Appl. Crystallogr. 2012, 45, 627–643. [Google Scholar] [CrossRef]
- Acar, P.; Ramazani, A.; Sundararaghavan, V. Crystal plasticity modeling and experimental validation with an orientation distribution function for ti-7al alloy. Metals 2017, 7, 459. [Google Scholar] [CrossRef]
- Kapoor, K.; Sangid, M.D. Initializing type-2 residual stresses in crystal plasticity finite element simulations utilizing high-energy diffraction microscopy data. Mater. Sci. Eng. A 2018, 729, 53–63. [Google Scholar] [CrossRef]
- Frydrych, K.; Maj, M.; Urbański, L.; Kowalczyk-Gajewska, K. Twinning-induced anisotropy of mechanical response of AZ31B extruded rods. Mater. Sci. Eng. A 2020, 771, 138610. [Google Scholar] [CrossRef]
- Frydrych, K.; Kowalczyk-Gajewska, K.; Libura, T.; Kowalewski, Z.; Maj, M. On the role of slip, twinning and detwinning in magnesium alloy AZ31b sheet. Mater. Sci. Eng. A 2021, 813, 141152. [Google Scholar] [CrossRef]
- Cauvin, L.; Raghavan, B.; Bouvier, S.; Wang, X.; Meraghni, F. Multi-scale investigation of highly anisotropic zinc alloys using crystal plasticity and inverse analysis. Mater. Sci. Eng. A 2018, 729, 106–118. [Google Scholar] [CrossRef]
- Frydrych, K.; Jarzebska, A.; Virupakshi, S.; Kowalczyk-Gajewska, K.; Bieda, M.; Chulist, R.; Skorupska, M.; Schell, N.; Sztwiertnia, K. Texture-Based Optimization of Crystal Plasticity Parameters: Application to Zinc and Its Alloy. Metall. Mater. Trans. A 2021, 52, 3257–3273. [Google Scholar] [CrossRef]
- Nayebi, A.; El Abdi, R.; Bartier, O.; Mauvoisin, G. New procedure to determine steel mechanical parameters from the spherical indentation technique. Mech. Mater. 2002, 34, 243–254. [Google Scholar] [CrossRef]
- Nakamura, T.; Wang, T.; Sampath, S. Determination of properties of graded materials by inverse analysis and instrumented indentation. Acta Mater. 2000, 48, 4293–4306. [Google Scholar] [CrossRef]
- Kucharski, S.; Mróz, Z. Identification of material parameters by means of compliance moduli in spherical indentation test. Mater. Sci. Eng. A 2004, 379, 448–456. [Google Scholar] [CrossRef]
- Kucharski, S.; Mróz, Z. Identification of yield stress and plastic hardening parameters from a spherical indentation test. Int. J. Mech. Sci. 2007, 49, 1238–1250. [Google Scholar] [CrossRef]
- Ma, D.; Ong, C.W.; Lu, J.; He, J. Methodology for the evaluation of yield strength and hardening behavior of metallic materials by indentation with spherical tip. J. Appl. Phys. 2003, 94, 288–294. [Google Scholar] [CrossRef]
- Mata, M.; Alcalá, J. Mechanical property evaluation through sharp indentations in elastoplastic and fully plastic contact regimes. J. Mater. Res. 2003, 18, 1705–1709. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, B.; Yoshino, M.; Roy, S.; Lu, H.; Komanduri, R. Combined numerical simulation and nanoindentation for determining mechanical properties of single crystal copper at mesoscale. J. Mech. Phys. Solids 2005, 53, 2718–2741. [Google Scholar] [CrossRef]
- Petryk, H.; Stupkiewicz, S.; Kucharski, S. On direct estimation of hardening exponent in crystal plasticity from the spherical indentation test. Int. J. Solids Struct. 2017, 112, 209–221. [Google Scholar] [CrossRef]
- Chakraborty, A.; Eisenlohr, P. Evaluation of an inverse methodology for estimating constitutive parameters in face-centered cubic materials from single crystal indentations. Eur. J. Mech.-A/Solids 2017, 66, 114–124. [Google Scholar] [CrossRef]
- Engels, J.K.; Vajragupta, N.; Hartmaier, A. Parameterization of a Non-local Crystal Plasticity Model for Tempered Lath Martensite Using Nanoindentation and Inverse Method. Front. Mater. 2019, 6, 247. [Google Scholar] [CrossRef]
- Shahmardani, M.; Vajragupta, N.; Hartmaier, A. Robust optimization scheme for inverse method for crystal plasticity model parametrization. Materials 2020, 13, 735. [Google Scholar] [CrossRef]
- Frydrych, K.; Kowalczyk-Gajewska, K. Grain refinement in the equal channel angular pressing process: Simulations using the crystal plasticity finite element method. Model. Simul. Mater. Sci. Eng. 2018, 26, 065015. [Google Scholar] [CrossRef]
- Frydrych, K.; Dominguez, J.; Alava, M.; Papanikolaou, S. Multiscale nanoindentation modeling of concentrated solid solutions: A continuum plasticity model. arXiv 2022, arXiv:2206.11833. [Google Scholar]
- Stupkiewicz, S.; Lengiewicz, J.; Korelc, J. Sensitivity analysis for frictional contact problems in the augmented Lagrangian formulation. Comput. Methods Appl. Mech. Eng. 2010, 199, 2165–2176. [Google Scholar] [CrossRef]
- Lewandowski, M.; Stupkiewicz, S. Size effects in wedge indentation predicted by a gradient-enhanced crystal-plasticity model. Int. J. Plast. 2018, 109, 54–78. [Google Scholar] [CrossRef]
- Wang, Y.; Raabe, D.; Klüber, C.; Roters, F. Orientation dependence of nanoindentation pile-up patterns and of nanoindentation microtextures in copper single crystals. Acta Mater. 2004, 52, 2229–2238. [Google Scholar] [CrossRef]
- Liu, Y.; Varghese, S.; Ma, J.; Yoshino, M.; Lu, H.; Komanduri, R. Orientation effects in nanoindentation of single crystal copper. Int. J. Plast. 2008, 24, 1990–2015. [Google Scholar] [CrossRef]
- Lee, W.B.; Chen, Y.P. Simulation of micro-indentation hardness of FCC single crystals by mechanism-based strain gradient crystal plasticity. Int. J. Plast. 2010, 26, 1527–1540. [Google Scholar] [CrossRef]
- Demiral, M.; Roy, A.; Silberschmidt, V. Indentation studies in bcc crystals with enhanced model of strain-gradient crystal plasticity. Comput. Mater. Sci. 2013, 79, 896–902. [Google Scholar] [CrossRef]
- Gao, Y.; Larson, B.; Lee, J.; Nicola, L.; Tischler, J.; Pharr, G. Lattice rotation patterns and strain gradient effects in face-centered-cubic single crystals under spherical indentation. J. Appl. Mech. 2015, 82, 061007. [Google Scholar] [CrossRef]
- Xiao, X.; Chen, L.; Yu, L.; Duan, H. Modelling nano-indentation of ion-irradiated FCC single crystals by strain-gradient crystal plasticity theory. Int. J. Plast. 2019, 116, 216–231. [Google Scholar] [CrossRef]
- Cheng, J.; Lane, R.; Kesler, M.; Brechtl, J.; Hu, X.; Mirzaeifar, R.; Rios, O.; Momen, A.; Nawaz, K. Experiment and non-local crystal plasticity finite element study of nanoindentation on Al-8Ce-10Mg alloy. Int. J. Solids Struct. 2021, 233, 111233. [Google Scholar] [CrossRef]
- Stupkiewicz, S.; Petryk, H. A minimal gradient-enhancement of the classical continuum theory of crystal plasticity. Part II: Size effects. Arch. Mech. 2016, 68, 487–513. [Google Scholar]
- Ryś, M.; Stupkiewicz, S.; Petryk, H. Micropolar regularization of crystal plasticity with the gradient-enhanced incremental hardening law. Int. J. Plast. 2022, 156, 103355. [Google Scholar] [CrossRef]
- Wang, Q.; Cochrane, C.; Skippon, T.; Wang, Z.; Abdolvand, H.; Daymond, M.R. Orientation-dependent irradiation hardening in pure Zr studied by nanoindentation, electron microscopies, and crystal plasticity finite element modeling. Int. J. Plast. 2019, 124, 133–154. [Google Scholar] [CrossRef]
- Nie, J.; Lin, P.; Liu, Y.; Zhang, H.; Wang, X. Simulation of the irradiation effect on hardness of Chinese HTGR A508-3 steels with CPFEM. Nucl. Eng. Technol. 2019, 51, 1970–1977. [Google Scholar] [CrossRef]
- Xiao, X.; Li, S.; Yu, L. Effect of irradiation damage and indenter radius on pop-in and indentation stress-strain relations: Crystal plasticity finite element simulation. Int. J. Mech. Sci. 2021, 199, 106430. [Google Scholar] [CrossRef]

| [MPa] | [MPa] | [MPa] | [MPa] |
|---|---|---|---|
| 8 | 240 | 142 | 7.5 |
| [MPa] | [MPa] | [MPa] | [MPa] |
|---|---|---|---|
| 5–15 | 100–400 | 50–250 | 5–10 |
| Minimum | Maximum | Mean | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | |
| Population 1 | −7.275 | −0.101 | −0.049 | 0.671 | 0.073 | 0.074 | −0.700 | −0.044 | 0.008 |
| Population 2 | −4.466 | −0.154 | −0.023 | 1.042 | 0.755 | 0.185 | −0.126 | 0.154 | 0.017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frydrych, K.; Papanikolaou, S. Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals 2022, 12, 1341. https://doi.org/10.3390/cryst12101341
Frydrych K, Papanikolaou S. Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals. 2022; 12(10):1341. https://doi.org/10.3390/cryst12101341
Chicago/Turabian StyleFrydrych, Karol, and Stefanos Papanikolaou. 2022. "Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation" Crystals 12, no. 10: 1341. https://doi.org/10.3390/cryst12101341
APA StyleFrydrych, K., & Papanikolaou, S. (2022). Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals, 12(10), 1341. https://doi.org/10.3390/cryst12101341






