The Third-Order Elastic Constants and Mechanical Properties of 30° Partial Dislocation in Germanium: A Study from the First-Principles Calculations and the Improved Peierls–Nabarro Model

Abstract

The elastic constants, core width and Peierls stress of 30° partial dislocation in germanium has been investigated based on the first-principles calculations and the improved Peierls–Nabarro model. Our results suggest that the predictions of lattice constant and elastic constants given by LDA are in better agreement with experiment results. While the lattice constant is overestimated at about 2.4% and most elastic constants are underestimated at about 20% by the GGA method. Furthermore, when the applied deformation is larger than 2%, the nonlinear elastic effects should be considered. And with the Lagrangian strains up to 8%, taking into account the third-order terms in the energy expansion is sufficient. Except the original $\gamma$—surface generally used before (given by the first-principles calculations directly), the effective γ—surface proposed by Kamimura et al. derived from the original one is also used to study the Peierls stress. The research results show that when the intrinsic−stacking−fault energy (ISFE) is very low relative to the unstable−stacking−fault energy (USFE), the difference between the original $\gamma$—surface and the effective $\gamma$—surface is inapparent and there is nearly no difference between the results of Peierls stresses calculated from these two kinds of $\gamma$—surfaces. As a result, the original $\gamma$—surface can be directly used to study the core width and Peierls stress when the ratio of ISFE to the USFE is small. Since the negligence of the discrete effect and the contribution of strain energy to the dislocation energy, the Peierls stress given by the classical Peierls–Nabarro model is about one order of magnitude larger than that given by the improved Peierls–Nabarro model. The result of Peierls stress estimated by the improved Peierls–Nabarro model agrees well with the 2~3 GPa reported in the book of Solid State Physics edited by F. Seitz and D. Turnbull.

1. Introduction

The interest in the nonlinear elastic properties of materials dates from the beginning of modern solid state physics and has never weakened [1,2,3,4,5,6,7,8]. The third-order elastic constants (TOECs) are important quantities characterizing nonlinear elastic properties when large stresses and strains are involved [8]. Otherwise, They are also the basis for discussion of other anharmonic properties, such as phonon−phonon interactions, thermal expansion, the temperature dependence of elastic properties, etc. [9]. However, the measurements of the TOECs are subject potentially to larger errors [10]. This problem also exists for the TOECs of semiconductor germanium. Much theoretical and experimental research has been performed on studying the elastic constants of germanium. Several experimental methods, such as neutron scattering, optical interference and ultrasonic wave propagation, are used to measure the elastic constants of germanium, including the second-order elastic constants (SOECs) and TOECs [11,12,13]. First-principles calculations are also used to investigate the elastic constants of germanium [14,15]. Bhatti calculated the TOECs of germanium using the Keating theory [16]. However, for some TOECs, such as $C_{144}$ given by ref. [11] and $C_{123}$ given by ref. [12], the range of error is very large. In addition, the result of $C_{144}$ determined by the experimental method is negative, while the result obtained from Keating theory in ref. [11] is positive. Considering the wide applications of germanium, such as infrared detection and imaging, etc., the study of TOECs is still necessary.

Within the elastic limit, the mechanical response of materials can be reflected by the elastic constants, while in the process of plastic deformation, the mobility of dislocations plays a key role. The crucial problems of dislocation are the core structure and Peierls stress. However, the study of the core width and Peierls stress of dislocation in germanium is relatively less. The estimated Peierls stress reported in the book of Solid State Physics is about 2~3 GPa [17]. The Peierls stress ${\sigma }_P$ of ${30}^{\circ }$ partial dislocation in silicon given by Joos et al. and Ren et al. using the classical Peierls–Nabarro model is about 0.3~0.4 times of Shear modulus $\mu$ [18,19,20]. According to the universality in the yielding phenomenon of tetrahedrally bonded crystals, the value of ${\sigma }_P/\mu$ for ${30}^{\circ }$ partial dislocation in germanium should be of the same order of magnitude as that in silicon. The shear modulus of germanium is given in ref. [21] is 56.4 GPa, the Peierls stress ${\sigma }_P$ of ${30}^{\circ }$ partial dislocation in germanium is, therefore, estimated to be 17~23 GPa. Obviously, the Peierls stress estimated from the value of ${\sigma }_P/\mu$ results from the classical Peierls–Nabarro model is about one order of magnitude larger than the 2~3 GPa given in ref. [17]. The classical Peierls–Nabarro model is based on the linear elastic theory in which the discrete effect of the lattice is neglected. However, the dislocations in covalent materials are very narrow, and the influence of discrete effect on the structure and Peierls stress of dislocation must be considered. Research has shown that the agreement between the theoretical prediction of Peierls stress given by the improved Peierls–Nabarro model which has fully considered the discrete effect of the crystal and the experimental and numerical results can be improved significantly [22,23,24,25]. Similar to the dislocations in silicon, the glide dislocations in germanium are usually dissociated into ${30}^{\circ }$ and ${90}^{\circ }$ partials, which are responsible for the high temperature plasticity. Compared with ${90}^{\circ }$ partial dislocation, ${30}^{\circ }$ partial dislocation generally possesses higher Peierls stress and controls the deformation. Therefore, the improved Peierls–Nabarro model is applied to investigate the core width and Peierls stress of ${30}^{\circ }$ partial dislocation in germanium.

In this paper, the SOECs, TOECs, core width and Peierls stress of ${30}^{\circ }$ partial dislocation in germanium have been investigated based on the first-principles calculations and the improved Peierls–Nabarro model. The paper is organized as follows: In Section 2, the homogeneous deformation theory and computational methods are introduced. Besides, the results of elastic constants are listed and discussed. Section 3 is focused on the improved Peierls–Nabarro model and the results of dislocation width and Peierls stress. Section 4 is a summary and discussion. The last section is the conclusion.

2. Computational Methods and Results

In this work, the SOECs and TOECs are obtained from the finite-strain continuum elasticity theory [1,2,3,4,26,27]. The relation between the elastic constants and the strain-energy density $\Phi$ can be expressed as [1,2]

$$\Phi \left(\eta \right)=\frac{1}{2!}{\displaystyle \sum _{ijkl}{C}_{ijkl}}{\eta }_{ij}{\eta }_{kl}+\frac{1}{3!}{\displaystyle \sum _{ijklmn}{C}_{ijklmn}}{\eta }_{ij}{\eta }_{kl}{\eta }_{mn}+\cdots ,$$

(1)

where ${\eta }_{ij}$ defined as ${\displaystyle {\sum }_k\left(J_{ki}{J}_{kj}-{\delta }_{ij}\right)}/2$ is the Lagrangian strain tensor [3], here ${\delta }_{ij}$ is a unit matrix, $J_{ij}=\partial {x_i}^{\prime }/\partial x_j$ is the deformation tensor which relates the initial coordinate $x_i$ and final coordinate ${x_i}^{\prime }$ of the infinitesimal element in the deformed solid. The $\alpha \mathrm{th}-\mathrm{order}\left(\alpha \ge 2\right)$ elastic constants are defined by Brugger as [4]:

$$C_{ijklmn\dots }=C_{IJK\dots }=\frac{{\partial }^{\alpha }\Phi }{\partial {\eta }_{ij}\partial {\eta }_{kl}\partial {\eta }_{mn}\cdots }|{}_{\eta = 0},$$

(2)

where I, J and K are the Voigt subscripts, and the Lagranian strain tensor $\eta$ links this notation by:

$$\eta =\left(\begin{array}{ccc}{\eta }_1& {\eta }_6/2& {\eta }_5/2\\ {\eta }_6/2& {\eta }_2& {\eta }_4/2\\ {\eta }_5/2& {\eta }_4/2& {\eta }_3\end{array}\right).$$

(3)

For semiconductor germanium, there are three independent SOECs and six TOECs, namely $C_{11}$, $C_{12}$, $C_{44}$, $C_{111}$, $C_{112}$, $C_{123}$, $C_{144}$, $C_{155}$, $C_{456}$. As shown below, the elastic constants will be obtained from the first-principles calculations by applying some simple deformation strains to the bulk-crystal. For obtaining the solvable system of elastic constants, the number of applied strain tensors should be the same as that of independent TOECs. Accordingly, in this work the following six sets of deformations are considered:

$$\begin{array}{l}{\eta }_a=\left(\begin{array}{ccc}\zeta & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)\stackrel{}{},{{\displaystyle }}^{{{\displaystyle }}^{}}{\eta }_b=\left(\begin{array}{ccc}\zeta & 0& 0\\ 0& \zeta & 0\\ 0& 0& 0\end{array}\right)\stackrel{}{},{{\displaystyle }}^{{{\displaystyle }}^{}}{\eta }_c=\left(\begin{array}{ccc}\zeta & 0& 0\\ 0& \zeta & 0\\ 0& 0& \zeta \end{array}\right)\stackrel{}{},\\ {\eta }_d=\left(\begin{array}{ccc}\zeta & 0& 0\\ 0& 0& \frac{\zeta }{2}\\ 0& \frac{\zeta }{2}& 0\end{array}\right)\stackrel{}{},{{\displaystyle }}^{}{\eta }_e=\left(\begin{array}{ccc}\zeta & 0& \frac{\zeta }{2}\\ 0& 0& 0\\ \frac{\zeta }{2}& 0& 0\end{array}\right)\stackrel{}{},{{\displaystyle }}^{}{\eta }_f=\left(\begin{array}{ccc}0& \frac{\zeta }{2}& \frac{\zeta }{2}\\ \frac{\zeta }{2}& 0& \frac{\zeta }{2}\\ \frac{\zeta }{2}& \frac{\zeta }{2}& 0\end{array}\right)\stackrel{}{}.\end{array}$$

(4)

For each type of strain mode considered, the corresponding strain-energy density $\Phi$ can be expressed as:

$$\begin{array}{l}\Phi \left({\eta }_a\right)=\frac{1}{2}{C}_{11}{\zeta }^2+\frac{1}{6}{C}_{111}{\zeta }^3,\\ \Phi \left({\eta }_b\right)=\left(C_{11}+C_{12}\right){\zeta }^2+\left(\frac{1}{3}{C}_{111}+C_{112}\right){\zeta }^3,\\ \Phi \left({\eta }_c\right)=\left(\frac{3}{2}{C}_{11}+3C_{12}\right){\zeta }^2+\left(\frac{1}{2}{C}_{111}+3C_{112}+C_{123}\right){\zeta }^3,\\ \Phi \left({\eta }_d\right)=\left(\frac{1}{2}{C}_{11}+\frac{1}{2}{C}_{44}\right){\zeta }^2+\left(\frac{1}{6}{C}_{111}+\frac{1}{2}{C}_{144}\right){\zeta }^3,\\ \Phi \left({\eta }_e\right)=\left(\frac{1}{2}{C}_{11}+\frac{1}{2}{C}_{44}\right){\zeta }^2+\left(\frac{1}{6}{C}_{111}+\frac{1}{2}{C}_{155}\right){\zeta }^3,\\ \Phi \left({\eta }_f\right)=\frac{3}{2}{C}_{44}{\zeta }^2+C_{456}{\zeta }^3.\end{array}$$

(5)

In every case for deformation ${\eta }_{\iota }\left(\iota =a\mathrm{to}f\right)$, the Lagrangian strain parameter $\zeta$ is changed from −0.08 to 0.08 with the step of 0.008. For covalent materials, the maximal amplitude 0.08 of the deformations is enough to obtain the accurate TOECs. The SOECs and TOECs can be determined from the least-square polynomial of the strain-energy relation given by the first-principles calculations [28].

The first-principles calculations are performed using the ab-initio simulation package (VASP 4.6) based on the framework of the density functional theory (DFT) [29,30,31]. In order to compare the performance of two different density functionals in predicting the lattice constant and elastic constants, the generalized gradient approximation (GGA) in the form of the Perdew−Burke−Ernzerhof (PBE) and the local density approximation (LDA) are employed. A plane-wave basis set is employed within the framework of the full potential frozen-core projector augmented wave (PAW) [32,33]. The structure is relaxed without any symmetry constraints with a cutoff energy of 550 eV. The equilibrium theoretical structure is determined by minimizing the Hellmann−Feynman force on the atoms and stress on the unit cell, the convergence of energy and force are set to $1.0\times {10}^{-6} \mathrm{eV}$ and $1.0\times {10}^{-4} \mathrm{eV}/\AA$, respectively. For the Brillouin zone integrals, reciprocal space is represented by the Monkhorst−Pack special k-point scheme [34] with $21\times 21\times 21$ grid meshes. First-principles calculations based on the density-functional theory are always carried out at the temperature T = 0 K, and thus thermal expansion and zero-point anharmonic expansion corrections are not included.

The calculated lattice and elastic constants and the strain-energy relations are shown in

Table 1. The lattice constant, SOECs and TOECs obtained from our first-principles calculations in comparison with the previous calculations and experiments. The lattice constants and elastic constants are in unit of Å and GPa, respectively.

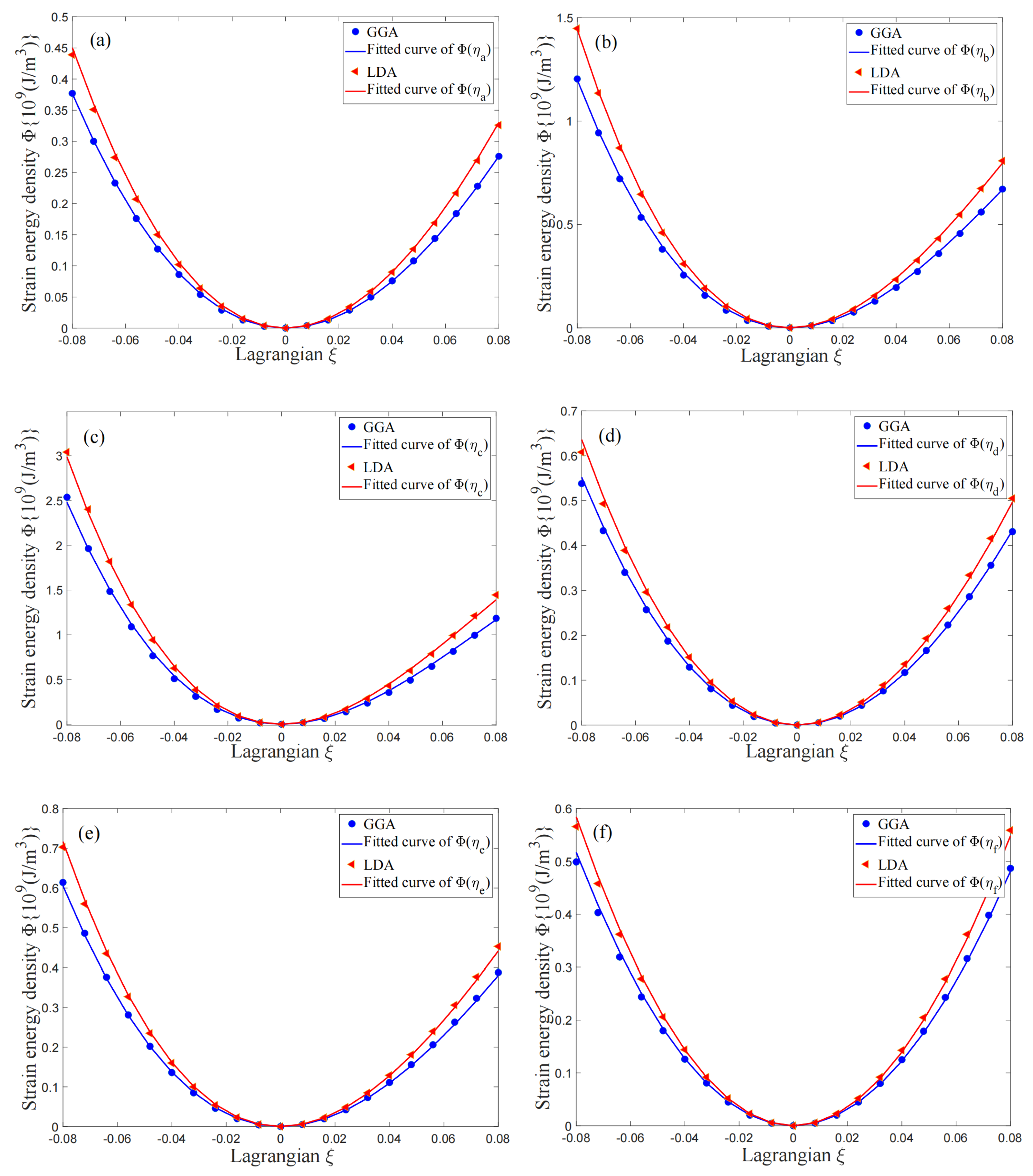
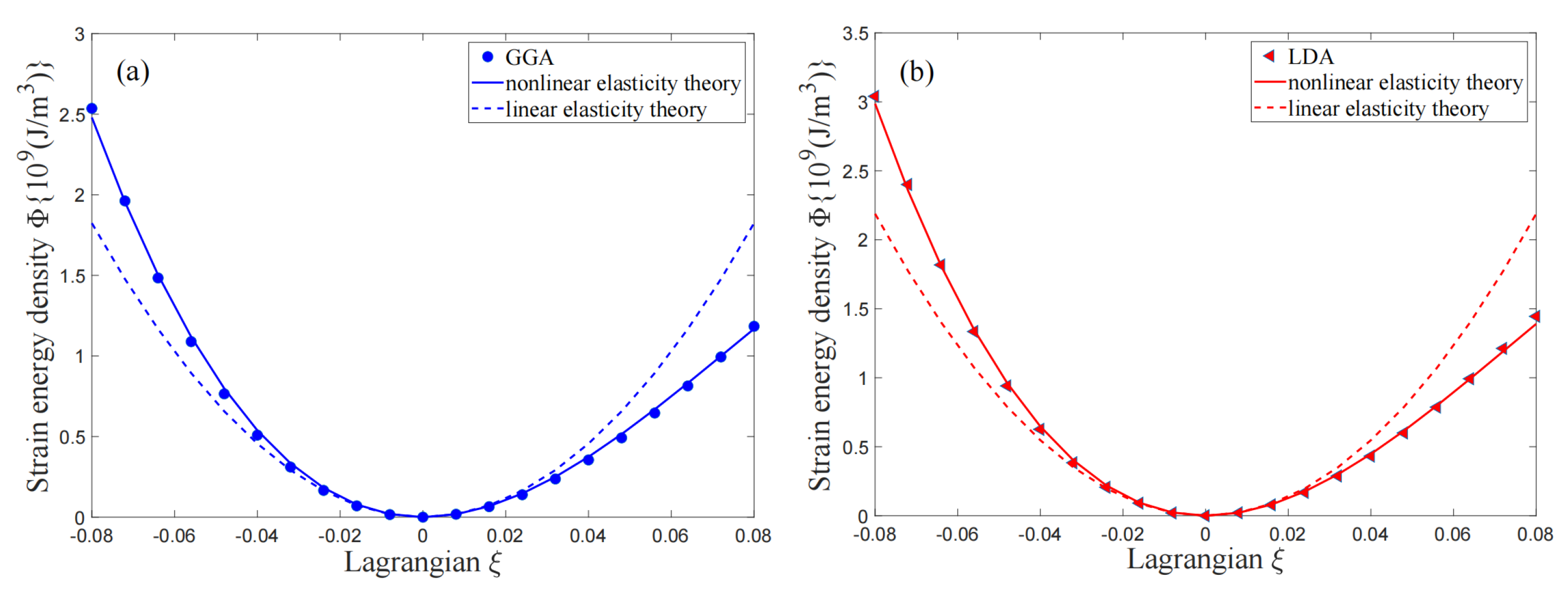
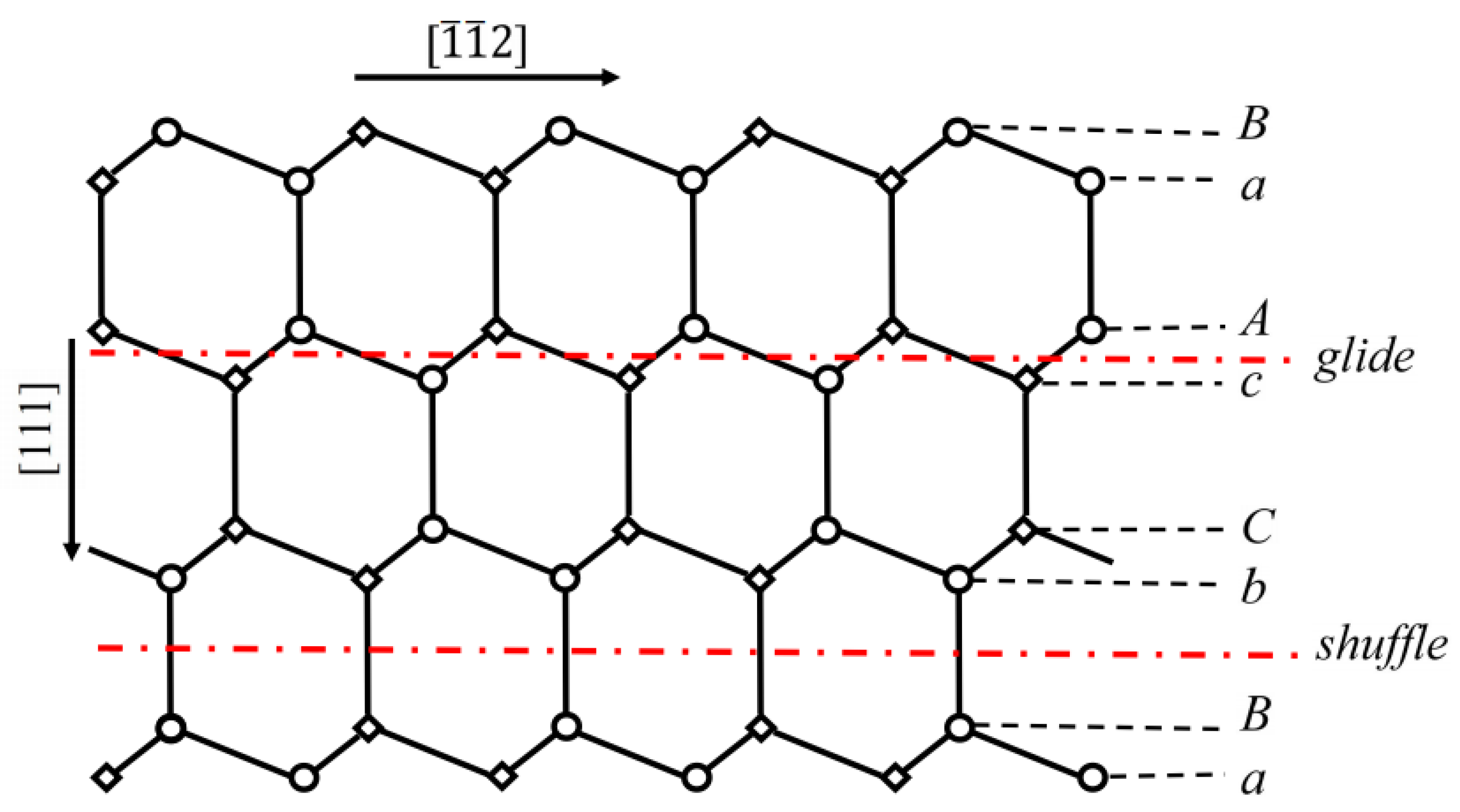
	Present Calculations	Previous Calculations	Experiments
$a_0$	5.785 a, 5.648 b	5.57 c, 5.763 e	5.66 f, 5.65 i
$C_{11}$	102 a, 122 b	129.92 c, 103.1 e	129 g, 128.35 j
$C_{12}$	44 a, 53 b	47.98 c, 36.8 e	48.3 g, 48.23 j
$C_{44}$	52 a, 59 b	67.17 c, 53.1 e	67.1 g, 66.66 j
$C_{111}$	−589 a, −705 b	−681 d	−710 ± 6 h, −716 ± 20 j, −714 k
$C_{112}$	−322 a, −396 b	−363 d	−389 ± 3 h, −403 ± 10 j, −388 k
$C_{123}$	−20 a, −19 b	−9 d	−18 ± 6 h, −18 ± 30 j, −34 k
$C_{144}$	−35 a, −37 b	9 d	−23 ± 16 h, −53 ± 5 j, −9 k
$C_{155}$	−244 a, −303 b	−323 d	−292 ± 8 h, −315 ± 5 j, −303 k
$C_{456}$	−35 a, −35 b	−45 d	−53 ± 7 h, −47 ± 10 j, −48 k

^a This work of GGA; ^b This work of LDA; ^c Ref [14] (LDA); ^d Ref [16] (Keating theory); ^e Ref [35] (PAW); ^f Ref [36]; ^g Ref [37]; ^h Ref [1] (T = 298 K); ⁱ Ref [38] (T = 298 K); ^j Ref [12] (T = 298 K); ^k Ref [13] (T = 298 K).

and Figure 1, respectively. The lattice constant is overestimated, SOECs and most of the TOECs are underestimated by GGA, it is consistent with the results of ref. [35]. The predictions of lattice constant and elastic constants given by LDA are in better agreement with experiment results in ref. [11]. One can see that when the Lagrangian strain is as high as 8%, it is sufficient to include the terms up to third order in the energy expansion. In order to examine the dominant range of the third-order effects, the curves of the linear elasticity comparison with the nonlinear elasticity of the deformation ${\eta }_c$ are shown in Figure 2. It is found that the third-order effects should be considered when the applied deformations are larger than 2%.

3. Mechanical Properties of ${30}^{\circ }$ Partial Dislocation in Germanium

In this section, the mechanical properties of ${30}^{\circ }$ partial dislocation in germanium have been investigated theoretically based on the improved Peierls–Nabarro model. The equation satisfied by the displacement field u of dislocation can be expressed as [39]

$$-\frac{\beta }{2}\frac{d^{2}u}{d{x}^2}-\frac{K\sigma }{2\pi }{\displaystyle {\int }_{-\infty }^{+\infty }\frac{{dx}^{\prime }}{x^{\prime }-x}}(\frac{du}{dx})|{}_{x = x^{\prime }}=f(u),$$

(6)

where the second-order derivative term is resulted from the interactions among atoms on the misfit plane and represents the correction from discrete effect. The discrete parameter $\beta$ for diamond structure crystals has been derived from a dynamics model [22]. For glide partial dislocations, the discrete parameter $\beta =\left(c_{11}-c_{12}\right)a^3{\sin }^2\theta /16.$ The energy factor $K=\mu [{\sin }^2\theta /\left(1-\nu \right)+{\cos }^2\theta )]$, where $\theta$, $\mu$ and $\nu$ are the dislocation angle, effective shear modulus and effective Poisson’s ratio in $\left\{111\right\}$ surface, respectively [21]. The derived effective shear modulus and Poison’s ratio are listed in

Table 2. The derived effective shear modulus and Poisson’s ratio in $\left\{111\right\}$ surface, $\mu$ is in unit of GPa.

GGA		LDA
$\mu$	$\nu$	$\mu$	$\nu$
39.5	0.269	44.5	0.286

. As suggested by Christian and Vitek [40], the nonlinear interaction force is given by the gradient of $\gamma$—surface as $f(u)=-\sigma ·\nabla \gamma \left(u\right)$, here $\sigma$ is the area of the primitive cell of the misfit plane.

There are two different slip sets for germanium due to its diamond-like structure, namely shuffle set and glide set, respectively (see Figure 3). For investigating the properties of ${30}^{\circ }$ partial dislocation, the $\gamma$—surface along the $1/2\langle 112\rangle$. direction on the glide set has been calculated with LDA and GGA method, respectively. The process of optimization is the same as that in Section 2. While for the Brillouin zone, the calculations of $\gamma$—surface employ $21\times 21\times 1$ grid meshes. In order to simulate the process of stacking fault, we employ a slab consisting of 12 atomic layers in the $\langle 111\rangle$ direction. The thickness of the vacuum layer is set to be 15 Å to avoid interactions between periodic images of the slabs. The $\gamma$—surface was generated by a set of rigid shifts of the upper half of the slab along $1/2\langle 112\rangle$ with respect to the lower half of the slab. For each step of the shift, we performed structural relaxation of the system allowing all atoms to move only in the $\langle 111\rangle$ direction by minimization of the Hellmann−Feynman forces on each atom.

The USFE given by GGA and LDA is 0.0803 eV/Ų and 0.0903 eV/Ų, the ISFE is 0.0051 eV/Ų and 0.0047 eV/Ų, respectively. The calculated $\gamma$—surface is shown in Figure 4. Kamimura et al. suggest that for the widely dissociated dislocation, the interaction effect between the trailing partial and the leading partial should be considered, the effective $\gamma$—surface is proposed accordingly [41]. The original and effective γ—surfaces can be approximately expressed as:

$$\gamma (u)={\gamma }_0{\cos }^2\frac{\pi u}{b}(1+{\gamma }_1{\cos }^2\frac{\pi u}{b}+{\gamma }_2{\cos }^4\frac{\pi u}{b}),$$

(7)

where b is the Burgers vector, the fitting curves of the $\gamma$—surfaces are shown in Figure 4 and the fitting parameters are listed in

Table 3. The fitting parameters of the $\gamma$ —surface, half width $\xi$ and Peierls stress ${\sigma }_P$ of ${30}^{°}$ partial dislocation in germanium. Original and Effective represent the original $\gamma$ —surface and effective $\gamma$ —surface, respectively; ${\xi }_0$ and ${\sigma }_P^0$ are the results calculated from the classical Peierls–Nabarro model. The Peierls stress is in unit of GPa.

		$${\mathit{\gamma }}_{\mathbf{0}}$$	$${\mathit{\gamma }}_{\mathbf{1}}$$	$${\mathit{\gamma }}_{\mathbf{2}}$$	$${\mathit{\xi }}_{\mathbf{0}}$$	$$\mathit{\xi }$$	$${\mathit{\sigma }}_{\mathit{P}}^{\mathbf{0}}$$	$${\mathit{\sigma }}_{\mathit{P}}$$
GGA	Original	0.0700	−0.73	0.30	0.18	0.24	17.4	1.6
	Effective	0.0685	−0.73	0.30	0.18	0.24	16.9	1.4
LDA	Original	0.0795	−0.74	0.31	0.18	0.24	20.1	1.6
	Effective	0.0775	−0.74	0.31	0.19	0.25	19.3	1.6

.

In order to investigate the difference between the original $\gamma$ —surface and the effective γ—surface, the core width and Peierls stress of 30° partial dislocation in germanium have been calculated by using these two γ—surfaces, respectively. The calculation methods of dislocation width and Peierls stress have been given in detail in ref. [22,39,42], and will not be repeated in this paper. The calculated half-width ξ and Peierls stress σ_p of 30° partial in germanium are listed in Table 3.

The ISFE of germanium is only about 5% to 6% of the USFE, therefore, the difference between the original γ—surface and the effective γ—surface is not obvious. Consequently, the dislocation widths and Peierls stresses calculated from these two γ—surfaces under the same calculation conditions are basically the same. Consequently, the original γ—surface can be directly used to study the dislocation structure and Peierls stress when the ratio of ISFE to USFE is small. While the ratio of ISFE to USFE is large, such as Cu, Ag and Au, etc. FCC metals, the effective γ—surface should be used when studying the Peierls stress. The 30° partial dislocation in germanium is very narrow, its core width is only a quarter of the Burgers vector, namely, only one in ten of the lattice constant. The narrow core of dislocation in germanium is reasonable due to the covalent interactions. Besides, the dislocation core and Peierls stress are widened and decreased by the discrete effect, respectively. The Peierls stress of 30° partial dislocation in germanium calculated from the classical Peierls–Nabarro model and improved Peierls–Nabarro model is about 17~20 GPa and 1.6 GPa, respectively. The result of 1.6 GPa agrees well with the experimental result 2~3 GPa reported in ref. [17]. According to the result of σ_p/μ of 30° partial dislocation in silicon given by Joos et al. and Ren et al. using the classical Peierls–Nabarro model [18,19,20], the Peierls stress of 30° partial in germanium is estimated to be 17~23 GPa, which is consistent with the result of 17~20 GPa in this paper calculated from the classical Peierls–Nabarro model. Obviously, the Peierls stress calculated from the classical Peierls–Nabarro model is about one order of magnitude larger than that calculated from the improved Peierls–Nabarro model. The main reason for such a big difference is the negligence of the discrete effect and the contribution of strain energy in the classical Peierls–Nabarro model [22].

4. Summary and Discussion

The elastic constants, core width and Peierls stress of 30° partial dislocation in germanium have been investigated based on the first-principles calculations and the improved Peierls–Nabarro model. The lattice constant calculated by the GGA method is about 2% larger than that calculated by LDA, and the elastic constants C₁₁, C₁₂, C₁₁₁, C₁₁₂, C₁₅₅ calculated by the GGA method are about 20% smaller than those calculated by LDA. The lattice constant is overestimated, the SOECs and most of the TOECs are underestimated by the GGA method, it is consistent with the results of ref. [36]. The predictions of lattice constant and elastic constants given by LDA are in better agreement with experiment results given in ref. [11]. Furthermore, when the Lagrangian strain is larger than 2% but lower than 8%, the nonlinear effects cannot be neglected and the third-order effects should be considered.

The ISFE is so low relative to the USFE that the difference between the original $\gamma$—surface and the effective $\gamma$—surface is very small, therefore, there is nearly no difference between the results calculated from these two $\gamma$—surfaces. Consequently, the original $\gamma$—surface can be directly used to study the dislocation structure and Peierls stress. The core width of the ${30}^{°}$ partial dislocation in germanium is very narrow (about one in ten of the lattice constant) due to the covalent interactions. The second-order elastic constants and $\gamma$—surface are used to calculate the Peierls stress based on the improved Peierls–Nabarro equation. Generally, the large second-order elastic constants may improve the discrete effects of crystals and thus lower the Peierls stress. On the contrary, the increase of unstable stacking fault energy prefers to enlarge the Peierls stress. That is to say, the second-order elastic constants and the $\gamma$—surface have opposite effects on the Peierls stress, leading to the same Peierls stress obtained from GGA and LDA methods. The Peierls stress of 30° partial dislocation in germanium calculated from the improved Peierls–Nabarro model agrees well with the experimental result reported in ref. [17]. While the result of the classical Peierls–Nabarro model is about ten times that of the improved Peierls–Nabarro model. The main reason for such a big difference is the negligence of the discrete effect and the contribution of strain energy in the classical Peierls–Nabarro model [22].

5. Conclusions

We studied the elastic constants, core width and Peierls stress of 30° partial dislocation in germanium based on the first-principles calculations and the improved Peierls–Nabarro model. The calculated results indicate that:

(1)

The lattice and elastic constants calculated by LDA method are in better agreement with the experimental results.

(2)

When the Lagrangian strain is larger than 2% but lower than 8%, the nonlinear effects cannot be neglected and the third-order effects should be considered.

(3)

If the ISFE is very low relative to the USFE, the original γ—surface can be directly used to study the dislocation structure and Peierls stress.

(4)

For the narrow dislocations in covalent materials, the discrete effect and the contribution of strain energy to the total energy of dislocation cannot be neglected.

The research method of this paper lays the foundation for theoretical research of the mechanical properties of the important third generation semiconductor gallium nitride.