Abstract
The parameters g-factor (
and ) together with the local structure of the Ce3+ center in BaWO4 single crystal (scheelite structure crystals) were theoretically investigated using a complete diagonalization procedure of energy matrix (CDM method). The intrinsic parameters were calculated. It is shown that the experimental and the calculated values of the g-factors are in good agreement. The angular distortion has also been calculated. It was found that the polar angles of the impurity–ligand bonding are smaller than in BaWO4 single crystal . The validity of the results and the changing in the local environment of the impurity–cerium ion is also discussed.
1. Introduction
The scheelite structure crystals, tungstate AWO4 (A = Ba, Sr, Ca, Pb) doped with trivalent rare-earth ions (Re3+), have received much interest thanks to their unusual properties such as luminescence, nonlinear optical activity, or scintillation [1,2,3,4,5,6] and for their application. The barium tungstate (BaWO4, BWO) is a very interesting inorganic optical material. Its potential applications include stimulated Raman scattering [7], scintillators and X-ray phosphor [8]. The blue and green PL emissions of BaWO4 are widely discussed for their importance in future optical applications [9,10,11]. The barium tungstate crystals (BaWO4) can also be used as a material for designing all solid-state lasers, especially for a wide variety of pump pulse durations in Raman laser pulses [12,13]. The barium tungstate (BaWO4) single crystals and nanocrystals have recently become the subject of intense scientific research [10,14]. More generally, many tungstate crystals like BaWO4, PbWO4, CaWO4, or SrWO4 are the subject of intense research because of their possible applications in optical devices such as lasers, or scintillators. Doping of tungstate crystals with rare earth elements (RE3+) like cerium (Ce3+), ytterbium (Yb3+), erbium (Er3+), etc., is a method of increasing their optical activity and their future applications.
The wolframite and scheelite structures are common structure types for ABO4 compounds [15]. The BaWO4 crystal crystallizes in tetragonal space group with C64h (I41/a) [16]. Lattice parameters of BWO are: a = b = 5.6148 Å, c = 12.721 Å [15,16]. Both Ba2+ and W6+ sites have S4 point symmetry. The Ba2+ ion is coordinated by eight O2- ions in the form of dodecahedron [BaO8] made of two rotated, interpenetrated tetrahedrons. The distance Ba–O is equal to 2.7857 Å and 2.8310 Å, respectively, for two tetrahedrons. Two tetrahedrons [BaO4] make up a dodecahedron [BaO8]. Apart from dodecahedrons [BaO8], [WO4] tetrahedrons are an important part in the unit cell of the BaWO4. The [WO4] tetrahedron has an almost regular shape only slightly distorted along the c (S4) axis. The distance between the W and the O ions is equal to 1.8230 Å [15]. Dodecahedrons [BaO8] are connected by their edges. Each O atom belongs to two dodecahedrons [BaO8] and one tetrahedron [WO4]. Figure 1 shows the unit cell structure of BaWO4 viewed along the b axis with marked dodecahedrons [BaO8] (blue). One can see that the unit cell of the BaWO4 has the biggest volume among ABO4 compounds (V = 401.0 Å3) [15].
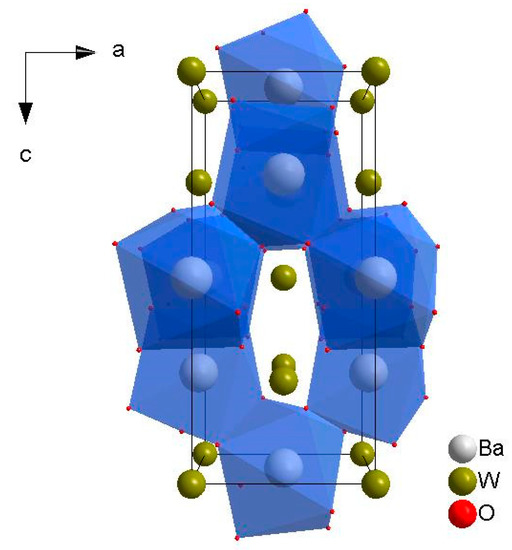
Figure 1.
Unit cell structure of BaWO4 viewed along the b axis with marked dodecahedrons [BaO8] (blue).
The present paper is a continuation of our research on the local structure of the BaWO4 single crystals doped and co-doped with ions of various elements. There are a few papers that have been investigating a local structure of BaWO4 single crystals doped and co-doped with, Ce, Na, Pr using EPR method [17,18,19]. Five paramagnetic centers with axial symmetry and about ten centers with low symmetry (C2) were found [17,18]. In the next step, we were investigated the connection between the g—shift and the environment of the Ce3+ centers with axial symmetry for four BaWO4 doped with Ce (cerium) and co-doped with Na (sodium) with different concentrations [20]. We also determined dislocations of Ce3+ ions. We were used a simplified method proposed by D. J. Newman [21]. Structural information can be obtained from spin–Hamiltonian parameters (and/or g-parameters) using a superposition model (SPM) [22,23] or perturbation methods (PM) up to second-order [24]. Previously, we used a simplified Newman model, a g-shift model [20]. In this paper, we choose to use superposition model (SPM) to obtain structural information on trivalent cerium ion (Ce3+) and its surroundings. Our investigations were focused on the most intense paramagnetic centers with axial symmetry presented in all four BaWO4 single crystals doped with Ce and co-doped with Na [17,18,19]. Obtained results will be compared with our previous results and other investigations.
We have found only one paper focused on rare-earth centers, this is Er3+ centers, in BaWO4 single crystals [25] and one other about similar, tetragonal Ce3+ centers in YPO4 and LuPO4 crystals [26]. However, one can find that there are several papers about: (a) Ce3+ and Yb3+ in garnets [27,28,29], (b) Ce3+, Yb3+ in YF3 crystal and Ce3+ in fluoride ligands [30,31], (c) Yb3+ in CaWO4 crystal [32], (d) Er3+ in CaWO4 and SrWO4 crystals [33], Er3+ in zircon-type compounds [34] or Er3+ in PbMoO4 and SrMoO4 [35], Er3+ at the Th4+ site in ThGeO4 [36], (e) Nb3+, Yb3+ in double tungstate’s and molybdates [37], (f) color centers in BaWO4 [38,39] and others [40,41]. All these papers are focused on analysis of spin–Hamiltonian parameters for the rare-earth ion surrounded by oxygen’s [ReO8] or fluoride’s dodecahedrons [ReF8]. It is interesting to compare our results with the results from these papers.
It is assumed that dopant ions such as rare earth ions (Re3+ like Ce3+, Er3+, or Yb3+) substitute in place of barium ions (Ba2+) [24,25,26,27,28,29,30]. Hence, two ReBa substitutions gives two excess positive charges, which are compensated by one the barium vacancy (VBa). The associated vacancies (VBa) do not necessarily affect the surroundings of the dopant ion, dodecahedron [ReO8]. In our previous articles, we described five paramagnetic centers (Ce3+) with axial symmetry detected in the EPR spectra of four BWO monocrystals doped with cerium and/or co-doped with sodium: (1) BaWO4: 0.5% at. Ce, (2) BaWO4: 1.0% at. Ce, (3) BaWO4: 0.5% at. Ce, 1.0% at. Na and (4) BaWO4: 1.0% at. Ce, 2.0% at. Na [17,18,19,20]. One of these centers is the strongest and occurs in all four monocrystals. It is g-factors are as follows: , . We will focus our analysis and calculations on this center with axial symmetry.
2. Calculations
Rare-earth ions (like Ce3+) substitute Ba2+ site in the elementary cell of the barium tungstate (BaWO4) [17,18,19,20,25,26,38]. The local symmetry of the CeBa site (Ba2+ place occupied by Ce3+) is S4 (tetragonal symmetry). However, the D2d symmetry approximation is often taken for many other rare-earth impurity ions (e.g., Yb3+, Er3+) in many scheelite-type oxygen and fluoride compounds because of the small distortion [25,26,38,39]. We will apply the D2d symmetry approximation here. Cerium ion (4f1 electronic configuration) in tetragonal symmetry has 2F5/2 ground state and 2F7/2 exited state. The crystal field with D2d symmetry splits the ground and exited states into three and four doublets, respectively. The Ce3+ ion has an effective spin S = ½, because only the lowest doublet is populated. The effective spin–Hamiltonian for Ce3+ ion in an external magnetic fields can be written as [42]:
where is free ion term, denotes spin–orbit interaction term, with —the spin-orbit coupling parameter, —crystal field term, and is Zeeman term. The Zeeman term is usually expressed as:
where is total angular momentum in the 2S+1LJ manifold. Therefore, we obtain 14 × 14 energy matrix and the energy levels (e.g., eigenvalues) can be calculated after diagonalization of spin–Hamiltonian matrices (1). Usually, the spin–Hamiltonian parameters for 4f1 ion are calculated using so-called complete diagonalization method (CDM), where the Zeeman term is not included to spin–Hamiltonian [26]. In this paper, the Zeeman term is added to spin–Hamiltonian and next the full spin–Hamiltonian is subject of complete diagonalization method (CDM) according H.G. Liu et al. [26]. Thus, no perturbation formula is needed. We get only g-factor parameters obtained from EPR measurements for Ce3+ in BaWO4 [17,18,19,20]. The g-factor can be obtained using CDM method using the following equations:
and are the Zeeman splitting between two the lowest energy levels (doublet) obtained by complete diagonalization the energy matrix from Equation (1), where the magnetic field is directed along the Z and the X axes, respectively. The crystal field interaction term for Ce3+ ion (4f1) in tetragonal symmetry (D2d) in terms of Stevens operator equivalent can be given as follows [22,42]:
there are the crystal field parameters, . According the superposition model (SPM), the crystal field parameters can be calculated as follows [21,22,23]:
the summation is only over the nearest neighbor ligands. In the case of the dodecahedron [CeO8] n = 8. The parameters and are the power law exponents and the intrinsic parameters, respectively. , called the reference distance, is often taken as a usual distance between the metal ion and the ligands. The parameters are the geometric coordination factors [23,24,26,43]. The Ce3+ ion is surrounded by eight O2− ions, and only these oxygens O2− ligands were included in the SPM model [20,28]. The dodecahedron [BaO8] is made in the form of two interpenetrated and rotated tetrahedrons. Figure 2 shows fragments of the BWO cell structure: a schematic view of the dodecahedron [BaO8] consisting of two rotated tetrahedrons with marked crystallographic axis Z (Z || c) and two polar angles .
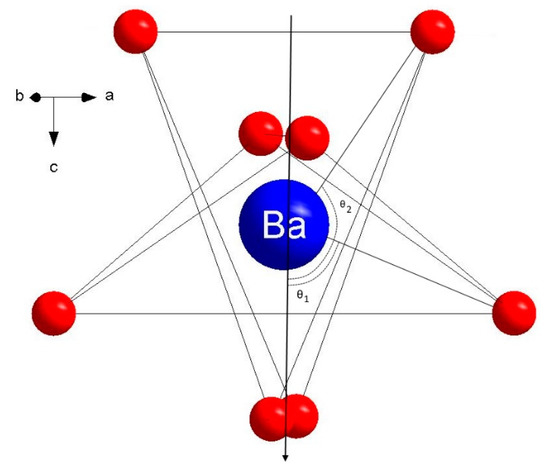
Figure 2.
Schematic view of the dodecahedron [BaO8] in BaWO4 single crystal consisting of two rotated tetrahedrons with marked crystallographic axis Z (Z || c) and two polar angles .
Therefore, we have two sets of the structural parameters: the distance and the polar angles , and the azimuthal angle , where means the first and the second tetrahedron, respectively. These polar and azimuthal angles are angles between the metal–ligand distance and Z (fourfold) axis and X axis of the crystal, respectively [25,44]. The values for the structural parameters [nm], , , and [nm], , , were obtained for the Ba2+ ion in the first and the second tetrahedron, respectively (see Figure 2) [44]. The ionic radii and the charge of the impurity rare-earth ion (like Ce3+) usually are different form host, e.g., barium ion (Ba2+). However, the local lattice relaxation arising from the size mismatch can be sufficiently good approximated from the equation [25,26]:
where and are the ionic radii of the impurity and the host ion, respectively. We assumed that [nm] and [nm] for Ce3+ and Ba2+ ions (both 6 coordination), respectively [43]. Now, one can estimate the distances for Ce3+ ion in both two tetrahedrons in BaWO4 single crystals according to Equation (6). The impurity–oxygens distances are changed. However, it is usually assumed that the polar angels and the azimuthal angles are the same as in the host crystal [25,44]. The structural data that were used in the calculations have been gathered in Table 1.

Table 1.
The structural data for Ce3+ ion in the barium site Ba2+ in the barium tungstate (BaWO4) [44].
(the reference distance) is taken as the average distance [nm]. The power law exponents were established as , , [22,23,26,28,40,41]. We also have to estimate the value of the spin–orbit coupling parameters. H. Ramanantoanina et al. calculated the value of the spin–orbit coupling in the Ce3+ ion embedded in the Cs2NaYCl6 crystal host [cm−1] [45]. Jun Wen et al. in the study of the Ce3+ ion doped in the various fluoride compounds estimated the value of [cm−1] [46]. H.G. Liu et al. in the investigation of the tetragonal Ce3+ centers in the YPO4 and LuPO4 crystals calculated the spin–orbit coupling parameter as [cm−1] and [cm−1] for YPO4 and LuPO4 crystals, respectively [26]. We decided to take the average of the two last spin–orbit coupling parameters, because YPO4 and LuPO4 crystals have similar zircon-type structure and the Ce3+ ion is surrounding by oxygens ligands, oxygens dodecahedron [CeO8] [26]. Therefore, we assumed that the spin–orbit coupling parameter (spin–orbit term in spin–Hamiltonian) is equal to [cm−1].
In first step, by substituting all these parameters into Equations (1)–(6), we can estimate the intrinsic parameters by fitting the EPR g-factors calculated using the new CDM method to the experimental values. Experimental and calculated values of the g-factor were calculated and have been gathered in Table 2, in the first and the second row. The differences between parallel and the perpendicular g-factor () have also been presented.

Table 2.
The EPR g factors for the axial Ce3+ center in BaWO4 single crystal.
The calculated intrinsic parameters for Ce3+ center in BaWO4 single crystal get values:
Table 2 shows that the calculated and observed g factor for Ce3+ center in BaWO4 single crystal are in quite a good agreement with each other, especially in the values of g parallel . In the next step, we tried to enhancing the fit, by varying the polar angles . The host metal–ligand polar angles (host–ligands) were replaced by polar angles (impurity–ligands) with small distortion: , there is the local angular distortion. We obtained the angular distortion:
It means that after decreasing the polar angles by one degree, we obtained the better fit to the experimental g-factors (Table 2, third row). The change is not so large, but visible. The difference in percentage between calculated and experimental values for the g perpendicular drop from 0.66% to 0.48% (see Table 2).
3. Discussion
The calculated g factors for above values of intrinsic parameters show good agreement with experimental values (see Table 2). However, the calculation based on the local distortion of the polar angels gives a slightly better fit to observed values of the g-factors. Hence, it is justifiable to say that the g-factor for tetragonal Ce3+ center in BaWO4 single crystal is quite well explained with additional information about the local structure of the Ce3+ ion in dodecahedron [CeO8]. There are several points that need further discussion.
First, the calculated intrinsic parameters fulfills inequality , where is order 600 [cm−1], and has a value of a few [cm−1]. Wu Shao-Yi et al. set the values of intrinsic parameters for Er3+ centers in BaWO4, CaWO4, and SrWO4 crystals [25,33]. H.G. Liu, W.C. Zheng and W.L. Feng calculated the intrinsic parameters from optical spectra for LuPO4: Ce, and YPO4: Ce single crystals with zircon structure [26]. We did not found other data regarding cerium ion, but there are many papers on rare-earth impurities, like Er3+, Yb3+, and Nd3+ in different oxide and fluoride crystals. The values of the (second rank) reach one thousand and more inverse centimeters (even [37]), while sixth rank intrinsic parameter reach a few inverse centimeters ( [37,40,41]. Therefore, the calculated values of intrinsic parameters (rank second, fourth and sixth) should be considered as reasonable and contained within the range of data.
The values of g-factors ( and ) for Ce3+ in BaWO4 single crystal, calculated and experimental are in good agreement (Table 2). For g parallel (), the fit is almost perfect. One can observe a small difference in the case of g perpendicular (, about 0.66 %). This difference decreases with the variation of the host metal–ligand polar angles with small distortion. The calculated angular distortion ° decrease a difference between experimental and calculated g perpendicular () to about 0.48 %. The calculated angular distortion for Ce3+ in BaWO4 agrees with angular distortion for other rare-earth ions. For example: angular distortion calculated for Er3+ in BaWO4 () [25], Ce3+ in Y3Al5O12 and Lu3Al5O12 garnets () [27], Yb3+ in Na3Sc2V3O12 garnet () [29], Er3+ in PbMoO4 and SrMoO4 (, respectively) [35]. It should be noticed that the angular distortion for Ce3+ in BaWO4 were calculated previously using a simplified SPM model () [20], from which follows that even a simplified SPM model can give a quite good angular distortion result useful for structural analysis. Our calculation shows that angular distortion of polar angles gives only a partial approximation to experimental values. The better approximation will be obtained by changing the azimuthal angles (), too. It means that oxygen ligands are not only coming slightly closer to a fourfold axis (Z or c axis), but oxygen tetrahedrons are also twisted (see Figure 2). Further calculations and structural analysis are required for further comprehension.
It should be pointed out that calculated intrinsic parameters were obtained only from the fitting procedure using SPM method to experimental EPR g-factors ( and ). These results should be considered as a first approximation and confirmed by fitting to results of the optical measurements. Unfortunately, we did not find the results of optical measurement of barium tungstate doped with cerium (BaWO4: Ce3+). If optical bands of BaWO4: Ce3+ will be recorded, our results could be a useful starting point. Our results could also be a useful help to structural analysis a local surroundings of the rare-earth ion (Ce3+), which substitute a Ba2+ site in oxygens dodecahedron [BaO8]. It may be important in further application of BaWO4: Ce3+ single crystals, for example in optical devices.
Author Contributions
Conceptualization, T.B.; Data curation, T.B.; Formal analysis, S.M.K.; Methodology, S.M.K.; Project administration, S.M.K.; Software, T.B.; Visualization, T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alencar, L.; Mesquita, A.; Feitosa, C.A.; Balzer, R.; Probst, L.F.; Batalha, D.C.; Rosmaninho, M.G.; Fajardo, H.V.; Bernardi, M.I. Preparation, characterization and catalytic application of Barium molybdate (BaMoO4) and Barium tungstate (BaWO4) in the gas-phase oxidation of toluene. Ceram. Int. 2017, 43, 4462–4469. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, I.; Sousa, R.; Matos, J.; Moura, J.; Freire, P.; Pinheiro, G.; Luz-Lima, C. Low-temperature induced phase transitions in BaWO4:Er3+ microcrystals: A Raman scattering study. J. Mol. Struct. 2020, 1204, 127498. [Google Scholar] [CrossRef]
- Tyagi, M.; Sangeeta, M.; Sabharwal, S. Luminescence properties of BaWO4 single crystal. J. Lumin. 2008, 128, 1528–1532. [Google Scholar] [CrossRef]
- Basiev, T.T.; Osiko, V.; Prokhorov, A.M.; Dianov, E.M. Solid-State Mid-Infrared Laser Sources; Springer Science & Business Media: Berlin, Germany, 2003; Volume 89, pp. 359–408. [Google Scholar]
- Wang, L.; Cui, X.; Wesch, W.; Wendler, E. He beam annealing and self-healing of Kr implanted BaWO4 at low temperature. J. Appl. Phys. 2021, 129, 165102. [Google Scholar] [CrossRef]
- Dabre, K.; Dhoble, S.; Lochab, J. Synthesis and luminescence properties of Ce3+ doped MWO4 (M = Ca, Sr and Ba) microcrystalline phosphors. J. Lumin. 2014, 149, 348–352. [Google Scholar] [CrossRef]
- Cerný, P.; Jelínková, H.; Basiev, T.T.; Zverev, P.G. Highly efficient picosecond Raman generators based on the BaWO/sub 4/ crystal in the near infrared, visible, and ultraviolet. IEEE J. Quantum Electron. 2002, 38, 1471–1478. [Google Scholar] [CrossRef]
- Mikhailik, V.B.; Kraus, H. Performance of scintillation materials at cryogenic temperatures. Phys. Status Solidi B 2010, 247, 1583. [Google Scholar] [CrossRef] [Green Version]
- Basiev, T.T.; Danileiko, Y.K.; Doroshenko, M.E.; Fedin, A.V.; Gavrilov, A.V.; Osiko, V.V.; Smetanin, S.N. High-energy BaWO4 Raman laser pumped by a self-phase-conjugated Nd:GGG laser. SPIE Proc. 2004, 5481, 23–27. [Google Scholar] [CrossRef]
- Wlodarczyk, D.; Bulyk, L.-I.; Berkowski, M.; Głowacki, M.; Kosyl, K.M.; Kaczmarek, S.M.; Kowalski, Z.; Wittlin, A.; Przybylinska, H.; Zhydachevskyy, Y.; et al. High-Pressure Low-Temperature Optical Studies of BaWO4:Ce,Na Crystals. Inorg. Chem. 2019, 58, 5617–5629. [Google Scholar] [CrossRef]
- Yin, Y.; Gan, Z.; Sun, Y.; Zhou, B.; Zhang, X.; Zhang, D.; Gao, P. Controlled synthesis and photoluminescence properties of BaXO4 (X = W, Mo) hierarchical nanostructures via a facile solution route. Mater. Lett. 2010, 64, 789–792. [Google Scholar] [CrossRef]
- Du, S.; Shi, Y.; Zhang, D.; Li, Q.; Feng, B.; Zhang, J.-Y.; Zang, J.-C. High-peak power multi-wavelength picosecond pulses generated from a BaWO4 Raman-seeded optical parametric amplifier. Opt. Commun. 2009, 282, 2960–2963. [Google Scholar] [CrossRef]
- Gao, L.; Wang, Q.P.; Zhang, X.Y.; Liu, Z.J.; Bai, F.; Chen, X.H.; Shen, H.B.; Lan, W.X. High-power Nd:YVO4/BaWO4 intracavity Raman laser emitting at 1103 nm. Appl. Phys. A 2012, 109, 9–13. [Google Scholar] [CrossRef]
- Vidya, S.; Solomon, S.; Thomas, J.K. Synthesis, Characterization, and Low Temperature Sintering of Nanostructured BaWO4 for Optical and LTCC Applications. Adv. Condens. Matter Phys. 2013, 2013, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Sleight, A.W. Accurate cell dimensions for ABO4 molybdates and tungstates. Acta Cryst. 1972, B28, 2899. [Google Scholar] [CrossRef]
- Chauhan, A. Czochralski growth and radiation hardness of BaWO4 Crystals. J. Cryst. Growth 2003, 254, 418–422. [Google Scholar] [CrossRef]
- Kaczmarek, S.M.; Leniec, G.; Bodziony, T.; Fuks, H.; Kowalski, Z.; Drozdowski, W.; Berkowski, M.; Głowacki, M.; Witkowski, M.E.; Makowski, M. BaWO4:Ce Single Crystals Codoped with Na Ions. Crystals 2019, 9, 28. [Google Scholar] [CrossRef] [Green Version]
- Leniec, G.; Kaczmarek, S.M.; Bodziony, T.; Fuks, H.; Kowalski, Z.; Berkowski, M.; Głowacki, M. Site Symmetries of Cerium Ions in BaWO4 Single Crystals Codoped with Sodium Ions. Appl. Magn. Reson. 2018, 50, 819–833. [Google Scholar] [CrossRef]
- Kaczmarek, S.; Witkowski, M.E.; Głowacki, M.; Leniec, G.; Berkowski, M.; Kowalski, Z.; Makowski, M.; Drozdowski, W. BaWO4: Pr single crystals co-doped with Na. J. Cryst. Growth 2019, 528, 125264. [Google Scholar] [CrossRef]
- Bodziony, T.; Kaczmarek, S.M. Structural Analysis of the BaWO4 Crystal Doped with Ce and Codoped with Na Ions Based on g-shift Parameters. Crystals 2020, 10, 789. [Google Scholar] [CrossRef]
- Newman, D.J. On the g-shift of S-state ions. J. Phys. C Solid State Phys. 1977, 10, L315–L318. [Google Scholar] [CrossRef]
- Newman, D.J.; Ng, B. Crystal Field Handbook; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Newman, D.; Urban, W. Interpretation of S-state ion E.P.R. spectra. Adv. Phys. 1975, 24, 793–844. [Google Scholar] [CrossRef]
- Wu, S.-Y.; Zheng, W.W. EPR parameters and defect structures for two trigonal Er3+ centers in LiNbO3 and MgO or ZnO codoped LiNbO3 crystals. Phys. Rev. B 2002, 65, 224107. [Google Scholar]
- Wu, S.-Y.; Dong, H.-N. Theoretical investigations of the EPR g factors and the local structure for Er3+ in BaWO4. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2004, 60, 1991–1994. [Google Scholar] [CrossRef]
- Liu, H.G.; Zheng, W.C.; Feng, W.L. Investigations of the optical spectra and EPR g-factors for the tetragonal Ce3+ centers in YPO4 and LuPO4 crystals. Philos. Mag. Lett. 2009, 89, 306–311. [Google Scholar] [CrossRef]
- Liu, H.-G.; Mei, Y.; Zheng, W.-C. Link between EPR g-factors and local structure of the orthorhombic Ce3+ center in Y3Al5O12 and Lu3Al5O12 garnets. Chem. Phys. Lett. 2012, 554, 214–218. [Google Scholar] [CrossRef]
- Liu, H.-G.; Paweł, G.; Czeslaw, R. Crystal field parameters for Yb3+ ions at orthorhombic centers in garnets—Revisited. J. Lumin. 2011, 131, 2690–2696. [Google Scholar] [CrossRef]
- Liu, H.G.; Zheng, W.C.; Feng, W.L. Spin-Hamiltonian parameters of Yb3+ions in trigonally-distorted octahedral sites of Na3Sc2V3O12 garnet. Philos. Mag. 2008, 88, 3075–3080. [Google Scholar] [CrossRef]
- Liu, H.G.; Zheng, W.C. Theoretical investigations of the optical and EPR spectra for trivalent cerium and ytterbium ions in orthorhombic YF3 crystal. Phys. B 2016, 496, 15–19. [Google Scholar] [CrossRef]
- Wen, J.; Ning, L.; Huang, Y.; Zhan, S.; Zhang, J.; Duan, C.-K.; Yin, M. Crystal field interactions between Ce3+ ion and fluoride ligands: A theoretical investigation. Mater. Res. Express 2015, 2, 086202. [Google Scholar] [CrossRef]
- Dong, H.-N.; Wu, S.-Y. Investigation of the spin Hamiltonian parameters of Yb3+ in CaWO4 crystal. Naturforschung 2004, 59, 943–946. [Google Scholar] [CrossRef]
- Wu, S.-Y.; Dong, H.-N.; Yan, W.-Z.; Gao, X.-Y. Theoretical studies of the spin-Hamiltonian parameters for Er3+ in CaWO4 and SrWO4. Phys. Status Solidi (b) 2004, 241, 1073–1077. [Google Scholar] [CrossRef]
- Wu, S.-Y.; Zheng, W.C. Investigations of the g factors and hyperfine structure parameters for Er3+ ion in zircon-type compounds. Spectrochim. Acta Part A 2002, 58, 3179–3183. [Google Scholar]
- Wu, S.-Y.; Dong, H.-N.; Wei, W.-H. Investigations on the local structures and the EPR parameters for Er3+ in PbMoO4 and SrMoO4. J. Alloy Compd. 2004, 375, 39–43. [Google Scholar] [CrossRef]
- Wu, S.-Y.; Dong, H.-N.; Wei, W.-H. Investigations of the spin-Hamiltonian parameters for Er3+ at the Th4+ site in ThGeO4. Spectrochim. Acta Part A 2005, 61, 2886–2890. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.-G.; Rudowicz, C.; Gnutek, P. Determination of the g-factors measured by EPR based on theoretical crystal field and superposition model analyses for lanthanide-based magnetically concentrated crystals—case study: Double tungstates and molybdates. Philos. Mag. 2018, 99, 224–246. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, T.; Zhang, Q.; Wang, X.; Yin, J.; Song, M.; Guo, X. First-principles study on electronic structures of BaWO4 crystals containing F-type color centers. J. Phys. Chem. Solids 2008, 69, 1815–1819. [Google Scholar] [CrossRef]
- Lin, X.S.; Chen, J.L.; Zhuang, N.F.; Zhao, B.; Chen, J.Z. Growth and characterization of Yb:BaWO4 single crystal. J. Cryst. Growth 2005, 277, 223–227. [Google Scholar] [CrossRef]
- Magnani, N.; Amoretti, G.; Baraldi, A.; Capelletti, R. Crystal-field and superposition model analysis of: BaY F (= Er, Dy, Nd). Eur. Phys. J. B 2002, 29, 79–84. [Google Scholar] [CrossRef]
- Magnani, N.; Amoretti, G.; Baraldi, A.; Capelletti, R. Superposition-model analysis of rare-earth doped BaY 2 F 8. Radiat. Eff. Defects Solids 2002, 157, 921–926. [Google Scholar] [CrossRef]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Clarendon Press: Oxford, UK, 1970. [Google Scholar]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. J. Acta Crystallogr. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Vishwamittar; Puri, S.P. Investigation of the crystal field in rare-earth doped scheelites. J. Chem. Phys. 1974, 61, 3720. [Google Scholar] [CrossRef]
- Ramanantoanina, H.; Urland, W.; García-Fuente, A.; Cimpoesu, F.; Daul, C. Calculation of the 4f1→4f05d1 transitions in Ce3+-doped systems by Ligand Field Density Functional Theory. Chem. Phys. Lett. 2013, 588, 260–266. [Google Scholar] [CrossRef]
- Wen, J.; Ning, L.; Duan, C.-K.; Chen, Y.; Zhang, Y.; Yin, M. A Theoretical Study on the Structural and Energy Spectral Properties of Ce3+ Ions Doped in Various Fluoride Compounds. J. Phys. Chem. C 2012, 116, 20513–20521. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).