High-Throughput Computation of New Carbon Allotropes with Diverse Hybridization and Ultrahigh Hardness
Abstract
:1. Introduction
2. Computational Procedure and Methods
- Step 1: Initially, the RG2 code generated 1598 carbon allotropes in total with different hybridization states.
- Step 2: We perform first-principles calculations to fully optimize those structures with low Monkhorst-pack k-mesh. The k-mesh in low-resolution DFT calculations depends on total number of atoms in the cell. Specifically, for numbers of atoms , , , and , the k-mesh was , , , and , respectively. After this step, we had 1576 carbon allotropes.
- Step 3: We continued to perform first-principles calculations to fully optimize the structures that were successfully optimized in the previous step, with high Monkhorst-pack k-mesh. The k-mesh in high-resolution DFT calculations depends on the length of lattice of the cell. Specifically, the product of the k-mesh in each direction and lattice size was approximately 60 Å. This was equivalent to the k-mesh of for diamond with an 8-atom conventional cell, which was high enough for global structure optimization. After this step, we had 1461 carbon allotropes.
- Step 4: After global structure optimization was finished, we cross-checked the 1461 carbon structures and also compared the structures with those downloaded from the SACADA database [29]. We found that some of the finally optimized structures had been already identified or reported in previous studies. After cross-checking and screening, we had 1105 new and unique carbon allotropes.
- Step 5: We finally calculated the elastic constants with conventional unit cells for all 1105 unique structures. Again, the k-mesh in each direction was determined by the same procedure as in Step 3. After this step, we successfully obtained the elastic constants of 1105 carbon allotropes.
- Step 6: Some structures had unreasonable universal anisotropy [32] so we decided to only report the carbon allotropes with universal anisotropy between 0 and 3. Finally, 904 carbon allotropes remained from all the screening processes.
3. Results and Discussion
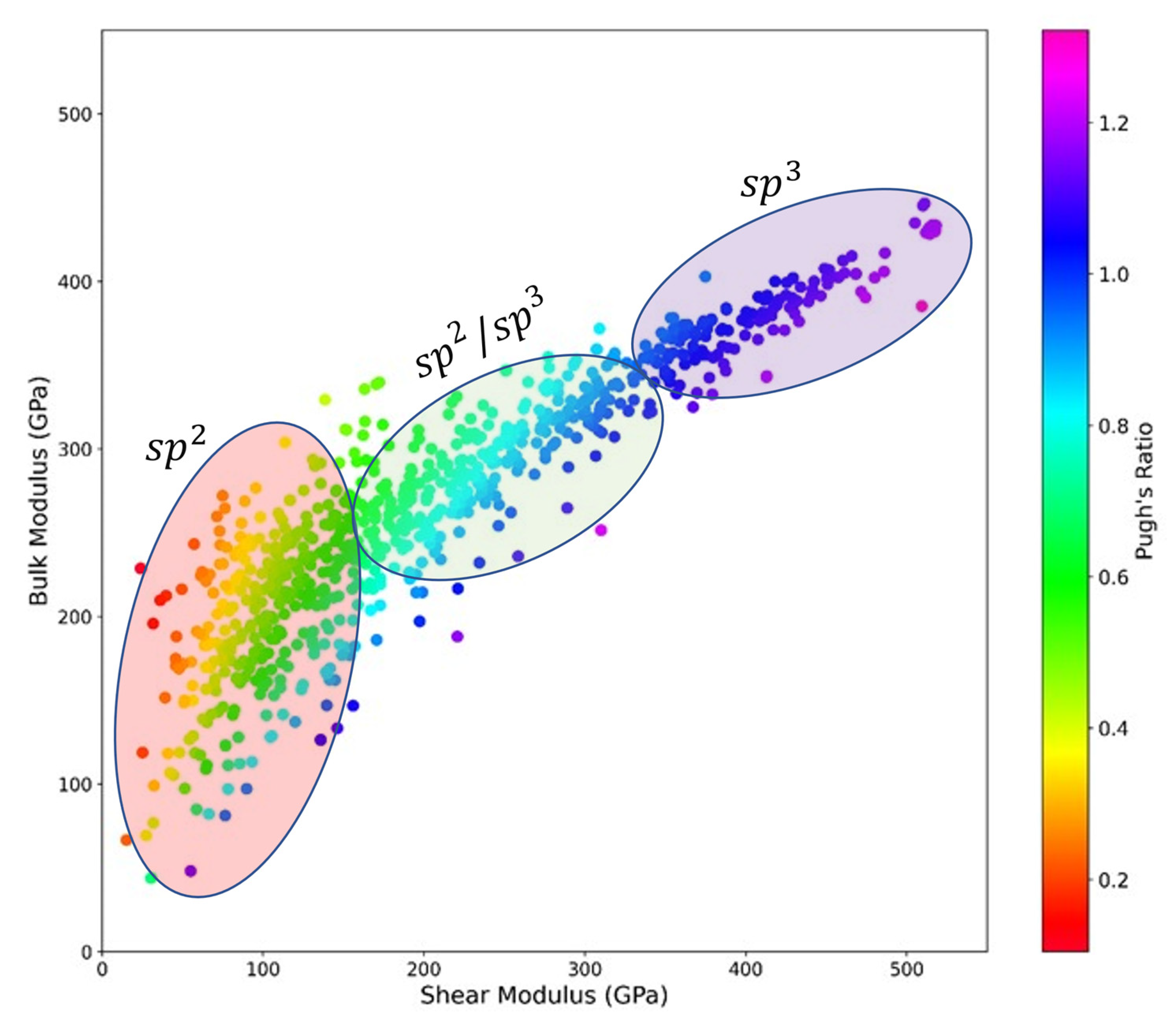
3.1. Ground-State Energy and Thermodynamic Stability
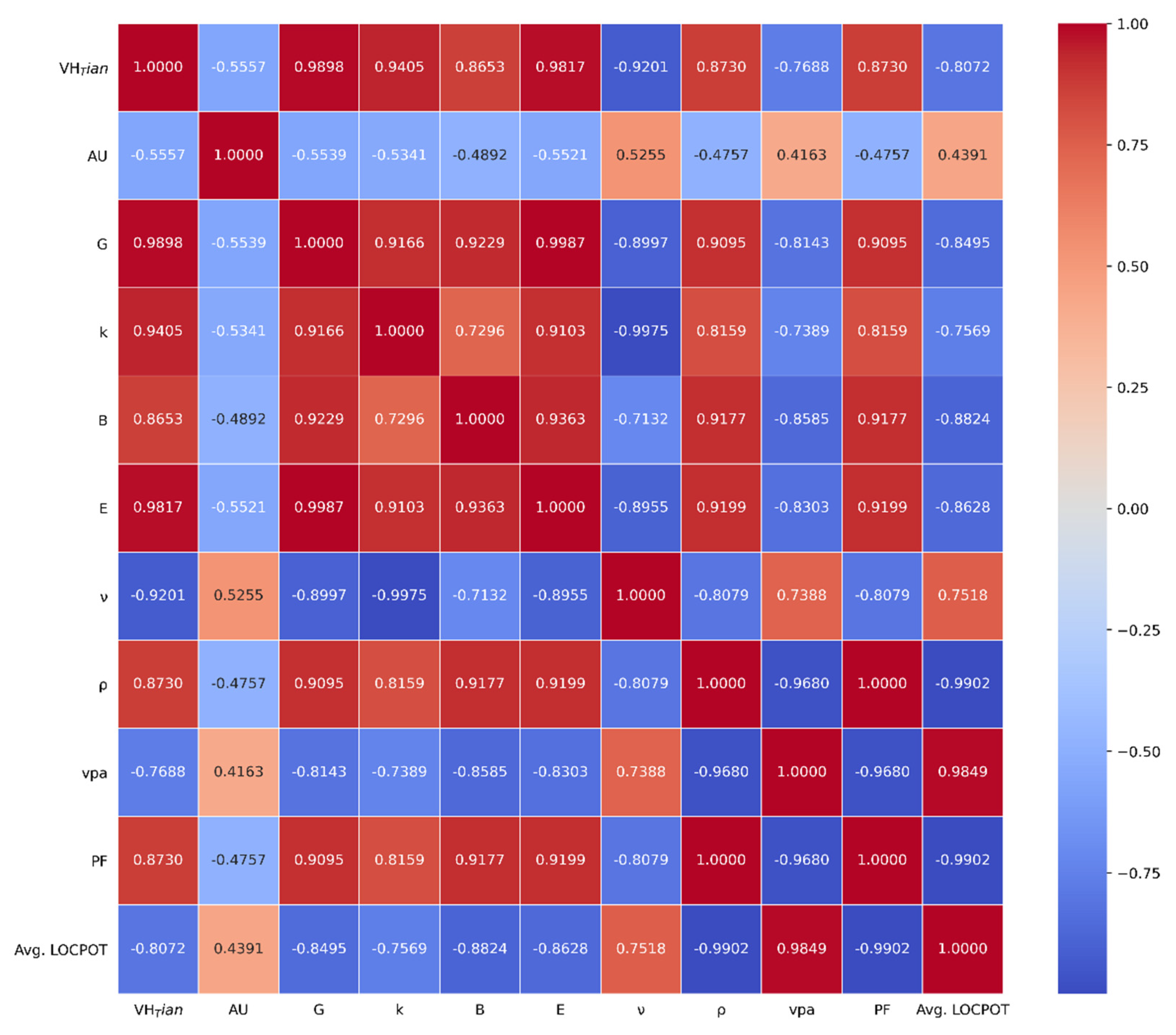
3.2. Pearson Correlation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Z.; Xu, B.; Wang, L.-M.; Zhou, X.-F.; He, J.; Liu, Z.; Wang, H.-T.; Tian, Y. Three dimensional carbon-nanotube polymers. ACS Nano 2011, 5, 7226–7234. [Google Scholar] [CrossRef]
- Miller, E.D.; Nesting, A.D.C.; Badding, J. Quenchable transparent phase of carbon. Chem. Mater. 1997, 9, 18–22. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Tait, K.; Liao, X.; Schiferl, D.; Zha, C.; Downs, R.T.; Qian, J.; Zhu, Y.; Shen, T. A quenchable superhard carbon phase synthesized by cold compression of carbon nanotubes. Proc. Natl. Acad. Sci. USA 2004, 101, 13699–13702. [Google Scholar] [CrossRef] [Green Version]
- Ivanovskaya, V.V.; Ivanovskii, A.L. Simulation of novel superhard carbon materials based on fullerenes and nanotubes. J. Superhard Mater. 2010, 32, 67–87. [Google Scholar] [CrossRef]
- Li, Q.; Ma, Y.; Oganov, A.R.; Wang, H.; Wang, H.; Xu, Y.; Cui, T.; Mao, H.-K.; Zou, G. Superhard monoclinic polymorph of carbon. Phys. Rev. Lett. 2009, 102, 175506. [Google Scholar] [CrossRef] [Green Version]
- Sheng, X.-L.; Yan, Q.-B.; Ye, F.; Zheng, Q.-R.; Su, G. T-Carbon: A novel carbon allotrope. Phys. Rev. Lett. 2011, 106, 155703. [Google Scholar] [CrossRef] [Green Version]
- Umemoto, K.; Wentzcovitch, R.M.; Saito, S.; Miyake, T. Body-centered tetragonal C4: A viable sp3 carbon allotrope. Phys. Rev. Lett. 2010, 104, 125504. [Google Scholar] [CrossRef]
- Zhou, X.-F.; Qian, G.-R.; Dong, X.; Zhang, L.; Tian, Y.; Wang, H.-T. Ab initio study of the formation of transparent carbon under pressure. Phys. Rev. B 2010, 82, 134126. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Oganov, A.R.; Salvadó, A.M.; Pertierra, P.; Lyakhov, A.O. Denser than diamond: Ab initio search for superdense carbon allotropes. Phys. Rev. B 2011, 83, 193410. [Google Scholar] [CrossRef] [Green Version]
- Mao, W.L.; Mao, H.-K.; Eng, P.J.; Trainor, T.P.; Newville, M.; Kao, C.-C.; Heinz, D.L.; Shu, J.; Meng, Y.; Hemley, R.J. Bonding changes in compressed superhard graphite. Science 2003, 302, 425–427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diederich, F.; Kivala, M. All-carbon scaffolds by rational design. Adv. Mater. 2010, 22, 803–812. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, A. The era of carbon allotropes. Nat. Mater. 2010, 9, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.T.; Chen, C.F.; Kawazoe, Y. Low-temperature phase transformation from graphite to sp3 orthorhombic carbon. Phys. Rev. Lett. 2011, 106, 075501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Z.; Xu, B.; Zhou, X.; Wang, L.-M.; Wen, B.; He, J.; Liu, Z.; Wang, H.-T.; Tian, Y. Novel superhard carbon: C-centered orthorhombic C8. Phys. Rev. Lett. 2011, 107, 215502. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.T.; Chen, C.F.; Kawazoe, Y. Orthorhombic carbon allotrope of compressed graphite: Ab initio calculations. Phys. Rev. B 2012, 85, 033410. [Google Scholar] [CrossRef] [Green Version]
- Kanyanta, V. Hard, superhard and ultrahard materials: An overview. In Microstructure-Property Correlations for Hard, Superhard, and Ultrahard Materials; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–23. [Google Scholar]
- Tehrani, A.M.; Brgoch, J. Hard and superhard materials: A computational perspective. J. Solid State Chem. 2019, 271, 47–58. [Google Scholar] [CrossRef]
- Haines, J.; Leger, J.M.; Bocquillon, G. Synthesis and design of superhard materials. Annu. Rev. Mater. Res. 2001, 31, 1–23. [Google Scholar] [CrossRef]
- Vepřek, S. Nanostructured superhard materials. In Handbook of Ceramic Hard Materials; Riedel, R., Ed.; Wiley: Weinheim, Germany, 2000; p. 109. [Google Scholar]
- Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. Thermodynamic model of hardness: Particular case of boron-rich solids. J. Superhard Mater. 2010, 32, 167–176. [Google Scholar] [CrossRef]
- Li, K.; Wang, X.; Zhang, F.; Xue, D. Electronegativity identification of novel superhard materials. Phys. Rev. Lett. 2008, 100, 235504. [Google Scholar] [CrossRef]
- Šimůnek, A.; Vackář, J. Hardness of covalent and ionic crystals: First-principle calculations. Phys. Rev. Lett. 2006, 96, 085501. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; He, J.; Wu, E.; Liu, S.; Yu, D.; Li, D.; Zhang, S.; Tian, Y. Hardness of covalent crystals. Phys. Rev. Lett. 2003, 91, 015502. [Google Scholar] [CrossRef] [PubMed]
- Teter, D.M. Computational alchemy: The search for new superhard materials. MRS Bull. 1998, 23, 22–27. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Shi, X.; He, C.; Pickard, C.J.; Tang, C.; Zhong, J. Stochastic generation of complex crystal structures combining group and graph theory with application to carbon. Phys. Rev. B 2018, 97, 014104. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Shi, X.; Clark, S.J.; Li, J.; Pickard, C.J.; Ouyang, T.; Zhang, C.; Tang, C.; Zhong, J. Complex low energy tetrahedral polymorphs of group IV elements from first principles. Phys. Rev. Lett. 2018, 121, 175701. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, R.; Kabanov, A.A.; Golov, A.A.; Proserpio, D.M. Homo citans and carbon allotropes: For an ethics of citation. Angew. Chem. Int. Ed. 2016, 55, 10962–10976. [Google Scholar] [CrossRef]
- Wang, J.-T.; Chen, C.; Kawazoe, Y. New carbon allotropes with helical chains of complementary chirality connected by ethene-type π-conjugation. Sci. Rep. 2013, 3, 3077. [Google Scholar] [CrossRef] [Green Version]
- Carey, F.A.; Sundberg, R.J. Advanced Organic Chemistry; Springer: New York, NY, USA, 2007. [Google Scholar]
- Ranganathan, S.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.; Shi, X.; He, C.; Martinez-Canales, M.; Li, J.; Pickard, C.J.; Tang, C.; Ouyang, T.; Zhang, C.; Zhong, J. Stone-Wales graphene: A two-dimensional carbon semimetal with magic stability. Phys. Rev. B 2019, 99, 041405. [Google Scholar] [CrossRef] [Green Version]
- Zhou, N.; Zhou, P.; Li, J.; He, C.; Zhong, J. Si-Cmma: A silicon thin film with excellent stability and Dirac nodal loop. Phys. Rev. B 2019, 100, 115425. [Google Scholar] [CrossRef]
- Ouyang, T.; Cui, C.; Shi, X.; He, C.; Li, J.; Zhang, C.; Tang, C.; Zhong, J. Systematic enumeration of low-energy graphyne allotropes based on a coordination-constrained searching strategy. Phys. Status Solidi Rapid Res. Lett. 2020, 14. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Page, Y.L.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials fromab initiocalcula-tions of stress. Phys. Rev. B 2002, 65. [Google Scholar]
- Zhang, S.; Zhang, R. AELAS: Automatic ELAStic property derivations via high-throughput first-principles computation. Comput. Phys. Commun. 2017, 220, 403–416. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Reuss, A.; Angew, Z. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Zener, C.M.; Siegel, S. Elasticity and anelasticity of metals. J. Phys. Chem. 1949, 53, 1468. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The elastic anisotropy of crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ward, L.; Dunn, A.; Faghaninia, A.; Zimmermann, N.E.; Bajaj, S.; Wang, Q.; Montoya, J.; Chen, J.; Bystrom, K.; Dylla, M.; et al. Matminer: An open source toolkit for materials data mining. Comput. Mater. Sci. 2018, 152, 60–69. [Google Scholar] [CrossRef] [Green Version]
- Doll, K.; Saunders, V.R.; Harrison, N.M. Analytical Hartree-Fock gradients for periodic systems. Int. J. Quantum Chem. 2000, 82, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Yang, Z.; Yuan, K.; Meng, J.; Zhang, X.; Tang, D.; Hu, M. Why thermal conductivity of CaO is lower than that of CaS: A study from the perspective of phonon splitting of optical mode. Nanotechnology 2020, 32, 025709. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Qin, G.; Li, G.; Wang, Q.; Hu, M. Low thermal conductivity of monolayer ZnO and its anomalous temperature dependence. Phys. Chem. Chem. Phys. 2017, 19, 12882–12889. [Google Scholar] [CrossRef] [PubMed]
- Yue, S.-Y.; Qin, G.; Zhang, X.; Sheng, X.; Su, G.; Hu, M. Thermal transport in novel carbon allotropes with sp2 or sp3 hybridization: An ab initio study. Phys. Rev. B 2017, 95, 085207. [Google Scholar] [CrossRef]
- Zhao, Y.; Al-Fahdi, M.; Hu, M.; Siriwardane, E.; Song, Y.; Nasiri, A.; Hu, J. High-throughput discovery of novel cubic crystal materials using deep generative neural networks. Adv. Sci. 2021, in press. [Google Scholar]
- Emery, A.A.; Wolverton, C. High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data 2017, 4, 170153. [Google Scholar] [CrossRef] [Green Version]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77, 733–742. [Google Scholar] [CrossRef]
- Gilman, J.J. Hardness e a strength microprobe. In The Science of Hardness Testing and its Research Applications; Westbrook, J.H., Conrad, H., Eds.; American Society of Metal: Metal Park, OH, USA, 1973; Chapter 4. [Google Scholar]
- Liu, A.Y.; Cohen, M.L. Prediction of new low compressibility solids. Science 1989, 245, 841–842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, F.M.; Gao, L.H. Microscopic models of hardness. J. Superhard Mater. 2010, 32, 148–166. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.-C.; Fecher, G.H.; Naghavi, S.S.; Felser, C. Elastic properties and stability of Heusler compounds: Cubic Co2YZ compounds with L21 structure. J. Appl. Phys. 2019, 125, 082523. [Google Scholar] [CrossRef] [Green Version]
- Nye, J.F.; Lindsay, R.B. Physical properties of crystals: Their representation by tensors and matrices. Phys. Today 1957, 10, 26. [Google Scholar] [CrossRef]

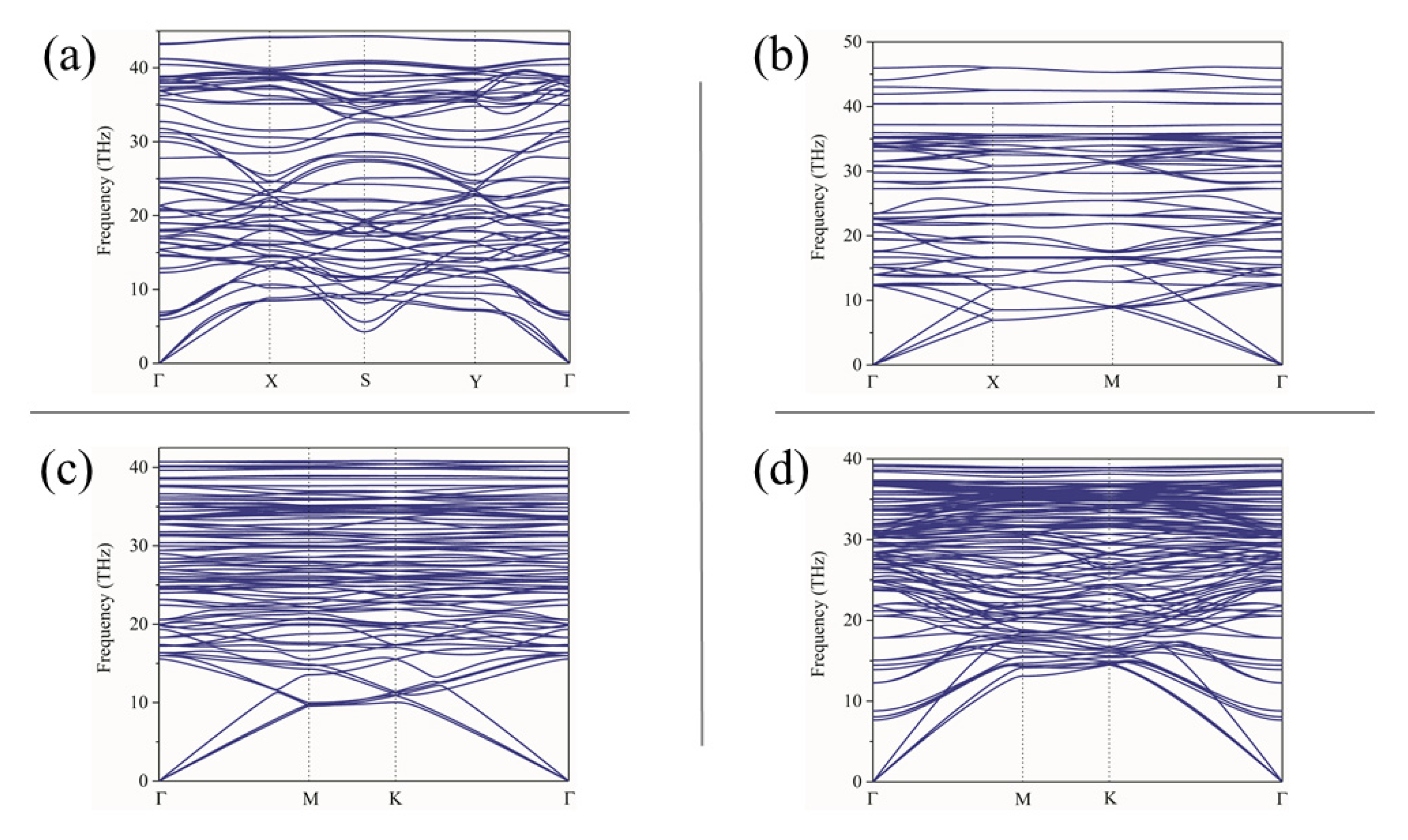

| Materials | Hybridizations | Vickers’ Hardness, (GPa) | Ground-State Energy, (eV) | Average Local Potential, (eV) |
|---|---|---|---|---|
| (a) 135-3-40-C-r89-np-id355667 | 30.88994 | −341.2203 | −11.7709 | |
| (b) 136-3-20-C-r689-np-id545421_1 | Hybrid / | 69.35087 | −175.5362 | −12.7828 |
| (c) 179-3-36-C-r6789-p-id545421 | 90.11029 | −320.6033 | −12.9213 | |
| (d) 165-3-28-C-r68-np-id545421 | 90.10081 | −245.7932 | −13.1631 |
| Materials | Vickers’ Hardness, (GPa) | Universal Anisotropy | Bulk Modulus, (GPa) | Elastic Modulus, (GPa) | Poisson’s Ratio | Volume Per Atom | Packing Fraction | Average Local Potential, (eV) | |
|---|---|---|---|---|---|---|---|---|---|
| 206-1-16-C-r0-np-id355667 | 104.302 | 0.00457 | 385.28 | 1060.73 | 0.04114 | 3.5534 | 5.61272 | 0.25595 | −13.467 |
| 181-1-6-C-r0-p-id224838_1 | 94.8507 | 0.04505 | 429.82 | 1108.01 | 0.07036 | 3.9125 | 5.71263 | 0.2515 | −13.185 |
| 154-1-6-C-r0-p-id224838 | 94.36159 | 0.044264 | 431.9735 | 1109.813 | 0.071805 | 3.496109 | 5.704695 | 0.251855 | −13.195 |
| 180-1-12-C-r0-p-id224838 | 94.16793 | 0.055942 | 428.2763 | 1102.033 | 0.071136 | 3.485896 | 5.72141 | 0.251119 | −13.169 |
| 182-1-12-C-r6x-p-id224838 | 94.13454 | 0.084798 | 433.4282 | 1111.486 | 0.072599 | 3.487636 | 5.718554 | 0.251244 | −13.169 |
| Materials | Vickers’ Hardness, (GPa) | Universal Anisotropy | Bulk Modulus, (GPa) | Elastic Modulus, (GPa) | Poisson’s Ratio | Volume Per Atom | Packing Fraction | Average Local Potential (eV) | |
|---|---|---|---|---|---|---|---|---|---|
| 224-3-72-C-r69-np-id355667 | 2.99986 | 1.56873 | 99.07801 | 87.23116 | 0.353262 | 1.561686 | 12.77097 | 0.112502 | −8.092 |
| 131-2-48-C-r68x-np-id224838 | 3.082382 | 2.944065 | 170.7716 | 125.9887 | 0.37704 | 2.074342 | 9.61473 | 0.149433 | −9.773 |
| 207-3-72-C-r689-np-id224838 | 1.162879 | 1.085925 | 66.67588 | 42.13926 | 0.394666 | 1.276296 | 15.62666 | 0.091943 | −6.915 |
| 222-3-112-C-r6x-np-id355667 | 1.541133 | 1.974846 | 118.8571 | 70.42662 | 0.401245 | 1.477887 | 13.4951 | 0.106465 | −7.750 |
| 155-3-54-C-r6x-p-id355667 | 3.318981 | 2.33672 | 69.3944 | 72.49172 | 0.325894 | 1.541569 | 12.93762 | 0.111052 | −8.030 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Fahdi, M.; Rodriguez, A.; Ouyang, T.; Hu, M. High-Throughput Computation of New Carbon Allotropes with Diverse Hybridization and Ultrahigh Hardness. Crystals 2021, 11, 783. https://doi.org/10.3390/cryst11070783
Al-Fahdi M, Rodriguez A, Ouyang T, Hu M. High-Throughput Computation of New Carbon Allotropes with Diverse Hybridization and Ultrahigh Hardness. Crystals. 2021; 11(7):783. https://doi.org/10.3390/cryst11070783
Chicago/Turabian StyleAl-Fahdi, Mohammed, Alejandro Rodriguez, Tao Ouyang, and Ming Hu. 2021. "High-Throughput Computation of New Carbon Allotropes with Diverse Hybridization and Ultrahigh Hardness" Crystals 11, no. 7: 783. https://doi.org/10.3390/cryst11070783
APA StyleAl-Fahdi, M., Rodriguez, A., Ouyang, T., & Hu, M. (2021). High-Throughput Computation of New Carbon Allotropes with Diverse Hybridization and Ultrahigh Hardness. Crystals, 11(7), 783. https://doi.org/10.3390/cryst11070783







