Wave Dispersion in One-Dimensional Nonlinear Local Resonance Phononic Crystals with Perturbation Method
Abstract
1. Introduction
2. Dispersion Relation of Linear Mass-in-Mass Lattice Model
3. Nonlinear Mass-in-Mass Lattice Analysis with the Perturbation Method
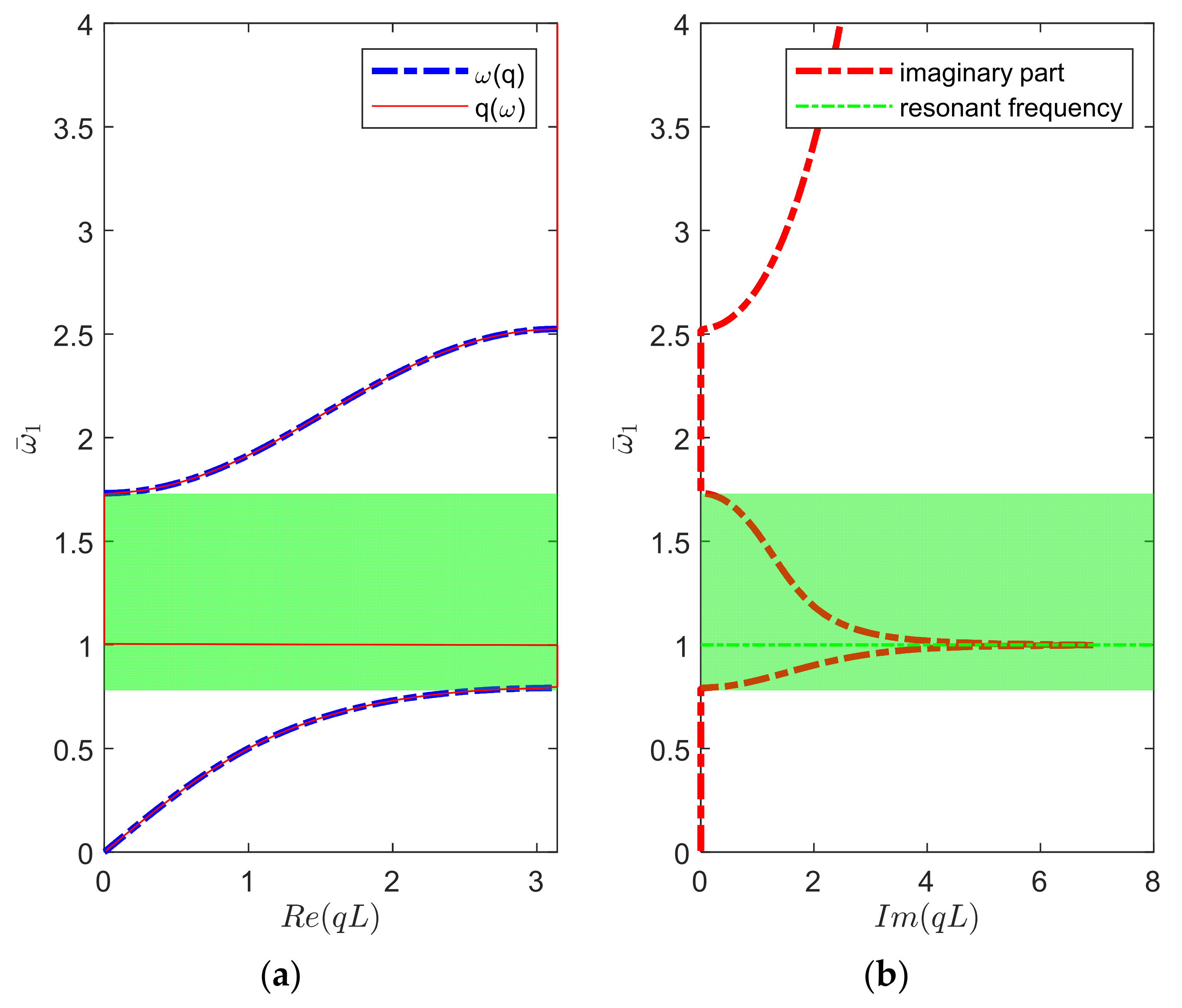
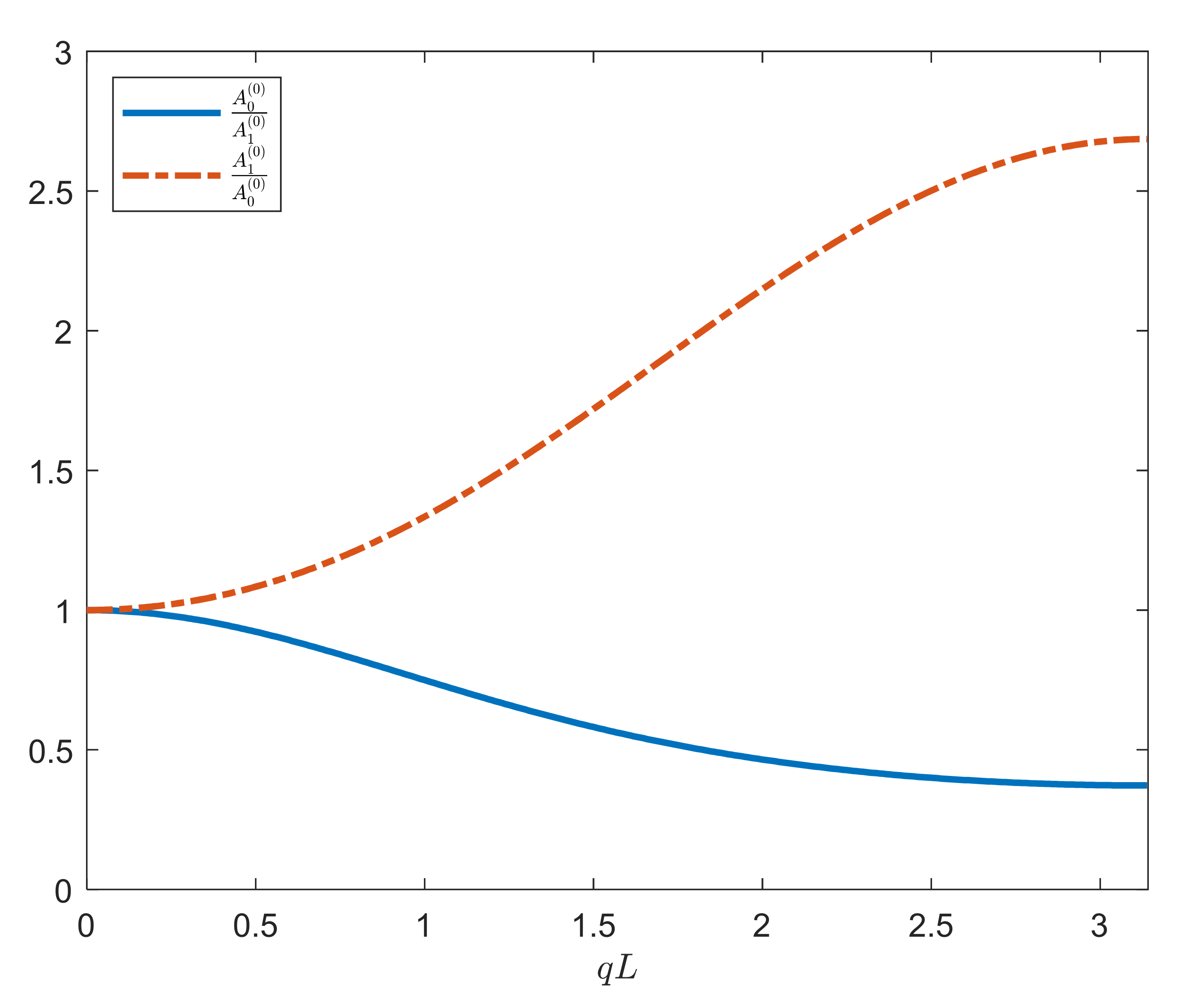
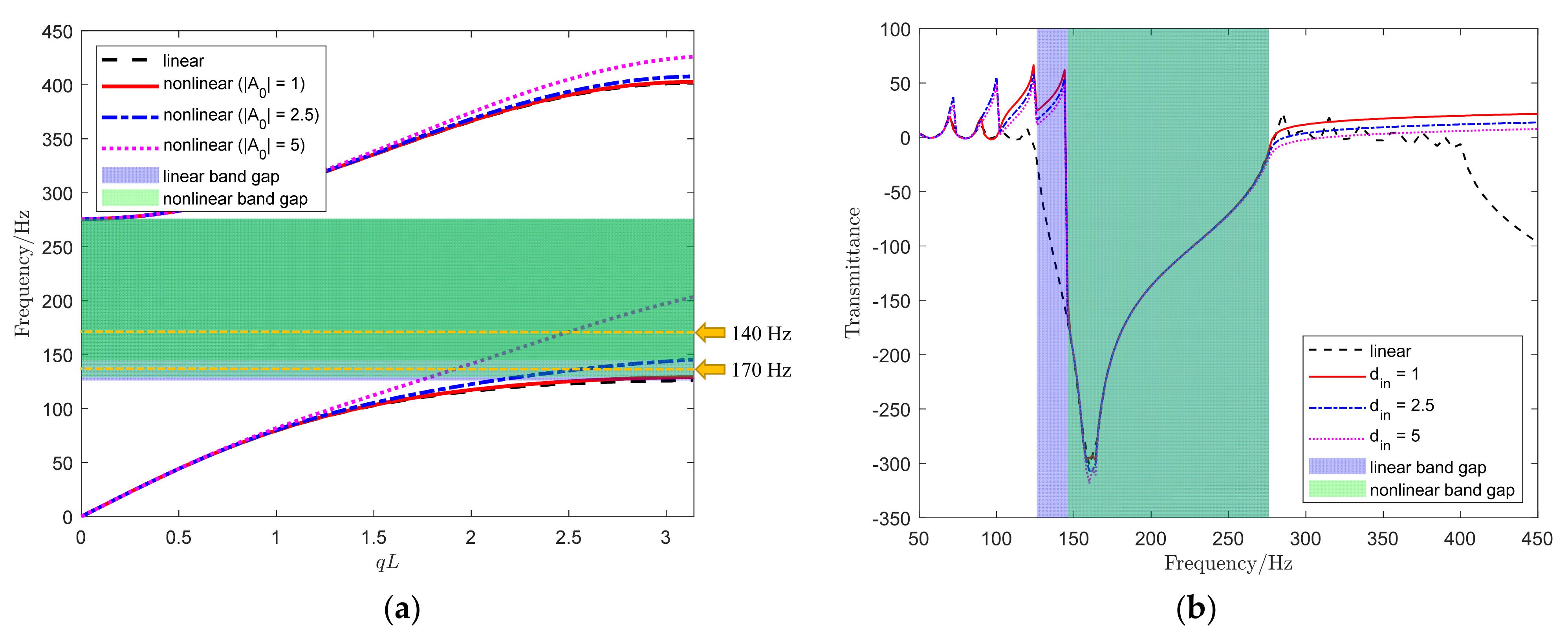
3.1. Nonlinear Dispersion Relations
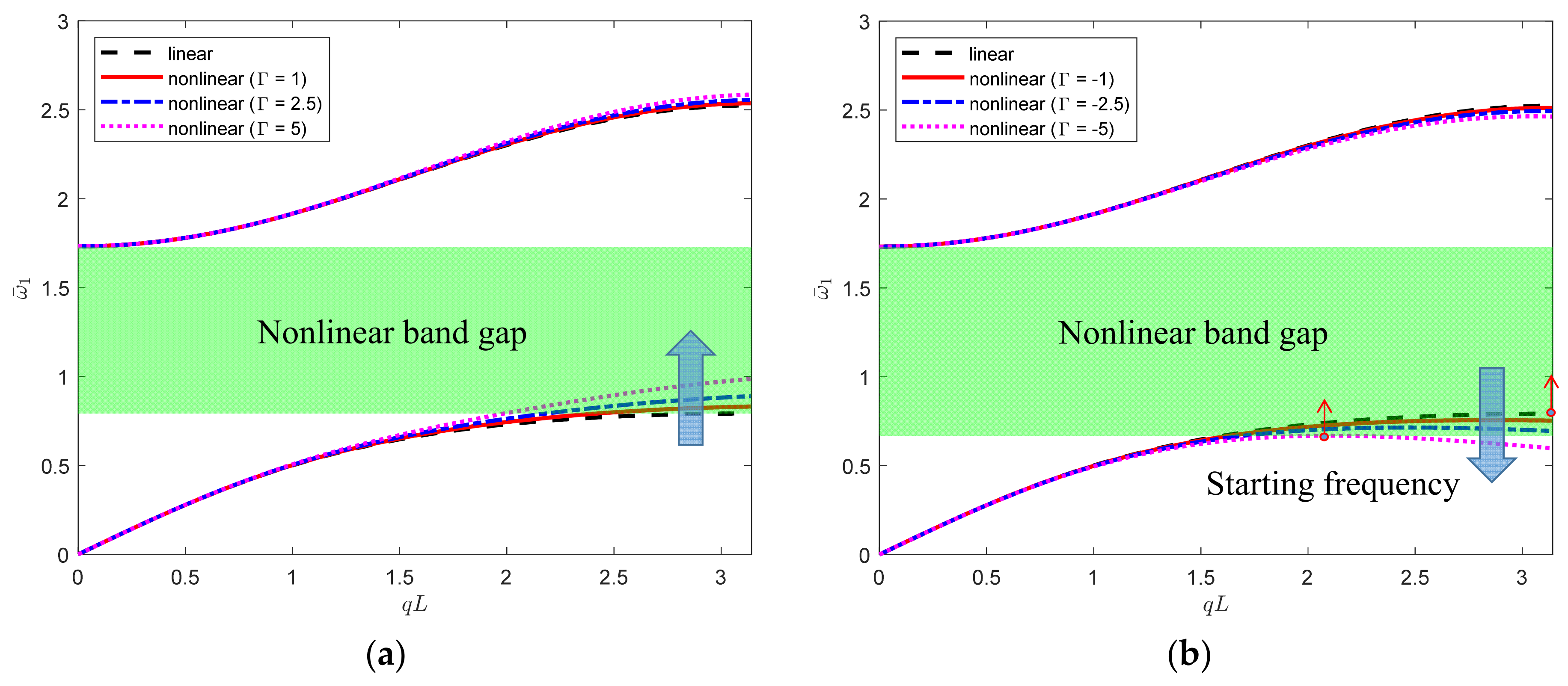
3.2. Effect of the Degree of Nonlinearity
3.3. Effect of the Wave Amplitude
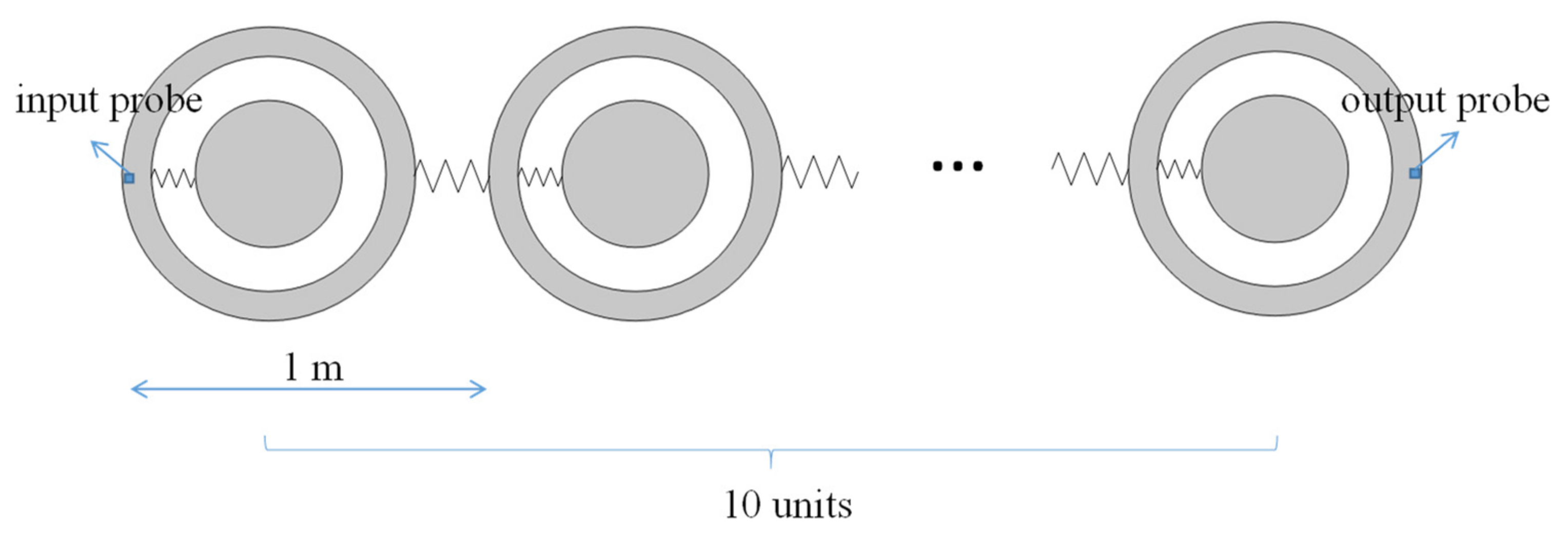
4. Transmittance Based on Finite Element Model
4.1. Transmittance with Linear Spring Constant
4.2. Transmittance with Nonlinear Spring Coefficient
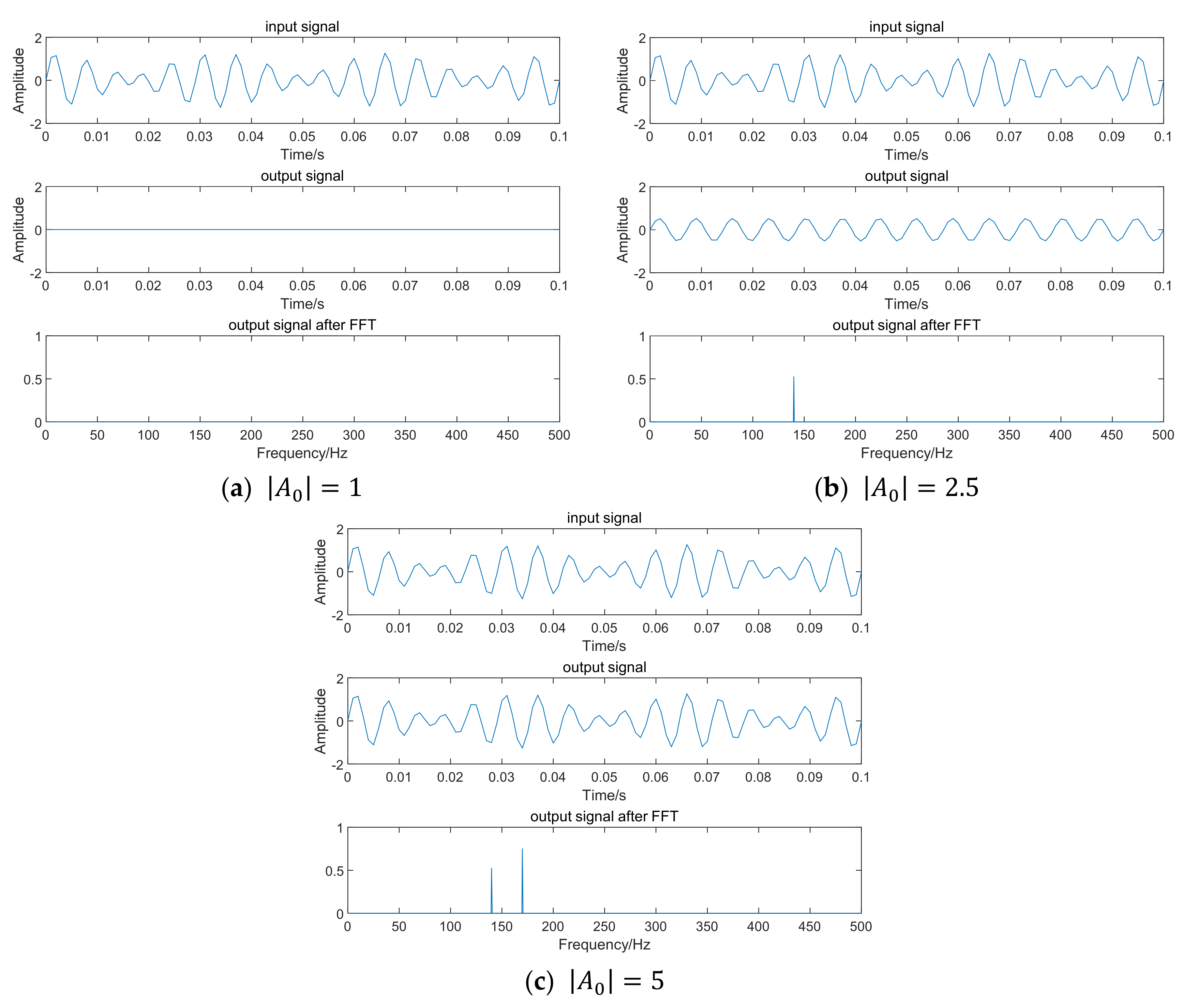
5. Application Example Based on Nonlinear Dispersion Relations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sheng, P.; Zhang, X.X.; Liu, Z.; Chan, C.T. Locally resonant sonic materials. Phys. B Condens Matter 2003, 338, 201–205. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T. Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J. Phys. 2009, 11. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Wang, G.; Cai, L.; Qiu, J. Low frequency torsional vibration gaps in the shaft with locally resonant structures. Phys. Lett Sect. A Gen. At. Solid State Phys. 2006, 348, 410–415. [Google Scholar] [CrossRef]
- Shao, H.B.; He, H.; Chen, Y.; Chen, G.P. A novel multi-cavity Helmholtz muffler. Chin. Phys. B 2019, 28. [Google Scholar] [CrossRef]
- Liang, B.; Yuan, B.; Cheng, J.C. Acoustic diode: Rectification of acoustic energy flux in one-dimensional systems. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Boechler, N.; Theocharis, G.; Daraio, C. Bifurcation-based acoustic switching and rectification. Nat. Mater. 2011, 10, 665–668. [Google Scholar] [CrossRef] [PubMed]
- Luongo, A.; Rega, G.; Vestroni, F. On nonlinear dynamics of planar shear indeformable beams. J. Appl. Mech. Trans. ASME 1986, 53, 619–624. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, K.; Xu, D.; Ouyang, H. Local resonator with high-static-low-dynamic stiffness for lowering band gaps of flexural wave in beams. J. Appl. Phys. 2017, 121. [Google Scholar] [CrossRef]
- Vakakis, A.F.; King, M.E. Nonlinear wave transmission in a monocoupled elastic periodic system. J. Acoust. Soc. Am. 1995, 98, 1534–1546. [Google Scholar] [CrossRef]
- Romeo, F.; Rega, G. Wave propagation properties in oscillatory chains with cubic nonlinearities via nonlinear map approach. Chaos Solitons Fractals 2006, 27, 606–617. [Google Scholar] [CrossRef][Green Version]
- Wang, G.; Yu, D.; Wen, J.; Liu, Y.; Wen, X. One-dimensional phononic crystals with locally resonant structures. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2004, 327, 512–521. [Google Scholar] [CrossRef]
- Manktelow, K.; Leamy, M.J.; Ruzzene, M. Multiple scales analysis of wave-wave interactions in a cubically nonlinear monoatomic chain. Nonlinear Dyn. 2011, 63, 193–203. [Google Scholar] [CrossRef]
- Narisetti, R.K.; Ruzzene, M.; Leamy, M.J. Study of wave propagation in strongly nonlinear periodic lattices using a harmonic balance approach. Wave Motion 2012, 49, 394–410. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, W.; Lim, C.W. Active control for acoustic wave propagation in nonlinear diatomic acoustic metamaterials. Int. J. Non Linear Mech. 2020, 125, 103535. [Google Scholar] [CrossRef]
- Zhou, G.; Wu, J.H.; Lu, K.; Tian, X.; Huang, W.; Zhu, K. Broadband low-frequency membrane-type acoustic metamaterials with multi-state anti-resonances. Appl. Acoust. 2020, 159, 107078. [Google Scholar] [CrossRef]
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adapt. Syst. Signal Process. Commun. Control Symp. (Cat. No.00EX373), Lake Louise, AB, Canada, 4 October 2020; pp. 153–158. [Google Scholar] [CrossRef]
- Elachi, C. Waves in Active and Passive Periodic Structures: A Review. Proc. IEEE 1976, 64, 1666–1698. [Google Scholar] [CrossRef]
- Shao, H.; He, H.; Chen, G.; Chen, Y. Two new designs of lamp-type piezoelectric metamaterials for active wave propagation control. Chin. J. Phys. 2020, 65, 1–13. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Li, G.; Sun, R.; Chen, G. Wave Dispersion in One-Dimensional Nonlinear Local Resonance Phononic Crystals with Perturbation Method. Crystals 2021, 11, 774. https://doi.org/10.3390/cryst11070774
Chen Y, Li G, Sun R, Chen G. Wave Dispersion in One-Dimensional Nonlinear Local Resonance Phononic Crystals with Perturbation Method. Crystals. 2021; 11(7):774. https://doi.org/10.3390/cryst11070774
Chicago/Turabian StyleChen, Yan, Gen Li, Rujie Sun, and Guoping Chen. 2021. "Wave Dispersion in One-Dimensional Nonlinear Local Resonance Phononic Crystals with Perturbation Method" Crystals 11, no. 7: 774. https://doi.org/10.3390/cryst11070774
APA StyleChen, Y., Li, G., Sun, R., & Chen, G. (2021). Wave Dispersion in One-Dimensional Nonlinear Local Resonance Phononic Crystals with Perturbation Method. Crystals, 11(7), 774. https://doi.org/10.3390/cryst11070774





