The Depth-Dependent Mechanical Behavior of Anisotropic Native and Cross-Linked HheG Enzyme Crystals

Abstract

Enzymes are able to catalyze various specific reactions under mild conditions and can, therefore, be applied in industrial processes. To ensure process profitability, the enzymes must be reusable while ensuring their enzymatic activity. To improve the processability and immobilization of the biocatalyst, the enzymes can be, e.g., crystallized, and the resulting crystals can be cross-linked. These mechanically stable and catalytically active particles are called CLECs (cross-linked enzyme crystals). In this study, the influence of cross-linking on the mechanical and catalytic properties of the halohydrin dehalogenase (HheG) crystals was investigated using the nanoindentation technique. Considering the viscoelastic behavior of protein crystals, a mechanical investigation was performed at different indentation rates. In addition to the hardness, for the first time, depth-dependent fractions of elastic and plastic deformation energies were determined for enzyme crystals. The results showed that the hardness of HheG enzyme crystals are indentation-rate-insensitive and decrease with increases in penetration depth. Our investigation of the fraction of plastic deformation energy indicated anisotropic crystal behavior and higher irreversible deformation for prismatic crystal faces. Due to cross-linking, the fraction of elastic energy of anisotropic crystal faces increased from 8% for basal faces to 68% for prismatic crystal faces. This study demonstrates that mechanically enhanced CLECs have good catalytic activity and are, therefore, suitable for industrial use.

1. Introduction

Halohydrin dehalogenases (HHDHs) (E.C. 4.5.1.-) are bacterial lyases that belong to the superfamily of short-chain dehydrogenases and reductases [1]. Apart from the degradation of toxic halogenated compounds, the industrial relevance of these lyases is based on their epoxide ring opening activities with a wide range of different nucleophiles enabling the formation of novel C–C, C–N, C–O, and C–S bonds [2]. Here, halohydrin dehalogenase HheG from Ilumatobacter coccineus is of special interest due to its ability to accept cyclic and other sterically demanding epoxide substrates such as vicinally di-substituted epoxides, further broadening the accessible product range of β-substituted alcohols [3,4,5]. Moreover, HheG is able to catalyze the α-regioselective ring-opening of different styrene oxide derivatives, with cyanate yielding the corresponding oxazolidinones [6]. The resulting products represent important compounds for the synthesis of fungicides and antibiotics [7,8]. Moreover, oxazolidinones are used as chiral auxiliaries in chemical synthesis [9]. Due to the wide range of its use, this enzyme is of special interest for future industrial applications.

To reach their full industrial potential, enzymes must meet various requirements for industrial applications, such as shear force resistance in a bioreactor and reusability. For this reason, soluble enzymes can be immobilized on a carrier or cross-linked as protein particles, either as crystals (CLECs) or aggregates (CLEAs) [10]. The mechanical behavior of protein crystals or aggregates depends on the structure of the individual protein molecules, the packing density, and the conformation within the three-dimensional structure of the protein particles [11] and must, therefore, be investigated individually. Since the mechanical stability of particulate biocatalysts is a fundamental property required for industrial applications, knowledge of the mechanical properties of these biocatalysts is of great interest. Previous studies have reported on the micromechanics of native protein crystals [12,13,14,15,16,17], as well as their fragility and sensitivity to environmental changes [18,19]. In recent years, there has been increasing interest in enhancing mechanical stability by cross-linking enzyme crystals [20,21]. This immobilization method offers stabilization of the crystalline enzyme structure while maintaining catalytic activity [20,22]. This technology is complementary to protein engineering methods that aim at boosting the inherent stability of an enzyme [23]. One of the most commonly used linkers for the immobilization of enzyme crystals described in the current literature is glutaraldehyde [24,25] because of its low cost, ease of handling, and high efficacy [26]. Morozov et al. were the first to use a resonance technique to measure parent (native) and cross-linked triclinic lysozyme crystals, as well as the Young’s modulus of the parent protein crystals in a range of 290−1400 MPa. The authors also reported no significant influence from the cross-linking of protein crystals on this value range [27]. In contrast, Lee et al. investigated the breakage probability of cross-linked yeast alcohol dehydrogenase (YADH) crystals through shearing with a rotating disc device. The authors observed no breakage of rod-shaped CLECs but did record the breakage of hexagonal CLECs at energy dissipation rates above 0.1 MW·kg⁻¹. The authors also studied non-cross-linked YADH crystals and noted a significant shift of the particle size distribution toward smaller particle sizes compared to those of cross-linked YADH [28]. Kubiak et al. measured the micromechanical properties of different CLECs (distinct PGA variants, Lysozyme, and HheG) using atomic force microscopy-based (AFM) nanoindentation. The determined differences in the mechanical behaviors of distinct protein crystals were correlated with the different crystal structures and properties, such as water content and the number of lysine residues able to be cross-linked [29,30]. Furthermore, the authors identified the anisotropic mechanical behaviors of the different HheG crystal faces, which were caused partly by the crystal structure and partly by the cross-linking time [31].

The cross-linking of enzyme crystals has an influence on the crystal’s mechanical properties and catalytic activity. An increase in cross-linking time leads to improved mechanical stability, but excessive cross-linking may cause protein precipitation and a loss in activity [32]. To use a biocatalyst successfully in an industrial process, both properties, mechanical stability and catalytic activity, must be present. In the context of this publication, the mechanical and catalytic properties of native and cross-linked enzyme crystals based on the HheG wildtype were examined, and the influence of cross-linking on the crystal properties was determined. For this purpose, a Nanoindenter was used as a tool to relate structural changes to variations in material properties due to this device’s ability to accurately measure micromechanical properties at various length scales [33]. This study compares the micromechanical properties of native and cross-linked protein crystals, which were examined under the same conditions using the nanoindentation technique. To the best of our knowledge, we are the first to evaluate the depth-dependent elastic and plastic functionality of indentation. Moreover, the catalytic properties of the designed CLECs are examined to fully characterize an industrially relevant HheG enzyme.

2. Materials and Methods

2.1. Crystallization and Cross-Linking

Halohydrin dehalogenase HheG from Ilumatobacter coccineus (HheG) was heterologously produced in Escherichia coli BL21(DE3) and purified to homogeneity as described previously [4]. Crystallization of the HheG wildtype was performed using the sitting drop method. A 20 µL droplet composed of protein stock solution (32 mg/mL) and precipitation solution (PEG 4000 (10% (w/v) in a HEPES buffer (10 mM, pH 7.3)) was placed on the cover slide and equilibrated against the reservoir solution (500 µL) at 5 °C. After 24 to 72 h, hexagonal crystals with an average size of 70 µm, as seen in Figure 1, were observed under an optical microscope and prepared for cross-linking using a gentle vapor diffusion method, based on the work of Lusty et al. [34]. For cross-linking, crystallization microplates equipped with microbridges in single wells were used. Crystals grown on a cover slide were washed on ice three times using a precipitation solution to remove the mother liquor and non-crystalized protein. Our experience has shown that cooling the crystals on ice is necessary to avoid crystal breakage caused by osmotic shock during the washing step [35]. After crystal washing, 10 µL of the fresh precipitation solution was added to the crystals. Then, 25 µL of a 25% aqueous glutaraldehyde solution (glutaraldehyde diluted in precipitation solution, pH~3 adjusted with HCl (1M)) was added to the well of the microbridge. According to Monsan et al., in an acidic pH solution, glutaraldehyde is present as a free aldehyde [36]. Finally, the cover slide containing the washed crystals was sealed over the well of a microplate. The microplate was then immediately turned over to allow the crystals to cross-link for approximately 24 h at 5 °C as a sitting droplet.

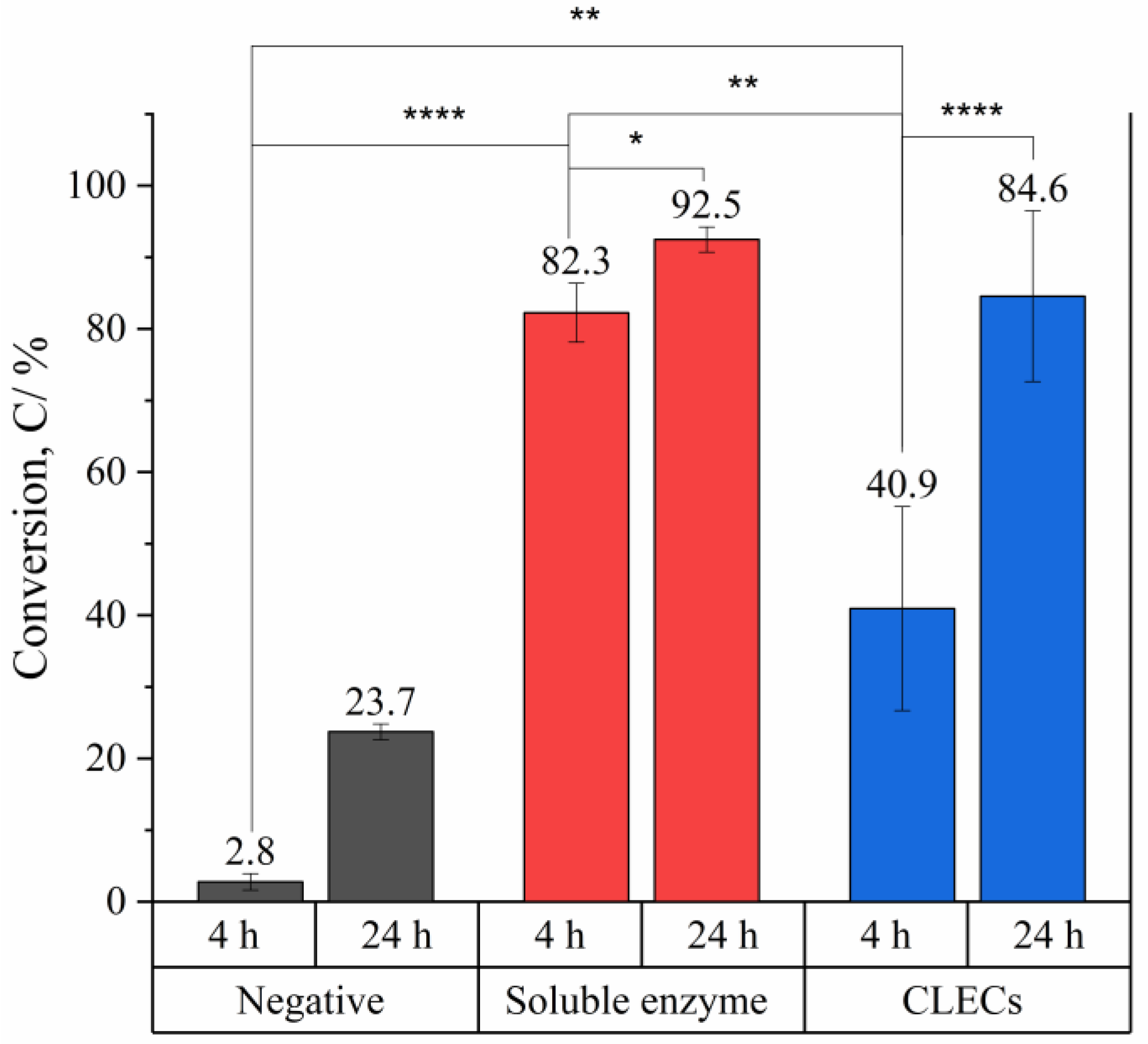
2.2. Bioconversion of Cyclohexene Oxide Using HheG CLECs

Conversion of the cyclohexene oxide using HheG CLECs was carried out at a 1 mL scale, and the reactions were analyzed by gas chromatography (GC) [37]. Reactions were performed at 22 °C and 900 rpm in a Tris·SO₄ buffer (50 mM, pH 7.0) containing cyclohexene oxide (20 mM) and sodium azide (40 mM) as a nucleophile. According to the reaction, we applied all HheG CLECs obtained from one crystallization and cross-linking batch, starting from the 320 µg soluble HheG. For comparison, a reaction using 100 µg of soluble HheG was performed as a positive control. However, the negative control reactions performed to investigate the chemical background did not contain the enzyme. After 4 and 24 h, samples of each 400 µL solution were taken and extracted with an equal volume of tert-butyl methyl ether (TBME) containing 0.1% dodecane as an internal standard. After drying the organic extracts over MgSO₄, the samples were analyzed by GC.

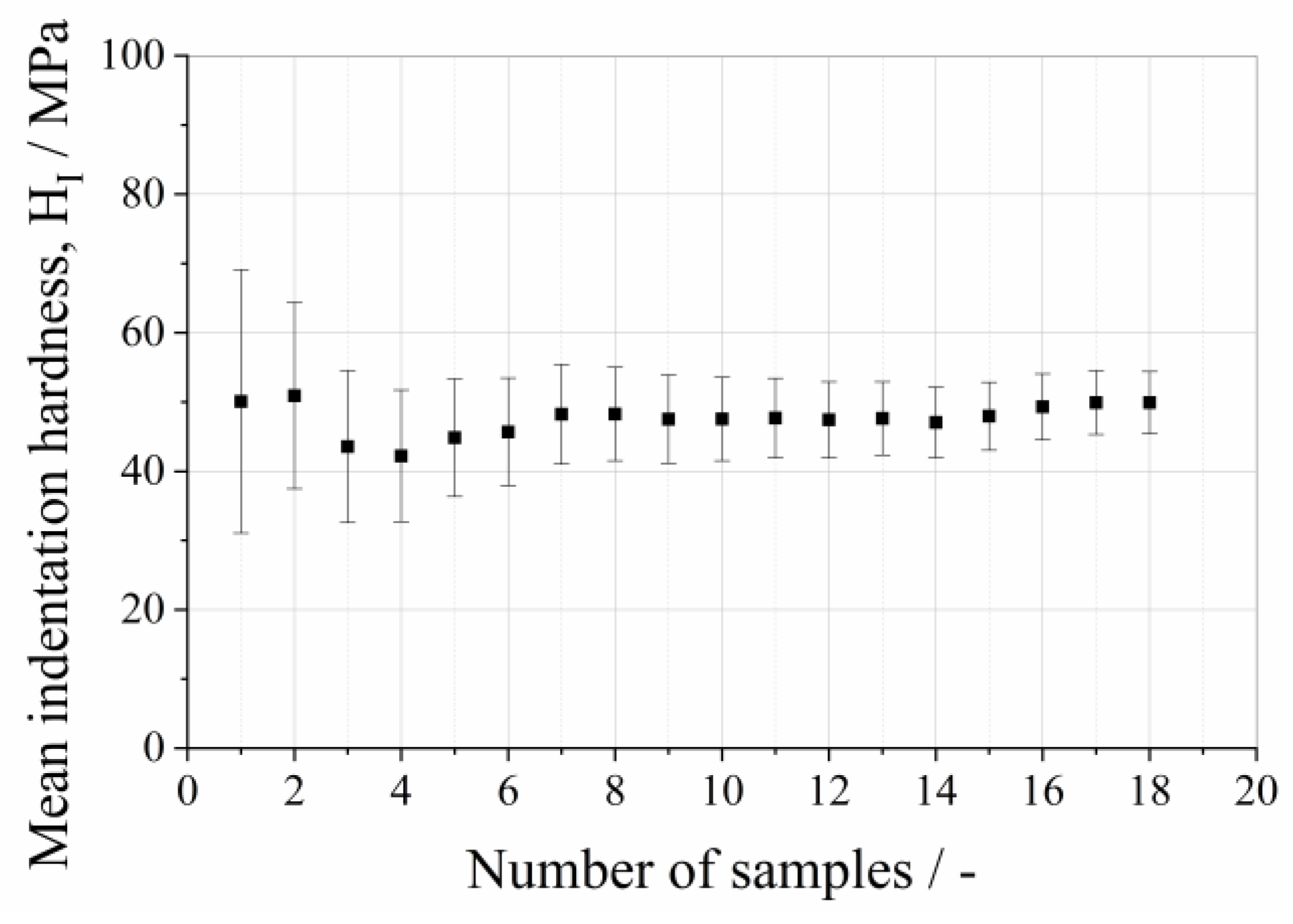
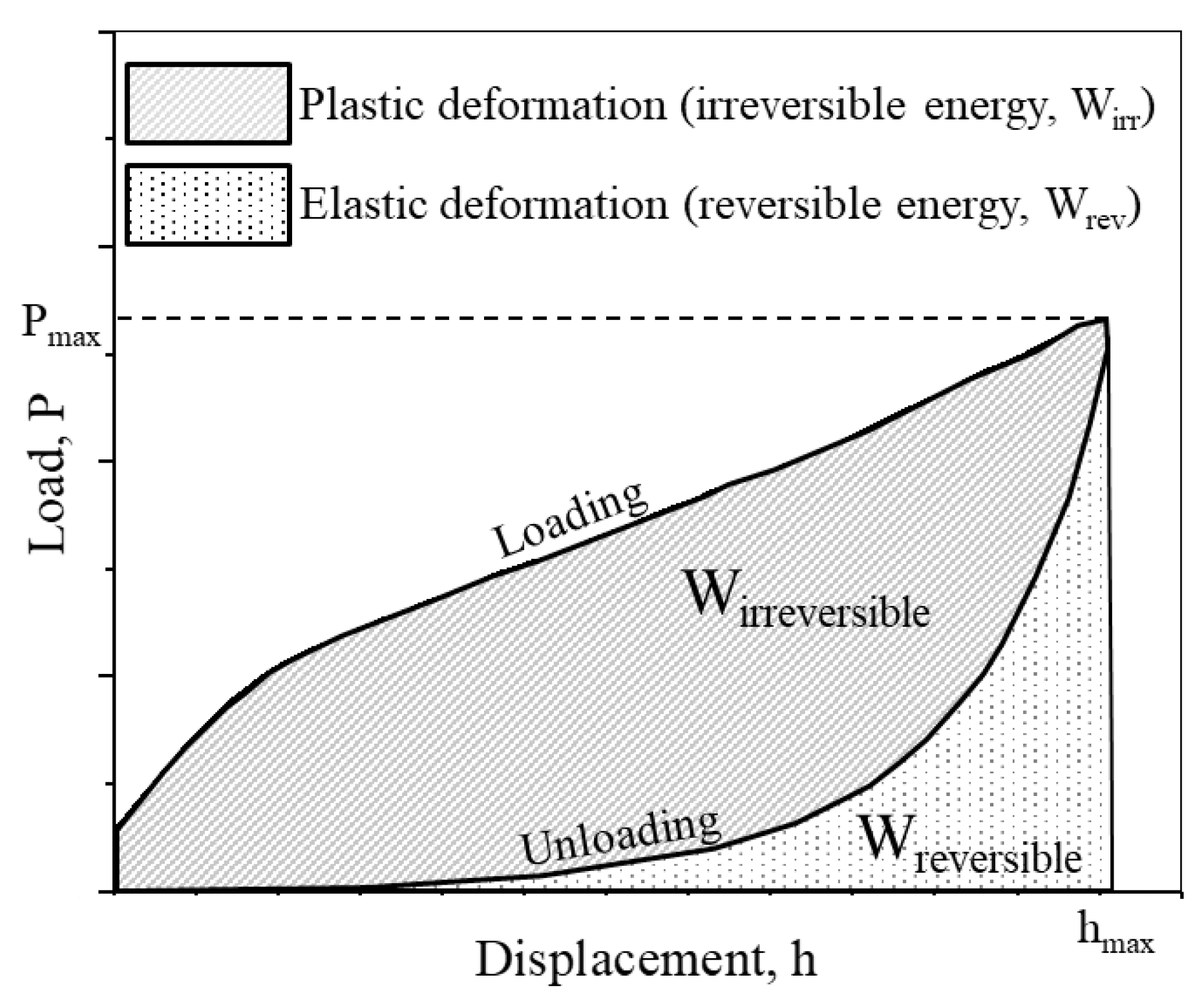
2.3. Mechanical Analysis on Single Protein Crystals

A Hysitron TriboIndenter Ti900 equipped with a Berkovich tip was used for the nanoindentation tests of native and cross-linked enzyme crystals. To avoid mechanical interventions, the crystals were indented on the cover slide upon which they grew. Since the crystals were grown on a siliconized slide in a sitting droplet, they adhered to the surface and were ‘immobilized’, which is needed for reliable indentation measurements. The cover slide was then mounted on a heating–cooling stage, which had a temperature of 5 °C. Because the indentation was performed in a viscous liquid (a PEG solution for native crystals), a preload of 5 µN was set for surface detection. Measurements at lower forces were not possible due to frequently according errors in surface detection, which resulted in a loss of contact between the Berkovich tip and the crystal surface during the measurement. To quantify the indentation size effect, indentation depths from 100 to 900 nm were set as a pattern (3 × 3 with gaps of 10 µm) on each single crystal face. The maximum penetration depth was set as 900 nm to avoid breakage of the native crystals. For this reason, the displacement-controlled mode was applied for the mechanical examination. Additionally, to investigate the influence of the indentation rate on the mechanical behavior of viscoelastic enzyme crystals, different displacement rates were applied for the measurements. It was not possible to use very fast indentation rates at small penetration depths (100–300 nm) because of machine compliance, which required an indentation duration time of 0.2 s or less. For this reason, the measurements were performed with either a constant displacement rate of 180 nm/s or a constant segment time of 0.55 s, meaning that each measurement was performed with an increased displacement rate, starting with 180 nm/s at a penetration depth of 100 nm up to 1636 nm/s at 900 nm, as shown in Figure 2.

For each indentation mode, nine measurements were taken on each of the approximately 18 crystals, distinguishing between basal and prismatic crystal faces. Based on the recorded force–displacement curves, the indentation hardness was calculated according to the Oliver and Pharr theory [38]. Using the example of hardness, Figure 3 shows that this number of indentations per penetration depth ensures sufficient statistical certainty—i.e., both the mean value and the standard deviation assume a constant value. Since the standard deviation is a measure of the distribution of values, this is the crucial point at which distributions must be compared with each other.

Additionally, elastic and plastic indentation work were calculated according to Formula (1) [39]:

$${\mathrm{E}}_{\mathrm{elastic}}={\int }_0^{{\mathrm{h}}_{\max }}{\mathrm{F}}_{\mathrm{unload}}\left(\mathrm{h}\right){\mathrm{dhE}}_{\mathrm{plastic}}={\int }_0^{{\mathrm{h}}_{\max }}{\mathrm{F}}_{\mathrm{load}}\left(\mathrm{h}\right)-{\mathrm{F}}_{\mathrm{unload}}{\mathrm{dhE}}_{\mathrm{total}}$$

(1)

where h_max is the maximum displacement during indentation, F_load and F_unload are the indentation forces during loading and unloading of the sample, elastic deformation is defined as the area under the unloading curve, and plastic deformation is defined as the area enclosed between loading and unloading curves, as shown in Figure 4.

All results are presented as a boxplot, which is explained in Figure 5.

The measurements at a penetration depth of 100 nm were discarded because of the temperature drift of the indenter tip during the first measurement, which was caused by transferring the tip from room temperature to the droplet with a temperature of 5 °C.

3. Results and Discussion

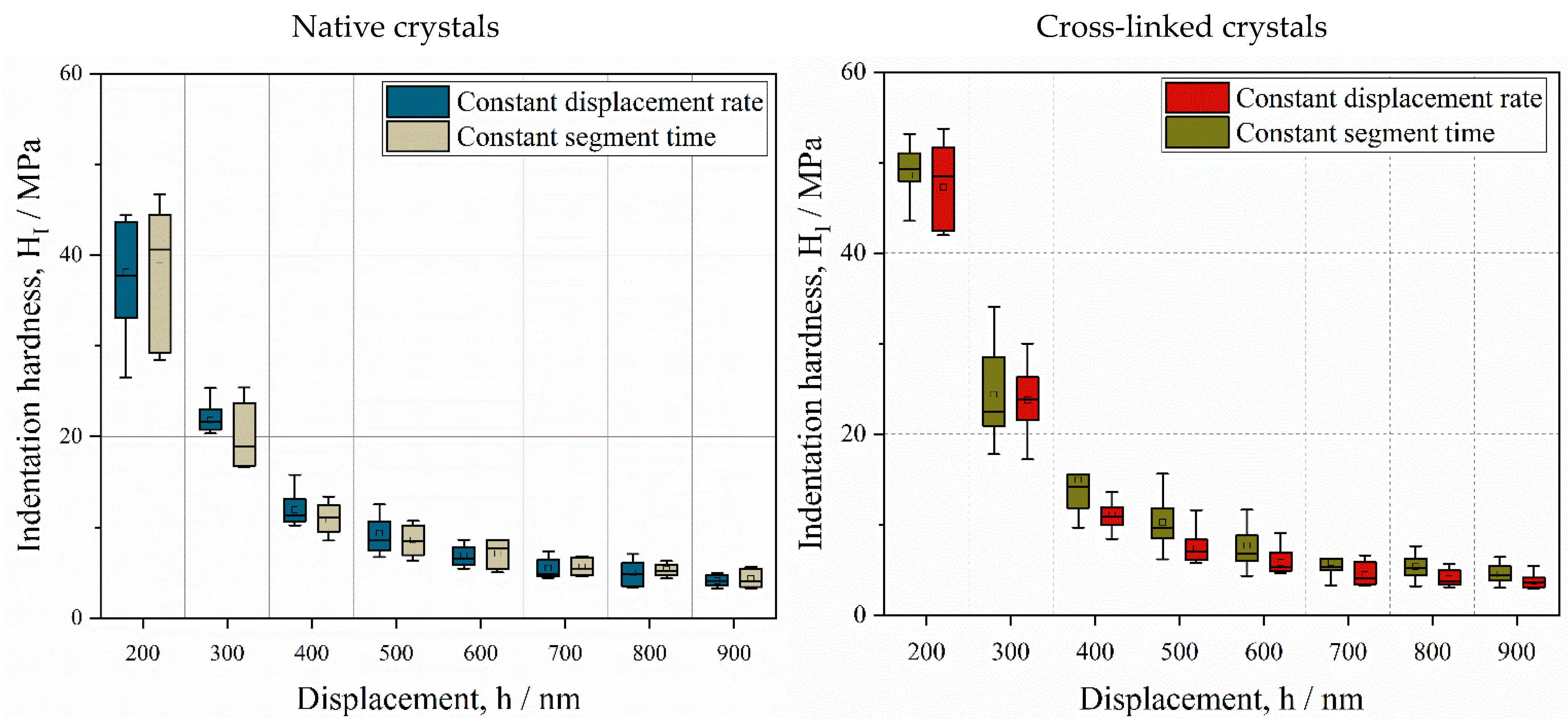
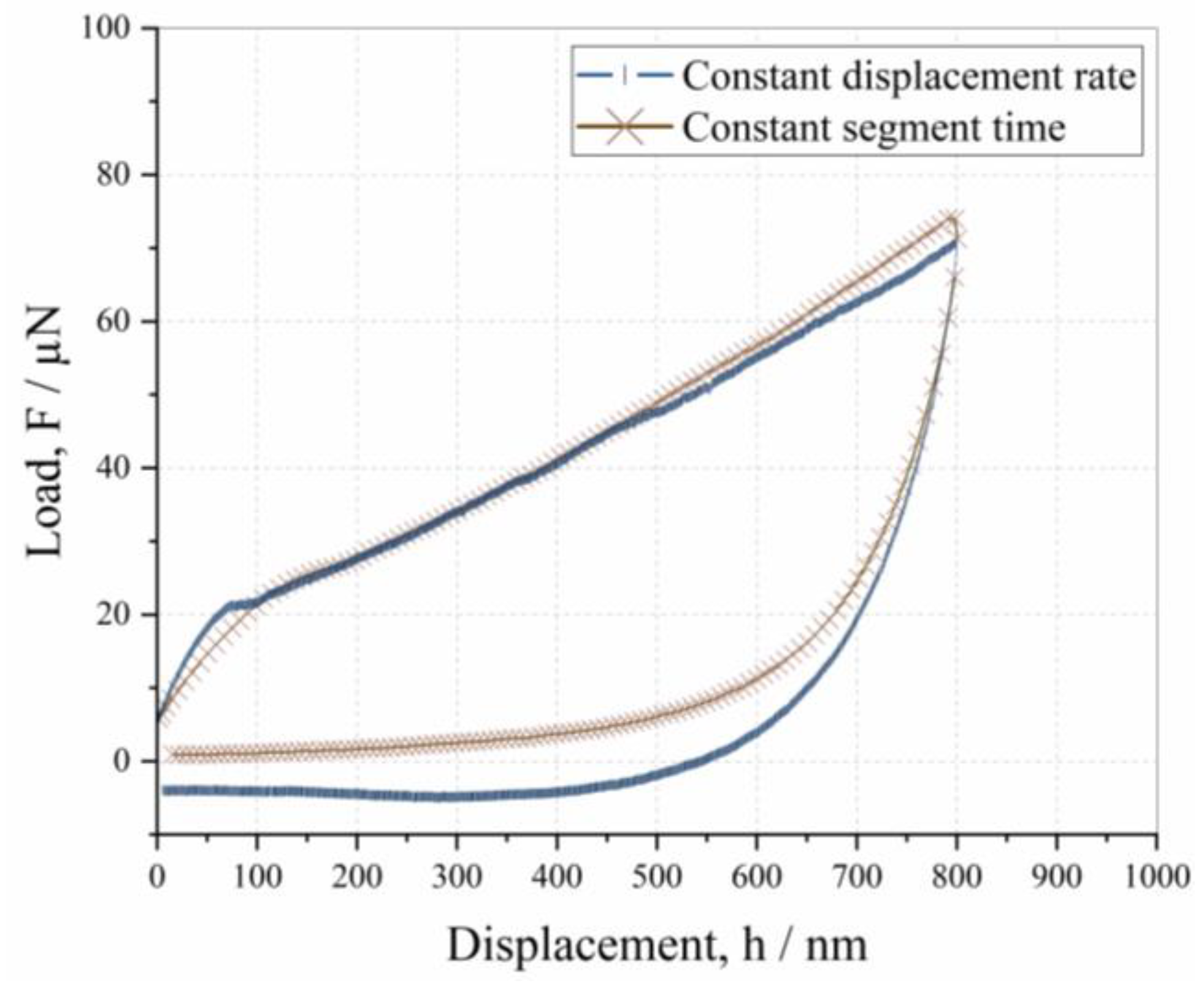
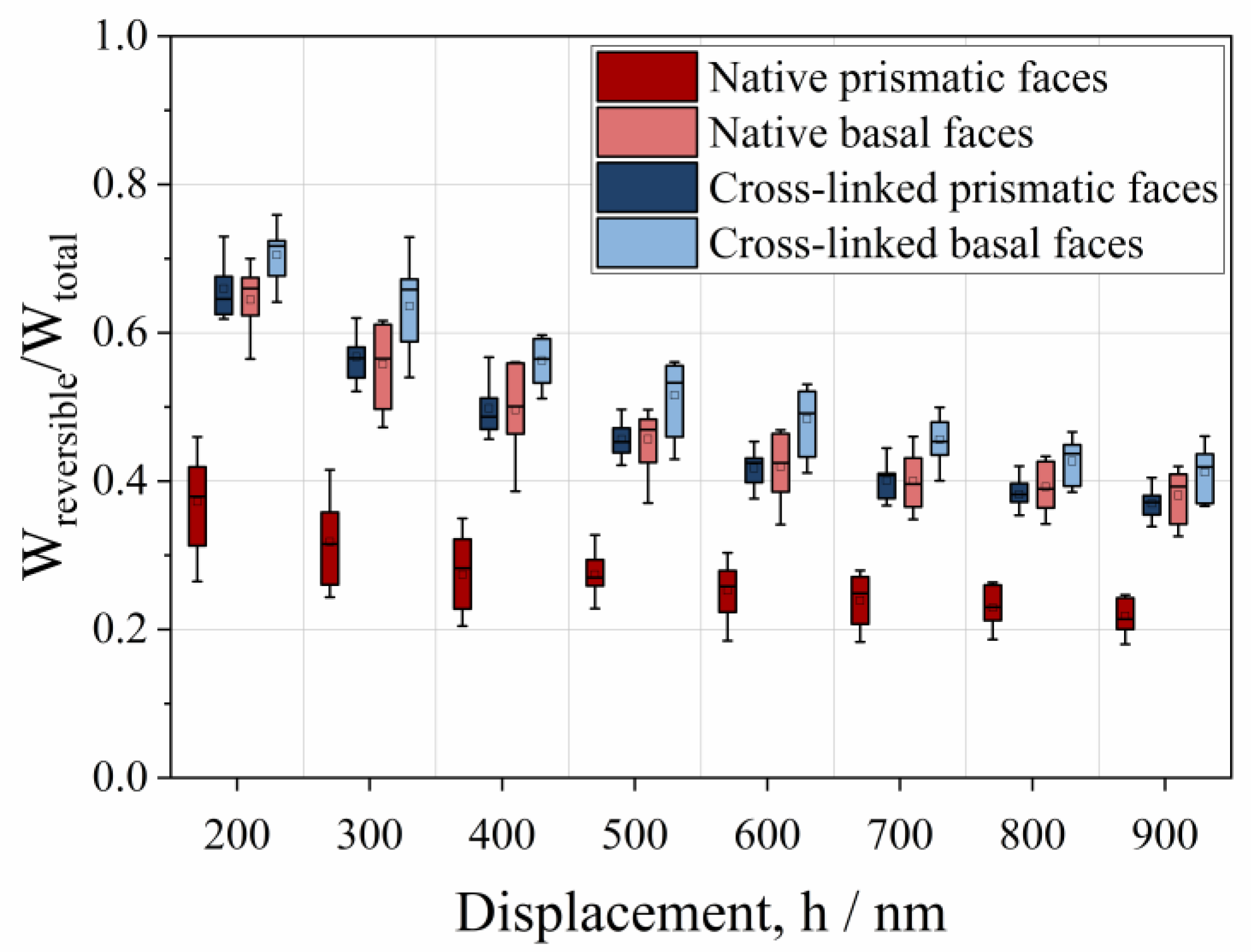
3.1. Influence of Displacement Rate on Depth-Dependent Mechanical Response

The time-dependent properties of protein crystals, such as their viscoelastic behaviors and creep, have been noted in many previous studies [12,27,40]. Although creep seems to have no significant impact on mechanical responses at small scales [29], it could affect measurements at large penetration depths. To establish the guidelines for further measurements, we first investigated and analyzed the influence of the displacement rate on mechanical properties in detail. Figure 6 presents the indentation hardness of native and cross-linked prismatic crystal faces measured at different penetration depths and displacement rates. Notably, under a constant segment time of 0.55 s, the displacement rate increased, as shown in Figure 2.

Here, we can observe three effects: (1) the tendency of hardness to decrease with an increase in penetration depth, (2) the higher hardness of cross-linked HheG crystals only at small penetration depths, and (3) the insensitivity of indentation hardness to the indentation rate. For both measurement modes, the indentation hardness decreases from ca. 39 MPa (mean value) for native crystals and 48 MPa for cross-linked crystals at a penetration depth of 200 nm to 4 MPa at high displacements of 900 nm. This so-called indentation size effect (ISE) has been widely examined and modeled using, e.g., the concepts of statistically stored dislocations (SSTs) and geometrically necessary dislocations (GNDs) [41]. SSTs are homogenously distributed in materials and dependent upon the material and processing conditions. Geometrically necessary dislocations (GNDs) are dislocations that must be present near the indentation to accommodate the volume of material displaced by the indenter at the surface [41]. The basic principle underlying this model is that the GNDs exist in addition to the usual statistically stored dislocations (SSDs) produced under uniform strain, giving rise to an extra hardening component that becomes larger as the contact impression decreases in size. The dislocation density is generally defined as the quotient of the dislocation length and volume in which the dislocations are stored. Thus, the geometrically necessary dislocation density (ρ_G) for an indentation with a conical indenter is defined as follows:

$${\mathsf{\rho }}_{\mathrm{G}}=\left(3{\tan }^2\mathsf{\theta }\right)/\left(2\mathrm{bh}\right)$$

(2)

where b is the Burger’s vector, h is the penetration depth, and θ is the angle between the indenter and the deformed surface. According to formula 2, the hardness increases at small depths because the geometrically necessary component of the dislocation density is inversely proportional to the depth and increases when the contact is minimal [41].

Regarding the magnitude of hardness, there are no comparable data showing depth-dependent hardness of protein crystals, especially HheG crystals. Nevertheless,

Table 1. Summary of the hardness results for the native and cross-linked lysozyme and HheG crystals.

Enzyme Crystal	Specifics	Measuring Method	Hardness/MPa	Literature
Lysozyme	Native, wet triclinic crystals	Micro-Vickers hardness	25–28	[42]
Lysozyme	Native, wet orthorombic crystals	Micro-Vickers hardness	6–10	[43]
Lysozyme	Native, wet tetragonal crystals	Nanoindenter	15	[12]
Lyzozyme	Cross-linked tetragonal crystals in liquid	AFM Nanoindentation	11	[29]
HheG	Cross-linked prismatic crystal faces	AFM Nanoindentation	8	[31]

summarizes some of the hardness results of native and cross-linked lysozyme and HheG crystals. According to the lysozyme results, the hardness strongly depends on the crystal structure. For example, the Vickers microhardness of the (010) plane of triclinic (tri-) HEWL crystals is over 4 times greater than the hardness of the (010) plane of orthogonal (O-) HEWL crystals [42,43]. In the cited studies, the hardness was measured in deep regions of the crystals (about 700 nm) via nanoindenter measurements [12]. For this reason, the HheG hardness at a penetration depth of 900 nm should be compared with the values in the literature. The hardness in the deep regions of native HheG crystals is about 4 MPa, which is comparable to the hardness of the (110) plane of O-HEWL crystals (6 MPa) [43]. According to Suzuki et al., hardness is an intrinsic property related to the habit planes and, therefore, is also related to anisotropy due to molecular packing and intracrystalline water [42]. The slightly lower hardness of HheG crystals can be explained by the high solvent content of the HheG crystals (65%) compared to the O-HEWL crystals (43%) [44].

There is good agreement between the hardness of the cross-linked HheG crystals studied with the help of nanoindentation and that studied using AFM. (4 vs. 8 MPa). However, the hardness was measured in the submicrometer range using a nanoindenter, and the results of AFM were obtained at a nanometer scale. By using the spherical tip instead of the Berkovich indenter, the indentation size effect, caused in part by the geometry of the tip, can be reduced. According to Swadener et al., the spherical indenter uniquely shows no depth dependence on hardness but does show dependence on the radius of the sphere [45]. This well-known effect provides an increase in hardness with a decrease in the tip radius [46]. This phenomenon explains why the hardness measured with the Berkovich tip (with a tip radius of ca. 50 nm) at low penetration depths of 200 nm was five times higher than the AFM hardness (with a tip radius of ca. 150 nm).

The last factor is the influence of cross-linking on the hardness of HheG crystals. Cross-linking increased the hardness by about 20% near the crystal surface at a penetration depth of 200 nm. In deeper regions (e.g., from ca. 400 nm), there was no significant difference in the hardness values. To provide a better understanding, this phenomenon is explained in Section 3.3. based on the many results presented in later parts of this manuscript.

The most surprising aspect of the data is the insensitivity to the displacement rate. While the present results are consistent with the findings of Raut et al., who examined organic crystals using the nanoindentation technique with a quasi-static load, they are at odds with the intrinsic time-dependent behavior of the crystals [47]. Raut et al. examined the strain-rate sensitivity of anorganic crystals. The authors reported that a lack of strain-rate sensitivity in crystals correlates with very low intermolecular interactions, such as van der Waals and hydrogen bonds, which can break easily such that plastic deformation occurs through the shearing of specific crystallographic planes [47]. An atomistic study of a protein dimer was previously published by Buehler et al. [48]. Although, in mechanical terms, protein crystals behave somewhat differently from individual proteins in their overall construction, deformation can be facilitated by the motion of individual molecules. Thus, interactions at the smallest scale, such as those within a protein dimer, can be considered in this context. The aforementioned study demonstrated the dependence of force–strain curves on pulling speed only above a velocity of a 1 m/s [48]. Moreover, the authors explained the unfolding process in terms of its dependence on the pulling speed. While at large velocities, unfolding occurs through the sequential breaking of hydrogen bonds one by one, at lower velocities (under 0.161 m/s), all hydrogen bonds are stretched equally and fail simultaneously [48]. However, although there was no detectable correlation between the applied displacement rate and the indentation hardness of enzyme crystals in the investigated range, different behavior could potentially be measured at significantly higher or lower displacement rates. Moreover, the penetration rate may have an influence on adhesion. During the data analysis, we noted that the tendency towards adhesion was higher at lower indentation rates. Figure 7 provides an example comparison of the representative force displacement curves at slow (180 nm/s) and fast (1273 nm/s) displacement rates.

It can be clearly seen that the force–displacement curve of the constant displacement rate measurement mode shows adhesion and a slight deviation from the almost smooth loading curve of the constant segment time mode. The latter result indicates that the tendency for dislocations to occur increases with an increase in contact time between the indenter tip and the specimen. Considering that the rate of displacement has no effect on the mechanical properties and that low displacement rates may cause adhesion, only the results of the constant segment time mode are presented in the following portion of the manuscript.

Due to the depth-dependence of mechanical measurements, in subsequent graphs, the fraction of elastic deformation in the indentation work is shown instead of the elastic modulus. Moreover, the indentation hardness, which is correlated with the elastic modulus [49], is replaced by the fraction of plastic deformation of an indentation. Hence, all subsequent results are presented using the elastic and plastic fractions of deformation energy.

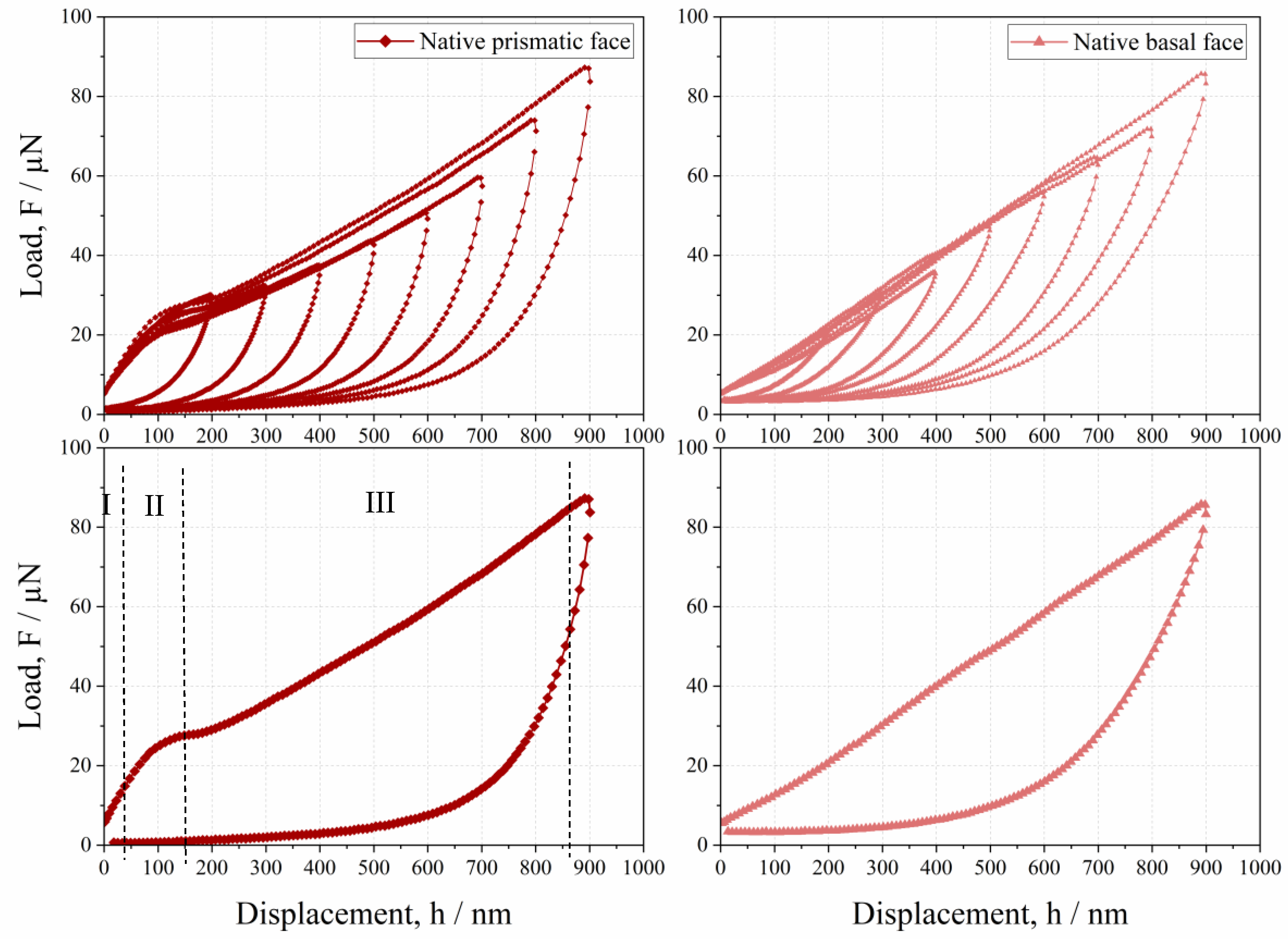
3.2. Anisotropic Behavior of Native HheG Crystals

To determine the changes in mechanical behavior due to cross-linking, we first investigated the mechanical behaviors of both faces of the native crystals. Figure 8 compares the energy fraction of the irreversible deformation of the prismatic and basal crystal faces. As expected, an increased fraction of plastic deformation energy with an increase in displacement is observable in the data for both crystal faces. The fraction of irreversible plastic deformation energy of the basal and prismatic faces starts at 36% and 63% and then increases to 62% and 78%, respectively. Interestingly, compared with the prismatic face, the basal face exhibits about 43% lower plastic deformation energy at relatively small penetration depths of 200 nm. This difference becomes smaller with an increase in penetration depth—ending at only 15%, at a depth of 900 nm.

There are two fundamental reasons for the observed anisotropy. Anisotropy can be related to either molecular packing or the intermolecular forces between the proteins, which can be different in each direction. Many publications have described the anisotropy of molecular crystals in the context of hydrogen bonds [50,51,52,53]. In the following section, the individual factors of this phenomenon will be discussed in more detail. Previously, Buehler studied an atomistic model of protein crystals and reported that plastic deformation is caused by chain unfolding [54], which indicates that permanent deformation occurs at a molecular scale. However, the experimental results presented in our manuscript contradict the atomistic modeling results provided by Buehler, who described the uniaxial strain of a perfect protein crystal of a small protein α-conotoxin PnIB from conus pennaceus in various directions [54]. Based on the simulated strain–stress curves, a comparable elastic modulus was observed for small deformations in all crystallographic orientations along with very different mechanical behaviors for large deformations [54]. As illustrated in Figure 8, the anisotropic faces show a greater difference in mechanical deformation under small than large deformations. This result is the opposite of the results in our study. Because no experimental data on the mechanical behavior of the crystals were provided in the aforementioned study, it could not be clarified whether these differences were due to the different behaviors of the distinct protein crystals or due to the inaccurate force fields used to model the crystal’s deformations. According to the author, future studies could be focused on using more accurate force fields that offer the possibility of bond breaking and formation for modeling deformation [54].

Hence, a mechanism for anisotropic plastic deformation that considers the sliding of crystallographic planes should be additionally considered and discussed. For this purpose, the mechanical behavior is first analyzed on the basis of the force–displacement curves. Figure 9 provides example force–displacement curves of nanoindentation on native prismatic and basal crystal faces.

Since the original studies by G. I. Taylor [55,56], numerous attempts have been made to explain the work-hardening phenomena in terms of dislocation mechanisms. Assuming that the deformation behaviors of organic and inorganic crystals are comparable [57], we analyzed and interpreted the deformation behavior of protein crystals using the typical stress–strain curves of an FCC metal crystal. In the case of the prismatic face (see Figure 9), nearly complete elastic behavior up to penetration depth of ca. 100 nm was measured (region I). In this case, the critical resolved shear stress was exceeded, allowing us to observe the yield strength. According to Taylor’s theory, flattening of the loading curve indicates that only one slip system is active in a given region and that dislocations migrate to a favorable oriented slip plane (region II). At a penetration depth of ca. 150–200 nm, as seen in Figure 9, a further increase in force is required for indentation (region III). The higher the penetration depth (and hence, the displacement rate) is in the constant-segment time mode, the higher the required force will be. Based on the theory of Taylor, this is a result of multiple gliding, where several slip systems are deformed simultaneously [55,56]. This phenomenon can be observed because the slip planes have no time for reorientation, as previously unfavorably located slip planes can now be displaced into more favorable positions. As a result, mutual hindrance of the dislocation movements leads to increased force. Here the stress decreases, unlike in region I, where the slope of the loading curve is much higher. In contrast, the loading curves of the basal face do not indicate any significant hindrance of slip movements. Moreover a much higher elastic fraction can be seen in Figure 9. These results can be explained by the fact that the anisotropic properties correlate with the crystal packing. Previous studies reported the dependence of hardness on the indented crystal plane [13,15,17,43,57]. These past studies showed a relationship between plastic deformation, dislocation multiplication, and motion in inducing a slip. Unfortunately, there is no detailed discussion on the correlation between the hardness and dislocation motion in each slip system within a protein crystal. However, the crystal packing shown in Figure 10 indicates that anisotropic deformation may be related to slip planes with different arrangements.

Xia et al. examined FCC metal using a nanoindenter equipped with a spherical diamond tip and categorized the plastic flow for each slip plane by the inclination angle of that plane to the surface [58]. The authors reported that the flow direction transformed from forward motion to sideways motion at a transition angle of 55° to 58° [58]. The graph shows that the indentation plane of the prismatic face is aligned parallel to the slip plane [010], indicating a sideways and hampered flow. In the case of a basal face, the indenter load is aligned orthogonally to the slip plane [001], where a forward flow (and easy gliding) can be expected.

HheG enzymes are large homotetramer molecules with a molecular weight of 299.37 kDa. These enzymes crystallize in a trigonal crystal system with the space group P3₁21. As a result, the crystals exhibited significant solvent content of 65% [4]. Nanev reported that intra-crystalline water works as a “lattice glue” and helps to hold the crystal structure together [59]. This effect is based on the dynamic hydrogen bond chains that form between some intra-crystalline water molecules, which are likely to become elongated to connect the amino-acid residues of adjacent protein molecules in the crystal lattice [59]. This effect is expected to be observed within very small channels and gaps where the molecules are at an appropriate distance to each other to be connected. These results show that there are many possible reasons for anisotropy and that the directional differences in mechanical behavior are most likely due to the interplay between the structure and the resulting crystal contacts.

3.3. Mechanical and Catalytic Properties of Cross-Linked HheG Crystals

Figure 11 summarizes all the results for the fraction of the reversible (elastic) indentation energy of native and cross-linked HheG crystals. First, it can be observed that the elastic energy decreases with an increase in penetration depth for both kinds of crystals. Second, it is evident from the figure that both faces of the cross-linked crystals exhibit higher elastic deformation energy than the native crystals. Indeed, the elastic energy of the basal faces shows the highest fraction and ranges from 72% to 42%. Next highest are the prismatic faces, ranging from 66% to 37%. The native basal faces of the crystals have similar properties, where the fraction of elastic energy decreases from 64% to 39%. The native prismatic surfaces of the crystals exhibit the lowest fraction of elastic energy, which decreases in the investigated range from 37% to 22%. The third and most surprising aspect of this study is the order of magnitude by which the native prismatic faces were reinforced. Due to cross-linking, the elastic energy of prismatic faces increased by about 78% at a penetration depth of 200 nm to 68% at high penetration depths. Moreover, cross-linking strengthened the crystal lattice against fractures. This was determined after none of the examined crystals presented cracks or fractures.

As mentioned in previous literature, due to cross-linking, strong covalent bonds become inserted into the crystal lattice [21,60,61]. Cross-linking bonds can occur intramolecularly (between groups in the same protein molecule) or intermolecularly (between different protein molecules) [62], where the latter are necessary to maintain the crystal packing in environments different from those of the crystallization liquor [23]. Kubiak et al. developed a mathematical model for calculating theoretical crystal strength based on the potential cross-linking bonds between three residual pairs: the ε-amines of lysine residues (Lys–Lys), two neighboring arginine residues (Arg–Arg), and arginine and lysine residues (Arg–Lys). Using the MATLAB toolbox, the authors analyzed the distance and direction of possible cross-linking bonds. From this analysis, the dominant crystal faces were determined, showing that higher number of perpendicular bond fractions yields a crystal face with greater strength. A summary of the direction-dependent crystal-strength results for the considered residual pairs is provided in

Table 2. Direction-dependent theoretical crystal strength due to the anisotropic cross-linking bonds between three residual pairs: arginine–arginine, arginine–lysine, and lysine–lysine. Surf 1 is the basal face, and Surf 2–3 are the three prismatic faces. Reprinted with permission from [31]. Copyright (2019) American Chemical Society.

Crystal Face	Arg–Arg	Arg–Lys	Lys–Lys	Sum
Surf 1	271.77	142	145.4	559.17
Surf 2	231.63	137.81	107.04	476.48
Surf 3	230.52	140.01	105.47	476.00
Surf 4	230.49	141.84	107.97	480.30

[31].

Assuming that all the bonds in deep crystal regions contribute to stabilizing the crystal structure, the basal face (Surf 1~560) has about a 15% higher fraction of anisotropic cross-linking bonds than the prismatic faces (Surf 2–Surf 4~477) [31]. This would result in a basal crystal face with higher strength, which agrees with our experimental results for cross-linked crystals. Mechanical analysis of the cross-linked anisotropic faces showed that the elastic fraction of deformation energy was ca. 15% higher for the basal faces than the prismatic faces.

We also identified most of these bonds near large and small channels within the crystal, as shown in Figure 12 [31].

Due to the strong covalent bonds, it seems possible to hold the crystallographic slips together such that the cross-linked prismatic faces exhibit much stronger elastic recovery than the native prismatic faces. This mechanical response can be clearly seen on the force displacement curves shown in Figure 13.

Compared to the force–displacement curves of native crystals, the loading and unloading curve of the cross-linked crystals shows a significantly higher elasticity fraction, higher forces required to create an indentation, and no flattening curve section. The shape of the stress curve of the cross-linked crystals is similar to that of polycrystalline materials, in which multi-gliding occurs immediately after elastic deformation. It can thus be suggested that cross-linking bonds, which lead to a decrease in the effective “pore” size of the channels [22], enclose the mobile water within a crystal lattice, which is why the crystal behaves like a damper against plastic deformation. Another possibility is that cross-linking bridges formed randomly within the crystal can transmit forces in all directions. In this way, strong covalent bonds contribute to a reduction in plastic deformation.

The hardness of the cross-linked HheG crystals in Figure 6 present higher hardness than the hardness of native crystals only at low penetration depths. This is caused by the strongly elastic recovery of the cross-linked crystals, especially at penetration depths of 200 and 300 nm. As a consequence, the slope of the unloading curve (P–h curve) is significantly smaller than that of native crystals. When calculating hardness according to the Oliver and Pharr method, the slope is used to determine the contact area—i.e., the smaller the slope is, the smaller the contact area will be. According to this definition, hardness refers to the maximum force obtained at the indentation in relation to the contact area. Therefore, the smaller the slope and contact area are, the greater the hardness will be.

Apart from an improved mechanical stability due to cross-linking, it is necessary for the CLECs to retain their catalytic activity for them to be used in biocatalytic reactions. To investigate the catalytic activity of the formed HheG CLECs, they were applied in opening the ring of cyclohexene oxide with azide as a nucleophile. The conversion data using different forms of HheG (soluble, CLECs) are presented in Figure 14.

Positive control reactions using 100 µg of soluble HheG yielded a mean conversion value of 90% after 24 h. This reaction was previously reported to reach product yields up to 98% within 24 h [4]. By comparison, the HheG CLECs achieved a conversion of 85% after 24 h (Figure 14). This result confirms the high residual activity of HheG CLECs compared to negative control reactions without the enzyme, which exhibited only 23% conversion after 24 h. In contrast, the HheG CLECs yielded only 41% conversion after 4 h of reaction, whereas a two times higher conversion rate (83%) was achieved using the soluble enzyme. This result indicates reduced HheG activity within the cross-linked enzyme crystal. This assumption is further underlined by the fact that the CLECs required a much longer reaction time to reach near completion of the reaction. Based on the literature, three main parameters seem to influence the activity of crystallized enzymes—crystal size, substrate size, and enzyme conformation [60]. The first two parameters are related to the diffusion limitations within the crystals and were addressed in several publications [22,63,64]. One possible solution to overcome diffusional limitations is the use of smaller enzyme crystals [65,66,67]. For example, Kasvinsky and Madsen reported that enzyme crystals of glycogen phosphorylase with a crystal size of 10 µm did not show diffusion limitations [65]. Mass transfer was also dependent on substrate concentration. Choosing a substrate concentration much higher than the respective K_m value of the enzyme seems to overcome diffusional limitations [10]. Besides mass transfer limitations, another explanation for reduced HheG activity could be the use of the cross-linker, glutaraldehyde. Glutaraldehyde reacts with the ε-amino groups of lysines but can also interact with the guanidyl groups of arginines [68] and tyrosines [68]. As Tyr165 and Arg169 are part of the catalytic triad of HheG [4], cross-linking of these residues with glutaraldehyde would also reduce enzyme activity and lead to reduced conversion when using CLECs compared to soluble enzymes. As our focus within this project was not to optimize CLEC activity but to investigate the influence of cross-linking on the mechanical behaviors of enzyme crystals, glutaraldehyde was used as a cross-linker. For the growth of crystals, a compromise had to be made between a crystal size that still showed sufficient catalytic activity and a size that could be reliably measured using a nanoindentation technique.

4. Conclusions

This project was undertaken to design robust and catalytically active CLECs and evaluate the differences in mechanical behavior between native and cross-linked enzyme crystals. Using the nanoindentation technique, the depth-dependent mechanical properties of anisotropic chemically treated and untreated enzyme crystals were investigated. This study provides several findings:

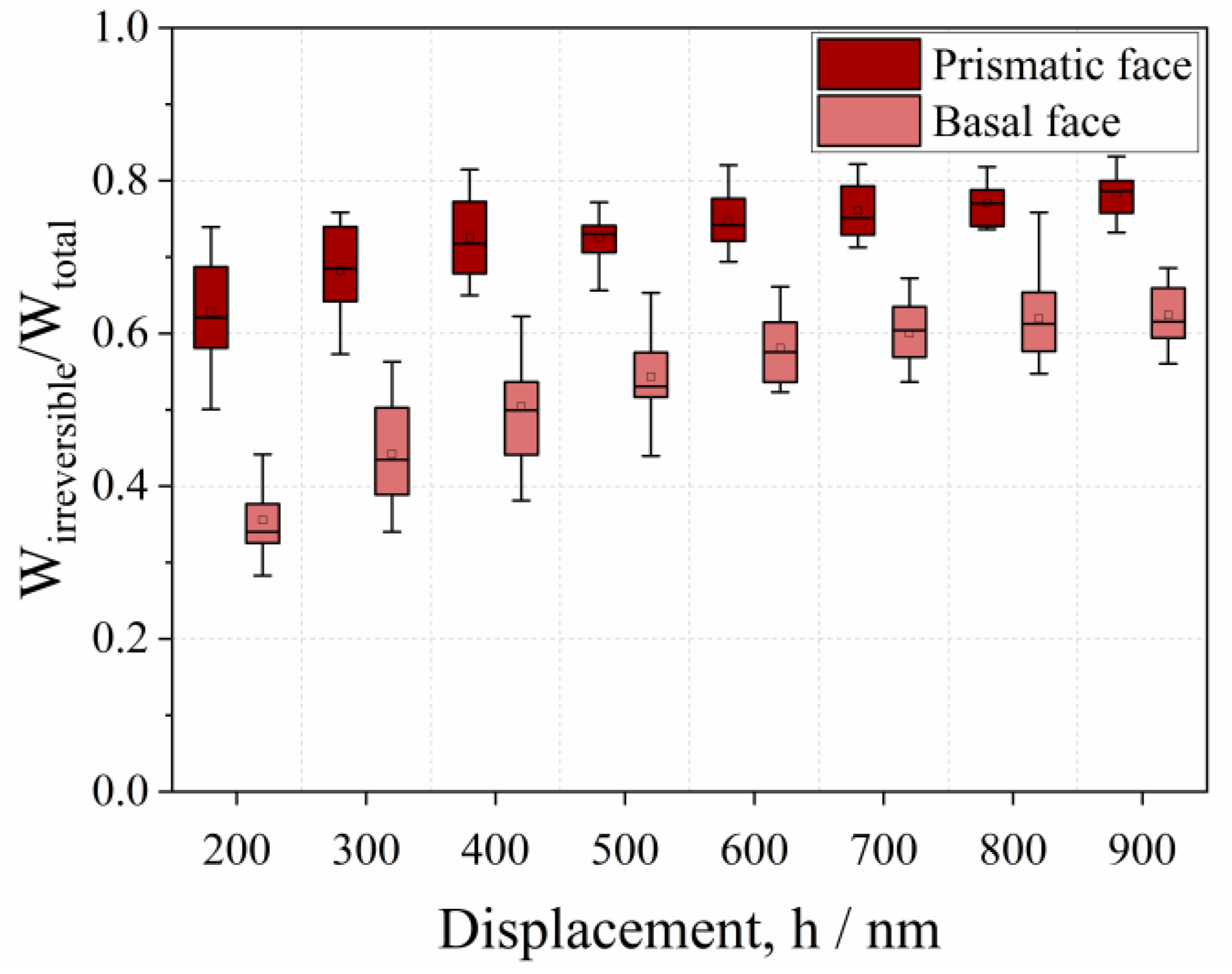
• The mechanical properties of native and cross-linked enzyme crystals, such as hardness and the fractions of elastic and plastic energy, decrease with an increase in penetration depth, meaning that they exhibit an indentation size effect (ISE).
• The mechanical properties are not dependent on the indentation rate, but the tendency toward adhesion increases at a slower displacement rate.
• Native crystals show anisotropic mechanical behaviors, where the basal face is more elastic than the prismatic one.
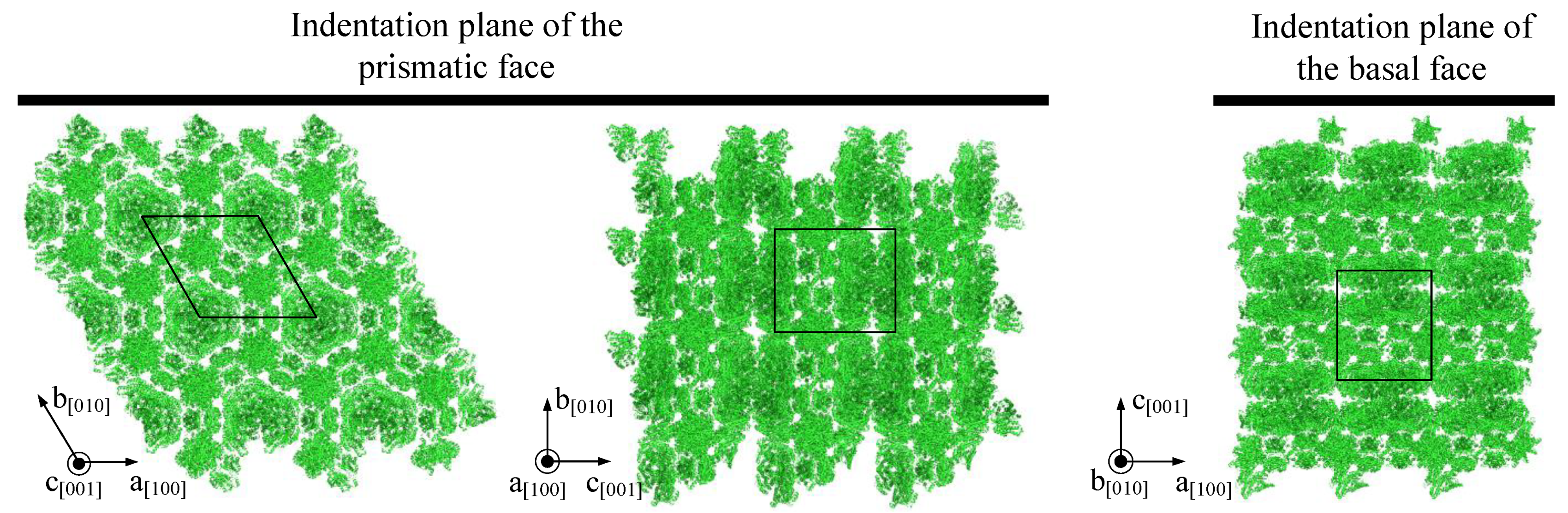
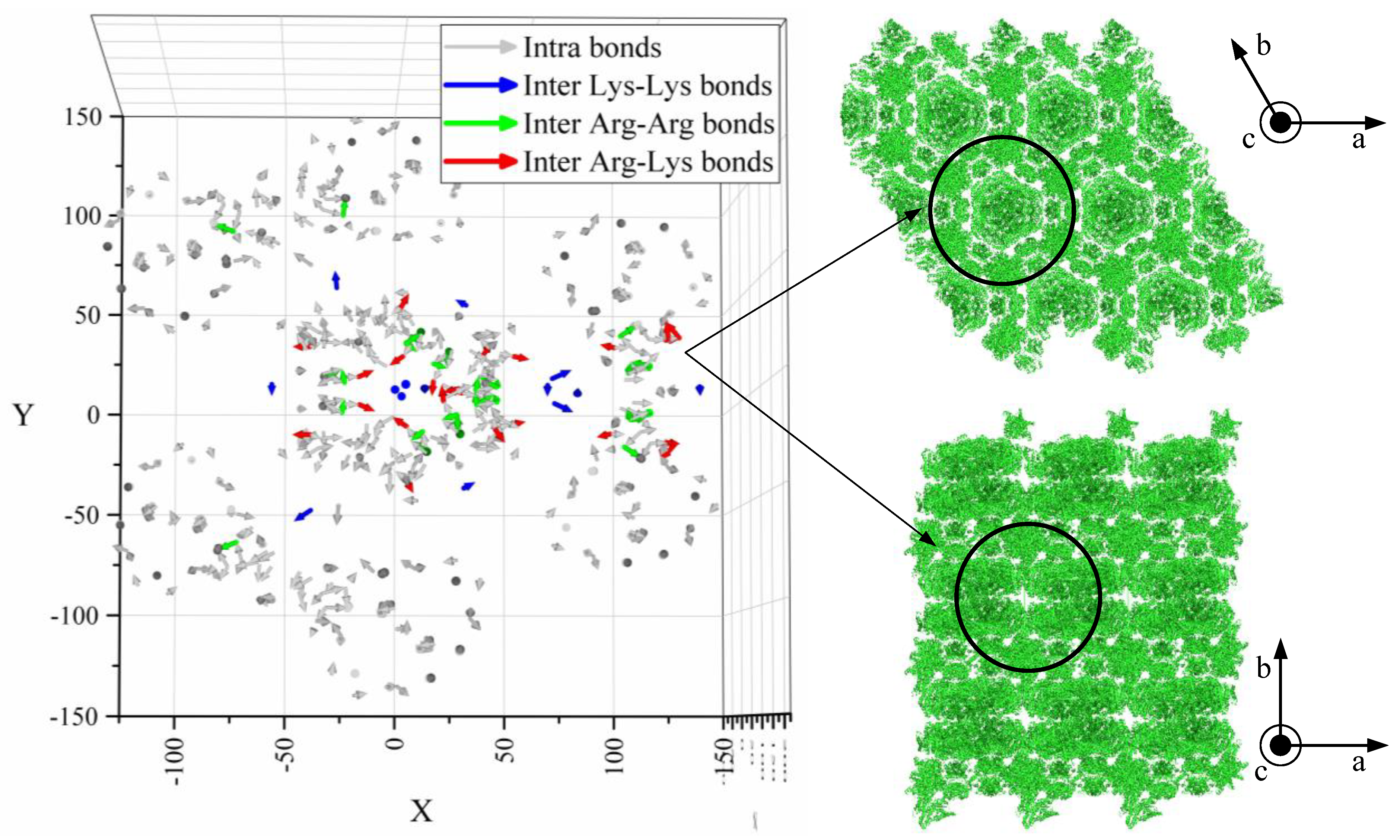
• The lower resistance of prismatic faces against plastic deformation seems to be caused by anisotropic crystallographic planes and intermolecular water.
• Cross-linking increases the fraction of the reversible indentation energy of prismatic and basal faces by approximately 68% and 8%, respectively.
• HheG CLECs cross-linked with glutaraldehyde showed high catalytic activity under a conversion time of 24 h. Due to diffusion limitations, a longer reaction time was required to complete the reaction compared to that when using a soluble enzyme.

Using a nanoindenter, we systematically identified the weakest spots on the HheG crystal surfaces and correlated those spots with the crystal structure. We also showed that the crystals’ flaws due to cross-linking can be significantly reduced using glutaraldehyde. This is the first study reporting process-relevant properties, such as the elastic and plastic deformation energy of enzyme crystals, and extends our understanding of ways to enhance their mechanical performance under cross-linking while maintaining catalytic activity. This knowledge will be necessary if CLECs are to be successfully used in industrial processes.