Optoelectronic Properties of Ultrathin Indium Tin Oxide Films: A First-Principle Study
Abstract
1. Introduction
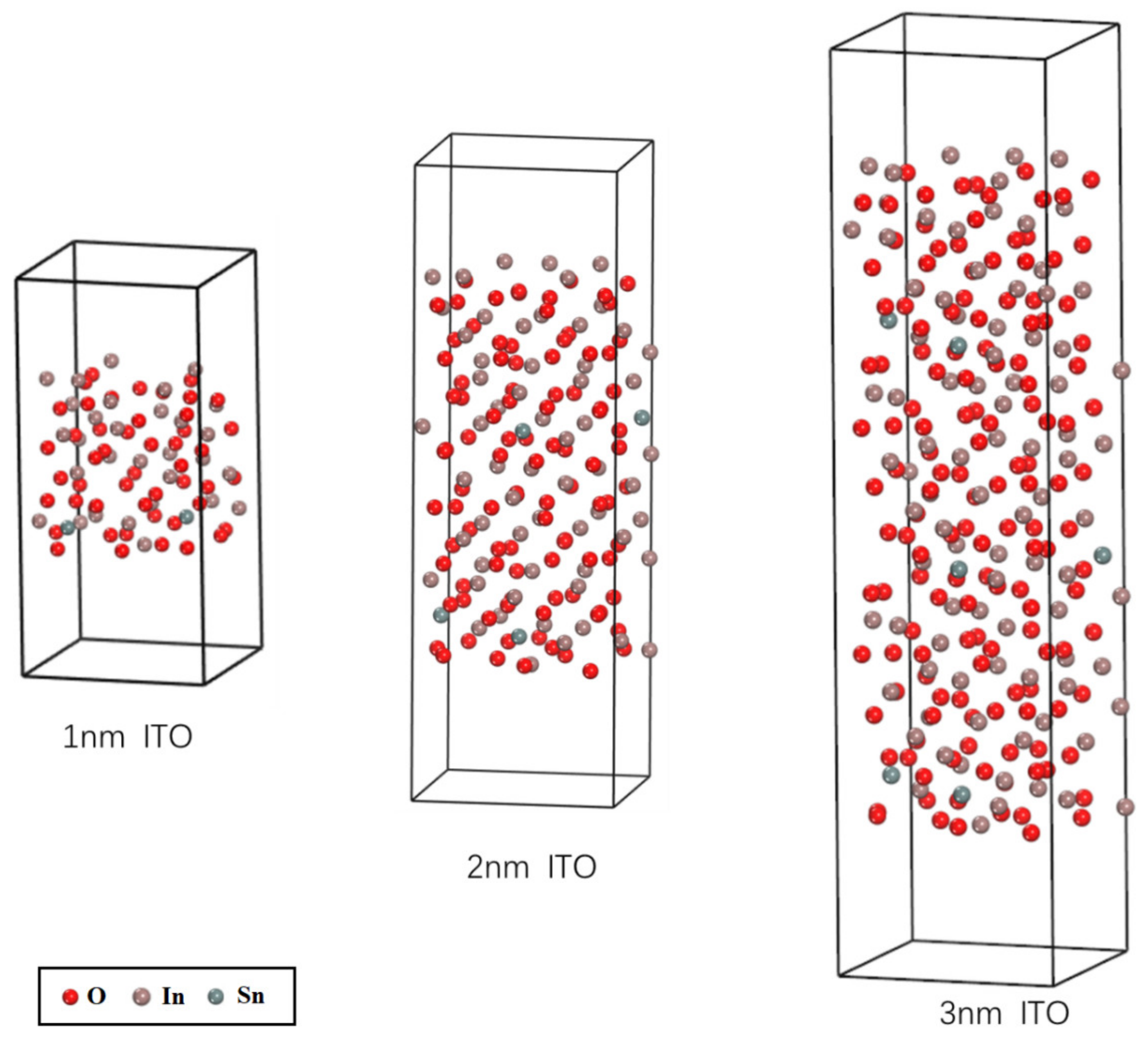
2. Materials and Methods
3. Results and Discussions
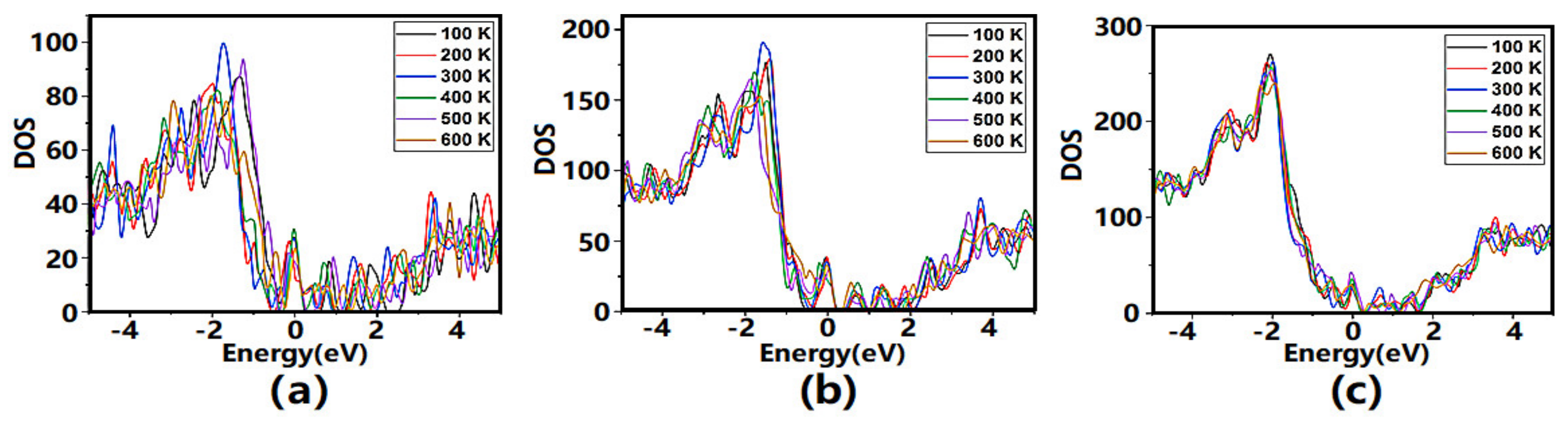
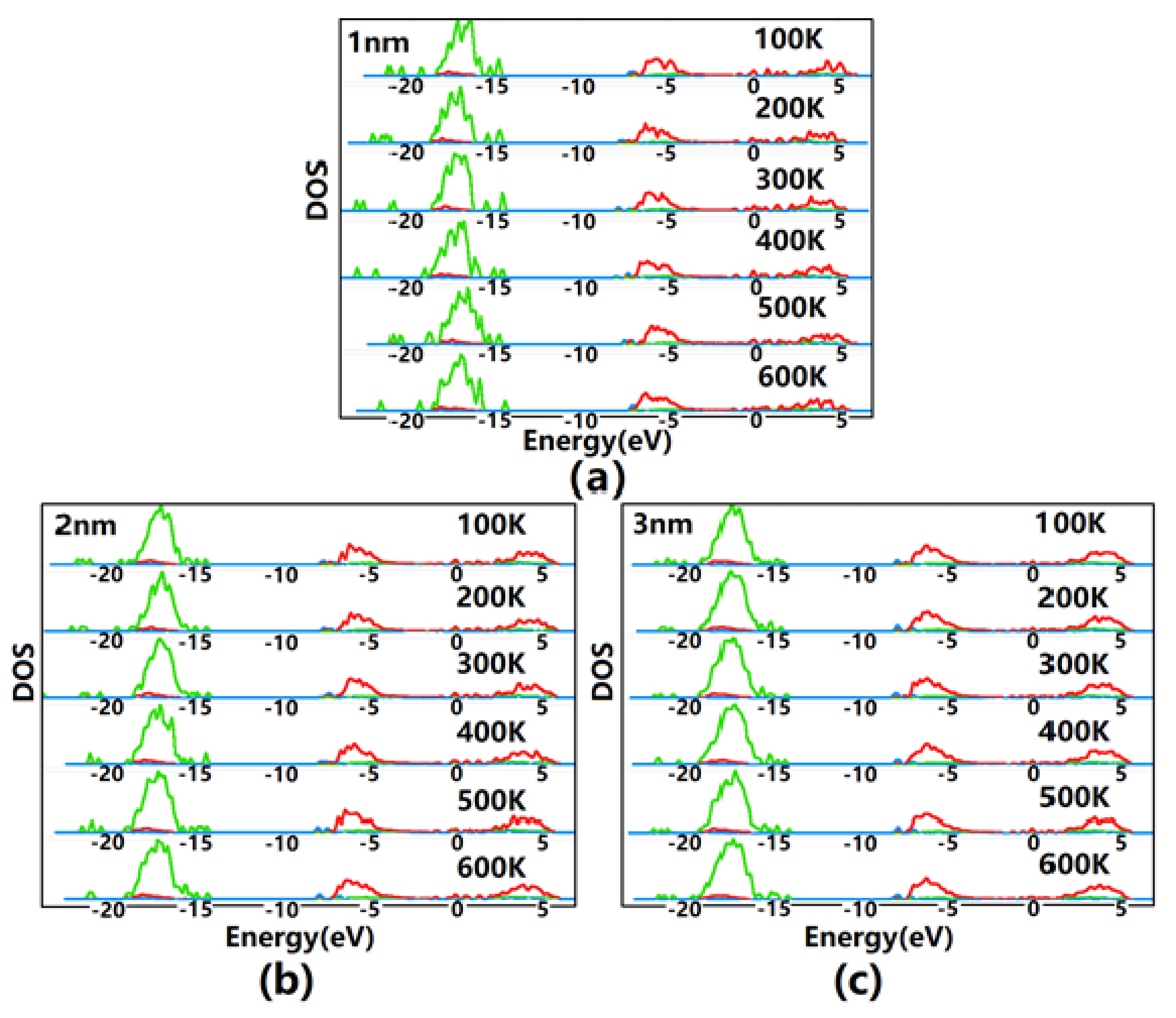
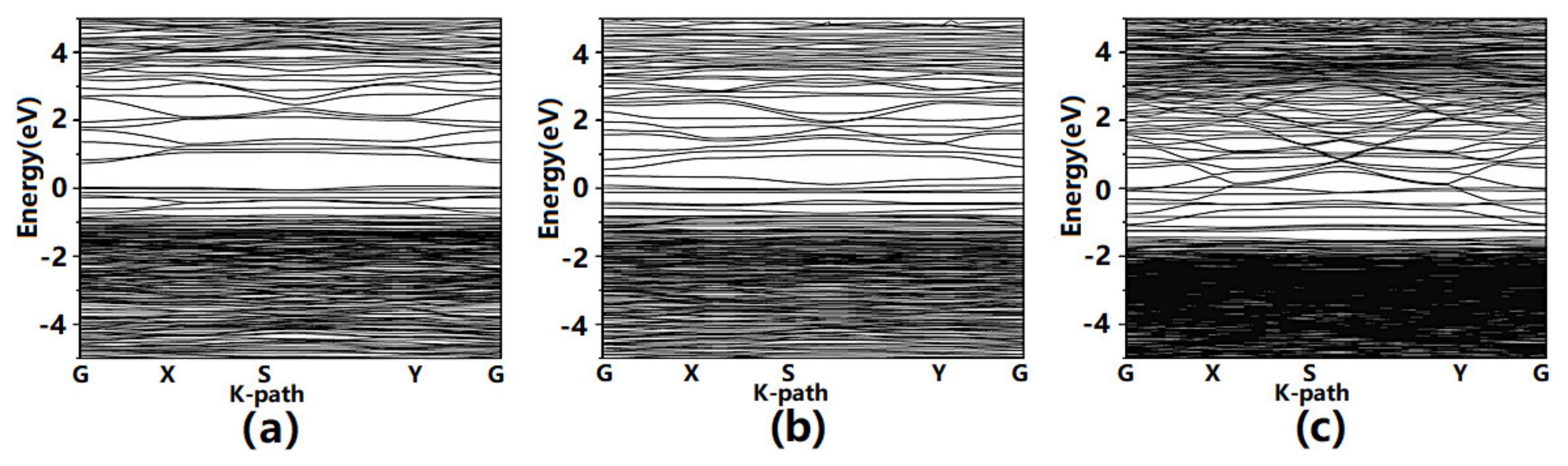
3.1. Electronic Structure Properties of Ultrathin Films of ITO
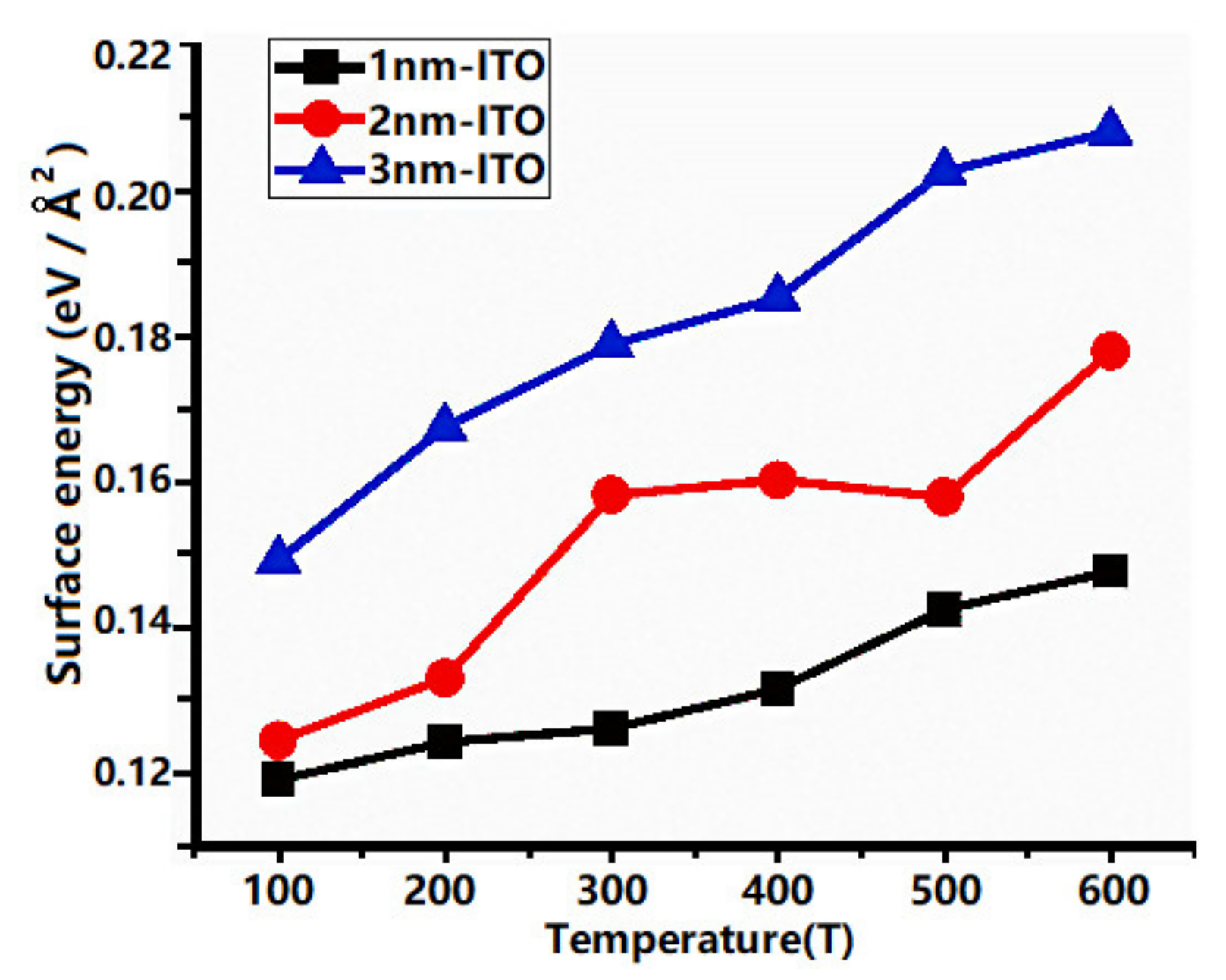
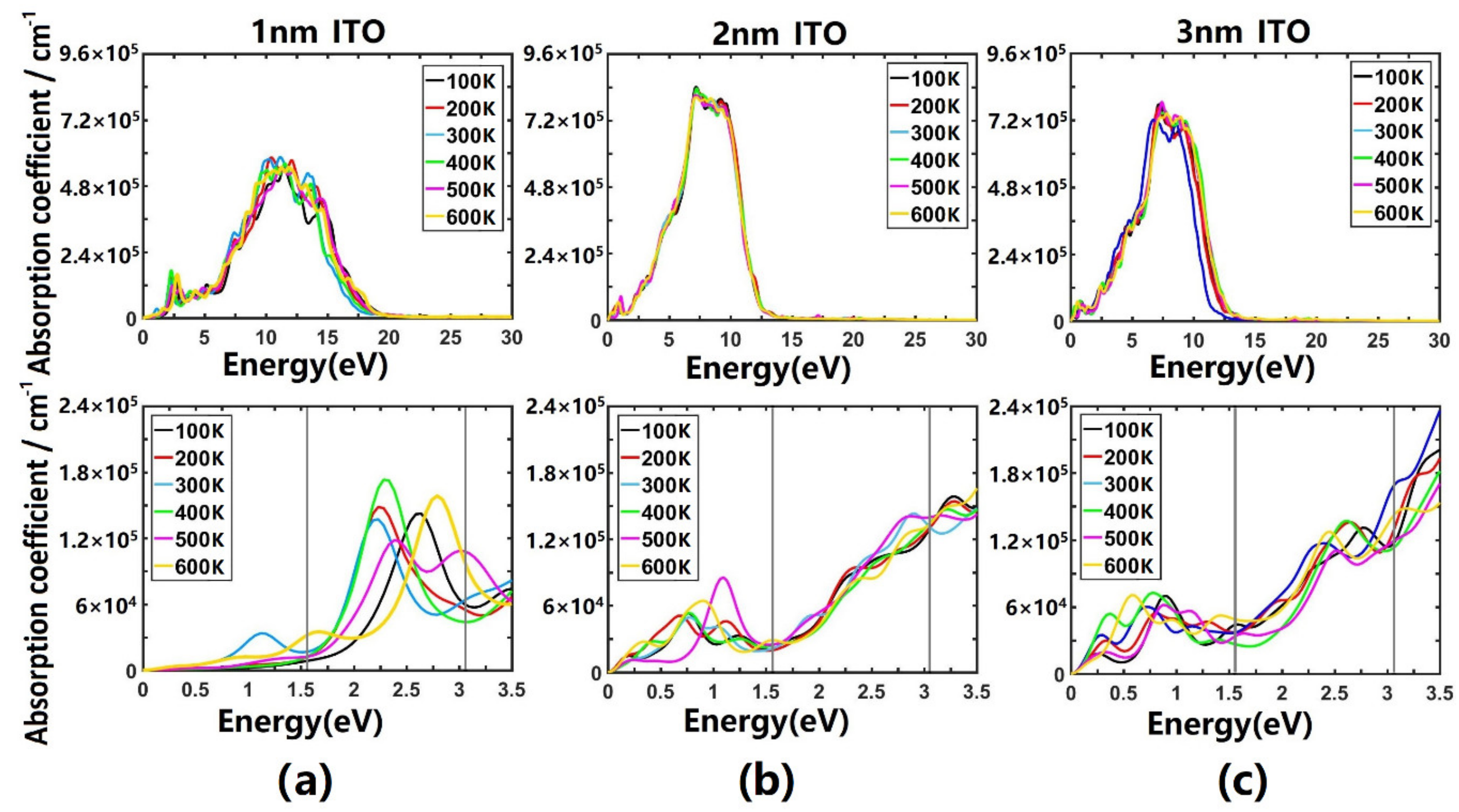
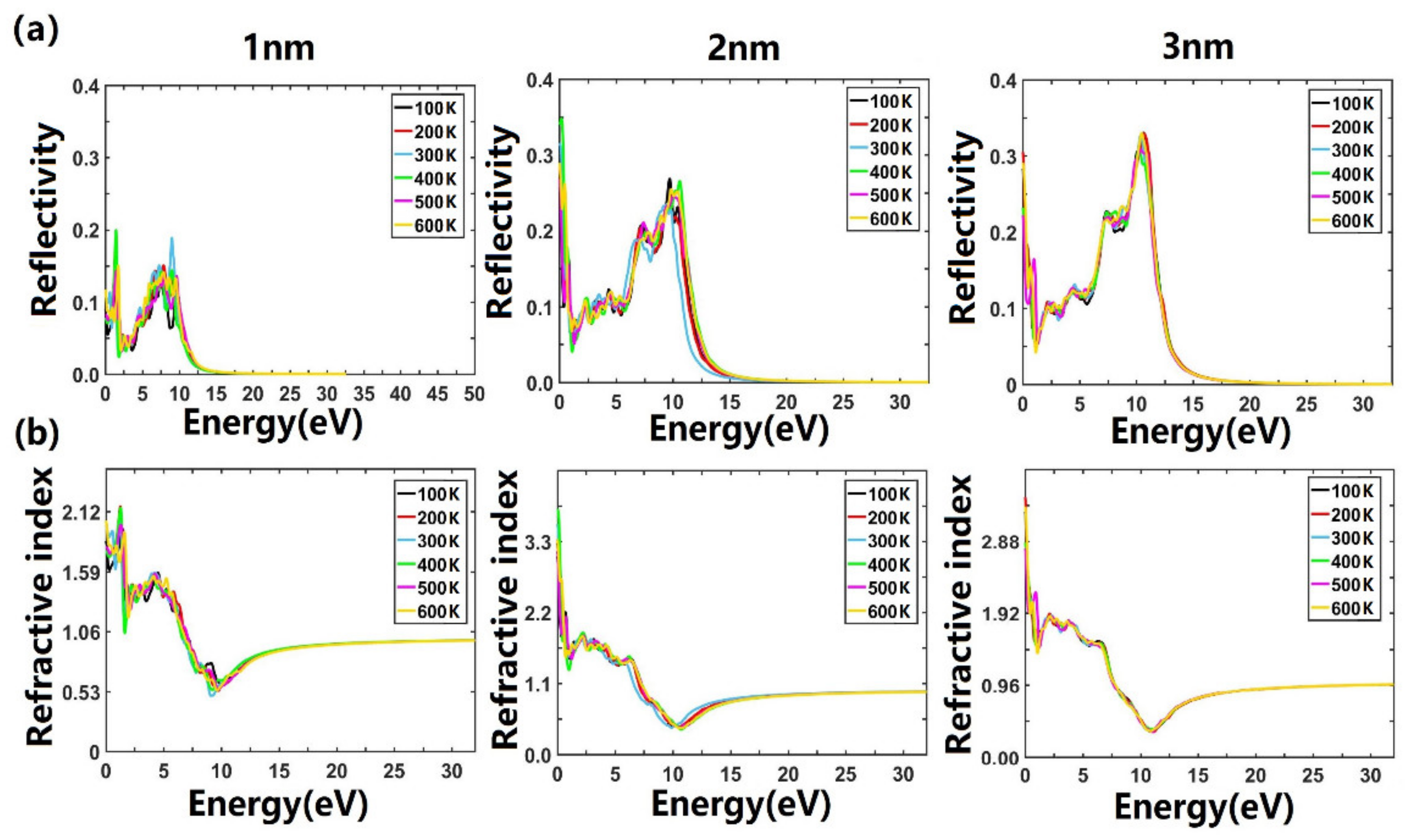
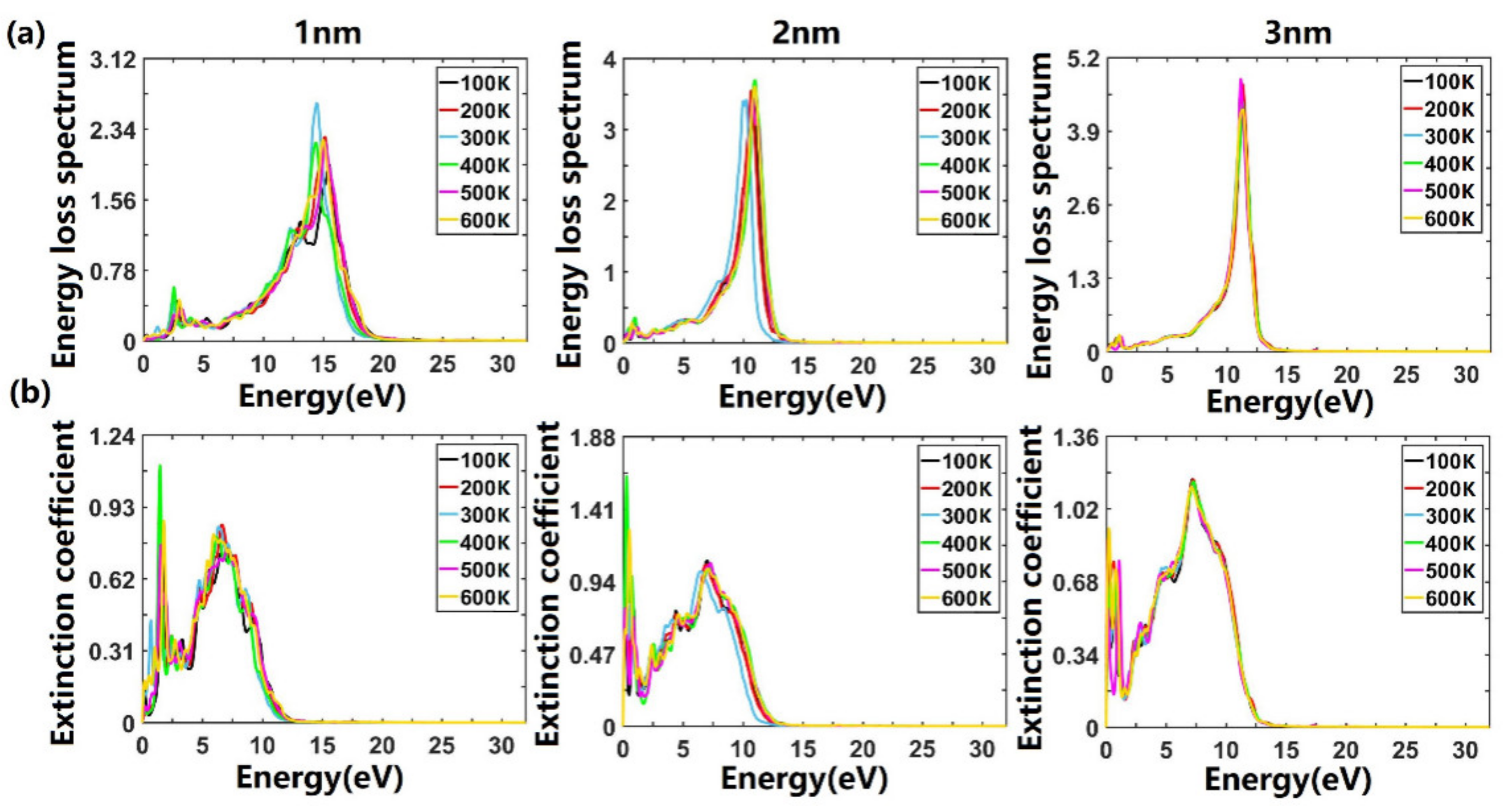
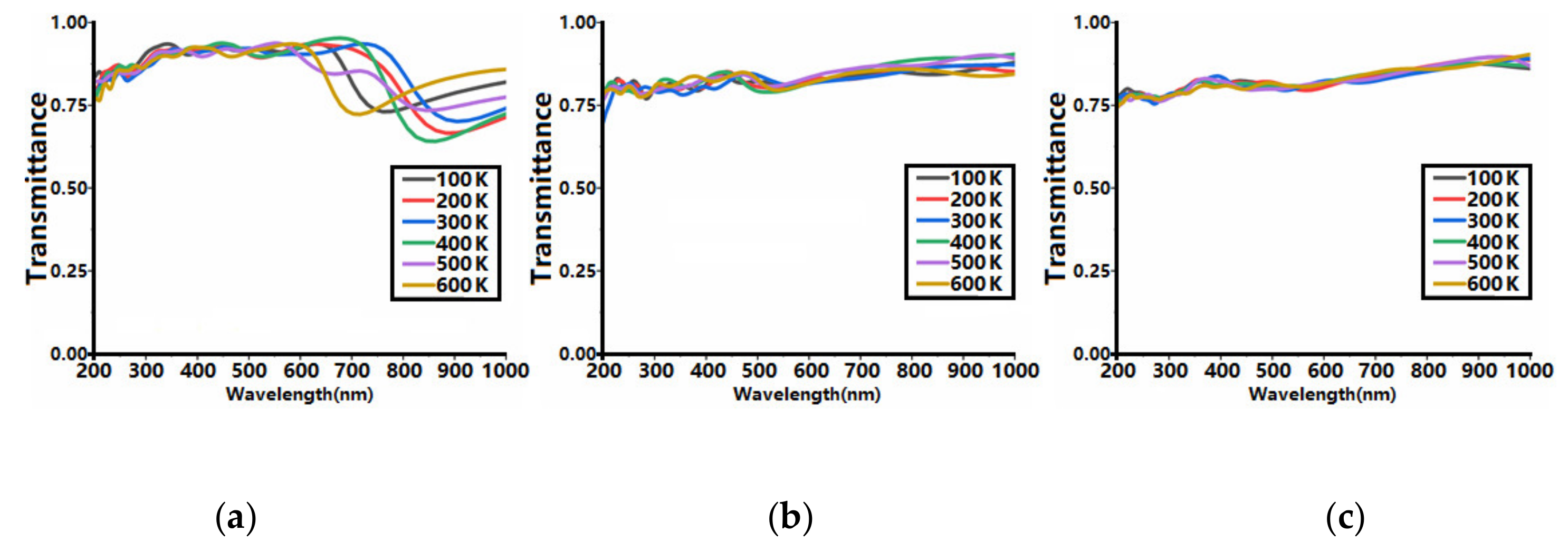
3.2. Optical Properties of Ultrathin Films of ITO
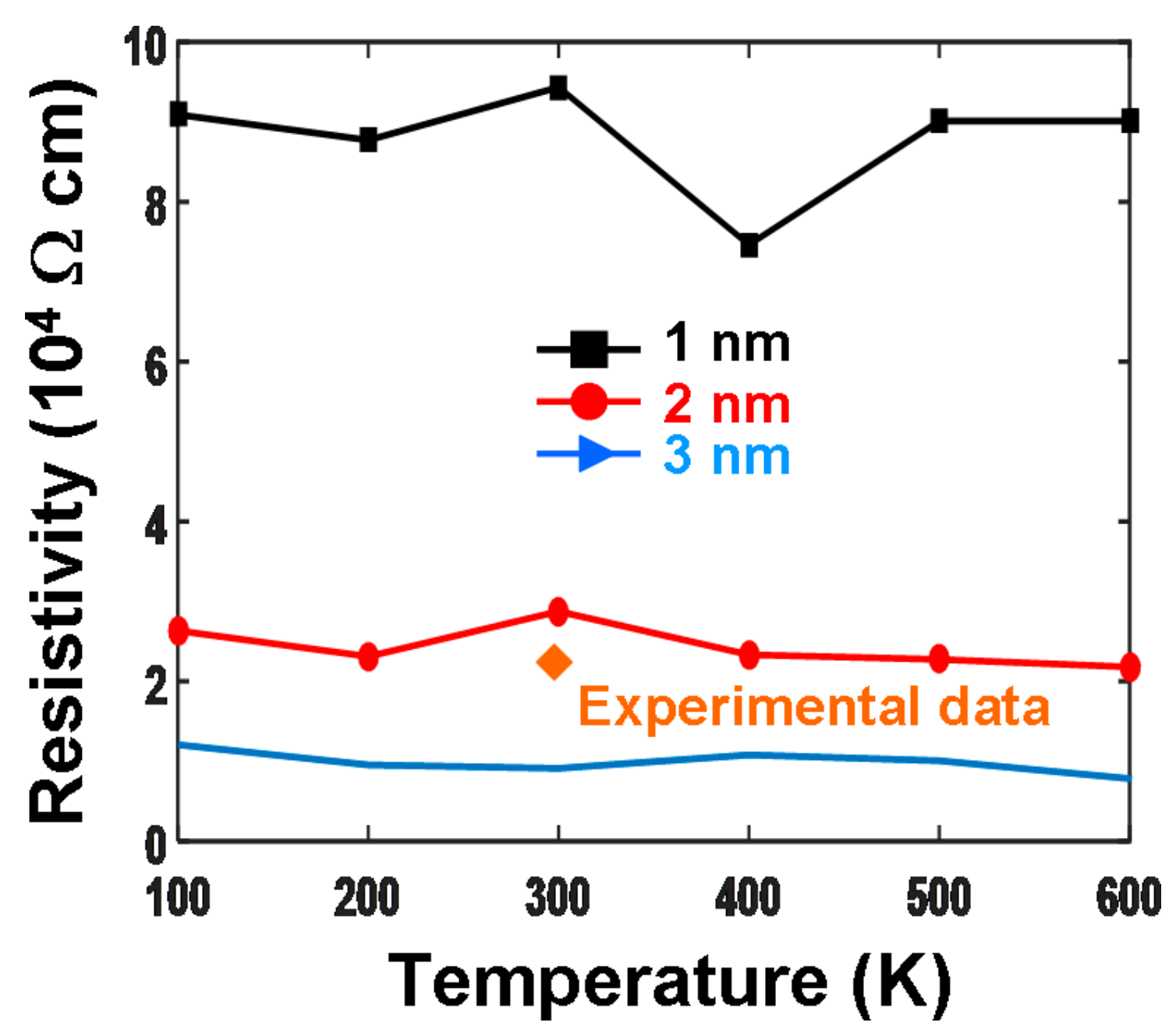
3.3. Electrical Transport Properties of Ultrathin Films of ITO
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gokceli, G.; Karatepe, N. Improving the properties of indium tin oxide thin films by the incorporation of carbon nanotubes with solution-based techniques. Thin Solid Films 2020, 697, 137844. [Google Scholar] [CrossRef]
- Woong, S.J.; Anthony, H.F. Is indium tin oxide a suitable electrode in organic solar cells? Photovoltaic properties of interfaces in organic p/n junction photodiodes. Appl. Phys. Lett. 2006, 88, 093504. [Google Scholar]
- Hong, C.H.; Shin, J.H.; Ju, B.K.; Kim, K.H.; Park, N.M.; Kim, B.S.; Cheong, W.S. Index-matched indium tin oxide electrodes for capacitive touch screen panel applications. J. Nanosci. Nanotechnol. 2013, 13, 7756–7759. [Google Scholar] [CrossRef]
- Semenza, P. New transparent conductors take on ITO for touch-screen and display applications. Inf. Disp. 2013, 29, 40–42. [Google Scholar] [CrossRef]
- Ji, H.Y.; Parida, B.; Park, S.; Kim, M.J.; Chung, S.J.; Kim, K. Enhancement effect of short-circuit currents of Si solar cells with inclusion of indium tin oxide layers on metal-semiconductor interfaces. Jpn. J. Appl. Phys. 2015, 54, 100306. [Google Scholar] [CrossRef]
- Kenji, N.; Hiromichi, O.; Kazushige, U.; Toshio, K.; Masahiro, H.; Hideo, H. Thin-film transistor fabricated in single-crystalline transparent oxide semiconductor. Science 2003, 300, 1269–1272. [Google Scholar]
- Hosseini, P.; Wright, C.D.; Bhaskaran, H. An optoelectronic framework enabled by low-dimensional phase-change films. Nature 2014, 511, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Carrillo, S.G.C.; Trumby, L.; Au, Y.Y.; Nagareddy, V.K.; Rodriguez-Hemandez, G.; Hosseini, P.; Rios, C.; Bhaskaran, H.; Wright, C.D. A nonvolatile phase-change metamaterial color display. Adv. Opt. Mater. 2019, 7, 41801782. [Google Scholar] [CrossRef]
- Rios, C.; Youngblood, N.; Cheng, Z.G.; le Gallo, M.; Pernice, W.H.P.; Wright, C.D.; Sebastian, A.; Bhaskaran, H. In-memory computing on a photonic platform. Sci. Adv. 2019, 5, eaau5759. [Google Scholar] [CrossRef]
- Madhvendra, N.T.; Kazuhito, S.; Ryoji, S.; Hiroshi, M.; Yoshiyuki, K. First-principles analysis of structural and opto-electronic properties of indium tin oxide. J. Appl. Phys. 2012, 111, 103110. [Google Scholar]
- Tripathi, M.N.; Bahramy, M.S.; Shida, K.; Sahara, R.; Mizuseki, H.; Kawazoe, Y. Optoelectronic and magnetic properties of Mn-doped indium tin oxide: A first-principles study. J. Appl. Phys. 2012, 112, 073105. [Google Scholar] [CrossRef]
- Bai, L.N.; Wei, Y.P.; Lian, J.S.; Jiang, Q. Stability of indium-tin-oxide and its optical properties: A first-principles study. J. Phys. Chem. Solids 2013, 74, 446–451. [Google Scholar] [CrossRef]
- Warschkow, O.; Ellis, D.E.; Gonzalez, G.B.; Mason, T.O. Defect cluster aggregation and nonreducibility in tin-doped indium oxide. J. Am. Chem. Soc. 2003, 86, 1707–1711. [Google Scholar] [CrossRef]
- Nadaud, N.; Lequeux, N.; Nanot, M.; Jove, J.; Roisnel, T. Structural studies of tin-doped indium oxide (ITO) and In4Sn3O12. J. Solid State Chem. 1998, 135, 140–148. [Google Scholar] [CrossRef]
- Karazhanov, S.Z.; Ravindran, P.; Vajeeston, P.; Ulyashin, A.; Finstad, T.G.; Fjelivag, H. Phase stability electronic structure, and optical properties of indium oxide polytypes. Phys. Rev. B 2007, 76, 075129. [Google Scholar] [CrossRef]
- McGuinness, C.; Stagarescu, C.B.; Ryan, P.J.; Downes, J.E.; Fu, D.F.; Smith, K.E.; Egdell, R.G. Influence of shallow core-level hybridization on the electronic structure of post-transition-metal oxides studied using soft X-ray emission and absorption. Phys. Rev. B 2003, 68, 165104. [Google Scholar] [CrossRef]
- Barr, T.L.; Liu, Y.L. An X-ray photoelectron spectroscopy study of the valence band structure of indium oxides. J. Phys. Chem. Solids 1989, 50, 657–664. [Google Scholar] [CrossRef]
- Hamberg, I.; Granqvist, C.G.; Berggren, K.F.; Sernelius, B.E.; Engstrom, L. Band-gap widening in heavily Sn-doped In2O3. Phys. Rev. B 1984, 30, 3240–3246. [Google Scholar] [CrossRef]
- Wang, L.; Yu, L.; Wu, J.Z.; Wen, J.; Xiong, B.S. Scanning near-field optical microscopy based phase-change optical memory. Appl. Phys. Express 2019, 12, 095002. [Google Scholar] [CrossRef]
- Rios, C.; Hosseini, P.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. On-chip photonic memory elements employing phase-change materials. Adv. Mater. 2014, 26, 1372–1377. [Google Scholar] [CrossRef]
- Rios, C.; Stegmaier, M.; Hosseini, P.; Wang, D.; Scherer, T.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. Integrated all-photonic non-volatile multi-level memory. Nat. Photonics 2015, 9, 725–733. [Google Scholar] [CrossRef]
- Li, X.; Youngblood, N.; Rios, C.; Cheng, Z.G.; Wright, C.D.; Pernice, W.H.P.; Bhaskaran, H. Fast and reliable storage using a 5 bit, nonvolatile photonic memory cell. Optica 2019, 6, 1–6. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Agoston, P.; Erhart, P.; Klein, A.; Albe, K. Geometry, electronic structure and thermodynamic stability of intrinsic point defects in indium oxide. J. Phys. Condens. Matter 2009, 21, 455801. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Persson, K.; Berkeley, C.A. Materials Data on In2O3 (SG:206) by Materials Project (United States). 2014. Available online: https://materialsproject.org/materials/mp-22598/ (accessed on 11 November 2020). [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Efficient projector expansion for the ab initio LCAO method. Phys. Rev. B 2005, 72, 045121. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Ozaki, T. Continued fraction representation of the Fermi Dirac function for large scale electronic structure calculations. Phys. Rev. B 2007, 75, 035123. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large scale electronic structures. Phys. Rev. B 2003, 67, 155108–155192. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, Philip, J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Cond. Mat. 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Peng, W.; Li, L.X.; Yu, S.H.; Zheng, H.R.; Yang, P. Structure, binding energy and optoelectrical properties of p-type CuI thin films: The effects of thickness. Appl. Surf. Sci. 2020, 502, 144424. [Google Scholar] [CrossRef]
- Knickerbocker, S.A.; Kulkarni, A.K. Calculation of the figure of merit for indium tin oxide films based on basic theory. J. Vac. Sci. Technol. A 1995, 13, 1048–1052. [Google Scholar] [CrossRef]
- Sipe, J.E.; Shkrebtii, A.I. Second-order optical response in semiconductors. Phys. Rev. B 2000, 61, 5337–5338. [Google Scholar] [CrossRef]
- Ravindran, P.; Delin, A.; Johansson, B.; Eriksson, O.; Wills, J.M. Electronic structure, chemical bonding, and optical properties of ferroelectric and antiferroelectric NaNO2. Phys. Rev. B 1999, 513, 1776–1778. [Google Scholar] [CrossRef]
- Guo, E.-J.; Guo, H.Z.; Lu, H.B.; Jin, K.J.; He, M.; Yang, G.Z. Structure and characteristics of ultrathin indium tin oxide films. Appl. Phys. Lett. 2011, 98, 011905. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, L.; Tong, Y. Optoelectronic Properties of Ultrathin Indium Tin Oxide Films: A First-Principle Study. Crystals 2021, 11, 30. https://doi.org/10.3390/cryst11010030
Liu X, Wang L, Tong Y. Optoelectronic Properties of Ultrathin Indium Tin Oxide Films: A First-Principle Study. Crystals. 2021; 11(1):30. https://doi.org/10.3390/cryst11010030
Chicago/Turabian StyleLiu, Xiaoyan, Lei Wang, and Yi Tong. 2021. "Optoelectronic Properties of Ultrathin Indium Tin Oxide Films: A First-Principle Study" Crystals 11, no. 1: 30. https://doi.org/10.3390/cryst11010030
APA StyleLiu, X., Wang, L., & Tong, Y. (2021). Optoelectronic Properties of Ultrathin Indium Tin Oxide Films: A First-Principle Study. Crystals, 11(1), 30. https://doi.org/10.3390/cryst11010030




