Single-Crystal Growth and Small Anisotropy of the Lower Critical Field in Oxypnictides: NdFeAsO_{1 − x}F_x

Abstract

High-quality single crystals of the unconventional superconductor NdFeAsO_{1 − x}F_x were grown. We developed a new optimized flux technique to overcome the difficulties in single-crystal growth and the sample quality limitations of NdFeAsO_{1 − x}F_x. The normal state of the F-doped samples exhibits simple metallic behavior upon cooling down from room temperature, followed by a sharp superconducting transition. The values of residual resistivity ratio (RRR) is 3.2, 6.4, and 10.3 for x = 0.1, 0.15, and 0.2, respectively. Both the large RRR and the narrow superconducting transition signpost the high quality of the crystals. We have examined the in- and out-of-plane lower critical fields, and the field at which vortices penetrate the sample of NdFeAsO_{1 − x}F_x (x = 0.1). The anisotropy ratio [γ_Hc1 (0)] increased slightly with increasing temperature from 0.8 Tc to Tc. The temperature dependence of the first vortex penetration field was obtained under the static magnetic field, H, parallel to the c- and ab- axis, and pronounced changes in the H_c1(T) curvature were observed, which are attributed to the multi-band superconductivity.

1. Introduction

In many correlated electron materials, several ground states are often competing with each other. Thus, adjusting certain parameters may allow switching from one ground state to another. Typical control parameters include the magnetic field, pressure, electron density, and chemical composition [1]. Searching for quaternary materials containing iron arsenide (FeAs) fluorite-type layers has brought new insights to the high-T_C superconductivity community [2]. The NdFeAsO_{1 − x}F_x compound is one of the 1111 iron pnictides: type-II superconductors containing sets of two-dimensional iron arsenide layers that exhibit a tetragonal structure at ambient conditions [3,4]. This compound shows a sharp superconducting (SC)transition [5]. Although the magnetic structure is the same as LaFeAsO, an ordered magnetic moment of 0.25 µ_B was measured for this compound, which is one of the lowest observed in this type of material to date [6]. The resistivity measurements reveal quite a small anisotropy and a huge upper critical field, and thus, encourage several applications of this compound [7]. The detailed chemical composition of the NdFeAsO_{1 − x}F_x samples with different x-values, as well as their electrical transport characterization, showed the emergence of superconductivity with fluorine doping at the level of 13–20% [8]. Direct current (DC) magnetometry and muon-spin spectroscopy (µSR) measurements revealed that, unlike the other Ln-1111 family members, in the intermediate F-doping regime of Nd-1111, there is a strong indication of fluctuating magnetism on the µSR time scale [9]. Studying the magnetic structure of Nd in the parent compound NdFeAsO revealed a strong interplay between Nd and Fe moments at low temperatures (T = 1.7–15 K). Although Nd moments aligned along the crystallographic c-axis at a low temperature (1.7 K), increasing the temperature allowed the moment to reorient towards the crystallographic c-axis [10].

The main challenge in understanding unconventional superconductors is to have large and high-quality single-phase crystals. The lack of such samples has been a central impediment in resolving several issues in the field of unconventional superconductivity. For example, the structure of the gap function in the Brillouin zone is not known at a high resolution. Oxypnictides, LnFePnO (Ln: lanthanide, Pn: pnictogen), abbreviated as 1111, are the most attractive materials among the discovered Fe-based superconductors due to their high SC transition temperatures, as well as their high upper critical fields, which make them suitable for high-field magnet applications. The main problems with the single-crystal growth of 1111 systems are the following [11]:

• The compounds decompose above ~1200 °C, well below the melting point;
• The presence of stable secondary phases (i.e., stable rare earth oxides compounds);
• The multicomponent phase diagrams are unknown.

Two main methods for the single-crystal growth of the 1111 compounds are as follows:

• Growth by the flux method using metallic Tin (Sn), an equivalent mixture of sodium and potassium chlorides (NaCl/KCl), and iodides (NaI/KI), and sodium arsenide (NaAs) as the flux. The following points were noticed:
  • Sodium arsenide (NaAs) was shown to yield large and well-shaped single crystals [11]. However, the quality of these crystals is under debate. Unfortunately, F-doping was not yet possible using this flux;
  • Tin (Sn) is a suitable flux for the CeFe(As_{1 − x}P_x)O system, but not for the LaFeAsO compound [12];
  • NaI/KI flux was shown to give crystals with several 100 μm lengths [13]. High temperatures need to be applied to increase the solubility of the elements in the salt flux.
• High-pressure crystal growth using the NaCl/KCl flux [14,15]. This method is favorable for the single-crystal growth of the 1111 systems. Using this technique, F-doped crystals were grown to crystal sizes below 500 μm. However, this is still too small for several experiments.

Among the widely studied superconducting 1111 compounds, a systematic investigation of the crossover region between the superconducting and the antiferromagnetic (AFM) phases for the Ln = Nd, La, and Ce cases is missing. Sphinx will fill this gap by focusing on the growth of sizeable high-quality single crystals of LnFeAsO_{1 − y}F_x (Ln = La, Ce, Nd) and LnFe(As_{1 − x}Pn_x)O (Pn = P, Sb) compounds. These compounds have a relatively small number of publications so far. None of which address these important challenges concerning the mechanism of superconductivity, and there is no agreement on a generic electronic phase diagram as a function of chemical doping.

The flux growth method is one of the frequently used techniques for growing crystals of iron pnictides. High-temperature solution growth allows for a wide variety of flux materials and relatively low growth temperature, as well as a relatively small quantity of reactants, providing a new route for single-crystal growth from incongruently melting reactants. Although the flux growth method produces single crystals free from thermal strain, the produced crystals are relatively small. However, by optimizing the amount of flux, the temperature profile may increase the size and the quality of the product.

In this work, we report the growth of a relatively large single crystal of the NdFeAsO_1-xF_x compound with different nominal fluorine doping. These crystals were grown by the flux method using alkali metal chlorides (NaCl/KCl) eutectic flux. The superconducting properties of the prepared samples were investigated and indicated the appearance of diamagnetic properties.

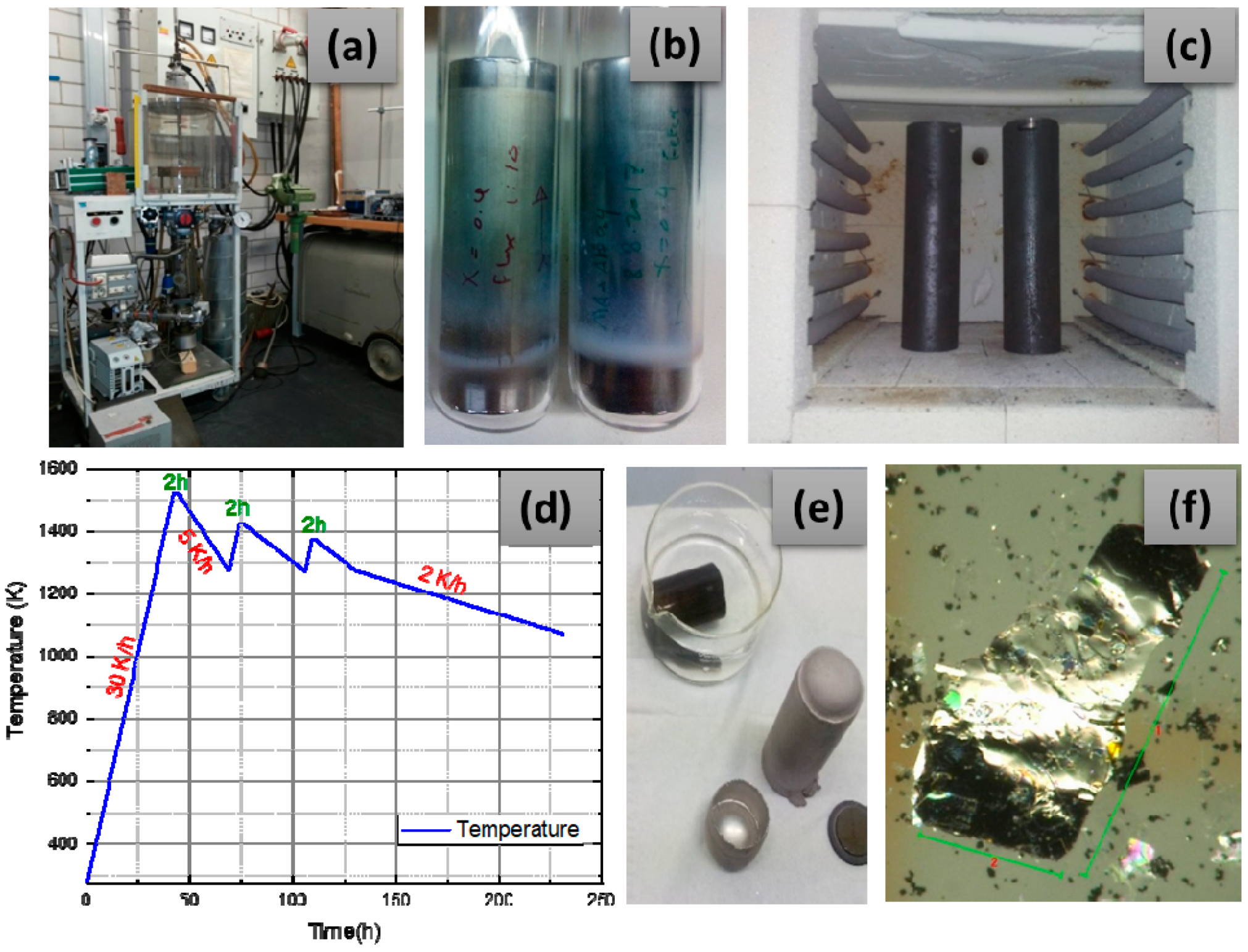
2. Materials and Methods

The growth of NdFeAsO_1-xF_x single crystals was done according to the previously reported method by Adamski et al. [16,17], with some modifications on both the flux stoichiometry and the temperature profile. Taking into consideration the safety precautions for handling arsenic, all procedures related to the sample preparation were performed under an argon atmosphere. The starting materials were neodymium metal (Nd), arsenic metal (As), iron (III) oxide (Fe₃O₄), iron fluoride (FeF₂), potassium chloride (KCl), and sodium chloride (NaCl). The purity of the materials was 99.9% and was used without further purification. These materials were cut, weighed, and mixed inside an Argon filled glove box under a controlled level of O₂ and H₂O (0.5 ppm). The molar ratio of reactants and the flux were modified to be 1:10, instead of 1:7 in the previously reported data.

Figure 1 summarizes the crystal growth process. The mixture of the precursors and the flux were added to a glassy carbon crucible (20 mm) with a lid. To decrease the oxidation of the sample, the crucible was inserted into a niobium ampoule and covered. The ampoule was then sealed using an arc-welding machine. Finally, the whole sample was sealed under a vacuum inside a quartz tube using a quartz welding station and then transferred into a box furnace. For the protection of the furnace, the samples were kept inside a stainless-steel shield with a cover.

The development of a suitable profile was quite challenging. The analysis of the powder diffraction patterns indicated that NdFeAsO_1-xF_x is a major phase, which means that the flux can dissolve most of the precursors. However, some relatively large and pure crystals were obtained. Most of the previous growth experiments using the flux method used a single step for crystallization which produced a large number of small-sized crystals. Since we could not increase temperature due to the decomposition of the compound, we tried to develop a way to increase both the nucleation and the growth time without increasing the temperature. The multistep temperature profile enhanced the crystal size. On one hand, heating the mixture after crystallization allowed the dissolving of smaller seeds formed in the first step, thus decreasing the number of possible crystallization sites. On the other hand, during the growth phase, melting can crystallize a smaller number of relatively large seeds which increases the size of the final crystal.

The growth process was carried out by applying a modified temperature profile using the Sawtooth profile, as shown in Figure 1d. In this profile, the sample was introduced at three crystalization steps at 1523, 1423, and 1373 K, respectively, with a dwell time of 2 h each. The sample was then cooled gradually to 1073 K at 2 K/h and then cooled rapidly to room temperature. The ampoule was cut using a stainless-steel cutting knife and the flux was dissolved by rinsing with distilled water. The crystals were separated by filtration and checked using an optical microscope. Relatively large single crystals were found (800 × 350 µm²), compared to the previously reported crystals produced using the same technique (250 × 250 µm²). X-ray powder diffraction patterns (XRD) were collected at ambient conditions using a Siemens D 500 diffractometer with 2θ in the range of 20–80 degrees. Electron probe microanalysis (EPMA) was carried out using a Jeol JX 8900 R microprobe equipped with four different probes. Both magnetic and transport measurements were carried out using a quantum design physical property measurement system (PPMS) instrument at the Institute of Physics, Goethe University Frankfurt. The measurements were carried out in the range between 2 and 300 K under different applied magnetic fields. The temperature dependence of the magnetic susceptibility, χ, and isothermal magnetization, M, versus the magnetic field, H, measurements were performed both in-plane and out-of-plane, parallel to the applied field. The transport measurements were measured by making four gold leads (10 µm) using an Epo-Tek H20E silver epoxy.

3. Results and Discussion

3.1. Crystal Quality

The purity phase of the single crystals and the exact amount of the fluorine dopant were confirmed by both EPMA and powder X-ray diffraction. The electron probe microanalyzer (EPMA) determined the exact amount of fluorine and oxygen in each crystal. Figure 2 represents the powder diffraction patterns of the different compounds. The diffraction patterns indicated a slight change in the lattice parameters and a regular shift in the Bragg peaks with different doping concentrations. These changes are attributed to the change in fluorine content as a result of replacing oxygen in the lattice, according to the previously reported data by Ponce-Flores and Conde-Gallardo [8].

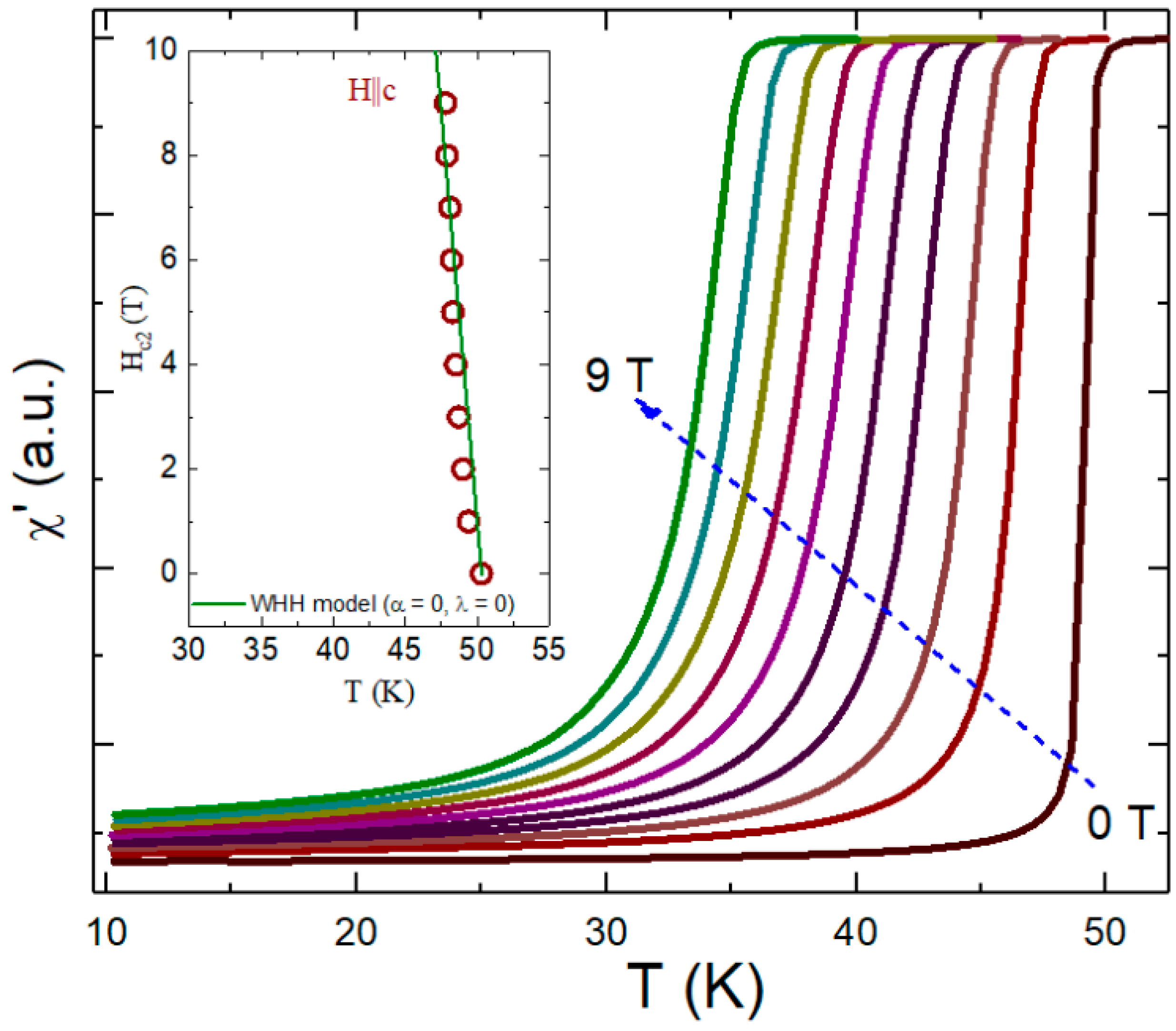
3.2. Transport Properties

Figure 3a elucidates the temperature dependence of the in-plane resistance measurements upon heating the NdFeAsO_{1 − x}F_x single crystals. Obviously, in the undoped NdFeAsO system, the anomaly at 142 K in resistance measurements attributed to the phase transition from tetragonal P4/nmm to orthorhombic Cmma. The second anomaly found at T_N ≈ 130 K corresponds to the onset of the well-known spin-density-wave (SDW) stripe-like Fe order [18]. In the absence of an externally applied field, the doped samples show a typical cooldown resistance curve for NdFeAsO_1−xF_x (x = 0.1, 0.15, and 0.2) single crystals. Both the spin density waves and the structural transition have been suppressed upon increasing the doping. In all doping samples, one can see that the normal state exhibits a simple metallic behavior upon cooling down to room temperature, followed by a sharp SC transition at Tc 45.4, 50.4 and 52.8 K (90% of the normal state resistivity) for x = 0.1, 0.15 and 0.2, respectively, shown in Figure 2b. The values of residual resistivity ratio (RRR) is 3.2, 6.4 and 10.3 for x = 0.1, 0.15 and 0.2, respectively. Both the large RRR and narrow superconducting transition confirm the good quality of the samples investigated here.

3.3. AC Measurements

Figure 4 represents the temperature dependence of the complex ac-susceptibility components of NdFeAsO_0.8F_0.2. The measurement was done in 5 Oe ac field amplitude and 1 kHz field frequency. The data were collected upon warming in the different dc magnetic fields after cooling in a zero magnetic field. The inset in Figure 4 presents the magnetic phase diagram of the temperature dependence of the upper critical field of NdFeAsO_0.8F_0.2. The data were fitted according to the Werthamer–Helfand–Hohenberg (WHH) theory (solid line) [16]. The WHH theory predicts the behavior of H_c2(Tc) by considering paramagnetic and orbital pair breaking. The investigated sample indicated a very high upper critical field, H_c2. Using a fit to the data in the whole measurement range for negligible spin-paramagnetic effects (α = 0) and spin-orbit scattering (λ = 0) yielded μ₀H_c2 = 95 T for x = 0.2. [18].

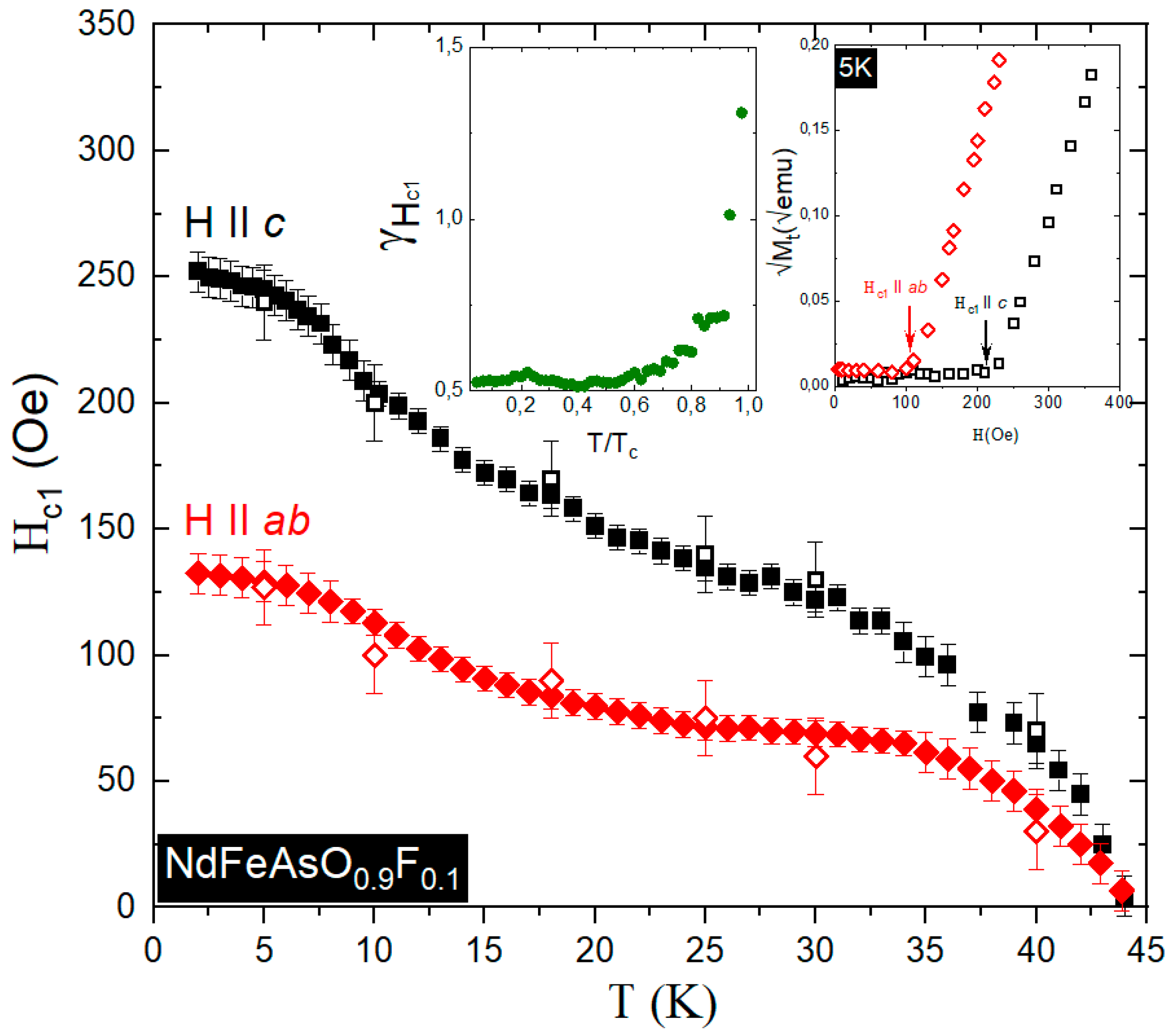
3.4. Experimental Determination of the Lower Critical Field

The lower critical field, H_c1, is a valuable parameter giving essential information about the bulk thermodynamic properties of the material [19,20,21,22]. The lower critical field, H_c1, was reliably determined from the magnetization measurements using two independent methods [16]. Once we experimentally obtained the values of H_c1, we corrected them by accounting for the demagnetization effects. The low-temperature section of Figure 5 shows the flat behavior and the temperature dependence of the first vortex penetration field of both orientations. This shows a pronounced change of the H_c1(T) curvature, which is attributed to the multi-band superconductivity [16]. The inset in Figure 5 shows that the anisotropy of H_c1: γ_Hc1 = H_c1^||c/H_c1^||ab has a small value. Similar behaviors have been reported in LiFeAs [23], MgB₂ [24], and PrFeAsO_1−y [25]. Such behaviors indicate a signature of multiband superconductivity. This could be due to the presence of Fermi surfaces of different sizes [26].

4. Conclusions

In summary, we developed a new optimized flux technique to overcome the difficulties in single-crystal growth and the limitation of the sample quality of NdFeAsO_{1 − x}F_x. The temperature dependence of the first vortex penetration field was experimentally obtained by two independent methods, and the corresponding lower critical field was deduced. This study confirmed the small anisotropy ratio of the lower critical fields in NdFeAsO_0.9F_0.1. The results were consistent with those reported previously.