First Principles Study on the Thermodynamic and Elastic Mechanical Stability of Mg2X (X = Si,Ge) Intermetallics with (anti) Vacancy Point Defects
Abstract
1. Introduction
2. Computational Method
3. Results and Discussion
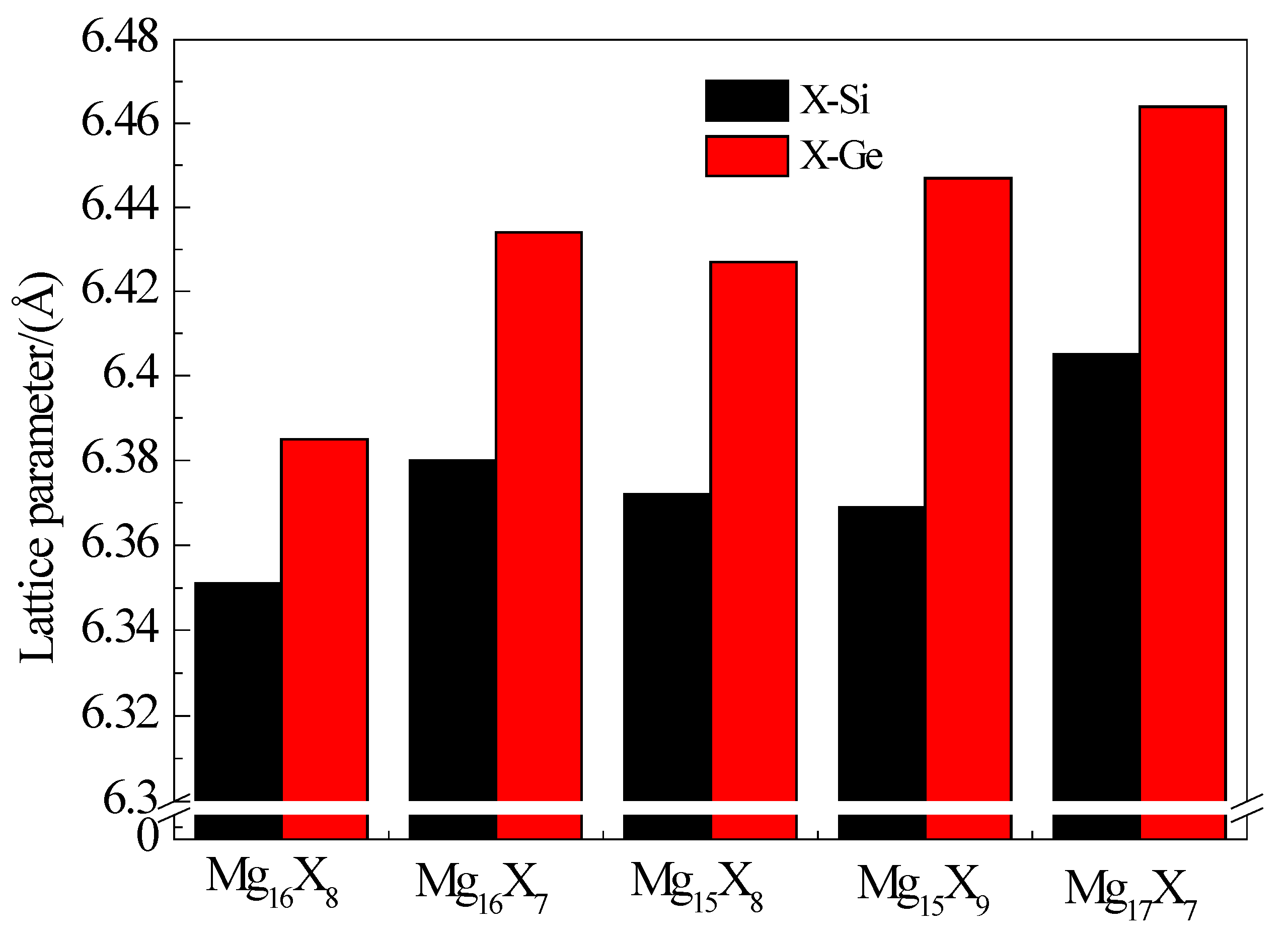
3.1. Equilibrium Lattice Stability of Intermetallics with or without Point Defects
3.2. Effects of Vacancy and Anti-Site Points Defects on Thermodynamic Stability
3.3. Effects of Vacancy and Anti-Site Points Defects on Elastic Mechanical Stability
3.3.1. Elastic Constants of Stability Criteria
3.3.2. Elastic Modulus of Mechanical Stability
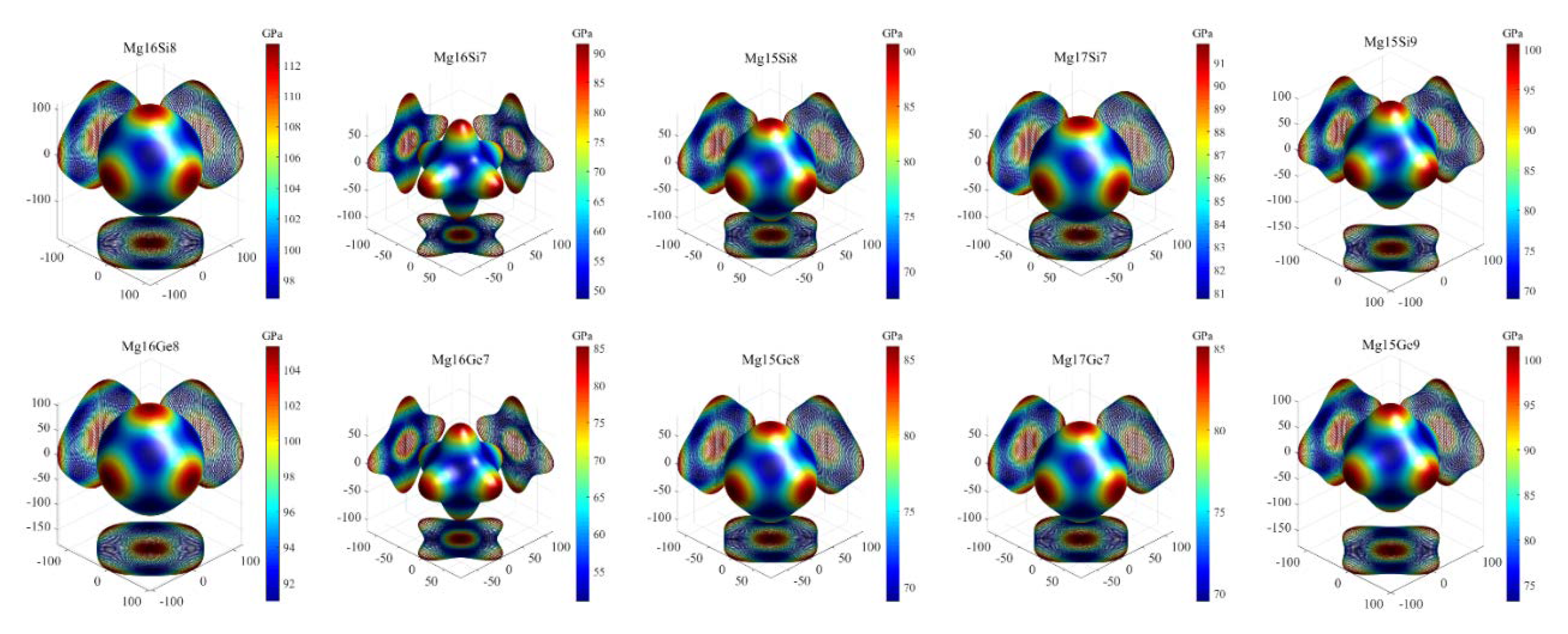
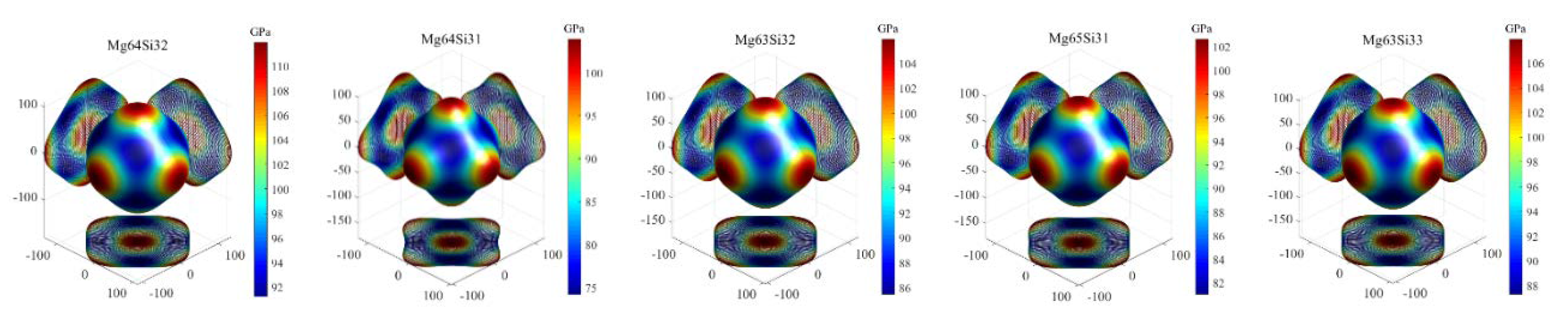
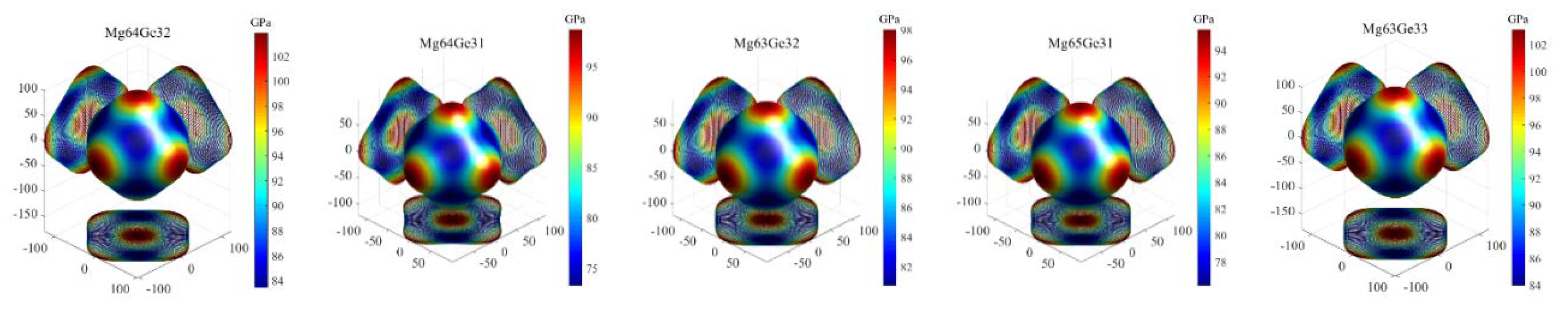
3.3.3. Elastic Anisotropy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cheng, P.; Zhao, Y.H.; Lu, R.P.; Hou, H.; Bu, Z.Q.; Yan, F. Effect of Ti addition on the microstructure and mechanical properties of cast Mg-Gd-Y-Zn alloys. Mater. Sci. Eng. A 2017, 708, 482–491. [Google Scholar] [CrossRef]
- Bell, L.E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 2008, 321, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Vantomme, A.; Mahan, J.E.; Langouche, G.; Becker, J.P.; Van Bael, M.; Temst, K.; Van Haesendonck, C. Thin film growth of semiconducting Mg2Si by codeposition. Appl. Phys. Lett. 1997, 70, 1086–1088. [Google Scholar] [CrossRef]
- Yu, R.; Li, G.; Guo, X.; Deng, K.Q.; Pang, A.M.; Zhai, P.C. An improved interatomic potential function for thermoelectric Mg2Si: A combination study of ab-initio and molecular dynamics method. Comput. Mater. Sci. 2018, 149, 49–56. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Sofo, J.O.; Zhu, T.; Chen, L.Q.; Zhao, X. First-principles studies of lattice dynamics an-d thermal properties of Mg2Si1−xSnx. J. Mater. Res. 2015, 30, 2578–2584. [Google Scholar] [CrossRef]
- Gu, X.; Li, X.; Yang, R. Phonon transmission across Mg2Si/Mg2Si1−xSnx interfaces: A first-principles-base-d atomistic Green’s function study. Phys. Rev. B 2015, 91, 205313. [Google Scholar] [CrossRef]
- Kaur, K.; Dhiman, S.; Kumar, R. Strain engineering on thermoelectric performance of Mg2Si. Mater. Res. Express 2017, 4, 075509. [Google Scholar] [CrossRef]
- Chen, Q.; Xie, Q.; Zhao, F.J.; Cui, D.; Li, X. First-principles calculations of electronic structure and optic-al properties of strained Mg2Si. Chin. Sci. Bull. 2010, 55, 2236–2242. [Google Scholar] [CrossRef]
- Huan, T.D.; Tuoc, V.N.; Le, N.B.; Minh, N.V.; Woods, L.M. High-pressure phases of Mg2Si from first principles. Phys. Rev. B 2016, 93, 094109. [Google Scholar] [CrossRef]
- Jun, L.W.; Lin, J.Z.; Qi, J.L.; Yuan, Z.C.; Ru, S.; Zhu, H.; Xiu, R.L. Pressure-induced metallization transition in Mg2Ge. Acta Phys. Sin. 2017, 66, 166201. [Google Scholar] [CrossRef]
- Hirayama, N.; Iida, T.; Morioka, S.; Sakamoto, M.; Nishio, K.; Kogo, Y. First-principles investigation of structural, electronic, and thermoelectric properties of n-and p-type Mg2Si. J. Mater. Res. 2015, 30, 2564–2577. [Google Scholar] [CrossRef]
- Hirayama, N.; Iida, T.; Funashima, H.; Morioka, S.; Sakamoto, M.; Nishio, K.; Hamada, N. Theoretical analysis of structure and formation energy of impurity-doped Mg2Si: Comparison of first-principles codes for material properties. Jpn. J. Appl. Phys. 2015, 54, 07JC05. [Google Scholar] [CrossRef]
- Murtaza, G.; Sajid, A.; Rizwan, M.; Takagiwa, Y.; Khachai, H.; Jibran, M.; Omran, S.B. First principles study of Mg2X (X = Si,Ge,Sn,Pb): Elastic, optoelectronic and thermoelectric properties. Mater. Sci. Semicond. Proc. 2015, 40, 429–435. [Google Scholar] [CrossRef]
- Jund, P.; Viennois, R.; Colinet, C.; Hug, G.; Fèvre, M.; Tedenac, J.C. Lattice stability and formation energies of intrinsic defects in Mg2Si and Mg2Ge via first principles simulations. J. Phys. Condens. Matter 2012, 25, 035403. [Google Scholar] [CrossRef] [PubMed]
- Chernatynskiy, A.; Phillpot, S.R. Anharmonic properties in Mg2X (X = C,Si,Ge,Sn,Pb) from first-principles calculations. Phys. Rev. B 2015, 92, 064303. [Google Scholar] [CrossRef]
- Guo, S.D. Electronic structure and thermoelectric properties of (Mg2X)2/(Mg2Y)2(X,Y = Si, Ge, Sn) superlattices from first-principle calculations. Eur. Phys. J. B 2016, 89, 134. [Google Scholar] [CrossRef]
- Yu, F.; Sun, J.X.; Chen, T.H. High-pressure phase transitions of Mg2Ge and Mg2Sn: First-principles calculations. Phys. B Condens. Matter 2011, 406, 1789–1794. [Google Scholar] [CrossRef]
- Pulikkotil, J.J.; Singh, D.J.; Auluck, S.; Saravanan, M.; Misra, D.K.; Dhar, A.; Budhani, R.C. Doping and temperature dependence of thermoelectric properties in Mg2(Si, Sn). Phys. Rev. B 2012, 86, 155204. [Google Scholar] [CrossRef]
- Zwolenski, P.; Tobola, J.; Kaprzyk, S. KKR–CPA study of electronic structure and relative stability of Mg2X (X= Si, Ge, Sn) thermoelectrics containing point defects. J. Alloy. Compd. 2015, 627, 85–90. [Google Scholar] [CrossRef]
- Liu, X.; Xi, L.; Qiu, W.; Yang, J.; Zhu, T.; Zhao, X.; Zhang, W. Significant roles of intrinsic point defects in Mg2X (X = Si,Ge,Sn) thermoelectric materials. Adv. Electron. Mater. 2016, 2, 1500284. [Google Scholar] [CrossRef]
- Viennois, R.; Jund, P.; Colinet, C.; Tédenac, J.C. Defect and phase stability of solid solutions of Mg2X with an antifluorite structure: An ab initio study. J. Solid State Chem. 2012, 193, 133–136. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Liu, X.; Yu, L.; Li, H.; Liu, Y. Investigation on AlP as the heterogeneous nucleus of Mg2Si in Al–Mg2Si alloys by experimental observation and first-principles calculation. Res. Phys. 2018, 8, 146–152. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, Z.; Wang, S.; Shao, G. Simulation of planar Si/Mg2Si/Si pin heterojunction solar cells for high efficiency. Solar Energy 2017, 158, 654–662. [Google Scholar] [CrossRef]
- Xia, Z.; Li, K. First-principles study on Al4Sr as the heterogeneous nucleus of Mg2Si. Mater. Res. Express 2016, 3, 126503. [Google Scholar] [CrossRef]
- Kessair, S.; Arbouche, O.; Amara, K.; Benallou, Y.; Azzaz, Y.; Zemouli, M.; Bouazza, B.S. First principles prediction of a new high-pressure phase and transport properties of Mg2Si. Indian J. Phys. 2016, 90, 1403–1415. [Google Scholar] [CrossRef]
- Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Wen, Z.Q.; Hua, H.; Tian, J.Z.; Zhao, Y.H.; Li, H.J.; Han, P.D. First-principles investigation of martensitic transformation and magnetic properties of Ni2XAl (X= Cr, Fe, Co) Heusler compounds. Intermetallics 2018, 92, 15–19. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Wang, S.; Zhang, B.; Yuan, Y.; Guo, Q.; Hou, H. The anisotropy of three-component medium entropy alloys in AlCoCrFeNi system: First-principle studies. J. Solid State Chem. 2019, 276, 232–237. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748. [Google Scholar] [CrossRef]
- Madelung, O. Numerical data and functional relationships in science and technology. N. Ser. 1982, New Series III (17), 571–619. [Google Scholar]
- Rowe, D.M. Thermoelectrics Handbook: Macro to Nano; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Zhao, Y.H.; Deng, S.; Liu, H.; Zhang, J.; Guo, Z.; Hou, H. First-principle investigation of pressure and temperature influence on structural, mechanical and thermodynamic properties of Ti3AC2 (A=Al and Si). Comput. Mater. Sci. 2018, 154, 365–370. [Google Scholar] [CrossRef]
- Zhang, C.; Han, P.; Yan, X.; Wang, C.; Xia, L.; Xu, B. First-principles study of typical precipitates in creep resistant magnesium alloys. J. Phys. D Appl. Phys. 2009, 42, 125403. [Google Scholar] [CrossRef]
- Duan, L.J.; Liu, Y.C. Relationships between Elastic Constants and EAM/FS Potential Functions for Cubic Crystals. Acta Metall. Sin. 2020, 56, 112–118. [Google Scholar] [CrossRef]
- Boulet, P.; Verstraete, M.J.; Crocombette, J.P.; Crocombette, J.P.; Briki, M.; Record, M.C. Electronic properties of the Mg2Si thermoelectric material investigated by linear-response density-functional theory. Comput. Mater. Sci. 2011, 50, 847–851. [Google Scholar] [CrossRef]
- Hill, R. The elastic behavior of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Hou, H.; Wen, Z.; Zhao, Y.; Zhao, Y.; Fu, L.; Wang, N.; Han, P. First-principles investigations on structural, elastic, thermodynamic and electronic properties of Ni3X (X= Al, Ga and Ge) under pressure. Intermetallics 2014, 44, 110–115. [Google Scholar] [CrossRef]
- Zhang, H.; Shang, S.; Saal, J.E.; Saengdeejing, A.; Wang, Y.; Chen, L.Q.; Liu, Z.K. Enthalpies of formation of magnesium compounds from first-principles calculations. Intermetallics 2009, 17, 878–885. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and Sufcient Elastic Stability Conditions in Various Crystal Systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R.; Vahldiek, F.W.; Mersol, S.A. Anisotropy in Single Crystal Refractory Compounds; Plenum: New York, NY, USA, 1968; p. 328. [Google Scholar]
- Tian, J.Z.; Zhao, Y.H.; Hou, H.; Wang, B. The effect of alloying elements on the structural stability, mechanical properties, and Debye temperature of Al3Li: A first-principles study. Materials 2018, 11, 1471. [Google Scholar] [CrossRef] [PubMed]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar] [CrossRef]
- Tian, J.Z.; Zhao, Y.H.; Hou, H.; Han, P.D. First-principles investigation of the structural, mechanical and thermodynamic properties of Al2Cu phase under various pressure and temperature conditions. Solid State Commun. 2017, 268, 44–50. [Google Scholar] [CrossRef]
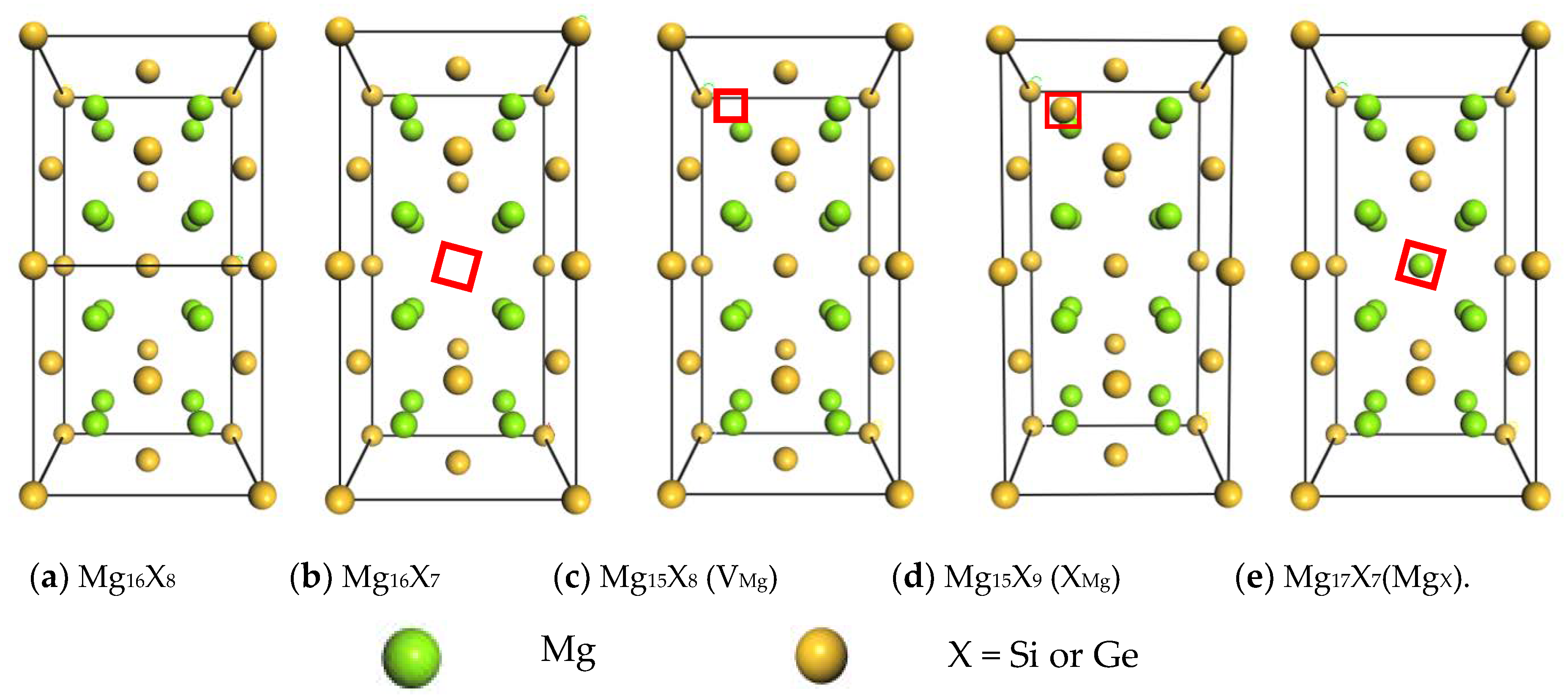

| Intermetallics | a (Å) | b (Å) | c (Å) | V (Å3) |
|---|---|---|---|---|
| Mg16Si8 | 6.351 | 6.351 | 12.702 | 512.338 |
| Mg16Si7(VSi) | 6.380 | 6.380 | 12.764 | 519.551 |
| Mg15Si8(VMg) | 6.372 | 6.372 | 12.758 | 518.005 |
| Mg15Si9(SiMg) | 6.369 | 6.369 | 12.962 | 525.793 |
| Mg17Si7(MgSi) | 6.405 | 6.405 | 13.140 | 539.056 |
| Mg16Ge8 | 6.385 | 6.385 | 12.770 | 520.586 |
| Mg16Ge7(VGe) | 6.434 | 6.434 | 12.793 | 529.584 |
| Mg15Ge8(VMg) | 6.427 | 6.427 | 12.872 | 531.695 |
| Mg15Ge9(GeMg) | 6.447 | 6.447 | 12.894 | 535.924 |
| Mg17Ge7(MgGe) | 6.464 | 6.464 | 13.229 | 552.751 |
| Intermetallics | A = b = c (Å) | V (Å3) | Intermetallics | a = b = c (Å) | V (Å3) |
|---|---|---|---|---|---|
| Mg64Si32 | 12.741 | 2068.290 | Mg64Ge32 | 12.771 | 2083.054 |
| Mg64Si31(VSi) | 12.761 | 2078.015 | Mg64Ge31(VGe) | 12.870 | 2131.974 |
| Mg63Si32(VMg) | 12.768 | 2081.463 | Mg63Ge32(VMg) | 12.879 | 2136.209 |
| Mg63Si33(SiMg) | 12.760 | 2077.480 | Mg63Ge33(GeMg) | 12.884 | 2138.745 |
| Mg65Si31(MgSi) | 12.808 | 2100.947 | Mg65Ge31(MgGe) | 12.918 | 2155.592 |
| 1 × 1 × 2 Intermetallics | 2 × 2 × 2 Intermetallics | ||||
|---|---|---|---|---|---|
| Mg16Si8 | −0.180 | −3.113 | Mg64Si32 | −0.170 | -2.949 |
| Mg16Si7(VSi) | −0.084 | −2.911 | Mg64Si31(VSi) | −0.148 | -2.899 |
| Mg15Si8(VMg) | −0.092 | −3.078 | Mg63Si32(VMg) | −0.155 | −2.947 |
| Mg17Si7(MgSi) | −0.072 | −2.852 | Mg65Si31(MgSi) | −0.142 | −2.880 |
| Mg15Si9(SiMg) | −0.108 | −3.103 | Mg63Si33(SiMg) | −0.155 | −2.945 |
| Mg16Ge8 | −0.281 | −2.953 | Mg64Ge32 | −0.259 | −2.761 |
| Mg16Ge7(VGe) | −0.167 | −2.756 | Mg64Ge31(VGe) | −0.236 | −2.716 |
| Mg15Ge8(VMg) | −0.197 | −2.910 | Mg63Ge32(VMg) | −0.248 | −2.761 |
| Mg17Ge7(MgGe) | −0.155 | −2.708 | Mg65Ge31(MgGe) | −0.230 | −2.700 |
| Mg15Ge9(GeMg) | −0.211 | −3.002 | Mg63Ge33(GeMg) | −0.248 | −2.753 |
| Intermetallics | |||||
|---|---|---|---|---|---|
| 1 × 1 × 2 | Mg16Si8 | 3.68 | 7.82 | −2.23 | 6.57 |
| Mg16Ge8 | 3.45 | 7.24 | −1.68 | 5.90 | |
| 2 × 2 × 2 | Mg64Si32 | 3.09 | 7.67 | −2.55 | 6.62 |
| Mg64Ge32 | 2.77 | 7.02 | −2.10 | 5.83 | |
| Supercell | Intermetallics | C11 | C12 | C13 | C33 | C44 | C66 |
|---|---|---|---|---|---|---|---|
| - | Mg2Si | 113.40 | 22.71 | - | - | 45.09 | - |
| - | Cal. [42] | 114.07 | 19.56 | - | - | 33.32 | - |
| 1 × 1 × 2 | Mg16Si7(VSi) | 91.55 | 27.67 | 21.98 | 94.37 | 19.64 | 28.76 |
| Mg15Si8(VMg) | 90.70 | 27.25 | 29.12 | 89.98 | 29.91 | 33.24 | |
| Mg17Si7(MgSi) | 91.83 | 24.34 | 25.26 | 84.48 | 38.07 | 31.50 | |
| Mg15Si9(SiMg) | 100.74 | 27.37 | 27.37 | 97.76 | 29.78 | 30.69 | |
| 2 × 2 × 2 | Mg64Si31(VSi) | 103.94 | 24.76 | 32.46 | |||
| Mg63Si32(VMg) | 105.98 | 25.23 | 38.96 | ||||
| Mg63Si33(SiMg) | 107.95 | 23.45 | 39.83 | ||||
| Mg65Si31(MgSi) | 102.69 | 25.95 | 36.64 | ||||
| - | Mg2Ge | 105.32 | 20.83 | - | - | 42.58 | 105.32 |
| - | Cal. [43] | 107.3 | 21.1 | - | - | 41.8 | 107.3 |
| 1 × 1 × 2 | Mg16Ge7(VGe) | 86.30 | 24.62 | 19.36 | 89.24 | 22.13 | 86.30 |
| Mg15Ge8(VMg) | 84.38 | 25.08 | 26.89 | 83.96 | 29.24 | 84.38 | |
| Mg17Ge7(MgGe) | 83.71 | 21.32 | 25.99 | 80.78 | 32.83 | 83.71 | |
| Mg15Ge9(GeMg) | 94.53 | 25.42 | 24.64 | 92.92 | 30.48 | 94.53 | |
| 2 × 2 × 2 | Mg64Ge31(VGe) | 98.69 | 22.22 | 32.46 | |||
| Mg63Ge32(VMg) | 98.05 | 23.14 | 37.08 | ||||
| Mg63Ge33(GeMg) | 103.14 | 22.97 | 38.42 | ||||
| Mg65Ge31(MgGe) | 95.57 | 23.53 | 34.59 |
| Supercell | Intermetallics | B/GPa | G/GPa | E/GPa | G/B | ʋ |
|---|---|---|---|---|---|---|
| - | Mg2Si | 52.94 | 45.19 | 105.54 | 0.854 | 0.168 |
| - | Cal. [42] | 51.06 | 46.12 | 108.35 | 0.903 | 0.150 |
| 1 × 1 × 2 | Mg16Si7(VSi) | 46.74 | 27.33 | 68.62 | 0.585 | 0.255 |
| Mg15Si8(VMg) | 49.15 | 31.00 | 76.85 | 0.631 | 0.239 | |
| Mg17Si7(MgSi) | 46.38 | 34.41 | 82.77 | 0.742 | 0.202 | |
| Mg15Si9(SiMg) | 51.49 | 35.53 | 83.61 | 0.752 | 0.239 | |
| 2 × 2 × 2 | Mg64Si31(VSi) | 51.16 | 35.14 | 85.79 | 0.687 | 0.221 |
| Mg63Si32(VMg) | 52.15 | 39.52 | 94.65 | 0.758 | 0.198 | |
| Mg65Si31(MgSi) | 51.53 | 37.32 | 90.19 | 0.724 | 0.208 | |
| Mg63Si33(SiMg) | 51.62 | 40.78 | 96.84 | 0.790 | 0.187 | |
| - | Mg2Ge | 49.00 | 42.45 | 98.81 | 0.866 | 0.164 |
| - | Cal. [43] | 49.80 | 42.30 | 98.90 | 0.847 | - |
| 1 × 1 × 2 | Mg16Ge7(VGe) | 43.48 | 28.17 | 69.50 | 0.648 | 0.234 |
| Mg15Ge8(VMg) | 45.47 | 29.51 | 72.79 | 0.649 | 0.233 | |
| Mg17Ge7(MgGe) | 43.88 | 30.16 | 73.62 | 0.688 | 0.220 | |
| Mg15Ge9(GeMg) | 47.28 | 32.76 | 79.84 | 0.693 | 0.219 | |
| 2 × 2 × 2 | Mg64Ge31(VGe) | 47.71 | 34.66 | 83.71 | 0.727 | 0.208 |
| Mg63Ge32(VMg) | 48.11 | 37.23 | 88.78 | 0.774 | 0.193 | |
| Mg65Ge31(MgGe) | 47.54 | 35.15 | 84.61 | 0.739 | 0.203 | |
| Mg63Ge33(GeMg) | 49.69 | 39.08 | 92.88 | 0.786 | 0.189 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Tian, J.; Bai, G.; Zhang, L.; Hou, H. First Principles Study on the Thermodynamic and Elastic Mechanical Stability of Mg2X (X = Si,Ge) Intermetallics with (anti) Vacancy Point Defects. Crystals 2020, 10, 234. https://doi.org/10.3390/cryst10030234
Zhao Y, Tian J, Bai G, Zhang L, Hou H. First Principles Study on the Thermodynamic and Elastic Mechanical Stability of Mg2X (X = Si,Ge) Intermetallics with (anti) Vacancy Point Defects. Crystals. 2020; 10(3):234. https://doi.org/10.3390/cryst10030234
Chicago/Turabian StyleZhao, Yuhong, Jinzhong Tian, Guoning Bai, Leting Zhang, and Hua Hou. 2020. "First Principles Study on the Thermodynamic and Elastic Mechanical Stability of Mg2X (X = Si,Ge) Intermetallics with (anti) Vacancy Point Defects" Crystals 10, no. 3: 234. https://doi.org/10.3390/cryst10030234
APA StyleZhao, Y., Tian, J., Bai, G., Zhang, L., & Hou, H. (2020). First Principles Study on the Thermodynamic and Elastic Mechanical Stability of Mg2X (X = Si,Ge) Intermetallics with (anti) Vacancy Point Defects. Crystals, 10(3), 234. https://doi.org/10.3390/cryst10030234




