From Equilibrium Liquid Crystal Formation and Kinetic Arrest to Photonic Bandgap Films Using Suspensions of Cellulose Nanocrystals
Abstract
1. Introduction
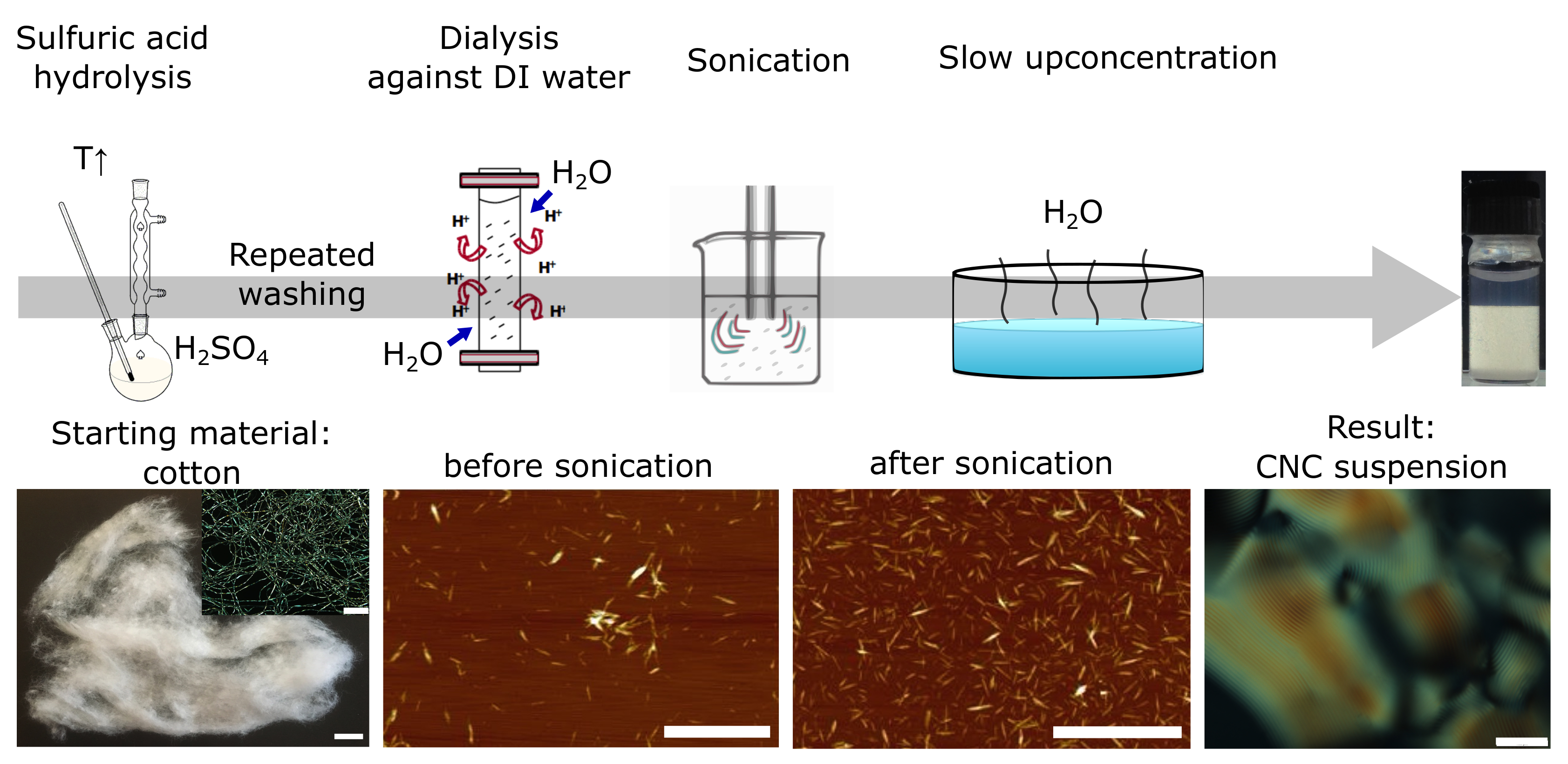
2. What Are Cellulose Nanocrystals and How Are They Made?
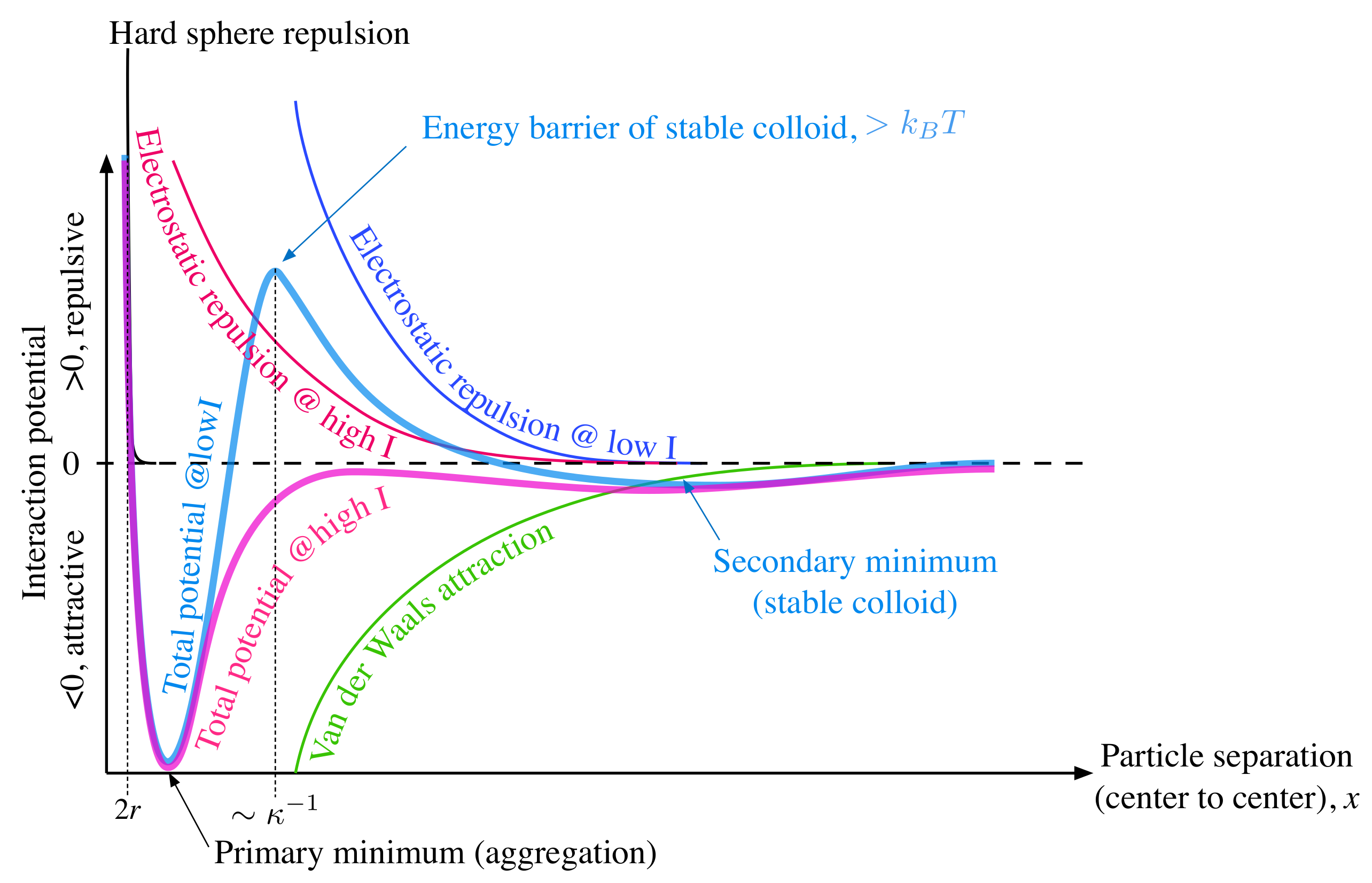
3. A Brief Reminder of the Factors Governing Electrostatic Stabilization of Colloids: the Debye Screening Length and the Ionic Strength
4. Liquid Crystal Formation in CNC Suspensions and Other Colloidal Nanorod Suspensions
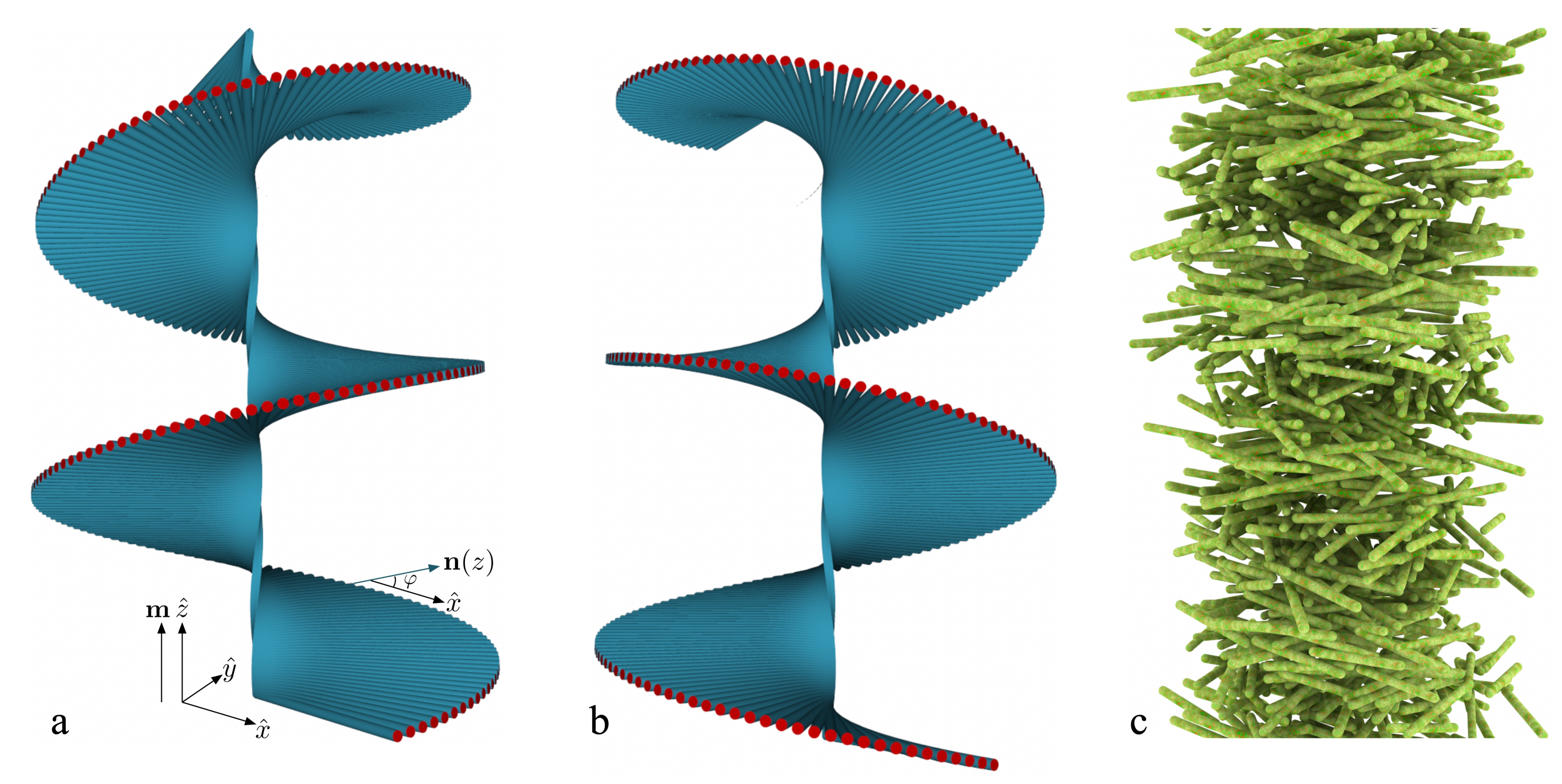
4.1. Long-Range Orientational, Short-Range Positional Order: The (Chiral) Nematic Phase
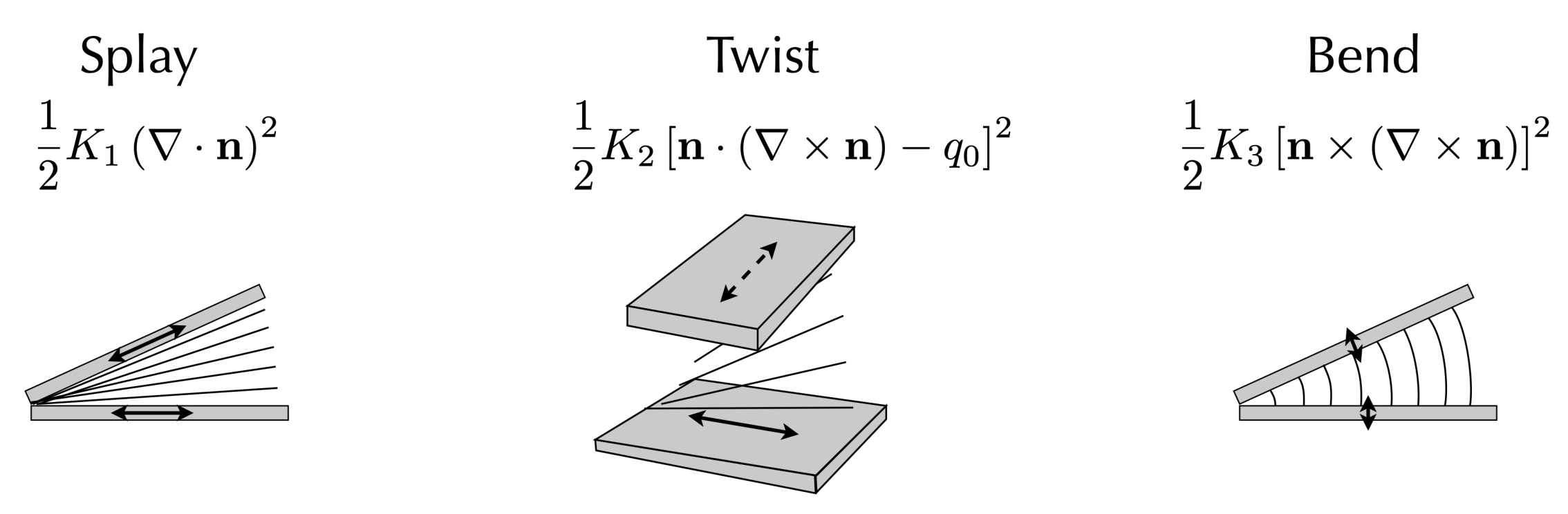
4.2. Nematic Elasticity
4.3. The Origin of Nematic Phase Formation According to Onsager
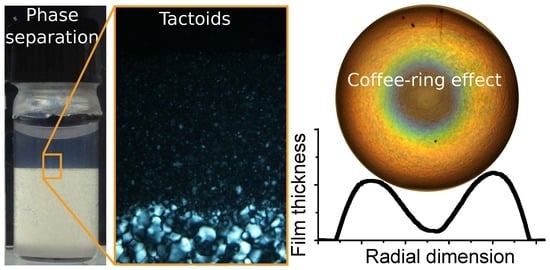
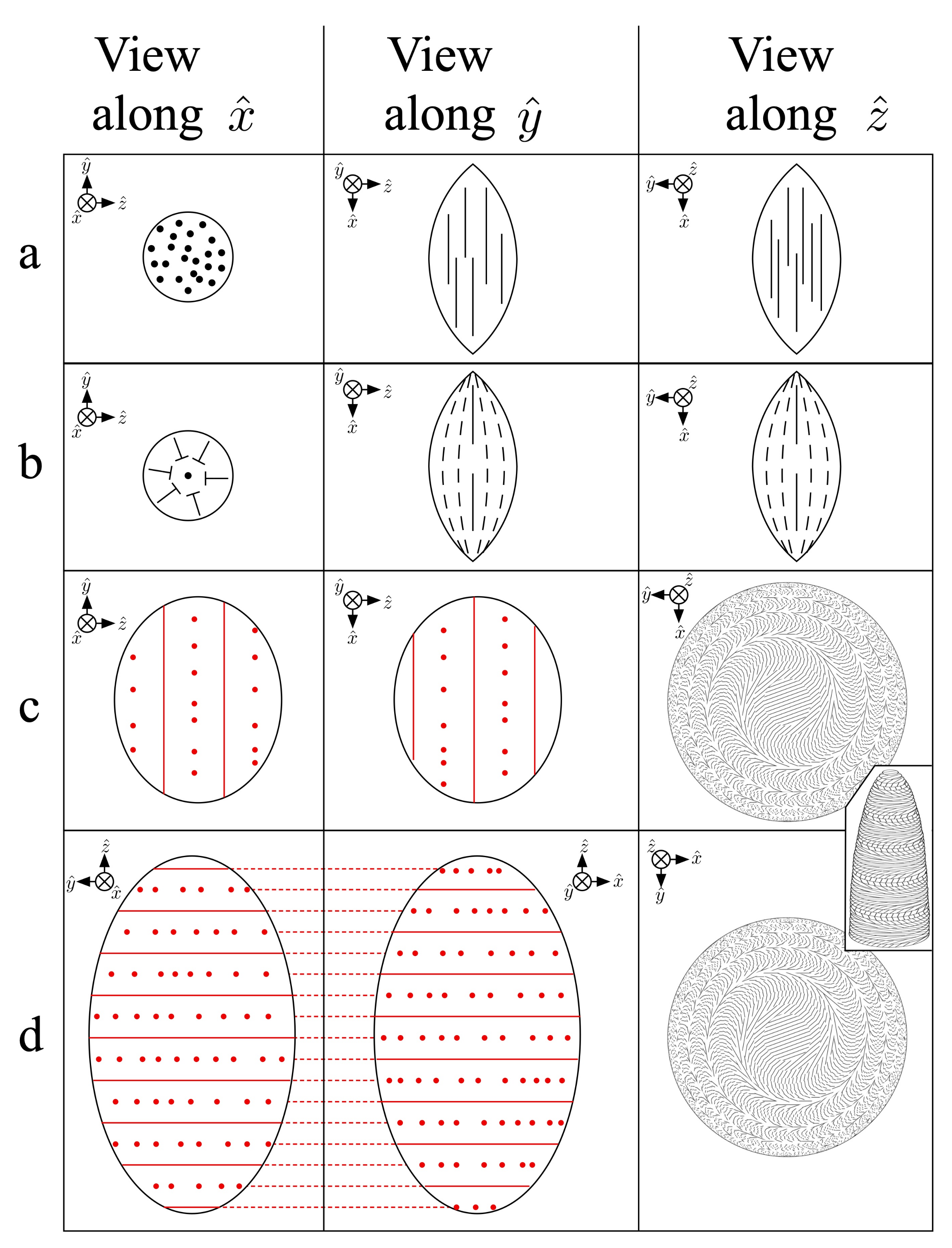
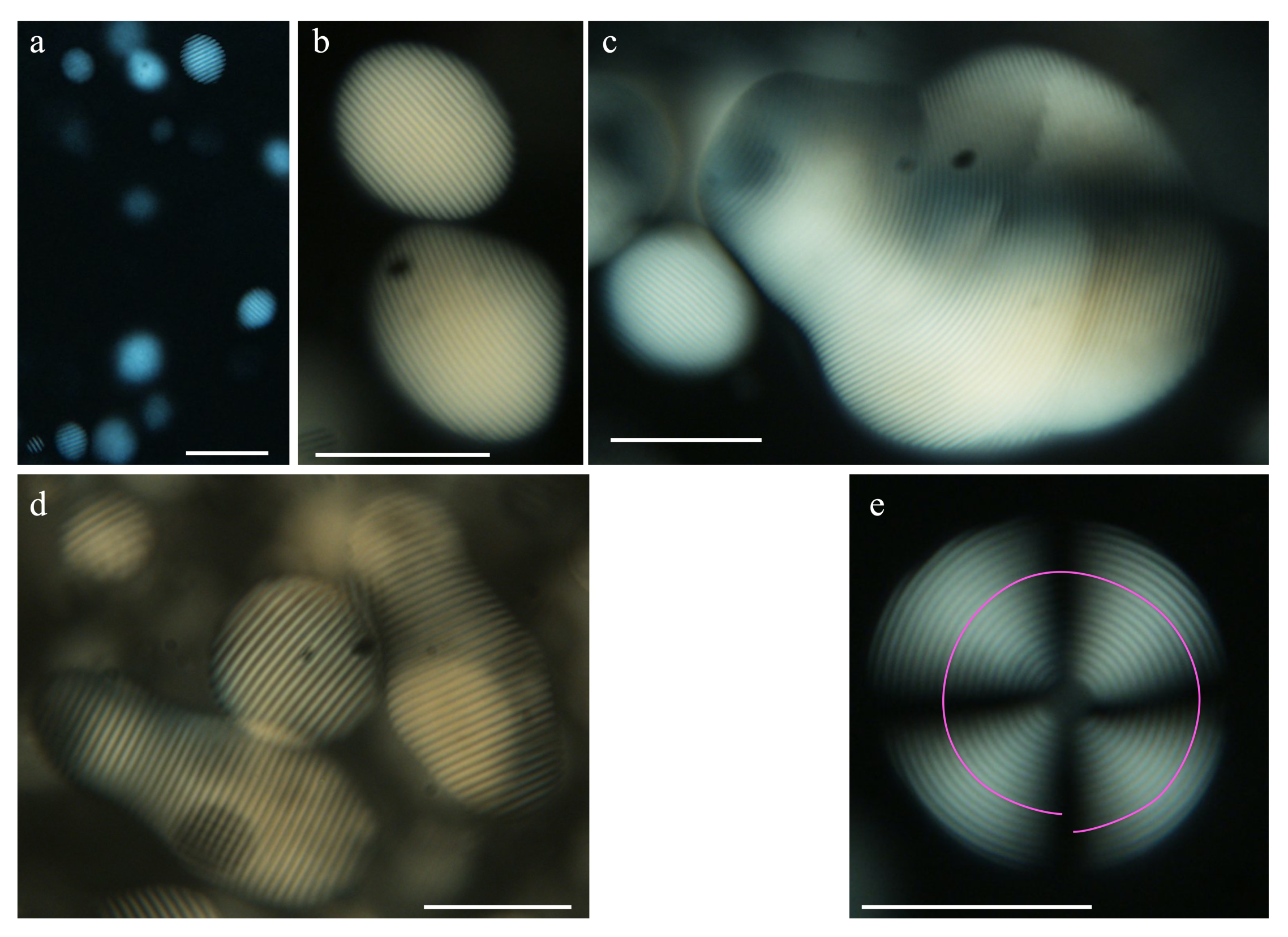
4.4. Isotropic–Nematic Phase Coexistence and the Nucleation of Tactoids
4.5. CNC Fractionation by Liquid Crystal Phase Separation and the Impact of Aspect Ratio on Phase Sequence
5. The End of Equilibrium: Kinetic Arrest, Percolation, Gel Formation and Glass Transitions
5.1. Percolation and Kinetic Arrest in CNC Suspensions
5.2. Kinetic Arrest by Glass Transition or Gelation?
5.3. How Do We Detect Kinetic Arrest Experimentally?
6. Tuning the Equilibrium Behavior—And Its Range—By Modifying the Solvent
6.1. The Challenge of Preparing Non-Aqueous CNC Suspensions and How to Overcome It
6.2. Liquid Crystallinity and Kinetic Arrest of Non-Aqueous CNC Suspensions
6.3. The Response of the Equilibrium Phase Diagram and Helix Pitch to Selected Solutes in the Aqueous Phase
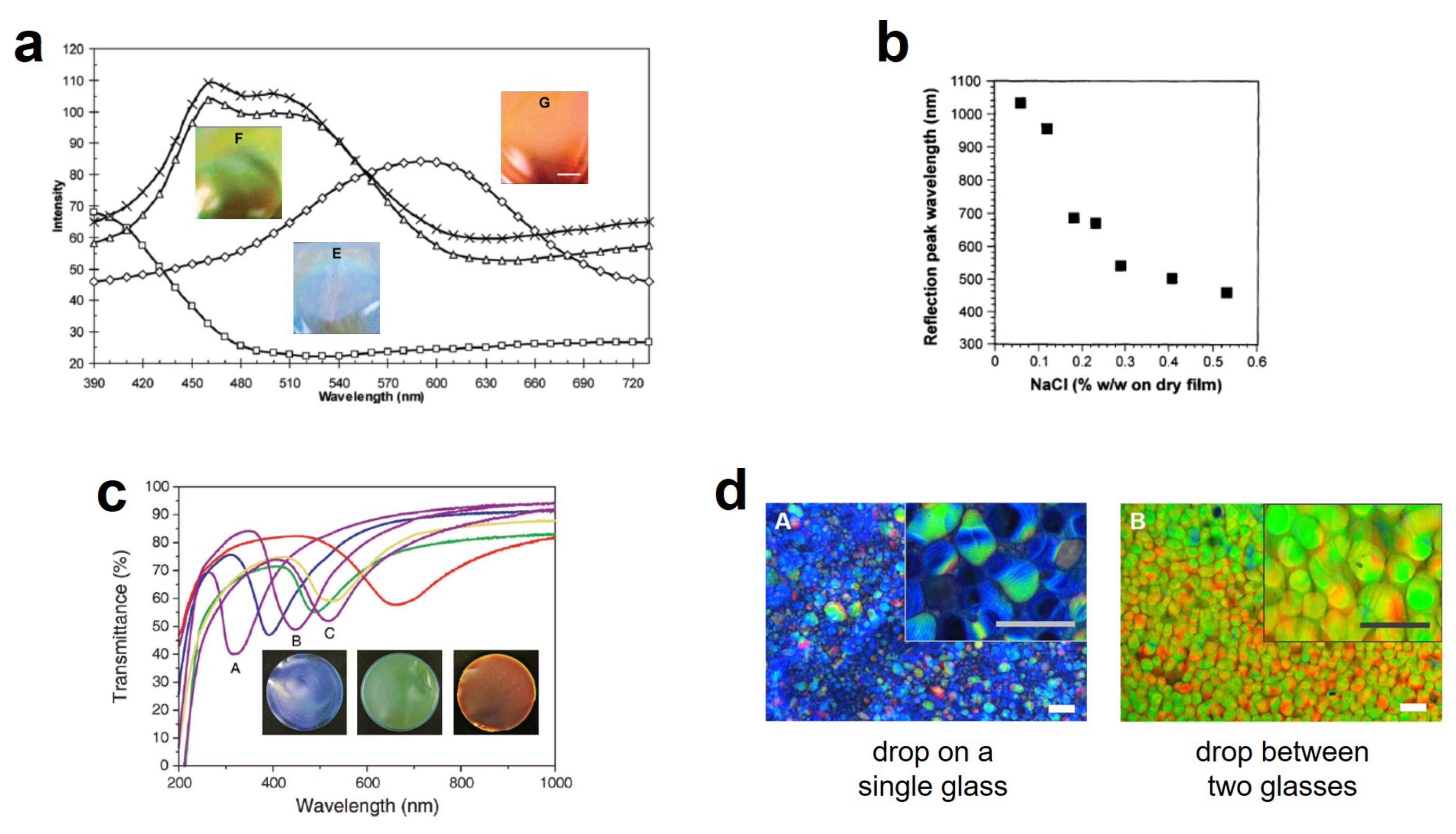
7. Creating Color with CNCs by Drying Suspensions Into Solid Films: Where Intriguing Science Meets Promising Applications
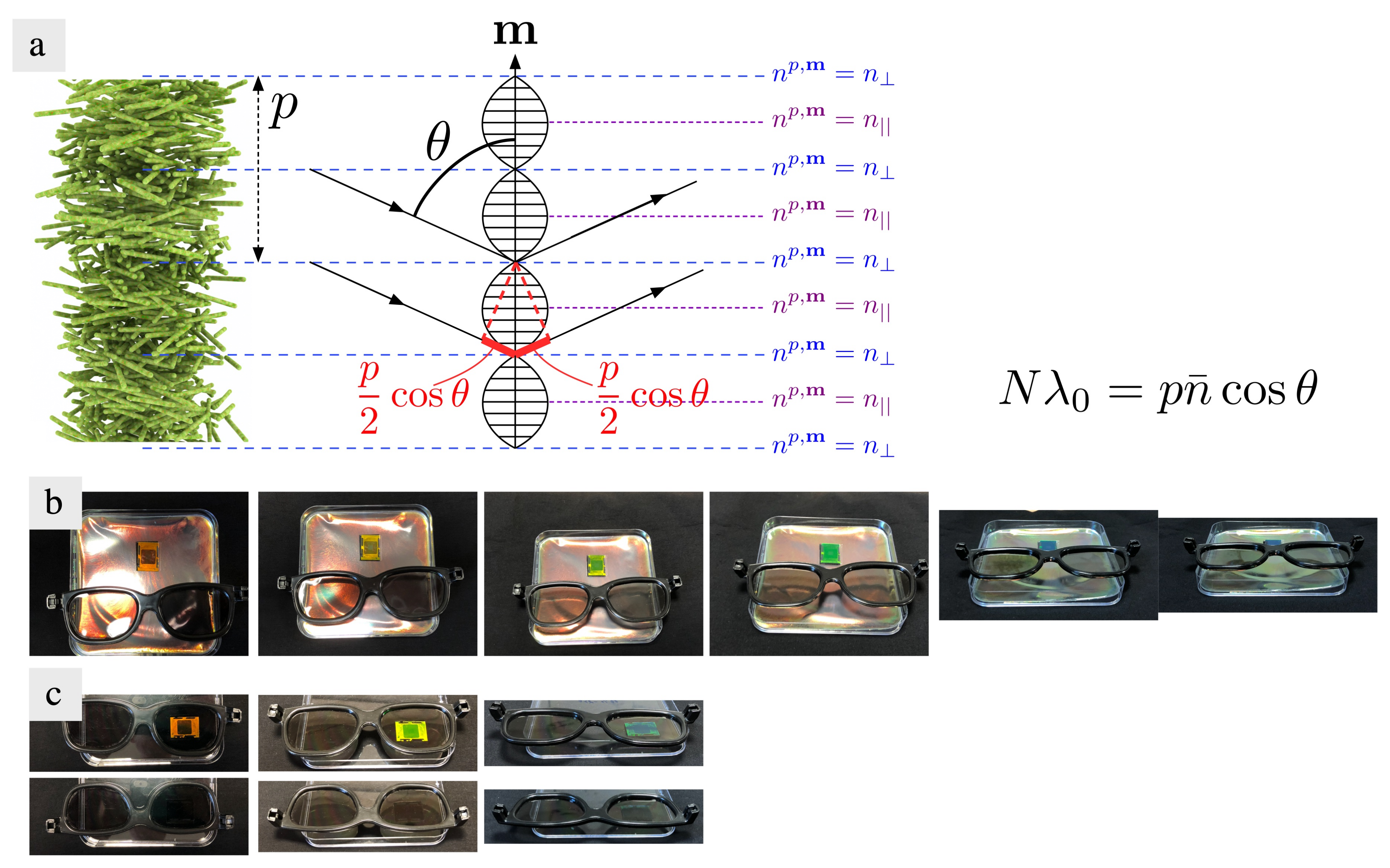
7.1. Bragg Reflection and Structural Color in Cholesteric Liquid Crystals
- Light incident along the helix axis, m, with a wavelength , as measured inside the cholesteric, that is identical to the helix pitch p, is separated into two eigenmodes that are perfectly circularly polarized, one right-handed and one left-handed. The mode with handedness opposite to that of the helix propagates unobstructed, but the one with the same handedness cannot propagate at all; it is totally back-reflected. This means that analysis of the reflected light through circular polarizers will show the reflected color if the polarizer has the handedness of the helix, while it will show no reflection if the polarizer has the opposite handedness.
- Because the cholesteric is birefringent and thus does not have one single refractive index, the condition is not uniquely defined when considering light wavelengths in air, prior to entering the cholesteric. Therefore, we find a band of air wavelengths that satisfy the reflection condition, from to (assuming ). This gives us a reflection band of width for the air wavelengths around that are selectively reflected, where the average refractive index is calculated as . (To calculate the average refractive index we must first calculate the average dielectric permittivity, , which is the proper material constant for use with Maxwell’s equations, and then take the square root, .) Considering that visible light wavelengths in air range from about 400 nm (violet) to about 700 nm (deep red), and that the average refractive index in dry CNC films can be expected to be (based on values reported for and for crystalline cellulose [14]), this means that the helix pitch in the film should be in the range nm in order to see selective reflection at normal incidence.
- For oblique incidence, i.e., if the incoming light beam does not enter along m but at an angle from the helix axis, the mean selective reflection wavelength, as measured in air, varies approximately according to Bragg’s law:Here, N is an integer that can be greater than 1 for oblique incidence, i.e., higher-order reflections may occur under these conditions. For normal incidence, strictly, because the perfectly sinusoidal modulation of the refractive index along the helix has no harmonics [177].
- The polarizations of the eigenmodes at oblique incidence, , are elliptical rather than circular. This means that, since any elliptical polarization different from circular can be separated into one left- and one right-handed circular component, neither of which is zero, analysis of the reflected light through circular polarizers should not give perfect extinction with the polarizer that has opposite handedness of the helix. However, for a well-aligned ideal cholesteric helix, the deviation from circular polarization is very small even up to large angles, hence the effect is practically negligible, see Figure 10c. Thus, even at oblique incidence, circular polarizers are very useful for assessing the quality of a cholesteric film.
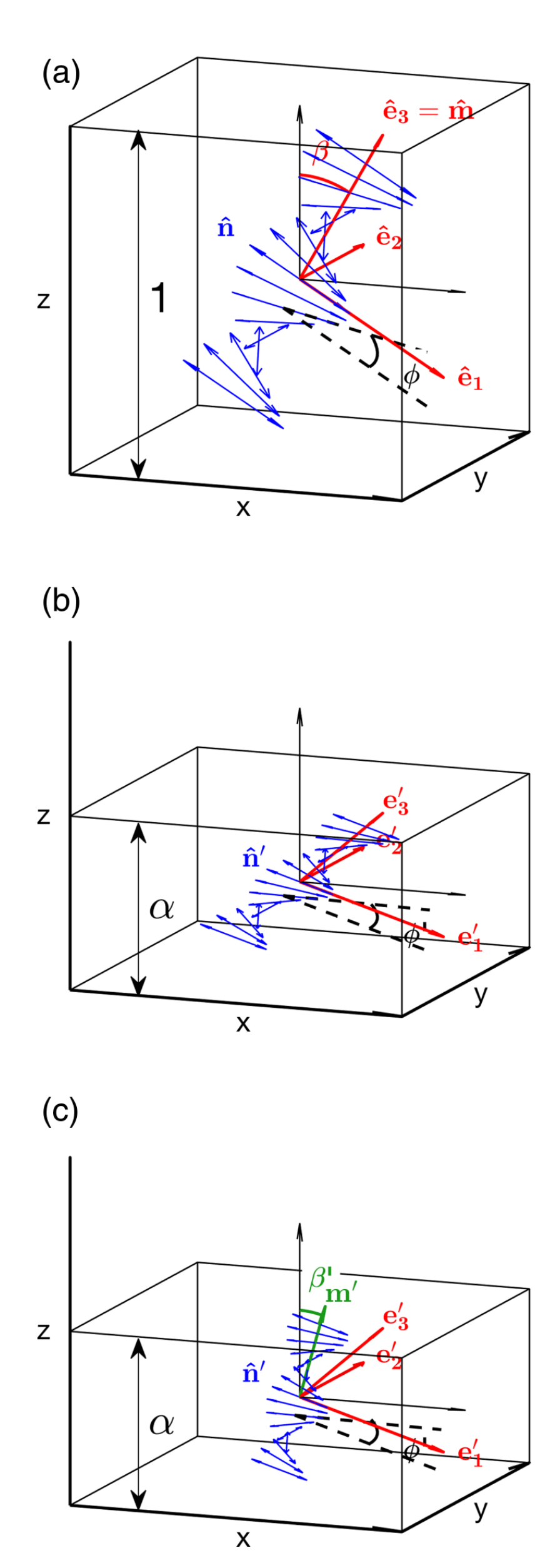
- If the helix axis m is in the plane of the sample, no selective reflection will be seen. If the pitch is smaller than light wavelengths, the light averages the effect of the helix and experiences regular birefringence where m is the optic axis, with extraordinary component for polarization along m and ordinary component for polarization perpendicular to m. (The refractive indices and , and through them also , still refer to orientations with respect to n.) Note that this means that the birefringence of the short-pitch cholesteric observed perpendicular to m is negative. On the other hand, if the pitch is longer than light wavelengths, light will resolve the variations of optic axis orientation, and the sample appears with the characteristic ’fingerprint’ texture that we have seen in, e.g., Figure 8, where dark bands correspond to n normal to the sample plane, along the light incidence, and bright bands are seen for n in the sample plane (assuming that m is parallel to neither polarizer nor analyzer). This means that the distance between two consecutive dark (or bright) bands is ().
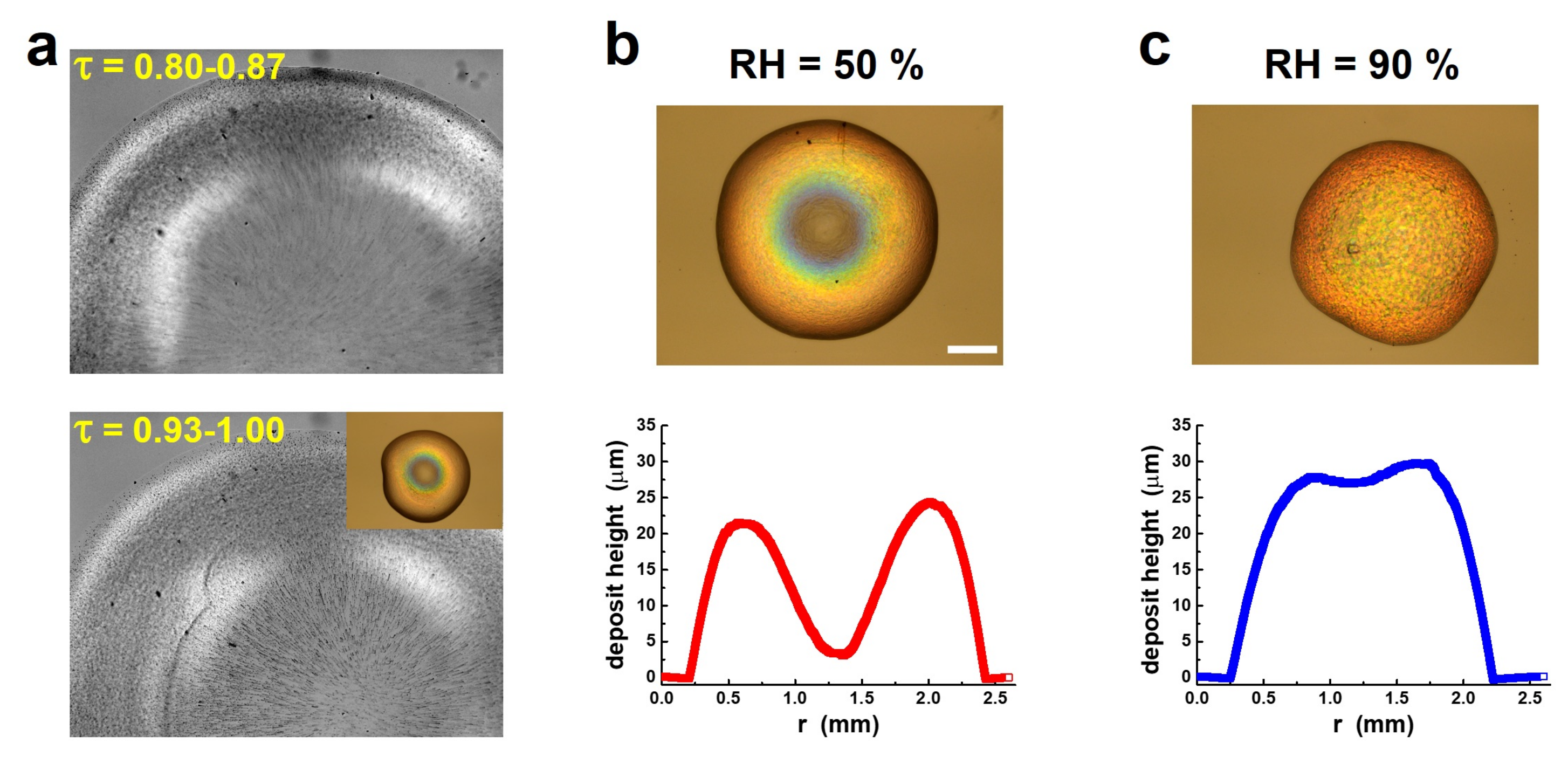
7.2. Drying a Cholesteric Gel: The Appearance of Color and Its Dependence on Drying Conditions
7.3. The Coffee-Ring Effect and How to Avoid It
7.4. To What Extent Can We Tune the Properties of CNC Films?
7.5. Parameters and Effects Meriting Further Investigations
8. Summary and Outlook
Author Contributions
Funding
Conflicts of Interest
References and Notes
- Zugenmaier, P. Crystalline Cellulose and Derivatives: Characterization and Structures; Springer Series in Wood Science; Springer: Berlin, Germany, 2010; p. 285. [Google Scholar]
- Revol, J.; Bradford, H.; Giasson, J.; Marchessault, R.; Gray, D. Helicoidal self-ordering of cellulose microfibrils in aqueous suspension. Int. J. Biol. Macromol. 1992, 14, 170–172. [Google Scholar] [CrossRef]
- Revol, J.F.; Godbout, L.; Gray, D. Solid self-assembled films of cellulose with chiral nematic order and optically variable properties. J. Pulp Pap. Sci. 1998, 24, 146–149. [Google Scholar]
- Bardet, R.; Roussel, F.; Coindeau, S.; Belgacem, N.; Bras, J. Engineered pigments based on iridescent cellulose nanocrystal films. Carbohydr. Polym. 2015, 122, 367–375. [Google Scholar] [CrossRef]
- Frka-Petesic, B.; Vignolini, S. So much more than paper. Nat. Photon. 2019, 13, 365–367. [Google Scholar] [CrossRef]
- Giese, M.; Blusch, L.K.; Khan, M.K.; MacLachlan, M.J. Functional Materials from Cellulose-Derived Liquid-Crystal Templates. Angew. Chem. Int. Ed. 2015, 54, 2888–2910. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.P.; Chodavarapu, V.P.; Kirk, A.G.; Andrews, M.P. Nanocrystalline cellulose for covert optical encryption. SPIE Org. Photonic Mater. Devices XIV 2012, 8258, 825808. [Google Scholar]
- Zhang, Y.P.; Chodavarapu, V.P.; Kirk, A.G.; Andrews, M.P. Structured color humidity indicator from reversible pitch tuning in self-assembled nanocrystalline cellulose films. Sens. Actuators B 2013, 176, 692–697. [Google Scholar] [CrossRef]
- Zhao, T.H.; Parker, R.M.; Williams, C.A.; Lim, K.T.P.; Frka-Petesic, B.; Vignolini, S. Printing of Responsive Photonic Cellulose Nanocrystal Microfilm Arrays. Adv. Funct. Mater. 2018, 29, 1804531. [Google Scholar] [CrossRef]
- Giese, M.; Blusch, L.; Khan, M.; Hamad, W.; MacLachlan, M. Responsive mesoporous photonic cellulose films by supramolecular cotemplating. Angew. Chem. Int. Ed. 2014, 53, 8880–8884. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Schütz, C.; Salajkova, M.; Noh, J.; Park, J.H.; Scalia, G.; Bergström, L. Cellulose nanocrystal-based materials: From liquid crystal self-assembly and glass formation to multifunctional thin films. NPG Asia Mater. 2014, 6, e80. [Google Scholar] [CrossRef]
- Srinivasarao, M. Nano-optics in the biological world: Beetles, butterflies, birds, and moths. Chem. Rev. 1999, 99, 1935–1961. [Google Scholar] [CrossRef] [PubMed]
- Mitov, M. Cholesteric liquid crystals in living matter. Soft Matter 2017, 13, 4176–4209. [Google Scholar] [CrossRef] [PubMed]
- Parker, R.; Guidetti, G.; Williams, C.; Zhao, T.; Narkevicius, A.; Vignolini, S.; Frka-Petesic, B. The Self-Assembly of Cellulose Nanocrystals: Hierarchical Design of Visual Appearance. Adv. Mater. 2017, 30, 1704477. [Google Scholar] [CrossRef] [PubMed]
- Reid, M.; Villalobos, M.; Cranston, E. Benchmarking Cellulose Nanocrystals: From the Laboratory to Industrial Production. Langmuir 2017, 33, 1583–1598. [Google Scholar] [CrossRef] [PubMed]
- Nickerson, R.F.; Habrle, J.A. Cellulose Intercrystalline Structure. Ind. Eng. Chem. 1947, 39, 1507–1512. [Google Scholar] [CrossRef]
- Rånby, B.; Ribi, E. Über den Feinbau der Zellulose. Experientia 1950, 6, 12–14. [Google Scholar] [CrossRef]
- Marchessault, R.; Morehead, F.; Walter, N. Liquid crystal systems from fibrillar polysaccharides. Nature 1959, 184, 632–633. [Google Scholar] [CrossRef]
- Liu, Q.; Campbell, M.; Evans, J.; Smalyukh, I. Orientationally ordered colloidal co-dispersions of gold nanorods and cellulose nanocrystals. Adv. Mater. 2014, 26, 7178–7184. [Google Scholar] [CrossRef]
- Moon, R.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef]
- Wicklein, B.; Salazar-Alvarez, G. Functional hybrids based on biogenic nanofibrils and inorganic nanomaterials. J. Mater. Chem. A 2013, 1, 5469–5478. [Google Scholar] [CrossRef]
- Eichhorn, S.J. Cellulose nanowhiskers: Promising materials for advanced applications. Soft Matter 2011, 7, 303–315. [Google Scholar] [CrossRef]
- Klemm, D.; Kramer, F.; Moritz, S.; Lindstrom, T.; Ankerfors, M.; Gray, D.; Dorris, A. Nanocelluloses: A New Family of Nature-Based Materials. Angew. Chem. Int. Ed. 2011, 50, 5438–5466. [Google Scholar] [CrossRef] [PubMed]
- Nishiyama, Y.; Langan, P.; Chanzy, H. Crystal structure and hydrogen-bonding system in cellulose Iβ from synchrotron X-ray and neutron fiber diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. [Google Scholar] [CrossRef] [PubMed]
- Atalla, R.; Vanderhart, D. Native cellulose: A composite of two distinct crystalline forms. Science 1984, 223, 283–285. [Google Scholar] [CrossRef] [PubMed]
- Eichhorn, S.; Dufresne, A.; Aranguren, M.; Marcovich, N.; Capadona, J.; Rowan, S.; Weder, C.; Thielemans, W.; Roman, M.; Renneckar, S.; et al. Review: Current international research into cellulose nanofibres and nanocomposites. J. Mater. Sci. 2010, 45, 1–33. [Google Scholar] [CrossRef]
- Yamamoto, H.; Horii, F. CPMAS carbon-13 NMR analysis of the crystal transformation induced for Valonia cellulose by annealing at high temperatures. Macromolecules 1993, 26, 1313–1317. [Google Scholar] [CrossRef]
- Yamamoto, H.; Horii, F.; Hirai, A. In situ crystallization of bacterial cellulose II. Influences of different polymeric additives on the formation of celluloses Iα and Iβ at the early stage of incubation. Cellulose 1996, 3, 229–242. [Google Scholar] [CrossRef]
- Majoinen, J.; Haataja, J.; Appelhans, D.; Lederer, A.; Olszewska, A.; Seitsonen, J.; Aseyev, V.; Kontturi, E.; Rosilo, H.; Österberg, M.; et al. Supracolloidal multivalent interactions and wrapping of dendronized glycopolymers on native cellulose nanocrystals. J. Am. Chem. Soc. 2014, 136, 866–869. [Google Scholar] [CrossRef]
- Usov, I.; Nyström, G.; Adamcik, J.; Handschin, S.; Schütz, C.; Fall, A.; Bergström, L.; Mezzenga, R. Understanding nanocellulose chirality and structure-properties relationship at the single fibril level. Nat. Commun. 2015, 6, 7564. [Google Scholar] [CrossRef]
- Belton, P.S.; Tanner, S.F.; Cartier, N.; Chanzy, H. High-resolution solid-state carbon-13 nuclear magnetic resonance spectroscopy of tunicin, an animal cellulose. Macromolecules 1989, 22, 1615–1617. [Google Scholar] [CrossRef]
- Abitbol, T.; Kam, D.; Levi-Kalisman, Y.; Gray, D.; Shoseyov, O. Surface Charge Influence on the Phase Separation and Viscosity of Cellulose Nanocrystals. Langmuir 2018, 34, 3925–3933. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Burger, C.; Hsiao, B.S.; Chu, B. Characterization of TEMPO-oxidized cellulose nanofibers in aqueous suspension by small-angle X-ray scattering. J. Appl. Crystallogr. 2014, 47, 788–798. [Google Scholar] [CrossRef]
- Schütz, C.; Agthe, M.; Fall, A.; Gordeyeva, K.; Guccini, V.; Salajková, M.; Plivelic, T.; Lagerwall, J.; Salazar-Alvarez, G.; Bergström, L. Rod Packing in Chiral Nematic Cellulose Nanocrystal Dispersions Studied by Small-Angle X-ray Scattering and Laser Diffraction. Langmuir 2015, 31, 6507–6513. [Google Scholar] [CrossRef] [PubMed]
- Elazzouzi-Hafraoui, S.; Nishiyama, Y.; Putaux, J.; Heux, L.; Dubreuil, F.; Rochas, C. The shape and size distribution of crystalline nanoparticles prepared by acid hydrolysis of native cellulose. Biomacromolecules 2008, 9, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Zakri, C.; Poulin, P. Phase behavior of nanotube suspensions: From attraction induced percolation to liquid crystalline phases. J. Mater. Chem. 2006, 16, 4095–4098. [Google Scholar] [CrossRef]
- Barry, E.; Dogic, Z. Entropy driven self-assembly of nonamphiphilic colloidal membranes. Proc. Natl. Acad. Sci. USA 2010, 107, 10348–10353. [Google Scholar] [CrossRef] [PubMed]
- Edgar, C.; Gray, D. Influence of dextran on the phase Behavior of suspensions of cellulose nanocrystals. Macromolecules 2002, 35, 7400–7406. [Google Scholar] [CrossRef]
- Beck-Candanedo, S.; Viet, D.; Gray, D. Induced phase separation in cellulose nanocrystal suspensions containing ionic dye species. Cellulose 2006, 13, 629–635. [Google Scholar] [CrossRef]
- Beck-Candanedo, S.; Viet, D.; Gray, D. Induced phase separation in low-ionic-strength cellulose nanocrystal suspensions containing high-molecular-weight blue dextrans. Langmuir 2006, 22, 8690–8695. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Burlington, MA, USA, 2010. [Google Scholar]
- Kang, K.; Wilk, A.; Patkowski, A.; Dhont, J. Diffusion of spheres in isotropic and nematic networks of rods: Electrostatic interactions and hydrodynamic screening. J. Chem. Phys. 2007, 126, 214501. [Google Scholar] [CrossRef]
- Sluckin, T.J.; Dunmur, D.A.; Stegemeyer, H. Crystals that Flow: Classic Papers from the History of Liquid Crystals; Taylor and Francis: London, UK, 2004. [Google Scholar]
- Lagerwall, J.P.; Scalia, G. Introduction. In Liquid Crystals with Nano and Microparticles: (In 2 Volumes); Lagerwall, J.P., Scalia, G., Eds.; World Scientific: Singapore, 2016. [Google Scholar]
- Lagerwall, J.P.F.; Giesselmann, F. Current topics in smectic liquid crystal research. ChemPhysChem 2006, 7, 20–45. [Google Scholar] [CrossRef] [PubMed]
- De France, K.; Yager, K.; Hoare, T.; Cranston, E. Cooperative Ordering and Kinetics of Cellulose Nanocrystal Alignment in a Magnetic Field. Langmuir 2016, 32, 7564–7571. [Google Scholar] [CrossRef] [PubMed]
- Lagerwall, S.T. On some important chapters in the history of liquid crystals. Liq. Cryst. 2013, 40, 1698–1729. [Google Scholar] [CrossRef]
- Enz, E.; La Ferrara, V.; Scalia, G. Confinement-Sensitive Optical Response of Cholesteric Liquid Crystals in Electrospun Fibers. ACS Nano 2013, 7, 6627–6635. [Google Scholar] [CrossRef] [PubMed]
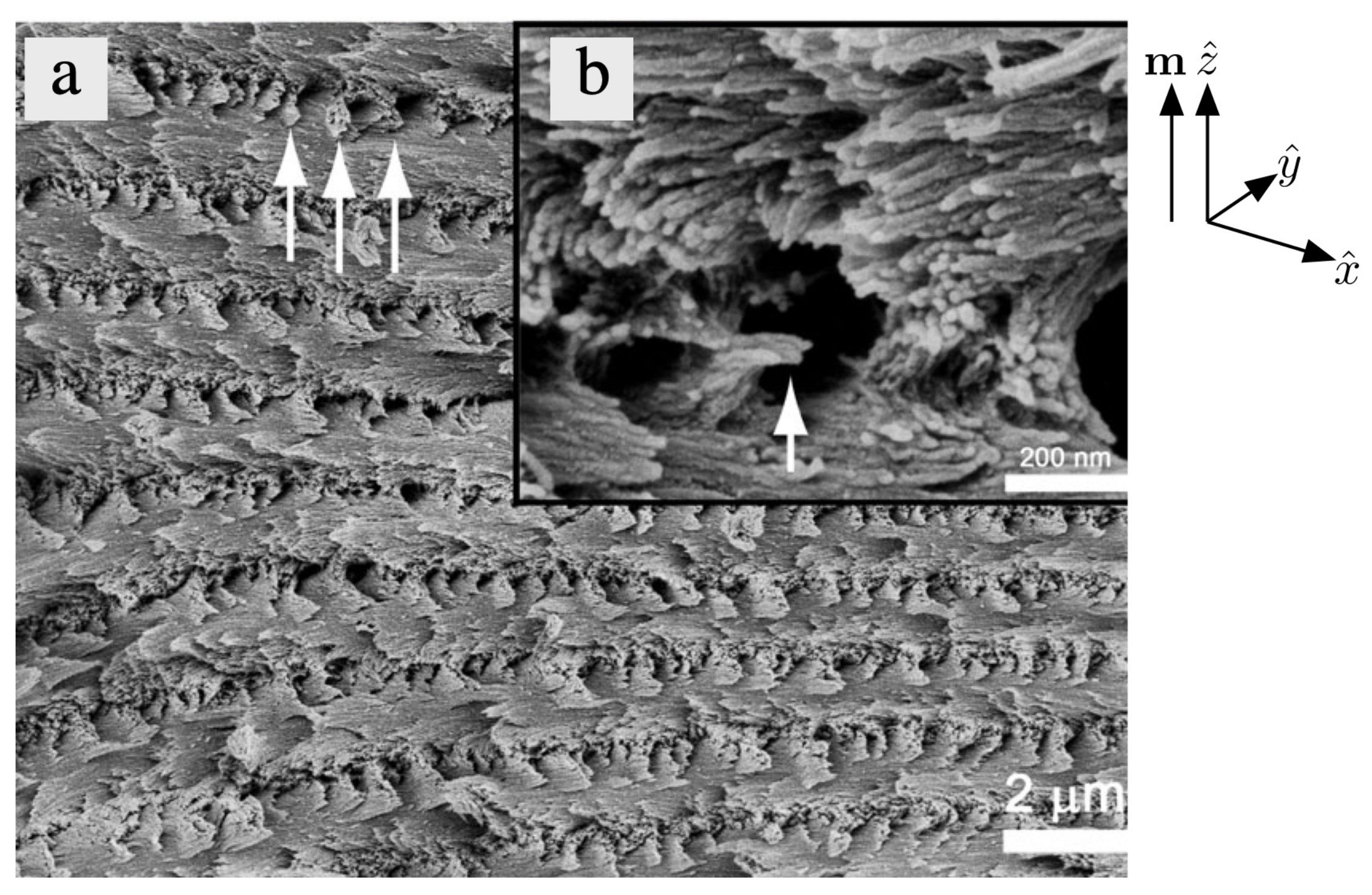
- Majoinen, J.; Kontturi, E.; Ikkala, O.; Gray, D.G. SEM imaging of chiral nematic films cast from cellulose nanocrystal suspensions. Cellulose 2012, 19, 1599–1605. [Google Scholar] [CrossRef]
- de Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Nayani, K.; Chang, R.; Fu, J.; Ellis, P.; Fernandez-Nieves, A.; Park, J.; Srinivasarao, M. Spontaneous emergence of chirality in achiral lyotropic chromonic liquid crystals confined to cylinders. Nat. Commun. 2015, 6, 8067. [Google Scholar] [CrossRef]
- Jeong, J.; Kang, L.; Davidson, Z.; Collings, P.; Lubensky, T.; Yodh, A. Chiral structures from achiral liquid crystals in cylindrical capillaries. Proc. Natl. Acad. Sci. USA 2015, 112, E1837–E1844. [Google Scholar] [CrossRef]
- Davidson, Z.; Kang, L.; Jeong, J.; Still, T.; Collings, P.; Lubensky, T.; Yodh, A. Chiral structures and defects of lyotropic chromonic liquid crystals induced by saddle-splay elasticity. Phys. Rev. E 2015, 91, 050501. [Google Scholar] [CrossRef]
- Prinsen, P.; van der Schoot, P. Shape and director-field transformation of tactoids. Phys. Rev. E 2003, 68, 021701. [Google Scholar] [CrossRef]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Dong, X.; Kimura, T.; Revol, J.; Gray, D. Effects of ionic strength on the isotropic-chiral nematic phase transition of suspensions of cellulose crystallites. Langmuir 1996, 12, 2076–2082. [Google Scholar] [CrossRef]
- Dong, X.; Gray, D. Effect of counterions on ordered phase formation in suspensions of charged rodlike cellulose crystallites. Langmuir 1997, 13, 2404–2409. [Google Scholar] [CrossRef]
- Yang, C.H.; Wang, M.X.; Haider, H.; Yang, J.H.; Sun, J.Y.; Chen, Y.M.; Zhou, J.; Suo, Z. Strengthening Alginate/Polyacrylamide Hydrogels Using Various Multivalent Cations. ACS Appl. Mater. Interfaces 2013, 5, 10418–10422. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J.; Abe, A. Statistical thermodynamics of mixtures of rodlike particles. 1. Theory for polydisperse systems. Macromolecules 1978, 11, 1119–1122. [Google Scholar] [CrossRef]
- Lekkerkerker, H.N.W.; Coulon, P.; Van Der Haegen, R.; Deblieck, R. On the isotropic-liquid crystal phase separation in a solution of rodlike particles of different lengths. J. Chem. Phys. 1984, 80, 3427–3433. [Google Scholar] [CrossRef]
- Odijk, T.; Lekkerkerker, H.N. Theory of the isotropic-liquid crystal phase separation for a solution of bidisperse rodlike macromolecules. J. Phys. Chem. 1985, 89, 2090–2096. [Google Scholar] [CrossRef]
- Vroege, G.J.; Lekkerkerker, H.N.W. Phase-transitions in lyotropic colloidal and polymer liquid-crystals. Rep. Prog. Phys. 1992, 55, 1241–1309. [Google Scholar] [CrossRef]
- Bates, M.A.; Frenkel, D. Influence of polydispersity on the phase behavior of colloidal liquid crystals: A Monte Carlo simulation study. J. Chem. Phys. 1998, 109, 6193–6199. [Google Scholar] [CrossRef]
- Wensink, H. Effect of Size Polydispersity on the Pitch of Nanorod Cholesterics. Crystals 2019, 9, 143. [Google Scholar] [CrossRef]
- Neto, A.M.F.; Salinas, S.R.A. The Physics of Lyotropic Liquid Crystals: Phase Transitions and Structural Properties (Monographs on the Physics and Chemistry of Materials); Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Maier, W.; Saupe, A. Eine einfache molekulare Theorie des nematischen kristallinflüssigen Zustandes. Z. Für Naturforschung A 1958, 13, 564–566. [Google Scholar] [CrossRef]
- Zocher, H.; Jacobsohn, K. Über Taktosole. Kolloidchem. Beihäfte 1929, 28, 167–206. [Google Scholar] [CrossRef]
- Zocher, H. Über freiwillige Strukturbildung in Solen (Eine neue Art anisotrop flüssiger Medien). Z. Für Anorg. Und Allg. Chem. 1925, 147, 91–110. [Google Scholar] [CrossRef]
- Puech, N.; Grelet, E.; Poulin, P.; Blanc, C.; van der Schoot, P. Nematic droplets in aqueous dispersions of carbon nanotubes. Phys. Rev. E 2010, 82, 020702. [Google Scholar] [CrossRef] [PubMed]
- Kaznacheev, A.; Bogdanov, M.; Taraskin, S. The nature of prolate shape of tactoids in lyotropic inorganic liquid crystals. J. Exp. Theor. Phys. 2002, 95, 57–63. [Google Scholar] [CrossRef]
- Robinson, C. Liquid-crystalline structures in solutions of a polypeptide. Trans. Faraday Soc. 1956, 52, 571. [Google Scholar] [CrossRef]
- Nyström, G.; Arcari, M.; Mezzenga, R. Confinement-induced liquid crystalline transitions in amyloid fibril cholesteric tactoids. Nat. Nanotechnol. 2018, 13, 330–336. [Google Scholar] [CrossRef] [PubMed]
- Mosser, G.; Anglo, A.; Helary, C.; Bouligand, Y.; Giraud-Guille, M. Dense tissue-like collagen matrices formed in cell-free conditions. Matrix Biol. 2006, 25, 3–13. [Google Scholar] [CrossRef]
- Sonin, A. Inorganic lyotropic liquid crystals. J. Mater. Chem. 1998, 8, 2557–2574. [Google Scholar] [CrossRef]
- Lehmann, O. Flüssige Kristalle und die Theorien des Lebens; Johann Ambrosius Barth: Leipzig, Germany, 1908. [Google Scholar]
- Friedel, G. Les états mésomorphes de la matière. Ann. Phys. 1922, 18, 273–474. [Google Scholar] [CrossRef]
- Blanc, C. Interplay between Growth Mechanisms and Elasticity in Liquid Crystalline Nuclei. Prog. Theor. Phys. Suppl. 2008, 175, 93–102. [Google Scholar] [CrossRef][Green Version]
- Langmuir, I. The Role of Attractive and Repulsive Forces in the Formation of Tactoids, Thixotropic Gels, Protein Crystals and Coacervates. J. Chem. Phys. 1938, 6, 873–896. [Google Scholar] [CrossRef]
- Chen, W.; Gray, D.G. Interfacial tension between isotropic and anisotropic phases of a suspension of rodlike particles. Langmuir 2002, 18, 633–637. [Google Scholar] [CrossRef]
- Lavrentovich, O. Topological defects in dispersed liquid crystals, or words and worlds around liquid crystal drops. Liq. Cryst. 1998, 24, 117–125. [Google Scholar] [CrossRef]
- Kurik, M.V.; Lavrentovich, O. Defects in liquid crystals: Homotopy theory and experimental studies. Physics-Uspekhi 1988, 31, 196–224. [Google Scholar] [CrossRef]
- Volovik, G.; Lavrentovich, O. Topological dynamics of defects: Boojums in nematic drops. Zh Eksp Teor Fiz 1983, 85, 1997–2010. [Google Scholar]
- Kurik, M.; Lavrentovich, O. Negative-positive monopole transitions in cholesteric liquid-crystals. JETP Lett. 1982, 35, 444–447. [Google Scholar]
- Bouligand, Y.; Livolant, F. The organization of cholesteric spherulites. J. Phys. 1984, 45, 1899–1923. [Google Scholar] [CrossRef]
- Xu, F.; Crooker, P. Chiral nematic droplets with parallel surface anchoring. Phys. Rev. E 1997, 56, 6853–6860. [Google Scholar] [CrossRef]
- Xu, F.; Kitzerow, H.S.; Crooker, P. Director configurations of nematic-liquid-crystal droplets: Negative dielectric anisotropy and parallel surface anchoring. Phys. Rev. E 1994, 49, 3061. [Google Scholar] [CrossRef]
- Drzaic, P.S. Liquid Crystal Dispersions; World Scientific: Singapore, 1995. [Google Scholar]
- Bezic, J.; Zumer, S. Structures of the cholesteric liquid crystal droplets with parallel surface anchoring. Liq. Cryst. 1992, 11, 593–619. [Google Scholar] [CrossRef]
- Robinson, C.; Ward, J.; Beevers, R. Liquid crystalline structure in polypeptide solutions. Part 2. Discuss. Faraday Soc. 1958, 25, 29–42. [Google Scholar] [CrossRef]
- Lopez-Leon, T.; Fernandez-Nieves, A. Drops and shells of liquid crystal. Colloid Polym. Sci. 2011, 289, 345–359. [Google Scholar] [CrossRef]
- Urbanski, M.; Reyes, C.G.; Noh, J.; Sharma, A.; Geng, Y.; Jampani, V.S.R.; Lagerwall, J.P. Liquid crystals in micron-scale droplets, shells and fibers. J. Phys. Condens. Matter 2017, 29, 133003. [Google Scholar] [CrossRef]
- Candau, S.; Roy, P.; Debeauvais, F. Magnetic Field Effects in Nematic and Cholesteric Droplets Suspended in a Isotropic Liquid. Mol. Cryst. Liq. Cryst. 1973, 23, 283–297. [Google Scholar] [CrossRef]
- Jamali, V.; Behabtu, N.; Senyuk, B.; Lee, J.; Smalyukh, I.; van der Schoot, P.; Pasquali, M. Experimental realization of crossover in shape and director field of nematic tactoids. Phys. Rev. E 2015, 91, 042507. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Davidson, Z.; Collings, P.; Lubensky, T.; Yodh, A. Chiral symmetry breaking and surface faceting in chromonic liquid crystal droplets with giant elastic anisotropy. Proc. Natl. Acad. Sci. USA 2014, 111, 1742–1747. [Google Scholar] [CrossRef]
- Nayani, K.; Fu, J.; Chang, R.; Park, J.; Srinivasarao, M. Using chiral tactoids as optical probes to study the aggregation behavior of chromonics. Proc. Natl. Acad. Sci. USA 2017, 114, 3826–3831. [Google Scholar] [CrossRef]
- Araki, J.; Kuga, S. Effect of Trace Electrolyte on Liquid Crystal Type of Cellulose Microcrystals. Langmuir 2001, 17, 4493–4496. [Google Scholar] [CrossRef]
- Lettinga, M.P.; Kang, K.; Imhof, A.; Derks, D.; Dhont, J.K. Kinetic pathways of the nematic–isotropic phase transition as studied by confocal microscopy on rod-like viruses. J. Phys. Condens. Matter 2005, 17, S3609. [Google Scholar] [CrossRef]
- Tran, A.; Hamad, W.; MacLachlan, M. Tactoid Annealing Improves Order in Self-Assembled Cellulose Nanocrystal Films with Chiral Nematic Structures. Langmuir 2018, 34, 646–652. [Google Scholar] [CrossRef]
- Li, Y.; Jun-Yan Suen, J.; Prince, E.; Larin, E.; Klinkova, A.; Thérien-Aubin, H.; Zhu, S.; Yang, B.; Helmy, A.; Lavrentovich, O.; et al. Colloidal cholesteric liquid crystal in spherical confinement. Nat. Commun. 2016, 7, 12520. [Google Scholar] [CrossRef] [PubMed]
- Lagerwall, J.P. A phenomenological introduction to liquid crystals and colloids. In Liquid Crystals with Nano and Microparticles: (In 2 Volumes); Lagerwall, J.P., Scalia, G., Eds.; World Scientific: Singapore, 2016; pp. 11–93. [Google Scholar]
- De Vries, H. Rotary power and other optical properties of certain liquid crystals. Acta Cryst. 1951, 4, 219–226. [Google Scholar] [CrossRef]
- Wang, P.; Hamad, W.; MacLachlan, M. Structure and transformation of tactoids in cellulose nanocrystal suspensions. Nat. Commun. 2016, 7, 11515. [Google Scholar] [CrossRef] [PubMed]
- O’Keeffe, O.; Wang, P.; Hamad, W.; MacLachlan, M. Boundary Geometry Effects on the Coalescence of Liquid Crystalline Tactoids and Formation of Topological Defects. J. Phys. Chem. Lett. 2019, 10, 278–282. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Revol, J.; Gray, D. Effect of microcrystallite preparation conditions on the formation of colloid crystals of cellulose. Cellulose 1998, 5, 19–32. [Google Scholar] [CrossRef]
- Hirai, A.; Inui, O.; Horii, F.; Tsuji, M. Phase Separation Behavior in Aqueous Suspensions of Bacterial Cellulose Nanocrystals Prepared by Sulfuric Acid Treatment. Langmuir 2009, 25, 497–502. [Google Scholar] [CrossRef]
- Honorato-Rios, C.; Lehr, C.; Schütz, C.; Sanctuary, R.; Osipov, M.A.; Baller, J.; Lagerwall, J.P.F. Fractionation of cellulose nanocrystals: Enhancing liquid crystal ordering without promoting gelation. NPG Asia Mater. 2018, 10, 455–465. [Google Scholar] [CrossRef]
- Beck-Candanedo, S.; Roman, M.; Gray, D. Effect of reaction conditions on the properties and behavior of wood cellulose nanocrystal suspensions. Biomacromolecules 2005, 6, 1048–1054. [Google Scholar] [CrossRef]
- Shafiei-Sabet, S.; Hamad, W.Y.; Hatzikiriakos, S.G. Rheology of Nanocrystalline Cellulose Aqueous Suspensions. Langmuir 2012, 28, 17124–17133. [Google Scholar] [CrossRef]
- Khandelwal, M.; Windle, A.H. Self-assembly of bacterial and tunicate cellulose nanowhiskers. Polymer 2013, 54, 5199–5206. [Google Scholar] [CrossRef]
- Finner, S.; Schilling, T.; van der Schoot, P. Connectivity, Not Density, Dictates Percolation in Nematic Liquid Crystals of Slender Nanoparticles. Phys. Rev. Lett. 2019, 122, 097801. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.; Dhont, J.K.G. Glass Transition in Suspensions of Charged Rods: Structural Arrest and Texture Dynamics. Phys. Rev. Lett. 2013, 110, 015901. [Google Scholar] [CrossRef] [PubMed]
- Purdy, K.; Fraden, S. Isotropic-cholesteric phase transition of filamentous virus suspensions as a function of rod length and charge. Phys. Rev. E 2004, 70, 061703. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, K.; Hagedorn, H.; Heuck, C.C.; Hinrichsen, M.; Ludwig, H. The ionic properties of the filamentous bacteriophages Pf1 and fd. J. Biol. Chem. 1986, 261, 1653–1655. [Google Scholar] [PubMed]
- Nordenström, M.; Fall, A.; Nyström, G.; Wågberg, L. Formation of Colloidal Nanocellulose Glasses and Gels. Langmuir 2017, 33, 9772–9780. [Google Scholar] [CrossRef]
- Lokanathan, A.; Nykänen, A.; Seitsonen, J.; Johansson, L.; Campbell, J.; Rojas, O.; Ikkala, O.; Laine, J. Cilia-mimetic hairy surfaces based on end-immobilized nanocellulose colloidal rods. Biomacromolecules 2013, 14, 2807–2813. [Google Scholar] [CrossRef]
- Petrova, A.; Herold, C.; Petrov, E. Conformations and membrane-driven self-organization of rodlike fd virus particles on freestanding lipid membranes. Soft Matter 2017, 13, 7172–7187. [Google Scholar] [CrossRef]
- Honorato-Rios, C.; Kuhnhold, A.; Bruckner, J.R.; Dannert, R.; Schilling, T.; Lagerwall, J.P. Equilibrium Liquid Crystal Phase Diagrams and Detection of Kinetic Arrest in Cellulose Nanocrystal Suspensions. Front. Mater. 2016, 3, 21. [Google Scholar] [CrossRef]
- Lettinga, M.P. Kolloid-Tagung 2019. In Proceedings of the 49th Conference of the German Colloid Society, Stuttgart, Germany, 23–25 September 2019. [Google Scholar]
- Phan-Xuan, T.; Thuresson, A.; Skepö, M.; Labrador, A.; Bordes, R.; Matic, A. Aggregation behavior of aqueous cellulose nanocrystals: The effect of inorganic salts. Cellulose 2016, 23, 3653–3663. [Google Scholar] [CrossRef]
- Urena-Benavides, E.E.; Ao, G.; Davis, V.A.; Kitchens, C.L. Rheology and Phase Behavior of Lyotropic Cellulose Nanocrystal Suspensions. Macromolecules 2011, 44, 8990–8998. [Google Scholar] [CrossRef]
- Shafeiei-Sabet, S.; Hamad, W.Y.; Hatzikiriakos, S.G. Influence of degree of sulfation on the rheology of cellulose nanocrystal suspensions. Rheol. Acta 2013, 52, 741–751. [Google Scholar] [CrossRef]
- Bruckner, J.; Kuhnhold, A.; Honorato-Rios, C.; Schilling, T.; Lagerwall, J. Enhancing Self-Assembly in Cellulose Nanocrystal Suspensions Using High-Permittivity Solvents. Langmuir 2016, 32, 9854–9862. [Google Scholar] [CrossRef] [PubMed]
- Habibi, Y. Key advances in the chemical modification of nanocelluloses. Chem. Soc. Rev. 2014, 43, 1519–1542. [Google Scholar] [CrossRef] [PubMed]
- Eyley, S.; Thielemans, W. Surface modification of cellulose nanocrystals. Nanoscale 2014, 6, 7764–7779. [Google Scholar] [CrossRef] [PubMed]
- Heux, L.; Chauve, G.; Bonini, C. Nonflocculating and chiral-nematic self-ordering of cellulose microcrystals suspensions in nonpolar solvents. Langmuir 2000, 16, 8210–8212. [Google Scholar] [CrossRef]
- Elazzouzi-Hafraoui, S.; Putaux, J.L.; Heux, L. Self-assembling and Chiral Nematic Properties of Organophilic Cellulose Nanocrystals. J. Phys. Chem. B 2009, 113, 11069–11075. [Google Scholar] [CrossRef]
- Frka-Petesic, B.; Jean, B.; Heux, L. First experimental evidence of a giant permanent electric-dipole moment in cellulose nanocrystals. EPL 2014, 107, 28006. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Hamad, W.Y.; MacLachlan, M.J. CdS Quantum Dots Encapsulated in Chiral Nematic Mesoporous Silica: New Iridescent and Luminescent Materials. Adv. Funct. Mater. 2014, 24, 777–783. [Google Scholar] [CrossRef]
- Shopsowitz, K.E.; Kelly, J.A.; Hamad, W.Y.; MacLachlan, M.J. Biopolymer Templated Glass with a Twist: Controlling the Chirality, Porosity, and Photonic Properties of Silica with Cellulose Nanocrystals. Adv. Funct. Mater. 2014, 24, 327–338. [Google Scholar] [CrossRef]
- Shopsowitz Kevin, E.; Stahl, A.; Hamad Wadood, Y.; MacLachlan Mark, J. Hard Templating of Nanocrystalline Titanium Dioxide with Chiral Nematic Ordering. Angew. Chem. Int. Ed. 2012, 51, 6886–6890. [Google Scholar] [CrossRef]
- Kelly, J.A.; Shopsowitz, K.E.; Ahn, J.M.; Hamad, W.Y.; MacLachlan, M.J. Chiral Nematic Stained Glass: Controlling the Optical Properties of Nanocrystalline Cellulose-Templated Materials. Langmuir 2012, 28, 17256–17262. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.; Roy, X.; Shopsowitz, K.E.; Hui, J.K.H.; MacLachlan, M.J. Liquid-Crystal Templating in Ammonia: A Facile Route to Micro- and Mesoporous Metal Nitride/Carbon Composites. Angew. Chem. Int. Ed. 2010, 49, 9740–9743. [Google Scholar] [CrossRef] [PubMed]
- Shopsowitz, K.; Qi, H.; Hamad, W.; MacLachlan, M. Free-standing mesoporous silica films with tunable chiral nematic structures. Nature 2010, 468, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Yao, K.; Meng, Q.; Bulone, V.; Zhou, Q. Flexible and Responsive Chiral Nematic Cellulose Nanocrystal/Poly(ethylene glycol) Composite Films with Uniform and Tunable Structural Color. Adv. Mater. 2017, 29, 1701323. [Google Scholar] [CrossRef]
- Wu, T.; Li, J.; Li, J.; Ye, S.; Wei, J.; Guo, J. A bio-inspired cellulose nanocrystal-based nanocomposite photonic film with hyper-reflection and humidity-responsive actuator properties. J. Mater. Chem. C 2016, 4, 9687–9696. [Google Scholar] [CrossRef]
- Giese, M.; De Witt, J.; Shopsowitz, K.; Manning, A.; Dong, R.; Michal, C.; Hamad, W.; MacLachlan, M. Thermal switching of the reflection in chiral nematic mesoporous organosilica films infiltrated with liquid crystals. ACS Appl. Mater. Interfaces 2013, 5, 6854–6859. [Google Scholar] [CrossRef]
- Kelly, J.; Shukaliak, A.; Cheung, C.; Shopsowitz, K.; Hamad, W.; MacLachlan, M. Responsive photonic hydrogels based on nanocrystalline cellulose. Angew. Chem. Int. Ed. 2013, 52, 8912–8916. [Google Scholar] [CrossRef]
- Cheung, C.C.Y.; Giese, M.; Kelly, J.A.; Hamad, W.Y.; MacLachlan, M.J. Iridescent Chiral Nematic Cellulose Nanocrystal/Polymer Composites Assembled in Organic Solvents. ACS Macro Lett. 2013, 2, 1016–1020. [Google Scholar] [CrossRef]
- Giese, M.; Khan Mostofa, K.; Hamad Wadood, Y.; MacLachlan Mark, J. Imprinting of Photonic Patterns with Thermosetting Amino-Formaldehyde-Cellulose Composites. ACS Macro Lett. 2013, 2, 818–821. [Google Scholar] [CrossRef]
- Khan, M.; Giese, M.; Yu, M.; Kelly, J.; Hamad, W.; MacLachlan, M. Flexible mesoporous photonic resins with tunable chiral nematic structures. Angew. Chem. Int. Ed. 2013, 52, 8921–8924. [Google Scholar] [CrossRef]
- Shopsowitz Kevin, E.; Hamad Wadood, Y.; MacLachlan Mark, J. Flexible and Iridescent Chiral Nematic Mesoporous Organosilica Films. J. Am. Chem. Soc. 2012, 134, 867–870. [Google Scholar] [CrossRef] [PubMed]
- Terpstra, A.S.; Arnett, L.P.; Manning, A.P.; Michal, C.A.; Hamad, W.Y.; MacLachlan, M.J. Iridescent Chiral Nematic Mesoporous Organosilicas with Alkylene Spacers. Adv. Opt. Mater. 2018, 6, 1800163. [Google Scholar] [CrossRef]
- Rao, A.; Divoux, T.; McKinley, G.; Hart, A. Shear melting and recovery of crosslinkable cellulose nanocrystal-polymer gels. Soft Matter 2019, 15, 4401–4412. [Google Scholar] [CrossRef] [PubMed]
- Okita, Y.; Fujisawa, S.; Saito, T.; Isogai, A. TEMPO-Oxidized Cellulose Nanofibrils Dispersed in Organic Solvents. Biomacromolecules 2011, 12, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Song, R.; Xu, Z.; Jing, Y.; Dai, H.; Fang, G. Fluorescent cellulose nanocrystals with responsiveness to solvent polarity and ionic strength. Sens. Actuators B 2018, 275, 490–498. [Google Scholar] [CrossRef]
- Espinosa, S.C.; Kuhnt, T.; Foster, E.J.; Weder, C. Isolation of Thermally Stable Cellulose Nanocrystals by Phosphoric Acid Hydrolysis. Biomacromolecules 2013, 14, 1223–1230. [Google Scholar] [CrossRef] [PubMed]
- Viet, D.; Beck-Candanedo, S.; Gray, D. Dispersion of cellulose nanocrystals in polar organic solvents. Cellulose 2007, 14, 109–113. [Google Scholar] [CrossRef]
- Sánchez, P.; Tsubaki, S.; Pádua, A.; Wada, Y. Kinetic analysis of microwave-enhanced cellulose dissolution in ionic solvents. Phys. Chem. Chem. Phys. 2020, 22, 1003–1010. [Google Scholar] [CrossRef]
- Lethesh, K.; Evjen, S.; Venkatraman, V.; Shah, S.; Fiksdahl, A. Highly efficient cellulose dissolution by alkaline ionic liquids. Carbohydr. Polym. 2020, 229, 115594. [Google Scholar] [CrossRef]
- Rajeev, A.; Basavaraj, M.G. Confinement effect on spatio-temporal growth of spherulites from cellulose/ionic liquid solutions. Polymer 2019, 185, 121927. [Google Scholar] [CrossRef]
- Okura, H.; Wada, M.; Serizawa, T. Dispersibility of HCl-treated Cellulose Nanocrystals with Water-dispersible Properties in Organic Solvents. Chem. Lett. 2014, 43, 601–603. [Google Scholar] [CrossRef]
- Gauche, C.; Felisberti, M.I. Colloidal Behavior of Cellulose Nanocrystals Grafted with Poly(2-alkyl-2-oxazoline)s. ACS Omega 2019, 4, 11893–11905. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Berry, R.M.; Pelton, R.; Cranston, E.D. One-Pot Water-Based Hydrophobic Surface Modification of Cellulose Nanocrystals Using Plant Polyphenols. ACS Sustain. Chem. Eng. 2017, 5, 5018–5026. [Google Scholar] [CrossRef]
- Fumagalli, M.; Sanchez, F.; Boisseau, S.M.; Heux, L. Gas-phase esterification of cellulose nanocrystal aerogels for colloidal dispersion in apolar solvents. Soft Matter 2013, 9, 11309. [Google Scholar] [CrossRef]
- Frka-Petesic, B.; Radavidson, H.; Jean, B.; Heux, L. Dynamically Controlled Iridescence of Cholesteric Cellulose Nanocrystal Suspensions Using Electric Fields. Adv. Mater. 2017, 29, 1606208. [Google Scholar] [CrossRef]
- Kovalenko, A. Predictive Multiscale Modeling of Nanocellulose Based Materials and Systems. IOP Conf. Ser. Mater. Sci. Eng. 2014, 64, 012040. [Google Scholar] [CrossRef]
- Gousse, C.; Chanzy, H.; Excoffier, G.; Soubeyrand, L.; Fleury, E. Stable suspensions of partially silylated cellulose whiskers dispersed in organic solvents. Polymer 2002, 43, 2645–2651. [Google Scholar] [CrossRef]
- Yi, J.; Xu, Q.; Zhang, X.; Zhang, H. Chiral-nematic self-ordering of rodlike cellulose nanocrystals grafted with poly(styrene) in both thermotropic and lyotropic states. Polymer 2008, 49, 4406–4412. [Google Scholar] [CrossRef]
- Xu, Q.; Yi, J.; Zhang, X.; Zhang, H. A novel amphotropic polymer based on cellulose nanocrystals grafted with azo polymers. Eur. Polym. J. 2008, 44, 2830–2837. [Google Scholar] [CrossRef]
- Goffin, A.; Habibi, Y.; Raquez, J.; Dubois, P. Polyester-grafted cellulose nanowhiskers: A new approach for tuning the microstructure of immiscible polyester blends. ACS Appl. Mater. Interfaces 2012, 4, 3364–3371. [Google Scholar] [CrossRef]
- Ljungberg, N.; Bonini, C.; Bortolussi, F.; Boisson, C.; Heux, L.; Cavaillé, J. New nanocomposite materials reinforced with cellulose whiskers in atactic polypropylene: Effect of surface and dispersion characteristics. Biomacromolecules 2005, 6, 2732–2739. [Google Scholar] [CrossRef] [PubMed]
- Araki, J.; Wada, M.; Kuga, S. Steric stabilization of a cellulose microcrystal suspension by poly (ethylene glycol) grafting. Langmuir 2001, 17, 21–27. [Google Scholar] [CrossRef]
- Siqueira, G.; Bras, J.; Dufresne, A. New process of chemical grafting of cellulose nanoparticles with a long chain isocyanate. Langmuir 2010, 26, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Fu, S.; Habibi, Y.; Lucia, L. Polymerization topochemistry of cellulose nanocrystals: A function of surface dehydration control. Langmuir 2014, 30, 14670–14679. [Google Scholar] [CrossRef]
- Blachechen, L.S.; de Mesquita, J.P.; de Paula, E.L.; Pereira, F.V.; Petri, D.F.S. Interplay of colloidal stability of cellulose nanocrystals and their dispersibility in cellulose acetate butyrate matrix. Cellulose 2013, 20, 1329–1342. [Google Scholar] [CrossRef]
- Braun, B.; Dorgan, J. Single-step method for the isolation and surface functionalization of cellulosic nanowhiskers. Biomacromolecules 2009, 10, 334–341. [Google Scholar] [CrossRef]
- Yuan, H.; Nishiyama, Y.; Wada, M.; Kuga, S. Surface acylation of cellulose whiskers by drying aqueous emulsion. Biomacromolecules 2006, 7, 696–700. [Google Scholar] [CrossRef]
- Zhou, Q.; Brumer, H.; Teeri, T.T. Self-Organization of Cellulose Nanocrystals Adsorbed with Xyloglucan Oligosaccharide-Poly(ethylene glycol)-Polystyrene Triblock Copolymer. Macromolecules 2009, 42, 5430–5432. [Google Scholar] [CrossRef]
- Salajkova, M.; Berglund Lars, A.; Zhou, Q. Hydrophobic cellulose nanocrystals modified with quaternary ammonium salts. J. Mater. Chem. 2012, 22, 19798–19805. [Google Scholar] [CrossRef]
- Xu, Y.; Dai, Y.; Nguyen, T.; Hamad, W.; MacLachlan, M. Aerogel materials with periodic structures imprinted with cellulose nanocrystals. Nanoscale 2018, 10, 3805–3812. [Google Scholar] [CrossRef]
- There is a confusing discrepancy between the plotted data, from which these numbers were taken, and the text, which states a pitch change from ∼80 μm to ∼10 μm
- Mu, X.; Gray, D. Formation of chiral nematic films from cellulose nanocrystal suspensions is a two-stage process. Langmuir 2014, 30, 9256–9260. [Google Scholar] [CrossRef] [PubMed]
- The percentage is given as 10% w/v without further clarification. While this mixing of mass and volume in a percent indication is quite commonly used in some communities, it causes problems because the meaning is not clearly defined. In addition, a percentage should be dimensionless, whereas here we have the dimension kg/m3. We assume that 1% here means 1 g in 100 mL, but this interpretation may be incorrect
- Frka-Petesic, B.; Kamita, G.; Guidetti, G.; Vignolini, S. Angular optical response of cellulose nanocrystal films explained by the distortion of the arrested suspension upon drying. Phys. Rev. Mater. 2019, 3, 045601. [Google Scholar] [CrossRef]
- Oseen, C.W. The theory of liquid crystals. Trans. Faraday Soc. 1933, 29, 883. [Google Scholar] [CrossRef]
- Fergason, J.L. Cholesteric Structure-1 Optical Properties. Mol. Cryst. 1966, 1, 293–307. [Google Scholar] [CrossRef]
- Dreher, R.; Meier, G. Optical properties of cholesteric liquid crystals. Phys. Rev. A 1973, 8, 1616. [Google Scholar] [CrossRef]
- Berreman, D.; Scheffer, T. Bragg reflection of light from single-domain cholesteric liquid-crystal films. Phys. Rev. Lett. 1970, 25, 577–581. [Google Scholar] [CrossRef]
- Berreman, D.W.; Scheffer, T.J. Reflection and Transmission by Single-Domain Cholesteric Liquid Crystal Films: Theory and Verification. Mol. Cryst. Liq. Cryst. 1970, 11, 395–405. [Google Scholar] [CrossRef]
- Kim, S.T.; Finkelmann, H. Cholesteric liquid single-crystal elastomers (LSCE) obtained by the anisotropic deswelling method. Macromol. Rapid Commun. 2001, 22, 429–433. [Google Scholar] [CrossRef]
- Finkelmann, H.; Kim, S.; Munoz, A.; Palffy-Muhoray, P.; Taheri, B. Tunable mirrorless lasing in cholesteric liquid crystalline elastomers. Adv. Mater. 2001, 13, 1069–1072. [Google Scholar] [CrossRef]
- Kizhakidathazhath, R.; Geng, Y.; Jampani, V.S.R.; Charni, C.; Sharma, A.; Lagerwall, J.P.F. Facile Anisotropic Deswelling Method for Realizing Large-Area Cholesteric Liquid Crystal Elastomers with Uniform Structural Color and Broad-Range Mechanochromic Response. Adv. Funct. Mater. 2019, 1909537. [Google Scholar] [CrossRef]
- Mao, Y.; Terentjev, E.M.; Warner, M. Cholesteric elastomers: Deformable photonic solids. Phys. Rev. E 2001, 64, 041803. [Google Scholar] [CrossRef] [PubMed]
- Revol, J.; Godbout, L.; Dong, X.; Gray, D.; Chanzy, H.; Maret, G. Chiral Nematic Suspensions of Cellulose Crystallites—Phase-separation and Magnetic-field Orientation. Liq. Cryst. 1994, 16, 127–134. [Google Scholar] [CrossRef]
- Kimura, F.; Kimura, T.; Tamura, M.; Hirai, A.; Ikuno, M.; Horii, F. Magnetic alignment of the chiral nematic phase of a cellulose microfibril suspension. Langmuir 2005, 21, 2034–2037. [Google Scholar] [CrossRef] [PubMed]
- Frka-Petesic, B.; Guidetti, G.; Kamita, G.; Vignolini, S. Controlling the Photonic Properties of Cholesteric Cellulose Nanocrystal Films with Magnets. Adv. Mater. 2017, 29, 1701469. [Google Scholar] [CrossRef] [PubMed]
- Larson, R.G. Transport and deposition patterns in drying sessile droplets. AIChE J. 2014, 60, 1538–1571. [Google Scholar] [CrossRef]
- Anyfantakis, M.; Baigl, D. Manipulating the Coffee-Ring Effect: Interactions at Work. ChemPhysChem 2015, 16, 2726–2734. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Contact line deposits in an evaporating drop. Phys. Rev. E 2000, 62, 756. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Capillary flow as the cause of ring stains from dried liquid drops. Nature 1997, 389, 827–829. [Google Scholar] [CrossRef]
- Mu, X.; Gray, D.G. Droplets of cellulose nanocrystal suspensions on drying give iridescent 3-D “coffee-stain” rings. Cellulose 2015, 22, 1103–1107. [Google Scholar] [CrossRef]
- Dupas, Lagerwall and Anyfantakis, in preparation
- Shimura, K.; Uchiyama, N.; Kasai, K. Prevention of evaporation of small-volume sample solutions for capillary electrophoresis using a mineral-oil overlay. Electrophoresis 2001, 22, 3471–3477. [Google Scholar] [CrossRef]
- Gençer, A.; Schütz, C.; Thielemans, W. Influence of the Particle Concentration and Marangoni Flow on the Formation of Cellulose Nanocrystal Films. Langmuir 2016, 33, 228–234. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Larson, R.G. Marangoni effect reverses coffee-ring depositions. J. Phys. Chem. B 2006, 110, 7090–7094. [Google Scholar] [CrossRef] [PubMed]
- Varanakkottu, S.; Anyfantakis, M.; Morel, M.; Rudiuk, S.; Baigl, D. Light-Directed Particle Patterning by Evaporative Optical Marangoni Assembly. Nano. Lett. 2016, 16, 644–650. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Hamad, W.; Straus, S. Parameters Affecting the Chiral Nematic Phase of Nanocrystalline Cellulose Films. Macromolecules 2010, 43, 3851–3858. [Google Scholar] [CrossRef]
- Beck, S.; Bouchard, J.; Berry, R. Controlling the Reflection Wavelength of Iridescent Solid Films of Nanocrystalline Cellulose. Biomacromolecules 2011, 12, 167–172. [Google Scholar] [CrossRef]
- Hirscher, M.; Becher, M.; Haluska, M.; Dettlaff-Weglikowska, U.; Quintel, A.; Duesberg, G.; Choi, Y.; Downes, P.; Hulman, M.; Roth, S. Hydrogen storage in sonicated carbon materials. Appl. Phys. A Mater. Sci. Process. 2001, 72, 129–132. [Google Scholar] [CrossRef]
- Nguyen, T.; Hamad, W.; MacLachlan, M. Tuning the iridescence of chiral nematic cellulose nanocrystals and mesoporous silica films by substrate variation. Chem. Commun. 2013, 49, 11296–11298. [Google Scholar] [CrossRef]
- Saha, P.; Davis, V.A. Photonic Properties and Applications of Cellulose Nanocrystal Films with Planar Anchoring. ACS Appl. Nano Mater. 2018, 1, 2175–2183. [Google Scholar] [CrossRef]
- Guidetti, G.; Atifi, S.; Vignolini, S.; Hamad, W. Flexible Photonic Cellulose Nanocrystal Films. Adv. Mater. 2016, 28, 10042–10047. [Google Scholar] [CrossRef]
- Bardet, R.; Belgacem, N.; Bras, J. Flexibility and color monitoring of cellulose nanocrystal iridescent solid films using anionic or neutral polymers. ACS Appl. Mater. Interfaces 2015, 7, 4010–4018. [Google Scholar] [CrossRef]
- Mitov, M. Cholesteric Liquid Crystals with a Broad Light Reflection Band. Adv. Mater. 2012, 24, 6260–6276. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, S.; Almeida, P.; Monge, N.; Aguirre, L.; Reis, D.; de Oliveira, C.; Neto, A.; Pieranski, P.; Godinho, M. Mind the Microgap in Iridescent Cellulose Nanocrystal Films. Adv. Mater. 2017, 29, 1603560. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.H.; Lim, H.C.; Lee, H.W.; Lee, S.J. Evaporation-induced saline Rayleigh convection inside a colloidal droplet. Phys. Fluids 2013, 25, 042001. [Google Scholar] [CrossRef]
- Song, W.; Lee, J.K.; Gong, M.S.; Heo, K.; Chung, W.J.; Lee, B.Y. Cellulose Nanocrystal-Based Colored Thin Films for Colorimetric Detection of Aldehyde Gases. ACS Appl. Mater. Interf. 2018, 10, 10353–10361. [Google Scholar] [CrossRef]
- Hoeger, I.; Rojas Orlando, J.; Efimenko, K.; Velev Orlin, D.; Kelley Steve, S. Ultrathin film coatings of aligned cellulose nanocrystals from a convective-shear assembly system and their surface mechanical properties. Soft Matter 2011, 7, 1957–1967. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schütz, C.; Bruckner, J.R.; Honorato-Rios, C.; Tosheva, Z.; Anyfantakis, M.; Lagerwall, J.P.F. From Equilibrium Liquid Crystal Formation and Kinetic Arrest to Photonic Bandgap Films Using Suspensions of Cellulose Nanocrystals. Crystals 2020, 10, 199. https://doi.org/10.3390/cryst10030199
Schütz C, Bruckner JR, Honorato-Rios C, Tosheva Z, Anyfantakis M, Lagerwall JPF. From Equilibrium Liquid Crystal Formation and Kinetic Arrest to Photonic Bandgap Films Using Suspensions of Cellulose Nanocrystals. Crystals. 2020; 10(3):199. https://doi.org/10.3390/cryst10030199
Chicago/Turabian StyleSchütz, Christina, Johanna R. Bruckner, Camila Honorato-Rios, Zornitza Tosheva, Manos Anyfantakis, and Jan P. F. Lagerwall. 2020. "From Equilibrium Liquid Crystal Formation and Kinetic Arrest to Photonic Bandgap Films Using Suspensions of Cellulose Nanocrystals" Crystals 10, no. 3: 199. https://doi.org/10.3390/cryst10030199
APA StyleSchütz, C., Bruckner, J. R., Honorato-Rios, C., Tosheva, Z., Anyfantakis, M., & Lagerwall, J. P. F. (2020). From Equilibrium Liquid Crystal Formation and Kinetic Arrest to Photonic Bandgap Films Using Suspensions of Cellulose Nanocrystals. Crystals, 10(3), 199. https://doi.org/10.3390/cryst10030199