Conditional Cooperation and Framing Effects
Abstract
1. Introduction
2. The Experiment
2.1. The Public Good Game
2.2. The FGF Method and the Experimental Treatments
2.3. The One-Shot Public-Good Game
2.4. Procedures
3. Results
3.1. Distribution of Types
3.2. Non-Monotonic Contribution Profiles
3.3. Comparing Contribution Schedules and One-Shot Contributions
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
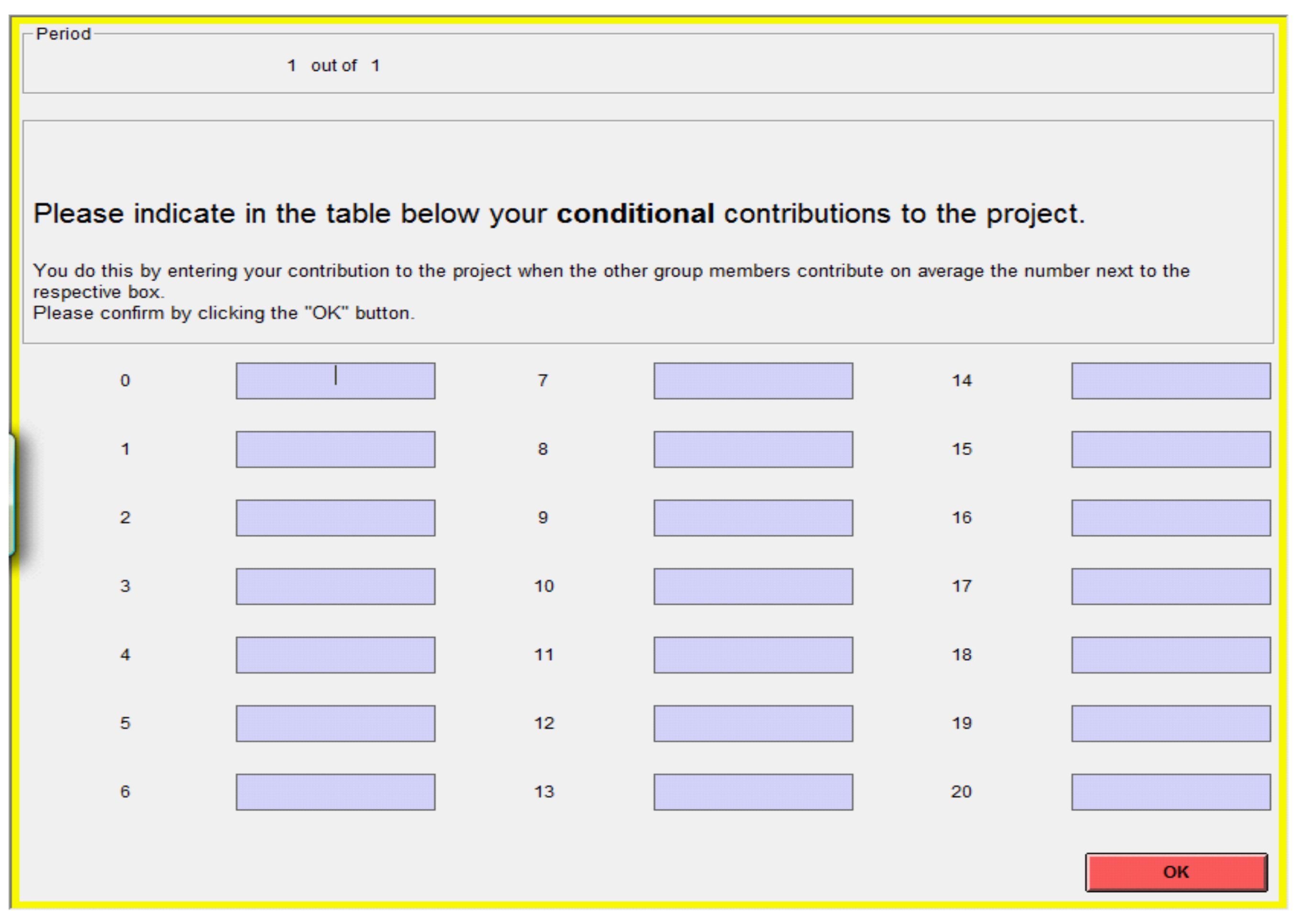
Appendix A Screenshot of the Contribution Table
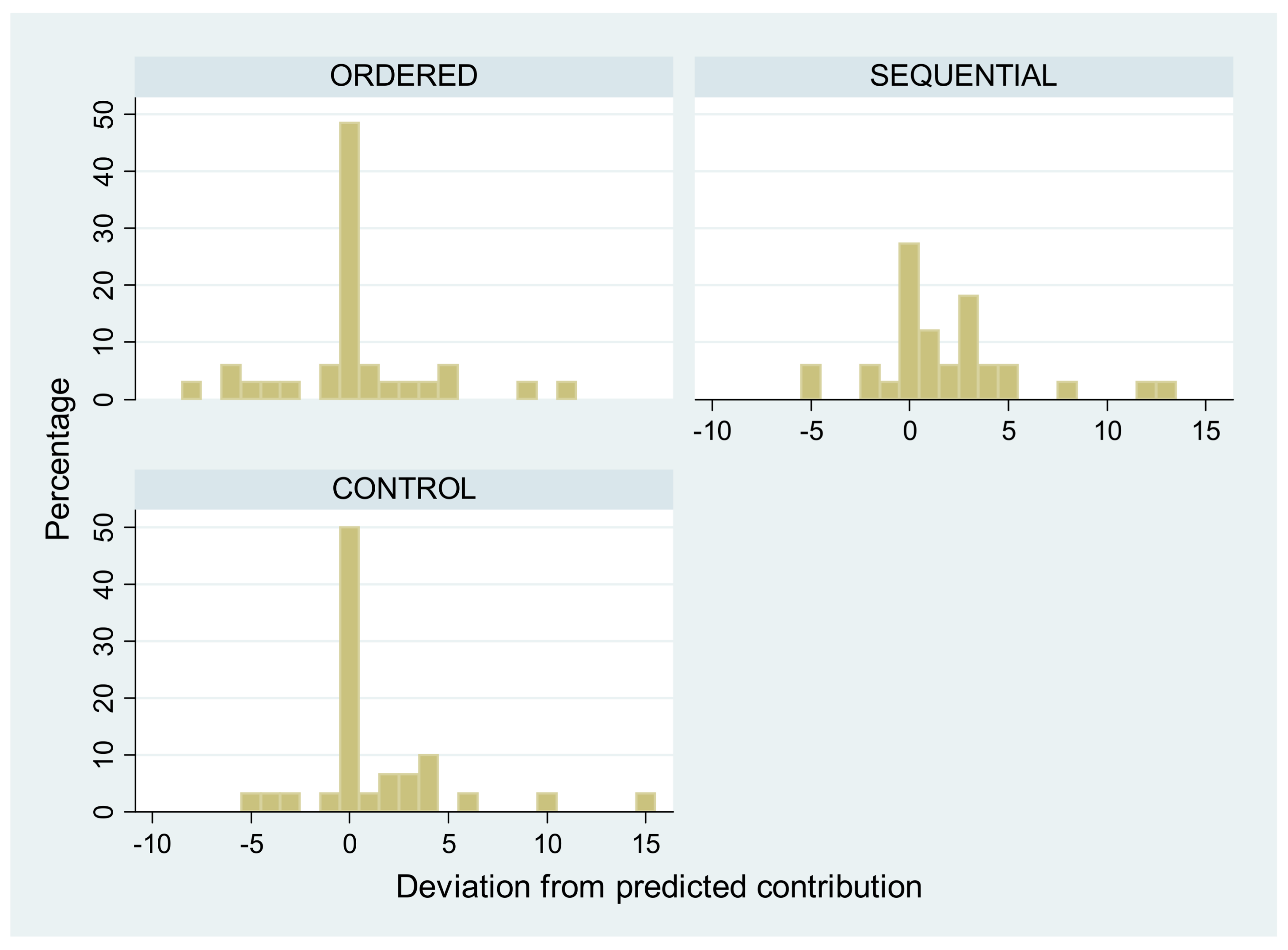
Appendix B Additional Statistics
| Unc. cont. (Part 1) | Beliefs (Part 1) | Cont. (Part 2) | Beliefs (Part 2) | |
|---|---|---|---|---|
| CONTROL | 6.2 (6.5) | 7.2 (5.2) | 4.9 (5.7) | 6.0 (5.0) |
| ORDERED | 4.4 (6.0) | 5.0 (4.6) | 3.9 (5.7) | 5.8 (5.2) |
| SEQUENTIAL | 6.6 (5.8) | 8.0 (4.4) | 5.8 (4.8) | 6.7 (4.5) |
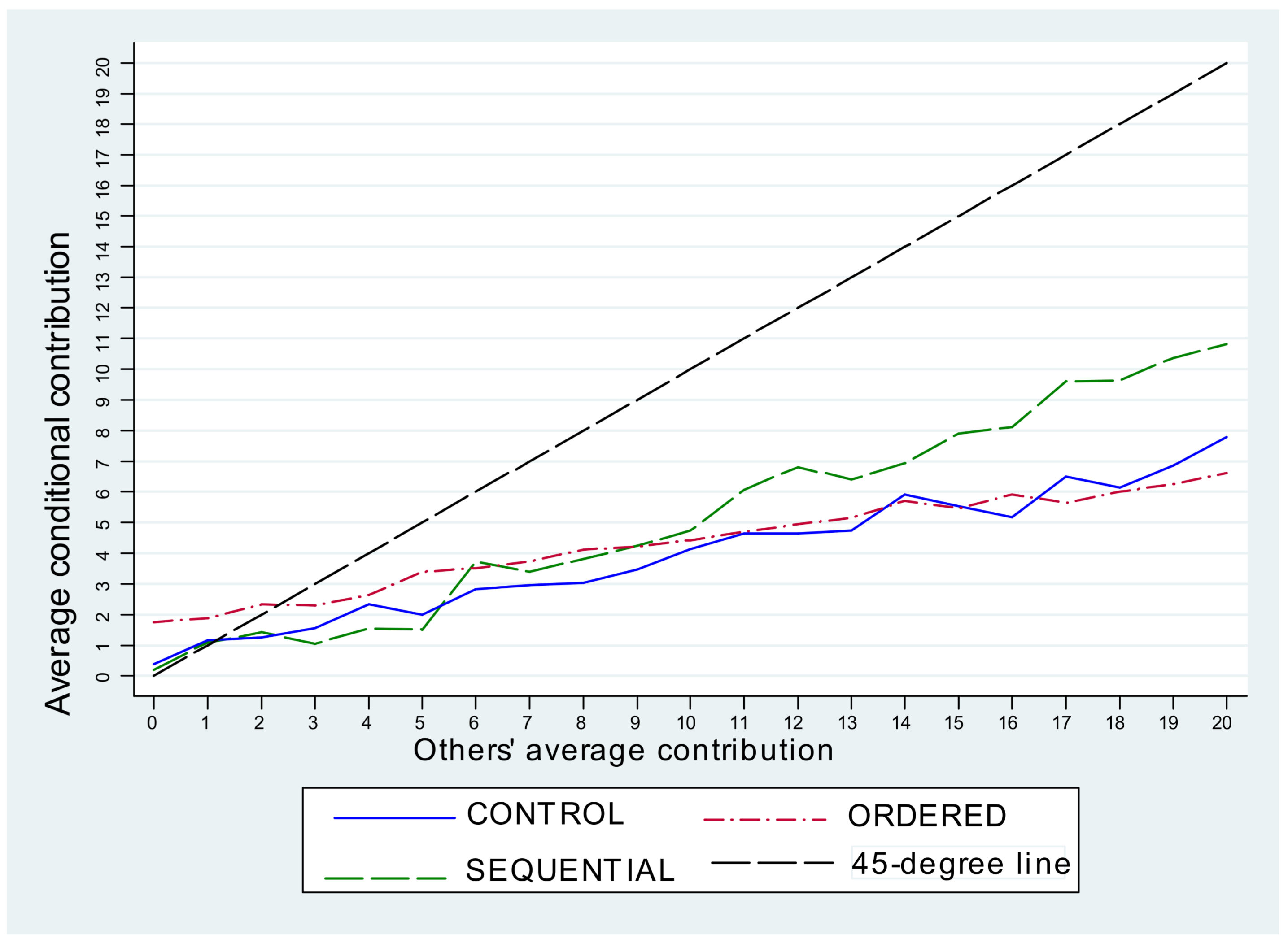
Appendix C Average Conditional Contribution by Treatment
Appendix D Individual Contribution Schedules

References
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people Conditionally Cooperative? Evidence from a Public Goods Experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Cherry, T.L.; McEvoy, D.M.; Sælen, H. Conditional cooperation and cultural worldviews. Econ. Lett. 2017, 158, 51–53. [Google Scholar] [CrossRef]
- Kocher, M.G.; Cherry, T.; Kroll, S.; Netzer, R.J.; Sutter, M. Conditional cooperation on three continents. Econ. Lett. 2008, 101, 175–178. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Quercia, S. The behavioral validity of the strategy method in public good experiments. J. Econ. Psychol. 2012, 33, 897–913. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Conditional strategies and the evolution of cooperation in spatial public goods games. Phys. Rev. E 2012, 85, 026104. [Google Scholar] [CrossRef] [PubMed]
- Szolnoki, A.; Perc, M. Effectiveness of conditional punishment for the evolution of public cooperation. J. Theor. Biol. 2013, 325, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Perc, M. Evolution of conditional cooperation under multilevel selection. Sci. Rep. 2016, 6, 23006. [Google Scholar] [CrossRef] [PubMed]
- Zizzo, D.J. Experimenter demand effects in economic experiments. Exp. Econ. 2010, 13, 75–98. [Google Scholar] [CrossRef]
- Fosgaard, T.; Gårn Hansen, L.; Wengström, E. Framing and Misperceptions in a Public Good Experiments. Scand. J. Econ. 2017, 119, 435–456. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S. Social Preferences, Beliefs and the Dynamics of Free Riding in Public Good experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef]
- Gächter, S.; Kölle, F.; Quercia, S. Reciprocity and the Tragedies of Maintaining and Providing the Commons. Nat. Hum. Behav. 2017, 1, 650–656. [Google Scholar] [CrossRef] [PubMed]
- Wolff, I. What are the equilibria in public-good experiments? Econ. Lett. 2017, 150, 83–85. [Google Scholar] [CrossRef]
- Cheung, S.L. New insights into conditional cooperation and punishment from a strategy method experiment. Exp. Econ. 2014, 17, 129–153. [Google Scholar] [CrossRef]
- Andreoni, J. Warm-Glow Versus Cold-Prickle: The Effects of Positive and Negative Framing on Cooperation in Experiments. Q. J. Econ. 1995, 110, 1–21. [Google Scholar] [CrossRef]
- Ellingsen, T.; Johannesson, M.; Mollerstrom, J.; Munkhammar, S. Social Framing Effects: Preferences or Beliefs? Games Econ. Behav. 2012, 76, 117–130. [Google Scholar] [CrossRef]
- Dufwenberg, M.; Gächter, S.; Hennig-Schmidt, H. The Framing of Games and the Psychology of Play. Games Econ. Behav. 2011, 73, 459–478. [Google Scholar] [CrossRef]
- Fosgaard, T.; Gårn Hansen, L.; Wengström, E. Understanding the nature of cooperation variability. J. Public Econ. 2014, 120, 134–143. [Google Scholar] [CrossRef]
- Nikiforakis, N. Feedback, Punishment and Cooperation in Public Good Experiments. Games Econ. Behav. 2010, 68, 689–702. [Google Scholar] [CrossRef]
- Cartwright, E. A comment on framing effects in linear public good games. J. Econ. Sci. Assoc. 2016, 2, 73–84. [Google Scholar] [CrossRef]
- Lévy-Garboua, L.; Maafi, H.; Masclet, D.; Terracol, A. Risk aversion and framing effects. Exp. Econ. 2012, 15, 128–144. [Google Scholar] [CrossRef]
- Holt, C.A.; Laury, S.K. Risk aversion and incentive effects. Am. Econ. Rev. 2002, 92, 1644–1655. [Google Scholar] [CrossRef]
- Cartwright, E.J.; Lovett, D. Conditional cooperation and the marginal per capita return in public good games. Games 2014, 5, 234–256. [Google Scholar] [CrossRef]
- Cartwright, E.; Patel, A. Imitation and the incentive to contribute early in a sequential public good game. J. Public Econ. Theory 2010, 12, 691–708. [Google Scholar] [CrossRef]
- Dariel, A.; Nikiforakis, N. Cooperators and reciprocators: A within-subject analysis of pro-social behavior. Econ. Lett. 2014, 122, 163–166. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A Theory of Fairness, Competition, and Cooperation. Q. J. Econ. B 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The strategy versus the direct-response method: A first survey of experimental comparisons. Exp. Econ. 2011, 14, 375–398. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Experimental economics 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Gneezy, U.; Imas, A.; Madarasz, K. Conscience Accounting: Emotion Dynamics and Social Behavior. Manag. Sci. 2014, 60, 2645–2658. [Google Scholar] [CrossRef]
| 1 | |
| 2 | As the reviewer of this paper points out, the impact of a demand effect can be more severe in the FGF method where previous studies have documented considerable levels of confusion among subjects (e.g., Fosgaard, Hansen, and Wengström, 2017) [9]. |
| 3 | Similarly, Wolff (2017) [12] used the FGF method to estimate the fraction of conditional cooperators and determined the “revealed preference” Nash equilibria of the public good game. He concluded: “The data show that multiple equilibria are relatively frequent even in a standard three-player setting. In this perspective, the common finding of close-to omnilateral defection at the end of repeated public-good games is surprising” (p. 83). |
| 4 | Cheung (2014) [13] used a variant of the FGF method where instead of the others’ average contribution, subjects are shown the others’ individual contributions. He found that about a third of his sample can be classified as conditional cooperators and half as selfish. He attributed this primarily to his Australian subject pool, but another explanation is that, in his experiment, conditionality was far less salient than in FGF. In addition, Fosgaard, Hansen, and Wengström (2017) [9] employed the FGF method using a positive–negative frame inspired by Andreoni (1995) [14], and found that this manipulation affects subjects’ contribution schedules, although this is partly due to misperception of the incentives of the game. Similarly, Gächter, Kölle, and Quercia (2017) [11] found that framing the public good game as a Maintenance or a Provision problem affects the elicited contribution profiles. |
| 5 | Different kinds of framing effects have been shown to affect contributions in public good games (e.g., Andreoni 1995 [14]; Ellingsen et al., 2012 [15]; Dufwenberg et al. 2011 [16]; Fosgaard, Hansen, Wengström, 2014 [17]; Nikiforakis, 2010 [18]). For an extensive list of references, see Cartwright (2016) [19]. |
| 6 | |
| 7 | The parameters in the present study were different from those of FGF, who used groups of four players and a marginal per-capita return of 0.4. See the studies of Cartwright and Lovett (2014), [22] and Wolff (2017), [12] for evidence on how changes in the marginal per-capita return affect contribution profiles elicited with the FGF method. |
| 8 | For instance, consider the model by Fehr and Schmidt (1999) [25]. A dislike for disadvantageous inequality (i.e., a sufficiently high ) could rationalize conditional cooperation in the public-good game. An individual with sufficiently high is predicted to contribute more in the contribution table for a given level of others’ contributions than someone with as well as in the one-shot game, controlling for beliefs, to avoid suffering disutility from earning more than his group members. |
| 9 | Since the FGF classification procedure for selfish subjects is very strict, requiring that subjects always contribute zero, I ran individual level regressions to explore the relationship between others’ and own contribution. If the fraction of subjects with insignificant slopes (selfish people would be among them) is compared using a Fisher’s-exact test, it is find that there are significantly fewer in SEQUENTIAL than in CONTROL (p-value = 0.081) or ORDERED (p-value = 0.015). |
| 10 | For example, an individual who always contributes has a weakly monotonic schedule. A perfect conditional cooperator contributes and has a strictly monotonic schedule. An individual who contributes and has a non-monotonic schedule. |
| 11 | The large fraction of non-monotonic schedules in SEQUENTIAL may be partly attributed to the fact that individuals could not revise their choices once made. However, it should be noted that: (i) subjects knew in advance all the choices they would be asked to make; and (ii) that half of the participants also failed to report a weakly monotonic schedule even in the CONTROL where revisions were possible. |
| 12 | This difference between SEQUENTIAL and CONTROL is not statistically significant (p-value = 0.330). |
| CONTROL | ORDERED | SEQUENTIAL | |
|---|---|---|---|
| Free riders | 30.00 | 36.36 | 3.03 |
| Conditional cooperators | 46.66 | 42.42 | 78.79 |
| Triangle contributors | 3.33 | 3.03 | 0.00 |
| Others | 20.00 | 18.18 | 18.18 |
| # of groups | 10 | 11 | 11 |
| # of subjects | 30 | 33 | 33 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dariel, A. Conditional Cooperation and Framing Effects. Games 2018, 9, 37. https://doi.org/10.3390/g9020037
Dariel A. Conditional Cooperation and Framing Effects. Games. 2018; 9(2):37. https://doi.org/10.3390/g9020037
Chicago/Turabian StyleDariel, Aurélie. 2018. "Conditional Cooperation and Framing Effects" Games 9, no. 2: 37. https://doi.org/10.3390/g9020037
APA StyleDariel, A. (2018). Conditional Cooperation and Framing Effects. Games, 9(2), 37. https://doi.org/10.3390/g9020037




