Abstract
Imitation of the successful choices of others is a simple and superficially attractive learning rule. It has been shown to be an important driving force for the strategic behavior of (young) adults. In this study we examine whether imitation is prevalent in the behavior of children aged between 8 and 10. Surprisingly, we find that imitation seems to be cognitively demanding. Most children in this age group ignore information about others, foregoing substantial learning opportunities. While this seems to contradict much of the literature in the field of psychology, we argue that success-based imitation of peers may be harder for children to perform than non-success-based imitation of adults.
1. Introduction
Imitation learning can be an attractive heuristic in many circumstances; it saves on decision costs and requires relatively low cognitive ability.1 Offerman and Schotter [2] have thus, referred to it as “poor man’s rationality”. Imitation learning is however far from being flawless, as under particular adverse circumstances it may lead to suboptimal outcomes. For instance, in Offerman and Schotter [2] a random idiosyncratic component to payoffs may lead imitators to adopt actions that only performed well due to luck. Similarly, Vega-Redondo [3] observed that in Cournot games, imitation learning leads to the emergence of Walrasian states with payoffs lower than those obtained in the Nash equilibrium. Much of the experimental-empirical literature in economics has consequently focused on circumstances under which imitation is harmful.
In contrast, scholars in other disciplines are less pessimistic about the merits of imitation learning. In the words of Albert Bandura [4], “Man’s capacity to learn by observation enables him to acquire large, integrated, units of behavior by example without having to build up the patterns gradually by tedious trial and error.”
We have thus decided to cast our study in a setting where imitation is not self-harming, but will in fact lead to outcomes with strictly higher payoffs than those received under rules that ignore information received by others. In particular, we study a multi-armed bandit problem where the distribution of payoffs across urns is unknown to subjects. In this setting, imitation is not only superficially attractive as in previously studied settings but indeed payoff-improving as compared to only reinforcing one’s own previously successful actions.
Our main contribution lies in showing that imitation is not necessarily a straightforward heuristic subjects are able to apply, regardless of their age. In particular, we compare the behavior of children between the ages of 8 and 10 (the vast majority of whom are aged 9) with that of university students. We identify imitative behavior through two treatment variations. In the Baseline treatment subjects cannot observe other participants, such that imitation cannot occur. In the Observation treatment, subjects do observe the choice and outcome of one other subject, such that imitation is possible and desirable.
While university students make efficient use of being able to observe others, we find that most children almost completely ignore the feedback they receive about others and refrain from imitation—despite clear evidence that they do understand the rules of the game and use the feedback they receive about their own choices in a rational manner. There is, however, a subgroup of children from elite schools that does better on average but still does not imitate as efficiently as university students.
1.1. Related Literature
Imitation has been studied in economics, psychology, anthropology, and many related fields. As a comprehensive review of the literature is beyond the scope of the current paper, we try to focus here on the experimental literature that is most relevant to the current study. For our purposes it is useful to divide the literature on imitation into two strands: (1) success-based imitation, where imitation is based on the success other people were observed as having with a given action, and (2) non-success-based imitation, where actions are imitated regardless of their success. The latter includes conformity-based imitation (Asch, [5]) or reflex-driven, automatic imitation (Ray and Heyes, [6]). Most of the evidence from child psychology also falls into this category since infants mostly imitate parents or other adults without accounting for or even observing the (relative) success of an action. For example, Meltzoff [7] in a famous experiment found that infants imitated adults by using their foreheads to switch on a lamp. However, Gergely et al. [8], by studying a setting where the adult’s hands are visibly occupied during the head action, show that imitation of the head action is less pronounced, thus documenting sophisticated rational imitation among children.
A second important dimension in the imitation literature is the question of who the role models are. Most studies in child psychology use adults as models.2 With adults as models, children may assume that it is a good idea to imitate even if they do not observe or understand the success of an action, simply because they trust the adult as having a reason for choosing a certain action. When peers are role models, this is much less clear. Zmyj and Seehagen [10] review the literature on children’s imitation of peers. One of their main conclusions is that young children are more likely to imitate adults than peers when the setting is unfamiliar.
In the experimental economics literature, imitation has also been an important agenda, mostly in the form of success-based imitation of peers. Huck et al. [11] and Offerman et al. [12] consider various scenarios where subjects differ in the information they receive in Cournot games. If subjects do not know how payoffs are determined but are informed about profits and quantities in the market, imitation learning is a good predictor of actual behavior, and convergence to the Walrasian state can be observed. Apesteguia et al. [13] show that it matters both empirically and theoretically whether agents observe their competitors or firms in different markets.
The experiment by Offerman and Schotter [2] is relatively close to the current design as it also studies success-based imitation in a decision problem where payoffs are stochastic. Imitation in their context leads to a situation where suboptimal strategies, which happened to have performed well in one instance, are adopted by a large fraction of society.
Our paper also contributes to recent work in the literature that studies decision-making in children. Harbaugh et al. [14] document strategic sophistication in bargaining games in children as young as 8. Fehr et al. [15] show that egalitarianism in simple distributional conflicts increases between the ages of 3 and 8. Almås et al. [16] show how children when they enter adolescence start to accept inequality that is the result of effort differentials as fair and how efficiency concerns are acquired in adolescence. Sutter et al. [17] show how adolescents’ risk attitudes, ambiguity attitudes, and time preferences correlate with their real-life behavior. Lergetporer et al. [18] study how third-party punishment in children can increase cooperation rates in prisoner’s dilemma games. Finally, Sher et al. [19] analyze how children’s ability to reason about other’s incentives and thinking develops in a strategic setting with age.
2. Experimental Design
In total, 162 subjects participated in the experiment, of which 82 were fourth-grade school children from four different elementary schools in Vienna. The comparison group consisted of 80 adults recruited from the subject pool of the experimental lab at the Department of Economics, University of Vienna. The average age of the school children was 9.6 (SD = 0.47 with a minimum age of 8.8 and a maximum of 11.1) and 37.8% were female. The average age of the adults was 25.5 (SD ) and 41.0% were female.
The task for all subjects was to repeatedly choose among six different “urns”, . Each urn i contained two balls that determined payoffs, That is, the worst urn either yielded a payoff of 1 or 2 while the best urn yielded a payoff of 6 or 7. Urns were labeled with a circle, a triangle, a cross, a square, a star, and a hexagon. Subjects did not know how the labels corresponded to the potential payoffs. There were 10 rounds and the points from all rounds were added up to obtain the final payoff. In each round subjects chose one of the six urns. After their choice, one of the two balls that were contained in their chosen urn was randomly drawn with 50–50 probabilities and subjects received feedback about the drawn ball and their payoff. The task was, thus, to find over time better and better urns. We have selected a decision problem that is easy to explain even to children yet fairly hard to solve optimally. In fact, we did not expect anyone (even the university students) to use the optimal solution.3
There were two treatments. In the Baseline treatment, subjects only received feedback from their own chosen urn. In the Observation treatment, subjects received additional information about the choice and payoff from one (fixed) other subject who was facing the exact same decision problem. That is, after each round, subjects received a sheet detailing “...what one of the other kids in class who plays the exact same game as you do, chose to do in the previous period and how many points this kid earned with its choice.” See Figure A1 in Appendix A for a feedback/decision sheet for the Observation treatment. It is important to note that in the context of this game, this was useful information. Indeed, the information about the other’s choice and payoff was as informative as the information about one’s own payoff. Both should have received equal weight.
For the school children, the experiment was conducted with pen and paper within the familiar environment of the classroom. Upon arrival the tables were arranged to face the blackboard. Partition walls were put up (see Figure 1). Six different urns were set up on a table clearly visible to all children. The instructions were read out aloud. To illustrate the distribution of balls across urns, the experimenter reached into each of the urns and presented the balls in front of the children. The distribution was also displayed on the blackboard and remained visible for the entire duration of the experiment. When explaining the random selection of balls by the computer, the experimenter reached into a random urn while blindfolded, displayed the drawn ball to the subjects, and put it back into the urn. The children were paid in vouchers for a book and stationary chain and made aware of the exchange rate between points and vouchers (10-cent vouchers for each point). On average, children received vouchers with a value of €5.41.

Figure 1.
The classroom experimental setting.
The experiment lasted approximately 90 min including instructions, questionnaire, and payment of subjects. We used an Excel program to calculate payoffs and to gather and print feedback information. In each period we first provided the children with the feedback/decision sheet containing information on the previous round. Each period, we gave them 30 s to go through the previous period’s information and choose an urn. In between these decision periods children were allowed to either read a comic or draw something on sheets of paper provided beforehand. After the last period they were handed a questionnaire (see Figure A2 in Appendix A), which was filled in with the assistance of the experimenters. At the end of the experiment each child was handed an envelope containing her vouchers. In addition, we also asked teachers to fill in questionnaires about all children. In particular, we asked them whether they expected that a child was likely to be accepted for the “Gymnasium”, the higher (selective) track in the Austrian school system which is attended by about one third of pupils.
The instructions (see Appendix B) were carefully adjusted to the children’s age group.
The university students received almost the same instructions, with the only difference being the use of the German polite form of address. The experiments with adults were conducted in six sessions at the Vienna VCEE experimental lab. Adults received monetary payoffs with an exchange rate of 25 cents per point. Average payoffs were of €14.74.
3. Results
Table 1 shows the overall means and standard deviations of the chosen urn’s number, 6 being the best, 1 being the worst. For children, we distinguish between pupils who were assessed by their teachers as suitable for the “Gymnasium” and all other pupils. In terms of their cognitive abilities, “Gymnasium” children are, when adjusted for age, probably closer to university students than other children.

Table 1.
Summary statistics with respect to urn choice.
We found that university students significantly outperformed all children in both treatments (Mann-Whitney U-test, two-sided, for the Baseline and Observation treatments).4 Also, university students did better in the Observation treatment than in the Baseline treatment, as predicted by imitation (). In contrast, we did not find a significant difference between the Baseline and Observation treatments for the children, regardless of whether they were “Gymnasium” ( or other children ().5 Figure 2 plots the corresponding histograms of urn choices for the six different cells. In all six cells, the best urn is also the most frequently chosen one. The histograms also show that the incidence of the optimal urn vastly increases for university students when they receive additional information about another subject in the Observation treatment. This is not the case for children where, as shown above, the two distributions are not significantly different.
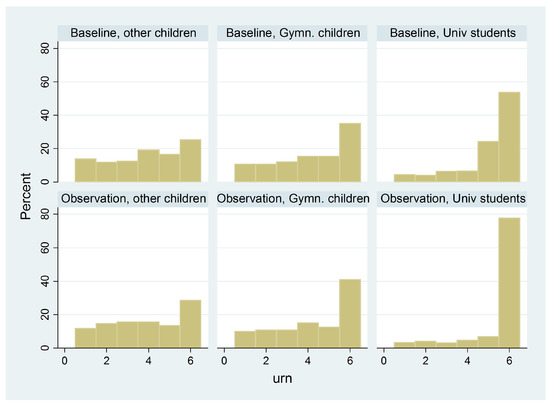
Figure 2.
Histograms of urn choices.
In order to study learning dynamics, we first examined how the average choice moves over time. Figure 3 plots the development of the average choice for children and adults.6 Fundamentally, the figure reveals that all subjects are able to learn. Learning is steeper for university students and steepest for university students in the Observation treatment. In contrast, there are no treatment differences in the development of the average choice for children over time.7 Further evidence for learning on the individual level is provided by the fact that 90% of the “Gymnasium” children and 84% of all other children by the end of the experiment chose either the same urn or a better urn than they started out with. University students did slightly better in this measure as well, with 100% of subjects choosing a weakly better urn by the end of the experiment.
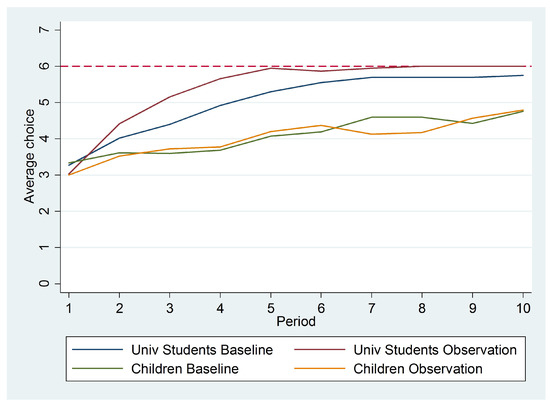
Figure 3.
Average choices over time.
While the absence of treatment differences in children is strongly indicative of the absence of imitation, the evidence is, of course, indirect. Direct evidence can be obtained by examining how often subjects copy others’ behavior when others have found a better urn. We define the rule “imitate the best” as follows.8 Subjects always pick one of the actions that yielded maximal payoff in the previous period. If the partner’s payoff was higher, they should adopt the partner’s urn. If their own payoff was higher, they should stick to their own urn. If both obtained the same payoff, either urn could be chosen. All other urns constitute experimentation. In Figure 4 we show the percentage of choices that are compatible with “imitate the best” depending on the difference in payoffs (=observed payoff − own payoff). While university students stick to their choices when they have earned significantly more than the other player and imitate others with higher payoffs, the picture is much noisier with children. An MWU test comparing the distribution of the shares of choices compatible with “imitate the best” (taking each subject pair as one observation) across children and university students confirms this difference (). This becomes most apparent at the two extremes of the distribution of payoff differences where children display a much stronger taste for experimentation. They do not imitate the other’s action as much as one would expect when the difference in payoffs is 6 or 5, nor do they stick to their action as much as one would expect when they are actually the ones earning the maximum payoff difference of and . It is further insightful to classify deviations from the “imitate the best” rule as either errors or explorations. We define errors as clearly suboptimal behavior and explorations as behavior that is neither imitation nor an error. Given that feedback was only provided about round , we count the following as errors:9 If one sees a payoff of 7 in (as one’s own or the partner’s payoff), one should use the corresponding urn in t. If one does not, this counts as an error. Likewise, if one sees a 1, one should not choose this urn in t. Finally, if one sees payoffs from two different urns in (in the Observation treatment) and chooses the one with lower payoff in t, that counts as an error. This definition of errors partitions the choices into three categories: errors, “imitate-the-best”, and exploration. As one can see in Figure 5, children (in particular those not on track for “Gymnasium”) both make more errors and explore more. Note the monotonic relation of error rates, exploration, and imitation rates across subject groups.
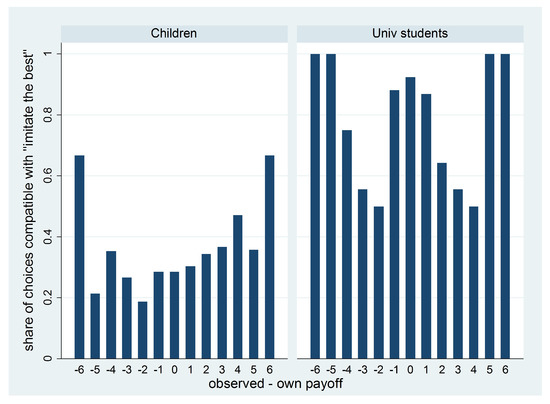
Figure 4.
Share of choices that are compatible with “imitate the best” depending on payoff difference (=observed payoff − own payoff from previous period).
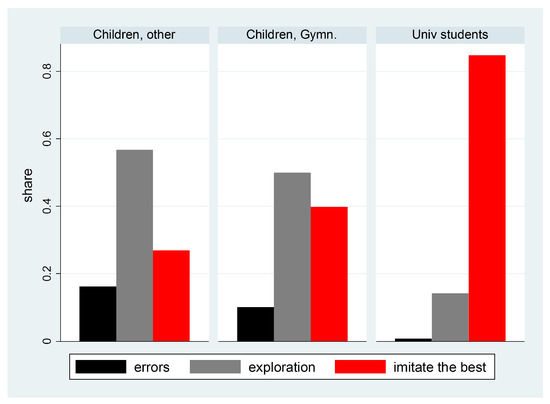
Figure 5.
Share of choices that are compatible with errors, exploration, and “imitate-the-best”.
As can be inferred from Figure 6, error rates are fairly heterogeneous across children. While some make no errors, some make errors in up to 33% of their decisions.
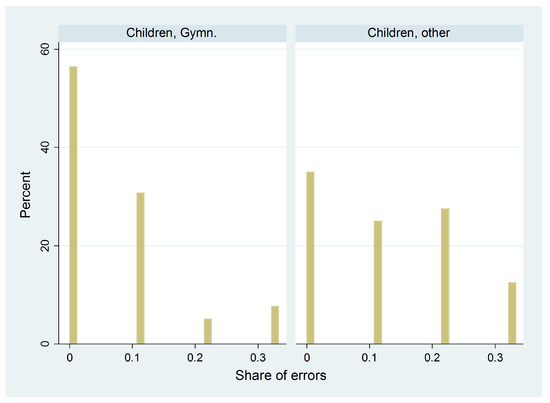
Figure 6.
Distribution of errors across children.
We now investigate whether the differences between university students and children can be accounted for by the composition of treatment groups in terms of “Gymnasium” and “non-Gymnasium” rather than age. To do so, we employ the entire data set and regress urn choice on treatments and dummies for university students and children viewed as suitable for higher school education (“Gymnasium”) and also include interaction terms that capture heterogeneous treatment effects. The results are shown in Table 2. The results show that while more able children generally do better in our task than those predicted not to reach the “Gymnasium”, they fail to do better in the Observation treatment. That is, they, too ignore the additional information from others’ urn choices. In other words, our finding that, in contrast to adults, children at the age of 10 are unable to engage in rational imitation is not due to selection bias in our sample. Smarter children do better at the learning task but still fail to make use of feedback about others’ choices and outcomes which is, in principle, as valuable as their own feedback.

Table 2.
Random effect regression: urn choice.
4. Conclusions
While much of the recently growing literature on economic and strategic decision-making in children points to various forms of sophistication being acquired early on in life, we document that children at the age of around 9 fail to engage in success-based imitation of peers, that is, they are unable to extract relevant information from peers’ choices and outcomes. Given the prevalence of other forms of imitation in child behavior, we find this surprising and we realize that our finding seems to contradict much of the earlier literature. Nevertheless, we believe such contradictory findings need to be published (in particular to avoid publication bias).
We document that our result is not due to selection bias. Even the most able children do not gain an advantage through rational imitative behavior. Instead, all children appear to discard information that stems from others’ choices even though the symmetry between own and others’ actions is made explicit. One may further wonder whether our results are an artifact of the urn choice setting. In fact, we had run an earlier pilot study based on a Cournot game. The fact that we found no evidence for children imitating their peers led us to study the simpler urn choice task. We are thus confident that our results may carry over to more general and more complex environments.
We believe that multiple aspects may account for our findings. First, our experiment studied success-based imitation. This is cognitively more demanding than automatic imitation as it does not only require subjects to copy others but bases the decision on the relative success of the observed behavior. Further, in our experiment children had to learn from observing peers. Most of the literature in child psychology uses adults as role models. Moreover, in line with previous literature in psychology, it has been argued that in unfamiliar settings, children trust their peers less and rely more on their own experience. We speculate that evolution might have forced prepubescent children to focus very carefully on own feedback. The wealth of new information provided to children at this age is enormous and a clear focus on feedback about own behavior might have been extremely useful (and perhaps still is). We believe that more research is required to find out which of these factors determine imitation in children.
Acknowledgments
We are grateful to two anonymous referees, Maarten Janssen, Wieland Müller, Karl Schlag, Matthias Sutter and a seminar audience at the Econometric Society World Congress in Montreal for useful comments and discussions. We thank Johannes Leutgeb for excellent research assistance. Financial support from the Vienna Science and Technology Fund (WWTF) under project fund MA 09-017 is gratefully acknowledged.
Author Contributions
All authors conceived and designed the experiments; E.W. and S.W. performed the experiments. All authors analyzed the data and contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Supplementary Material
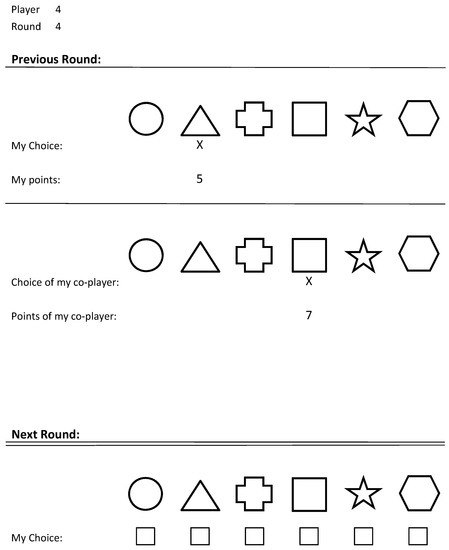
Figure A1.
Feedback/decision sheet in the Observation treatment.

Figure A2.
Questionnaire.
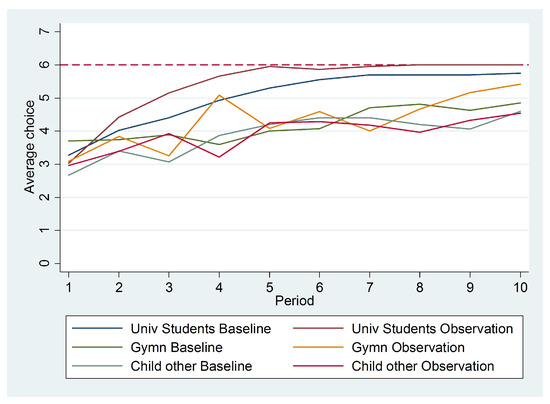
Figure A3.
Average choices over time.

Table A1.
Random effects regression: time trend in urn choices.
Table A1.
Random effects regression: time trend in urn choices.
| Children | University Students | |||
|---|---|---|---|---|
| Baseline | Observation | Baseline | Observation | |
| Period | 0.16 *** | 0.16 *** | 0.26 *** | 0.26 *** |
| Constant | 3.21 *** | 3.13 *** | 3.60 *** | 3.98 *** |
| N | 420 | 400 | 400 | 380 |
Clustered standard errors in parentheses, *** significant at 1% level.
Appendix B. Instructions
Instructions for the BASELINE Treatment—Additional Text for the OBSERVATION Treatment in [ ].
The non-verbal part of the instructions is in italics.
Hello, my name is (Name of Instructor) and these are (Name Helper 1) and (Name Helper 2). Thanks for letting us visit you in class today. Maybe your teacher has already told you, we’re working at the University of Vienna and we would like to play a game with you today.
In our game you will have the possibility to earn points. These points will be transferred into LIBRO vouchers at the end of the game. Do all of you guys know the LIBRO store? You can buy pencils, CDs or little toys there. Each point in the game will give you a 10-cent voucher. The vouchers look like this (show the kids some sample vouchers). The colorful vouchers are worth €1 or €5. The more points you earn in the game the more vouchers you will get by the end of the game and the more vouchers you can yourself spend in the store.
Before we can start to play the game, I will explain the rules.
From now on, I would like to ask you not to talk to any of you classmates anymore. If one of you is talking to any other child in class we will exclude this person from the game and he or she will not get any vouchers at the end of the game. Please listen carefully to my instructions. The better you listen to me and understand the game the more points you can earn and the more vouchers you can spend in store afterwards.
Please raise your hand if you do have a question concerning the game. One of us is going to come to your table and answer this question in private. Otherwise you just stay silent and listen carefully.
First, I’m going to explain the rules of the game to you. Then, we will play 10 rounds of the game. After we’ve finished the game we will fill in a questionnaire together and each child will get an envelope with his vouchers.
Everything ok so far? Let us talk about the game itself then.
(Draw on the blackboard: six bowls with two balls inside each.)
- There are six urns in our game (point at the urns on the blackboard).
- There are two balls in each of these urns (point at the balls in the urns on the blackboard).
- Inside one of these urns there is a ball worth one point and a ball that gives you two points (label the balls in one of the urns on the blackboard with numbers one and two).
- Inside another one of these urns there is a ball worth two points and a ball that gives you three points (label the balls in one of the urns on the blackboard with numbers two and three).
- Inside a further one of these urns there is a ball worth three points and a ball that gives you four points (label the balls in one of the urns on the blackboard with numbers three and four).
- Inside another one of these urns there is a ball worth four points and a ball that gives you five points (label the balls in one of the urns on the blackboard with numbers four and five).
- Inside one of these urns there is a ball worth five points and a ball that gives you six points (label the balls in one of the urns on the blackboard with numbers five and six).
- Inside another one of these urns there is a ball worth six points and a ball that gives you seven points (label the balls in one of the urns on the blackboard with numbers six and seven).
- Your task in each period is to choose one of the urns.
- After you’ve chosen one of the urns the computer is going to draw one of the balls inside the urn at random and you will get the points stated on that ball.
(Place six bowls with two tennis balls inside each, numbered from 1–7 and covered with colored lids, in front of the class.)
- You can think of the game as follows. Here are six urns.
- If you, for example, decide to choose the red urn, then the computer will compute your points as if it would randomly draw a ball out of this urn (draw a ball out of the red bowl with covered eyes and show the ball with its associated number to the kids). After having drawn the ball and after having allocated the associated points to you, the computer will put the ball back into the same urn and the next period of the game will be about to begin (put the ball back into the bowl).
- If you decide to choose the blue urn in the next period, then the computer will draw a ball out of the blue urn. You get the points that are written on this ball, and the ball will be placed back into the urn (draw a ball with covered eyes out of the blue bowl, show the ball with its associated number to the kids, and put the ball back into the bowl).
- If you decide to choose the blue urn again in the next period, then the computer will again draw one of the two balls. You get the points that are written on this ball and the ball will be placed back into the urn (again, draw a ball out of the blue bowl with covered eyes, show the ball with its associated number to the kids, and put the ball back into the bowl).
(Draw the six different signs (circle, square, triangle, cross, star, hexagon) on the blackboard).
- However, the urns in our game will not be differentiated by colors. But each urn will be associated with a sign. We have one urn marked with a circle (point to the circle on the blackboard), one urn with a square (point to the square on the blackboard), one urn with a triangle (point to the triangle on the blackboard), one urn with a cross (point to the cross on the blackboard), one urn with a star (point to the star on the blackboard) and one urn with a hexagon (point to the hexagon on the blackboard). The urns will have the same sign throughout the whole game. But we will not tell you which sign belongs to which urn.
- What you know is that there is one urn with a ball labeled 1 and a ball labeled 2. There is one urn with a ball labeled 2 and a ball labeled 3. In one urn there is a ball labeled 3 and a ball labeled 4. In one urn there is a ball labeled 4 and a ball labeled 5. In one urn there is a ball labeled 5 and a ball labeled 6 and in one urn there is a ball labeled 6 and a ball labeled 7.
- In order for you to decide on one urn and to get to know how many points you’ve earned with one of the urn’s balls, we will provide you with a decision sheet at the beginning of each period (show a period 1 decision sheet).
- On top of the sheet you will find your unique player’s number, which lets the computer know who you are and you will find the period in which we’re currently in.
- Underneath you will see the six signs of the urns. In each period your task is going to be to decide on one of the signs. As soon as you’ve decided on one of the signs, you tick off the box underneath the sign and wait for us to collect your decision sheet.
- From the second period on, you will find some more information on your decision sheet. On top of the sheet you will again find your player’s number and the current period (show a period 2 decision sheet).
- Underneath, you will see what happened in the previous period.
- You can see what urn you did choose. The sheet tells you “my choice” and shows you a ticked off box underneath your previous period’s sign.
- You can have a look on how many points you did get with your choice. The sheet says “my points”.
- Underneath, you will again find the six signs of the urns and you can again decide on an urn’s sign.
- [Only in the Observation treatment: Additionally, we will tell you what one of the other kids in class who plays the exact same game as you do chose to do in the previous period and how many points this kid earned with her choice.]
- The game will last 10 periods. We will tell you when the last period is going to be.
- The important thing is that you understand that different urns can give you different numbers of points.
Before we start to play the game, each of you is going to be provided with a comic book and some sheets of paper. Whenever there isn’t any decision sheet on your table you’re allowed to read the comic or color on the blank sheets of paper. You will have to close the comic books, put away the drawings, and concentrate on the new decision sheet as soon as I tell you that a new period of the game is going to start, until we pick up the decision sheet again.
Each game period is going to last for 30 s. In this time you will carefully read through the previous period’s information and decide on an urn for the current period afterwards.
Remember, in each period you can decide on one of the urn’s signs. There are no guidelines on which sign to choose when or how often. It is completely up to you if you want to choose a different sign in each period or if you want to go for the same sign in some consecutive periods.
Remember, the more points you earn in the game, the more money in form of voucher you will get by the end of the game. If anybody has any more questions raise your hand now. Otherwise I wish you the best of luck and don’t forget not to talk to any other kids.
Before every new period: Please close the comic book and put away all the drawings (wait for some seconds). We will now provide you with the decision sheets for the next period. Please read carefully through the information’s provided and decide which sign you would like to choose in this period. (After the last period) The game’s last period is now over. First, we will collect the comic books. Second, we will provide you with a questionnaire. Since we will fill it in together, please wait until everybody is provided with the questionnaire. In the mean time, the computer is going to calculate your earnings. When we are finished filling in the questionnaires, each child is going to get an envelope with his vouchers.
(Before giving away the envelopes) Before each of you is going to get his envelope we would like to thank you for being able to be with you today and also say thanks to your teacher for allowing us to visit your class. We will now hand each of you an envelope with your player number on the outside. Inside the envelope you will find a sheet of paper that tells you how many points you’ve earned in the whole game and how many vouchers this number of points is going to give you. The vouchers look like that (show them sample vouchers). They are labeled €5 or €1. We wish you a lot of fun with your envelopes and the vouchers.
References
- Alós-Ferrer, C.; Schlag, K. Imitation and Learning. In The Handbook of Rational and Social Choice; Anand, P., Pattanaik, P., Puppe, C., Eds.; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Offerman, T.; Schotter, A. Imitation and luck: An experimental study on social sampling. Games Econ. Behav. 2009, 65, 461–502. [Google Scholar] [CrossRef]
- Vega-Redondo, F. The Evolution of Walrasian Behavior. Econometrica 1997, 65, 375–384. [Google Scholar] [CrossRef]
- Bandura, A. Social Learning Theory; General Learning Press: New York, NY, USA, 1971. [Google Scholar]
- Asch, S. Social Psychology; Prentice Hall: Englewood Cliffs, NJ, USA, 1952. [Google Scholar]
- Ray, E.; Heyes, C. Imitation in infancy: The wealth of the stimulus. Dev. Sci. 2011, 14, 92–105. [Google Scholar] [CrossRef] [PubMed]
- Meltzoff, A.N. Infant imitation after a 1-week delay: Long-term memory for novel acts and multiple stimuli. Dev. Psychol. 1988, 24, 470. [Google Scholar] [CrossRef] [PubMed]
- Gergely, G.; Bekkering, H.; Király, I. Developmental psychology: Rational imitation in preverbal infants. Nature 2002, 415, 755. [Google Scholar] [CrossRef] [PubMed]
- Hanna, E.; Meltzoff, A.N. Peer imitation by toddlers in laboratory, home, and day-care contexts: Implications for social learning and memory. Dev. Psychol. 1993, 29, 701. [Google Scholar] [CrossRef] [PubMed]
- Zmyj, N.; Seehagen, S. The role of a model’s age for young children’s imitation: A research review. Infant Child Dev. 2013, 22, 622–641. [Google Scholar] [CrossRef]
- Huck, S.; Normann, H.T.; Oechssler, J. Learning in Cournot Oligopoly—An Experiment. Econ. J. 1999, 109, C80–C95. [Google Scholar] [CrossRef]
- Offerman, T.; Potters, J.; Sonnemans, J. Imitation and Belief Learning in an Oligopoly Experiment. Rev. Econ. Stud. 2002, 69, 973–997. [Google Scholar] [CrossRef]
- Apesteguia, J.; Huck, S.; Oechssler, J. Imitation—Theory and experimental evidence. J. Econ. Theory 2007, 136, 217–235. [Google Scholar] [CrossRef]
- Harbaugh, W.T.; Krause, K.; Vesterlund, L. Learning to bargain. J. Econ. Psychol. 2007, 28, 127–142. [Google Scholar] [CrossRef]
- Fehr, E.; Bernhard, H.; Rockenbach, B. Egalitarianism in young children. Nature 2008, 454, 1079–1083. [Google Scholar] [CrossRef] [PubMed]
- Almås, I.; Cappelen, A.W.; Sørensen, E.Ø.; Tungodden, B. Fairness and the development of inequality acceptance. Science 2010, 328, 1176–1178. [Google Scholar]
- Sutter, M.; Kocher, M.G.; Glätzle-Rützler, D.; Trautmann, S.T. Impatience and uncertainty: Experimental decisions predict adolescents’ field behavior. Am. Econ. Rev. 2013, 103, 510–531. [Google Scholar] [CrossRef]
- Lergetporer, P.; Angerer, S.; Glätzle-Rützler, D.; Sutter, M. Third-party punishment increases cooperation in children through (misaligned) expectations and conditional cooperation. Proc. Natl. Acad. Sci. USA 2014, 111, 6916–6921. [Google Scholar] [CrossRef] [PubMed]
- Sher, I.; Koenig, M.; Rustichini, A. Children’s strategic theory of mind. Proc. Natl. Acad. Sci. USA 2014, 111, 13307–13312. [Google Scholar] [CrossRef] [PubMed]
- Alós-Ferrer, C.; Weidenholzer, S. Imitation and the role of information in overcoming coordination failures. Games Econ. Behav. 2014, 87, 397–411. [Google Scholar] [CrossRef]
| 1. | See Alós-Ferrer and Schlag [1] for a broad review. |
| 2. | There are a number of exceptions (see e.g., Hanna and Meltzoff [9], and the review by Zmyj and Seehagen [10]) where peers are used as models. |
| 3. | In fact, one would have to assume a particular utility function to solve the problem. Even then, it is extremely tedious, although possible, to solve the problem via backward induction. |
| 4. | For non-parametric tests, we considered the average choice of one subject (in the Baseline treatment) or one pair of subjects (in the Observation treatment) as one independent observation. |
| 5. | Moreover, we did not find a treatment effect for any of the questions contained in the children’s questionnaire. |
| 6. | Differentiating between “Gymnasium” and “non-Gymnasium” children does not change much (see Figure A3 in Appendix A). |
| 7. | Random effect regressions with clustered standard errors and a period variable (reported in Table A1 in the Appendix A) show that average choices for all groups in Figure 3 display a significant upward trend. |
| 8. | See Vega-Redondo [3] for earlier work utilizing the “imitate the best” rule and see Apesteguia et al. [13] and Alós-Ferrer and Weidenholzer [20] for a further discussion and axiomatization of related imitation rules. |
| 9. | We could also define errors more broadly by assuming that subjects memorize outcomes of pervious rounds. However, this would assume that we know how long the memory of the subject is and would complicate the analysis substantially. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).