Team Incentives under Moral and Altruistic Preferences: Which Team to Choose?

Abstract

This paper studies incentives provision when agents are characterized either by homo moralis preferences, i.e., their utility is represented by a convex combination of selfish preferences and Kantian morality, or by altruism. In a moral hazard in a team setting with two agents whose efforts affect output stochastically, I demonstrate that the power of extrinsic incentives decreases with the degrees of morality and altruism displayed by the agents, thus leading to increased profits for the principal. I also show that a team of moral agents will only be preferred if the production technology exhibits decreasing returns to efforts; the probability of a high realization of output conditional on both agents exerting effort is sufficiently high; and either the outside option for the agents is zero or the degree of morality is sufficiently low.

1. Introduction

Teamwork permeates economic activities. In some cases, different skills are needed complementing each other to complete a project; in other cases, division of labor plays a crucial role in timely delivery of a product. Partnerships, group projects and team sports are but a few examples in which individuals team up to achieve a certain goal. With the exception of partnerships, it falls upon an employer to hire the team of employees to fulfill the task at hand. In particular, as expenditure in recruitment and assessment surges1, with U.S. companies spending on average around US$\$4000$ per hire, an increase of nearly $15\%$ in the last four years, it is clear that recruitment and talent research divisions have turned their attention to more than the job applicants’ professional abilities. As a matter of fact, common practice includes the analysis of criminal2 and credit histories3, and more recently, social networks as well4.

While employees’ technical skills are important, interest in their personal characteristics other than job-relevant skills may be related to the now widespread knowledge that economic agents are not purely selfish, often displaying other-regarding preferences [3,4,5,6,7]. The literature in behavioral and experimental economics strongly suggests that social preferences affect outcomes in standard economic models [8,9]. The works in [10,11,12,13] analyze, in particular, the role other-regarding preferences play in interactions among employees in models of the workplace. The main findings in this literature show that the employees’ concerns towards one another affect not only the provision of effort, but also the compensation schemes that are offered. Thus, it is only natural to wonder what an ideal team would look like, for a given set of skills: Would it be a team composed of selfish individuals, whose only concern is their own gains, or maybe a group of altruistic agents, who would be content with increasing their workmates’ wellbeing? Perhaps a crew of moral employees deriving satisfaction in choosing actions they think are the right ones? These are the questions I address in this paper.

In view of the overwhelming experimental evidence of behaviors that are incompatible with purely selfish preferences [4,5,14,15], it is important to understand how prosocial preferences affect behavior in the workplace and, by extension, the design of contracts in the workplace. I propose a model to address this question.

Specifically, I focus on the optimal compensation schemes that should be used in a standard moral hazard setting to incentivize the employees to fulfill their tasks. In doing so, I am able to compare the profits obtained by the employer from a team composed of individuals with different kinds of prosocial preferences. Although I do not study the recruitment process per se, I am able to make predictions about which preferences the principal would prefer.

The framework utilized is the multiagent moral hazard model, as first proposed by [16,17], where a risk-neutral principal hires a team of two risk-averse agents. The agents can exert costly effort in order to stochastically affect the realization of output. By assumption, efforts are simultaneously and independently chosen by the agents and cannot be observed by the principal. On the other hand, output is observable by third parties after being realized and can thus be contracted upon.

In the behavioral economics literature, several classes of prosocial preferences have been proposed. I analyze two of them. The first one is altruism [18]5, a class that has been extensively used in the literature on the voluntary contribution of public goods. This is natural since one can think of efforts made in the context of teamwork in a firm as contributions to a public good (the firm’s profit). Second, in light of recent results by [20,21], who show that a particular, novel, class of preferences stands out as being favored by evolution, I compare the optimal contract under altruism with the optimal contract under this class of homo moralis preferences, a convex combination of selfishness and morality. In sum, my model allows addressing the following questions: if an employer could choose between a team of two moral agents and a team of two altruists, which team would he/she prefer and why6?

I characterize the optimal contract for a team of equally altruistic agents and a team of equally moral agents and compare them. First, I find that the trade-off between risk-sharing and incentive provision is present, as in the case with standard selfish preferences. However, as intuition would suggest, I find that high-powered incentives are less needed to induce effort as the agents become more concerned about the right thing to do or about each other’s material payoff, and that the principal’s expected profit obtained from the interaction with each team is increasing in the team’s degree of morality or altruism. Second, if efforts are symmetric and could be contracted upon, the principal would be better off hiring a team of altruistic agents over the other ones, for any degrees of morality and altruism, because altruism towards one’s partner reduces the payment necessary to induce participation, one effect that is not present with selfish or moral preferences. On the other hand, when efforts are not observable, which team is going to be preferred depends on the production technology: in particular, if the stochastic production technology displays increasing returns to efforts, the altruistic team is the least expensive to hire. This is a consequence of the different nature of each class of preferences. While altruistic agents derive benefits from increased material payoffs of their fellows, moral agents take satisfaction in doing the right thing. Intuitively, a higher effort under increasing returns drastically increases the expected material payoff of the agents, on which altruism is based. Meanwhile, the choice of the right thing to do depends only on the contract offered by the principal, and not on the production’s underlying technology. Therefore, under increasing returns, altruistic agents possess higher intrinsic motivation to exert the high level of effort, thus demanding a less high-powered contract and saving costs for the principal.

This paper is closely related to the moral hazard literature, in particular to two of its strands: moral hazard in teams and moral hazard with prosocial preferences. References [17,23] characterize the basic results on moral hazard in teams that are used to build the model below7. References [25,26,27,28] study optimal incentive schemes under different prosocial preferences: the first three focus on inequity aversion, while the last models agents exhibiting reciprocity concerns towards each other. References [29,30,31] consider moral hazard in team problems where the agents can monitor one another and, therefore, study the effects of peer pressure on the optimal contract design. Furthermore, [32,33,34] study problems where the agents’ prosocial preferences are private information and give conditions for separating equilibria and self-selection by different types. None of them, however, raises the question of which preferences yield the least cost to the principal.

The analysis below differs from the previous literature in three crucial points: first, it considers homo moralis preferences, which has not, to the best of my knowledge, been done before in a contracting setting, thus presenting a simple environment where the principal can profitably explore idiosyncrasies generated by those and altruistic preferences. Second, it does not allow for monitoring, nor private information about the agents’ preferences, so that I can focus solely on the effect of the prosocial preferences on the optimal contract design. Last, and more importantly, the analysis contrasts the optimal contracts under each class of preferences, and derives conditions under which the principal would prefer hiring one team over the other, therefore providing a rationale for firms to collect soft information on potential employees to compose teams that will minimize the total payments to be made.

I proceed as follows. Section 2 presents the environment, while Section 3 and Section 4 study the optimal contract assuming efforts are contractible and non-contractible, respectively. Section 5 concludes. For the ease of exposition, all proofs are relegated to Appendix C.

2. The Model

I analyze the interaction between a principal and two agents, denoted by $i\in \{A,B\}$. The principal hires the two agents to work on a joint task, which generates revenue $x\in \{x^H,x^L\}$ for the principal, where $x^H>x^L$. Each agent can exert either a low or a high effort level $e_i\in \{0,1\}$. Efforts determine revenues stochastically, according to the following probability distribution:

$$\begin{array}{cc}& \begin{array}{cc}\hspace{1em}{e}_B=1& e_B=0\hspace{1em}\end{array}\\ \begin{array}{c}{e}_A=1\\ e_A=0\end{array}\hfill & \begin{array}{ccc}(& \begin{array}{cc}{p}_2\hspace{1em}& \hspace{1em}{p}_1\\ p_1\hspace{1em}& \hspace{1em}{p}_0\end{array} & )\end{array}\end{array}$$

Throughout, I assume that revenue is never certain and that the probability of achieving a high outcome is increasing in the total effort exerted by the agents: $1>p_2>p_1>p_0>0$.

If effort is costless, the assumption above indicates a preference of the principal for both agents to exert effort. However, effort is costly to each agent; for each $i=A,B$8,

$$c\left(e_i\right)=\left\{\begin{array}{cc}c>0\hfill & \mathrm{if}{e}_i=1,\hfill \\ 0\hfill & \mathrm{if}{e}_i=0.\hfill \end{array}\right.$$

The principal offers the agents contracts $w_i\left(x\right)$, $i=A,B$, specifying payments that will follow each realization of revenues. The principal is assumed to be risk neutral, and his/her payoff is given by:

$$V(x,w_A\left(x\right),w_B\left(x\right))=x-w_A\left(x\right)-w_B\left(x\right).$$

Denote by $\pi (e_i,e_j,w_i\left(x\right))$ the expected material payoff accruing to agent i from the effort choices $(e_i,e_j)$ and wage schedule $w_i\left(x\right)$, for $i,j\in \{A,B\},i\ne j$. I restrict attention to wage schedules pairs ${\mathbf{w}}_i=(w_i^H,w_i^L)$ determining the payments following good and bad realizations of revenues. In what follows, the material payoff function takes the expected additively separable form:

$$\pi (e_i,e_j,{\mathbf{w}}_i)=p_{e_i+e_j}\left[u\left(w_i^H\right)-c\left(e_i\right)\right]+(1-p_{e_i+e_j})\left[u\left(w_i^L\right)-c\left(e_i\right)\right],$$

(1)

where $u:{\mathbb{R}}_{+}\to \mathbb{R}$ is the function that associates the agent’s consumption utility with each amount of money. The dependence of i’s expected material payoff on $e_j$ comes from the effect of the other agent’s effort on the probability distribution of revenues. The agents are risk averse towards wages: $u\left(w\right)$ is assumed to be twice-continuously differentiable, strictly increasing and strictly concave9.

The principal faces either a team consisting of two agents characterized by homo moralis preferences with degree of morality ${\kappa }_i\in [0,1]$, represented by the utility function:

$$U^{HM}(e_i,e_j,{\mathbf{w}}_i,{\kappa }_i)=(1-{\kappa }_i)\pi (e_i,e_j,{\mathbf{w}}_i)+{\kappa }_i\pi (e_i,e_i,{\mathbf{w}}_i),$$

(2)

a team comprised of two altruistic agents, whose preferences are summarized by the utility function:

$$U^{Alt}(e_i,e_j,{\mathbf{w}}_i,{\mathbf{w}}_j,{\alpha }_i)=\pi (e_i,e_j,{\mathbf{w}}_i)+{\alpha }_i\pi (e_j,e_i,{\mathbf{w}}_j),$$

(3)

for ${\alpha }_i\in [0,1]$ and $i,j\in \{A,B\}$, $i\ne j$. Both specifications take the standard selfish preferences as a special case (${\kappa }_i={\alpha }_i=0$), and this will allow comparisons between the results to be presented below and the benchmark moral hazard problem.

As pointed in [20,22], this specification of preferences for altruistic agents gives rise to the behavioral equivalence between homo moralis preferences and altruism for ${\alpha }_i={\kappa }_i$ in many classes of games. With that in mind, I will make the following assumption for the rest of the exposition.

Assumption 1.

${\alpha }_A={\alpha }_B={\kappa }_A={\kappa }_B=\theta$.

Thus, the agents’ utility functions are simplified to:

$$\begin{array}{c}{U}^{HM}(e_i,e_j,{\mathbf{w}}_i,\theta )=(1-\theta )\pi (e_i,e_j,{\mathbf{w}}_i)+\theta \pi (e_i,e_i,{\mathbf{w}}_i),\hfill \end{array}$$

(4)

$$\begin{array}{c}{U}^{Alt}(e_i,e_j,{\mathbf{w}}_i,{\mathbf{w}}_j,\theta )=\pi (e_i,e_j,{\mathbf{w}}_i)+\theta \pi (e_j,e_i,{\mathbf{w}}_j).\hfill \end{array}$$

(5)

The relationship among the three parties unfolds as follows. First, the principal offers each agent a contract ${\mathbf{w}}_{\mathbf{i}}$, which can be either accepted or rejected by the agents. If at least one agent rejects the contract, the game ends, and every party receives his/her own reservation utility. If both agents accept the principal’s offers, they play a normal form game10: both of them must simultaneously and independently choose an effort level, from which revenues will be realized according to the probability distribution given by the production technology above. Payments are made according to the schedules proposed by the firm, and the agents’ payoffs in the normal form game are given by their expected utilities with regard to received wages, efforts and preferences. While each agent’s effort choice is private information, revenues and wages are publicly observable. It is also assumed that the agents’ preferences are common knowledge11.

3. Studying the Benchmark: The Contractible Effort Case

As a starting point, I derive the optimal contract assuming efforts are observable and contractible by the principal, to serve as a benchmark for later results. In what follows, I assume that each agent possesses an outside option that gives him/her utility $\overline{u}\ge 0$ if he/she does not accept the principal’s contract offer. Therefore, agent $i\in \{A,B\}$ is willing to participate in the proposed relationship iff:

$$U(e_i,e_j,{\mathbf{w}}_i,{\mathbf{w}}_j,\theta )\ge \overline{u}.$$

(IR)

As discussed in the previous section, standard selfish preferences are a particular case of both homo moralis and altruistic preferences, and for the ease of exposition, I begin this and the next section by analyzing the optimal contract for that instance. Thus, under contractible efforts, the standard Borch rule:

$$\frac{p(e_i,e_j)}{u^{\prime }\left(w_i^H\right)p(e_i,e_j)}=\frac{1-p(e_i,e_j)}{u^{\prime }\left(w_i^L\right)[1-p(e_i,e_j)]}$$

gives:

$$\begin{array}{}({BR}_S)& \frac{u^{\prime }\left(w_i^H\right)}{u^{\prime }\left(w_i^L\right)}=1,\end{array}$$

which implies $w_i^H=w_i^L=w_i=u^{-1}\left(\overline{u}+c\left(e_i\right)\right)$ for $e_i\in \{0,1\}$. The intuition here is the same as in the classical moral hazard problem with one principal and one agent: if effort is contractible, the principal optimally offers a constant wage schedule remunerating the agent according to his/her reservation utility and the cost of the principal’s desired level of effort.

When the principal faces a team of altruistic agents, he/she solves:

$$\begin{array}{cc}{\max }_{{\mathbf{w}}_A,{\mathbf{w}}_B}\hfill & p(e_A,e_B)\left(x_H-w_A^H-w_B^H\right)+(1-p(e_A,e_B))\left(x_L-w_A^L-w_B^L\right)\hfill \\ s.t.\hfill & \left[p(e_A,e_B)u\left(w_A^H\right)+(1-p(e_A,e_B))u\left(w_A^L\right)-c\left(e_A\right)\right]\hfill \\ \left(I{R}_A\right)& \hfill & +\theta \left[p(e_A,e_B)u\left(w_B^H\right)+(1-p(e_A,e_B))u\left(w_B^L\right)-c\left(e_B\right)\right]\ge \overline{u}\hfill \hfill & \left[p(e_A,e_B)u\left(w_B^H\right)+(1-p(e_A,e_B))u\left(w_B^L\right)-c\left(e_B\right)\right]\hfill \\ \left(I{R}_B\right)& \hfill & +\theta \left[p(e_A,e_B)u\left(w_A^H\right)+(1-p(e_A,e_B))u\left(w_A^L\right)-c\left(e_A\right)\right]\ge \overline{u}\hfill \end{array}$$

An interior solution is characterized by the KKT first-order conditions:

$$\begin{array}{c}-p(e_i,e_j)+{\lambda }_{i}p(e_i,e_j)u^{\prime }\left(w_i^H\right)+{\lambda }_j\theta p(e_i,e_j)u^{\prime }\left(w_i^H\right)=0\hfill \\ -[1-p(e_i,e_j)]+{\lambda }_i[1-p(e_i,e_j)]u^{\prime }\left(w_i^L\right)+{\lambda }_j\theta [1-p(e_i,e_j)]u^{\prime }\left(w_i^L\right)=0,\hfill \end{array}$$

so the Borch rule becomes12:

$$\begin{array}{}({\mathit{BR}}_{\mathit{Alt}})& \frac{u^{\prime }\left(w_i^H\right)}{u^{\prime }\left(w_i^L\right)}=1,\end{array}$$

for any choices of effort $(e_A,e_B)\in {\{0,1\}}^2$ and $i,j\in \{A,B\}$, $i\ne j$. Therefore, if agents are altruistic, the optimal contract under verifiable efforts proposes a constant wage schedule, just as was the case in the benchmark selfish preferences, given by:

$$w^{Alt}=u^{-1}\left(\frac{1}{1+\theta }\overline{u}+c\left(e_i\right)\right),$$

(6)

which is well-defined for all $\theta \in [0,1]$. It is easy to see that for $\theta =0$, this is exactly the same expression as for the optimal contract under verifiable efforts in the benchmark case, while that for any positive degree of altruism is lower than it would be for selfish agents. Intuitively, each altruistic agent recognizes that by participating in the relationship, his partner’s material payoff increases, and therefore, the wage demanded for participation declines when the degree of altruism becomes larger.

Finally, consider the team with homo moralis preferences, in which agent $i\in \{A,B\}$ is willing to participate in the proposed relationship iff:

$$U^{HM}(e_i,e_j,{\mathbf{w}}_i,\theta )=(1-\theta )\pi (e_i,e_j,{\mathbf{w}}_i)+\theta \pi (e_i,e_i,{\mathbf{w}}_i)\ge \overline{u},$$

i.e., iff

$$u\left(w_i^H\right)[(1-\theta )p(e_i,e_j)+\theta p(e_i,e_i)]+u\left(w_i^L\right)[(1-\theta )(1-p(e_i,e_j))+\theta (1-p(e_i,e_i))]-c\left(e_i\right)\ge \overline{u}.$$

Some points are noteworthy. First, as mentioned before, in the case where $\theta =0$, this participation constraint reduces to the usual $\left(IR\right)$ constraint in the benchmark moral hazard problem, since the selfish preference is a particular case of this framework. Second, for $\theta =1$, $U^{\kappa }(e_i,e_j,{\mathbf{w}}_i,1)=\pi (e_i,e_i,{\mathbf{w}}_i)$. In this case, agent i’s choice of effort does not depend on agent j’s effort choice, and choosing $e_i$ becomes an individual decision problem. Third, if $e_i=e_j=e\in \{0,1\}$, the participation constraint collapses into:

$$p(e,e)u\left(w_i^H\right)+(1-p(e,e))u\left(w_i^L\right)-c\left(e\right)\ge \overline{u},$$

Note here that the agents’ degrees of morality are irrelevant, and the participation constraints are exactly the same as those that would be obtained in a symmetric equilibrium in the benchmark moral hazard problem: by imposing $e_i=e_j$, both expected material payoffs terms are identical, and since the utility function is constructed as a convex combination of these functions, the expressions above are obtained.

By Assumption 1, every agent in each team is identical to his/her partner, since the only source of heterogeneity in the general formulation was given by the preferences. Therefore, I will restrict attention to symmetric choices of effort $e_A=e_B$ in the rest of the discussion13.

Proposition 1.

Suppose Assumption 1 holds. Then, there exists $c^{\ast }>0$ such that for all $c\in (0,c^{\ast })$, the principal induces agents in the teams of moral or altruistic agents to exert high effort by means of a constant wage.

This result is not surprising: if efforts are contractible, the principal compensates the agents with a fixed transfer in case they exert the desired level of effort or punishes them if there is a deviation. Furthermore, if the cost of exerting effort is small, then the amount the principal has to transfer back to the agents in order to have an increased chance of obtaining a high realization of revenues is also small and, thus, profitable to implement. Moreover, since I restrict attention to symmetric equilibria, the degree of morality plays no role when I consider a team of homo moralis agents: the compensation schedule and effort choices are exactly the same as those obtained in the benchmark problem.

Now, I can focus on the central question of the paper: given the optimal contracts that induce the desired level of effort, which team should the principal hire?

Proposition 2.

Suppose Assumption 1 holds, efforts are verifiable and the principal wants both agents to make the high effort. For any $\theta \in [0,1]$, the principal prefers hiring the team of altruistic agents over the team of selfish or moral agents.

Intuitively, in situations where someone fails to do the right thing, a moral agent derives part of his/her utility from contemplating what would happen if everyone did the right thing. If both agents do in fact exert high effort, the contemplation in question does not add utility beyond the material utility that the agents thus obtain. By contrast, for altruistic agents, any choice but high effort decreases the material payoff of both agents and, consequently, all of the utility of each altruistic employee. Therefore, intrinsic motivation is larger for altruistic agents, and a team comprised of such employees is less costly for the principal.

4. Moving to the Second Best: Non-Contractible Efforts

Throughout the rest of the exposition, I focus on contracts that induce both agents to participate in the relationship and also exert the high level of effort ($e=1$).

As a benchmark, focus first on standard selfish preferences. If efforts are non-contractible and the principal wishes to induce both agents to exert effort, he/she must solve, for $i,j\in \{A,B\}$, $i\ne j$,

$$\begin{array}{cc}{\max }_{{\mathbf{w}}_A,{\mathbf{w}}_B}\hfill & p_2(x^H-w_A^H-w_B^H)+(1-p_2)(x^L-w_A^L-w_B^L)\hfill \\ s.t.\hfill & p_2\left[u\left(w_i^H\right)-c\right]+(1-p_2)\left[u\left(w_i^L\right)-c\right]\ge p_{1}u\left(w_i^H\right)+(1-p_1)u\left(w_i^L\right)\hfill & \hfill \left(I{C}_i\right)\\ \hfill & p_2\left[u\left(w_i^H\right)-c\right]+(1-p_2)\left[u\left(w_i^L\right)-c\right]\ge \overline{u}.\hfill & \hfill \left(I{R}_i\right)\end{array}$$

Manipulating the incentive compatibility constraint yields:

$$\begin{array}{}\left(I{C}_i\right)& u\left(w_i^H\right)-u\left(w_i^L\right)\ge \frac{c}{p_2-p_1}.\hfill \end{array}$$

By assumption, $c>0$ and $p_2>p_1$. Thus, the incentive compatibility constraint implies a monotonicity constraint on the wages following a good and a bad realization of output, since $u(·)$ is assumed to be strictly increasing. Standard arguments show that both the incentive compatibility and the individual rationality constraints must bind at the optimum, so that the solution to the principal’s problem is a contract ${\mathbf{w}}_S=(w_S^H,w_S^L)$ such that:

$$\begin{array}{cc}\hfill u\left(w_S^L\right)& =\overline{u}-\frac{p_{1}c}{p_2-p_1},\hfill \\ \hfill u\left(w_S^H\right)& =\overline{u}+\frac{(1-p_1)c}{p_2-p_1}.\hfill \end{array}$$

Given the incentive compatibility constraint, it is clear that $\Delta w_S\equiv w_S^H-w_S^L>0$.

Of course, if the principal wishes to induce the agents not to exert effort, a constant wage schedule $w^H=w^L=w=u^{-1}\left(\overline{u}\right)$ would be optimal. Comparison of the principal’s profits when agents exert effort and shirk show that the former is preferred by the employer for any $c\le {\overline{c}}_S$, $0<{\overline{c}}_S<c^{\ast }$.

Under altruistic preferences for the agents, the principal’s problem is:

$$\begin{array}{cc}{\max }_{w^H,w^L}\hfill & p_2(x^H-2w^H)+(1-p_2)(x^L-2w^L)\hfill \\ \left(IR\right)& s.t.\hfill & (1+\theta )[p_{2}u\left(w^H\right)+(1-p_2)u\left(w^L\right)-c]\ge \overline{u}\hfill \hfill & (1+\theta )\left[p_{2}u\left(w^H\right)+(1-p_2)u\left(w^L\right)-c\right]\ge \hfill \\ \left(IC\right)& \hfill & \left[p_{1}u\left(w^H\right)+(1-p_1)u\left(w^L\right)\right]+\theta \left[p_{1}u\left(w^H\right)+(1-p_1)u\left(w^L\right)-c\right].\hfill \end{array}$$

Rewrite the incentive compatibility constraint as:

$$u\left(w^H\right)-u\left(w^L\right)\ge \frac{c}{(1+\theta )(p_2-p_1)},$$

(7)

and notice that the right-hand side is strictly decreasing in the degree of altruism $\alpha$. The intuition behind this is the tradeoff between explicit and intrinsic incentives. Indeed, as the agent cares less about his/her own material payoff relative to that of his/her teammate, the intrinsic incentive derived from an increase in the probability of a high realization of output (and a consequent increase in the expected material benefit of his/her partner) becomes larger than the explicit incentives given by a high powered contract in inducing the agent to exert the high level of effort.

The proposition below characterizes the optimal contract14.

Proposition 3.

Suppose Assumption 1 holds. There exists ${\overline{c}}_{Alt}>{\overline{c}}_S$ such that, for all $c<{\overline{c}}_{Alt}$, it is optimal for the principal to induce both altruistic agents to exert effort, $e_A=e_B=1$, by means of a contract ${\mathbf{w}}_{\mathbf{Alt}}^{\ast }=(w_{Alt}^H,w_{Alt}^L)$ such that:

$$\Delta w_{Alt}\equiv w_{Alt}^H-w_{Alt}^L\le \Delta w_S$$

$\forall \theta \in [0,1]$, with strict inequality for any $\theta >0$.

Close inspection of the incentive compatibility constraint shows that any contract that would induce a selfish agent to exert the high effort would also induce an altruistic employee to do the same. Furthermore, for any given contract, an increase in $\theta$ would increase the utility of each agent. Hence, the principal can profit by reducing both wages15. This argument is formally stated below.

Corollary 1.

Suppose Assumption 1 holds. Then, the principal’s expected profits are strictly increasing in θ.

Last, I consider homo moralis preferences. The principal must choose wage vectors ${\mathbf{w}}_A,{\mathbf{w}}_B$ to solve:

$$\begin{array}{cc}{\max }_{{\mathbf{w}}_A,{\mathbf{w}}_B}\hfill & p_2\left(x_H-w_A^H-w_B^H\right)+(1-p_2)\left(x_L-w_A^L-w_B^L\right)\hfill \\ s.t.\hfill & (1-\theta )\left[p_2(u\left(w_i^H\right)-c)+(1-p_2)(u\left(w_i^L\right)-c)\right]\hfill \\ \hfill & +\theta \left[p_2(u\left(w_i^H\right)-c)+(1-p_2)(u\left(w_i^L\right)-c)\right]\ge \hfill \\ \hfill & (1-\theta )\left[p_{1}u\left(w_i^H\right)+(1-p_1)u\left(w_i^L\right)\right]\hfill \\ \left(I{C}_i\right)& \hfill & +\theta \left[p_{0}u\left(w_i^H\right)+(1-p_0)u\left(w_i^L\right)\right]\hfill \hfill & (1-\theta )\left[p_2(u\left(w_i^H\right)-c)+(1-p_2)(u\left(w_i^L\right)-c)\right]\hfill \\ \left(I{R}_i\right)& \hfill & +\theta \left[p_2(u\left(w_i^H\right)-c)+(1-p_2)(u\left(w_i^L\right)-c)\right]\ge \overline{u}\hfill \end{array}$$

for $i=A,B$. Note that the individual rationality constraint can be rewritten in the simpler form:

$$p_{2}u\left(w_i^H\right)+(1-p_2)u\left(w_i^L\right)-c\ge \overline{u},$$

since, in equilibrium, the principal’s offer induces the symmetric effort choice $e_A=e_B=1$.

The incentive compatibility constraint also simplifies to:

$$\begin{array}{c}{p}_{2}u\left(w_i^H\right)+(1-p_2)u\left(w_i^L\right)-c\ge \hfill \\ (1-\theta )\left[p_{1}u\left(w_i^H\right)+(1-p_1)u\left(w_i^L\right)\right]+\theta \left[p_{0}u\left(w_i^H\right)+(1-p_0)u\left(w_i^L\right)\right].\hfill \end{array}$$

The right-hand side of this inequality highlights an interesting fact: a positive degree of morality implies the agent internalizes the cost of choosing a low effort by evaluating what would happen if the other agent also were to make the same decision. This is very different in nature to how an altruistic agent evaluates any deviation: while the latter considers only the effects of his/her own deviation on his/her own material payoff and on his/her partner’s, the former would consider the effect of the same deviation being made by his/her partner on his/her own payoff. Besides, by force of the assumptions presented above, further manipulation of $\left(I{C}_i\right)$ yields:

$$u\left(w_i^H\right)-u\left(w_i^L\right)\ge \frac{c}{(p_2-p_1)+\theta (p_1-p_0)},$$

(8)

where $\frac{c}{(p_2-p_1)+\theta (p_1-p_0)}>0$. Because of the strict concavity of $u(·)$, the incentive compatibility constraint for moral agents also implies a monotonicity condition on the optimum compensation schedules offered by the principal, even when the agents display the highest degree of morality. This last remark implies that the intrinsic incentives of the most moral agent are not sufficiently large to overcome the need to provide him/her with explicit incentives to exert the high level of effort.

Proposition 4.

Suppose Assumption 1 holds. There exists ${\overline{c}}_{HM}>{\overline{c}}_S$ such that, for all $c<{\overline{c}}_{HM}$, it is optimal for the principal to induce both moral agents to exert effort, $e_A=e_B=1$, by means of a contract ${\mathbf{w}}_{\mathbf{HM}}^{\ast }=(w_{HM}^H,w_{HM}^L)$, such that:

$$\Delta w_{HM}\equiv w_{HM}^H-w_{HM}^L\le \Delta w_S$$

$\forall \theta \in [0,1]$, and strict inequality for $\theta >0$.

The intuition behind the monotonicity constraint is the same as in the benchmark model: if wages following a low realization of revenues were larger than their counterpart after a good realization, then agents would prefer to exert low effort in order to receive this higher compensation and save in the cost of exerting effort.

The novelty in the results relates to how the compensation schedules vary with respect to the degree of morality $\theta$. Keeping in mind that $u^{\prime }>0$, one can see that as $\theta$ increases, the right-hand side of $\left(I{C}_i\right)$ becomes ever smaller, albeit positive. This implies that the gap in wages following good and bad realizations of revenues must decrease, since the incentive compatibility constraint binds, but monotonicity still holds. Intuitively, the principal can reduce the compensation over high realizations of revenues given to an agent who is very concerned about doing the right thing. However, at the same time, he/she must increase wages after bad outcomes in order to satisfy the participation constraint.

Because of this diminishing wage gap, intuition would suggest that the first-best result is obtained for a sufficiently high degree of morality. However, this is not the case. To see this, take $\theta =1$, where agent i’s preferences are purely Kantian, and thus, his/her utility is completely characterized by the expected material payoff $\pi (e_i,e_i)$. Although the participation constraint does not vary with the agent’s degree of morality16, the same is not true for the incentive compatibility constraint. Now, when considering the pros and cons of a deviation in terms of effort choice, agent i internalizes what would happen if agent j were to do the same. Specifically, this entails a reduction in the probability of the good revenue being realized from $p_2$ to $p_0$, instead of the reduction to $p_1$ in the selfish term. This internalization is reflected in the $\left(I{C}_i\right)$ constraint, which becomes:

$$u\left(w_i^H\right)-u\left(w_i^L\right)=\frac{c}{p_2-p_0}>0.$$

The denominator on the right-hand side is exactly the difference in the probabilities discussed above. Taking $\theta =1$ makes the incentive compatibility constraint for a team of moral agents as easy to satisfy as possible, but it still binds, thus pushing the optimal contract away from the first-best one (constant wage schedule).

Given this behavior of wage schedules with respect to the degree of morality, a natural question to be asked is whether the principal is better off with highly moral agents or not. The answer is unconditional and presented in the following result.

Corollary 2.

The principal’s expected profit is strictly increasing in θ.

Corollary 2 contrasts with the contractible effort case, where the principal’s profits were identical when hiring a team of selfish agents or a team of moral agents, for any degree of morality the last would display. Mathematically, the result is a consequence of the individual rationality constraints being identical in both cases, while the incentive compatibility constraint has a smaller right-hand side under moral agents than under selfish ones. Intuitively, the principal exploits the agents’ morality, as he/he did with altruistic employees, as well, to induce high effort by means of less high-powered incentives, while inducing participation with a slightly increased payment after a bad realization of output. Thus, one concludes that the expected savings in wages after a good realization made by the principal by choosing a high morality agent offsets the expected increase in payments after low revenues.

One remark is in order here. Because of the assumption that $1>p_2>p_1>p_0>0$ and the monotonicity condition implied by the incentive compatibility constraints for each preferences, it is the case that $U(0,1,\mathbf{w};\theta )\ge U(0,0,\mathbf{w};\theta )$, where $\mathbf{w}$ is the optimal contract offered by the principal. Thus, using the $\left(IC\right)$ constraints again, I have that $U(1,1,\mathbf{w};\theta )\ge U(0,0,\mathbf{w};\theta )$, so the agents have no incentives to jointly deviate to shirking. The same is also true for altruistic agents.

So far, I have showed that the principal can attain higher profits by exploiting the agents’ morality or altruism, thus reducing high-powered explicit incentives in the optimal contract in such a way that participation and incentives to exert high effort are still satisfied. Therefore, from the employer’s perspective, knowing which class of preferences demands the least amount of explicit incentives is crucial. Lemma 1 tells us that the answer to that question depends on the stochastic production technology.

Lemma 1.

Under Assumption 1, $\left[u\left(w_{HM}^H\right)-u\left(w_{HM}^L\right)\right]-\left[u\left(w_{Alt}^H\right)-u\left(w_{Alt}^L\right)\right]$ has the same sign as $\left(p_2-p_1\right)-\left(p_1-p_0\right)$.

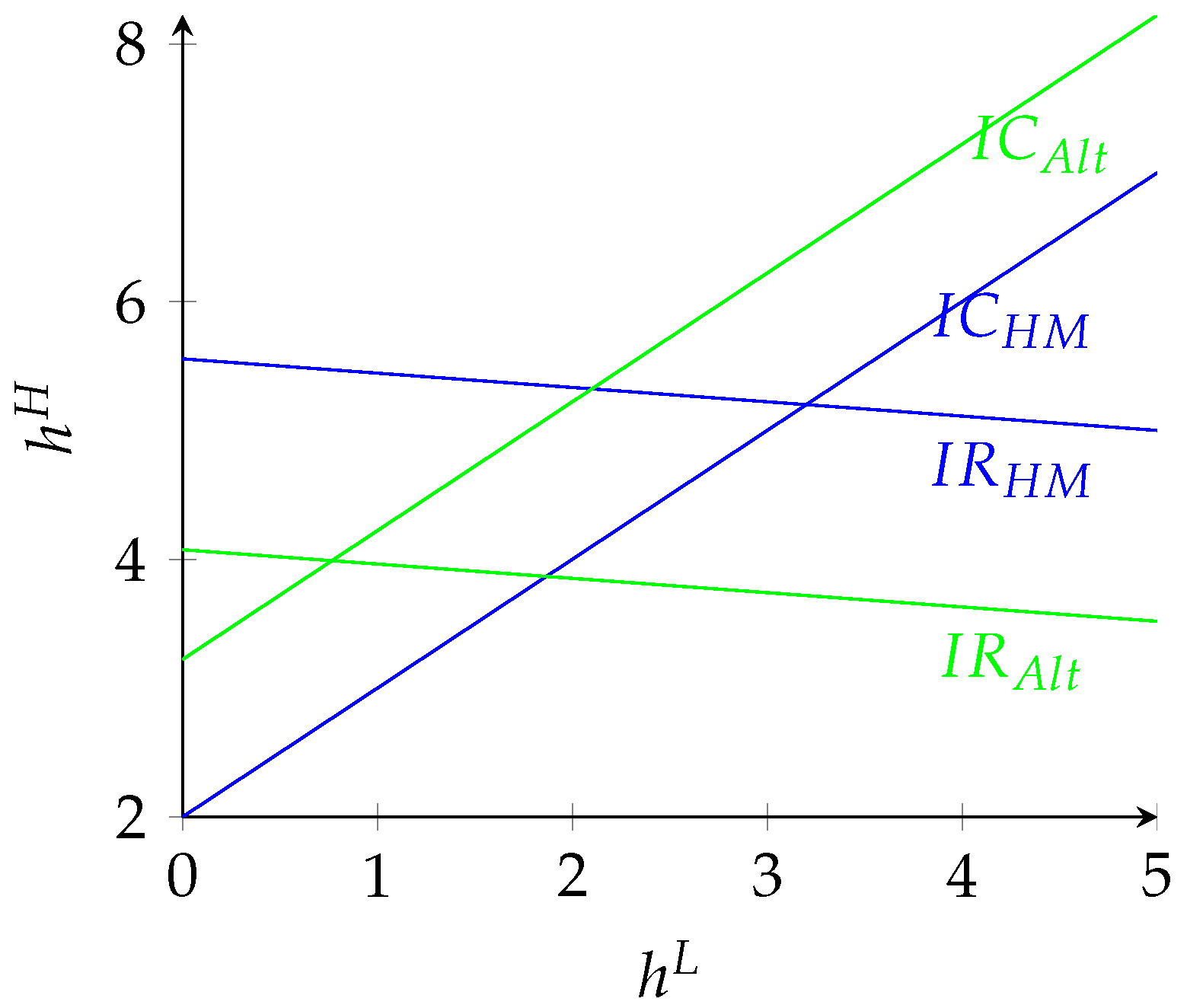
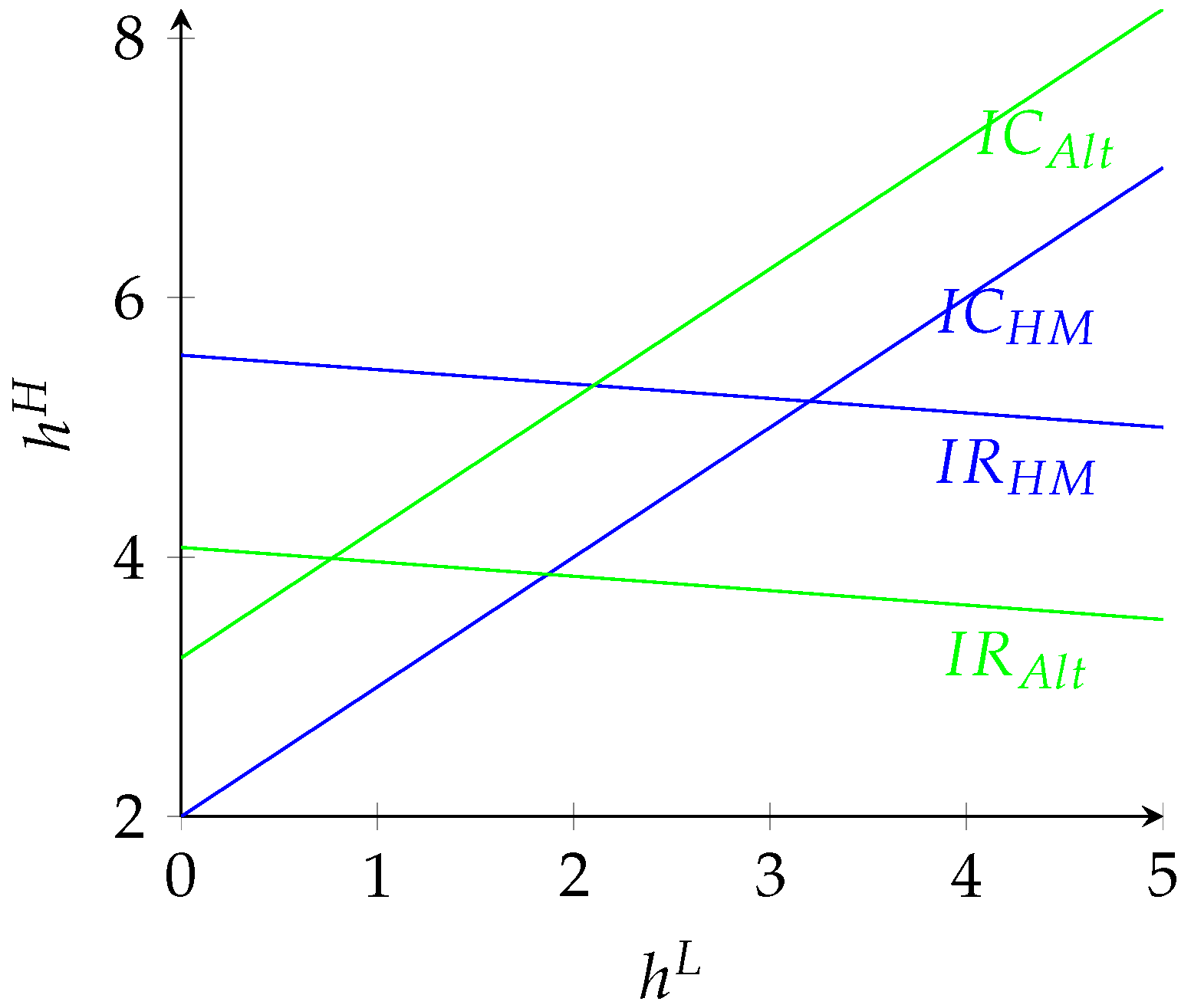
In other words, if the stochastic technology presents increasing returns on aggregate efforts, the optimal contract under homo moralis preferences is (weakly) more high-powered than its counterpart under altruism when $\kappa =\alpha$: any contract inducing moral agents to exert high effort would do the same to altruistic employees. The converse is true if the technology has decreasing returns on efforts. This can be seen in Figure 1. The middle (green) line represents the incentive compatibility constraint for altruistic agents, whose format is not affected by the production technology. The top (red) and the bottom (blue) lines are the graphic representations of the $\left(IC\right)$ constraint for moral agents when $p_2-p_1>p_1-p_0$ and $p_2-p_1<p_1-p_0$, respectively17.

Given the result above, one would expect that the principal’s expected payoff will be uniformly higher if the agents are altruistic rather than moral when the production technology presents increasing returns to efforts, while the opposite would be true if decreasing returns are present. The flaw with such a logic is not considering the effects of the binding individual rationality constraints, which implied under contractible efforts that the team of altruistic agents was always the least expensive to hire. In particular, remember that for altruistic agents, the outside option $\overline{u}$ is divided by $1+\theta$ in the participation constraint, a factor that is not present under selfish and moral preferences. This implies that $w_{Alt}^L$ should also be smaller than $w_{HM}^L$18. However, the principal has clear preferences over the composition of the team, and the result below precisely states when one team is preferred over the other.

Theorem 1.

Assume the principal offers contracts ${\mathbf{w}}_{HM}$ and ${\mathbf{w}}_{Alt}$ to homo moralis and altruistic agents, respectively, inducing them to exert the high level of effort. Furthermore, assume Assumption 1 holds. Then, if the stochastic production technology exhibits:

1.

increasing returns to efforts ($p_2-p_1\ge p_1-p_0$), the principal is better off hiring a team of altruistic agents over a team of moral agents,

2.

decreasing returns to efforts ($p_2-p_1<p_1-p_0$) and

• the outside option is zero ($\overline{u}=0$), the principal prefers a team of moral agents; or
• the outside option is positive, and the degree of morality is sufficiently low ($\overline{u}>0$, $\kappa \to 0$); the principal prefers a team of moral agents only if $p_2>{\overline{p}}_2\in (0,1)$.

Under increasing returns to efforts, an altruistic team is less expensive for the principal because of two reasons. First, the wage that must be paid after a bad realization of output is smaller than its counterparts under selfish or moral preferences, and this is a consequence of the fact that the former’s consideration with regards to the payoff of his/her partner slackens the participation constraint. On he other hand, such a concern also slackens the incentive compatibility constraint in this case, because exerting efforts drastically increases the probability of being successful, thus providing implicit incentives for the altruistic worker to exert effort and requiring a less high-powered contract to be proposed by the employer.

Such a difference in the intrinsic incentives to exert effort disappear when the production technology has constant returns, so that the power of the contract remains the same for both teams. However, it is still the case that the principal exploits the fact that altruistic agents derive utility from each other’s material payoff and can thus pay them less.

The third case, with decreasing returns to efforts, is the most interesting, because the preference of the principal results from the net effect of two opposing forces. While it is still true that $w_{Alt}^L\le w_{HM}^L$, Lemma 1 states that now, the power of the contract required by moral agents is smaller than the one for altruistic agents. In the range where such a reduction is the most drastic, the principal will prefer the team of moral agents rather than altruistic ones. The first condition for this to happen is that the probability of a success when both agents are exerting effort is sufficiently high, as can be seen from the incentive compatibility constraints. The second condition is that either the outside option for the agents is zero or if it is positive, the degree of morality or altruism is close to zero. If both cases, the participation constraints for moral and altruistic agents become arbitrarily close (identical if $\overline{u}=0$) so that the exploitability of altruistic preferences, described in the preceding paragraph, becomes small, and the principal profits by hiring the agents demanding the least powered contracts: the moral agents in this case.

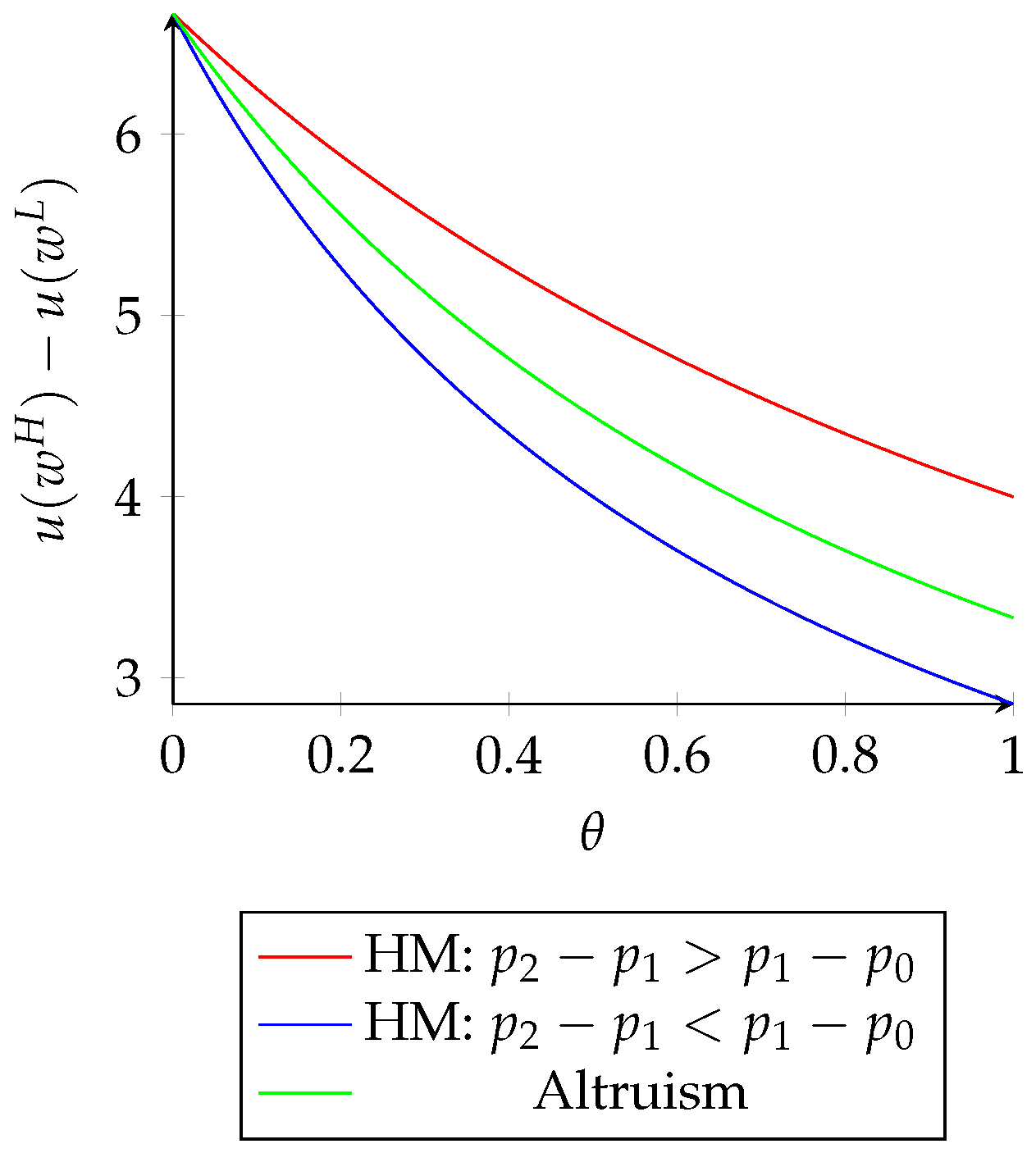
Figure 2a–c provides an example of Theorem 1 for $u\left(w\right)=\sqrt{w}$. Figure 2a represents the case where the production technology exhibits increasing returns to efforts. With the exception of $\theta =0$, where both teams are identical to the selfish agents, the principal’s profit is higher with a team of altruistic agents ($V^{Alt}$) than with a team of moral agents ($V^{HM}$).

Figure 2b exemplifies the case with decreasing returns to efforts, the zero outside option for the agents and a high probability of success if both agents exert effort (namely, I set $p_2=0.9$). As Theorem 1 states, under these conditions, $V^{HM}\left(\theta \right)\ge V^{Alt}\left(\theta \right)$ for all equal degrees of morality and altruism.

Finally, Figure 2c plots the ratio $V^{HM}/V^{Alt}$ for decreasing returns to efforts and $\overline{u}=0.2$. Contrary to the previous case where $\overline{u}=0$, the difference in the participation constraints for moral and altruistic agents makes it unprofitable for the employer to hire the moral team if $\theta$ becomes larger, since the decrease in $w_{Alt}^L$ would be, in expected terms, sufficient to compensate the savings related to the power of the contract. This is represented by the region in the figure in which $V^{HM}/V^{Alt}\le 1$.

Therefore, a rationale in terms of the principal’s expected profits is given for trying to sort employees with respect to their preferences. If the production technology exhibits increasing returns with respect to efforts, the principal’s choice is straightforward: always choose to employ altruistic agents. However, if the condition does not hold, employing moral individuals may lead to higher profits in comparison to both altruistic and purely selfish agents.

5. Concluding Remarks

This paper presents a comparison between the optimal contracts offered to teams of agents, who may be characterized by either homo moralis preferences or altruism towards each other. These contracts were explored in situations where the teams have only two agents with binary choices of efforts, affecting stochastically the revenues accrued by the principal.

Under contractible efforts, I show that altruistic agents are more exploitable by the principal, in the sense that the employers need to pay a smaller wage to induce the participation of the those agents when compared to the case where he/she would hire a team of selfish or moral employees. When efforts are no longer contractible, this exploitability also shows up for moral agents, and I show that the larger the degree of altruism or morality displayed by the members of each team, the higher the expected profits for the principal. Then, the natural question is which class of preferences would require smaller wages to exert effort and participate in the contractual relationship?

The main finding is that the principal obtains a higher expected profit hiring a team composed of moral agents under restrictive conditions: first, the stochastic technology exhibits decreasing returns with respect to efforts; second, the outside option of the agents yields zero utility; or third, the degree of morality is sufficiently low.

It is noteworthy that even in such a simple environment, prosocial preferences affect the contractual design, by adding a third channel to the traditional trade-off between risk-sharing and incentive provision. In effect, the principal will be better off employing a team of either altruistic or moral agents instead of a team composed solely of selfish employees, since a higher degree of morality and altruism decreases the amount of explicit incentives provided by the optimal contracts to induce the agents to exert effort. However, this additional channel is not enough to completely extinguish the need for explicit incentives even when the agents are purely moral or altruistic. Because it is more costly to the principal to hire a team of selfish agents, the exploitability of prosocial preferences can thus explain the costly acquisition of job applicants’ soft information in the labor market.