The Monty Hall Problem as a Bayesian Game

Abstract

This paper formulates the classic Monty Hall problem as a Bayesian game. Allowing Monty a small amount of freedom in his decisions facilitates a variety of solutions. The solution concept used is the Bayes Nash Equilibrium (BNE), and the set of BNE relies on Monty’s motives and incentives. We endow Monty and the contestant with common prior probabilities (p) about the motives of Monty and show that, under certain conditions on p, the unique equilibrium is one in which the contestant is indifferent between switching and not switching. This coincides and agrees with the typical responses and explanations by experimental subjects. In particular, we show that our formulation can explain the experimental results in Page (1998), that more people gradually choose switch as the number of doors in the problem increases.

1. Introduction

The “Monty Hall” problem is a famous scenario in decision theory. It is a simple problem, yet people confronted with this dilemma almost overwhelmingly seem to make the incorrect choice. This paper provides justification for why a rational agent may actually be reasoning correctly when he or she makes this ostensibly erroneous choice.

This notorious problem arrived in the public eye in the form of a September, 1990 column published by Marilyn vos Savant in Parade Magazine1 (vos Savant (1990) [5]). vos Savant’s solution drew a significant amount of ire, as people vehemently disagreed with her answer. The ensuing debate can be recounted in several subsequent articles by vos Savant [6,7], as well as in a 1991 New York Times article by James Tierney [8]. The problem draws its name from the former host of the TV show “Let’s Make a Deal”, Monty Hall, and is formulated as follows:

There is a contestant (whom we shall call Amy (A)) on the show and its famous host Monty Hall (M). Amy and Monty are faced on stage by three doors. Monty hides a car behind one of the doors at random, and a goat behind the other two doors. Amy selects a door, and then, before revealing to Amy the outcome of her choice, Monty opens one of the other unopened doors to reveal a goat. Amy is then given the option of switching to the other unopened door, or of staying on her current choice. Should Amy switch?

There are a significant number of papers in both the economics and psychology literatures that look at the typical person’s answers to this question. The overwhelming result presented in these bodies of work, including [9,10,11], is that that subjects confronted with the problem solve it incorrectly and fail to recognize that Amy should switch. The typical justification put forward by the subjects is that the likelihood of success if they were to switch doors is the same as if they were to stay with their original choice of door. This mistake is often cited as an example of the equiprobability bias heuristic ([12,13,14]) as described in Lecoutre (1992) [15]. Other possible causes for this mistake mentioned in the literature are the “illusion of control” ([10,16,17]), the “endowment effect” ([9,10,11,14,18]), or a misapplication of Laplace’s “principle of insufficient reason” ([10]).

It is important to recognize; however, that in the scenario presented above, as in vos Savant’s columns, Selvin’s articles, and many other formulations of the problem, it is unclear whether Monty must reveal a goat and allow Amy to switch. However, their subsequent analysis and solutions imply that this is an implicit condition on the problem.

One of the first properties of the model formulated by our paper is that the game show host is also a strategic player, in addition to the game’s contestant. Indeed this agrees with the New York Times [8] article, in which the eponymous host Monty, himself, notes that he had a significant amount of freedom. To model this problem, we will formulate it as a non-cooperative game, as developed by Nash, von Neumann and others. There have been several other papers that model this scenario as a game: notably by Fernandez and Piron (1999) [19], Mueser and Granberg (1999) [20], Bailey (2000) [21], and Gill (2011) [22]. The most similar of these works to this paper is [19]. There, Fernandez and Piron also note Monty’s freedom to choose, and in fact allow him to manipulate various behavioral parameters of Amy’s. In addition to giving Monty this wide array of strategy choices, the authors also introduce a third player, “the audience”. Monty’s objective as a host is to make the situation difficult for the audience to predict, and this incentive, combined with Monty’s menu of options, allow for a variety of equilibria.

In this paper, we are able to generate our results simply by giving Monty the option to allow or prevent Amy from switching choices. We note that Monty’s incentives and personality matter, and show that his disposition towards Amy’s success affects the equilibria of the game. We model this by considering a game of Incomplete Information2. Both Monty and Amy share a common prior about whether Monty is “sympathetic” or “antipathetic” towards Amy, but only Monty sees the realization of his “type” before the game is played. Using this, we are able to show that there may be an equilibrium where it is not optimal for Amy to always switch from her initial choice following a revelation by Monty. There is an equilibrium under which Amy’s payoffs under switching and staying are the same (as people are wont to claim). We also generalize the three door problem to one with n doors, and show that our formulation agrees with the experimental evidence in Page (1998) [24]. As the number of doors increases, the range of prior probabilities in support of an equilibrium where Amy always switches grows. Concurrently, as the number of doors increases, the range of prior probabilities under which there is an equilibrium where Amy does not always switch, shrinks. Moreover, there is a cutoff number of doors, beyond which the only equilibrium is the one where Amy always switches.

Furthermore, in Appendix B we show that the results established in this paper are not dependent on the specific assumptions made about Monty’s preferences. We relax our original conditions on Monty’s preferences and endow him with a continuum of types which model a much broader swath of possible motives. As before, the size of the set of prior probabilities in support of the “always switch” equilibrium increases as the number of doors increases. Furthermore, the size of the set of priors in support of an equilibrium where Amy does not always switch is decreasing in the number of doors.

There are several contributions made by this paper. Unlike other papers in the literature, this paper allows for uncertainty about Monty’s motives. In contrast to our formulation, the modal construction of the Monty Hall scenario is as a static zero-sum game (as in [21,22]), with no uncertainty whatsoever about Monty’s motives. While the paper by Mueser and Granberg (1999) [20] compares briefly the Nash Equilibria in games where Monty is respectively neutral and antipathetic, they assume that his preferences are common knowledge in each. In contrast to [20], we assume only that the contestant has a set of priors over Monty’s motives.

We also examine how the number of doors affects the equilibria in the problem. Experimental results in [24] show that the number of doors in the scenario affects play, and this paper is the first to show how these results can arise naturally as equilibrium play by rational agents. In addition, our formulation of the scenario in Appendix B captures a variety of Monty’s possible preferences beyond the simple sympathetic/antipathetic dichotomy, and we show that our results hold even in this general environment.

The structure of this paper is as follows. In Section two, we formalize the problem as one where Monty may choose whether to reveal a goat and examine the cases where Monty derives utility from Amy’s success or failure, respectively. In the next section, we further extend the model by allowing there to be uncertainty about whether Monty is sympathetic or antipathetic. We also then extend this analysis beyond the three door case to the more general n door case. Finally, in Appendix B we further generalize the model by allowing for a continuum of Montys, each with different preferences.

2. The Model

We consider the onstage scenario, where Monty (M) hides two goats and one car among three doors and Amy (A) must then select a door. Suppose that following the initial selection of a door by Amy, Monty has two choices:

• Reveal a goat behind one of the unselected doors, what we shall call “reveal” $\left(r\right)$.
• Not reveal a goat $\left(h\right)$.

Amy has different feasible strategies, depending on what Monty’s choice is: If Monty reveals a goat, then Amy may

• Switch $\left(s\right)$.
• Not switch (or keep) $\left(k\right)$.

If Monty does not reveal (choice h), then Amy has no option to switch choices and must keep her original selection. This is the same assumption as is made in [19]. Note that few papers in the literature address Monty’s protocol if revealing a goat and allowing Amy to switch is not mandatory. Moreover, as noted in [20], whether Monty must reveal a goat and allow Amy to switch is itself ambiguous in a significant number of papers (as well as in the column published by vos Savant and various popular retellings of the problem).

To simplify the analysis, we impose that Monty must hide the car completely at random. Consequently, we can model this situation as a game of Incomplete Information:

Amy’s initial pick can be modeled as a random draw or a “move of nature”. With probability $1/3$, her first pick is correct and with probability $2/3$, it is incorrect. Monty is able to observe the realization of this draw prior to making his decision and see whether or not Amy is correct. Thus, this game can be modeled as a sequential Bayesian game, where Amy and Monty have the common prior ${\theta }_1=1/3$ and ${\theta }_2=2/3$. We can rephrase this by saying that Amy’s initial pick determines Monty’s type, which is given by the binary random variable $\theta$,

$$\begin{array}{cc}\hfill \theta & \in \left\{{\theta }_1,{\theta }_2\right\}\hfill \\ \hfill \mathrm{Pr}(\theta ={\theta }_1)& =\frac{1}{3},\mathrm{Pr}(\theta ={\theta }_2)=\frac{2}{3}\hfill \end{array}$$

(1)

The Monty of type ${\theta }_1$ is the Monty in the scenario where Amy has made the correct initial guess, and conversely, the Monty of type ${\theta }_2$ is the one where Amy was incorrect initially. Monty knows his type, but Amy only knows the distribution over types. That is, Monty is able to view the “draw” realization, i.e., whether or not Amy is correct, before choosing his action. Amy cannot observe the outcome and has only her prior to go by. We may formally write the sets of strategies for Amy and type ${\theta }_i$ of Monty as $S_A$3 and $S_M$, respectively:

$$\begin{array}{cc}\hfill S_A& =\left\{s,k\right\}\hfill \\ \hfill S_M& =\left\{r,h\right\}\hfill \end{array}$$

(2)

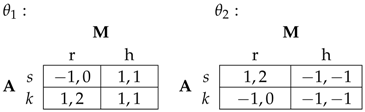
Before going further, we need to specify the two players’ preferences in this strategic interaction. Naturally, Amy prefers to end up with the car than with the goat4. Assigning Amy to be player 1 and Monty, player 2, we write this formally as:

$$\begin{array}{cc}\hfill u_A(k,r)=u_A(k,h)=u_A(s,h)& >u_A(s,r)\mathrm{for}\theta ={\theta }_1\hfill \\ \hfill u_A(s,r)>u_A(k,r)=u_A(k,h)& =u_A(k,r)\mathrm{for}\theta ={\theta }_2\hfill \end{array}$$

(3)

It is reasonable to suppose that Monty would slightly prefer to reveal a goat5, and thereby give Amy the option of switching, than to not reveal a goat, and prevent Amy from switching. However, we also endow Monty with preferences over Amy’s success or failure (he cares whether Amy ultimately ends up with a car or goat), and moreover, we stipulate that these preferences are in a sense stronger than Monty’s desire to reveal. Given Amy’s choice of keep, Monty would always prefer to allow her to switch (since the outcome of Amy’s choice would not change):

$$u_M(k,r)>u_M(k,h)$$

(4)

However, given Amy’s choice of switch, Monty would prefer to allow her to switch (choice r) only if Amy switching would result in Monty’s desired outcome.

We now divide the analysis into two cases:

Case 1:

This is what we will call the Sympathetic Case: Monty and Amy’s preferences are aligned in the sense that all else equal Monty would prefer that Amy be correct rather than incorrect.

Case 2:

We call this the Antipathetic Case: Here, all else equal, Monty would prefer that Amy be incorrect. Their preferences are not aligned.

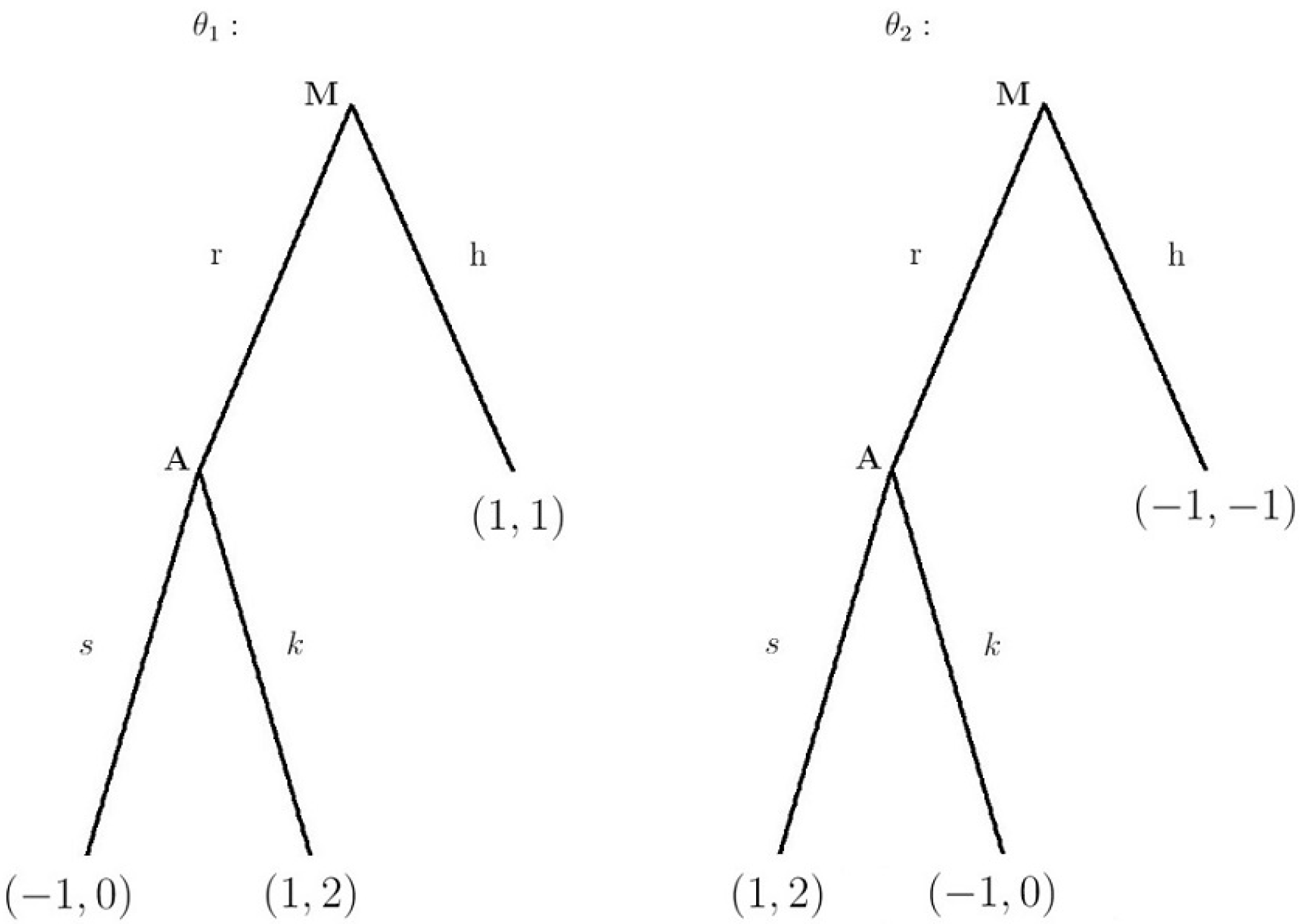
2.1. Case 1, Sympathetic

We stipulate that all parameters of the game are common knowledge, including Monty’s preferences; i.e., it is common knowledge that Monty is a sympathetic player. As the sympathetic player, Monty would prefer that Amy be successful. Consequently, in the state of the world where Amy’s initial guess is correct (${\theta }_1$), Monty would prefer that Amy not switch. Likewise, in the state of the world where Amy guesses wrong initially (${\theta }_2$), Monty would rather Amy switch. We write explicitly

$$\begin{array}{c}For\theta ={\theta }_1,u_M(s,j)\le u_A(k,j),j\in \left\{r,h\right\}\hfill \\ For\theta ={\theta }_2,u_M(k,j)\le u_A(s,j),j\in \left\{r,h\right\}\hfill \end{array}$$

(5)

As above, Amy’s and Monty’s sets of strategies $S_A$ and $S_M$ are

$$\begin{array}{cc}\hfill S_A& =\left\{s,k\right\}\hfill \\ \hfill S_M& =\left\{r,h\right\}\hfill \end{array}$$

(6)

and in Figure 1 we present the game in extensive form.

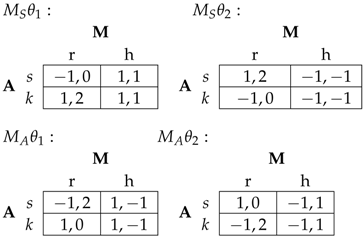
The corresponding payoff matrix is:

Lemma 1.

The unique Bayes-Nash Equilibrium is in pure strategies6; it is

$$(s,(h,r\left)\right)$$

(7)

Amy always switches, type ${\theta }_1$ of Monty chooses not to reveal, and type ${\theta }_2$ of Monty chooses to reveal. It is clear that following Monty’s choice, Amy knows exactly whether her initial choice was correct. Monty’s choice completely reveals to Amy the state of the world.

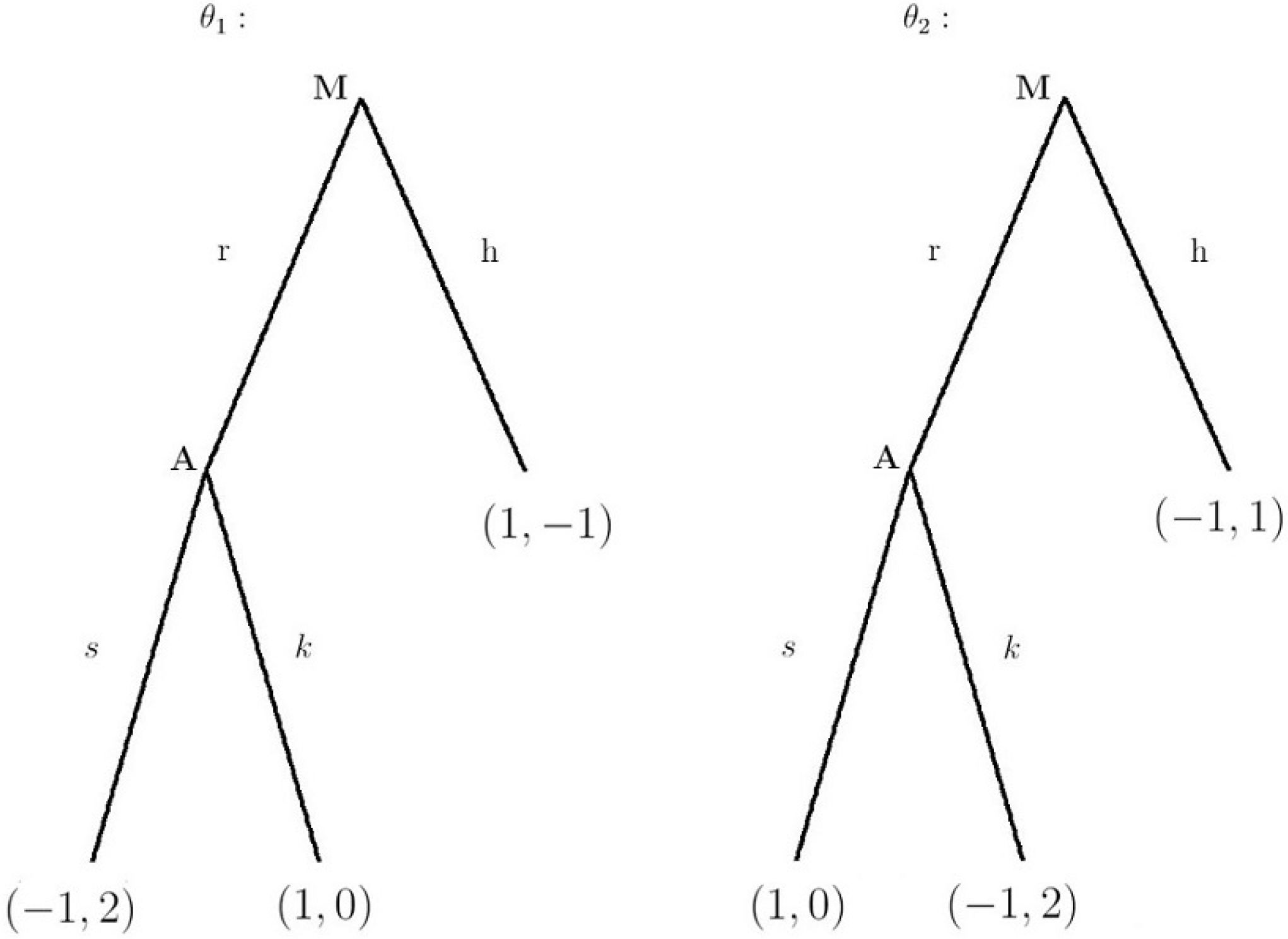
2.2. Case 2, Antipathetic

As in Case 1 (Section 2.1), Monty’s preferences are common knowledge; i.e., that he is antipathetic towards Amy. In contrast to Monty’s preferences as a sympathetic player (Section 2.1), as an antipathetic player, Monty would prefer that Amy be unsuccessful. Accordingly, in the state of the world where Amy’s initial guess is correct (${\theta }_1$), Monty would prefer that Amy switch. Consonantly, in the state of the world where Amy guesses wrong initially (${\theta }_2$), Monty would rather Amy not switch. We write explicitly

$$\begin{array}{c}For\theta ={\theta }_1,u_M(k,j)\le u_A(s,j),j\in \left\{r,h\right\}\hfill \\ For\theta ={\theta }_2,u_M(s,j)\le u_A(k,j),j\in \left\{r,h\right\}\hfill \end{array}$$

(8)

Defining Amy and Monty’s strategies as before, in Figure 2 we present the game in extensive form.

The corresponding payoff matrix is:

Interestingly, there are no pure strategy Bayes-Nash Equilibria.

Lemma 2.

The unique BNE is in mixed strategies7; it is:

$$\left(\underset{A}{\mathrm{Pr}}(s)=\frac{1}{2},(r,\underset{M}{\mathrm{Pr}}(r)=\frac{1}{2})\right)$$

(9)

Amy switches half the time, while type ${\theta }_1$ of Monty chooses to reveal, and type ${\theta }_2$ of Monty chooses to reveal half of the time. Using Bayes’ law, we write:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left(Correct\right|Reveal)& =\frac{\mathrm{Pr}\left(Reveal\right|Correct\left)\mathrm{Pr}\right(Correct)}{\mathrm{Pr}\left(Reveal\right)}=\frac{1(1/3)}{1(1/3)+(1/2)(2/3)}=\frac{1}{2}\hfill \\ \hfill \mathrm{Pr}\left(Correct\right|NotReveal)& =\frac{\mathrm{Pr}\left(NotReveal\right|Correct\left)\mathrm{Pr}\right(Correct)}{\mathrm{Pr}\left(NotReveal\right)}=\frac{0(1/3)}{1/3}=0\hfill \end{array}$$

(10)

Thus, a completely rational Amy knows that if Monty chooses to reveal a goat, there is a 50 percent chance that her initial choice was correct. Simply by allowing Monty the option to not reveal, we have shown that if Monty and Amy’s preferences are opposed, the unique equilibrium is one where Amy does not always switch. Moreover, this equilibrium is one under which Amy’s beliefs are exactly those proposed so often by subjects in the many experiments: that her chances of success are equal under her decision to switch or not.

3. Uncertainty about Monty’s Motives

We now take the framework from the previous section and extend it as follows. Suppose now that Amy is unsure about whether Monty is sympathetic or antipathetic. We model this by saying that Amy and Monty have a common prior p, defined as

$$p=\mathrm{Pr}(M=M_S)$$

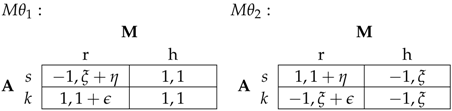
p is the probability that Monty is sympathetic (type $M_S$); and naturally, $1-p$ is the probability that Monty is antipathetic (type $M_A$). Consequently, there are 4 states of the world: $\left\{{\theta }_1,{\theta }_2\right\}\times \left\{M_S,M_A\right\}$ Thus, we may present the game matrices:

We write the following lemma:

Lemma 3.

Given uncertainty about Monty’s motives as formulated above, there is a pure strategy BNE,

$$(s,h,r,r,h)$$

for $p\ge \frac{1}{3}$.

We see that if Amy is sufficiently optimistic about the nature of Monty, there is a pure strategy equilibrium where she switches.

There may also be mixed strategy BNE, and we write:

Lemma 4.

Given uncertainty about Monty’s motives as formulated above, there is a mixed strategy BNE,

$$\left(\underset{A}{\mathrm{Pr}}\left(s\right)=\frac{1}{2},(\alpha ,r,r,\beta )\right)$$

where type $M_S{\theta }_1$ plays $\mathrm{Pr}\left(r\right)=\alpha$ and type $M_S{\theta }_2$ plays $\mathrm{Pr}\left(r\right)=\beta$, where α, β satisfy

$$-p\alpha +3p+2\beta -2p\beta -1=0$$

(11)

Equation (11) has a solution8 in acceptable (i.e., $\alpha ,\beta \in [0,1]$) α and β for all $p\le \frac{1}{2}$.

How should we interpret these equilibria? We see that as long as Amy believes that there is at least a 50 percent chance that Monty is antipathetic, there is an equilibrium where she switches half of the time. Interestingly, as long as the common belief as to Monty’s type falls in that range, Amy’s mixing strategy is independent of the actual value of p. Amy mixes equally regardless of whether p is 0 or $\frac{1}{2}$. On the other hand, Monty’s strategies are not independent of p. We may rearrange Equation (11) and take derivatives to see how Monty’s optimal choice of $\alpha$ and $\beta$ vary depending on p. Rearranging (11), we obtain,

$$\beta (p,\alpha )=\frac{1+p\alpha -3p}{2-2p}$$

(12)

Then,

$$\frac{\partial \beta }{\partial p}=\frac{2\alpha -4}{2-2p^2}$$

(13)

This is strictly less than 0 for all $p\ne \frac{1}{2}$ and for all permissible $\alpha$. Similarly,

$$\alpha (p,\beta )=\frac{3p+2\beta -2p\beta -1}{p}$$

(14)

Then,

$$\frac{\partial \alpha }{\partial p}=\frac{1-2\beta }{p^2}$$

(15)

This is greater than or equal to 0 for $\beta \le \frac{1}{2}$ and for all p. However, we show later (in Appendix A.3) that $\beta$ must be less than or equal to $\frac{1}{2}$, and a brief examination of Equation (14) shows that $\beta$ cannot equal $\frac{1}{2}$. Therefore, Equation (15) is positive for all acceptable values of the parameters.

As the common belief that Monty is sympathetic increases, type $M_S{\theta }_1$ plays reveal more often. Likewise, as p increases, type $M_A{\theta }_2$ plays reveal more often. Both relationships are somewhat counter-intuitive: as p increases, the sympathetic Monty reveals more often in the state where Amy was correct, and the unsympathetic Monty reveals less in the state where Amy is incorrect.

Generalizing to n Doors

We now generalize the previous scenario to one with $n-1$ doors ($n\ge 3$) concealing goats and one door concealing a car. Monty has hidden a car behind one of n doors, and a goat behind each of the remaining $(n-1)$ doors. As before, Amy selects a door, but before the outcome of her choice is revealed, Monty may open $(n-2)$ of the $(n-1)$ remaining doors to reveal goats. If Monty reveals the goats, Amy has the option of switching to the other unopened door or remaining with her current choice of door. This formulation agrees with the scenario faced by experimental subjects in Page (1998)9 [24].

It is easy to obtain the following lemma:

Lemma 5.

The unique pure strategy BNE is

$$(s,(h,r,r,h\left)\right)$$

for $p\ge \frac{1}{n}$.

As before, there may also be a mixed strategy BNE, presented in the lemma,

Lemma 6.

There is a set of mixed strategy BNE given by:

$$\left(\underset{A}{\mathrm{Pr}}\left(s\right)=\frac{1}{2},(\alpha ,r,r,\beta )\right)$$

where type $M_S{\theta }_1$ plays $\mathrm{Pr}\left(r\right)=\alpha$ and type $M_S{\theta }_2$ plays $\mathrm{Pr}\left(r\right)=\beta$. This equation defines a BNE for all acceptable α, β (i.e., $\alpha ,\beta \in [0,1]$) satisfying

$$-p\alpha +np+(n-1)\beta -(n-1)p\beta -1=0$$

(16)

As a corollary,

Corollary 1.

Equation (16),

$$-p\alpha +np+(n-1)\beta -(n-1)p\beta -1=0$$

has a solution in acceptable α and β for all p that satisfy:

$$\begin{array}{cc}\hfill \frac{1}{n-\alpha }& \ge p\hfill \\ \hfill \frac{1-(n-1)\beta }{(n-1)-(n-1)\beta }\ge p& \ge \frac{1-(n-1)\beta }{n-(n-1)\beta }\hfill \end{array}$$

(17)

Note that the second inequality in Corollary 1 requires that $\beta \le \frac{1}{n-1}$. The proof of this corollary is simple and may be found in Appendix A.3.

Define set ${\mathcal{A}}_n$ as

$${\mathcal{A}}_n=\left[\frac{1}{n},1\right]$$

(18)

That is, for a given situation with n doors, ${\mathcal{A}}_n$ is the set of priors, p, under which there is a pure strategy BNE where Amy switches. We can then obtain the following theorem:

Theorem 1.

As the number of doors increases, the set of priors that support a BNE where Amy switches is monotonic in the following sense:

$${\mathcal{A}}_n\subset {\mathcal{A}}_{n+1}$$

(19)

Moreover, in the limit, as the number of doors goes to infinity, we see that any interior probability supports a BNE where Amy switches.

Now, take the derivatives of the three constraints on the set of priors, p, given by Equation (17). They are:

$$\begin{array}{c}-\frac{1}{{(n-\alpha )}^2}\hfill \\ \frac{1}{(\beta -1){(n-1)}^2}\hfill \\ -\frac{1}{{((\beta -1)n-\beta )}^2}\hfill \end{array}$$

(20)

Evidently, each of these is negative for all acceptable values of the parameters and therefore, we see that the constraints are all strictly decreasing in n. We shall also find it useful to look at the limit of the two possible upper bounds for p:

$$\underset{n\to \infty }{\lim }\frac{1}{n-\alpha }=0$$

(21)

$$\underset{n\to \infty }{\lim }\frac{1-(n-1)\beta }{(n-1)-(n-1)\beta }=-\frac{\beta }{1-\beta }$$

(22)

The term in Equation (21) is strictly positive for all values of n, whereas the term in Equation (22) is less than 0 for all n greater than some cutoff value. Thus, there must be some cutoff value $\widehat{n}$, beyond which the first constraint, that $\frac{1}{n-\alpha }\ge p$, does not bind. Indeed, it is simple to derive the following lemma:

Lemma 7.

The constraint $\frac{1}{n-\alpha }\ge p$ does not bind for all $n>\widehat{n}$, where $\widehat{n}$ is given by

$$\widehat{n}=\frac{1}{2}\left(\alpha +2+\sqrt{\frac{\beta {\alpha }^2-4\alpha +4}{\beta }}\right)$$

(23)

Define the set ${\mathcal{B}}_n$ as the interval of prior probabilities p, that satisfy the conditions (A6) in Corollary 1 for a given number of doors n, $n>\widehat{n}$. Because $n>\widehat{n}$, the constraint

$$\frac{1-(n-1)\beta }{(n-1)-(n-1)\beta }\ge p\ge \frac{1-(n-1)\beta }{n-(n-1)\beta }$$

binds. Let b denote the left hand side of this expression and a the right hand side:

$$b=\frac{1-(n-1)\beta }{(n-1)-(n-1)\beta }a=\frac{1-(n-1)\beta }{n-(n-1)\beta }$$

(24)

Thus, ${\mathcal{B}}_n$ is defined as

$${\mathcal{B}}_n=[a,b]$$

(25)

We can now state a natural corollary to Lemma 7:

Corollary 2.

There is a finite number $N\in \mathbb{N}$ such that if $n>N$, ${\mathcal{B}}_n=\varnothing$

Proof. 

This corollary follows immediately from Lemma 7 and Equations (A7) and (A9) (monotonicity of the constraints, and behavior of left-hand side constraint in the limit). ☐

Since each set ${\mathcal{B}}_n$ is a closed interval, it is natural to define the size of the set, ${\nu }_n$, as the Lebesgue measure of the interval. That is, if a, b are the two endpoints of the interval ${\mathcal{B}}_n$,

$${\nu }_n=|b-a|$$

(26)

We can obtain the following theorem:

Theorem 2.

${\nu }_n>{\nu }_{n+1}$. That is, the size of the set of priors under which there is a mixed strategy BNE is strictly decreasing in n.

Proof may be found in Appendix A.4.

This theorem, in conjunction with Theorem 1, above, supports the experimental evidence from Page (1998) [24]. There, the author finds evidence that supports the hypotheses that people’s performance on the Monty Hall problem increases as the number of doors increases, and that, moreover, their improvement in performance is gradual in nature. Both findings follow from Theorems 1 and 2 in our paper. If we view the prior probability p as itself being drawn from some population distribution of prior probabilities, we see that as the number of doors increases, the likelihood that there is a BNE where Amy always switches is strictly increasing. The probability that the random draw of p falls in the required interval is strictly increasing for a fixed distribution, since the interval grows monotonically as n increases.

4. Conclusions

In this paper we have developed and pursued several ideas. The first is that even a small amount of freedom on the part of Monty begets equilibria that differ from the canonical “always switch” solution. Moreover, given this freedom, Monty’s incentives and preferences matter, and affect optimal play.

One of the characteristics of a mixed strategy equilibrium in games in which agents have two pure strategies is that each player’s mixing strategy leaves the other player (or player’s) indifferent between their two pure strategies. Thus, in a sense, the equiprobability bias may not be as irrational as it seems. When the agent is confronted with a strategic adversary, and the decision problem becomes a game, in an equilibrium, any mixed strategy yields for the agent the exact same expected reward. Indeed, the frequent remarks and comments in the literature by subjects confronted with this problem coincide exactly with this equality of reward in expectation.

Of course, that is not to say that the participants in these experiments must be correct in doing so. In the variations posed there is almost always at least an implicit restriction requiring Monty to reveal a goat (and often an explicit restriction). In such phrasings of the problem, regardless of Monty’s motivation, the situation is merely a decision problem on the part of Amy, and the optimal solution is the one where she should always switch. However, many decision-making situations encountered by people in social settings, perhaps especially atypical ones—think of a sales situation—are strategic in nature and so it could be that mistakes such as the equiprobability heuristic are indicative of this. That is, so many situations are strategic that decision makers treat every situation as if it were strategic.

Continuing with this line of reasoning, results established in this paper could also explain findings in the literature examining learning in the Monty Hall dilemma. There have been numerous studies, including [10,11,12,13,16], that show that subjects going through repeated iterations of the Monty Hall problem increase their switching rate over time, as they learn to play the problem optimally. In the model presented in this paper, uncertainty about Monty’s incentives drives the participant Amy to not play the “always switch” strategy. Through repeated play, Monty’s preferences and type become more apparent, and as it becomes more and more clear to Amy that Monty is not malevolent, the strategy of always switching becomes the unique equilibrium. This also agrees with the “Eureka moment” described in Chen and Wang (2010) [26]. There, they find that in the 100-door version of the Monty problem subjects do not play always switch for the first $(n-1)$ periods of play. Once the subjects have played $(n-1)$ repetitions of the game they reach an “epiphany” point, after which they play always switch. This is just the behavior that one would expect in a learning model where one player has an unknown type—experimentation until a cutoff belief is reached. One possible future avenue of research would be the further development of this idea by writing a formal model of this scenario, and analyzing the equilibria of that game.

The experimental results in Mueser and Granberg (1999) [20] provide support for the assumptions made in the above paragraph. In their experiment, they differentiate between phrasings of the problem where Monty must always open a door and ones where Monty need not always open a door. Furthermore, they describe explicitly to the subjects the motives of Monty, and categorize him as having either neutral, positive, or negative intent. They find that when Monty is not forced to open a door, his intent is significant in its effect on the subjects decisions. Moreover, subjects behave as our model predicts they should, and are “...much less likely to switch when the host is attempting to prevent them from winning the prize than when he wishes to help them.” ([20]). Extending this idea, another research idea that could be pursued would be the examination of learning in a scenario similar to that in [20]—one where the subjects are aware of Monty’s motives.

Finally, one possible alternative explanation for why the results shown in Page (1998) [24] occur is that in the 100 door scenario, it becomes more obvious to the subject that information was revealed, for instance, to an subject using the “Principle of Restricted Choice”10 [27]. However, this explanation does not satisfactorily explain why subjects are not able to transfer their knowledge from the 100-door problem to the 3-door problem, as detailed in [24]. The model constructed in this paper is able to explain that occurrence: it is because in the three door case the relative importance of Monty’s motives becomes more important. Having more doors makes an unknown piece of information (Monty’s disposition) less important or relevant, and thereby clarifies the situation for Amy. It should be possible to design an experiment that highlights to the subjects Monty’s motives and level of freedom, and in that context examine how their decision making is affected by increasing the number of doors.