Ignorance Is Bliss, But for Whom? The Persistent Effect of Good Will on Cooperation
Abstract
:1. Introduction
2. Model
2.1. Main Idea
2.2. Cooperation on Graphs
2.3. Indirect Reciprocity
- Defectors never cooperate with any agent
- Unconditional cooperators (UCs) cooperate with all agents
- Conditional cooperators (CCs) cooperate only with an agent i if i is “good”, i.e.,
2.4. Updating Mechanism
2.4.1. Birth-Death
2.4.2. Death-Birth
2.4.3. Imitation
3. Simulation
3.1. Overview
3.2. Parameters
3.3. Assumptions
- All agents start with a “good” reputation.
- Agents who do not know the reputation of another (which happens with probability of ) assume that the reputation of the other is “good”.
- Only the previous action when the agent was the donor determines its reputation.
- Donors that do not cooperate with defectors receive a “bad” reputation.
- Agents do not make mistakes, neither in their perception nor in their actions.
- There is no mutation in the updating of strategies.
4. Results
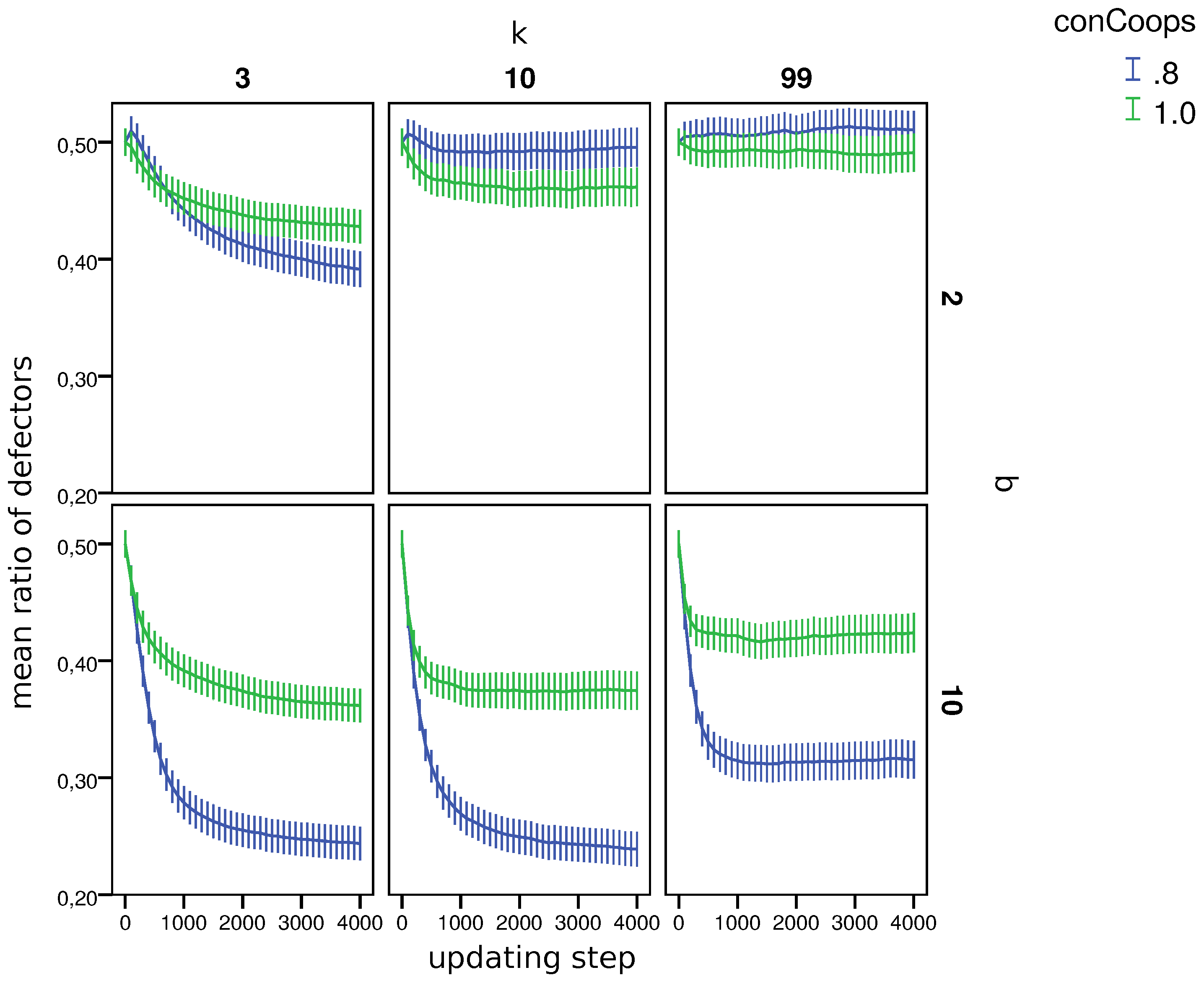
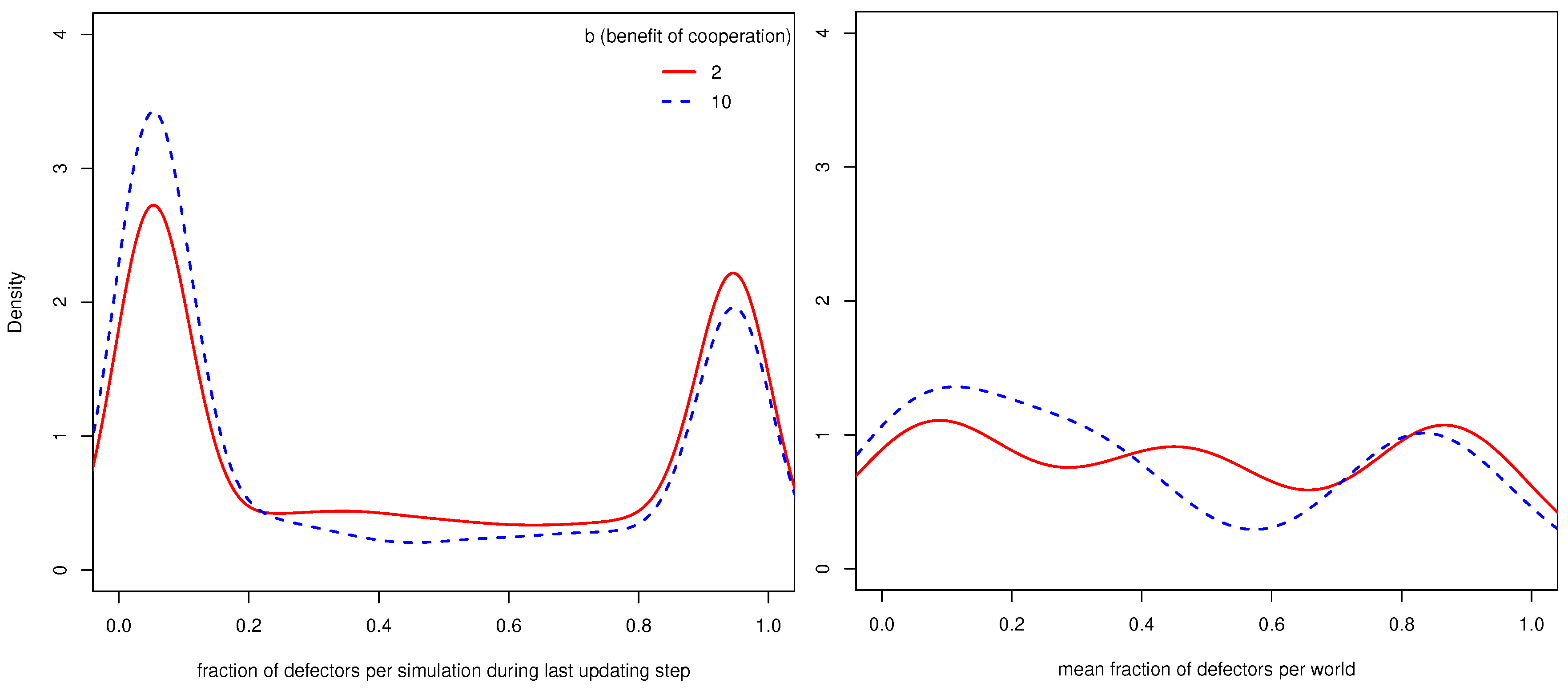
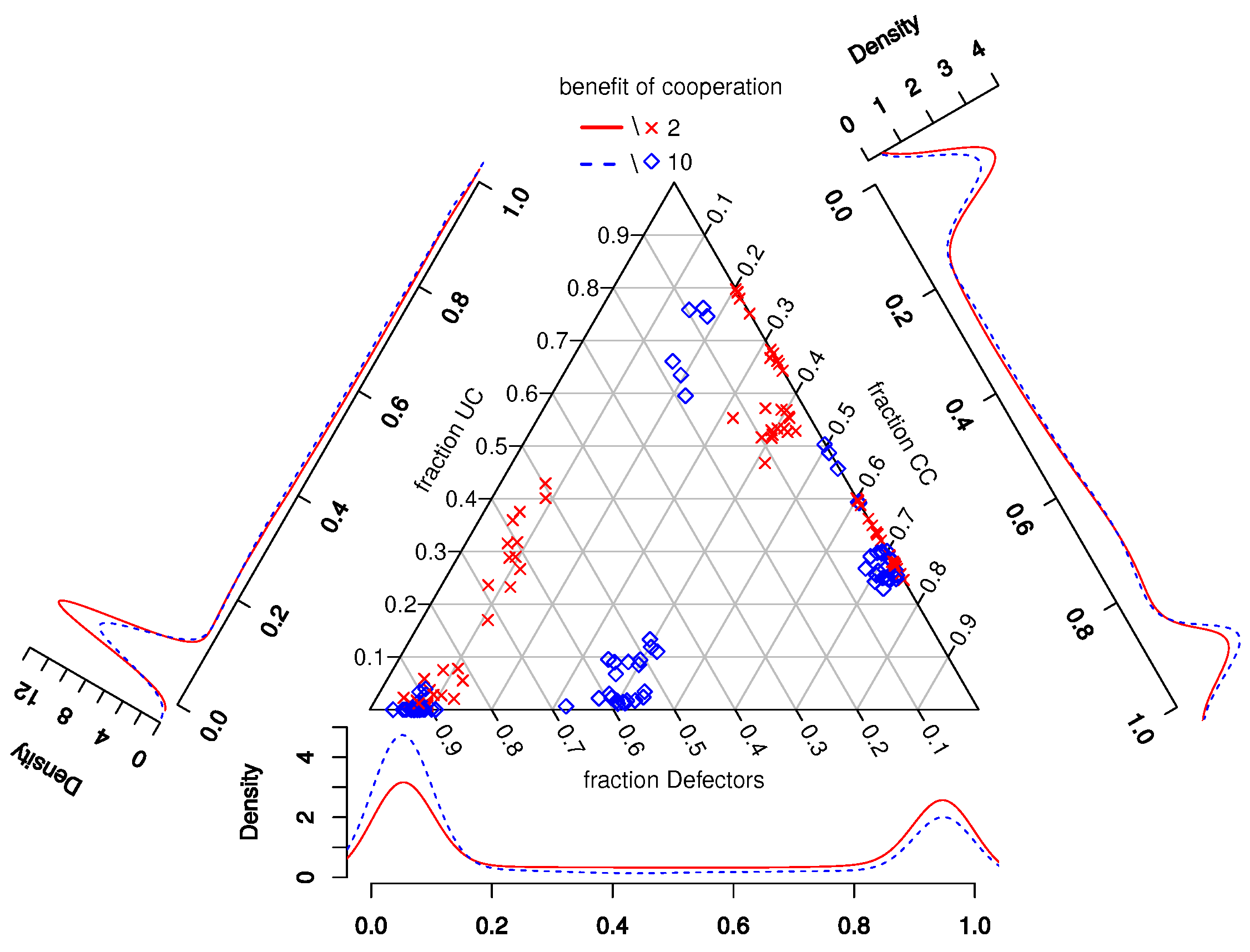
4.1. General Results
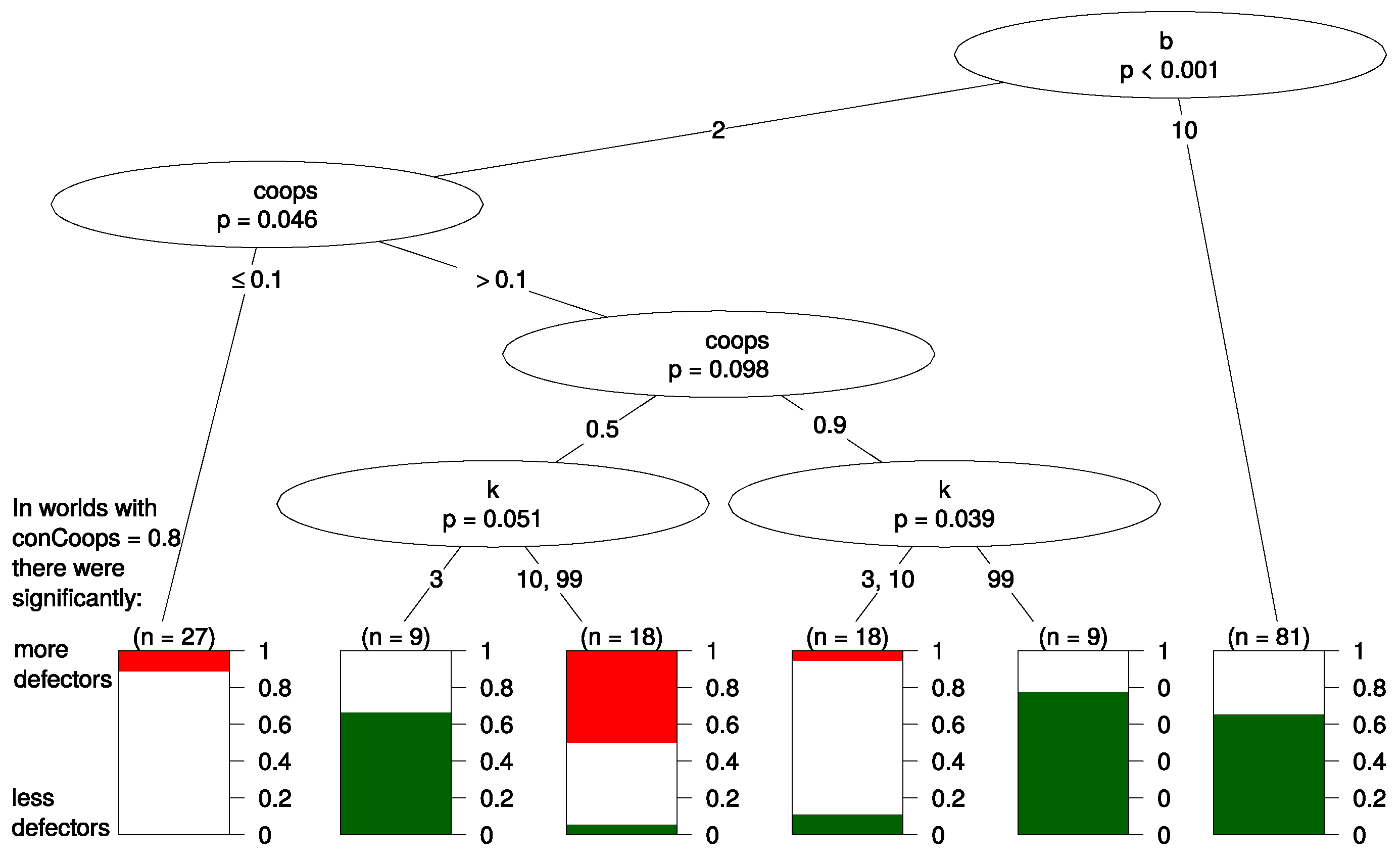
4.2. Regression Tree
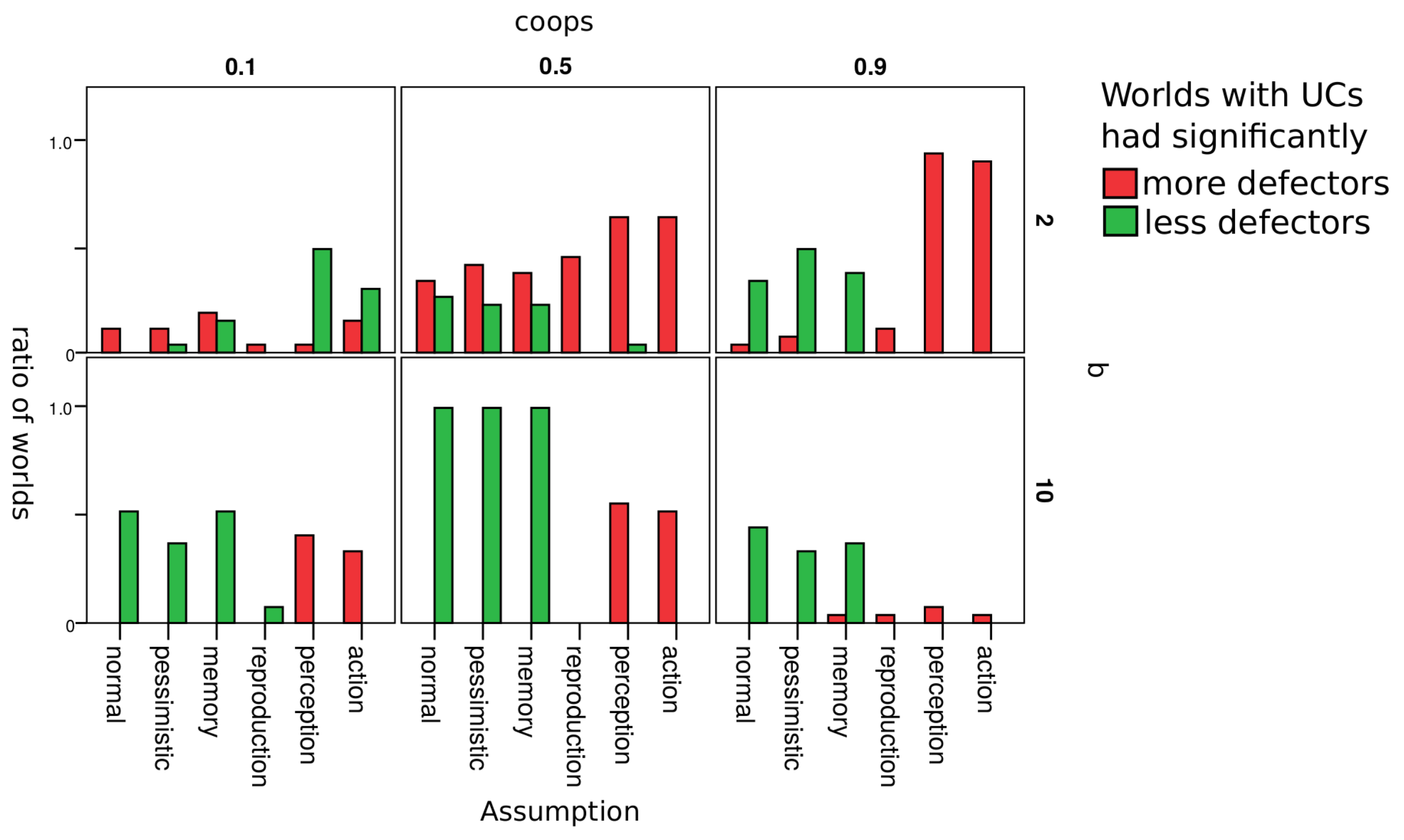
4.3. Robustness Check
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Pseudo-Code of Simulation
| Pseudo-code: main() is executed initially |
|
Appendix B. Per World Comparison
| 3 | k | ||||||||||
| BD | DB | IM | Updating | ||||||||
| 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | conCoop | ||
| 0.1 | 10 | −1 | 0 | −1 | 0 | ||||||
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||
| 0.5 | 10 | 0 | 0 | 0 | 0 | ||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 0 | |||||
| 0.9 | 10 | 0 | 0 | 0 | 0 | ||||||
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 10 | k | ||||||||||
| BD | DB | IM | Updating | ||||||||
| 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | conCoop | ||
| 0.1 | 10 | 0 | 0 | ||||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |||
| 0.5 | 10 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||
| 0.9 | 10 | 0 | 0 | ||||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | ||||
| 99 | k | ||||||||||
| BD | DB | IM | Updating | ||||||||
| 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | conCoop | ||
| 0.1 | 10 | 0 | 0 | 0 | 0 | ||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ||||
| 0.5 | 10 | 0 | 0 | 0 | 0 | ||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||||
| 0.9 | 10 | 0 | 0 | ||||||||
| 2 | 0 | 1 | 0 | 0 | −1 | 0 | 1 | −1 | |||
| q | b | ||||||||||
Appendix C. Detailed Robustness Check
Appendix C.1. Default Assumption of CCs
Appendix C.2. Error in Action
Appendix C.3. Error in Perception
Appendix C.4. Errors during Reproduction
Appendix C.5. Memory Span
Appendix C.6. Standing
Appendix D. Updating
References
- Grossman, Z.; van der Weele, J.J. Self-Image and Strategic Ignorance in Moral Dilemmas; Technical Report; Available at SSRN 2237496; University of California: Oakland, CA, USA, 2013. [Google Scholar]
- Cohen, S. States of Denial: Knowing About Atrocities and Suffering; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Carrillo, J.D.; Mariotti, T. Strategic Ignorance as a Self-Disciplining Device. Rev. Econ. Stud. 2000, 67, 529–544. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolutionary Dynamics of Biological Games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sigmund, K. Evolutionary game dynamics. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
- Maynard Smith, J. Evolution and the Theory of Games, 1st ed.; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Maynard Smith, J. The theory of games and the evolution of animal conflicts. J. Theor. Biol. 1974, 47, 209–221. [Google Scholar] [CrossRef]
- Maynard Smith, J. Group selection and kin selection. Nature 1964, 201, 1145–1147. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity by image scoring. Nature 1998, 393, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Nowak, M.A. Direct reciprocity on graphs. J. Theor. Biol. 2007, 247, 462–470. [Google Scholar] [CrossRef] [PubMed]
- Han, T.A.; Moniz Pereira, L.; Santos, F.C. Intention recognition promotes the emergence of cooperation. Adapt. Behav. 2011, 19, 264–279. [Google Scholar]
- Han, T.A.; Tran-Thanh, L.; Jennings, N.R. The Cost of Interference in Evolving Multiagent Systems. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems (AAMAS ’15), Istanbul, Turkey, 4–8 May 2015; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2015; pp. 1719–1720. [Google Scholar]
- Phelps, S.; Mcburney, P.; Parsons, S. Evolutionary Mechanism Design: A Review. Auton. Agents Multi-Agent Syst. 2010, 21, 237–264. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 437, 1291–1298. [Google Scholar] [CrossRef] [PubMed]
- Ghang, W.; Nowak, M.A. Indirect reciprocity with optional interactions. J. Theor. Biol. 2015, 365, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, M.; Yoeli, E.; Nowak, M.A. Cooperate without looking: Why we care what people think and not just what they do. Proc. Natl. Acad. Sci. USA 2015, 112, 1727–1732. [Google Scholar] [CrossRef] [PubMed]
- Panchanathan, K.; Boyd, R. A tale of two defectors: The importance of standing for evolution of indirect reciprocity. J. Theor. Biol. 2003, 224, 115–126. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y.; Nowak, M.A. Indirect reciprocity provides only a narrow margin of efficiency for costly punishment. Nature 2009, 457, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. The Dynamics of Indirect Reciprocity. J. Theor. Biol. 1998, 194, 561–574. [Google Scholar] [CrossRef] [PubMed]
- Saavedra, S.; David, S.; Felix, R.T. Cooperation under Indirect Reciprocity and Imitative Trust. PLoS ONE 2010, 5, e13475. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Five Rules for the Evolution of Cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Van Doorn, G.S.; Taborsky, M. The evolution of generalized reciprocity on social interaction networks. Evolution 2012, 66, 651–664. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, K. Indirect Reciprocity Game Modelling for Cooperation Stimulation in Cognitive Networks. IEEE Trans. Commun. 2011, 59, 159–168. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Liu, K.J.R. An indirect reciprocity game theoretic framework for dynamic spectrum access. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 1747–1751.
- Traag, V.; Van Dooren, P.; Nesterov, Y. Indirect reciprocity through gossiping can lead to cooperative clusters. In Proceedings of the 2011 IEEE Symposium on Artificial Life (ALIFE), Paris, France, 11–15 April 2011; pp. 154–161.
- Lotem, A.; Fishman, M.A.; Stone, L. From reciprocity to unconditional altruism through signalling benefits. Proc. R. Soc. Lon. B Biol. Sci. 2003, 270, 199–205. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.C.; Pacheco, J.M.; Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Fu, F.; Wang, L.; Nowak, M.A.; Hauert, C. Evolutionary dynamics on graphs: Efficient method for weak selection. Phys. Rev. E 2009, 79, 046707. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; May, R.M. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Nakamaru, M.; Nogami, H.; Iwasa, Y. Score-dependent Fertility Model for the Evolution of Cooperation in a Lattice. J. Theor. Biol. 1998, 194, 101–124. [Google Scholar] [CrossRef] [PubMed]
- Durrett, R.; Levin, S. The Importance of Being Discrete (and Spatial). Theor. Popul. Biol. 1994, 46, 363–394. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Nowak, M.A.; Pacheco, J. Breaking the Symmetry between Interaction and Replacement in Evolutionary Dynamics on Graphs. Phys. Rev. Lett. 2007, 98, 108–106. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Nowak, M.A. Evolutionary games on cycles. Proc. R. Soc. B Biol. Sci. 2006, 273, 2249–2256. [Google Scholar] [CrossRef] [PubMed]
- Hassell, M.P.; Comins, H.N.; May, R.M. Species coexistence and self-organizing spatial dynamics. Nature 1994, 370, 290–292. [Google Scholar] [CrossRef]
- May, R.M. Network structure and the biology of populations. Trends Ecol. Evol. 2006, 21, 394–399. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Borsos, I. Evolutionary potential games on lattices. Phys. Rep. 2016, 624, 1–60. [Google Scholar] [CrossRef]
- Szabó, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Roca, C.P.; Cuesta, J.A.; Sánchez, A. Evolutionary game theory: Temporal and spatial effects beyond replicator dynamics. Phys. Life Rev. 2009, 6, 208–249. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Nowak, M.A. The replicator equation on graphs. J. Theor. Biol. 2006, 243, 86–97. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Nowak, M.A. Evolutionary stability on graphs. J. Theor. Biol. 2008, 251, 698–707. [Google Scholar] [CrossRef] [PubMed]
- Tisue, S.; Wilensky, U. Netlogo: A simple environment for modeling complexity. In Proceedings of the International Conference on Complex Systems, Boston, MA, USA, 16–21 May 2004; pp. 16–21.
- Imhof, L.A.; Fudenberg, D.; Nowak, M.A. Tit-for-tat or win-stay, lose-shift? J. Theor. Biol. 2007, 247, 574–580. [Google Scholar] [CrossRef] [PubMed]
- Imhof, L.A.; Fudenberg, D.; Nowak, M.A. Evolutionary cycles of cooperation and defection. Proc. Natl. Acad. Sci. USA 2005, 102, 10797–10800. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Wild, G.; Taylor, P.D. Fitness and evolutionary stability in game theoretic models of finite populations. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2004, 271, 2345–2349. [Google Scholar] [CrossRef] [PubMed]
- Nakamaru, M.; Matsuda, H.; Iwasa, Y. The Evolution of Cooperation in a Lattice-Structured Population. J. Theor. Biol. 1997, 184, 65–81. [Google Scholar] [CrossRef] [PubMed]
- Mohtashemi, M.; Mui, L. Evolution of indirect reciprocity by social information: The role of trust and reputation in evolution of altruism. J. Theor. Biol. 2003, 223, 523–531. [Google Scholar] [CrossRef]
- Brandt, H.; Sigmund, K. Indirect reciprocity, image scoring, and moral hazard. Proc. Natl. Acad. Sci. USA 2005, 102, 2666–2670. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Iwasa, Y. How should we define goodness?—Reputation dynamics in indirect reciprocity. J. Theor. Biol. 2004, 231, 107–120. [Google Scholar] [CrossRef] [PubMed]
- Leimar, O.; Hammerstein, P. Evolution of cooperation through indirect reciprocity. Proc. R. Soc. Lond. B Biol. Sci. 2001, 268, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Brandt, H.; Sigmund, K. The logic of reprobation: Assessment and action rules for indirect reciprocation. J. Theor. Biol. 2004, 231, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Sugden, R. The Economics of Rights, Co-Operation and Welfare; Palgrave Macmillan: New York, NY, USA, 1986. [Google Scholar]
- Farjam, M.; Faillo, M.; Sprinkhuizen-Kuyper, I.; Haselager, P. Punishment mechanisms and their effect on cooperation: A simulation study. J. Artif. Soc. Soc. Simul. 2015, 18, 5. [Google Scholar] [CrossRef]
- Matsuda, H.; Ogita, N.; Sasaki, A.; Sato, K. Statistical Mechanics of Population: The Lattice Lotka-Volterra Model: Invited Papers. Prog. Theor. Phys. 1992, 88, 1035–1049. [Google Scholar] [CrossRef]
- Harada, Y.; Ezoe, H.; Iwasa, Y.; Matsuda, H.; Sato, K. Population Persistence and Spatially Limited Social Interaction. Theor. Popul. Biol. 1995, 48, 65–91. [Google Scholar] [CrossRef] [PubMed]
- 2.Further fundamental papers using indirect reciprocity are Nowak and Sigmund [9,14], Ghang and Nowak [15], Hoffman et al. [16], Panchanathan and Boyd [17], Ohtsuki et al. [18], Nowak and Sigmund [19], Saavedra et al. [20], Nowak [21]. Closely related to this paper is work on indirect reciprocity like Van Doorn and Taborsky [22], who study reciprocity on social interaction networks; Chen and Liu [23] use indirect reciprocity for cooperation stimulation in cognitive networks; and Zhang et al. [24] are applying this theory for dynamics spectrum access Traag et al. [25] and are observing cooperative clusters by using gossiping as indirect reciprocity.
- 3.The individual interactions of agents are presented in a symmetric way even though each interaction is asymmetric as the recipient can only obtain resources or not. However, each agent will eventually meet the same agent, and hence, the interaction can be seen as symmetric.
- 4.Indeed, there exists a substantial body of literature in evolutionary game theory in spatial settings looking at well-mixed and not well-mixed populations, like in Fu et al. [29], Nowak and May [30], Hauert and Doebeli [31], Nakamaru et al. [32]. Evolutionary game theory on graphs uses research in this area, like Durrett and Levin [33], Ohtsuki et al. [34], Ohtsuki and Nowak [35], Hassell et al. [36]. For an overview of its use in population biology and network structure, see May [37]. It should be noted that many results in evolutionary games are subject to change dependent on the exact parametrization of the model; even more so, when studying graphs [38,39,40]. Our study should therefore be seen only as a first attempt with regard to the exact influence and interactions of certain parameters.
- 5.This may seem like a rather bold assumption. One might think that the agent who lacks information determines the reputation of the interaction partner, e.g., randomly. However, Nowak and Sigmund [9] show that agent i will outperform agent j if agent i is more optimistic about the reputation of others and that optimistic agents evolve for that reason by themselves. Nevertheless, we also check the robustness of this assumption in our analysis.
- 6.Note that this updating mechanism is formally identical to pairwise comparison (PC), meaning that two random partners are chosen, and the partner with lower fitness adopts the strategy of the “stronger” partner [10].
- 7.This updating mechanism corresponds to the score-dependent fertility model by Nakamaru et al. [32].
- 8.We do not know of any mathematical solutions for several strategies on a non-well-mixed population.
- 9.Similar to other papers analyzing multiple strategies in co-presence [44,45], we also find that in many worlds, the population does not reach a stable distribution of strategies, but oscillates between states with more and less cooperation/defection. Since as we are interested in the general influence of UCs on cooperation, we compare the mean fractions of strategies during the last updating step per world (i.e., 110 simulations).
- 10.Appendix B, Table B1 shows the result of the test per world.
- 12.For the generation of the tree we used the R package ctree and a minimum information criterion of 0.8.
| Share | Not Share | |||
|---|---|---|---|---|
| share | b | |||
| not share | 0 | |||
| b | 0 | |||
| Parameter | Meaning |
|---|---|
| b | resources agents receive from donors |
| c | resources donors pay to donate |
| k | number of agents with which an agent can interact |
| reputation of agent i | |
| q | probability that d of a neighboris known |
| strategy of agent i | |
| rule that defines updating mechanism | |
| m | games per updating step |
| Parameter | Meaning | Value |
|---|---|---|
| n | number of agents in the simulation | 100 |
| m | games per updating step | 125 |
| updating steps per simulation | 4000 | |
| c | resources donors pay to donate | 1 |
| b | resources agents receive from donors | |
| k | number of agents an agent can interact with | |
| q | probability that d of a neighboris known | |
| type of updating mechanism | ||
| fraction of agents that are either CCs or UCs | ||
| fraction of that are CCs |
| Assumption | Description |
|---|---|
| normal | Simulations with assumption as described in Section 3.3 |
| pessimistic | Unknown reputations are assumed to be bad (good in normal) |
| memory | Reputations of agents depend on the last 3 actions (1 action in normal) |
| reproduction | With a 1% chance, offspring will have a random strategy from {UC, CC, defectors} (0% in normal) |
| perception | With a 5% chance the agent perceives the other agent as good if it is bad and vice versa (0% in normal) |
| action | With a 5% chance the agent cooperates when he/she wanted to defect and vice versa (0% in normal) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farjam, M.; Mill, W.; Panganiban, M. Ignorance Is Bliss, But for Whom? The Persistent Effect of Good Will on Cooperation. Games 2016, 7, 33. https://doi.org/10.3390/g7040033
Farjam M, Mill W, Panganiban M. Ignorance Is Bliss, But for Whom? The Persistent Effect of Good Will on Cooperation. Games. 2016; 7(4):33. https://doi.org/10.3390/g7040033
Chicago/Turabian StyleFarjam, Mike, Wladislaw Mill, and Marian Panganiban. 2016. "Ignorance Is Bliss, But for Whom? The Persistent Effect of Good Will on Cooperation" Games 7, no. 4: 33. https://doi.org/10.3390/g7040033
APA StyleFarjam, M., Mill, W., & Panganiban, M. (2016). Ignorance Is Bliss, But for Whom? The Persistent Effect of Good Will on Cooperation. Games, 7(4), 33. https://doi.org/10.3390/g7040033





