The Influence of Mobility Rate on Spiral Waves in Spatial Rock-Paper-Scissors Games
Abstract
:1. Introduction
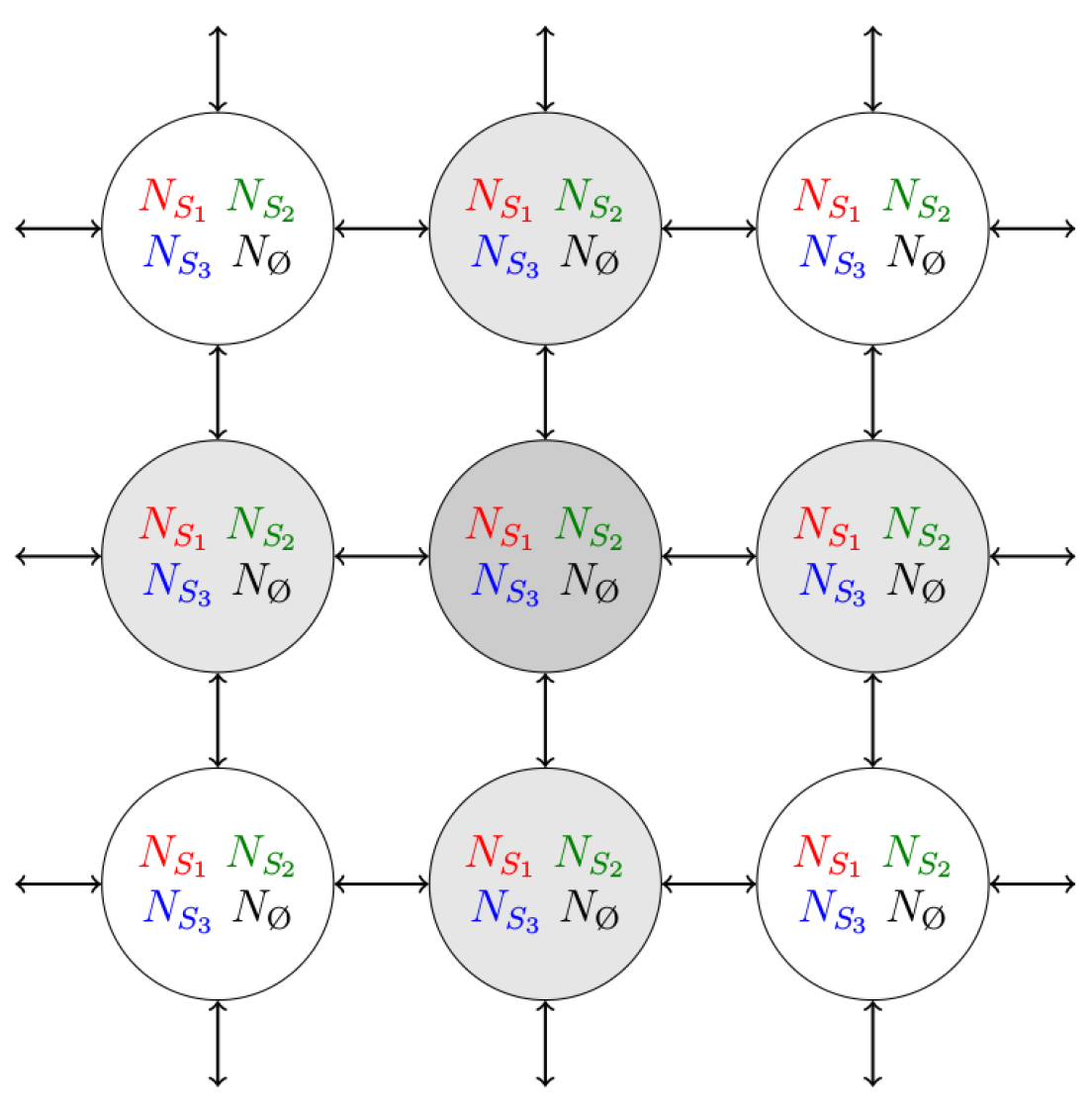
2. Model
3. Spiraling Patterns and the Complex Ginzburg-Landau Equation
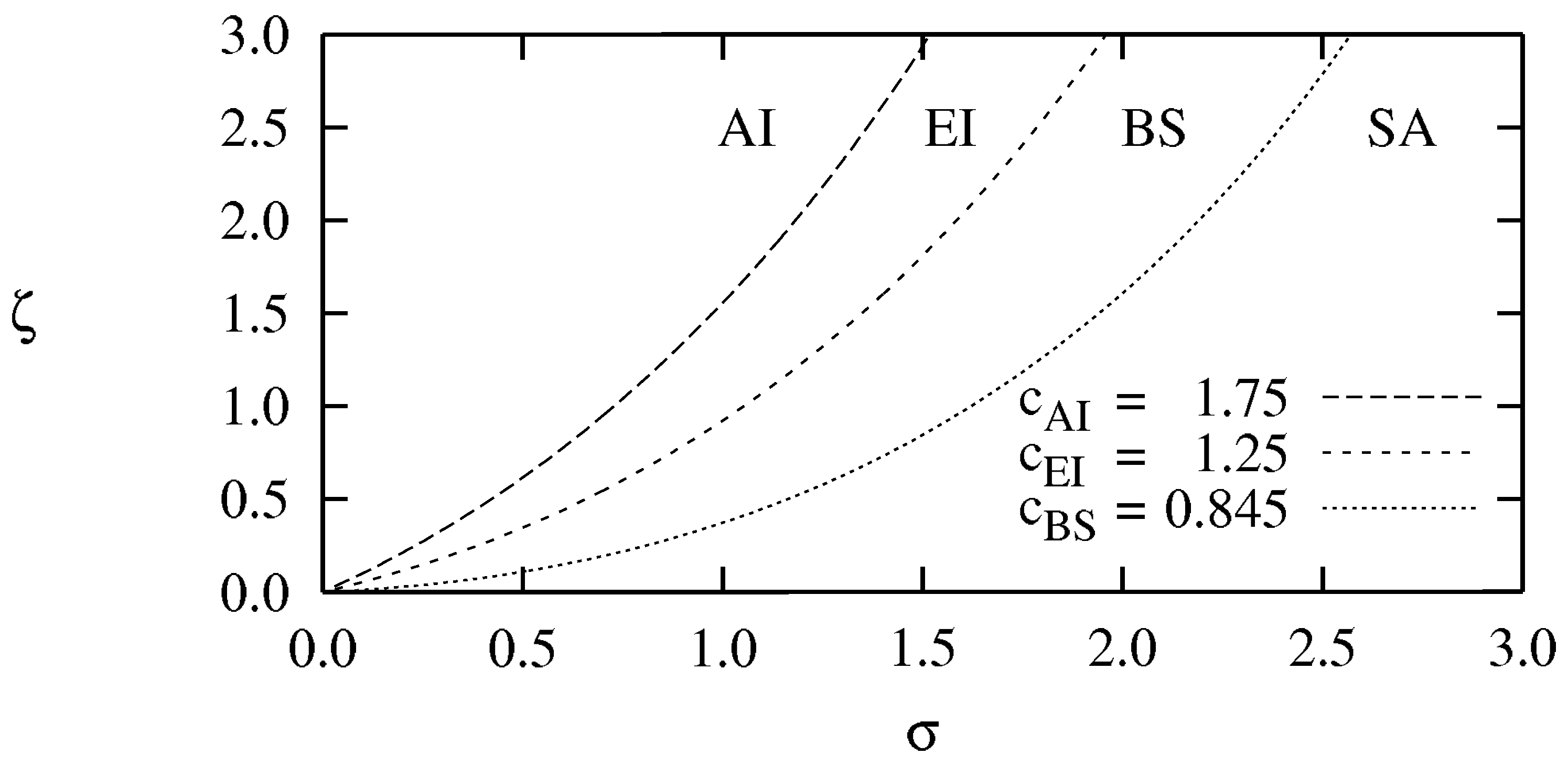
- For (close to the HB) [43]: There are four phases separated by the three critical values , as shown in the phase diagram of Figure 2: No spiral waves can be sustained in the “absolute instability (AI) phase” (); spiral waves are convectively unstable in the Eckhaus instability (EI) phase with ; stable spiral waves are found in the bound state (BS) phase (); while spiral waves annihilate when they collide in the spiral annihilation (SA) phase when .
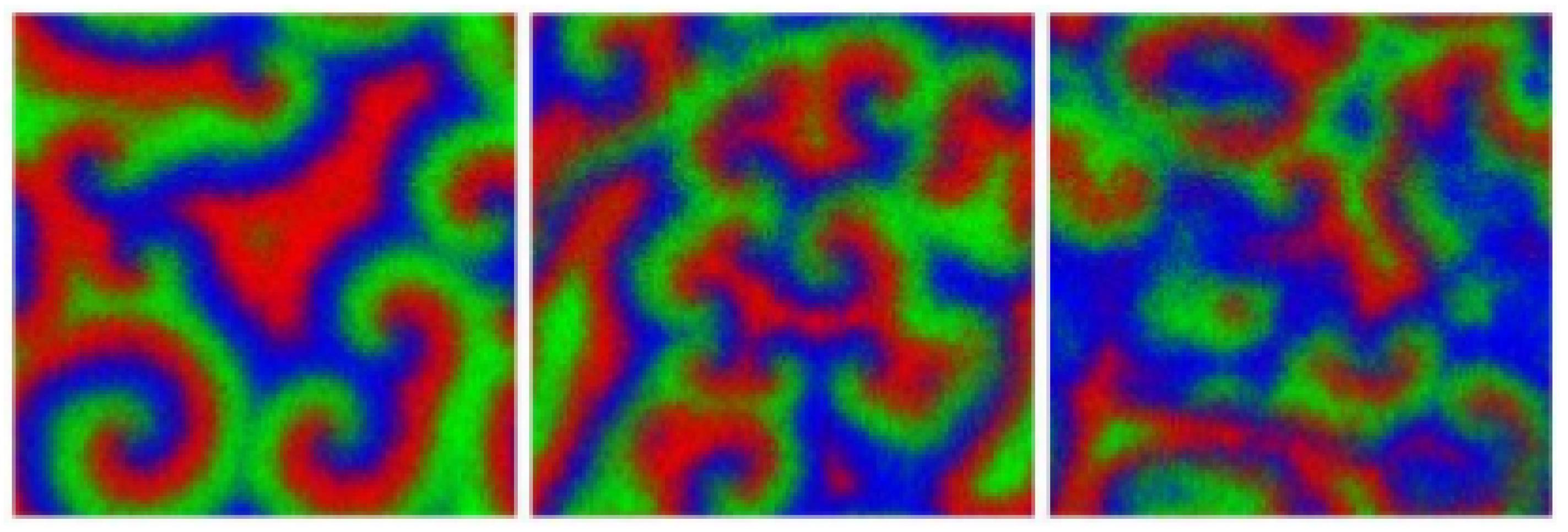
- For (away from the HB) [45]: The AI, EI and BS phases are still present even away from the HB whose boundaries are essentially the same as in the vicinity of the HB, see Figure 3. At low mutation rate, there is no spiral annihilation and the SA phase is generally replaced by an extended BS phase (with far-field breakup of the spiral waves when ).
4. How Does Pair-Exchange Influence the Formation of Spiral Waves on a Grid?
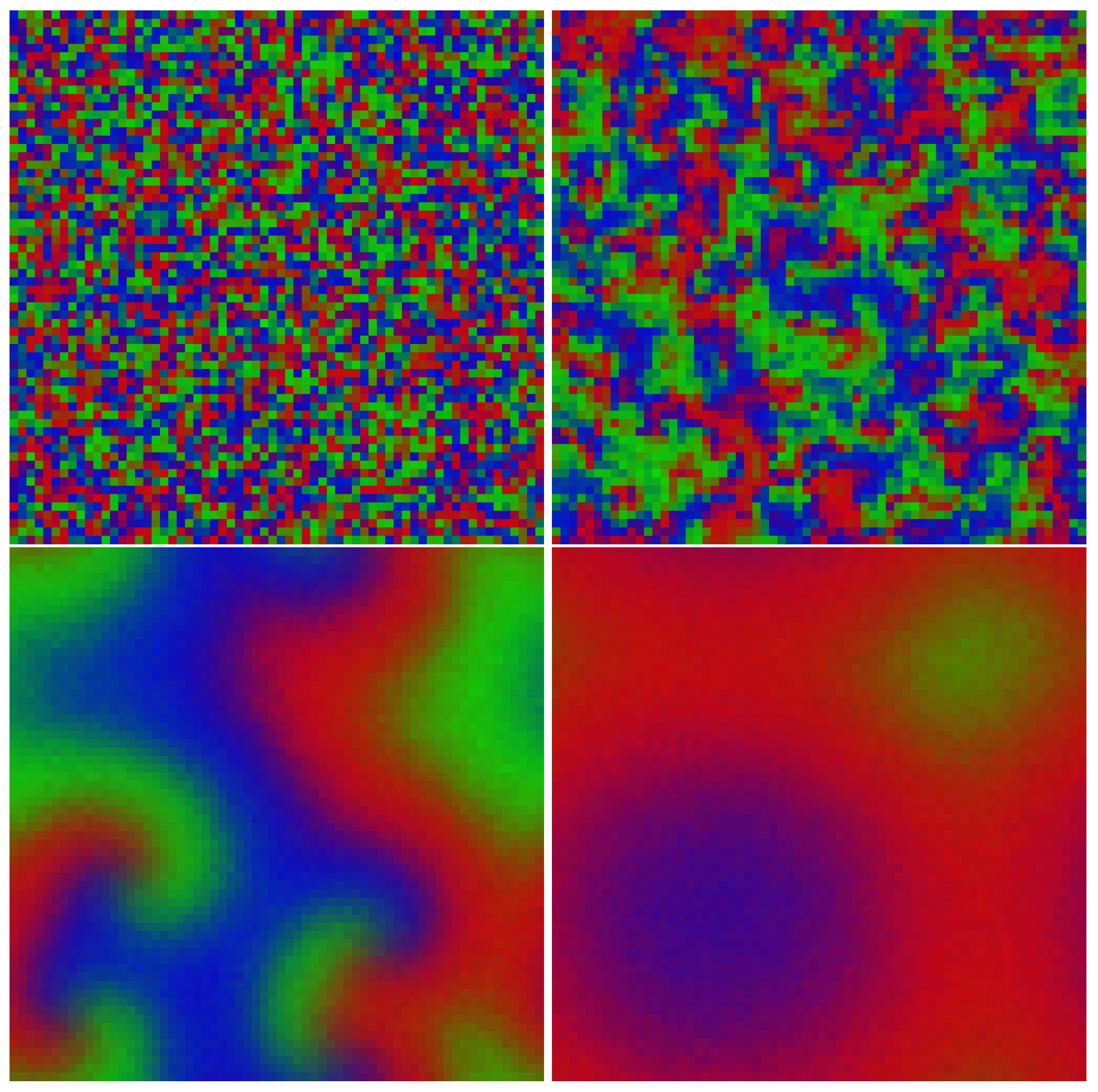
4.1. Resolution Issues
4.2. Far-Field Breakup of Spiral Waves under Weak Pair-Exchange Rate
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pennisi, E. What Determines Species Diversity? Science 2005, 309, 90. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nowak, R.M. Evolutionary Dynamics; Belknap Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Frey, E. Evolutionary game theory: Theoretical concepts and applications to microbial communities. Phys. A 2010, 389, 4265–4298. [Google Scholar] [CrossRef]
- Sinervo, B.; Lively, C.M. The rock-paper-scissors game and the evolution of alternative male strategies. Nature 1996, 380, 240–243. [Google Scholar] [CrossRef]
- Kerr, B.; Riley, M.A.; Feldman, M.W.; Bohannan, B.J.M. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature 2002, 418, 171–174. [Google Scholar] [CrossRef] [PubMed]
- Kerr, B.; Neuhauser, C.; Bohannan, B.J.M.; Dean, A.M. Local migration promotes competitive restraint in a host-pathogen ’tragedy of the commons. Nature 2006, 442, 75–78. [Google Scholar] [CrossRef] [PubMed]
- Nahum, J.R.; Harding, B.N.; Kerr, B. Evolution of restraint in a structured rock-paper-scissors community. Proc. Natl. Acad. Sci. USA 2011, 108, 10831–10838. [Google Scholar] [CrossRef] [PubMed]
- Sinervo, B.; Miles, D.B.; Frankino, W.A.; Klukowski, M.; DeNardo, D.F. Testosterone, Endurance, and Darwinian Fitness: Natural and Sexual Selection on the Physiological Bases of Alternative Male Behaviors in Side-Blotched Lizards. Horm. Behav. 2000, 38, 222–233. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.B.C.; Buss, L. Allelopathy and spatial competition among coral reef invertebrates. Proc. Nat. Acad. Sci. USA 1975, 72, 5160–5163. [Google Scholar] [CrossRef] [PubMed]
- Frean, M.; Abraham, E.D. Rock-scissors-paper and the survival of the weakest. Proc. R. Soc. Lond. B 2001, 268, 1323–1327. [Google Scholar] [CrossRef] [PubMed]
- Ifti, M.; Bergensen, B. Survival and extinction in cyclic and neutral three–species systems. Eur. Phys. J. E 2003, 10, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Mobilia, M.; Frey, E. Coexistence versus extinction in the stochastic cyclic Lotka-Volterra model. Phys. Rev. E 2006, 74, 051907. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Mobilia, M.; Frey, E. Stochastic effects on biodiversity in cyclic coevolutionary dynamics. Banach Cent. Publ. 2008, 80, 259–264. [Google Scholar] [CrossRef]
- Berr, M.; Reichenbach, T.; Schottenloher, M.; Frey, E. Zero-One Survival Behavior of Cyclically Competing Species. Phys. Rev. Lett. 2009, 102, 048102. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.P.O.; Gallas, J.A.C. How community size affects survival chances in cyclic competition games that microorganisms play. Phys. Rev. E 2010, 82, 052901. [Google Scholar] [CrossRef] [PubMed]
- Turing, A.M. The Chemical Basis of Morphogenesis. Phil. Trans. R. Soc. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology; Springer-Verlag: New York, NY, USA, 1993. [Google Scholar]
- Koch, A.J.; Meinhardt, H. Biological pattern formation: From basic mechanisms to complex structures. Rev. Mod. Phys 1994, 66, 1481–1507. [Google Scholar] [CrossRef]
- Levin, S.A.; Segel, L.A. Hypothesis to explain the origin of planktonic patchness. Nature 1976, 259, 659–663. [Google Scholar] [CrossRef]
- Hassel, M.P.; Comins, H.N.; May, R.M. Species coexistence and self-organizing spatial dynamics. Nature 1994, 370, 290–292. [Google Scholar] [CrossRef]
- Maron, J.L.; Harrison, S. Spatial pattern formation in an insect host-parasitoid system. Science 1997, 278, 1619–1621. [Google Scholar] [CrossRef] [PubMed]
- Kirkup, B.C.; Riley, M.A. Antibiotic-mediated antagonism leads to a bacterial game of rock-paper-scissors in vivo. Nature 2004, 428, 412–414. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Mobilia, M.; Frey, E. Mobility promotes and jeopardizes biodiversity in rock-paper-scissors games. Nature 2007, 448, 1046–1049. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Mobilia, M.; Frey, E. Noise and correlations in a spatial population model with cyclic competititon. Phys. Rev. Lett. 2007, 99, 238105. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Mobilia, M.; Frey, E. Self-organization of mobile populations in cyclic competititon. J. Theor. Biol. 2008, 254, 368–383. [Google Scholar] [CrossRef] [PubMed]
- May, R.M.; Leonard, W.J. Nonlinear aspects of competition between three species. SIAM J. Appl. Math. 1975, 29, 243–253. [Google Scholar] [CrossRef]
- Peltomäki, M.; Alava, M. Three-and four-state rock-paper-scissors games with diffusion. Phys. Rev. E 2008, 78, 031906. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Zhou, T.; Perc, M.; Huang, X.; Wang, B. Emergence of target waves in paced populations of cyclically competing species. New J. Phys. 2009, 11, 103001. [Google Scholar] [CrossRef]
- He, Q.; Mobilia, M.; Täuber, U.C. Co-existence in the two-dimensional May–Leonard model with random rates. Eur. Phys. J. B 2011, 82, 97–105. [Google Scholar] [CrossRef]
- He, Q.; Täuber, U.C.; Zia, R.K.P. On the relationship between cyclic and hierarchical three-species predator-prey systems and the two-species Lotka-Volterra model. Eur. Phys. J. B 2012, 85, 141–153. [Google Scholar] [CrossRef]
- Tainaka, K.I. Stationary pattern of vortices or strings in biological systems: Lattice version of the Lotka-Volterra Model. Phys. Rev. Lett. 1989, 63, 2688–2691. [Google Scholar] [CrossRef] [PubMed]
- Tainaka, K.I. Vortices and strings in a model ecosystem. Phys. Rev. E 1994, 50, 3401–3409. [Google Scholar] [CrossRef]
- Frachebourg, L.; Krapivsky, P.L.; Ben-Naim, E. Segregation in a one-dimensional model of interacting species. Phys. Rev. Lett. 1996, 77, 2125–2128. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Szolnoki, A. Three-state cyclic voter model extended with Potts energy. Phys. Rev. E 2002, 65, 036115. [Google Scholar] [CrossRef] [PubMed]
- Perc, M.; Szolnoki, A.; Szabó, G. Cyclical interactions with alliance specific heterogeneous invasion rates. Phys. Rev. E 2007, 75, 052102. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Mobilia, M.; Täuber, U.C. Spatial rock-paper-scissors models with inhomogeneous reaction rates. Phys. Rev. E 2010, 82, 051909. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Wang, W.X.; Lai, Y.C.; Grebogi, C. Cyclic competition of mobile species on continuous space: Pattern formation and coexistence. Phys. Rev. E 2010, 82, 066211. [Google Scholar] [CrossRef] [PubMed]
- Venkat, S.; Pleimling, M. Mobility and asymmetry effects in one-dimensional rock-paper-scissors games. Phys. Rev. E 2010, 81, 021917. [Google Scholar] [CrossRef] [PubMed]
- Mitarai, N.; Gunnarson, I.; Pedersen, B.N.; Rosiek, C.A.; Sneppen, K. Three is much more than two in coarsening dynamics of cyclic competitions. Phys. Rev. E 2016, 93, 042408. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Frey, E. Instability of spatial patterns and its ambiguous impact on species diversity. Phys. Rev. Lett. 2008, 101, 058102. [Google Scholar] [CrossRef] [PubMed]
- Rulands, S.; Zielinski, A.; Frey, E. Global attractors and extinction dynamics of cyclically competing species. Phys. Rev. E 2013, 87, 052710. [Google Scholar] [CrossRef] [PubMed]
- Szczesny, B.; Mobilia, M.; Rucklidge, A.M. When does cyclic dominance lead to stable spiral waves? EPL (Europhys. Lett.) 2013, 102, 28012. [Google Scholar] [CrossRef]
- Szczesny, B.; Mobilia, M.; Rucklidge, A.M. Supplementary material: When does cyclic dominance lead to stable spiral waves? Available online: https://dx.doi.org/10.6084/ m9.figshare.96949 (accessed on 4 August 2016). [CrossRef]
- Szczesny, B.; Mobilia, M.; Rucklidge, A.M. Characterization of spiraling patterns in spatial rock-paper-scissors games. Phys. Rev. E 2014, 90, 032704. [Google Scholar] [CrossRef] [PubMed]
- Szolnoki, A.; Mobilia, M.; Jiang, L.-L.; Szczesny, B.; Rucklidge, A.M.; Perc, M. Cyclic dominance in evolutionary game: A review. J. R. Soc. Interface 2014, 11, 20140735. [Google Scholar] [CrossRef] [PubMed]
- Szczesny, B. Coevolutionary Dynamics in Structured Populations of Three Species. Ph.D. Thesis, University of Leeds, Leeds, UK, 2014. [Google Scholar]
- Avelino, P.P.; Bazeia, D.; Losano, L.; Menezes, J.; Oliveira, B.F. Junctions and spiral patterns in generalized rock-paper-scissors models. Phys. Rev. E 2012, 86, 036112. [Google Scholar] [CrossRef] [PubMed]
- Roman, A.; Dasgupta, A.; Pleimling, M. Interplay between partnership formation and competition in generalized May-Leonard games. Phys. Rev. E 2013, 87, 032148. [Google Scholar] [CrossRef]
- Mowlaei, S.; Roman, A.; Pleimling, M. Spirals and coarsening patterns in the competition of many species: A complex Ginzburg-Landau approach. J. Phys. A: Math. Theor. 2014, 47, 165001. [Google Scholar] [CrossRef]
- Siegert, F.; Weijer, C.J. Spiral and concentric waves organize multicellular Dictyostelium mounds. Curr. Biol. 1995, 5, 937–943. [Google Scholar] [CrossRef]
- Igoshin, O.A.; Welch, R.; Kaiser, D.; Oster, G. A biochemical oscillator explains several aspects of Myxococcus xanthus behavior during development. Proc. Natl. Acad. Sci. USA 2004, 101, 15760–15765. [Google Scholar] [CrossRef] [PubMed]
- Hanski, I. Metapopulation Ecology; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Mobilia, M. Oscillatory dynamics in rock-paper-scissors games with mutations. J. Theor. Biol. 2010, 264, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Toupo, D.F.P.; Strogatz, S.H. Nonlinear Dynamics of the Rock-Paper-Scissors Game with Mutations. Phys. Rev. E 2015, 91, 052907. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. A General Method for Numerically Simulating the Stochastic Time Evolution of Coupled Chemical Reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Gardiner, C. Handbook of Stochastic Methods, 2nd ed.; Springer: Heidelberg, Germany, 1985. [Google Scholar]
- Lugo, C.A.; McKane, A.J. Quasicycles in a spatial predator-prey model. Phys. Rev. E 2008, 78, 051911. [Google Scholar] [CrossRef] [PubMed]
- Butler, T.; Goldenfeld, N. Robust ecological pattern formation induced by demographic noise. Phys. Rev. E 2009, 80, 030902. [Google Scholar] [CrossRef] [PubMed]
- Miller, P. Applied Asymptotic Analysis, Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2006. [Google Scholar]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef]
- Postlethwaite, C.M.; Rucklidge, A.M. Spirals and heteroclinic cycles in a spatially extended rock-paper-scissors model of cyclic dominance. Phys. Rev. Lett. to be submitted.
- Szabó, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Perc, M.; Szolnoki, A. Coevolutionary games—A mini review. BioSystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Szolnoki, A.; Izsák, R. Rock-scissors-paper game on regular small-world networks. J. Phys. A Math. Gen. 2004, 37, 2599–2609. [Google Scholar] [CrossRef]

| Wavelength λ | Mobility Rate δ | Diffusion Coefficient D () | Patterns on Grid |
|---|---|---|---|
| Clumps of activity | |||
| Stable spirals | |||
| Planar waves |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mobilia, M.; Rucklidge, A.M.; Szczesny, B. The Influence of Mobility Rate on Spiral Waves in Spatial Rock-Paper-Scissors Games. Games 2016, 7, 24. https://doi.org/10.3390/g7030024
Mobilia M, Rucklidge AM, Szczesny B. The Influence of Mobility Rate on Spiral Waves in Spatial Rock-Paper-Scissors Games. Games. 2016; 7(3):24. https://doi.org/10.3390/g7030024
Chicago/Turabian StyleMobilia, Mauro, Alastair M. Rucklidge, and Bartosz Szczesny. 2016. "The Influence of Mobility Rate on Spiral Waves in Spatial Rock-Paper-Scissors Games" Games 7, no. 3: 24. https://doi.org/10.3390/g7030024
APA StyleMobilia, M., Rucklidge, A. M., & Szczesny, B. (2016). The Influence of Mobility Rate on Spiral Waves in Spatial Rock-Paper-Scissors Games. Games, 7(3), 24. https://doi.org/10.3390/g7030024






