Abstract
A recurring argument in the global debate is that climate deterioration is likely to make social conflicts over diminishing natural resources more common in the future. The exact mechanism behind such a development has so far not been successfully characterized in the literature. In this paper, we present a general model of a community populated by farmers and herders who can either divide up land in a market economy or in autarky. The key insight from our model is that decreasing resources can make trade between the two groups collapse, which in turn makes each group’s welfare independent of that of the other. Predictions from the model are then applied to the conflict in Darfur. Our analysis suggests that three decades of drought in the area can at least partially explain the observed disintegration of markets and the subsequent rise of social tensions.
JEL:
Classification codes: P16; O41
1. Introduction
Recent research has shown that climate change increases the risk of social conflicts. For instance, a study by Burke et al. (2009) [1] on Africa predicts that a one degree Celsius increase in temperature (with an associated decline in the carrying capacity of African land) will result in about a 50 percent increase in the risk of civil war 1. In a very extensive meta-study, using data from 60 existing studies with available data, Hsiang et al. (2013) [4] demonstrate that a one standard deviation in temperature towards warmer temperatures or more extreme rainfall is associated with an increase in inter-group conflict by 14 percent 2. Using long-term data from the period 1400–1900 AD for the Northern Hemisphere, Zhang et al. (2007) [6] show that cold periods are associated with declines in agricultural yields, population decreases and, eventually, war 3.
The underpinnings of this “neo-Malthusian” hypothesis from the point of view of economic theory must, however, be regarded as quite vague. In the standard models of conflict in the literature, players typically compete over a prize, for instance the rents from a valuable natural resource, and the more valuable the prize, the greater the incentives to engage in predation rather than in production (Skaperdas, 1996 [12]; Olsson and Congdon Fors, 2004 [13]). Conflict over natural resources is sometimes also included in the literature on renewable resources and population dynamics, following the work of Brander and Taylor (1998) [14]. For instance, Reuveny and Maxwell (2001) [15] integrate a conflict between two groups over a harvested resource into the Brander and Taylor framework and show that the steady-state conflict effort increases as the carrying capacity of the area increases. None of the papers above provide any explanation of how social tension might rise as resource scarcity increases 4.
In this paper, we offer a model of a “Ricardian” mechanism through which climate change potentially causes conflict over diminishing natural resources in a traditional economy operating in a vulnerable environment 5. The mechanism highlights the roles of markets and trade for creating a social fabric and a mutual interdependence among groups that decrease the risk of conflictual outcomes. Our model outlines an ancient resource allocation problem between a farming and a herding community that can either share land equally and produce according to their comparative advantage in a market solution or grab as much land as their political strength allows and then produce in autarky. Starting from a market scenario where communities interact in trade, we show how declining resources, perhaps due to climate change, remove the basis for peaceful trade and eventually cause integrated markets to collapse. In autarky, each community’s level of welfare becomes mutually independent of that in the other community, and the division of the resource will thus be purely conflictual. A collapse of markets further implies a redistribution of resources towards politically powerful groups.
When some of the implications from the model are applied to a narrative case study of the Darfur region in Sudan, we find that effective land resources appear to have diminished drastically since the 1970s due to a 20 percent decline in precipitation. We argue that this might at least partially explain the observed disintegration of a market-like economy and the onset of appropriative conflicts from the 1980s and onwards in Darfur, culminating in the 2003 war. We also believe that our model is relevant for understanding the potential deterioration of markets in the wake of climate change in other vulnerable environments around the world.
The theoretical, as well as the empirical parts are related to a number of existing works. Rodrik (1999) [18] discusses on a macro level how negative shocks (like climate change) might be extra harmful in countries with deep social divisions, since any change in the joint pool of resources will necessarily involve painful negotiations that can become even more harmful to growth than the initial negative shock. Our market integration model is similar to Dalgaard and Olsson (2013) [19], who in turn have exploited insights from empirical findings, showing that rich capitalist economies tend to have a higher degree of political cohesion than poorer countries. However, Dalgaard and Olsson’s model (2013) [19] is primarily exploited to discuss how market integration in the Western world eventually prevailed over self-sufficiency and how this was associated with the emergence of less conflictual societies 6. In this paper, on the other hand, it is the change in the level of the resource itself that is crucial and that might bring about a different market regime.
Copeland and Taylor (2009) [21] outline a model where property rights to a renewable resource evolve endogenously in response to harvesting capacity and other factors. Our model is similar in the sense that the division of a given level of resources is also endogenously determined, but in our framework, the resource dynamics are determined by climate change beyond agents’ control rather than by a harvesting function. Our model further highlights the conflictual nature of land division 7.
Several other articles deal with farmer-herder conflicts in the Sahel. Van den Brink et al. (1995) [23] analyze theoretically the efficiency of exclusionary property rights to land in an environment where herders naturally have a preference for institutions that allow for flexible adjustments if rains should fail. Turner (2004) [24] provides an overview of the political ecology literature in relation to farmer-herder relations in the Sahel.
The specific situation in Darfur has rendered increased attention in the literature. Olsson and Siba (2013) [25] analyze the determinants of attacks on more than 500 villages in Southwestern Darfur and show that violence appears to have been directed mainly at certain ethnic groups. Olsson (2010) [26] and Alix-Garcia et al. (2013) [27] are both concerned with the long-run socioeconomic effects of this violence. In a recent paper, De Juan (2015) [28] studies the change in vegetation intensity before 2002 and shows that subsequent conflict was more intense in areas where vegetation coverage had improved 8. Based on interviews among refugees in Chad, Vanrooyen et al. (2008) [30] analyze in detail the nature of the attacks and the scope of human and resource losses in three villages.
We believe that our paper makes at least two broad contributions to the literature: Firstly, it offers a general modeling framework for analyzing the links between climate change and market integration among agents with diverse livelihoods in vulnerable agricultural environments. Secondly, it is the first systematic modeling attempt that is applied to enhance our understanding of the Darfur crisis.
2. A Market Integration Model
2.1. The Setting
In this section, we present the intuition behind the market integration model, which is the key contribution of the paper. The basic setting is a land populated by two distinct groups with historically given differences in livelihood strategies and production technologies. In order to produce the goods necessary for survival, they both need an essential, rival natural resource, like land or water.
The central question that we address is how the nature of economic cooperation between groups is affected by changes in the level of the rival natural resource when the effective level is subject to exogenous shocks, for instance due to climate change. More specifically, we are concerned with the issue of under what conditions a cooperative market economy, based on specialization and peaceful trade, might arise and when it might break down.
The key choices that we model below are, first, the choice of production regime (i.e., autarky or specialization with market exchange) and, second, the allocation of the resource between groups. We argue that it is reasonable to think of them as a joint decision where the choice of production regime is made by the groups, taking into consideration the effects that this choice will have on the subsequent division of the resource. In autarky, there is no matching of interests, and the division of the rival resource is conflictual. In a market regime, the groups become interdependent through trade, and the division of the resource will be made in the joint interest of all parties. The groups consider these two options when they make the first fundamental decision about the production regime.
We argue that the default option throughout history has been to produce independently in isolation. If any of the two groups prefer to do so, then even the group that preferred exchange will have to produce in autarky, since there is no one else with whom to trade. A market regime with an exchange of goods and specialization based on comparative advantages will only arise if both groups unanimously decide to trade. This will happen if both groups realize that market exchange with a consensual division of the resource will actually benefit them both compared to autarky. Furthermore, trade is impossible without a mutual interest between at least two parties, whereas autarky production is inevitable if only one out of two parties opts for it.
What is the motivation for assuming the particular sequence of events? We argue that the first basic choice situation might be seen as reflecting the fundamental decision whether two groups should form a joint (economic) community or not. If they choose to enter such a mutual cooperation, based on a commitment towards specialization and trade, the next political issue is necessarily how to divide and potentially redistribute resources in the joint interest of both groups. Arguably, such a process is indeed similar to how many larger polities have formed throughout history. If no such joint community is formed, the division of resources in the next stage becomes conflictual, and the groups with the strongest bargaining power (or military strength) grab most of the resource.
Why do the two groups not first divide the resource and then decide on the market regime? Although we do not rule out that this might perhaps be a suitable description of certain historical situations, we believe that it is reasonable to assume that the nature of political bargaining over resources should be conditional on what type of economic regime that the agents are in, rather than the other way around. The sequence of events that we model here would also rule out somewhat unrealistic situations where, for instance, a redistribution of resources based on political power would happen before the groups decide on whether to form an economic community or not. 9
2.2. Sequence of Events
In this section, we will present in more detail the players, their potential strategies and the sequence of events in the market integration model. Let us consider a geographically-bounded economy with two population groups that each consume two essential goods. For simplicity, we might think of the population groups as being farmers (denoted as f) and herders (denoted as h). Farmers have a comparative advantage (defined below) in producing crops, whereas herders have a comparative advantage in producing meat. Both farmers and herders need, however, to consume both crops and meat. Both activities further require a rival natural resource with weakly-defined property rights; in the case at hand, land.
There are two basic choices to be made. Firstly, farmers and herders choose in which type of (economic) community they prefer to be. More specifically, they need to decide how much meat and crops they should produce within their group. There are two possible regimes: either that both groups produce both goods in autarky, so that farmers also keep some cows and herders grow some crops, or that both groups specialize in the production in which they have a comparative advantage and then trade goods with the other group in an open market economy.
The second key choice is how the two groups should divide the land between them. In the absence of clearly-defined property rights, there is no market for land 10. We assume that land allocation is determined in a Nash bargaining process between groups. Even here, there are two potential outcomes: the two groups can either grab as much as they can of the resource through political strength or brute force or they can engage in specialized production and peaceful trade, in which case, the resource will be divided in accordance with players’ comparative advantages.
The point of departure is a historical de facto division of the resource. The sequence of events in this model is the following:
- Nature (i.e., climate change) reveals the effective level of the central natural resource R.
- The two groups choose individually and simultaneously what production regime they prefer to be in: autarky or a market regime with an exchange of goods. The market regime will only arise if both groups unanimously choose this option; otherwise, the actual outcome will be autarky even if one group chooses market.
- The groups divide up the rival natural resource (R) through (Nash) bargaining.
- The two groups produce and consume (and potentially trade) within the regime chosen in the second stage and using the allocation of R determined in the third stage.
An informal game tree representation is shown in Figure 1. We assume rational individuals who can perfectly assess the effects of choices by both groups in each stage. Conflict is defined as a situation when a prevailing market equilibrium is replaced by an autarky equilibrium, which in turn results in a non-cooperative reallocation of land from a politically weaker group to a politically stronger group in Stage 3.
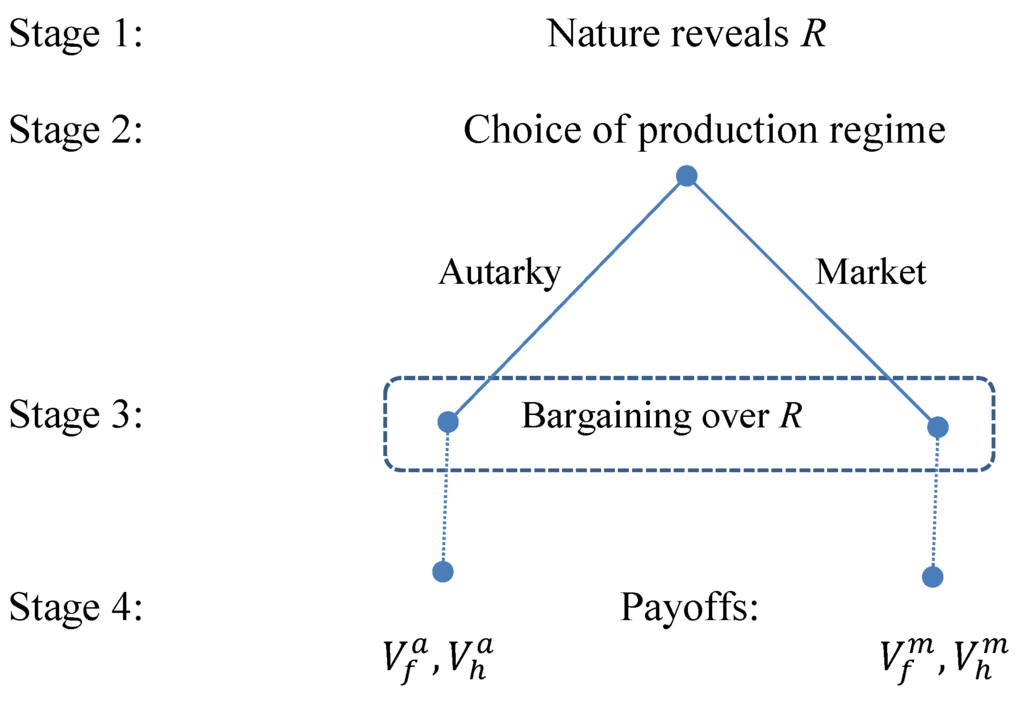
Figure 1.
The market integration game. The figure shows the four stages of the repeated market integration game, as described further in the text. In Stage 1, Nature (climate change) reveals the level of resources R during a particular year. In Stage 2, both players (groups) decide individually on what market regime in which to be. Only if both groups choose market will that regime be the outcome. In Stage 3, groups Nash bargain over the division of resources R. In Stage 4, production, consumption, prices and indirect payoffs in terms of indirect utilities V materialize for both groups. Players solve the game through backward induction, taking into account already in Stage 2 the effects of their choices in Stages 3–4.
The model is solved through backward induction. We therefore start below by solving for the production and consumption decisions in Stage 4.
2.3. Preferences and Production
There are adults in the farming community and adults in the herding community, so that We assume that there is no mobility between communities and that changes in population are exogenous. 11
Individuals in population group have the following Cobb–Douglas utility function:
Utility is gained in both regions from consuming positive amounts of crops and meat with respective elasticities η and and where . The level of η reflects the weight given to crops in total utility. We assume that farmers and herders have identical preferences in this regard. A straightforward motivation for this assumption is based on dietary needs; the consumption of crops provides calories, whereas meat provides protein. Both are essential for human survival. The utility function satisfies the usual assumptions of a positive, but diminishing marginal utility of each good.
All individuals in the two groups have one unit of time at their disposal for productive activities during adulthood. In a regime where the two groups produce in autarky, they will split their time between production of the two goods. Accordingly, individuals are then subject to a time constraint.
where represents time allocated to farming in community For instance, thus stands for time spent on herding cattle in a farming group.
The production technologies for the representative producer in the two groups are:
respectively. Since we want to keep the model as simple as possible, output is only a function of resources per capita and work effort 12.
is the amount of land in community i used for farming, and is the land used for herding, so that . is the total (working) population in group i. Land is assumed to be shared equally within each community, but it is a rival factor of production between modes of production and between communities 13 As will be discussed further below, , where R is the fixed effective supply of land in the economy as a whole during a particular year, reflecting both size and quality. In other setups, we might instead think of R as water, forest resources or indeed as an ecological complex of renewable resources that are used directly in production. In our model, climate change materializes through unpredictable increases or decreases in the effective level of R.
The source of comparative advantage is that in the farming community, one extra unit of land per worker has a higher output elasticity than one extra unit in herding, whereas in the herding community, an extra acre of herding land has a higher output elasticity than in farming:
For simplicity, we assume that there is a symmetry in these productivity differences, so that and and that . There is, however, always diminishing marginal returns to land. The elasticities of work effort x in farming and herding, γ and δ, are assumed to be identical in the two communities and have a level of γ,.
The representative individual consumes all production every year, hence and .
2.4. Optimization in Autarky
As discussed above, there are two basic regimes for organizing production: autarky, in which the two groups produce both goods in isolation from each other, and a market economy where trade between groups takes place and production is specialized.
Under an autarkic production regime, the optimization problem is to find, for both groups , the time allocations and and land allocations and that maximize utility in Equation (1), subject to the constraints and . The straightforward solutions for the time allocation problem turn out to be:
Maximizing utility in community i with respect to land allocation gives us:
The indirect utility for community i in autarky (with an index a) is therefore:
The expression in Equation (6) shows that the indirect utility of representative individuals in both the farming and herding communities depends positively on the level of effective resources per capita that the community has been able to obtain. Hence, the allocation of resources between communities is inherently conflictual, since one community’s utility gain of resources is mirrored by an equal loss in the other community.
2.5. Optimization in the Market Economy
In the market regime, people specialize in production in accordance with their comparative advantages, implying that farmers only produce crops and that herders only produce meat 14. While individual preferences are the same as in autarky, the budget constraints are different. For individuals in, for instance, community , total income () is divided between consumption of crops ( and meat :
where p is the relative price of meat, i.e., measured in terms of crops.
Farmers’ income derives from using their entire time endowment on production of crops, so that . Furthermore, all land is used for farming, so that . This means that total income is simply:
In a corresponding manner, herders will specialize in herding, and their relevant constraints are:
Solving the utility maximization problem of individuals in the two communities leads to the following demand equations for the two products:
In a competitive market equilibrium, the total supply of crops must equal total demand, so that . Total supply of crops is produced by farmers, whereas total demand comes from both the demand of farmers and from herders, who also consume crops. In a similar manner, total supply of meat is produced by specialized herders, whereas total demand comes from both farmers and herders.
Combining these equilibrium conditions, we can write an expression showing that total relative supply (left-hand side) must equal relative demand (right-hand side), where the price adjusts so as to clear markets:
In this expression, is total income of the farming community, whereas is the total income of the group of herders.
Since the right-hand side of Equation (10) collapses into just and since by Equation (5), we can derive the equilibrium relative market price of meat to be:
A key feature of this expression is that in the market economy, attempts by, for instance, farmers to get a larger share of total land, i.e., an increase in the -ratio, will cause a higher supply of crops, but also a lower aggregate supply of meat. This, in turn, will increase the relative price of meat, as shown in Equation (11). Since farmers also eat meat, they will be hurt by the price increase. We can thus get a sense of how the market institution will typically reduce incentives for engaging in an appropriative struggle for basic natural resources. The relative price will also be affected by the population ratio .
As in the previous section, we can now solve for the indirect levels of utility in the market economy:
From these expressions, it is clear that the utility of, for instance, farmers will be directly dependent not only on their own resource levels, but also on the corresponding level for the herders (. This effect comes about through the price mechanism: an increase in the -ratio implies that the production of crops increases, but it also implies that the relative price of meat in Equation (11) rises, which hurts farmers. This is the primary reason for the emergence of a stronger social integration and cohesion, as described below.
2.6. Resource Allocation
In Stage 3 of the model, farmers and herders divide up the resource stock in a political bargaining process 15. We assume that this process can be described as an asymmetric Nash bargaining function that is in place both during autarky and the market economy:
In this expression, and are simply the indirect utilities for farmers and herders, respectively, during economic regimes , as derived above. We write these as functions of the observed level of R, since in the normal cases, all of R can be fully exploited. What is new in Equation (14) are the threat points and that show each agent’s indirect utility in case the bargaining breaks down. The key assumption that we make is that such a non-cooperative situation is associated with both groups retreating to a safe homeland, leaving a share as an empty part that no party dares to use and, therefore, is wasted. The proportional level of λ is assumed to be the same regardless of whether the breakdown of bargaining takes place during autarky or during trade. The smaller the λ, the greater the fear of the other group and the stronger the incentives to agree through bargaining. Note that as the function is specified above, our threat point does not allow for switching economic regime 16.
The exponent reflects the relative bargaining strength and will play a key role for the outcome of the process. π might be thought of as capturing crude political strength, perhaps based on military advantage, government support, higher levels of education or historical reasons. One might, for instance, assume that π reflects the proportion of farmers in the total population, such that .
A natural question at this point is why we propose that resources are divided through a bargaining process and why there are no clear property rights to the resource? To begin with, it is generally recognized that property rights over resources like land tend to be weak in developing countries, in particular in peripheral regions of such countries. Secondly, even when there are formal entitlements to land, farmers and herders in these types of environments often find it mutually beneficial to reach agreements that formally violate property rights, for instance when farmers let herders graze on their land in exchange for meat and milk. We believe that the Nash bargaining process assumed here captures the special types of considerations that farmers and herders need to make under imperfect property rights reasonably well. Furthermore, π might be thought of as reflecting the formal property rights to land.
In autarky, substitutions of indirect utility levels in Equation (6) and the identity into Equation (14) give us the following maximization problem:
By taking the standard first-order conditions for maximum and solving for , we can obtain the following solutions:
The results imply that we can express a first proposition:
Proposition 1:
(i) The Nash bargaining equilibrium allocation of effective land to farmers during autarky increases with farmer bargaining strength π, with the strength of preferences for crops η, and with the total effective level of total resources R. (ii) The Nash bargaining equilibrium allocation of effective land to herders decreases with farmer bargaining strength π, with the strength of preferences for crops η, and increases with the total effective level of total resources
Proof:
The results follow from straightforward comparative statics on the basis of 15.
The division of the resource will strongly depend on bargaining strengths π and . The reason for the importance of this factor is the absence of any interdependence between the two groups due to the lack of trade. Although both players settle for this outcome during autarky, the allocation of R is inherently conflictual, since both farmers and herders would benefit from having more of the resource.
Furthermore, if the utility weight given to crops η is high among both farmers and herders, this will imply that herders can accept that a somewhat larger fraction of resources is retained by the farmers. Not surprisingly, an increase in the effective level of the land resource R will imply that both communities increase their access.
If the two groups specialize and trade in a market economy, however, we can infer from inspection of Equations (12) and (13) that the Nash bargaining process simply boils down to the following problem:
The solution becomes surprisingly simple:
Thus, regardless of bargaining strengths π, farmers and herders will agree to share the resource with each other according to their preference for the two goods, because this arrangement will maximize their welfare in a market economy. The intuition for this result is that the two communities’ welfare become interdependent. Trade introduces a solution that is mutually beneficial.
2.7. Market Exchange vs. Autarky
In Stage 2 of the game, the two groups observe the realized actual level of the natural resource R that was revealed in the first stage and that needs to be divided up. The representative agents in both groups choose individually what regime they prefer to be in; autarky or a market economy. By the backward induction logic and since the players can foresee what happens in the later stages, we therefore now insert the solutions for , and and compare indirect utilities. The market outcome will be chosen whenever the following condition applies:
In all other situations, autarky will prevail. Hence, only if both groups prefer to engage in trade will there be a market regime. The condition in Equation (16) further implicitly assumes that groups have solved their collective action problem, so that deviant choices cannot be made by individuals within the groups.
The indirect utility comparison for farmers is
is a clutter of parameters where, importantly, it might be noted that . The intuition for this is that when farmer bargaining power π is large, then farmers will be able to grab a great share of the resource in autarky and are hence more likely to prefer not to trade.
Analogously, the relevant comparison for herders is:
where it clearly is the case that .
The results in Equations (17) and (18) allow us to state the following key result:
Proposition 2:
A market solution is more likely if the level of the common resource R is high, if the size of comparative advantages is large and if there are relatively equal distributions of bargaining powers and population sizes, so that and
Proof:
Comparative statics shows that and since . The results regarding π, and follow from the fact that the outcome of the choice of a market regime will be determined (from Equation (16)) by whether or not . This minimum level is maximized when and .
The key result from the proposition above is that an increase in the level of effective natural resources R increases the probability of a cooperative market solution and that the positive impact of R will increase with the elasticity differences (or magnitude of comparative advantages) . Since we defined conflict above as a situation when a market equilibrium breaks down and causes a non-cooperative redistribution of land through the Nash bargaining process, an analogy to Proposition 2 is that conflict is likely to arise in response to a large fall in R. This implication differentiates our approach from the spirit of several theoretical contributions on the curse of natural resources where a greater resource abundance often leads to unproductive rent seeking and a less well functioning economy. 17
The intuition behind our result is essentially derived from the fact that the total output elasticity and productivity of land is greater in the specialized market economy than in autarky. The upper expressions of Equations (17) and (18) illustrate this insight. In a market economy, farmers will have access to of land resources, and the output elasticity is . In autarky, farmers have access to of land resources, and the elasticity of indirect utility with respect to land is since .
Note that if π is relatively large, the greater access to land through political power might compensate for the lower productivity of land for farmers during autarky. A higher aggregate R from one year to the next will however make the autarky solution less attractive to both farmers and herders, since the productivity difference between the two modes of production increases with R. A high level of R will give this factor of production a great weight in the production and indirect utility functions and make a market choice more likely.
On the other hand, if R falls due to climate change or some natural disaster, then the importance of R in the calculation above will generally fall, and the level of political power π will increase in importance. Eventually, a deep enough fall in R could cause a market economy to collapse. This is one of the most central insights from our model.
The results regarding the distribution of bargaining power π and population sizes are also fairly easy to grasp. Should farmers’ political and bargaining power π be very large, maybe even close to unity, then their interest in a more equal division of the resource in a market regime is relatively small, since they can obtain a lot more of R by choosing autarky. Equivalently, if is substantially greater than , then the relative price of meat from the herding community will be very high, which will decrease farmers’ willingness to participate in a market economy, regardless of the level of R. If both bargaining power and population levels are evenly distributed, there will neither be a large redistribution of land, nor a price shock to one of the groups in the case of a market economy, which makes such a regime more likely.
2.8. A Numerical Illustration
In order to clarify the implications of the model further, we include a numerical illustration of the main results. If we use the central expressions Equations (17) and (18), we can plot how the relative indirect utilities of a market outcome and depend on the level of resources R as in Figure 2 In this example, we have assumed that parameter levels are , , and . Starting with the elasticities, the assumed levels all satisfy the basic restrictions above and ensure that farmers have an advantage in farming and herders in herding. As for population levels, we just picked some number, but made the important assumption that the two groups should initially be equally large. Equal size is also reflected in the assumption of equal political power;
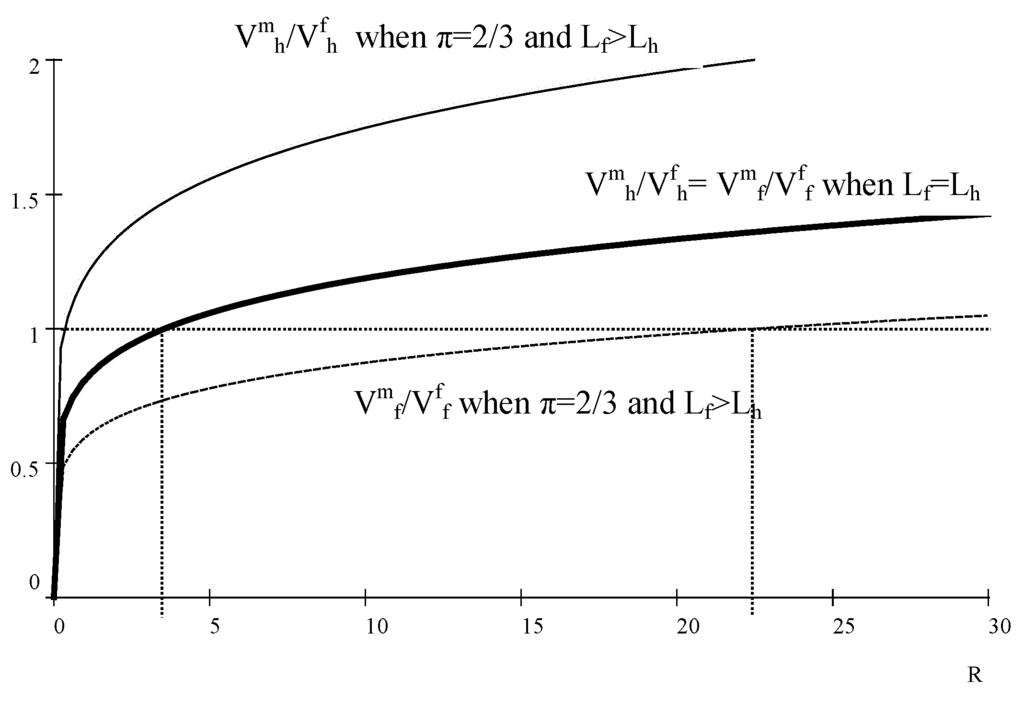
Figure 2.
Relative indirect utility of market integration as a function of resources R. The figure shows simulations of Equations (17) and (18) at different parameter values. The thick line in the middle shows the indirect utility functions / and / as functions of R when the assumed parameter values are ; ; ; . The dotted concave line on top and the thin concave line on the bottom show relative indirect utilities for herders and farmers, respectively, using the same parameter values as above with the only change being that we assume unequal levels of population and political power: ; , .
The thick line in the middle shows the relative utility comparisons for both groups since the lines coincide. In general, it is clear that the relative utility of a market is a positive and concave function of effective resources R. The crossing of this line with the horizontal line at indicates the critical level of R for a market solution to be preferred. During a year when the level of resources is at least 3.56, both groups will prefer trade, and they will share the resource equally. Since we assumed that , R was divided equally also during autarky. In this example, a switch from market to autarky would therefore not result in any redistribution and, hence, in no conflict.
When we modify these assumptions and instead assume that population levels are and , which is also reflected in political power, so that, for instance, , then the lines in Figure 2 diverge, so that the herders’ line rises, whereas the farmers’ line falls. Farmers are now much less willing to engage in trade, since meat produced by herders will be relatively expensive and since farmers’ larger political power ensures them 2/3 of the resource during autarky 18. Farmers will only opt for a market economy if They will then find it worthwhile to give up 1/6 of total resources and engage in trade with the herders. In total, a transition to a market economy will result in a resource reallocation amounting to of the total stock of resources with farmers giving up 1/6 and herders gaining 1/6. This illustrates graphically the result in the proposition above that a market solution is more likely to emerge when population sizes and political power are equally distributed.
However, why would a politically strong group voluntarily give up resources when making the transition to a market economy? The key reason is that if farmers keep as much resources as before, the price of meat will be unnecessarily high due to herders’ shortage of land and the price of crops too low. The benefits of a market economy are maximized when the division of the resource equals η, implying in the example above that farmers give up land in order to obtain a market situation where the price of meat (crops) is as low (high) as possible.
The figure also makes clear how climate deterioration might cause a market economy to collapse. If R is initially perhaps equal to 30, then farmers will prefer trade, specialization and an equal sharing of land resource with herders, even if their political power is large (). If the climate deteriorates in the following year, so that R falls to 20, farmers will be better off in autarky. Trade then breaks down, and farmers grab 1/3 of herder land. Such a year is thus characterized by a redistributive conflict.
What is the intuition behind the fact that farmers choose to grab more land when climate and R deteriorate? Once again, the ultimate tradeoff is between the greater productivity that specialization, trade and an equal sharing of resources bring, against the direct advantage of having access to more land in production. The higher the general quality of the land, i.e., the greater the importance of land in both groups’ production functions, the more weight is given to the advantages during the market regime. Analogously, a low R implies that the advantages of a market are relatively small, and autarky becomes more likely. When production is independent during autarky, farmers are no longer hurt by a higher price of meat if they grab more land, and hence, they have a stronger incentive to do so.
How robust are these results to the specific assumptions used in the model above? An important limitation of the current setup is that the model only compares two extreme situations; complete autarky and complete specialization with trade. How about a market regime with incomplete specialization, such that farmers and herders both produce crops and meat and then trade? The Appendix outlines the basic characteristics of such an extension. Given the more complex nature of the optimization problem in this scenario, analytical results are not easily interpreted. Hence, it needs to be recognized that we cannot rule out that our main results are to some extent influenced by the sharpness of the comparison between full autarky and specialization.
3. An Application to Darfur
The model above is meant to describe a general situation in traditional economies where production and welfare are particularly vulnerable to climate change. We believe the model could, for instance, be applied to many parts of the Sahel area in Africa where conflict between farmers and herders is common. The basic conflictual situation between sedentary and nomadic populations was further very common in all parts of the world before the rise of industrial production and might potentially be used for analyzing numerous historical developments.
In this section, we will briefly relate the model to one particular current conflict episode in a vulnerable environment: Darfur. There are at least three reasons for this choice of study object: Firstly, Darfur lies in the African Sahel region, which has been identified as one of the most vulnerable environments in the world in the years to come (Stern, 2006 [37]; IPCC, 2007 [38]). Secondly, several studies have indicated that conflict over scarce land has been a key factor in Darfur (UNEP, 2007 [39]). Thirdly, and most importantly, Darfur is arguably one of the most serious humanitarian disasters in the world during the last decade, with about 300,000 dead since 2003 and about two million people displaced (Degomme and Guha-Sapir, 2010 [40]).
3.1. Context
Darfur is located in western Sudan on the eastern edge of the Sahel cultural zone and is one of the most landlocked areas in the world. The heart of the region is the Jebel Marra massif, which has a quite different climate and vegetation from the surrounding Sahelian plain. It is estimated that Darfur harbors around 6–6.5 million people and that the population has increased by three million since 1983 (D-JAM, 2006 [41]). The population consists of a multitude of ethnic groups, some with their more or less recognized traditional homeland (dar). Land ownership within homelands is primarily communal, and the main livelihood strategies are subsistence agriculture and pastoralism.
In a very simplified sense, the region has traditionally been dominated by the farming Fur people and its allied ethnic groups who occupy the slopes of Jebel Marra, where they cultivate sorghum and millet. They are sedentary and refer to themselves as “African” in the Darfuri context. The “Arab” tribes in the area are typically cattle herders. 19
3.2. The Darfur Conflict
The key economic institutions prevailing in Darfur before the conflict are described in Olsson (2010) [26]. A central institution is the customary land tenure system, known as hakura, allotting land rights to certain named tribes rather than to individuals. This system had been in place already since before the colonial period and implied that dominant tribes, such as the Fur, had a dar (“homeland”) where they had usufructuary rights to land. However, during peaceful periods, individuals from many other tribes were also welcome to cultivate the land in these villages. The hakura system for sedentary farmers was combined with a practice that gave herders and their livestock the right to pass through and graze on farmers’ lands after harvest (talique). Moreover, it was a common practice during peace for farmers to leave their cattle in the hands of the herders in exchange for agricultural goods.
Recurring droughts in the area from the 1970s brought a serious disturbance to the fragile ecological balance between the pastoralist tribes and the farming communities. The pastoralist tribes typically moved from northern to southern Darfur with their herds over farming lands during February–March and then returned during May. The droughts forced farmers to intensify their cultivation, and attempts were made to seal off land from the pastoralists. Deadly clashes between farmers and herders were common during this period, killing thousands and making tens of thousands homeless (United Nations, 2004 [42]). In a recent paper, De Juan (2015) [28] shows that migration to central and western parts of Darfur increased up until the eve of the crisis in 2002.
The major conflict in Darfur is usually considered to have exploded in the first half of 2003, when hostilities from two rebel groups, dominated by farming tribes, caused the government to mobilize militias among the herders in the area for a counter-insurgency campaign. These “Janjaweed” fighters would typically target civilian villages. Destruction of property, rape and murder were common outcomes of such attacks (Prunier, 2007 [43]). After 2005, the conflict changed its nature and became less intense in terms of the severity of attacks and number of casualties.
3.3. Trends in Resources, Population and Power
The key variables in our model are effective resources R, relative population size and the distribution of political power, measured by π. In Darfur, the relevant natural resource is effective land, i.e., a composite stock of the quantity and quality of land where quality is influenced by rainfall, proximity to surface water, intensity of land use, degree of desertification, etc. As in most parts of Sudan, the land is typically arid or semi-arid, and the relatively most fertile areas are found on the Jebel Marra plateau in the heartland of the region. The majority of the population is either subsistence farmers or pastoralists, organized in geographically-bounded homelands (dars) within which land is primarily communal and where there are no strong individual property rights to land.
Whereas the total size of the land is more or less constant, precipitation varies from year to year and is the major factor determining land productivity over time 20. Rainfall data are further measured with a certain accuracy and have previously been shown to have an influence on economic growth rates and conflict risk (Miguel et al., 2004 [2]). The long-run pattern of precipitation in Darfur is summarized in an extremely condensed form in Figure 3. It shows that in all three Darfur states, the average annual rainfall has declined during the last thirty years as compared to the 1946–1975 period. Using more detailed data, Kevane and Gray (2008) [44] confirm that there indeed appears to have been a structural break in precipitation around 1972 whereupon rainfall appears to have decreased by about 20 percent. Their data further reveal that there were major drought episodes in 1975–1977, 1984–1985, around 1990 and again around the year 2000.
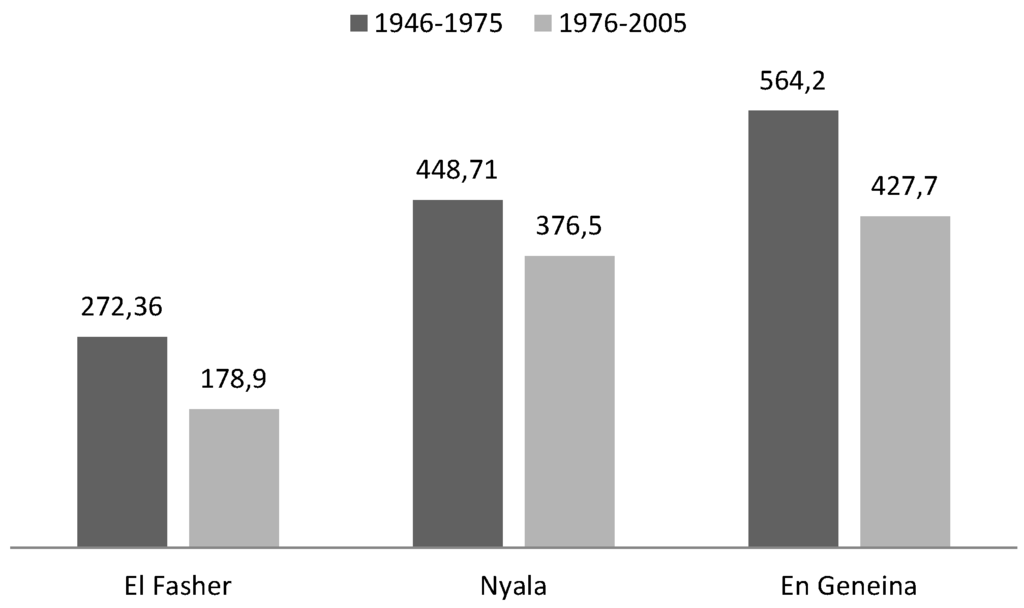
Figure 3.
Average precipitation (in mm) in the three Darfuri capitals by time period. Source: Time series constructed on the basis of data from UNEP (2007, Table 4).
Using satellite imagery of vegetation intensity (NDVI) for the 1982–2002 period on a disaggregated grid cell level, De Juan (2015) [28] confirms that there was indeed a notable reduction in vegetation cover in eastern and northern Darfur. However, the western parts around El-Geneina, which were the traditional homelands of the Fur and the Masalit, had actually increased their NDVI level during these years and had also experienced attacks during 2003–2004.
Population is another factor that plays a key role in our model. Figure 4 shows the population trend from 1956–2003, based on official data from D-JAM (2006) [41]. Noteworthy features are that population has increased by a factor of nearly five between 1973 and 2003 (from 1.34 million–6.48 million) and that there appears to have been a structural break in population growth around 1973. This is particularly remarkable, since the same period has had a marked decline in rainfall. If we assume that land productivity has decreased on average by 20 percent due to rain failure, effective resources per capita in 2003 should on average only be about one sixth of the level in 1973 21. This must be regarded as a quite remarkable deterioration.
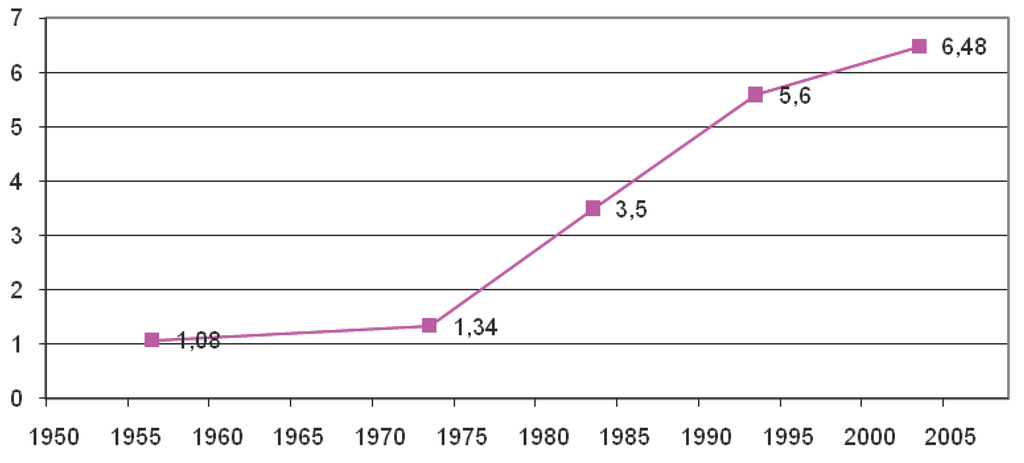
Figure 4.
Total population levels (in millions) in Darfur, 1956–2003. Source: constructed on the basis of data from D-JAM (2006, p. 12).
Why was there an increase in population growth rates in the early 1970s despite a downturn in the rainfall trend and a major drought around 1976? De Juan (2015) [28] offers some important explanations of this pattern. He shows that population increase was greatest in the central parts of Darfur around the major towns. Inflow was also large in the western parts, which unlike most of the region experienced an increase in vegetation cover, as mentioned above. Hence, the gradient between the best and the worst lands must have increased substantially, forcing herders from several regions in the Sahel to enter the greener lands of the Fur and the Masalit. The effect of this inflow was of course a lowering of in the western parts of Darfur. Even so, farmers still appear to have been in the majority. Data from Southwestern Darfur before 2003 suggests that African ethnic groups, who are most often farmers, outnumbered Arab populations by a factor of six to one (Olsson and Siba, 2013 [25]).
After the rebellion in 2003, it seems that the massive military support for the Janjaweed militia implied a substantial negative shock in π. Indeed, the empirical analysis in Olsson and Siba (2013) [25], as well as documents cited in Flint and de Waal (2008) [32] strongly suggest that the government actually supported an ethnic cleansing campaign on the African farming populations, indicating a drastic fall in π after 2003.
3.4. Market Integration
What do the trends above imply for market integration in Darfur? In order to answer this, let us briefly return to our model. Since we have established that farmers outnumber pastoralists in the area, they are most likely to be the group that benefits least from markets and, hence, make up the decisive group. This can be illustrated as in Figure 2, where and and Let us initially assume that the level of resources is . In this case, the community is initially in a market scenario, and land is shared equally, so that .
A fall in resources to 20 due to climate change would in this example be enough to push the economy into autarky. In the new bargaining situation, farmers would then reclaim 1/6 of available land (they increase their share from 3/6 in the market scenario to , perhaps through fencing their fields). Despite this reallocation, farmers lose units of land because of the fall in total resources. However, herders lose much more; units. The fall in and in π should however imply an upward shift in the curve, which, at the same time, should improve farmers’ willingness to engage in markets.
In order to test implications like these, one would ideally like to have access to time series data capturing various measures of trade intensity, resource stocks and exact relative population levels. Although resource and population data do exist, information on the functioning of markets is unfortunately not available for Darfur. We must therefore resort to using qualitative evidence and narratives from various works.
Many sources suggest that a kind of market integration was effectively in place before the 1970s. As expressed in a report from UNHCR/INTERSOS(2005, p 11) [45]:
“...before the 2003 crisis, the traditional system of managing resources facilitated the relatively peaceful coexistence between nomads and farmers. African farmers sold agricultural food items to the Arabs, who brought animals into the market. During the farming season, from July to February, nomadic movements were restricted to certain annually-marked traditional routes, called migration routes...During the rest of the year, nomads moved along the agreed upon migration routes. Water points were shared by everyone.”
There are also many indications of that this type of cooperation actually started to break down already during the 1970s, following the decline in effective resources.
Prunier (2007, p 56–57) describes a bit more in detail how the collapse of economic integration unfolded and how this affected the herding populations:
“The drought not only shrunk their grazing resources but upset their picture of the world. Farmers trying to hang on to all potential agricultural land now often blocked the traditional marahil (migratory route) which had once led to the southern pastures. The nomads called these fenced-off unused agricultural land zaraib al–hawa (literally “enclosures of air”), and for them it was a catastrophe. The world was suddenly closing up, with traditional pathways and temporary forage suddenly out of reach...In their eagerness to push towards the still wet south, they started to fight their way through the still blocked off marahil.”
As already documented above, there was further a very uneven inflow of people into Darfur during these decades. Nomadic pastoralist peoples were clearly the main immigrant group, causing the -ratio to fall. This leveling of population levels should have given the agricultural majority stronger incentives for cooperative trade. However, as was also discussed above, the massive support to the Janjaweed from 2003 had changed the bargaining power during autarky in strong favor of the pastoralist Arabs, causing a lower π. The effective level of π might even have become so low as to make herders the decisive group, and with resources continuing to fall, trade was no longer seen as a rational option.
In our model, we envisaged a bargaining between farmers and herders over land resources that took place after the effective level of R had been disclosed. In the real world, day-to-day interactions between the two groups on the fields and along the livestock migration routes are the equivalent of this bargaining, played out within the existing institutional structure of hakura and talique, as referred to above. The market regime, associated with agricultural fields open for grazing herds, farmer livestock cared for by the herders and peaceful trade, was under strong pressure already in the 1990s and eventually definitely collapsed in 2003 as a result of a steady decrease in R, changes in the -ratio and in political power π. This collapse also resulted in conflict and land redistribution. A new market equilibrium still seems to be an illusion in Darfur for years to come.
4. Concluding Remarks
In this paper, we have developed a simple model of the links between natural resources like land and market integration in vulnerable agricultural environments. Our model showed that if two different groups have distinct comparative advantages in their use of land, the two groups will typically have incentives for trading and for dividing the common land resource equally in a market economy. The main insight from the model is that if effective land resources decline, perhaps due to climate change, the basis for trade is weakened, and the market economy might potentially collapse. Agents then retreat to uncooperative autarky where political strength determines the allocation of resources.
Our model was motivated by the proposition in the literature that dwindling natural resources in vulnerable environments might cause conflict over these resources. We suggest a general mechanism for how economic exchange in societies might break down as a consequence of negative environmental developments. The model is applicable to any environment with a heavy reliance on natural resources. However, our model is not really a conflict model, since the agents do not exert any effort to fighting. In future theoretical work, the collapse of markets might be modeled as the first step in an escalating process that eventually leads to an appropriate conflict in the more conventional sense.
When the main results from our model were applied in an informal manner on the situation in Darfur, we argued that there appeared to be some support for our key hypothesis in the sense that market integration indeed has broken down at least partly because of decreasing effective land resources. Casual inference from other historical narratives, such as Jared Diamond’s (2005) description of the breakdown of advanced economies on such diverse places as Easter island and the Maya empire on the Yucatan peninsula, seem to suggest that similar cycles have been operating throughout history. Future work, using data on various indicators for market integration, should be able to shed further light on the underlying mechanisms at work. We believe that our theoretical framework might be a useful point of departure in this endeavor.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A Incomplete Specialization in the Market Regime
Although the assumption of complete specialization in a market economy enhances analytical clarity, it is admittedly somewhat strong. What if we were to relax this assumption to allow for a mixed regime?
Such a change of assumptions would imply that we now allow both farmers and herders to produce both crops and meat. In the clean cases of autarky and market regimes in the paper, the fourth stage of the model was relatively uncomplicated, since in autarky, there was no price mechanism to take into account, and in the market regime, there was no division of labor and land between activities. Now, however, we need to take into account also these effects, which greatly complicate the interactions between the agents.
To start with, we need to specify three additional stages after Stage 3 in the paper:
- 4.
- The two groups divide up the rival resource within the group between farming and herding production, and .
- 5.
- The two groups decide how much of their time to devote to farming and herding, and .
- 6.
- The two groups trade on the market and jointly determine a relative price p.
Since the incomplete specialization model is not a key feature of the paper, we will not provide a complete characterization of solutions at all these stages. We will however consider Stage 6 when trade occurs and prices are determined. The utility functions are the same as before, as well as the demand functions for crops and meat from farmers and herders:
The production functions are now the same as in the autarky regime for :
In other words, both farmers and herders split their time and their land and between farming and herding.
Total supply of crops in this market economy now comes from both farmers and herders:
whereas total supply of meat is:
The general equilibrium condition is now that:
From this condition, we can solve for the equilibrium relative price of meat:
The key difference between this expression and the price expression in the main text is that we allow for the possibility that , so that farmers use some land and spend some time for herding and herders use some land and spend some time farming 22.
This expression is much more complicated than the expression for in the main text where we had complete specialization. In this scenario, more land to the farmer group (i.e., an increase in and ) would by symmetry imply equivalently lower levels of and . From the expression above, it is not obvious how this would affect the price of meat. More to the point, should politically strong farmers consider grabbing land from the herders, the penalty in terms of a price increase in meat would be a lot less severe if farmers also produced some meat.
Inserting the demand functions and back into the utility functions give us:
Total individual income for the representative individual in group i now equals the value of total production of that group, so that . Combining the expressions for and , the utility function for farmers can be written as:
As one can easily imagine, every reallocation of resources will have complicated direct utility effects, as well as affecting the general equilibrium through the price mechanism. For instance, a reallocation within the farming community, so that increases at the expense of , while keeping total farming community resources constant, would increase the production of crops and decrease the production of meat. In addition, the relative price of meat would go up, which would affect both communities.
In Stage 5, the two groups would decide how much of their time to devote to farming and herding, and . For farmers, that would involve finding the and that maximize Equation (19). Not only would they have to take into account the direct effects of their time allocation on the production of crops and meat , they would also need to consider how their time allocation affected the equilibrium price.
In Stage 4, the groups would divide up the resource within their respective communities between farming and herding, taking into account the effects that this choice would have on time allocation and price formation.
Could complete specialization or autarky arise within the initially mixed economies as modeled in this Appendix? More specifically, could a situation arise when the representative agents in the communities choose to allocate all resources and time to one activity, as in the market regime in the paper?
Given the diminishing returns to each factor of production in the production functions above, such a solution would be impossible. Output elasticities of land and labor time all satisfy , which implies that as land or labor allocated to a certain activity approaches zero, the marginal product will, as usual, approach infinity. Hence, some resources are always devoted to such an activity, and specialization would not emerge endogenously.
In Stage 2 in the main model in the paper, groups decide on whether to opt for complete specialization or produce in autarky. Could we introduce a choice also here in Stage 2 between a market economy with incomplete specialization versus autarky? Such an analysis would imply that we solve for the allocations of resources and labor time and for the price and then compare the indirect utility of this scenario with the indirect utility in autarky. Unfortunately, such a comparison does not have clear analytical insights due to the very complicated nature of the expressions involved.
- 1.More specifically, their study predicts that the risk of civil war increases from an average of 11 percent per year to 17 percent. See also Miguel et al. (2004) [2] for the impact of precipitation on income and the risk of war in Africa and Blattman and Miguel (2010) [3] for an overview of the literature on civil war.
- 2.The conclusions of this study have been challenged by Buhaug et al. (2014) [5], who consider the meta-analysis methodology to be problematic and potentially suffering from a sample selection bias.
- 3.See also Kennett et al. (2012) [7] for an analysis of how a deteriorating climate caused the Maya pre-colonial civilization to disintegrate. Other more general works in this tradition include Schubert et al. (2008) [8] and Homer-Dixon (1991, 1994) [9,10]. Diamond (2005) [11] discusses several historical cases of how overexploitation of scarce resources has caused advanced economies to stagnate and even collapse.
- 4.There is a large literature in social psychology that studies the conditions for cooperative and non-cooperative behavior. In the classic “Robbers Cave”experiment, Sherif et al. (1961) [16] showed that conflict between groups could be mitigated by working on a common task that could not be completed without the other group (such as a market). Tajfel et al. (1971) [17] demonstrated that an in-group favoritism can very easily emerge even with arbitrary assignments into groups. In this paper, I present an economic explanation to the emergence of cooperation over a common task: the market.
- 5.We define a vulnerable environment as one where people have a production structure with a great deal of dependency on natural factors, such as rainfall and temperature and where people live close to some minimum subsistence level.
- 6.See also Rohner et al. (2013) [20] for a theoretical model where peaceful trade between ethnic groups hinges on human capital investments on both sides that facilitate interaction. Trade reduces the risk of conflict, but accidental conflicts might cause trade to break down.
- 7.See also Engel et al. (2006) [22] for a model of negotiations between local communities and companies over a natural resource under weak property rights.
- 8.See also De Waal et al. (2014) [29] for an analysis of conflict patterns during 2008–2009, using a novel dataset collected by the UN forces in the area.
- 9.A formal demonstration of how a change in the sequence of events would change the nature of the game in the model is available upon request.
- 10.As analyzed by van den Brink et al. (1995) [23], it is not obvious that herders actually want to have exclusionary property rights to a certain piece of land given their nomadic way of life. However, for the model to be relevant, it is enough that one of the groups (the farmers) will try to establish exclusive possession of land.
- 11.The assumption of no mobility might be regarded as a strong assumption. In a richer model, we could have endogenized the choice whether to be a herder or a farmer. In that case, it would be natural to assume that people shifted occupation in every period until marginal utility was equalized. However, it should also be recognized that being, for instance, a farmer is also associated with strong cultural markers in terms of language, customs, etc., that serve as barriers that are potentially hard to overcome, at least in the short run. Most of the major farming tribes further identify themselves as “African”, whereas herders typically identify themselves as “Arab” (Flint and de Waal, 2008 [32]).
- 12.In Dalgaard and Olsson (2013) [19], we also included human capital that accumulated over time through learning-by-doing. Since that is not the focus of this work, we refrain from using either human capital or productivity parameters here.
- 13.We do not allow for land rentals in this model. We acknowledge however that a system of renting land between communities could potentially change the terms of trade and provide more flexible solutions to the land allocation problem.
- 14.Such complete specialization is not often observed in reality, since even trading farming communities usually keep some cattle as a kind of insurance policy. We use the extreme specialization assumption, since it simplifies the analysis. See the Appendix for an analysis of the equilibrium price if we instead assumed incomplete specialization.
- 15.This bargaining process should be thought of as a very general characterization of social interactions that might, in reality, be much more complex than two parts on either side of a table.
- 16.One might, for instance, imagine that a breakdown of bargaining during a market regime would induce the players to revert back to autarky. In the spirit of Binmore et al. (1986) [31], we argue that this is not an appropriate modeling of threat points. A threat point should show the alternative to agreeing in the short run, which is simply producing under the economic regime at hand, but with less resources. In the long run, however, players might make a new choice in the first stage of the game and switch economic regime, as discussed below.
- 17.See, for instance, Collier and Hoeffler (2004) [33], Mehlum et al. (2006) [34] and Olsson (2007) [35]. Van der Ploeg (2011) [36] provides an overview of the resource curse literature. It should be noted though that natural resources are often proxied by valuable minerals for export in those studies rather than land, as in the current analysis.
- 18.A decrease in farmers’ political power would in this situation shift their curve upwards and the herders’ curve downwards, which would make a market regime more likely.
- 19.Apart from the two main types of farmer and herder groups, there are also other categories of people in Darfur, including tribes that declared themselves as “neutral” in the struggle between the farmer rebel groups and the Janjaweed (Olsson, 2010 [26]). These are however relatively unimportant in terms of population numbers, and I abstract from them in the analysis below.
- 20.Other natural processes, such as desertification, erosion, salinization and deforestation also affect the overall quality of land, but we will refrain from analyzing such factors here.
- 21.More specifically, let us normalize effective resources (land) per capita in 1973 to be 1/1 = 1. Whereas effective land depreciated by a factor 1,2 due to drought, total population increased by a factor of 4,836. Hence, effective resources per capita in 2003 are (1/1,2)/(1*4,836) = 0,172, i.e., slightly more than of the level in 1973.
- 22.Note that the utility maximizing level resource use and time has not been calculated in the expression above, but given the concave character of the functions, it is for certain that people in both communities will use some land and spend some time in the activity in which the group does not have a comparative advantage.
References
- Burke, M.B.; Miguel, E.; Satyanath, S.; Dykema, J.A.; Lobell, D.B. Warming Increases the Risk of Civil War in Africa. PNAS 2009, 106, 20670–20674. [Google Scholar] [CrossRef] [PubMed]
- Miguel, E.; Satyanath, S.; Sergenti, E. Economic Shocks and Civil Conflict: An Instrumental Variables Approach. J. Political Econ. 2004, 112, 725–753. [Google Scholar] [CrossRef]
- Blattman, C.; Miguel, E. Civil War. J. Econ. Lit. 2010, 48, 3–57. [Google Scholar] [CrossRef]
- Hsiang, S.; Burke, M.; Miguel, E. Quantifying the Influence of Climate on Human Conflict. Science 2013, 341, 13. [Google Scholar] [CrossRef] [PubMed]
- Buhaug, H.; Nordkvelle, J.; Bernauer, T.; Böhmelt, T.; Brzoska, M.; Busby, J.W.; Ciccone, A.; Fjelde, H.; Gartzke, E.; et al. One effect to rule them all? A comment on climate and conflict. Clim. Chang. 2014, 127, 391–397. [Google Scholar] [CrossRef]
- Zhang, D.D.; Brecke, P.; Lee, H.F.; He, Y.-Q.; Zhang, J. Global climate change, war, and population decline in recent human history. PNAS 2007, 104, 19214–19219. [Google Scholar] [CrossRef] [PubMed]
- Kennett, D.J.; Breitenbach, S.F.M.; Aquino, V.V.; Asmerom, Y.; Awe, J.; Baldini, J.U.L.; Bartlein, P.; Culleton, B.J.; Ebert, C.; Jazwa, C.; et al. Development and Disintegration of Maya Political Systems in Response to Climate Change. Science 2012, 338, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Schubert, R.; Schellnhuber, H.J.; Buchmann, N.; Epiney, A.; Grieβhammer, R.; Kulessa, M.; Messner, D.; Rahmstorf, S.; Schmid, J. Climate Change as a Security Risk, German Advisory Council on Global Change. 2008. Available online: http://www.wbgu.de/wbgu_jg2007_engl.html (accessed on 1 March 2008).
- Homer-Dixon, T. On the Threshold: Environmental Changes as Causes of Acute Conflict. Int. Secur. 1991, 16, 76–116. [Google Scholar] [CrossRef]
- Homer-Dixon, T. Environmental Scarcities and Violent Conflict: Evidence from Cases. Int. Secur. 1994, 19, 5–40. [Google Scholar] [CrossRef]
- Diamond, J. Collapse: How Societies Choose to Fail or Succeed; Penguin Group: New York, NY, USA, 2005. [Google Scholar]
- Skaperdas, S. Contest Success Functions. Econ. Theory 1996, 7, 283–290. [Google Scholar] [CrossRef]
- Olsson, O.; Congdon Fors, H. Congo: The Prize of Predation. J. Peace Res. 2004, 41, 321–336. [Google Scholar] [CrossRef]
- Brander, J.A.; Taylor, S. The Simple Economics of Easter Island: A Ricardo-Malthus Model or Renewable Resource Use. Am. Econ. Rev. 1998, 88, 119–138. [Google Scholar]
- Reuveny, R.; Maxwell, J.W. Conflict and Renewable Resources. J. Confl. Resolut. 2001, 45, 719–742. [Google Scholar] [CrossRef]
- Sherif, M.; Harvey, O.J.; White, B.J.; Hood, W.R.; Sherif, C.W. The Robbers Cave Experiment: Intergroup Conflict and Cooperation; Wesleyan University Press: Middletown, CT, USA, 1961. [Google Scholar]
- Tajfel, H.; Flament, C.; Billig, M.; Bundy, R. Social categorization and inter-group behavior. Eur. J. Soc. Psychol. 1971, 1, 149–178. [Google Scholar] [CrossRef]
- Rodrik, D. Where did all the growth go? External shocks, social conflict, and growth collapses. J. Econ. Growth 1999, 4, 385–412. [Google Scholar] [CrossRef]
- Dalgaard, C.-J.; Olsson, O. Why Are Rich Countries More Politically Cohesive? Scand. J. Econ. 2013, 115, 423–448. [Google Scholar] [CrossRef]
- Rohner, D.; Thoenig, M.; Zilibotti, F. War Signals: A Theory of Trade, Trust, and Conflict. Rev. Econ. Stud. 2013, 80, 1114–1147. [Google Scholar] [CrossRef]
- Copeland, B; Taylor, S. Trade, tragedy and the commons. Am. Econ. Rev. 2009, 99, 725–749. [Google Scholar]
- Engel, S.; Lopez, R.; Palmer, C. Community-Industry Contracting over Natural Resource Use in a Context of Weak Property Rights. Environ. Resour. Econ. 2006, 33, 73–93. [Google Scholar] [CrossRef]
- van den Brink, R.; Bromley, D.; Chavas, J.P. The Economics of Cain and Abel: Agro-Pastoral property Rights in the Sahel. J. Dev. Stud. 1995, 31, 373–399. [Google Scholar] [CrossRef]
- Turner, D. Political Ecology and the Moral Dimensions of Resource Conflicts: The Case of Farmer-Herder Conflicts in the Sahel. Political Geogr. 2004, 23, 863–889. [Google Scholar] [CrossRef]
- Olsson, O.; Siba, E. Ethnic cleansing or resource struggle in Darfur? An empirical analysis. J. Dev. Econ. 2013, 103, 299–312. [Google Scholar] [CrossRef]
- Olsson, O. After Janjaweed? Socioeconomic Impacts of the Conflict in Darfur. World Bank Econ. Rev. 2010, 24, 386–411. [Google Scholar] [CrossRef]
- Alix-Garcia, J.; Bartlett, A.; Saah, D. The Landscape of Conflict: IDPs, Aid, and Land-Use Change in Darfur. J. Econ. Geogr. 2013, 13, 589–617. [Google Scholar] [CrossRef]
- De Juan, A. Long-term Environmental Change and Geographical Patterns of Violence in Darfur, 2003–2005. Political Geogr. 2015, 45, 22–33. [Google Scholar] [CrossRef]
- De Waal, A.; Hazlett, C.; Davenport, C.; Kennedy, J. The Epidemiology of Lethal Violence in Darfur: Using Micro-Data to Explore Complex Patterns of Ongoing Armed Conflict. Soc. Sci. Med. 2014, 120, 368–377. [Google Scholar] [CrossRef] [PubMed]
- Vanrooyen, M.; Leaning, J.; Johnson, K.; Hirschfeld, K.; Tuller, D.; Levine, A.; Hefferman, J. Employment of a Livelihoods Analysis to Define Genocide in the Darfur Region of Sudan. J. Genocide Res. 2008, 10, 343–358. [Google Scholar] [CrossRef]
- Binmore, K.; Rubinstein, A.; Wolinsky, A. The Nash Bargaining Solution in Economic Modelling. Rand J. Econ. 1986, 17, 176–188. [Google Scholar] [CrossRef]
- Flint, J.; De Waal, A. Darfur: A New History of a Long War (Revised and Updated); Zed Books: New York, NY, USA, 2008. [Google Scholar]
- Collier, P.; Hoeffler, A. Greed and Grievance in Civil War. Oxf. Econ. Pap. 2004, 56, 563–595. [Google Scholar] [CrossRef]
- Mehlum, H.; Moene, K.; Torvik, R. Institutions and the Resource Curse. Econ. J. 2006, 116, 1–20. [Google Scholar] [CrossRef]
- Olsson, O. Conflict Diamonds. J. Dev. Econ. 2007, 82, 267–286. [Google Scholar] [CrossRef]
- van der Ploeg, F. Natural Resources: Curse of Blessing? J. Econ. Lit. 2011, 49, 366–420. [Google Scholar] [CrossRef]
- Stern, N. Stern Review on the Economics of Climate Change; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- IPCC. IPCC Fourth Assessment Report, Working Group II: Impacts, Adaptation and Vulnerablility; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- UNEP. Sudan: Post-Conflict Environmental Assessment; United Nations Environmental Programme: Nairobi, Kenya, 2007. [Google Scholar]
- Degomme, O.; Guha-Sapir, D. Patterns of Mortality Rates in Darfur Conflict. Lancet 2010, 375, 294–300. [Google Scholar] [CrossRef]
- D-JAM. Darfur Joint Assessment Mission: Status of Natural Resources and the Environment, Republic of Sudan. 2006. [Google Scholar]
- United Nations. Report of the International Commission of Inquiry on Darfur to the United Nations Secretary General; United Nations: Geneva, Switzerland, 2005.
- Prunier, G. Darfur: The Ambiguous Genocide; (Revised and Updated Edition); Cornell University Press: New York, NY, USA, 2007. [Google Scholar]
- Kevane, M.; Gray, L. Darfur: Rainfall and Conflict. Environ. Res. Lett. 2008, 3, 1–10. [Google Scholar] [CrossRef]
- UNHCR/INTERSOS. Return-Oriented Profiling in the Southern Part of West Darfur and Corresponding Chadian Border Area UNHCR/INTERSOS. 2005. Availiable online: http://webgis-darfur.intersos.org (accessed on 4 March 2009).
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).