1. Introduction
Understanding how social systems can affect the evolution of cooperation has attracted considerable attention in evolutionary biology and the social sciences [
1,
2,
3]. On the one hand, commitment is one of the most practical tools for maintaining social interactions and takes diverse forms (e.g., from a promise to a deposit and mortgage). Game-theoretical studies have shown that costly commitment can promote the evolution of cooperation in the context of the prisoner’s dilemma [
4,
5,
6,
7,
8]. This widely-studied commitment strategy works in a peer-to-peer fashion by allowing a personal proposer to ask his/her co-player to commit to cooperation, but also enforcing compensation if those who commit defect at a later stage. On the other hand, in various social systems, costly punishment has been widely studied in terms of governing the commons and maintaining the social order [
9,
10,
11,
12]. In contrast to this, relatively little is known about the effects of interaction between costly punishment and commitment technologies. Positive effects of the exclusion of non-committers [
7] and mixed strategies of peer punishment and commitment [
8] have recently been reported. However, it is unclear how prior agreement with the contribution to costly punishment, which itself is another crucial common good, can affect the evolution of cooperation.
Two major strands of costly punishment are peer punishment and pool punishment. Importantly, the systems for peer and pool punishment present a puzzling tradeoff between efficient punishment and effective discrimination of free riders [
13].
Peer punishment [
14,
15,
16] is a reactive and individualistic system for privately sanctioning a particular target in reaction to its past behavior in joint efforts. Peer punishment is however not so effective that it is likely to cause the so-called second-order free rider problem: freeloading on the efforts of others with respect to punishment undermines the equilibrium with peer punishment [
17,
18].
Pool punishment [
13,
19,
20] is proactive and institutional. In pool punishment, each person is initially offered an opportunity to proactively contribute to the pool punishment, regardless of whether free riders are present. This is effective in searching for and sanctioning second-order free riders. The pool punishment prevents second-order free riders from drifting into a resident population of costly punishers who may otherwise earn a payoff equal to that of the free riders. Pool punishment, however, is more wasteful compared to peer punishment, because all of the pooling is used for the system (e.g., wages for police officers). Indeed, once a cooperative state protected by pool punishment has been established, it is desirable to improve the unconditional pooling system.
For an improved solution, we turn to the commitment with a refundable deposit [
21]. We consider commitment to contribution in terms of not only cooperation, but also peer punishment. Such comprehensive commitment to a set of prosocial behaviors has not been explored in previous game-theoretical studies. In this manuscript, for comparison with pool punishment, we assume that players are offered an opportunity to commit by paying deposits to a neutral institution [
21], rather than offering mutual security to other players. In contrast to wasteful pool punishment, the deposit will be refunded, as long as players comply with the social rules. As such, we propose a novel model for the evolution of cooperation by deposit-based commitment to prosocial behaviors (see
Section 2). Punishment and commitment have already been compared by investigating the effective cost-to-effect ratio in the respective independent systems [
4]. We, for the first time, investigated replicator dynamics consisting of punishment and commitment to understand the competition of these (see
Section 3). In particular, we analyzed the conditions for an evolutionary transition from a homogeneous state of pool punishment to a homogeneous state of deposit-based commitment.
2. Materials and Methods
We consider infinitely large, well-mixed populations. The game sequence comprises the following three stages:
Commitment stage: First, each player is offered an opportunity to commit to the social rules by either making deposits or pooling for punishment.
Donation game (DG) stage: This is a one-shot DG [
22]. Each player interacts with a randomly-sampled co-player, both of whom decide independently whether to donate to the opponent at cost
to themselves. To donate means to play C; otherwise, they play D. Each donation leads to some benefits
b to the opponent with
. This is a social-dilemma situation,
i.e., irrespective of what others do, switching to playing D is more advantageous than is playing C by saving cost
c; nevertheless, the net payoff is 0, if both play D, whereas it is
, if both play C.
Punishment stage: Finally, each player interacts with a co-player chosen by means of another random sample and independent of the co-player in the DG stage. Both players independently decide whether to punish their opponent based on each of the opponent’s acts in the commitment and DG stages. We assume that their acts in the last two stages are perfectly known to each other (e.g., through reputation).
Thus, throughout the game sequence, there are four decisions to make: committing, playing C, punishing non-committers and punishing D-players (
Table 1). Particularly when using commitment with a refundable deposit, we can combine (i) reactive sanction-execution as in peer punishment and (ii) proactive target sensing as in pool punishment. In our model, the social rules with which committers must comply are to play C in the DG stage and to punish all non-committers and D-players in the punishment stage. If those who commit by making deposits behave as prescribed in these rules, they will have their deposits refunded; otherwise, they will not.
To investigate the effects of commitment through deposit and to compare these effects with peer and pool punishment, we consider the following typical strategies.
Defector (ALLD): non-committing, playing D and punishing neither non-committers nor D-players.
Cooperator (ALLC): non-committing, playing C and punishing neither non-committers nor D-players.
Peer punisher (PEER): non-committing, playing C and punishing D-players individually, but not non-committers. The PEER punishes a D-player through fines with personal fees .
Pool punisher (POOL): committing by pooling fees for punishing non-committers and for D-players, playing C and punishing non-committers and D-players institutionally. The implementation of punishment is done with the aid of a central authority (e.g., hired sheriff or police force). In the punishment stage, fines or are imposed on a non-committer or a D-player, respectively. If the opponent is a non-committer and D-player (e.g., ALLD), the corresponding fine and fee are and , respectively.
Faithful committer (COM): committing by making fixed deposits , playing C and punishing non-committers and D-players individually. The COM punishes a non-committer through fines with personal fees and punishes a D-player through fines with personal fees . If the opponent is a non-committer and D-player (e.g., ALLD), the corresponding fine and fee are and , respectively. Finally, the deposit will be returned without loss, without being used to carry out punishment, at the end of the punishment stage.
Fake committer (FAKE): committing by making fixed deposits , playing D and punishing neither non-committers nor D-players. The deposit made by FAKE is not returned at all.
It is assumed that the frequencies of these strategies evolve with the replicator dynamics [
23]. Let
and
be the frequency and expected payoff of strategy
S, with
ALLC, ALLD, PEER, POOL, COM or FAKE. The replicator equations are defined as
with
, where
is the average payoff across the population. See
Table 1 and
Table 2 for an overview of the definitions and precise expected payoff values for the strategies considered above.
Table 1.
Decisions and reactions of strategies. Non-committers (ALLD, ALLC and PEER) are punished by POOL and COM. D-players (ALLD and FAKE) are punished by PEER, POOL and COM. Fake committers (FAKE) are sanctioned by means of no refund.
Table 1.
Decisions and reactions of strategies. Non-committers (ALLD, ALLC and PEER) are punished by POOL and COM. D-players (ALLD and FAKE) are punished by PEER, POOL and COM. Fake committers (FAKE) are sanctioned by means of no refund.
| Strategy | Pre-Commit? | C or D in DG? | Punish Non-Committer? | Punish D-Player? | Punished by |
|---|
| ALLD | No | D | No | No | PEER, POOL, COM |
| ALLC | No | C | No | No | POOL, COM |
| PEER | No | C | No | Yes | POOL, COM |
| POOL | Yes (by pooling) | C | Yes | Yes (by central authority) | |
| COM | Yes (by deposit) | C | Yes | Yes | |
| FAKE | Yes (by deposit) | D | No | No | No refund |
Table 2.
Expected payoffs of strategies. We denote by , , , and d the coefficients of fines for non-committers, fines for D-players, fees for punishing non-committers, fees for punishing D-players and deposit, respectively. In the second column, B denotes the expected benefit in the DG, given by proportional to the fraction of C-players. Fines and are imposed, respectively, on non-committers (ALLC, ALLD and PEER) and D-players (ALLD and FAKE), depending on the fractions of punishers. PEER and COM incur fees for punishing D-players, while the latter also incurs fees for punishing non-committers. POOL pays constant fees for pooling, irrespective of the fractions of non-committers and D-players.
Table 2.
Expected payoffs of strategies. We denote by , , , and d the coefficients of fines for non-committers, fines for D-players, fees for punishing non-committers, fees for punishing D-players and deposit, respectively. In the second column, B denotes the expected benefit in the DG, given by proportional to the fraction of C-players. Fines and are imposed, respectively, on non-committers (ALLC, ALLD and PEER) and D-players (ALLD and FAKE), depending on the fractions of punishers. PEER and COM incur fees for punishing D-players, while the latter also incurs fees for punishing non-committers. POOL pays constant fees for pooling, irrespective of the fractions of non-committers and D-players.
| Strategy | DG | Punishment of Non-Committer | Punishment of D-Player | Deposit |
|---|
| ALLD | B | | | |
| ALLC | | | | |
| PEER | | | | |
| POOL | | | | |
| COM | | | | |
| FAKE | B | | | |
3. Results
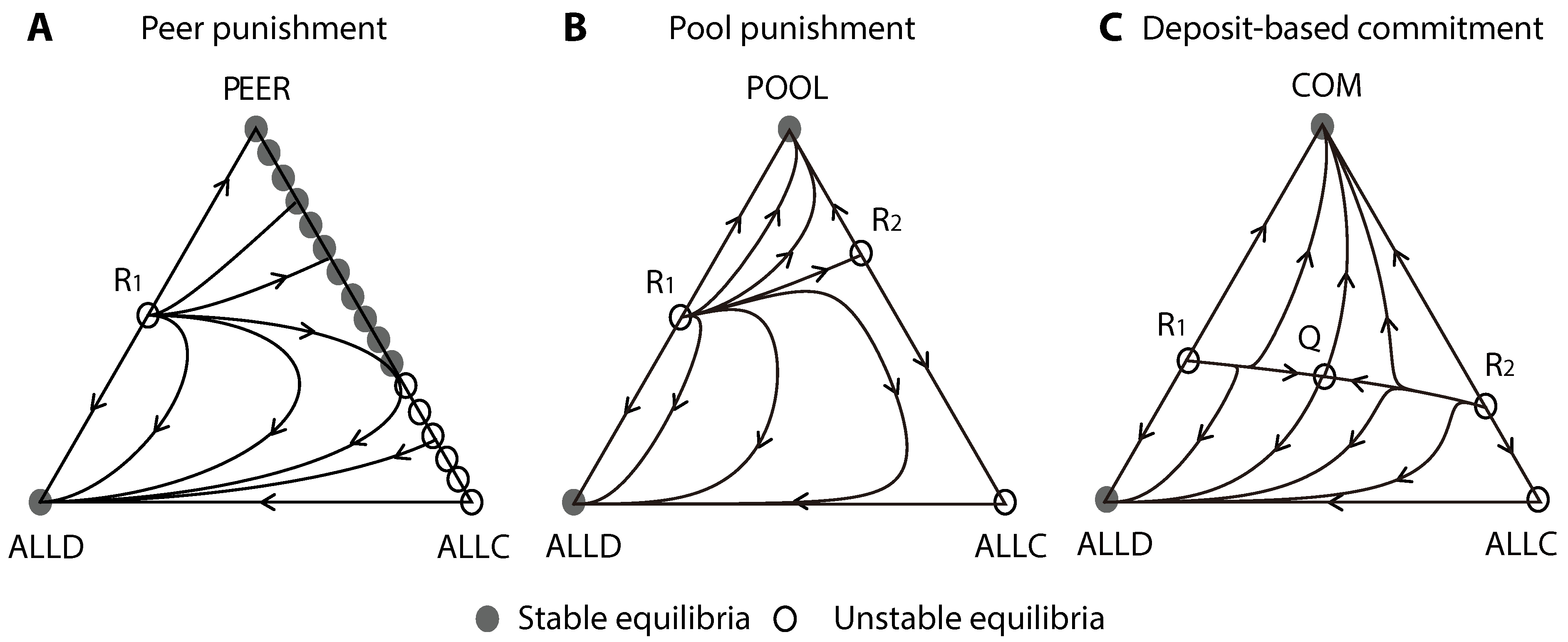
We analyze the replicator dynamics for three strategies, ALLC, ALLD and each of the sanctioning strategies, peer punishment (PEER), pool punishment (POOL) and faithful commitment (COM) (
Figure 1). See Section S1 of the Supplementary Materials for a detailed analysis of the COM case (
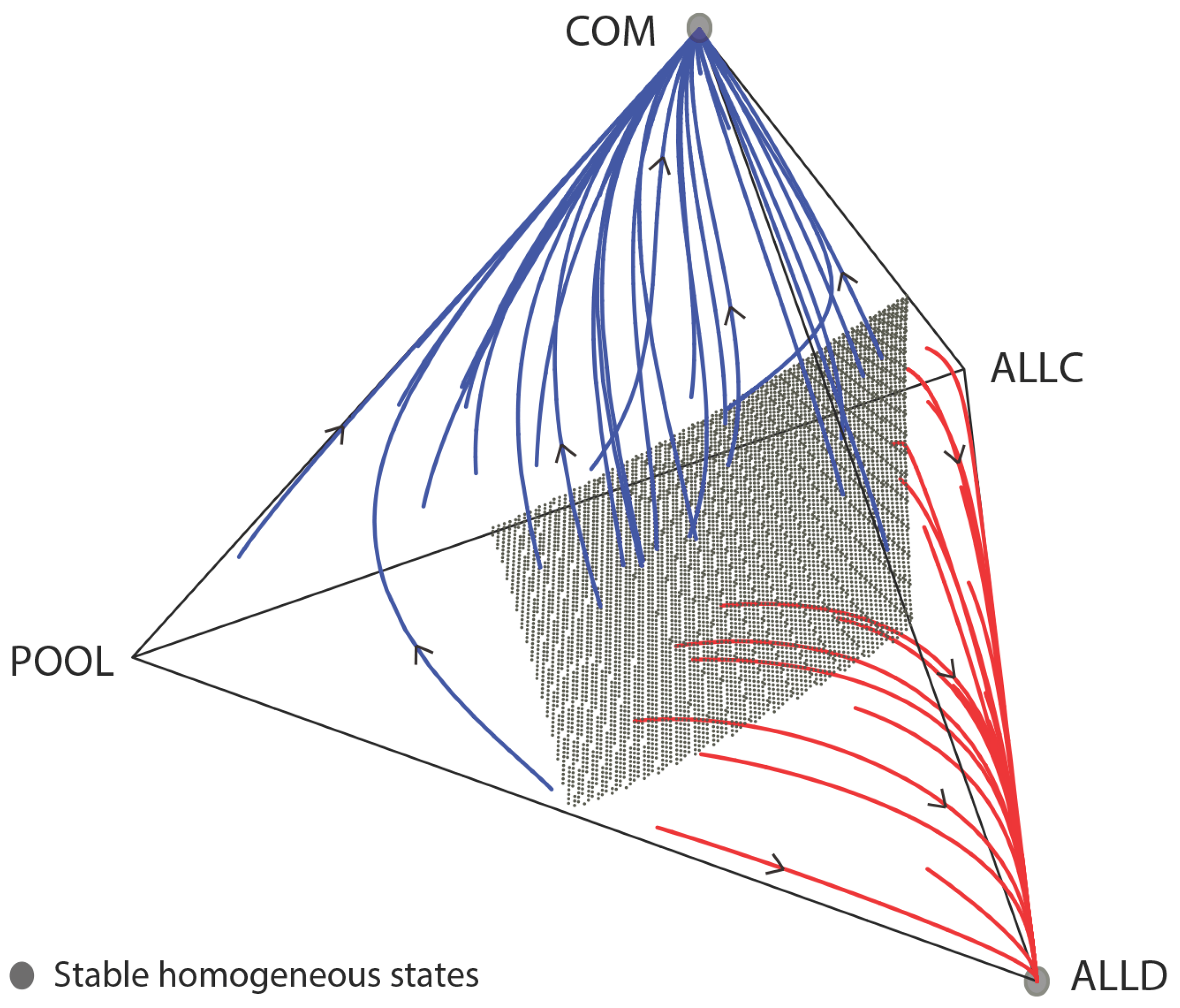
Figure 1C). We then look at the competition between POOL and COM in the replicator dynamics with ALLC and ALLD (
Figure 2). See Section S2 and Figure S1 of the Supplementary Materials for the replicator dynamics for ALLC, ALLD, PEER and COM. We note that ALLD dominates ALLC in any mixed population that consists exclusively of ALLD and ALLC. We also examine the robustness of the main results by considering fake commitment, antisocial punishment or pool punishment with tax refund.
Peer punishment (
Figure 1A): The presence of ALLD leads ALLC to outcompete PEER by saving the fee
for punishment. Thus, no interior equilibrium exists at which the three strategies coexist, and all interior orbits converge to the specific boundary areas of the state space. Parts of orbits are attracted to the ALLD node (a homogeneous state of ALLD). If the fine given to a D-player,
, is larger compared to the cost in the DG game,
c, that is,
the other orbits converge to the PEER node or its adjacent segment of the PEER-ALLC edge (mixed states of PEER and ALLC). In particular, on the PEER-ALLD edge, the population’s state with a sufficient proportion of PEERs, such that:
will evolve to the PEER node. In any mixture of PEER and ALLC, no costly punishment occurs; thus, these strategies are equivalent in terms of payoffs. From this neutrality, a population’s state on the edge can drift to its unstable segment adjacent to the ALLC node. This can result in leaving the edge and eventually reaching the ALLD node.
Pool punishment (
Figure 1B): Any mixed state consisting exclusively of POOL and ALLC is no longer in equilibrium because in the commitment stage, ALLC is identified as a non-committer to be punished by POOL. The POOL node can turn into a local attractor with sufficiently large fines on a D-player and non-committer, with
and:
In this case, the evolutionary dynamics are bi-stable. With a sufficient proportion of POOLs,
, the population’s state can evolve straightforwardly to the POOL node; otherwise, they evolve to the other attractor, the ALLD node. The thresholds are, for example,
for the population’s state on the POOL-ALLD edge and:
for the population’s state on the POOL-ALLC edge.
Figure 1.
Replicator dynamics in donation games with different sanctioning systems. (A) In peer punishment, with its small perturbation and neutral drift around the PEER-ALLC edge, the population’s state eventually converges to the ALLD node; (B) in pool punishment, the POOL-ALLC edge no longer consists of a continuum of equilibria, and instead, the POOL node turns into a local attractor; (C) in deposit-based commitment, the basin of attraction for the homogeneous state of punishers is broader than that in peer and pool punishment. For specific parameters, the interior state space can have a unique equilibrium Q that is a saddle point. Parameters: , , , , and .
Figure 1.
Replicator dynamics in donation games with different sanctioning systems. (A) In peer punishment, with its small perturbation and neutral drift around the PEER-ALLC edge, the population’s state eventually converges to the ALLD node; (B) in pool punishment, the POOL-ALLC edge no longer consists of a continuum of equilibria, and instead, the POOL node turns into a local attractor; (C) in deposit-based commitment, the basin of attraction for the homogeneous state of punishers is broader than that in peer and pool punishment. For specific parameters, the interior state space can have a unique equilibrium Q that is a saddle point. Parameters: , , , , and .
Faithful commitment (
Figure 1C): The COM-ALLC edge consists of no continuum of fixed points, as in pool punishment. Moreover, the COM node is a local attractor for sufficiently large fines on a D-player with
and any positive fines on a non-committer with:
Regarding the dependence on the initial conditions, sufficient COMs can overrun the population, converging to the COM node; otherwise, the population’s state will converge to the ALLD node. The thresholds are, for example,
for the population’s state on the COM-ALLD edge and:
for the population’s state on the COM-ALLC edge. The state space can have a unique interior equilibrium (
Figure 1C), which is generic and a saddle point (see the Supplementary Materials for details).
Figure 2.
Competition of pool punishment and deposit-based commitment. Populations are attracted to either a state of commitment-based cooperation (COM node) or one of mutual defection (ALLD node). The gray surface separates the basins of attraction for the COM and ALLD nodes. The relative size of the basin of attraction for the COM node is approximately 65% for the specific parameters. In particular, commitment-based cooperation outcompetes coercion-based cooperation (POOL node). Parameters are the same as those given in
Figure 1.
Figure 2.
Competition of pool punishment and deposit-based commitment. Populations are attracted to either a state of commitment-based cooperation (COM node) or one of mutual defection (ALLD node). The gray surface separates the basins of attraction for the COM and ALLD nodes. The relative size of the basin of attraction for the COM node is approximately 65% for the specific parameters. In particular, commitment-based cooperation outcompetes coercion-based cooperation (POOL node). Parameters are the same as those given in
Figure 1.
Efficiency and effectiveness: Equations (3)–(8) suggest the following. To stabilize a homogeneous state of COM for the invasion of a rare ALLC or PEER, it is sufficient that the punishment fine for non-committers is in Equation (6) (see also Section S2 and Figure S1 of the Supplementary Materials). In the case of such rare invasion, the expected punishment cost for COM is zero. In the case of POOL, the punishment fine should be larger than the tax in Equation (3). Therefore, deposit-based commitment requires a relatively lower running cost compared to the taxes in pool punishment. Deposit-based commitment is more efficient compared to pool punishment to maintain full cooperation. Furthermore, the threshold values in Equations (7) and (8) are smaller compared to those in Equations (4) and (5), leading to a wider range of parameters for reaching full cooperation (and thus more effective) than in pool punishment.
Competition in pool punishment and faithful commitment (
Figure 2): Here, we consider ALLC, ALLD, POOL and COM. It is obvious that when
, a rare COM can invade a homogeneous state of POOL and eventually overrun the population. In particular, COM earns a higher expected payoff compared to POOL in any heterogeneous population with POOL and COM, by COM’s conditional payment of
and
. Therefore, there is no interior equilibrium, and all of the interior orbits will converge to the boundary. From the boundary dynamics mentioned previously, it follows that the replicator dynamics can be bi-stable for the attractors, that is the COM and ALLD nodes.
Pool punishment with tax refund and public good games: The dominance of COM over POOL is robust even for a tuned pool punishment. Pool punishment can become more efficient, for instance, by considering a refund of unused taxes in the absence of free riders among interactions [
24]. In this case, pool punishers will pay net costs with
and
, where
α and
β describe the fractions of unused taxes. Considering payment for wages of hired sheriffs or police officers, it would be realistic to assume that
and
. This means that the expected payoff for pool punishers with the tax refund is less than or equal to that for COM (equality holds if and only if
). It is also clear that our main results that COM dominates POOL and that a 100%-COM state is stable in the system with ALLD and ALLC do not change throughout general public good games (that is, the expected benefit
B in the DG stage is the same for all, yet only C-players incur cost
c, as outlined in
Table 2).
Fake commitment: When the size of deposit
d is sufficiently large compared to some of the COM’s costs, a rare FAKE is not able to invade a homogeneous state of COM. The condition is that the loss of deposit outweighs the marginal benefit from switching to FAKE,
. We then derive a sufficient condition that a rare FAKE is not able to invade any state that consists exclusively of POOL and COM (that is, on the POOL-COM edge in
Figure 2). Considering that the taxes for POOL are constant, the sufficient condition is:
In this case, the transition of POOL and COM is robust against the invasion by a rare FAKE. It is obvious that these results hold as long as rare invaders are willing to play D, irrespective of actions in the punishment stage (even if the punishment is antisocial, as examined later). We note that this can be applied to a fake pool punisher who plays D because the fake pool punisher is worse off than is the fake committer who plays D and punishes.
This is not the case, however, when considering another complicated faker who is willing to commit and play C, yet not commit to punish non-committers, D-players or both. In the absence of non-committers and D-players, this type of faker can receive the same expected payoff as COM. In this case, the replicator dynamics are not able to select only for COM, possibly allowing those who punish to turn to those who do not punish, eventually destabilizing a 100%-COM state through the accumulation of neutral change (e.g., by mutation or exploration) in the punishing trend.
Antisocial punishment: The main results that COM dominates POOL and that a 100%-COM state in the system with ALLD and ALLC is stable are upheld even in the presence of antisocial punishers,
i.e., punishing prosocialists who are willing to contribute to social welfare, such as players with ALLC, PEER, POOL or COM in the model. Previous studies reported that antisocial punishment could prevent the evolution of costly peer punishment of free riders [
25,
26].
In commitment, it is clear that those who commit to cooperation and punishment of non-committers and D-players, yet carry out antisocial punishment (with fee
), are classified as a kind of fake committer; thus, their deposits will not be returned. Similar to Equation (9), the invasion by rare antisocial committers to the POOL-COM edge can be suppressed by setting a sufficiently large deposit, such that:
In this case, it is sufficient to update the rule that prohibits antisocial punishment.
In the case that antisocial punishers do not commit to the social rule, punishment with sufficiently large fines
and
for non-committers and D-players, respectively, will suffice to protect the POOL-COM edge. The sufficient conditions are:
for C-players with antisocial punishment and:
for D-players with antisocial punishment. As such, considering rare antisocial punishment does not affect the replicator dynamics for POOL and COM and the results for these. The results in Equations (11) and (12) can be generalized for non-committers by considering any combination of costly punishments (with total fee
), specifically whether to punish or not and who to punish.
4. Discussion
We investigated deposit-based commitment to cooperation and peer punishment, a novel mechanism for maintaining social order. Our analysis shows that considering such a mechanism can lead to stabilizing full cooperation in the system with classic unconditional defectors (ALLD) and cooperators (ALLC), as well as in pool punishment. This holds even when including antisocial punishment in the system. However, this is not the case when considering just peer punishment without pre-commitment. We assume that faithful committers from the outset have insurance that is powerful enough to cover any expected payoff loss relative to fake committers. To receive such insurance, faithful committers are required only to follow a social “code”. With commitment, faithful committers do not need to reciprocate such fake acts or rule-breakers, and for suitable deposits, they can form a sub-game perfect Nash equilibrium [
21]. This mechanism can prevent the infamous, infinite regress to higher-order free rider problems [
27]. Thus, true public enemies are those who are not willing to commit [
7]. In competition with non-committers, a faithful committer can no longer rely on the binding force of deposit; thus, it is necessary to disadvantage non-committers. Our model efficiently enables this by combining separate mechanisms for continuous discrimination through commitment and conditional sanction with peer punishment.
Studies of the effects of pre-commitment on the evolution of cooperation have recently started to report some results [
4,
5,
6,
7,
8]. A common basic feature throughout these models is a commitment-compensation strategy to pay for setting up a commitment that guarantees cooperation and enforces compensation for its default. In the models, players who accept the commitment yet later defect will have to compensate non-defaulting players. Players who do not accept the commitment will not interact anymore and will only earn a payoff of zero. The commitment-compensation mechanism is closely related to pool punishment in the sense that the cost of setting up a commitment occurs regardless of the existence of defaulting players, and it is not refunded (a sunk cost). Different from the commitment-compensation mechanism, in our model, a key factor is commitment to peer punishment, and its net cost occurs only in the presence of defaulting players. Moreover, non-committers are treated with peer punishment, as well, not refusal to interact.
We note that even without the commitment to punish, our model can maintain cooperation if participation in the commitment to cooperate is compulsory; otherwise, non-committers willing to defect can proliferate, as executing costly punishment is not credible. As is known, a popular norm in human societies is one that prescribes not to help the bad and assesses persons who intentionally help or overlook the bad as bad (e.g., the “standing” norm for reciprocity [
28]). Members who accept this kind of norm would not deviate, avoiding loss of one’s reputation (namely, deposits). Additionally, diverse religions often have the discipline of committing to punishment of evil people (e.g., by making no offering).
In this manuscript, for the sake of analytical simplicity, we assume a well-mixed model in which players interact with all other players with equal probability in the DG and punishment stages, and those matching in the different stages are not correlated. This contributes to analyzing the conditions by which the system’s transition from pool punishment to deposit-based commitment is robust, despite the presence of various antisocial punishers and fake players. In practice, however, it would be more realistic for sanctioning co-players to differ from (e.g., is higher than) sanctioning other individuals in terms of the probability of sanctioning. Future work should investigate the effects of considering specific assortments on the conditions for transitions of sanctioning systems.
Another limitation of our model is that an equilibrium state of faithful commitment can be invaded by some specific fake committers with neutral drift. Discriminating those unwilling to play C is relatively easy because the opportunity to choose C/D occurs unconditionally. Discriminating those unwilling to punish, however, is not that easy. In the absence of persons undergoing punishment (D-players or non-committers), the fake committers who do not punish can receive the same expected payoff as faithful committers who punish. In this case, Darwinian selection or social learning based only on the payoff difference confuses fake committers with faithful committers. A possible efficient solution in this regard that can save on social costs is to leave committers to prove their own willingness to punish. Although it is logically possible for fake committer to fake the self-certificate of willingness to punish, this would be costly and thus improbable. Indeed, it would take continuous efforts to keep such fakeness, if inspection of the willingness to punish may come about in any given moment throughout the game. To understand this aspect, further development of the model, particularly from the psychological and epistemic perspectives, would be required.
Faithful commitment to social rules is likely to emerge through a specific state in which full pool punishment has already been established (
Figure 2). Previous studies have reported that rewards, signaling, optional participation, modest punishment, and so on, can help establish costly punishment [
13,
24,
29,
30,
31,
32]. Previous findings have also indicated that binding through voting can affect endogenous choice or formation of a sanctioning institution [
33,
34]. Understanding how such inspiring measures can affect deformation of the existing institution remains to be explored.
Experimental work on the effects of commitment with refundable deposits for cooperation is not widespread, but the results from existing works correspond with our results. Cherry and McVoy [
35] evaluated the performance of a deposit-refund scheme that enforces compliance with public good games through laboratory experiments. Their results are consistent with the current theory, suggesting that considering refundable deposits can lead to maintaining nearly full cooperation without stark sanctioning systems. They further showed that the performance of the deposit-refund mechanism depends on the threshold number of participants necessary to form agreement. Unanimous agreement rather than partial agreement is more likely to achieve nearly full cooperation. In contrast to this, our model does not consider coordination failure in obtaining agreement, but instead, it considers agreement in punishment for those who do not join. It seems that the effects of sanctioning non-committers can complement those of unanimous agreement.
In the case of excludable goods, Shichijo
et al. [
36] recently showed, in theory and practice, that a deposit-refund scheme succeeds in overcoming the coordination-failure problem. In their model, the upfront payment of deposits also serves as a costly signal that proves the player’s type, and thereby, those who pay no deposit are not allowed to enter the contribution stage (which corresponds to the DG stage in our model). Their model and results are comparable with a variant of our model in which peers exclude rather than punish non-committers (
cf. [
7]).
An important implication of our model is the emergence of links between prosocial behaviors. It is known, on the one hand, that a fixed link between cooperation and punishment or incentives and meta-incentives can promote a prosocial state [
37,
38]. On the other hand, the significance of the correlation between cooperation and punishment has not yet been observed [
39,
40,
41]. We show that individuals are more likely to prefer prescribed prosocial behaviors considering deposit-based commitment rather than peer punishment alone.