Sequential Rationality in Continuous No-Limit Poker

Abstract

Newman’s (1959, Operations Research, 7, 557–560) solution for a variant of poker with continuous hand spaces and an unlimited bet size is modified to incorporate sequential rationality.

Newman [1] analyzes a model of ‘real’ poker, where a player may bet any amount without limit. In particular, each of two risk-neutral individuals, A and B, pays an ante of 1 unit into the pot in return for a private hand—x for A, y for B—dealt uniformly at random from the interval $(0,1)$. A then chooses a bet $\beta \ge 0$ to put into the pot. B finally decides either to call (matching the bet) or fold. If B calls, both players’ hands are revealed and the higher hand receives the pot of $2(\beta +1)$; if they have the same hand, the pot is split evenly between them. If B folds, the hands remain private and A wins the pot of $\beta +2$.

Newman provides a solution where A bets 0 if his hand lies in the interval $(1$/$7,4$/$7)$, and bets β with either hand $x_{\beta }^{-}=(1$/$7)(1-3{\xi }^2+2{\xi }^3)$ or $x_{\beta }^{+}=1-(3$/$7){\xi }^2$, where $\xi =2/(\beta +2)$; B then calls the bet β if and only if his hand exceeds $y_{\beta }^{*}=1-(6$/$7)\xi$.1 An increasing amount $\beta \left(x\right)$ is thus bet by A hands in the interval $(4$/$7,1)$, with an asymptote at 1, and these bets are mimicked by hands in the interval $(0,1$/$7)$, as illustrated in Figure 1.

Hence, B knows that the bet β was made by one of two possible hands, $x_{\beta }^{-}$ or $x_{\beta }^{+}$, but does not know which one; he is then indifferent at a cutoff $y_{\beta }^{*}$ somewhere in between the two possible hands. As Newman notes, his solution is a pure strategy for both A and B; hence, the solution exhibits the pure-strategy “bluffing” encountered, for instance, in the simple von Neumann and Morgenstern [2] (pp. 211–219) limited-bet model (and in the continuous case of the bounded bet space model of Bellman and Blackwell [3]).

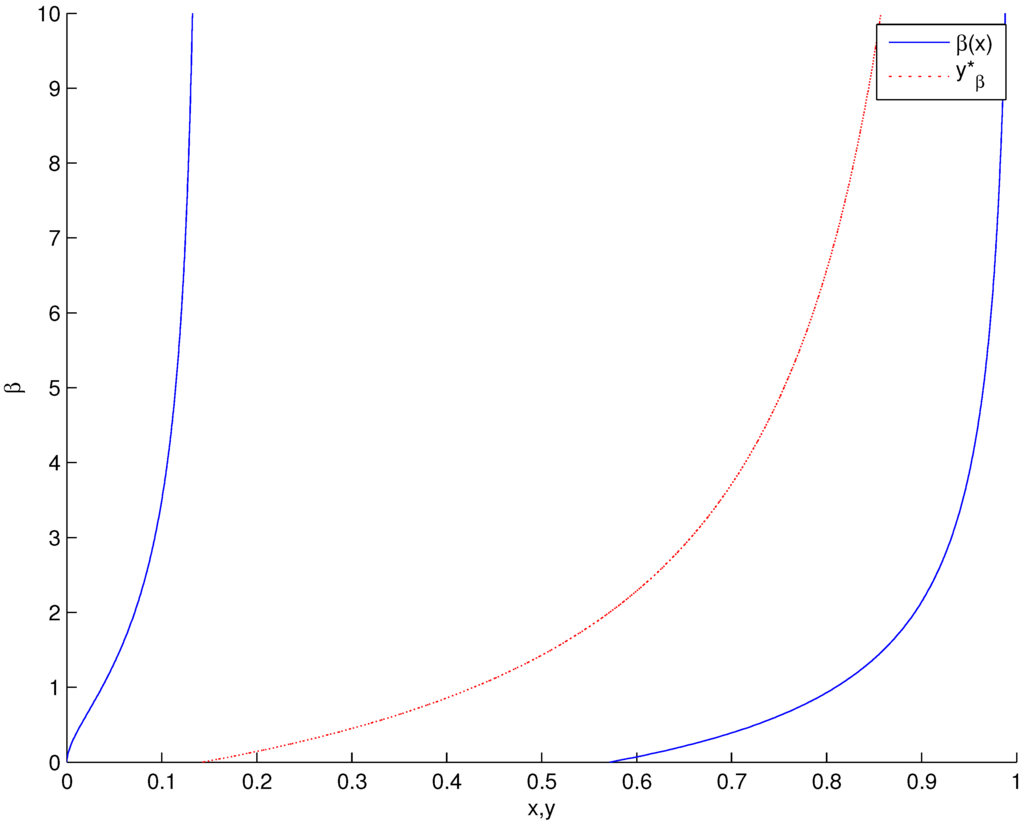
Figure 1. Newman’s solution.

Figure 1. Newman’s solution.

Since Newman’s original paper, however, a great deal of progress has of course been made in refining Nash equilibria to capture sequential rationality in finite extensive-form games with perfect recall [4,5]. Here I adapt sequential rationality for the infinite-game setting of Newman. A sequentially rational player must optimise not just in the game overall, but at each of his information sets. In Newman’s game, for a sequentially rational B, the cutoff hand $y_{\beta }^{*}$ must be indifferent between calling β and folding:

$$(2\beta +2)Pr\left(x<y_{\beta }^{*}\mid \beta \right)+0Pr\left(x>y_{\beta }^{*}\mid \beta \right)-\beta =0$$

(1)

and for (weak) consistency of beliefs, it must be the case that

$$\frac{Pr\left(x<y_{\beta }^{*}\right)Pr\left(\beta \mid x<y_{\beta }^{*}\right)}{Pr\left(\beta \right)}=\frac{\beta }{2\beta +2}$$

(2)

by Bayes’ rule. These are the requirements of a weak perfect Bayesian equilibrium [6,7]: strategies are sequentially rational and beliefs are derived from Bayes’ rule along the equilibrium path. If each information set were reached with strictly positive probability, such a weak perfect Bayesian equilibrium would automatically be a sequential equilibrium [5]; indeed, this would make Bayesian Nash equilibrium sufficient for sequential equilibrium.

With the infinite strategy set of A, however, whilst each of B’s information sets is along the equilibrium path under Newman’s solution, they are not all reached with strictly positive probability. Indeed, $Pr\left(\beta \right)=Pr(x=x_{\beta }^{-})+Pr(x=x_{\beta }^{+})=0$ for all $\beta >0$, and as a result, the left-hand side of Equation (2) is undefined. In response to this problem, I adopt the approach of Aumann [8], Jung [9] and González Díaz and Meléndez-Jiménez [10], and work directly with conditional probabilities. This is equivalent to the use of Bayes’ rule in finite games, but is also well-defined in infinite games; any conditionally updated beliefs must agree at information sets along the equilibrium path (even if they occur with probability zero). Now, a bet of β is equally likely to have been made by hands $x_{\beta }^{-}$ and $x_{\beta }^{+}$ (and no others) under Newman’s solution, so that Equation (1) implies

$$Pr\left(x<y_{\beta }^{*}\mid \beta \right)=\frac{\beta }{2\beta +2}=\frac{1}{2}$$

for all $\beta >0$, a contradiction. Newman’s solution thus violates sequential rationality under conditional updating. Since Bayesian Nash equilibrium requires such sequential rationality for almost every β in Newman’s game (i.e., except on a set of Lebesgue measure zero, given the uniform hand distribution and ${\left.\beta \left(x\right)\right|}_{(0,1/7)}={\left.\beta \left(x\right)\right|}_{(4/7,1)}$ a homeomorphism), his solution is not a Bayesian Nash equilibrium.

However, a modification of Newman’s solution does satisfy sequential rationality. To see this, note that the lowest that $y_{\beta }^{*}$ can be for positive β is 1/7, the lower limit of the interval of hands with which A checks. But then, given any bet $\beta >0$, A’s expected payoff from betting β is the same with any hand below 1/7; these hands win against the same folded B hands and lose against the same calling hands. In particular, all hands $x\in (0,1$$/7)$ win 2 when B folds and lose β when he calls; hence, they receive the expected payoff

$$2\left(1-\frac{6}{7}\xi \right)-\frac{6}{7}\xi \beta =\frac{2}{7}$$

(3)

from any bet $\beta >0$, which exceeds the $2x$ they get from betting 0. We are thus free to have each $x\in (0,1/7)$ mix between positive bets with the probabilities required for conditional updating of B’s beliefs. For instance, we might have each $x\in (0,1/7)$ play a mixed strategy putting probability $p_{\beta \left(x\right)}=\beta \left(x\right)/(\beta \left(x\right)+2)$ on Newman’s bet $\beta \left(x\right)$, with the complementary probability spread uniformly over a countably infinite subset $C\left(x\right)$ of ${\mathbb{R}}^{+}\backslash \left\{\beta \left(x\right)\right\}$, with ${\bigcap }_{x\in (0,1/7)}C\left(x\right)=\varnothing$.2 Thus, hand $x_2^{-}=1/14$ would bet 2 with probability $1/2$, and could spread the remaining $1/2$ probability uniformly over the set $\{\frac{1}{14},1\frac{1}{14},2\frac{1}{14},\dots \}$. Any $x\in [1/7,1)$, meanwhile, still bets according to Newman’s solution; the bet 2 would thus be made with probability 1 by hand $x_2^{+}=25/28$. With this strategy profile, a bet of $\beta >0$ is made with positive probability only by hands $x_{\beta }^{-}$ and $x_{\beta }^{+}$, with probabilities $p_{\beta }$ and 1 respectively (and with probability 0 by all other hands), so that B’s indifference condition

$$Pr\left(x<y_{\beta }^{*}\mid \beta \right)=\frac{p_{\beta }}{p_{\beta }+1}=\frac{\beta }{2\beta +2}$$

is satisfied for each $\beta >0$, giving sequential rationality under conditional updating.3

There are obviously infinitely many such equilibria, and infinitely many more where hands $x\in (0,1/7)$ play different mixed strategies that “average out” to the same conditionally updated beliefs for B, but these are all equivalent in terms of their outcome. This outcome admits the intuitive interpretation of low hands bluffing as a mixed—rather than a pure—strategy, consistent with the findings of Borel [11] and Chen and Ankenman [12] (pp. 154–157). Whilst Borel restricts the first player to a single possible bet (or fold), Chen and Ankenman study a game that differs from the present one only in the drawing of hands from the closed (rather than open) unit interval $[0,1]$. This means that a worst possible and best possible hand exist in their model, and a bet of infinity must be allowed by the player with the best possible hand, effectively imposing an upper limit on the bet. Their solution has similarities to the one presented here, but also an important difference: hands $x\in (0,1/7)$ can bet 0 with positive probability. This requires B hands $y\in (0,1/7)$ to fold to a bet of 0; otherwise $x\in (0,1/7)$ would prefer positive bets to 0 (see Equation (3)). This is irrational for $y\in (0,1/7)$, since they have a positive probability of winning the pot at zero cost by calling. In my solution, by contrast, all B hands call a bet of 0, and no $x\in (0,1/7)$ bets 0 with positive probability as a result.4

Finally, although Newman’s game has infinitely many equilibria, I claim that there are no equilibria giving a different outcome. To see this, note that each player has an infinite set of (measurable) pure Bayesian strategies, ${\sigma }_A:(0,1)\to [0,\infty )$ and ${\sigma }_B:[0,\infty )\times (0,1)\to \{\mathrm{call},\mathrm{fold}\}$ respectively. Each player’s set of mixed Bayesian strategies, P and Q respectively, is then a convex subset of a linear topological vector space. Moreover, B’s pure strategy space is an (uncountable) product of compact spaces, and hence compact by Tychonoff’s Theorem; endowing his mixed strategy space Q with the weak* topology, that too is compact. B’s expected gain $K:P\times Q\to \mathbb{R}$ from the game (net of his ante) is then continuous in each of its arguments, quasi-convex in p and quasi-concave in q (by linearity of expectation and of B’s gain in the players’ actions). It follows by Sion’s [13] general minimax theorem (see Raghavan [14], pp. 751–752) that the game has a value. The value of the game to A, net of the ante, is

$${\int }_0^{\frac{1}{7}}\frac{2}{7}dx+{\int }_{\frac{1}{7}}^{\frac{4}{7}}2xdx+{\int }_{\frac{4}{7}}^1\left(2(\beta +1)\left(x-1+\frac{6}{7}\xi \right)+(\beta +2)\left(1-\frac{6}{7}\xi \right)-\beta \right)dx-1=\frac{1}{7}$$

which is unchanged from Newman’s solution, because the mixed strategies of hands $x\in (0,1/7)$ have the same expected payoff as the corresponding pure strategies of Newman. The existence of a value here is less obvious than in Chen and Ankenman [12] (pp. 154–157), where both players’ strategy spaces are compact (the possibility of betting infinity providing the Alexandroff extension); nonetheless, the compactness of B’s strategy space in Newman’s game is enough to avoid the arms race in bet size that would make for nonexistence of the value.