Hierarchical Bayesian Analysis of Biased Beliefs and Distributional Other-Regarding Preferences
Abstract
:1. Introduction
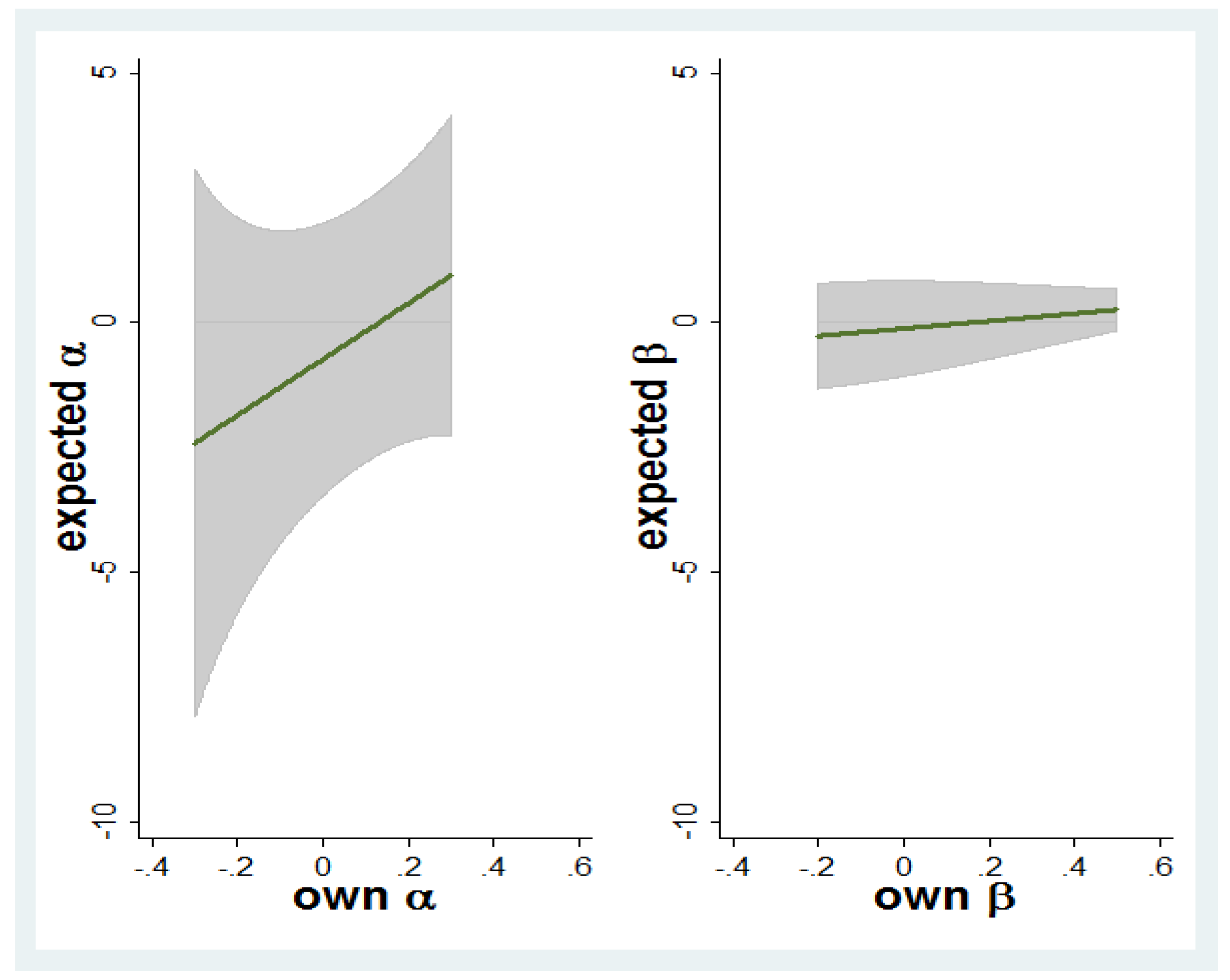
- Result 1: There is a strong increasing monotonic relationship between own other-regarding preferences and beliefs about average other-regarding preferences.
- Result 2: There is a U-shaped association between own other-regarding preferences and beliefs about the variance in others’ other-regarding preferences for one of the two parameters in the utility model, namely α. For the other β parameter, the same relationship is insignificant.
- Result 3: The utility model that we use and the model for beliefs that we develop below explain the choices and beliefs of subjects in binary Dictator Games adequately.
2. Method
2.1. Subjects
2.2. Procedure
3. Theoretical Model: Other-Regarding Preferences and Beliefs
3.1. Other-Regarding Preferences
3.2. Beliefs
4. Analyses and Results
4.1. Bayesian and Frequentist Analysis of Other-Regarding Preferences
| ML | Bayesian | ||||
| parameter | Coef. | S.E. | P.M. | P.SD. | |
| τ | .211 | .013 | .212 | .007 | |
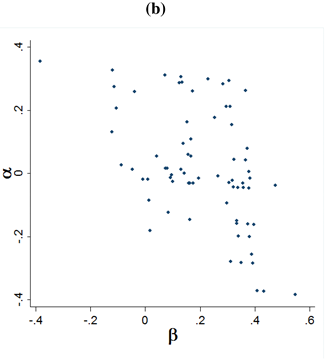
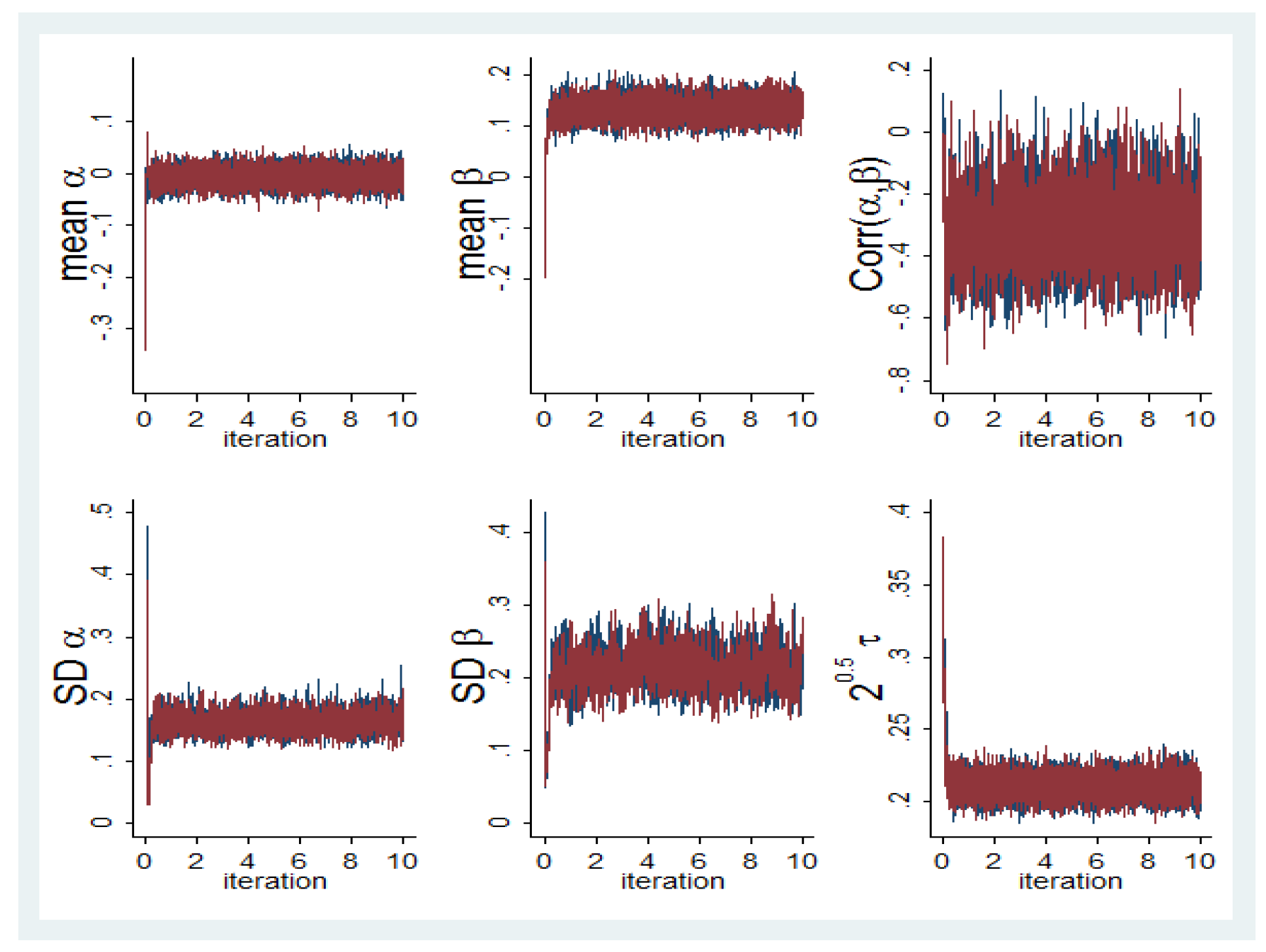
4.2. Bayesian Analysis of Other-Regarding Preferences and Beliefs
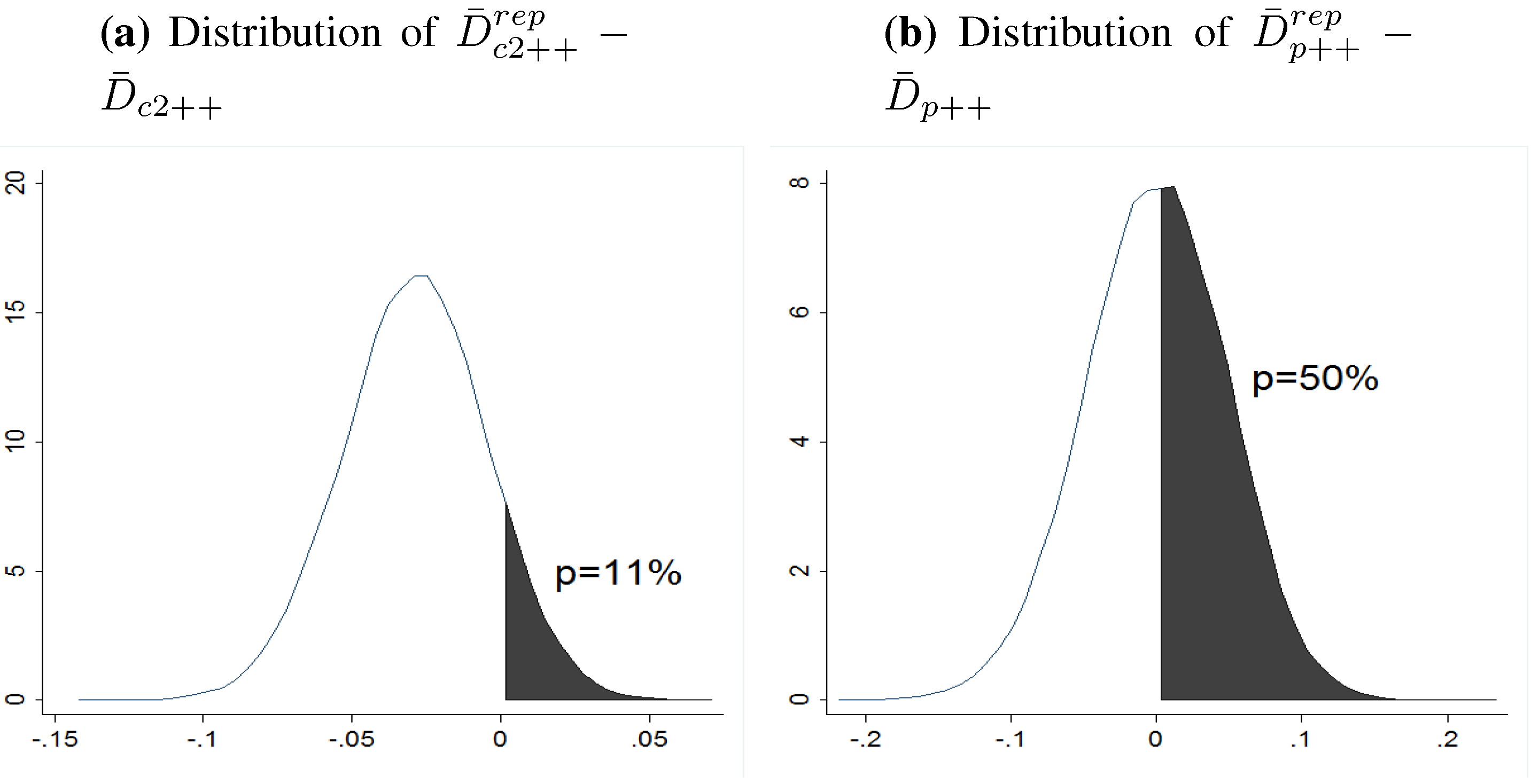
4.3. Bayesian Assessment of Fit: Posterior Predictive Checking
5. Discussion and Conclusions
6. Appendix
A. Dictator Games used in the Study
| You get | Other gets | You get | Other gets | α | β | A-choice | %A-choice | %A-choice | (choice,belief) | |
| 18 | 650 | 600 | 650 | 685 | .273 | 46.380 | 31.023 | 0.509 | ||
B. Instructions
| Example 1 | Option A | Option B |
| You get | 100 | 100 |
| Other participant gets | 200 | 1 |
| Your choice | [ ] | [ ] |
| % participants who choose option A: [____] | ||
Acknowledgements
References
- Iedema, J. The Perceived Consensus of One’s Social Value Orientation; Ph.D Dissertation; Tilburg University: Tilburg, Netherlands, 1993. [Google Scholar]
- Aksoy, O.; Weesie, J. Beliefs about the social orientations of others: A parametric test of the triangle, false consensus, and cone hypotheses. J. Exp. Soc. Psychol. 2012, 48(1), 45–54. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Kohler, S. Incomplete information about social preferences explains equal division and delay in bargaining. Games 2012, 3(3), 119–137. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Games with incomplete information played by Bayesian players. Manage. Sci. 1968, 14, 468–502. [Google Scholar]
- Ross, L.; Greene, D.; House, P. The false consensus effect: An egocentric bias in social perception and attribution processes. J. Pers. Soc. Psychol. 1977, 13, 279–301. [Google Scholar] [CrossRef]
- Kelley, H.H.; Stahelski, A.J. Social interaction basis of cooperators’ and competitors’ beliefs about others. J. Pers. Soc. Psychol. 1970, 16(1), 66–91. [Google Scholar] [CrossRef]
- Blanco, M.; Engelmann, D.; Koch, A.K.; Normann, H.T. Preferences and Beliefs in a Sequential Social Dilemma: A Within-Subjects Analysis; IZA Discussion Papers 4624; Institute for the Study of Labor (IZA): Bonn, Germany, 2009. [Google Scholar]
- Blanco, M.; Engelmann, D.; Normann, H.T. A within-subject analysis of other-regarding preferences. Game. Econ. Behav. 2011, 72, 321–338. [Google Scholar] [CrossRef]
- Danz, D.N.; Fehr, D.; Kuebler, D. Information and beliefs in a repeated normal-form game. Exp. Econ. 2012, 15, 622–640. [Google Scholar] [CrossRef]
- Hyndman, K.; Oezbay, E.Y.; Schotter, A.; Ehrblatt, W. Belief formation: An experiment with outside observers. Exp. Econ. 2012, 15, 176–203. [Google Scholar] [CrossRef]
- Dufwenberg, M.; Gneezy, U. Measuring beliefs in an experimental lost wallet game. Game. Econ. Behav. 2000, 30, 163–182. [Google Scholar] [CrossRef]
- Croson, R.T.A. Thinking like a game theorist: Factors affecting the frequency of equilibrium play. J. Econ. Behav. Organ. 2000, 41, 299–314. [Google Scholar] [CrossRef]
- Gaechter, S.; Renner, E. The effects of (incentivized) belief elicitation in public good experiments. Exp. Econ. 2010, 13(3), 364–377. [Google Scholar] [CrossRef]
- Ellingsen, T.; Johannesson, M.; Tjotta, S.; Torsvik, G. Testing guilt aversion. Game. Econ. Behav. 2010, 68, 95–107. [Google Scholar] [CrossRef]
- Bellemare, C.; Kroeger, S.; van Soest, A. Measuring inequity aversion in a heterogeneous population using experimental decisions and subjective probabilities. Econometrica 2008, 76(4), 815–839. [Google Scholar] [CrossRef]
- Offerman, T.; Sonnemans, J.; Schram, A. Value orientations, expectations and voluntary contributions in public goods. The Economic Journal 1996, 106, 817–845. [Google Scholar] [CrossRef]
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 100, 166–193. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. Inequality aversion, efficiency, and maximin preferences in simple distribution experiments. Am. Econ. Rev. 2004, 94(4), 857–869. [Google Scholar] [CrossRef]
- Falk, A.; Fischbacher, U. A theory of reciprocity. Game. Econ. Behav. 2006, 54, 293–315. [Google Scholar] [CrossRef]
- Rodriguez-Lara.; Moreno-Garrido, I. Modeling inequity aversion in a dictator game with production. Games 2012, 3(4), 138–149. [Google Scholar] [CrossRef]
- Schulz, U.; May, T. The recording of social orientations with ranking and pair comparison procedures. Eur. J. Soc. Psychol. 1989, 19, 41–59. [Google Scholar] [CrossRef]
- Aksoy, O.; Weesie, J. Social motives and expectations in one-shot asymmetric Prisoner’s Dilemmas. J. Math. Sociol. 2013, 37, 24–58. [Google Scholar] [CrossRef]
- Tutic, A.; Liebe, U. A theory of status-mediated inequity aversion. J. Math. Sociol. 2009, 33(3), 157–195. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, Second Edition; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Gelman, A.; Meng, X.L.; Stern, H. Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica 1996, 6, 733–807. [Google Scholar]
- Snijders, T.A.B.; Bosker, R.J. Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2012. [Google Scholar]
- Spiegelhalter, D.L.D.D.; Thomas, A.; Best, N. The BUGS project: Evolution, critique and future directions (with discussion). Stat. Med. 2009, 28, 3049–3082. [Google Scholar]
- Greiner, B. The online recruitment system ORSEE 2.0 a guide for the organization of experiments in economics. Working Paper Series in Economics; University of Cologne: Koln, Germany, 2004. [Google Scholar]
- Friedman, D.; Cassar, A. Economics Lab; Routledge: London, UK, 2004. [Google Scholar]
- Blanco, M.; Engelmann, D.; Koch, A.K.; Normann, H.T. Belief Elicitation in Experiments: Is there a Hedging Problem? IZA Discussion Papers 3517; Institute for the Study of Labor (IZA): Bonn, Germany, 2008. [Google Scholar]
- Oechssler, J. Finitely repeated games with social preferences. Exp. Econ. 2012. [Google Scholar] [CrossRef]
- Stahl, D.O.; Haruvy, E. Other-regarding preferences: Egalitarian warm glow, empathy, and group size. J. Econ. Behav. Organ. 2006, 61, 20–41. [Google Scholar] [CrossRef]
- McFadden, D. Conditional logit analysis of qualitative choice behavior. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: New York, NY, USA, 1974; pp. 105–142. [Google Scholar]
- McKelvey, R.D.; Palfrey, T.R. Quantal Response Equilibria for normal form games. Game. Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Rabe-Hesketh, S.; Skrondal, A.; Pickles, A. Reliable estimation of generalized linear mixed models using adaptive quadrature. SJ 2002, 2(1), 1–21. [Google Scholar]
- Kunreuther, H.; Silvasi, G.; Bradlow, E.T.; Small, D. Bayesian analysis of deterministic and stochastic Prisoner’s Dilemma games. Stat. Sci. 2009, 4(5), 363–384. [Google Scholar]
- Nilsson, H.; Rieskamp, J.; Wagenmakers, E.J. Hierarchical Bayesian parameter estimation for cumulative prospect theory. J. Math. Psychol. 2011, 55, 84–93. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences (with discussion). Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Morishima, Y.; Schunk, D.; Bruhin, A.; Ruff, C.C.; Fehr, E. Linking brain structure and activation in the temporoparietal junction to explain the neurobiology of human altruism. Neuron 2012, 75, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Aksoy, O.; Weesie, J. Simultaneous analysis of ones own social orientation and ones beliefs about the social orientations of others using Mplus: A supplementary reseach note for the JESP-paper.
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge: New York, NY, USA, 2006. [Google Scholar]
- Fox, J.P. Bayesian Item Response Modeling: Theory and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Dawes, R.M. Statistical criteria for establishing a truly false consensus effect. J. Exp. Soc. Psychol. 1989, 25, 1–17. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. The false consensus effect disappears if representative information and monetary incentives are given. Exp. Econ. 2000, 3, 241–269. [Google Scholar] [CrossRef]
- Kuhlman, D.M.; Brown, C.; Teta, P. Judgements of cooperation and defection in social dilemmas: The moderating role of judge’s social orientation. In Social Dilemmas, Theoretical Issues, and Research Findings; Liebrand, W., Messick, D.M., Wilke, H.A.M., Eds.; Pergamon: Oxford, UK, 1992. [Google Scholar]
- Laury, S. Pay one or pay all: Random selection of one choice for payment. Andrew Young School of Policy Studies Research Paper Series, Working Paper 06-13; Andrew Young School of Policy Studies, Georgia State University: Atlanta, GA, USA, January 2005. [Google Scholar]
- 1.In our analyses, we assume that subjects report their average beliefs, which we think is a natural response for most subjects. Theoretically, incentivising beliefs with a quadratic loss function would ensure reporting average beliefs. We opted for a linear but “spline-like" loss fuction rather than a quadratic loss function to make the incentive structure more accessible to the subjects. We do not think this is a major issue as the exact incentive function does not seem to influence the distribution of beliefs to a great extent. For example, [14] compares the distributions of incentivized and non-incentivized beliefs and reports some but not substantial differences.
- 2.In our theoretical model for own preferences, we assume that is multivariate normal. We ascertained that this normality assumption for own is reasonable by estimating with fixed effects, that is, without assuming normality. As own is normal, we see no reason to assume a different distribution for beliefs.
- 3.Besides these error terms, the means of the belief distribution depend only on . However, the model could be easily adapted to include other subject level covariates, such as age, gender, study field etc.
- 4.We fix in (3) to zero, otherwise the MCMC procedure failed to converge. We performed a sensitivity analysis and observed that assigning different fixed values for hardly influenced the parameters of interest.
- 5.Note again that the Bayesian results include not only P.M.s and P.SD.s but the entire posterior distributions of parameters. Thus, as in Figure 2, it is possible to obtain posterior density strips of all parameters which we omit for brevity.
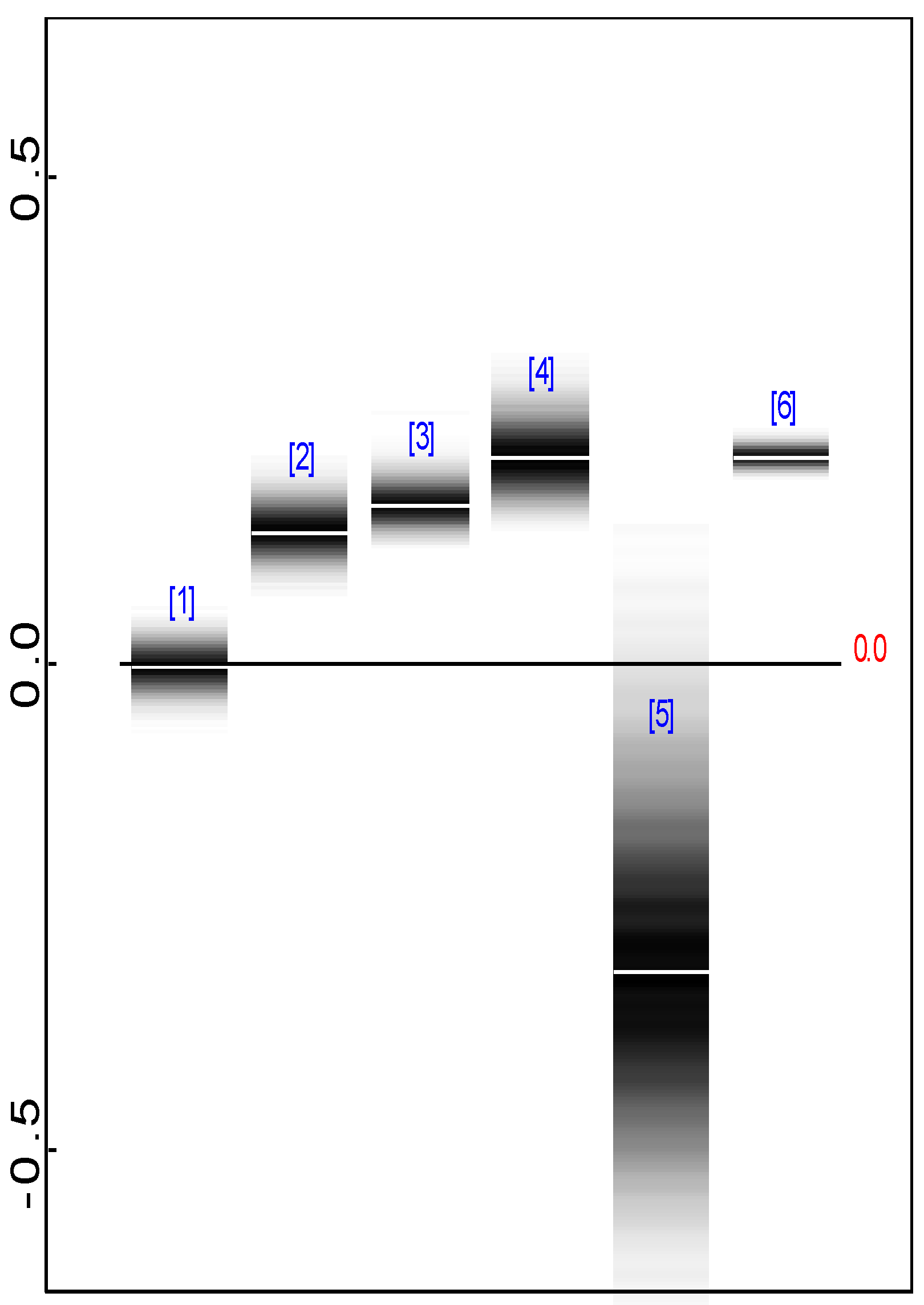
- 6.Note also that within the Bayesian framework the discrepancy statistics and are not single scores, but each has an entire posterior distribution.
- 7.[45] and [46] show that this effect is not necessarily false. That is, people use information on others’ choices and even assign higher weights to others’ choices than one’s own choice in forming beliefs. A truly false consensus effect would require ignoring information about others’ choices. In our case subjects did not receive feedback about others’ choices prior to belief elicitation.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aksoy, O.; Weesie, J. Hierarchical Bayesian Analysis of Biased Beliefs and Distributional Other-Regarding Preferences. Games 2013, 4, 66-88. https://doi.org/10.3390/g4010066
Aksoy O, Weesie J. Hierarchical Bayesian Analysis of Biased Beliefs and Distributional Other-Regarding Preferences. Games. 2013; 4(1):66-88. https://doi.org/10.3390/g4010066
Chicago/Turabian StyleAksoy, Ozan, and Jeroen Weesie. 2013. "Hierarchical Bayesian Analysis of Biased Beliefs and Distributional Other-Regarding Preferences" Games 4, no. 1: 66-88. https://doi.org/10.3390/g4010066
APA StyleAksoy, O., & Weesie, J. (2013). Hierarchical Bayesian Analysis of Biased Beliefs and Distributional Other-Regarding Preferences. Games, 4(1), 66-88. https://doi.org/10.3390/g4010066




