Hierarchical Bayesian Analysis of Biased Beliefs and Distributional Other-Regarding Preferences

Abstract

This study investigates the relationship between an actor’s beliefs about others’ other-regarding (social) preferences and her own other-regarding preferences, using an “avant-garde” hierarchical Bayesian method. We estimate two distributional other-regarding preference parameters, α and β, of actors using incentivized choice data in binary Dictator Games. Simultaneously, we estimate the distribution of actors’ beliefs about others’ α and β, conditional on actors’ own α and β, with incentivized belief elicitation. We demonstrate the benefits of the Bayesian method compared to it’s hierarchical frequentist counterparts. Results show a positive association between an actor’s own $(\alpha ,\beta )$ and her beliefs about average $(\alpha ,\beta )$ in the population. The association between own preferences and the variance in beliefs about others’ preferences in the population, however, is curvilinear for α and insignificant for β. These results are partially consistent with the cone effect [1,2] which is described in detail below. Because in the Bayesian-Nash equilibrium concept, beliefs and own preferences are assumed to be independent, these results cast doubt on the application of the Bayesian-Nash equilibrium concept to experimental data.

1. Introduction

Experimental evidence shows that utility models incorporating other-regarding preferences often explain choice data better than the classical economic model with selfish actors. Consequently, numerous social preference models have been proposed and many such model have received great attention in the literature. (For example, according to our most recent search of Google Scholar on November 21, 2012, Fehr and Schmidt’s [3] inequality aversion model is cited 5299 times, approaching the 7454 citations of Adam Smith’s “The Theory of Moral Sentiments”). It is also acknowledged that there is heterogeneity in preferences, i.e., some actors are selfish, whereas some actors have other-regarding preferences to varying degrees (e.g., [3,4]). This heterogeneity is often invoked as an important factor to explain why, under some experimental conditions, results seem to converge to the classical economic model’s predictions, while under other conditions, results deviate significantly from the classical model.

Introducing other-regarding preferences in micro-economic models and acknowledging heterogeneity in preferences, however, creates the need to also model actors’ beliefs about others’ preferences. In many cases (without dominant equilibria), predictions of micro-economic models depend strongly on actors’ beliefs about others’ behavior. Beliefs about others’ behavior, in turn, depend on actors’ beliefs about others’ preferences. Thus, modeling actors’ own preferences is necessary but not sufficient to obtain behavioral predictions. In addition to actors’ own preferences, actors’ beliefs about others’ preferences should also be dealt with. Otherwise, empirical tests of utility models are incomplete because the observed behavior could be the result of not only own preferences, but also beliefs about others’ preferences. In the behavioral economics literature uncertainty about others’ utilities, thus beliefs about others’ preferences are typically dealt with via the application of the Bayesian-Nash equilibrium [5] with “rational beliefs” (e.g., [3]). Beliefs are assumed to be independent of own preferences, and actors are assumed to know the actual distribution of preferences in the “population”. While making sense theoretically, this concept may not be empirically solid. Social psychology studies often demonstrate clear biases in expectations, as summarized by the “false” consensus hypothesis [6], the triangle hypothesis [7], or the Cone model of Iedema [1] indicating that actors’ own social preferences and expectations about others’ social preferences may not be independent. See also [8,9] for a critic of Bayesian-Nash equilibrium within the experimental economics context. We investigate actors’ beliefs about others’ preferences empirically. Particularly, we focus on the relationship between own preferences and beliefs about others’ preferences.

There is a rich literature on belief formation and learning (recent examples include [10,11]) which are not among the topics of the current paper. Comparable existing studies on beliefs in the micro-economics literature focus mainly on the relationship between the actor’s behavior and the actor’s beliefs about others’ behavior (e.g., [12,13,14,15]), or between the actor’s preferences and the actor’s beliefs about others’ behavior (e.g., [8,16,17]). In our view, a micro theory, such as a social utility model, should be the theoretical basis of the analysis of both the actor’s own behavior and the actor’s beliefs about others’ behavior. If we are to explain actors’ own behavior with a utility model, we should also explain actors’ beliefs with the same utility model. Thus, the distinctive feature of our study is that we explicitly analyze the relationship between actors’ own preferences and their beliefs about others’ preferences, nested in the same utility model. We estimate two other-regarding preference parameters for a variant of the Charness and Rabin [18], an extension of Fehr and Schmidt [3] utility specification, using choice data in binary Dictator Games. Simultaneously, we estimate the moments of the distribution of actors’ beliefs about others’ other-regarding preferences, conditional on own other-regarding preferences, with incentivized belief elicitation. To be clear, analyzing the relationship between preferences and beliefs about others’ preferences, we deviate from rational beliefs –yet rational beliefs remain a special case of our model where the aforementioned relationship is absent–. However, we do assume that people’s preferences are described by the utility model we use, and people think that other people’s preferences are given by the same utility model.

Because the main focus of this study is on the relationship between beliefs and preferences, we restrict our attention to a single utility model, namely a variant of Charness and Rabin [18], which is an extension of the inequality aversion model of Fehr and Schmidt [3]. Although we provide an assessment of empirical fit of the model, the primary aim of this paper is not testing the utility model used in this paper or finding the utility model that best explains our data. This has been done extensively in the literature. We are aware of other relevant social motives and other successful models of other-regarding preferences (e.g., [19,20,21,22]). Yet, because the model of Charness and Rabin [18], and of Fehr and Schmidt [3] which is contained in Charness and Rabin are among the most cited and applied social utility models, describing the relationship between actors’ own motives and beliefs within this framework is useful. In addition, in our study, we use data on simple Dictator Games. In such games, preferences given by the model used here are in line with other potentially relevant types of motives, e.g., maximin preferences and inequality aversion. Finally, variants of other-regarding preferences given by Charness and Rabin [18] are a common theme in other disciplines such as social psychology (e.g., [23]), and rational choice sociology (e.g., [24,25]). Thus, our results would be relevant for a variety of disciplines. In addition, the simple shape of the function we use yields substantial convenience in statistical analyses.

An important contribution of this paper, however, is it’s statistical methodology. We use a hierarchical Bayesian method to estimate the other-regarding preferences and the moments of the distribution of actors’ beliefs about others’ other-regarding preferences. Hierarchical Bayesian methods have some practical advantages over their hierarchical frequentist counterparts [26]. First and foremost, incorporating strong numerical estimation procedures, Bayesian methods are very flexible. They could be relatively easily applied to many complex statistical models. Relying on the maximum likelihood approach, however, frequentist methods are limited in this sense. For example, the simultaneous analysis of own other-regarding preferences and beliefs that we perform in this paper is nearly impossible within the frequentist framework. In addition, the Bayesian approach provides a strong and flexible tool to assess model fit via posterior predictive sampling [27], which we exploit in the current paper. Assessing model fit for relatively complex models as ours within the frequentist framework is, again, very difficult. In addition to those practical advantages of Bayesian methods, given that one uses fairly uninformative priors the results of the Bayesian methods converge to “would be" Maximum Likelihood estimates [26,28]. In other words, (some of) the Bayesian results obtained using uninformative priors may be interpreted as frequentist estimates. Our statistical analysis is implemented in OpenBugs [29]. We provide the estimation routine as a supplementary file so that other scholars could replicate, modify, and apply the routine.

The main results of the hierarchical Bayesian analysis are the following:

• Result 1: There is a strong increasing monotonic relationship between own other-regarding preferences and beliefs about average other-regarding preferences.
• Result 2: There is a U-shaped association between own other-regarding preferences and beliefs about the variance in others’ other-regarding preferences for one of the two parameters in the utility model, namely α. For the other β parameter, the same relationship is insignificant.
• Result 3: The utility model that we use and the model for beliefs that we develop below explain the choices and beliefs of subjects in binary Dictator Games adequately.

We want to elaborate on how this current paper improves on a previous study of the authors [2]. In the current paper we use a richer dataset, combining data from two experiments. Thus statistical power is improved. Second, [2] employs a different other-regarding preference model, namely the social orientation model, a model predominantly used in social psychological literature. In the social orientation model in [2], actors are interested in absolute inequality as they are assumed to not differentiate between advantageous and disadvantageous forms of inequality. Despite using a different utility model in this paper, we still find some support for the cone effect. This further reinforces the existence of the cone pattern, at least for some type of other-regarding preferences. Thirdly, and most importantly, [2] uses a two step estimation method that predicts individual social preference parameters in the first step, and in the second step uses these individual estimates to model beliefs. As we acknowledge in [2], this two step estimation procedure is flawed as in the second step it does not take into account measurement error in the first step. In this paper, the Bayesian estimation routine solves this problem as simultaneous estimation of preferences and beliefs becomes possible.

The organization of the paper is as follows. After describing the experimental procedure, we describe the model for other-regarding preferences and beliefs in detail. We then move on to the details of the hierarchical Bayesian analysis where we briefly compare the Bayesian method with a frequentist alternative. A final discussion of the main results concludes the paper.

2. Method

2.1. Subjects

The data come from two independent experiments. The only differences between the experiments are: (1) the first experiment reported in [2] was conducted in January 2010; the second experiment in May 2010, and (2) the second experiment was embedded in a larger set of experiments which included additional treatments. In this paper, we use a subset of data from the second experiment. This subset is collected using the identical procedure as in the first experiment. We performed careful statistical analyses to compare the data from the two experiments. These analyses –available from the authors– showed that when the parameters of the statistical models in this paper are considered, both for other-regarding preferences and beliefs, the hypothesis that the two samples come from the same population could not be rejected. Thus, we collapsed the data of the two experiments, and report below the results for this combined dataset. This yielded a sample of 187 subjects (155 from the 1st and 32 from the 2nd experiment) recruited using the Online Recruitment System for Economic Experiments (ORSEE) [30]. The two experiments comprised 10 sessions in total, each of which was run with 16 to 20 subjects who were seated randomly in one of the cubicles in the Experimental Laboratory for Sociology and Economics (ELSE) of Utrecht University. Since the experiment was conducted in the English language a good command of English was a prerequisite for participation.

2.2. Procedure

We followed the standard procedures of experimental economics, e.g., anonymity, real and anonymous partners, incentive compatibility, etc. [31]. Social preferences were measured with 18 different binary Dictator Games. Subjects were informed that for each Dictator Game, the recipient was a randomly selected participant. The outcomes in these 18 Dictator Games were chosen to (approximately) optimize the precision of statistical estimates of the other-regarding preference parameters, building on the previous evidence on the empirical distribution of such parameters. In 16 of the games, one option included an equal distribution, and the other option included inequity of varying degrees (see the Appendix for the parameters of these 18 Dictator Games and the rationale behind choosing these particular games). To measure beliefs, subjects were asked to guess the percentage of other participants taking part in the experiment who would choose each option in each of these 18 Dictator Games. Subjects earned points from their own decisions and were rewarded for the accuracy of their guesses regarding others’ behavior. More precisely, for each of the 18 Dictator Games, if a subject’s guess of how many other subjects would choose each option was equal to the actual percentage, she earned 500 points. For each percentage point of deviation from the actual percentage, the subject earned 20 fewer points. If the guess was off by more than 25%, the subject earned no points.1 In addition, next to their decisions as “senders” in the Dictator Games, as a subsequent step, subjects also passively earned points as “recipients” of other randomly selected participants. No feedback about the accuracy of the guesses or about the choices of others was given until all 18 games were complete. The order in which a subject received these 18 games was randomized.

Here we want to discuss three methodological issues that may concern the reader. First of all, we paid for both game outcomes and beliefs. One may argue that subjects might hedge by stating beliefs to insure against bad outcomes in the game. We do not think this is a major concern as [32] study this problem explicitly and show clearly that hedging in designs as ours is not a major problem. Secondly, we pay for all games instead of paying for a randomly selected Dictator Game. Our data analysis assumes that subjects treat each Dictator Game as a one-shot game independent from other games, rather than all games as one big game. Sophisticated readers might claim that if subjects are also sophisticated enough they may consider distributional outcomes not game by game but across the set of 18 games (see [33]. To stress the (assumed) one-shot nature of each decision, in the experiment the recipient was a randomly selected new participant in each Dictator Game, i.e., stranger matching. Alternatively we could pay for a randomly selected game, but that procedure is not free of problems either (e.g., [34]). Finally, in the experiment a subject decided as the sender in the Dictator Game, but also was a recipient of another person. This was done not to reduce the sample size by half. This feature of the design does not make the game strictly one-person and may potentially have some consequences. Yet, we believe that this does not influence our results in a substantial way. First of all, the recipient and the sender for whom the subject was a recipient were both randomly selected subjects, i.e., they were not necessarily the same person. Moreover, our parameter estimates are quite similar to those found in other studies and as we discuss below the statistical model fits data quite well. An otherwise finding would make us suspect such potential design effects. We will revisit these methodological issues in the discussion.

3. Theoretical Model: Other-Regarding Preferences and Beliefs

3.1. Other-Regarding Preferences

We use the following utility function for distributional other-regarding preferences. For an outcome allocation for the self (x) and the other (y), the (random) utility for actor i is:

$$\begin{array}{ccc}\hfill U^r(x,y;{\alpha }_i,{\beta }_i)& =& U(x,y;{\alpha }_i,{\beta }_i)+ϵ\hfill \\ & =& x-{\alpha }_{i}max(0,y-x)-{\beta }_{i}max(0,x-y)+ϵϵ\sim N(0,{\tau }^2).\hfill \end{array}$$

(1)

Following Charness and Rabin [18], for subjects with $0<\beta <\alpha$, this function reduces to the inequity aversion model of [3], where α and β capture the utility losses due to disadvantageous and advantageous inequity, respectively. Subjects with $\beta <0$ and $\alpha >0$ are competitive, that is, they prefer to receive higher outcomes than the other. Subjects with $\beta >0$ and $\alpha <0$ are motivated by so called “social welfare", that is, their utility increases in the outcomes of the other, irrespective of the other earns more or less than self, yet with different weights. Finally, those with $\beta =\alpha =0$ are selfish. To be able to use this utility function for statistical purposes, we included a stochastic term ϵ [35] in the function, which is assumed to be normally distributed with zero mean, independent across subjects, evaluations, and alternatives in the games. Then, the probability that actor i chooses option A over option B in a binary Dictator Game j will be,

$$\begin{array}{ccc}\hfill Pr(U_{ijA}^r>U_{ijB}^r)& =& \hfill \\ \hfill Pr\left(U_{jAB}^r({\alpha }_i,{\beta }_i)>0\right)& =& Pr\left(U(x_{jA},y_{jA};{\alpha }_i,{\beta }_i)-U(x_{jB},y_{jB};{\alpha }_i,{\beta }_{ij}+({ϵ}_{ijA}-{ϵ}_{ijB})>0\right)\hfill \\ & =& Pr\left({\Delta }_{jx}-{\alpha }_i·{\Delta }_{jyx}-{\beta }_i·{\Delta }_{jxy}+{\Delta }_{ijϵ}>0\right)\hfill \\ & =& \Phi \left(\frac{{\Delta }_{jx}-{\alpha }_i·{\Delta }_{jyx}-{\beta }_i·{\Delta }_{jxy}}{\sqrt{2}\tau }\right).\hfill \end{array}$$

(2)

where $x_{jA}$ is the outcome for the self in option A, $y_{jB}$ is the outcome for the other in option B, ${\Delta }_{jyx}=max(0,y_{jA}-x_{jA})-max(0,y_{jB}-x_{jB})$, ${\Delta }_{jxy}=max(0,x_{jA}-y_{jA})-max(0,x_{jB}-y_{jB})$, ${\Delta }_{ijϵ}={ϵ}_{jA}-{ϵ}_{jB}\sim N(0,2{\tau }^2)$ for subject i in game j, and Φ is the cumulative standard normal distribution. Note that this probability is equivalent to the Quantal Response Equilibrium prediction with normal distributed evaluation errors [36].

3.2. Beliefs

For each of the 18 Dictator Games, subjects guessed the percentage of other participants who preferred option A over option B. Let $p_{ij}$ be subject i’s stated belief about the percentage of others choosing option A in Dictator Game j. We define ${\pi }_{ij}$ as i’s belief about the probability that (2) holds. We assume that actor i’s beliefs about others’ α and β, $({\tilde{\alpha }}_i,{\tilde{\beta }}_i)$, are represented by a multivariate normal distribution $\left(\begin{array}{c}{\tilde{\alpha }}_i\\ {\tilde{\beta }}_i\end{array}\right)\sim N\left(\left(\begin{array}{c}{\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)\\ {\mu }_{{\tilde{\beta }}_i}({\beta }_i)\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)& {\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}\\ {\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}& {\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)\end{array}\right)\right)$ , where ${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$ and ${\mu }_{{\tilde{\beta }}_i}({\beta }_i)$ are i’s beliefs about the means of α and β, ${\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)$ and ${\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)$ are i’s beliefs about the variance of α and β, and ${\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}$ is i’s belief about the correlation between α and β.2 Then ${\pi }_{ij}$ satisfies

$$\begin{array}{ccc}\hfill {\pi }_{ij}& =& Pr\left(U_{AB}^r(\tilde{\alpha },\tilde{\beta })>0|\left(\begin{array}{c}\tilde{\alpha }\\ \tilde{\beta }\end{array}\right)\sim N\left(\left(\begin{array}{c}{\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)\\ {\mu }_{{\tilde{\beta }}_i}({\beta }_i)\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)& {\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}\\ {\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}& {\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)\end{array}\right)\right)\right)\hfill \\ {\Phi }^{-1}({\pi }_{ij})& =& \frac{{\Delta }_{jx}-{\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)·{\Delta }_{jyx}-{\mu }_{{\tilde{\beta }}_i}({\beta }_i)·{\Delta }_{jxy}}{\sqrt{2{\tilde{\tau }}^2+{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)·{\Delta }_{jyx}^2+{\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)·{\Delta }_{jxy}^2+2{\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}\sigma ({\tilde{\alpha }}_i)\sigma ({\tilde{\beta }}_i)·{\Delta }_{jyx}{\Delta }_{jxy}}}\end{array}$$

(3)

where $2{\tilde{\tau }}^2$ is the variance of $\widetilde{{ϵ}_A}-\widetilde{{ϵ}_B}$, the variance of the difference of random disturbances and ${\Phi }^{-1}$ is the inverse cumulative normal distribution. Ignoring boundary cases, we model ${\Phi }^{-1}(p_{ij})={\Phi }^{-1}({\pi }_{ij})+{\epsilon }_{ij}$ and assume that ${\epsilon }_{ij}$ is normally distributed with zero mean, thus

$$\begin{array}{ccc}\hfill {\Phi }^{-1}(p_{ij})& =& {\Phi }^{-1}({\pi }_{ij})+{\epsilon }_{ij}{\epsilon }_{ij}\sim N(0,{\tau }_p^2)\hfill \end{array}$$

(4)

Moreover, we model the moments of the subjective belief distribution given in (3) as polynomial functions of own social preference parameters. More precisely:

$$\begin{array}{ccc}\hfill {\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)& =& b_{a0}+b_{a1}{\alpha }_i+{\epsilon }_{\alpha i}{\epsilon }_{\alpha i}\sim N(0,{\tau }_{\alpha }^2)\hfill \\ \hfill {\mu }_{{\tilde{\beta }}_i}({\beta }_i)& =& b_{b0}+b_{b1}{\beta }_i+{\epsilon }_{\beta i}{\epsilon }_{\beta i}\sim N(0,{\tau }_{\beta }^2)\hfill \\ \hfill ln{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)& =& b_{sa0}+b_{sa1}{\alpha }_i+b_{sa2}{\alpha }_i^2\hfill \\ \hfill ln{\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)& =& b_{sb0}+b_{sb1}{\beta }_i+b_{sb2}{\beta }_i^2\hfill \\ \hfill {\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}& =& b_{c0}.\hfill \end{array}$$

(5)

In (5), ${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$ and ${\mu }_{{\tilde{\beta }}_i}({\beta }_i)$ depend on α and β in a linear form, whereas $ln{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)$ and $ln{\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)$ depend on α and β in a curvilinear form. We also performed analyses with higher order polynomial terms, but the functional forms above in (5) are sufficient to describe our main results. We will discuss this issue below in the results section.

Also note that there are stochastic error terms ${\epsilon }_{\alpha i}$ and ${\epsilon }_{\beta i}$ in the equation. For convenience, we assume that ${\epsilon }_{\alpha i}$ and ${\epsilon }_{\beta i}$ are independent. These error terms capture the possibility that two subjects who have the same values for $(\alpha ,\beta )$ may have different beliefs about average $(\alpha ,\beta )$ in the population.3 It is in principle possible to add similar error terms for $ln{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)$ and $ln{\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)$. We tried to do so. However adding so many random terms complicate analysis yielding estimation and convergence problems. Thus we included error terms only for ${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$ and ${\mu }_{{\tilde{\beta }}_i}({\beta }_i)$.

4. Analyses and Results

We will first discuss the analyses and the results for other-regarding preferences without introducing beliefs. In a subsequent step, we will provide the simultaneous analysis of other-regarding preferences and beliefs.

4.1. Bayesian and Frequentist Analysis of Other-Regarding Preferences

We assume a multivariate normality for β and α in our subject pool. Consequently, (2) yields a multilevel probit model with random coefficients for α and β. The dependent variable is a subject’s choice between options A and B, and the independent variables are the differences between the outcomes for the self and the two terms for outcome differences in options A and B as given in (2). Note that the coefficient of ${\Delta }_{jx}$ is 1. The parameters of (2) to be estimated are the means and (co)variances of $({\alpha }_i,{\beta }_i)$ and the variance of evaluation error ${\tau }^2$. Since (2) yields a fairly standard multilevel probit model with random coefficients, it can be fitted using the frequentist Maximum Likelihood approach as well as the Bayesian framework. To facilitate comparison and show indeed that the Bayesian approach with uninformative priors yield very similar results as the frequentists Maximum Likelihood approach, we present the results of both estimation procedures. When we introduce beliefs later on, however, estimation using the frequentist approach becomes infeasible, thus will provide only the Bayesian solution.

We fitted (2) with Maximum Likelihood using the Stata software GLLAMM [37] (also see: [2]). The hierarchical Bayesian estimation requires a more elaborate description, firstly because scholars are less familiar with it, and secondly it involves three main elements each of which should be described clearly. Thus, we spare somewhat more space for the Bayesian procedure. The three main elements of a Bayesian analysis are the prior distributions of the parameters, the likelihood of data, and the MCMC method to obtain the posterior distribution of the parameters. We used the following standard uninformative priors for the parameters of (2). The prior for the covariance matrix of $(\alpha ,\beta )$ is an inverse Wishart with 2 degrees of freedom with a scale matrix of ${10}^2·I_2$ where $I_2$ is the $2\times 2$ identity matrix [38]. For the mean vector of $(\alpha ,\beta )$, we used a multivariate normal prior with zero means and $10·I_2$ variances. For the variance of the evaluation error ${\tau }^2$, we used a Gamma(10,10) prior. The likelihood of data is implied by (2). We used OpenBugs [29], a freely available program, to obtain (draws from) the posterior distribution of the parameters. The estimated posterior distribution comprised 22.000 draws from two chains after a burn-in of 30.000 draws and recording every 10th draw in each chain [39]. Convergence was confirmed by visual inspection of the history of the draws from the two chains as well as using the [40] $\widehat{R}$ statistics. If the model has converged, the chains started from different values should mix and the posterior distribution should stabilize. This can be seen from figure 1, which includes the history of the draws for the parameters of (2) until the 10.000th iteration. In fact convergence is achieved as early as after a few hundred iterations. In addition, values of [40] $\widehat{R}$ statistics for the parameters after excluding the burn-in iterations are all smaller than 1.05, in fact all are virtually 1.

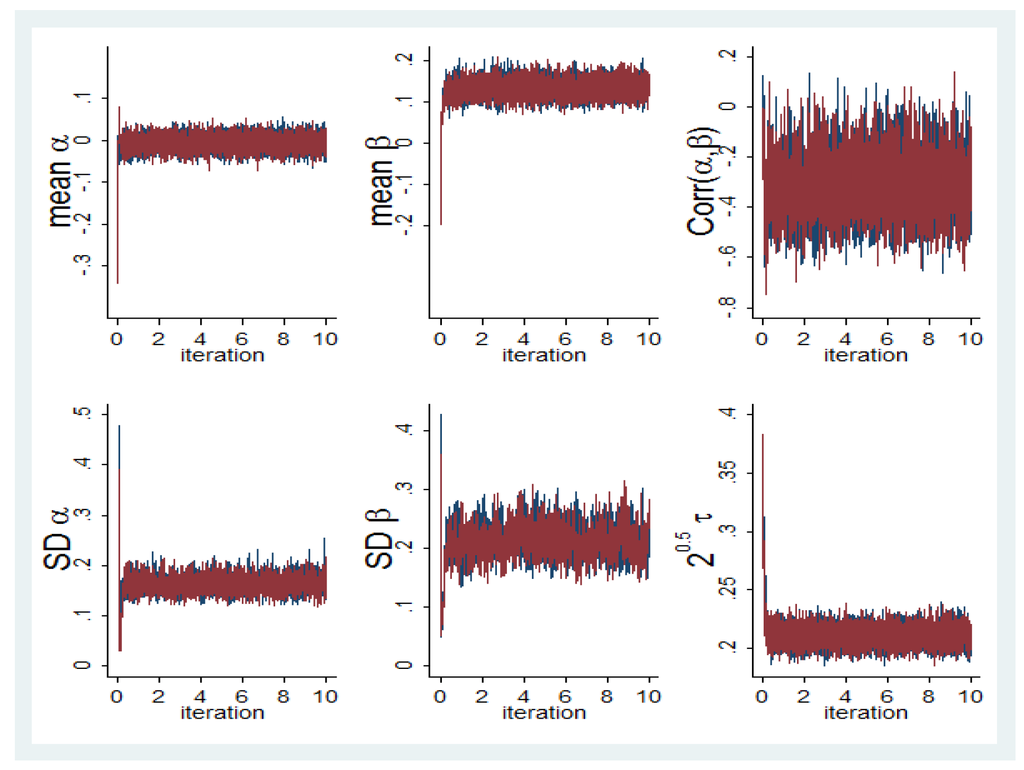
Figure 1. History of draws from the posterior distribution of parameters per ${10}^3$ iterations to assess convergence.

Figure 1. History of draws from the posterior distribution of parameters per ${10}^3$ iterations to assess convergence.

Table 1 includes the results of the frequentist and the Bayesian estimations, as well as the bivariate scatter plot of individual $({\alpha }_i,{\beta }_i)$ estimates obtained as empirical posterior means. For the Bayesian procedure Table 1-a includes the posterior means (P.M.) as point estimates of the parameters and posterior standard deviations (P.SD.) as standard errors of those point estimates [28]. The first thing to note is the extreme similarity of the Maximum Likelihood and Bayesian results. This is not surprising, given that we used uninformative priors. When uninformative priors are used, the results of Bayesian procedures converge to the frequentist results for relatively large samples [26]. Note that the Bayesian procedure yields an entire posterior distribution, not only posterior means or standard deviations. This is demonstrated in Figure 2, which presents the posterior density plots of the parameters.

Both the frequentist and Bayesian results show that the estimated mean of β is roughly .14. Also, there is significant variation among subjects with respect to β. The mean of ${\alpha }_i$ is estimated as -.01, which is statistically “insignificant", that is the estimate is not significantly different from zero (ML result), and the posterior density of the parameter is centered around zero (Bayesian result). However, albeit small, the estimated variance of ${\alpha }_i$ is statistically significant. Thus, although, on average, α is about zero, subjects differ significantly in terms of their α values. We also find a moderate negative correlation between α and β. Note, however, that the uncertainty/precision of this correlation parameter is somewhat high, reflected as a wider density strip (see Figure 2), and a larger posterior standard deviation and standard error (see Table 1).

Table 1. (a) Hierarchical Maximum Likelihood (ML) and hierarchical Bayesian estimates and their standard errors for the means and standard deviations of the other-regarding preference parameters $(\alpha ,\beta )$ and the standard deviation of the evaluation error (τ). (b) Bivariate scatter plot of empirical Bayes estimates of $(\alpha ,\beta )$.

(a)
	ML			Bayesian
parameter	Coef.	S.E.		P.M.	P.SD.
mean(${\beta }_i$ )	.140	.022		.134	.019
mean(${\alpha }_i$)	-.007	.016		-.010	.015
sd(${\beta }_i$)	.208	.023		.211	.024
sd(${\alpha }_i$)	.163	.015		.166	.013
corr(${\alpha }_i,{\beta }_i$)	-.303	.010		-.304	.093
τ	.211	.013		.212	.007

N(decision) = 3366, N(subject) = 187

Table 1. (a) Hierarchical Maximum Likelihood (ML) and hierarchical Bayesian estimates and their standard errors for the means and standard deviations of the other-regarding preference parameters $(\alpha ,\beta )$ and the standard deviation of the evaluation error (τ). (b) Bivariate scatter plot of empirical Bayes estimates of $(\alpha ,\beta )$.

(a)
	ML			Bayesian
parameter	Coef.	S.E.		P.M.	P.SD.
mean(${\beta }_i$ )	.140	.022		.134	.019
mean(${\alpha }_i$)	-.007	.016		-.010	.015
sd(${\beta }_i$)	.208	.023		.211	.024
sd(${\alpha }_i$)	.163	.015		.166	.013
corr(${\alpha }_i,{\beta }_i$)	-.303	.010		-.304	.093
τ	.211	.013		.212	.007

N(decision) = 3366, N(subject) = 187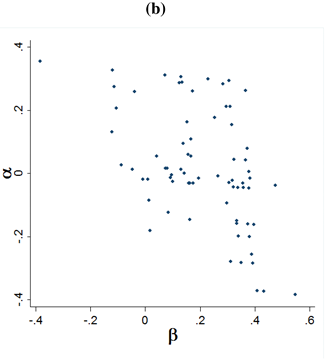

The utility function that we use is an extension of Fehr and Schmidt’s inequity aversion model, thus, we can assess to what extend the assumptions of Fehr and Schmidt hold. Our estimates show that the typical assumptions of Fehr & Schmidt on the distributions of α and β, e.g., $\alpha >0$, $\beta >0$, and $\alpha >\beta$, do not hold in the Dictator Games (see also Table 1-b). For example, a substantial portion of our sample has negative α estimates, and for quite some of our subjects $\alpha <\beta$. Although our results point to such deviations from the original assumptions of Fehr & Schmidt, they are in fact very close to the estimates obtained for the same utility function in a study that used a representative Dutch sample [16]. [16], for instance, also report negative α values for a large portion of their sample. Another recent study that estimates $({\alpha }_i,{\beta }_i)$ with Maximum Likelihood in a Swiss sample also yields a very similar $(\alpha ,\beta )$ distribution as ours where for may subjects $\beta >\alpha$ and for quite some $\alpha <0$ [41]. [9] also reports that the assumptions of Fehr and Schmidt on the distribution of $\alpha ,\beta$ are violated in a battery of games. This shows the usefulness of Charness and Rabin extension of the Fehr and Schmidt model.

As a side, we find no evidence of quadratic/nonlinear preferences; i.e., when added to the model, the coefficients of ${\Delta }_{xy}^2$ and ${\Delta }_{yx}^2$ were not significant. Additionally, remember that each subject received the 18 Dictator Games in random order. We checked whether the order that a subject received these games mattered and concluded that the game order did not influence the social preference parameters. The only, albeit small, order effect was that the variance of evaluation error, τ, decreased in the number of previous decisions. Yet, including this order effect on evaluation error in our models did not change our results in any substantial way. We will discuss below the fit of the other-regarding preference model in detail.

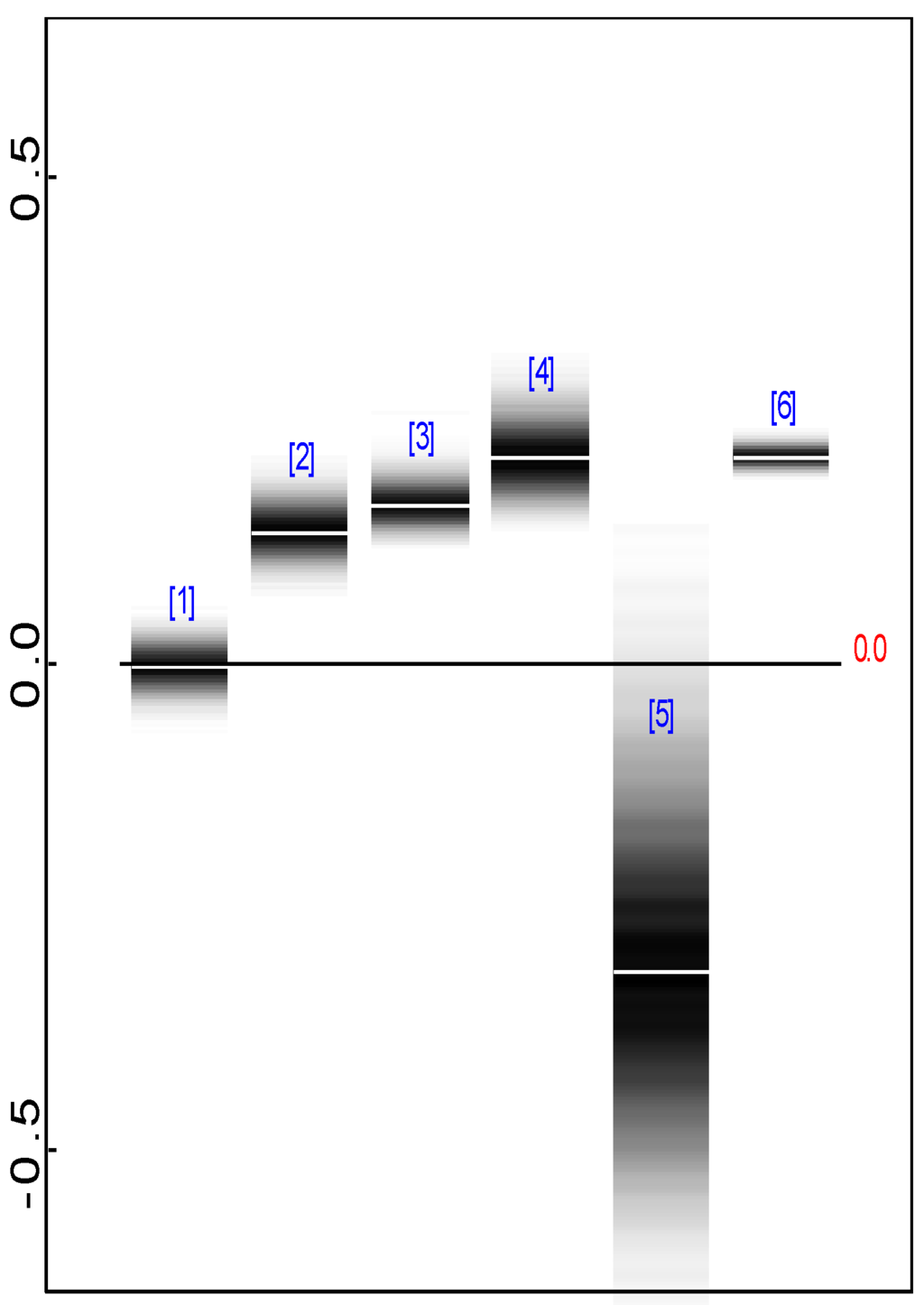
Figure 2. Density strips of the posterior distribution of parameters: [1]=${\mu }_{\alpha }$, [2]=${\mu }_{\beta }$, [3]=${\sigma }_{\alpha }$, [4]=${\sigma }_{\beta }$, [5]=Corr$(\alpha ,\beta )$, [6]=$\sqrt{2}\tau$.

Figure 2. Density strips of the posterior distribution of parameters: [1]=${\mu }_{\alpha }$, [2]=${\mu }_{\beta }$, [3]=${\sigma }_{\alpha }$, [4]=${\sigma }_{\beta }$, [5]=Corr$(\alpha ,\beta )$, [6]=$\sqrt{2}\tau$.

4.2. Bayesian Analysis of Other-Regarding Preferences and Beliefs

When the beliefs are entered in the model, statistical analysis becomes significantly difficult. First of all, now the analysis involves fitting four simultaneous equations, namely (2), (3), (4), and (5). Secondly, these four equations include highly nonlinear forms. If one wants to stay within the frequentist approach, options are very limited and those limited options are problematic, too [2]. The first option is a two-step procedure: in the first step fitting (2) and obtaining individual $(\alpha ,\beta )$ estimates as posterior means [37]; in the second step fitting (3), (4), and (5) with the nonlinear least squares method, feeding in individual estimates of $(\alpha ,\beta )$ obtained in the first stage as observed variables. This approach, however, would yield incorrect estimates, because in the second step the measurement error in $(\alpha ,\beta )$ is ignored. Moreover, in this two stage approach it is impossible to include the two error terms in (5), namely ${\epsilon }_{\alpha i}$ and ${\epsilon }_{\beta i}$. In other words, individual variation in beliefs has to be ignored, yielding potentially important biases. A second frequentist alternative is turning to (multilevel) structural equation modeling (SEM), which is a natural tool to solve for simultaneous equations within the frequentist framework [42]. Yet, it proves to be impossible to obtain convergence due to high number of unknowns and highly non-linear forms in (2), (3), (4), and (5). Thus, we do not discuss further the frequentist solutions for the simultaneous analysis of other-regarding preferences and beliefs.

The hierarchical Bayesian approach, on the other hand, is very flexible. The likelihood of data is given by (2), (3), (4), and (5). One still needs to assign priors to the unknowns in those equations and the strong MCMC tools incorporated in the Bayesian framework, i.e., MCMC and the Gibbs sampler take care of obtaining (draws from) the posterior distribution of the parameters. We now describe this procedure. As above, we used rather uninformative priors. The priors for the parameters of (2) are given in the previous subsection. The priors for the $b_{•}$ parameters in (5) are univariate normals with zero mean and ${10}^2$ variance, except $b_{c0}$ to which a Uniform[-1,1] prior is assigned. For the variances of error terms, ${\tau }_{•}$, in (5) and (4) we assigned Gamma(10,10) priors.4 As above after 30.000 burn-in draws from two MCMC chains and recording every 10th draw in each chain, a final posterior distribution with 56.000 draws is obtained using OpenBugs. As explained above, convergence is ascertained by visual inspection of the history of the draws from the two chains as well as using the [40] $\widehat{R}$ statistics. Table 2 shows the posterior means (P.M.) and posterior standard deviations (P.SD.) of the parameters of Equation 5.5

The strong positive relationship between own other-regarding preferences and expected average other-regarding preferences is apparent in Table 2 for both α and β. Those with larger other-regarding preference parameters also believe that the average other-regarding preferences in the population is higher. The variances of individual errors in average other-regarding preferences, ${\tau }_{\alpha }$ and ${\tau }_{\beta }$, are estimated as .77 and .08, respectively with relatively low standard errors/high precision. Thus, although beliefs depend on own preferences, there is significant variance in beliefs that cannot be totally explained by own preferences. One finding to be noted is the slope of ${\alpha }_i$ on ${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$, which is 5.6. Although this slope seems higher than what one would expect, in fact the variation in ${\alpha }_i$ is small. The difference between the two standard deviations below and above the average ${\alpha }_i$, that is the difference between

Table 2. Beliefs about others’ other-regarding preferences: Points estimates (posterior means) of the parameters of Equation 5. Posterior standard deviations are given in parentheses below as the standard errors of posterior means. N(decision) = 3366, N(subject) = 187.

${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$ =		−.737		+5.596 ${\alpha }_i$		$+{\epsilon }_{\alpha i}\sim N(0,.{770}^2)$
		(.105)		(.991)		(.107)
${\mu }_{{\tilde{\beta }}_i}({\beta }_i)$ =		−.117		+ .747 ${\beta }_i$		$+{\epsilon }_{\beta i}\sim N(0,.{075}^2)$
		(.024)		(.143)		(.018)
$ln{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)$ =		1.020		−1.788 ${\alpha }_i$		$+9.516{\alpha }_i^2$
		(.115)		(.732)		(4.203)
$ln{\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)$ =		−1.076		−1.622 ${\beta }_i$		$-3.325{\beta }_i^2$
		(.103)		(2.406)		(7.103)
${\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}$ =		.650
		(.106)

Table 2. Beliefs about others’ other-regarding preferences: Points estimates (posterior means) of the parameters of Equation 5. Posterior standard deviations are given in parentheses below as the standard errors of posterior means. N(decision) = 3366, N(subject) = 187.

${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$ =		−.737		+5.596 ${\alpha }_i$		$+{\epsilon }_{\alpha i}\sim N(0,.{770}^2)$
		(.105)		(.991)		(.107)
${\mu }_{{\tilde{\beta }}_i}({\beta }_i)$ =		−.117		+ .747 ${\beta }_i$		$+{\epsilon }_{\beta i}\sim N(0,.{075}^2)$
		(.024)		(.143)		(.018)
$ln{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)$ =		1.020		−1.788 ${\alpha }_i$		$+9.516{\alpha }_i^2$
		(.115)		(.732)		(4.203)
$ln{\sigma }_{{\tilde{\beta }}_i}^2({\beta }_i)$ =		−1.076		−1.622 ${\beta }_i$		$-3.325{\beta }_i^2$
		(.103)		(2.406)		(7.103)
${\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}$ =		.650
		(.106)

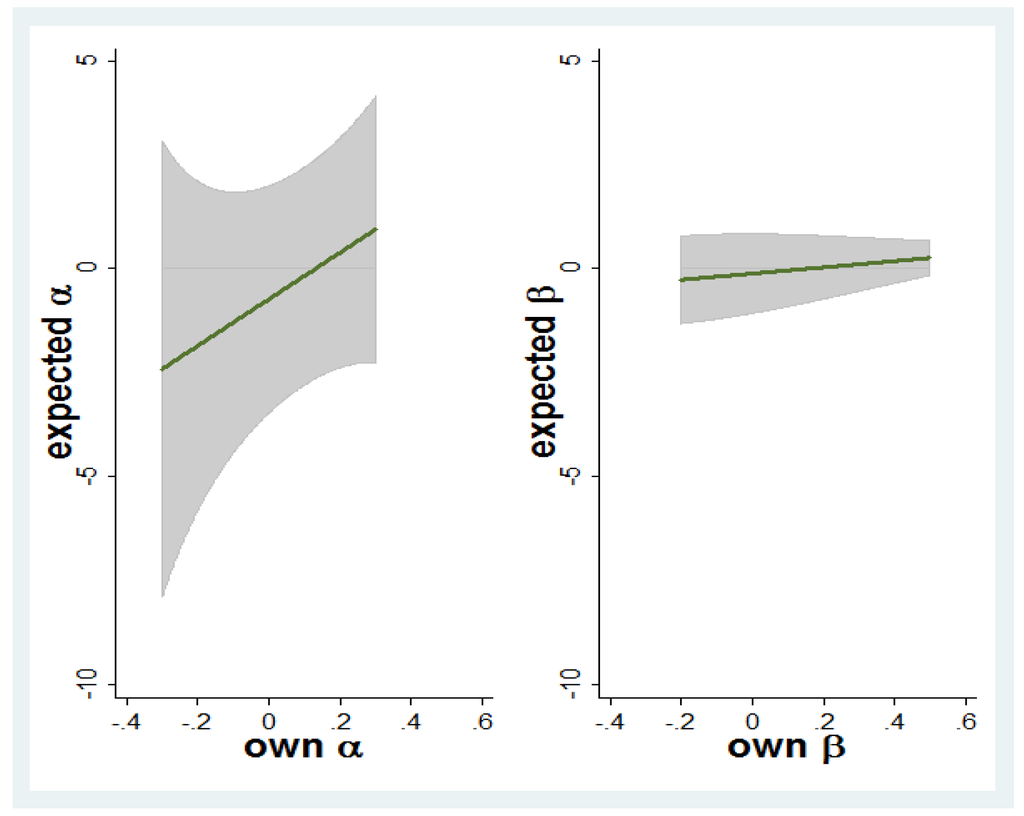
Figure 3. Expected other-regarding preferences versus own other-regarding preferences based on the posterior means of the parameters in Table 2. Grey shaded areas represent the relationship between expected variance (uncertainty) in others’ other-regarding preferences and own other-regarding preferences; i.e., the boundaries of the grey areas are: $\mu (\tilde{\alpha })\pm 1.65\sigma (\tilde{\alpha })$ and $\mu (\tilde{\beta })\pm 1.65\sigma (\tilde{\beta })$. Note that $\pm 1.65\sigma (\tilde{\beta })$ refer to 90% confidence intervals. The solid lines within these areas represent the relationship between average expected other-regarding preferences and own other-regarding preferences.

Figure 3. Expected other-regarding preferences versus own other-regarding preferences based on the posterior means of the parameters in Table 2. Grey shaded areas represent the relationship between expected variance (uncertainty) in others’ other-regarding preferences and own other-regarding preferences; i.e., the boundaries of the grey areas are: $\mu (\tilde{\alpha })\pm 1.65\sigma (\tilde{\alpha })$ and $\mu (\tilde{\beta })\pm 1.65\sigma (\tilde{\beta })$. Note that $\pm 1.65\sigma (\tilde{\beta })$ refer to 90% confidence intervals. The solid lines within these areas represent the relationship between average expected other-regarding preferences and own other-regarding preferences.

the lowest and highest likely ${\alpha }_i$ values is only about 0.64. Thus, although the slope is high, the difference in predicted ${\mu }_{{\tilde{\alpha }}_i}({\alpha }_i)$ is not that high due to the small size and variance of ${\alpha }_i$ estimates. The U-shaped association between own other-regarding preferences and beliefs about the variance in others’ other-regarding preferences for the α parameter is also apparent. The estimated polynomial function relating ${\sigma }^2(\tilde{\alpha })$ and α is $ln{\sigma }^2(\tilde{\alpha })=1.02-1.79\alpha +9.52{\alpha }^2$. The global minimum of this function is 0.09. In other words, those who have larger absolute values of α expect much more variation in the population than those with smaller absolute values of α. The relationship between ${\sigma }^2(\tilde{\beta })$ and β, however, is statistically insignificant.

Figure 3 describes the nature of the relationship between other-regarding preferences and beliefs in a graphical form. Figure 3 is obtained using the posterior means displayed in Table 2 as point estimates of the parameters. This curvilinear relationship between own other-regarding preferences and expected variance in others’ other-regarding preferences for the α parameter is depicted in Figure 3, with wider grey regions as absolute own other-regarding preferences increases. Although the variance in beliefs about β seems to decrease in own β, the relationship is highly insignificant. Note that the variance in beliefs is in general higher for the α parameter than for the β parameter.

To report, the estimate of ${\rho }_{{\tilde{\alpha }}_i,{\tilde{\beta }}_i}$, which is the belief regarding the correlation between α and β, is .65 with a posterior standard deviation of 0.11. ${\tau }_p$ is estimated as 1.19 with a posterior standard deviation of 0.02.

It is possible to improve the model in Table 2 by adding higher-order polynomial terms to Equation 5. For example, a representation where $\mu (\tilde{\alpha })$ is a third-order polynomial function of α yields a better fit. Yet, in this alternative representation, results still indicate a monotonic and increasing, though non-linear, relationship between $\mu (\tilde{\alpha })$ and α. Similarly, a model where $ln{\sigma }_{{\tilde{\alpha }}_i}^2({\alpha }_i)$ is a fourth-order polynomial function of α yields a better fit. But, again, the results of this model also indicate a U-shaped relationship between $ln{\sigma }^2(\tilde{\alpha })$ and α, with an almost identical local minimum. Thus, although it is possible to obtain a better fit with more complex polynomial representations, the model in Table (2) is sufficient to describe our main results. In the discussion below, we provide some insights on why this particular shape between other-regarding preferences and beliefs about others’ other-regarding preferences emerges.

4.3. Bayesian Assessment of Fit: Posterior Predictive Checking

The question examined here is how well our model for other-regarding preferences and beliefs fits data. If the discrepancy between our model and data is too high, then the results discussed above might be misleading. Consider the following discrepancy statistics for the choice of subject i in game j:

$$\begin{array}{ccc}\hfill D_{cij}& =& \frac{{(y_{ij}-Pr(U_{ijA}^r>U_{ijB}^r))}^2}{(Pr(U_{ijA}^r>U_{ijB}^r))(1-Pr(U_{ijA}^r>U_{ijB}^r))}\hfill \end{array}$$

(6)

where $Pr(U_{ijA}^r>U_{ijB}^r)$ is the predicted probability of choosing option A in a game j for subject i (cited from Equation 2, and $y_{ij}$ is the observed choice for i in game j. Statistics (6) is chosen for its similarity to Pearson’s ${\chi }^2$ statistics, a widely used statistics to assess fit. We construct an overall fit statistic, ${\overline{D}}_{c++}$, by averaging over all i and j.

A similar discrepancy statistics can be constructed for beliefs as below:

$$\begin{array}{ccc}\hfill D_{pij}& =& {({\Phi }^{-1}(p_{ij})-{\Phi }^{-1}({\pi }_{ij}))}^2\hfill \end{array}$$

(7)

where ${\Phi }^{-1}({\pi }_{ij})$ is the predicted inverse cumulative probability for subject i in game j that (2) holds and ${\Phi }^{-1}(p_{ij})$ is the observed inverse cumulative probability (see Equations 3 and 4. As above, an overall fit statistic, ${\overline{D}}_{p++}$, is constructed by averaging over all i and j.

Had we known the theoretical distributions of ${\overline{D}}_{c++}$ and ${\overline{D}}_{p++}$ under the null hypothesis that our model fits data, we could compare the ${\overline{D}}_{c++}$ and ${\overline{D}}_{p++}$ scores in our sample to the theoretical distributions and calculate a p-value for each discrepancy score. These p-values then would show how likely it is to observe the calculated or higher ${\overline{D}}_{c++}$ and ${\overline{D}}_{p++}$ scores, given that our model fits. However, only for very few such discrepancy statistics the theoretical distribution under the null is known and ${\overline{D}}_{c++}$ and ${\overline{D}}_{p++}$ are not among those few cases. Fortunately, the Bayesian framework offers an alternative, i.e., posterior predictive checking. Below we briefly describe this procedure and refer to [27] and [43] for a fuller treatment of the topic.

For each draw from the Markov Chain used to fit our model, we create a replicated dataset given our model. For each replicated dataset, we calculate the ${\overline{D}}_{c++}$ and ${\overline{D}}_{p++}$ scores, which we call ${\overline{D}}_{c++}^{rep}$ and ${\overline{D}}_{p++}^{rep}$, respectively. Subsequently, we obtain the discrepancy p-values for the parts of the model that explains the choices and beliefs of subjects by calculating $Pr({\overline{D}}_{c++}^{rep}>{\overline{D}}_{c++})$ and $Pr({\overline{D}}_{p++}^{rep}>{\overline{D}}_{p++})$.6 This procedure is very general and could be used for any (discrepancy) statistics. In fact, we used a slightly different smoother discrepancy statistics for choices of subjects, to deal with the boundary cases using $D_{c2ij}=\frac{{(y_{ij}-Pr(U_{ijA}^r>U_{ijB}^r))}^2}{(0.1+0.8Pr(U_{ijA}^r>U_{ijB}^r))(0.9-0.8Pr(U_{ijA}^r>U_{ijB}^r))}$. The exact form of the discrepancy statistics does not matter to calculate a p-value, since for any statistics posterior predictive samples could be created.

Figure 4 shows the distributions of ${\overline{D}}_{c2++}^{rep}-{\overline{D}}_{c2++}$ and ${\overline{D}}_{c++}^{rep}-{\overline{D}}_{c++}$, as well as $p_{c++}=Pr({\overline{D}}_{c2++}^{rep}>{\overline{D}}_{c2++})$ and $p_{p++}=Pr({\overline{D}}_{c++}^{rep}>{\overline{D}}_{c++})$. The discrepancy p-values are $p_{c++}=11\%$ and $p_{p++}=50\%$. Neither of these figures is low, which means that under the null hypothesis that the model fits, neither of the discrepancy statistics is extremely unlikely. In other words, we do not find much evidence against the hypothesis that the model fits, thus conclude that overall our model fits data relatively well.

It is also possible to obtain person fit statistics as ${\overline{D}}_{ci+}$, that is, for each subject averaging the discrepancy statistics over all games. Similarly, it is possible to obtain item fit statistics ${\overline{D}}_{c+j}$ by averaging the discrepancy statistics over all subjects for each Dictator Game [44]. Subsequently, discrepancy p-values could be calculated for each subject and each Dictator Game, using posterior predictive sampling. This way, subjects whose choices and beliefs are not captured by the model or games in which choices and beliefs of subjects deviate from the predictions of the model can be detected. Since the overall fit of our model is rather satisfactory, we do not pursue assessing fit at lower levels. However, we would like to stress that this aspect of posterior predictive sampling on assessing individual level and item/game level discrepancies is potentially very useful to assess fit at different levels.

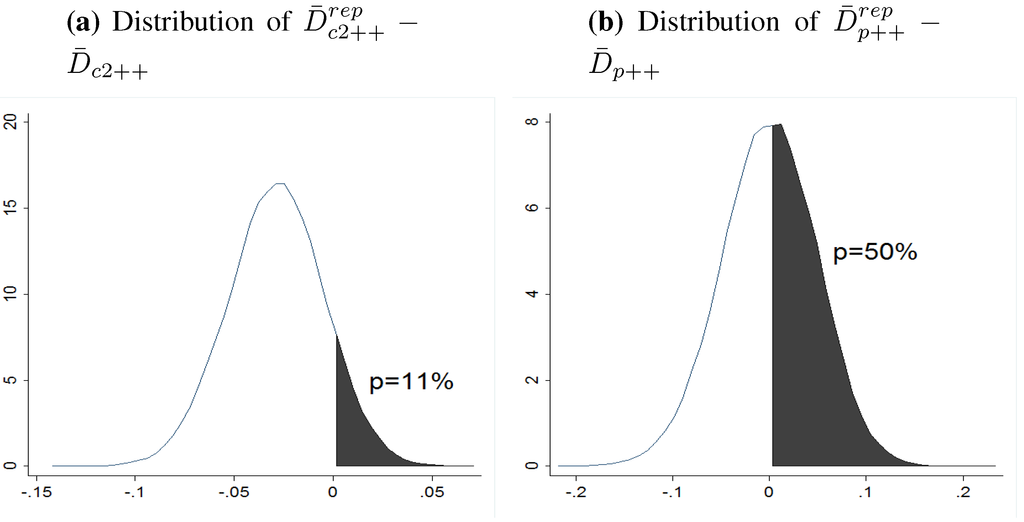
Figure 4. Posterior predictive checking: Distributions of ${\overline{D}}_{c2++}^{rep}-{\overline{D}}_{c2++}$ and ${\overline{D}}_{p++}^{rep}-{\overline{D}}_{p++}$, as well as corresponding discrepancy p-values.

Figure 4. Posterior predictive checking: Distributions of ${\overline{D}}_{c2++}^{rep}-{\overline{D}}_{c2++}$ and ${\overline{D}}_{p++}^{rep}-{\overline{D}}_{p++}$, as well as corresponding discrepancy p-values.

5. Discussion and Conclusions

In this study, we investigate the relationship between an actor’s beliefs about others’ other-regarding preferences and her own other-regarding preferences using a hierarchical Bayesian method. We estimated the other-regarding preferences parameters, α and β, of actors using choice data from binary Dictator Games. Simultaneously, we estimated the distribution of actors’ beliefs about others’ α and β, conditional on own α and β, with incentivized belief elicitation. We demonstrated some advantages of the Bayesian method over its hierarchical frequentist counterparts including its flexibility in dealing with relatively complex models with many free parameters, as well as the possibility of a sound assessment of model fit even for complex models using posterior predictive sampling.

Besides describing the benefits of the hierarchical Bayesian method, the paper presents interesting results. We found that there is a positive monotonic relationship between own other-regarding preferences and the belief about average other-regarding preferences. This is not an unprecedented finding (e.g., [8]), although our study is perhaps novel in demonstrating this relationship in light of a specific preference model. What is probably more novel is that we also found a strong U-shaped association between own other-regarding preferences and variance in beliefs about others’ other-regarding preferences for the α parameter. This result can also be interpreted in the following way. Selfish actors, i.e., those with approximately zero α, also expect most others to be selfish as well. Thus, these selfish actors fit the classical economic model in terms of both their preferences and their beliefs. As α deviate from selfishness, however, actors expect more variation in the population while still expecting others to be similar to themselves on average. The association between preferences and variance in beliefs for the β parameter however is insignificant. Another finding to be noted is that variance in beliefs is in general much higher for the α parameter than for the β parameter.

Why beliefs vary with own type and mechanisms yielding the particular relationships between own motives and beliefs that we describe in this paper is an open question. This question is tackled mainly within social psychology. We hope that our study will bring the social psychological literature on the relationship between types and beliefs about others’ types to the attention of experimental economists. The positive relationship between own preferences and beliefs about preferences in the population is in line with what social psychologists call the “false" consensus effect [6].7 The consensus effect literature typically does not investigate variance in beliefs (or uncertainty) about others’ preferences. Consequently, our result on the relationship between own other-regarding preferences and expected variance of others’ preferences is as novel in the social psychological literature as it is for economics. The triangle hypothesis [7], structured assumed similarity bias [47], and the cone model [1] are three hypotheses proposed in the social psychological literature each of which indirectly proposes a certain relationship between own preferences and expected variance in others’ preferences. We refer to [2] for a detailed description of those hypotheses. Among those three hypotheses, our results support partially the cone model. The cone effect, as discussed by [1] is caused by several factors. We apply those factors to the context of this paper. First, in line with the consensus effect all types –actors with certain values of $(\alpha ,\beta )$– expect their own type to be more common in the population. Secondly, in addition to their own types, all types expects selfishness to be another common type in the population, because selfishness is a common stereotype about others. These two effects overlap when the expectations of selfish people are considered. As a result, expected variance is smaller for selfish people. We should note, however, that the cone effect is observed for the α parameter. For the β parameter variance in beliefs is stable, that is, it does not depend on own β. Without further research, we can only speculate why the cone pattern emerges for the α parameter but not for the β parameter. As the social psychological literature shows, biases in beliefs such as the cone or the consensus effects are stronger for situations where information is scarce and uncertainty is high [6]. Our findings show that uncertainty about others’ preferences is much higher for the α parameter than that for the β parameter as the variance in beliefs is smaller for β than for α. In line with this, also the relationship between own other-regarding preferences and the belief about average other-regarding preferences is much stronger for α than for β. Thus, probably the cone and the consensus effects are stronger for the α parameter because subjects are more uncertain about others’ α than others’ β.

Irrespective of the exact causal mechanisms, these clear associations between own other-regarding preferences and beliefs about others’ other-regarding preferences that we document in this paper call for more elaborate and accurate application of other-regarding utility models. In the experimental economics literature, beliefs are typically assumed to be rational. That is, actors are assumed to know the actual distribution of preferences, and this distribution is independent of own preferences. We showed that these assumptions are problematic. If one disregards egocentric biases in beliefs by assuming rational expectations, one may obtain misleading results, such as incorrect predictions or inflated/incorrect estimates of social motives. Without modeling beliefs, modeling social preferences is not enough to derive accurate behavioral predictions for many interaction situations. We also hope that our findings on the distribution of own other-regarding preferences, beliefs about others’ other-regarding preferences, and the relationship between the two will provide an empirical basis for future theoretical work that may incorporate these biases in beliefs into more complex game-theoretic models.

Before closing, we want to address some methodological caveats. As we explicitly discuss in the methods section, in our experimental design subjects decide in multiple binary Dictator Games. Additionally, a subject is paired with multiple other subjects as a recipient. We pay for all decisions, dictator and recipient. We analyze data assuming that subjects treat each Dictator Game as a one-shot game, rather than all games as one big game. This is a potentially problematic assumption. We believe that this feature of our design corresponds to a more general and important methodological issue in the literature. To estimate other-regarding preference parameters with good statistical precision, one needs several conditionally independent observations from each subject and a relatively large subject pool. Similarly, constraining subjects to play in a single decision role, e.g., the dictator or the recipient role reduces the sample size substantially. Paying for all decisions has the potential drawback that a subject may not treat a particular game independent from other games, e.g., maximize utility over all sets of games. It is possible to devise statistical models to analyze choices taking potential dependence between games. Yet, we think it is unlikely that subjects are maximizing utility over all games. Thus, even one could adapt the statistical model to include potential dependences between a subjects’ choices over several games, such a model would be implausible, at least for most subjects. An alternative payment protocol, paying for a randomly selected game instead of all games may solve this potential dependence problem. In simple single person setups, paying for all or paying for a randomly selected game does not seem to matter [48]. However, paying for a randomly selected game has its own problems in situations that involve more than 1-person, such as Dictator Game. For example, [48] shows that introducing a random payment scheme may reduce the influence of game outcomes on choice by introducing potential path-dependent utility. Thus, it is not clear if random payment protocol solves the problem at all. We think that this is an important methodological issue and leave the discussion to future research that will systematically compare the repercussions of using alternative designs and payment methods.