Nonspecific Networking

Abstract

A new model of strategic networking is developed and analyzed, where an agent's investment in links is nonspecific. The model comprises a large class of games which are both potential and super- or submodular games. We obtain comparative statics results for Nash equilibria with respect to investment costs for supermodular as well as submodular networking games. We also study supermodular games with potentials. We find that the set of potential maximizers forms a sublattice of the lattice of Nash equilibria and derive comparative statics results for the smallest and the largest potential maximizer. Finally, we provide a broad spectrum of applications from social interaction to industrial organization.

To network or not to network, that is the question.

1. Introduction

Models of strategic network formation typically assume that each agent selects his direct links to other agents in which to invest. Yet in practice, a person's networking efforts may not only establish or strengthen desirable links to specific agents, but also create or reinforce links to many if not all other individuals. Beneficial links may come along with detrimental ones. For example, being better connected and more accessible implies potentially more calls from phone banks, more “spam”, more encounters with annoying or hostile people.

To illustrate the latter, consider a population of four persons where each has two friends and one enemy. Each individual i has a binary choice, to network and choose s_i = 1 at cost 1.5 or not to network and choose s_i = 0 at zero cost. The intensity of a link between two persons i and j is s_i + s_j. A person likes interacting with friends and dislikes interacting with enemies. Specifically, i enjoys the benefit +(s_i + s_j) when j is a friend and −(s_i + s_j) when j is an enemy. Friendship and enmity between persons are represented by the diagram s_i = 0 to s_i = 1, the person enjoys added benefits +2 from the two friends, −1 from the enemy, and incurs the cost 1.5. Hence the net gain is −0.5. However, a person does not internalize the externalities of her networking effort when she plays her strictly dominant strategy. A switch from s_i = 0 to s_i = 1 would create extra benefits +2 for her friends and −1 for her enemy. Hence efficiency requires that everybody is networking.

Nonspecific networking does not mean that an individual's networking effort affects everybody else. As a practical matter, networking may be possible between certain persons and not between others. We employ graphs to model restrictions on networking. Then formally, networking takes place within a given network or graph. Not only may different persons be affected differently by an individual's networking effort; but individuals may also differ in their networking efforts, even if the same range of effort levels is available to them. Both in traditional and in electronic interactions, some agents are much more active in networking than others and might be called “networkers”. Some might be considered designated networkers because they have higher benefits or lower costs from networking than others. To fix ideas, consider a population of four individuals. Their networking possibilities are described by a circular graph as follows where ↔ means that networking between the two persons is possible. ■ stands for a high cost person and □ stands for a low cost person or “natural networker”. Individuals are identical ex ante in all other respects.

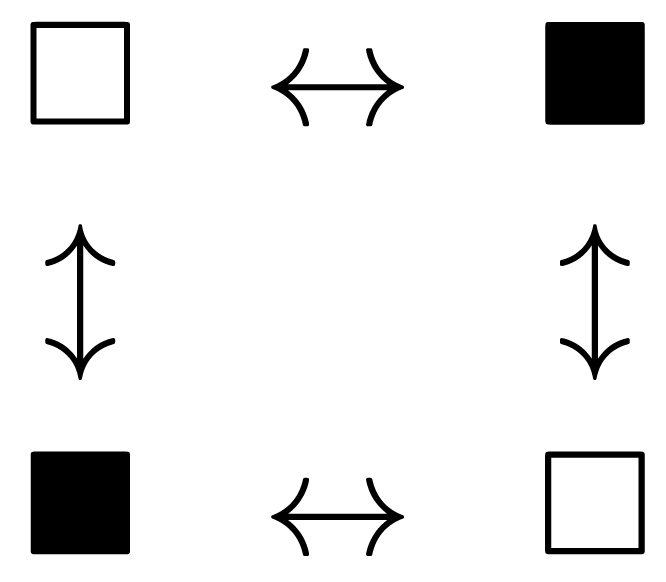
If benefits and costs of networking are positive, one would expect low cost □-persons are networking more (or at least not less) than high cost individuals. Indeed, this is the case for a wide range of model parameters. But it is not necessarily the case when low costs and high costs are very close. High cost individuals may be networking in equilibrium while low cost individuals are not. This intriguing result is driven by strategic substitutes in networking: In that case, if a □-person has two neighbors whose networking efforts are high, no effort may be the best response, and if a ■-person has two neighbors choosing zero effort, a significant effort may be the best response. For details, we refer to Example 2. A related yet different question is whether more networking occurs when ceteris paribus networking becomes less expensive in a society. The comparative statics in Section 5 addresses this question.

To recapitulate, we develop and analyze a new model of strategic network formation—or rather network utilization in many instances—where

• an agent's effort or investment in links is nonspecific;

• the intensity and impact of links can differ, possibly with a negative impact of certain links;

• networking may take place within a given network (graph).

Our model holds much promise for several reasons:

• A broad spectrum of applications.

• A rich class of games which are both potential and supermodular games.

• Possibility of comparative statics with respect to networking costs.

• Possibility of stochastic stability analysis.

• Possibility to explore networking within a “social structure”.

In the remainder of the section, we shall elaborate on these points.

Nonspecific networking games

Here we focus on nonspecific networking, meaning that an agent cannot select a specific subset of feasible links which he wants to establish or strengthen. Rather, each agent chooses an effort level or intensity of networking. In the simplest case, the agent faces a binary choice: to network or not to network. If an agent increases his networking effort, all direct links to other agents are strengthened to various degrees. We assume that benefits accrue only from direct links. The set of agents or players is finite. Each agent has a finite strategy set consisting of the networking levels to choose from. For any pair of agents, their networking levels determine the individual benefits which they obtain from interacting with each other. An agent derives an aggregate benefit from the pairwise interactions with all others. This aggregate benefit is a function of the chosen profile of networking levels. In addition, the agent incurs networking costs, which are a function of the agent's own networking level. The agent's payoff is his aggregate benefit minus his cost. The set of agents together with the individual strategy sets and payoff functions constitute a game in strategic form. Equilibrium means Nash equilibrium. 1

Instances of networking

Despite its apparent simplicity, our hitherto unexplored model of nonspecific networking covers a broad spectrum of applications. It allows for social networking where some persons are more attractive than others, and some even possess negative attraction. Attraction or repulsion can be mutual or not. Certain individuals can have greater advantages from networking or smaller costs of networking than others and, therefore, may be considered natural networkers. To the extent that benefits are positive, under-investment in links can occur in equilibrium. When one allows for the possibility that benefits from interactions with certain agents are negative, a player prefers not to have links and interactions with such “bad neighbors”. Therefore, agents may refrain from networking even when link formation is costless. But an agent cannot prevent bad neighbors from networking and, consequently, may suffer from their efforts. Thus, there can be over-investment in the sense that less investment would increase aggregate welfare. The above 4-player game among friends and enemies demonstrates that under-investment is a possibility as well. In Section 6, we shall present an example where under-investment by one group of agents and over-investment by a second group coexist in equilibrium. A person's social networking activities may consist in joining social or sports clubs. Our general framework encompasses such instances of social networking, like the example following Fact 1 in subsection 3.3. In addition to social interaction and networking, the model is applicable in economics, in particular in the context of industrial organization. We mention in Section 8 that the model encompasses specific cases of user network formation.

Potential and supermodular games

The model comprises a large class of games which are both potential and supermodular (strategic complements) games. Finite potential games and finite supermodular games have in common that a Nash equilibrium in pure strategies exists. The literature on games which share both properties is scarce. Dubey, Haimanko, and Zapechelnyuk [3] show that games of strategic substitutes or complements with aggregation are “pseudo-potential” games.2 As a consequence, they obtain existence of a Nash equilibrium and convergence to Nash equilibrium of certain deterministic best response processes. Brânzei, Mallozzi and Tijs [5] investigate the relationship between the class of potential games and the class of supermodular games. They essentially focus on two-person zero-sum games (and a special case of Cournot duopoly). Their main result is that two-player zero-sum supermodular games are potential games and conversely that two-player zero-sum potential games can be transformed into supermodular games. In our model, suitable assumptions on the benefits from pairwise interaction give rise to a novel class of games which are both potential and supermodular games. A different set of assumptions generates an equally rich family of networking games which have both a potential and the strategic substitutes property.

Potential maximization, if applicable, has several strong implications. First of all, the set of potential maximizers is a subset of the set of Nash equilibria. Hence potential maximization constitutes a refinement of Nash equilibrium in potential games.3 If in addition, the game is supermodular, the set of potential maximizers forms a sublattice of the lattice of Nash equilibria. Consequently, if the game is also a symmetric game, then it has at least one symmetric potential maximizer. Finally, again in the case of supermodular potential games, one obtains comparative statics results for the smallest and the largest potential maximizer.

Comparative statics

In Section 5, we obtain comparative statics results for Nash equilibria with respect to networking costs for either class of networking games, those with strategic complements and those with strategic substitutes. For networking games which are both potential and supermodular games, we obtain comparative statics results for the smallest and the largest potential maximizer.

Stochastic stability

If a finite strategic game and specifically a networking game is a potential game, then perturbed best response dynamics with logit trembles yield the maximizers of the potential as the stochastically stable states, as shown by Blume [7,8], Young [9], Baron et al. [10], among others. Hence in this case, all results for potential maximizers apply to stochastically stable states as well. Two qualifications are warranted. First the coincidence of the set of potential maximizers and the set of stochastically stable states need not hold if the potential is not exact or updating is not asynchronous (like in the above papers), as Alos-Ferrer and Netzer (2010) have shown. Second, this is not to say that the study of stochastically stable states under logit perturbations has to be confined to games with exact potentials. See Alós-Ferrer and Netzer [11], Baron et al. [12], and Section 7 of Baron et al. [10].

Social structure

Nonspecific networking admits a differential impact of an agent's networking efforts on the strength of links to various other agents. In particular, undirected graphs serve as a descriptive tool throughout the paper to distinguish between pairs of agents which can form links among themselves and those pairs which cannot reach each other. Such a graph represents a “social structure” in the sense of Chwe [13]. Chwe investigates which social structures are conducive to coordination in a “local information game”. In contrast to Chwe's, our model falls under the rubric of “local interaction games”. Our concern is not whether people coordinate, but who networks and how much, e.g., whether natural networkers invest more in networking than others.

Related Work

The model of Bramoullé and Kranton [14] is similar to ours in many respects, with one important exception: Interaction is not pairwise but rather with the entire group of one's neighbors. For further details, see Remark (c) at the end of Section 4. The model of Cabrales, Calvó-Armengol and Zenou [15] constitutes an instance of nonspecific networking, both with respect to network formation (socialization) and with respect to network utilization. In both respects, the model exhibits strategic complements and quadratic costs. The investments in networks (socialization) give rise to a weighted graph or network. Given the network, productive investments, say a parent's time spent on homework with their child not only affects their own child's scholarly achievement, but also the achievement of other children with whose parents the parent is linked via the network. Under certain conditions, the model has three Nash equilibria, an unstable one where nobody invests in networks and two stable ones with positive investments in networks, one with low levels of networks and production (resulting in under-investment relative to the efficient outcome) and one with high levels (resulting in over-investment). The model shares several traits with ours: Nash equilibrium, pairwise interactions, comparative statics, among others. Their model differs in that investment is in two dimensions, networks and production, payoffs are of a special functional form, and results obtain asymptotically, for replica games. Galeotti and Merlino [16] adopt the network formation (socialization) part of the Cabrales et al. [15] model, with linear costs and link weight or strength replaced by link reliability or probability. Then the investments in networks yield a random graph. In the realized network, a worker with a “needless job offer” can pass on the offer to an adjacent job seeker. The authors find that investment in the network is high and the resulting networks are well connected when the job destruction rate is at intermediate levels, whereas investment is low and the emerging networks are not well connected when the job destruction rate is either low or high. Goyal and Moraga-González [17] consider a finite number of quantity-setting firms. In the first stage of a three-stage game, costless specific (directed, earmarked) network formation occurs, with pairwise stability à la Jackson and Wolinsky as the equilibrium concept. At the second stage, each makes a costly investment in R&D which reduces its marginal cost of production in the third stage. There are non-specific networking effects in that the firm's investment not only reduces its own marginal costs but also those of other firms and more so the costs of its direct neighbors. If at the third stage, the firms operate in independent markets, the complete network is stable and serves them best. If at the third stage, all firms compete in the same market, then each faces a trade-off: To the extent it benefits from the marginal cost reduction efforts of its competitors, its own investment also reduces the marginal costs of the competitors. Hence, with more connectivity, firms invest less, which increases marginal costs and reduces equilibrium outputs. Therefore, while stable, the complete network is undesirable both in terms of industry profits and total surplus.

Outline

In Section 2, we introduce concepts which are of interest not only for networking games. We set the stage in Section 3, where we develop the general model and some of the main results about Nash equilibria, potentials, and potential maximizers. In Section 4, we examine the question of networkers and networking in a class of games with pairwise symmetry. Section 5 is devoted to comparative statics. In Section 6, we present two classes of games with linear benefits and costs. In Section 7, we elaborate on stochastic stability under logit perturbations. Section 8 contains conclusions and extensions.

2. Preliminaries

Here we collect definitions and results that are of interest beyond the investigation of nonspecific networking. Throughout, we consider finite games in strategic or normal form

$$G=(I,{(S_i)}_{i\in I},{(u_i)}_{i\in I})$$

(2.1)

where I is a finite non-empty set of players, S_i denotes the finite non-empty strategy set of player i and u_i denotes the payoff function of player i. The game G has joint strategy set S = ∏_j S_j. For player i, S_−i = ∏_j≠i S_j denotes the set of joint strategies of all players except i.

2.1. Lattices

Let X be a partially ordered set, with partial order ≥. That is, ≥ is a reflexive, transitive and antisymmetric binary relation on X. Antisymmetric means that for any x, y ∈ X, if x ≥ y and y ≥ x then x = y. Given elements x and z in X, denote by x ∨ z or sup{x, z} the least upper bound or join of x and z in X, provided it exists, and by x Λ z or inf {x, z} the greatest lower bound or meet of x and z in X, provided it exists. A partially ordered set X that contains the join and the meet of each pair of its elements is called a lattice. A lattice in which each nonempty subset has a supremum and an infimum is complete. In particular, a finite lattice is complete. If Y is a subset of a lattice X and Y contains the join and the meet with respect to X of each pair of elements of Y, then is Y is a sublattice of X.

2.2. Supermodular Games

Let X and Y be two partially ordered sets and U : X × Y → ℝ.

Definition 1

The function U satisfies decreasing differences (x,y) in ∈ X×Y if for all pairs (x,y) ∈ X×Y and (x′,y′) ∈ X×Y, it is the case that x ≥ x′ and y ≥ y′ implies

$$U(x,y)-U(x^{\prime },y)\le U(x,y^{\prime })-U(x^{\prime }-y^{\prime }).$$

The function U satisfies increasing differences in (x,y) ∈ X×Y if for all pairs (x,y) ∈ X×Y and (x′,y′) ∈ X×Y, it is the case that x ≥ x′ and y ≥ y′ implies

$$U(x,y)-U(x\prime ,y)\ge U(x,y^{\prime })-U(x^{\prime },y^{\prime }).$$

Definition 2

Let X be a lattice and U: X → ℝ. The function U is supermodular on X if for all pairs (x, y) ∈ X × X, it is the case that

$$U(sup\left\{x,y\right\})+U(inf\left\{x,y\right\}\ge U(x+U(y).$$

Let Euclidean spaces ℝ^l and subsets thereof be endowed with the canonical partial order. In the sequel, let S_i ⊆ ℝ, i = 1,…, N, with N > 1. Set S = S₁ × … × S_n ⊆ ℝ^N. For s = (s₁,…, s_N) ∈ S and i ∈ {1,…, N}, we adopt the game-theoretical notation s = (s_i, s_−i). Similarly, we shall write s = (s_i, s_j, s_−ij) in case i,j ∈ {1,…, N}, i ≠j, and S_−ij instead of ∏_k≠i,j S_k.

Definition 3

A function u: S → ℝ is pairwise supermodular if u(·,·, s_−ij): S_i × S_j → ℝ satisfies increasing differences for all pairs i, j ∈ {1,…, N}, i ≠ j and s_−ij ∈ S_−ij.

Since S = S₁ × … × S_N and S_i ⊆ ℝ for all i, the following two properties hold by Theorems 2.6.1, 2.6.2, and Corollary 2.6.1 of Topkis [18]:

$$u:S\to ℝ\text{is supermodular if and only if it is pairwise supermodular}$$

(2.2)

$$\text{If}u:S\to ℝ\text{is pairwise supermodular then}u\text{satisfies increasing differences in}(s_i,s_{-i})\in S_i\times S_{-i}\text{for all}i=1,\dots ,N.$$

(2.3)

For a finite N-player game G = (I, (S_i)_i∈I, (u_i)_i∈I) with I = {1,…, N} and S_i⊆ ℝ for all i ∈ I, supermodularity amounts to the following

Definition 4

The game G is supermodular if each payoff function u_i satisfies increasing differences in (s_i, s_−i) ∈ S_i × S_−i.4

Pairwise supermodularity is a strategic complements condition when reaction functions exist and equivalent to ∂²u_i/∂ s_j∂s_i ≥ 0 for i ≠ j when strategy sets are intervals and payoff functions are sufficiently smooth. For details and further references on lattices and supermodularity see Topkis [18] and Chapter 2 of Vives [19]. Notice that in our context, S is trivially compact and, therefore, Theorem 2 of Zhou [20] and its proof apply:

$$\text{The set of Nash equilibria of a supermodular game}G\text{is a nonempty complete lattice}.$$

(2.4)

2.3. Potential Games

When appropriate, we shall employ the concept of a potential P for a game G = (I, (S_i)_i∈I, (u_i) _i∈I) pioneered by Monderer and Shapley [21], i.e., a function P : S → ℝ such that

$$u_i(s_i,s_{-i})-u_i(s_i^{\prime },s_{-i})=P(s_i,s_{-i})-P(s_i^{\prime },s_{-i})$$

for all i ∈ I, s_i, s′_i ∈ S_i, s_−i ∈ S_−i. The game G is called a potential game if it has a potential. For a game G with potential P,

$$S^{*}=\underset{s\in S}{argmax}P(s)$$

denotes the set of potential maximizers. Notice that S* is a subset of the set of Nash equilibria and independent of the particular choice of the potential P.

3. The Networking Game

Our model of nonspecific networking constitutes a game in strategic form. There is a finite player set I = {1,…, N} where N > 1. Every player i ∈ I has strategy set

$$S_i=K=\left\{k_0,k_1,\dots ,k_T\right\},$$

with T ≥ 1 and 0 = k₀ < k₁,…,k_T. The T + 1 individual strategies 0, k₁,…, k_T are the networking levels a player can choose and are the same for all players. Depending on the context, a higher networking level may mean more effort in socializing, more investment in networking skills, more investment in communication and information hardware or software, subscription to better network services.

Players receive benefits from pairwise interaction with others: For any pair (i,j)∈I × I,i ≠ j, player i receives a benefit b_ij(s_i, s_j)∈ ℝ from interacting with j, if i chooses s_i ∈S_i and j chooses s_j ∈ S_j. At this preliminary stage, the benefit function b_ij should be viewed as a reduced form that convolutes several effects. Subsequently, special cases of benefit functions will be considered, where the different aspects of nonspecific networking become more explicit and transparent. Player i∈I incurs a cost c_i(s_i) when choosing s_i ∈ S_i. As a rule, the choice of a higher networking level is more costly: 0 = c_i(0) < c_i(k₁), …, c_i(k_T). However, in some applications, k₀, k₁,…, k_T may just be labels for different technologies, user networks, natural or artificial languages, etc. which cannot be unambiguously ranked in terms of benefits or costs. The payoff u_i(s) for player i depends on the strategy profile (joint strategy) of all players, s = (s₁,…, s_N)∈ S, and consists of i's total benefit from interacting with other players minus i's cost:

$$u_i(s)=\text{∑}_{j\ne i}{b}_{ij}(s_i,s_j)-c_i(s_i)$$

(3.1)

For specific interpretations, it proves advantageous to decompose benefit functions as follows:

$$b_{ij}(s_i,s_j)={\pi }_{ij}(s_i,s_j)·{\upsilon }_{ij}$$

(3.2)

where π_ij ≥ 0 can be viewed as the intensity of i interacting with j and υ_ij as i's benefit, appreciation or valuation of an interaction with j. If 0 ≤ π _ij < 1 and π_ij is interpreted as a probability, then player i receives benefit υ _ij with probability π_ij, zero benefit with probability 1 − π_ij, and expected benefit b_ij. It is possible that players are linked without any effort or investment, that is π_ij(0, 0) > 0. It is also possible that the strength or probability of certain links proves irresponsive to effort or investment, that is π_ij is constant.

The list G = (I, (S_i)_i∈I, (u_i)_i∈I) constitutes a game in strategic or normal form and summarizes our model of nonspecific networking. The game G will be referred to as the networking game. The equilibrium concept is Nash equilibrium. Let S^NE denote the set of Nash equilibria of G.

We adopt the standard notion of efficiency in the literature on networks. Let W : S → ℝ be the aggregate or utilitarian welfare function given by

$$W(s)={\text{∑}}_i{u}_i(s)$$

for s ∈ S. A strategy profile s is called efficient if it is a maximizer of W and called inefficient otherwise.

It proves convenient and instructive to distinguish the pairs (i,j) with b_ij ≠ 0 as the edges or links of an undirected graph on the player set I. To this end, we shall use the following terminology and notation related to graphs and networks. Let F = {J ⊆ I: |J| = 2}. A pair Γ = (I, E) with E ⊆ F is called an undirected graph with vertex set I and edge set E. Then the elements of I are called the vertices or nodes of the graph and the elements of E are called the edges or links of the graph. In case {i, j} ∈ E, i.e., in case {i, j} is an edge (link) of the graph, we also say that {i, j} “belongs to the graph” and that i and j are “neighbors” or “adjacent”. Throughout, without further mention, we are restricting ourselves to graphs without isolated nodes. In such a graph, every node has at least one neighbor. Finally, we use the shorthand notation ij for (i,j).

In the sequel, we frequently assume a graph (I, E) such that b_ij = 0 for all(i, j) with {i, j} ∈ F\E In that case networking takes place within the given network or graph E so that a player can only network with his neighbors in E. If two persons are not neighbors, then interaction between them may be impossible or to no avail. Infeasible could simply mean exorbitantly costly. One possible interpretation is that E represents a preexisting network and players decide to what extent they utilize the network. For example, the network could be a physical infrastructure, like fiber-optical cables, which determines who can network with whom. The network could reflect geographical, legal, language, and a variety of other barriers as well.

Several of the subsequent examples will be based on the circular network (I, E⁰) with

$$E^0=\left\{\left\{1,2\right\},\left\{2,3\right\},\dots ,\left\{N-1,N\right\}-\left\{N,1\right\}\right\}$$

where the players are arranged in a circle and i and j are neighbors if j = i ± 1 mod N. The circular graph or network figures prominently in the literature on local interaction games, especially in Ellison [22]. Schelling ([23], p. 147) explains the relevance of neighborhood size, referring to a dinner table where men and women are seated alternately: With one neighbor to the left and one to the right, every person has only neighbors of the opposite sex. Counting two neighbors on either side, every person has two neighbors of both sexes. Yet in his analysis of the dynamics of neighborhood segregation, Schelling does not use a circular city model and resorts to a linear city model and a rectangular lattice instead. The term circular city, found in Weidenholzer [24] for example, originated in the literature on spatial competition where it is associated with a model by Salop [25]. Berninghaus and Schwalbe [26] call E⁰ a one-dimensional interaction structure in contrast to two-dimensional interaction structures.

We are going to explore the implications of two opposite conditions, (A) and (B), on the benefits from networking. We will further consider condition (C) on networking costs and condition (D) on best responses:

• There exists an undirected graph (without isolated nodes) (I,E) such that b_ij = 0 for {i,j} ∉ E and b_ij satisfies increasing differences in (s_i, s_j) ∈ S_i × S_j for {i,j} ∈ E.

• There exists an undirected graph (without isolated nodes) (I,E) such that b_ij = 0 for {i,j} ∉ E and b_ij satisfies decreasing differences in (s_i,s_j) ∈ S_i × S_j for {i,j} ∈ E.

• There exist C₁ > 0,…, C_N > 0 such that c_i(s_i) = C_i·s_i for i∈I, s_i∈S_i.

• For i∈I, there exists a unique best response against each s_−i ∈ S_−i.

Let us consider Igor, player i who helps his daughter Olga with her homework. Similarly, José, player j, helps his daughter Laura with her homework. Olga and Laura are classmates. It is plausible to assume that greater effort by Igor improves Olga's scholarly achievement and greater effort by José improves Laura's. But there may also be cross-effects. First suppose, as is often assumed, that there exist positive peer effects: Laura's achievement motivates Olga the more the higher Laura's achievement and vice versa. For instance, if José makes a greater effort, then Laura does better, but this also enhances the positive impact of greater effort by Igor on Olga's performance. The same holds true for the cross-effect in the opposite direction. Under those circumstances, (A) is satisfied for i and j. Second, one can also imagine negative peer effects: Olga is frustrated and de-motivated by Laura's success and vice versa. Then (B) is satisfied by i and j. Condition (C) simply means positive linear networking costs. (D) implies that all Nash equilibria are strict. More interestingly, the condition helps strengthen some comparative statics results: Compare Propositions 4 and 5. Ceteris paribus, (D) is generically satisfied with respect to cost parameters.

3.1. Implications of Increasing Differences in Benefits

As a first result, we obtain

Proposition 1

Let G be a networking game where pairwise benefits satisfy (A). Then the set of Nash equilibria S^NE ⊆ S is nonempty and the partially ordered set S^NE is a lattice.

PROOF

The proof consists in verifying that the hypothesis of (2.4) is satisfied. S = ∏_i∈I S_i is a finite lattice as the cartesian product of finite lattices. Pick any i∈I. For each j ≠ i, u_i(s_i, s_j, s_−ij) satisfies increasing differences in (s_i,s_j) on S_i × S_j for each fixeds_−ij∈S_−ij because of the functional form (3.1) and assumption (A) which implies that u_i(s_i, s_−i) has increasing differences in (s_i, s_−i) on S_i × S_−i. Hence G is a supermodular game. The assertion follows from Zhou's Theorem (2.4). ■

Since S is finite, the lattice property of the set of Nash equilibria implies that there exists a Nash equilibrium where every player networks at least as much as in any other Nash equilibrium. If in addition, the game is symmetric, one obtains as a corollary that such an equilibrium is symmetric, hence existence of a symmetric equilibrium. The specific cases examined in subsection 3.4 and Section 6, and the examples given in Section 5 satisfy the assumptions of the proposition.

In general, a networking game need not have a Nash equilibrium in pure strategies:

Example 1

We consider a population of N = 4 players who form the circular network Γ = (I, E⁰). K = {0,1} so that each player has a binary choice, to network or not to network. The costs functions are c_i(s_i)= (3/2).s_i. Payoffs are such that even numbered players exhibit strategic substitutes and odd numbered players exhibit strategic complements:

$$\begin{array}{cc}\hfill b_{ij}(s_i,s_j)& =\sqrt{s_i+s_j}\text{for}\left\{i,j\right\}\in E,i\text{even};\hfill \\ \hfill b_{ij}(s_i,s_j)& =s_i{s}_j\text{for}\left\{i,j\right\}\in E,i\text{odd};\hfill \\ \hfill b_{ij}(s_i,s_j)& =0\text{for}\left\{i,j\right\}\notin E.\hfill \end{array}$$

In this example, S^NE is empty. Namely, if at least one of the even numbered players plays 0, then the best response of both odd numbered players is to play 0. Against the latter, the best response of both even numbered players is 1. In turn the best response of both odd numbered players is 1. Against the latter, the best response of both even numbered players is 0, and we have reached a cycle where players alternate their choices. If none of the even numbered players plays 1, we also reach a cycle where players alternate their choices.

3.2. Implications of Increasing Differences in Benefits and of the Existence of a Potential

Obviously, every finite potential game has a Nash equilibrium. Moreover, for a networking game that has a potential and satisfies assumption (A) of Proposition 1, the set S* of potential maximizers forms a nonempty sublattice of the equilibrium set S^NE:

Proposition 2

Suppose G is a networking game which has a potential P: S → ℝ and satisfies (A). Then:

• (α) The potential P is supermodular on S.

• (β) The set S* is a nonempty sublattice of S^NE and of S.

• (γ) Moreover, if u_i is supermodular on S for each i∈I, then the set of states s ∈ S which are both efficient and potential maximizing constitutes a sublattice of S.

PROOF

• (α): Pick any i ∈ I For all j ≠ i and for all s, s′ ∈ S such that $s_i\ge s_i^{\prime }$ and $s_j\ge s_j^{\prime }$, we have

  $$\begin{array}{cc}\hfill P(s_i,s_j,s_{-ij})& -P(s_i^{\prime },s_j,s_{-ij})\hfill \\ \hfill =u_i(s_i,s_j,s_{-ij})& -u_i(s_i^{\prime },s_j,s_{-ij})\hfill \\ \hfill \ge u_i(s_i,s_j^{\prime },s_{-ij})& -u_i(s_i^{\prime },s_j^{\prime },s_{-ij})\hfill \\ \hfill =P(s_i,s_j^{\prime },s_{-ij})& \hfill -P(s_i^{\prime },s_j^{\prime },s_{-ij}).\end{array}$$

  The two equalities follow from the definition of a potential P. The inequality follows from (A). This means that P satisfies increasing differences on S_i × S_j for each j ≠ i and each fixed s_−ij ∈ S_−ij. As this property holds for all i ∈ I, we conclude that P is pairwise supermodular and so supermodular on S by (2.2).

• (β): The set S* of maximizers of P is nonempty because S is a finite set. By (α) and Theorem 2.7.1 of Topkis [18], S* is a sublattice of S. Moreover, by Proposition 1, S^NE is a lattice with respect to the partial order induced by the partial order of S, but not necessarily a sublattice of S. Now S* ⊆ S^NE. Thus we have that S* ⊆ S^NE ⊆ S and S* is a sublattice of S^NE.

• (γ): Because the payoff function u_i is supermodular on S for each i ∈ I, the utilitarian welfare function W is supermodular on S as the finite sum of supermodular functions by Lemma 2.6.1 in Topkis [18]. It follows that S^∞ = arg max_s∈S W(s) is a sublattice of S by Theorem 2.7.1 in Topkis [18]. Now the set of states which are both efficient and potential maximizing is S^∞ ∩ S*. Because S* is a sublattice of S by (β) and we demonstrated that S^∞ is a sublattice of S as well, it follows that S^∞ ∩ S* is a sublattice of S as the intersection of sublattices of S by Lemma 2.2.2 in Topkis [18]. ■

Remarks

• Observe that if in addition, G is a symmetric game, then assertion (β) of the proposition implies that G has at least one symmetric potential maximizer.

• The result that the set of potential maximizers forms a nonempty sublattice of S (rather than merely a lattice), is also of some practical interest. Namely, then one can easily find a new potential maximizer knowing that two profiles (equilibria) are potential maximizers: If s = (s₁,…,s_N) and $s^{\prime }=(s_1^{\prime },\dots ,s_N^{\prime })$ are in S*, then so are ${sup}_S\left\{s,s^{\prime }\right\}=(max\left\{s_1,s_1^{\prime }\right\},\dots ,max\left\{s_N,s_N^{\prime }\right\})$ and ${inf}_S\left\{s,s^{\prime }\right\}=(min\left\{s_1,s_1^{\prime }\right\},\dots ,min\left\{s_N,s_N^{\prime }\right\})$. One cannot necessarily proceed this way within the equilibrium set S^NE. For the conclusion of Proposition 1 that the set of Nash equilibria S^NE is a nonempty lattice can be hardly replaced by the stronger assertion that S^NE is a sublattice of the set of strategy profiles S. The reason is that Zhou's Fixed-Point Theorem ([20], p. 297) cannot be generalized to the effect that the set of fixed points of an increasing correspondence from a nonempty complete lattice X into itself is a sublattice of X; see Zhou ([20], p. 298) and Example 2.5.1 of Topkis ([18], p. 40). For the specific case of a two-player supermodular game where players' strategy sets are totally ordered, Echenique [27] establishes that the set of Nash equilibria is a sublattice of the set of strategy profiles. But he observes that a supermodular game with more than two players need not have an equilibrium set that is a sublattice even if players' strategy sets are totally ordered.

• Part (γ) of Proposition 2 does not assert that S^∞ ∩ S* is nonempty. See particular instances of inefficient Nash equilibria (and potential maximizers) in subsection 6.1.

• The results contained in Propositions 1 and 2 do not depend on the particular form of the payoff functions (3.1). They also hold if (A) is replaced by the more general condition that each payoff function u_i satisfies increasing differences in (s_i, s_−i) ∈ S_i × S_−i.

• In general, a networking game satisfies neither condition (A) nor condition (B) as Example 1 demonstrates. A networking game need not be a potential game either. But which restrictions on benefit functions would yield a potential game?

3.3. Existence of a Potential

To formulate sufficient conditions on benefit functions for the existence of a potential of G, let us consider for any pair of distinct players ij, the two-player game G_ij with:

• player set I_ij = {i, j};

• strategy sets S_i = S_j = K;

• payoffs b_ij(s_i, s_j) for i and b_ji(s_j, s_i) for j when they play the joint strategy (s_i, s_j) K × K.

Suppose β_ij is a potential for G_ij. We say that β_ij is symmetric, if β_ij(s_i, s_j) = β_ij(s_j, s_i) for all (s_i, s_j) K × K. Existence of a symmetric potential for all pairwise interactions is sufficient for the existence of a potential of the entire networking game:

Fact 1

If for each distinct pair ij, β_ij is a symmetric potential of G_ij, then the function P given by

$$P(s)=\frac{1}{2}\text{∑}_i\text{∑}_j{\beta }_{ij}(s_i,s_j)-\text{∑}_i{c}_i(s_i)$$

(3.3)

for s S, is a potential of G.

PROOF

Analogous to proof of Proposition 1 in Baron et al. [10]. ■

Suppose that each player i has four choices s_i = 0,1,2,3. s_i = 0 stands for joining no club. s_i = 1 stands for joining only the chess club at cost c₁ > 0 and basic benefit b₁. s_i = 2 stands for joining only the tennis club at cost c₂ > c₁ and basic benefit b₂. s_i = 3 stands for joining both clubs at cost c₁ + c₂ and basic benefit b₃. Moreover, player i obtains an added benefit or (disutility) if a neighbor belongs to the same club(s). Neighbors i and j both enjoy the added benefit β_ij(s_i, s_j) which depends on the common club memberships. Set c_i (0) = 0, c_i(1)= c₁ − b₁, c_i(2) = c₂ − b₂, c_i(3) = c₁ + c₂ − b₃. Then each game G_ij has the symmetric potential β_ij and G has the potential (3.3). The games G_ij are congestion games in the sense of Rosenthal [28] which are potential games (and vice versa); see Rosenthal [28], Monderer and Shapley [21], and Voorneveld et al. [29].

Next we impose directly certain restrictions on the pairwise benefit functions and discuss how they relate to the existence of symmetric potentials. For any distinct pair of players ij, we consider the following three conditions:

• Identical Benefits:b_ij(s_i, s_j) = b_ji(s_j,s_i) for all (s_i,s_j) K × K.

• Symmetric Benefits: b_ij(s_i,s_j) = b_ji(s_i,s_j) for all (s_i,s_j) K × K.

• Interchangeable Actions: b_ij(s_i,s_j) = b_ij(s_j,s_i), b_ji(s_i,s_j) = b_ji(s_j,s_i) for all (s_i,s_j) K × K.

Condition (I) is tantamount to b_ij being a (not necessarily symmetric) potential of G_ij and b_ji being a (not necessarily symmetric) potential of G_ji. Condition (II) implies existence of a symmetric potential of G_ij in case T = 1, but not otherwise. Conditions (I) and (II) combined are equivalent to b_ij =b_ji being a symmetric potential of G_ij. Any two of the three conditions imply the third one. As an immediate consequence, we obtain

Lemma 1

If the conditions (I)–(III) hold, then the game G has a potential P of the form (3.3) with β_ij = b_ij.

While obviously restrictive, existence of a symmetric potential for G_ij still leaves a lot of flexibility in terms of functional form and interpretation. To illustrate the scope of applications, let us specialize and assume a decomposition (3.2) with π_ij ≥ 0. Then (I)–(III) have the following counter-parts:

• Identity: π_ij(s_i, s_j) = π_ji(s_j, s_i) for all (s_i, s_j) ∈ K × K.

• Symmetry: π_ij(s_i, s_j) = π_ji(s_i, s_j) for all (s_i, s_j) ∈ K × ?K.

• Interchangeability: π_ij(s_i, s_j) = π_ij(s_j, s_i), π_ji(s_i, s_j) = π_ji(s_j, s_i)for all (s_i, s_j) ∈ K × K.

  We also consider a symmetry condition for the valuations υ_ij:

• Mutual Affinity: υ_ij = υ_ji.

Mutual affinity can result, e.g., from similarity (kindred spirits) or from complementarity (attraction of opposites). There can be mutual lack of interest, υ_ij = υ_ji = 0, and mutual dislike or disadvantage, υ_ij = υ_ji < 0. Any two of the conditions (i)–(iii) imply the third one. Conditions (i)–(iv) imply (I)–(III).

3.4. Adversity

We repeatedly consider games exhibiting pairwise symmetry of the form (3.2) with (ii) and (iv). But part of the appeal of our approach rests on the fact that it encompasses asymmetric scenarios. For instance, case 2 of Example 2 below can be transformed into a strategically equivalent game where some players are more attractive to their neighbors than the neighbors are to them, which constitutes a violation of (iv). In the current subsection (and in subsection 6.2), we set out to study more systematically networking games with variably attractive players.

In certain pairwise interactions, one party gains when the other loses and vice versa. One can think of chess matches, instances of gambling, or mutual industrial espionage. This means that for such a pair of players ij, the game G_ij is a zero-sum game:5 b_ij(s_i, s_j) = −b_ji(s_j, s_i) for any pair of networking levels (s_i, s_j) ∈ K × K. If one assumes the functional form (3.2) and equal intensities of interaction, that is (i), then such an adversarial interaction amounts to υ_ij = −υ_ji. It turns out that if G_ij is zero-sum, then existence of a potential of G_ij and supermodularity of G_ij are equivalent.

Proposition 3

Suppose the game G_ij is zero-sum. Then the following properties are equivalent:

(α) G_ij has a potential.

(β) There exist functions f_ij: K → ℝand g_ij: K → ℝ such that b_ij(s_i, s_j) = f_ij(s_i) − g_ij(s_j), b_ji(s_j, s_i) = g_ij(s_j) − f_ij(s_i) for all (s_i, s_j) ∈ K × K.

(γ) G_ij is supermodular.

PROOF

By Theorem 1 of Brânzei et al. [5], (α) and (β) are equivalent. The separation property (β) implies increasing differences (in fact constant differences) and, since K ⊆ IR, supermodularity. Hence (β) implies (γ). By Theorem 4 of Brânzei et al. [5], (γ) implies (α). ■

If a zero-sum game G_ij has a potential, then the function β_ij(s_i, s_j) = f_ij(s_i) + g_ij(s_j), with f_ij and g_ij as in (β), is a potential. The potential is asymmetric unless f_ij and g_ij are identical up to an additive constant. Hence, in general, Proposition 1 will not apply. Nevertheless, if each basic game G_ij satisfies the separation property (β), then G has a potential given by

$$P(s)=\text{∑}_i\text{∑}_{j\ne i}{f}_{ij}(s_i)-\text{∑}_i{c}_i(s_i)$$

for s ∈ S. Moreover, then each player i has a nonempty set D_i of weakly dominant strategies and S* = S^NE = D₁ × … × D_N. Essentially the same conclusions hold if each basic game G_ij is constant-sum and a potential game.

4. Networkers and Networking

Both in traditional and in electronic interactions, some agents are much more active in networking than others and might be called “networkers”. Some might be considered designated or natural networkers because they have higher benefits or lower costs from networking than others. In the Introduction, we already raised the question whether natural networkers would necessarily network more. To address this question, we examine the following example.

Example 2

We consider a population of N = 2M players with M ≥ 2. The players form the circular undirected graph Γ = (I, E⁰). The set of available networking levels is K = {h/2: h = 0,1,…, 10}. The pairwise benefit functions constitute a special case of (3.2):

$$b_{ij}(s_{i,}{s}_j)=\sqrt{s_i+s_j}\cdot {\upsilon }_{ij}\text{for}\left\{i,j\right\}\in E^0;b_{ij}(s_i,s_j)=0\text{for}\left\{i,j\right\}\notin E^0.$$

Costs are of the linear form c_i(s_i) = C_i · s_i with C_i > 0.

CASE 1

υ_ij = 1 for all ij and C_i = 1 for all i.

Then the networking game G = (I, (S_i)_i∈I, (u_i)_i∈I) is symmetric and has the symmetric equilibrium $s^{*}=(s_1^{*},\dots ,s_N^{*})=(1/2,\dots ,1/2)$. G has at least two asymmetric equilibria, s^Δ = (0,1, 0,1,…, 0,1) and s^∇ = (1,0,1,0,…,1,0).6

All three equilibria are inefficient, with the same value W = 2N − M whereas the maximum value of W is 4N − 2N = 2N, since maximization of the welfare function W requires that s_i + s_j = 4 for {i, j} ∈ E⁰. The game has a potential P given by (3.3) and all three equilibria are maximizers of P.

CASE 2

υ_ij = 1 for all ij and C_i = 1 for i even, C_i = C < 1 for i odd.

Then the odd numbered players have a cost advantage and are the “natural networkers”.

• If the cost advantage is rather small, e.g., C = 0.9, then s*, s^Δ, and s^∇ are still Nash equilibria. In s^∇, the natural networkers are not networking while the other players are. However, the cost difference does have an impact: The Nash equilibrium s^Δ—where the natural networkers are networking and others are not — is the only potential maximizer.

• If the cost advantage is sufficiently large, then only natural networkers are networking in equilibrium. E.g., if C = 0.5, then s** = (4, 0, 4, 0,…, 4, 0) is the only Nash equilibrium and the only potential maximizer.

Remarks

• The equilibria s*, s^Δ, s^∇ and s** discussed in the example are inefficient in that there is under-investment in networking.

• If in CASE 2, the payoff function u_i of each odd numbered player i is replaced by u_i/C, then the Nash equilibria remain the same, although the game is no longer a potential game after these payoff transformations. In the modified game, all players have the same cost functions, but the odd numbered players have greater benefits from networking than the even numbered players. A possible interpretation is that the even numbered players are more attractive to their neighbors than the odd numbered players.

• Bramoullé and Kranton [14] consider a different way of nonspecific networking. They assume an undirected graph Γ = (I, E) with vertex set I and edge set E, continuous actions s_i ≥ 0 for i ∈ I, a C²-function B : ℝ₊ → ℝ₊ with B(0) = 0, B′ > 0, B″ < 0, and linear cost functions c_i(s_i) = C·s_i so that B′(e*) = C for some e* > 0. Player i ∈ I has payoffs

  $$U_i(s;E)=B\left(s_i+\text{∑}_{j\in N_i}{s}_j\right)-C\cdot s_i$$
  where N_i is the set of i′s neighbors in (I, E). If E is a circle, then equilibria similar to s*, s^Δ, and s^∇ above arise.

5. Comparative Statics in Networking Costs

Intuitively, one would expect that networking activities intensify if networking costs decline. This conjecture proves at least partially true in the presence of strategic substitutes in pairwise interactions. To be precise, we consider conditions (B)–(D). Notice that condition (B) constitutes the antithesis of condition (A). It is satisfied in Example 2. Both (A) and (B) hold for the linear models of subsections 6.1 and 6.2.

Proposition 4

Let G be a networking game satisfying (B)-(D) and let G′ be a second networking game that differs from G only in the marginal networking costs, which are $C_1^{\prime }>0,\dots ,C_N^{\prime }>0$ in G′. Further, let s ∈ S be an equilibrium of G and s′ ∈ S be an equilibrium G′. Suppose $C_i^{\prime }\le C_i$ for all i and s′ ≠ s. Then $s_i^{\prime }>s_i$ for some i.

PROOF

Let G, G′, C₁,…, C_N, $C_1^{\prime },\dots ,C_N^{\prime }$, s, s′ be as hypothesized. Since s ≠ s′, there is i ∈ I such that s_i ≠ s′_i. Consider this player i and suppose the conclusion is false, that is $s_j^{\prime }\le s_j$for all j ∈ I. We have:

$$\begin{array}{cc}\hfill 0& <\text{∑}_j{b}_{ij}(s_i,s_j)-C_i\cdot s_i-\left(\text{∑}_j{b}_{ij}(s_i^{\prime },s_j)-C_i\cdot s_i^{\prime }\right)\hfill \\ & =\text{∑}_j(b_{ij}(s_i,s_j)-b_{ij}(s_i^{\prime },s_j))-C_i\cdot s_i+C_i\cdot s_i^{\prime }\hfill \\ & \le \text{∑}_j(b_{ij}(s_i,s_j^{\prime })-b_{ij}(s_i^{\prime },s_j^{\prime }))-C_i\cdot s_i+C_i\cdot s_i^{\prime }\hfill \\ & \le \text{∑}_j(b_{ij}(s_i,s_j^{\prime })-b_{ij}(s_i^{\prime },s_j^{\prime }))-C_i^{\prime }\cdot s_i+C_i^{\prime }\cdot s_i^{\prime }\hfill \\ & =\text{∑}_j{b}_{ij}(s_i,s_j^{\prime })-C_i^{\prime }\cdot s_i-\left(\text{∑}_j{b}_{ij}(s_i^{\prime },s_j^{\prime })-C_i^{\prime }\cdot s_i^{\prime }\right)<0\hfill \end{array}$$

a contradiction. The first inequality follows from optimality of s_i at s_−i, $s_i\ne s_i^{\prime }$, and (D). The second inequality follows from (B). The third inequality is a consequence of $C_i^{\prime }\le C_i$. The last inequality follows from optimality of $s_i^{\prime }\text{at}{s}_{-i}^{\prime },s_i\ne s_i^{\prime }$, and (D). Hence, to the contrary, the conclusion has to be true. ■

The assumption (D) of unique best responses can be disposed of if one postulates strict cost reductions instead:

Proposition 5

Let G be a networking game that satisfies (B) and (C) and let G′ be a second networking game that differs from G only in the marginal networking costs, which are $C_1^{\prime }>0,\dots ,C_N^{\prime }>0$ in G′. Further, let s ∈ S be an equilibrium of G and s′ ∈ S be an equilibrium of G′. Suppose $C_i^{\prime }<C_i$ for all i and s′ ≠ s. Then $s_i^{\prime }>s_i$ for some i.

PROOF

Let G, G′, C₁,…, C_N, $C_1^{\prime },\dots ,C_N^{\prime }$, s, s′ be as hypothesized. Suppose the conclusion is false, that is $s_i^{\prime }\le s_i$ for all i ∈ I. Now take any i ∈ I. By assumption, s_i is a best response of i against s_−i in G. Since $s_j^{\prime }\le s_j$ for all j ≠ i and (B) and (C) hold, the largest best response ŝ_i of i against $s_{-i}^{\prime }$ in G satisfies ŝ_i ≥ s_i. Since $C_i^{\prime }<C_i$, (B) and (C) hold, and G and G′ differ only in marginal networking costs, one obtains s̃_i ≥ ŝ_j for any best response s̃_i of i against $s_{-i}^{\prime }$ in G′ and any best response ŝ_i of i against $s_{-i}^{\prime }$ in G. It follows that $s_i^{\prime }\ge s_i$ because $s_i^{\prime }$ is a best response of i against $s_{-i}^{\prime }$ in G′. But $s_i^{\prime }\ge s_i$ and $s_i^{\prime }\le s_i$ imply $s_i^{\prime }=s_i$. Since i was arbitrary, s′ = s, which contradicts the hypothesis of the proposition. Hence, to the contrary, the conclusion has to be true. ■

Notice that the conclusion of Propositions 4 and 5 cannot be substantially strengthened for two reasons. For one, G and G′ may have the same equilibria, even if $C_i^{\prime }<C_i$for all i. This follows from the discreteness of the model. Secondly, let G be the game of CASE 1 of Example 2 which satisfies (B)–(D) with C_i = 1 for all i. Let G′ be a game that differs from G only with respect to marginal networking costs. Specifically, set $C_i^{\prime }=1/2$ for i odd and $C_j^{\prime }=C^{\prime }<1$for j even. If C′ is sufficiently close to 1, then the conclusion in CASE 2 of Example 2 still applies: s** = (4, 0,…, 4, 0) is an equilibrium of G′ while s* = (2, 2,…, 2, 2) is an equilibrium of G. Obviously s** ≠ s*. But some players have lowered their efforts in s** relative to s*.

Without a strategic substitutes assumption, a cost decline is consistent with a universal reduction of networking activities. Next we provide a numerical example with this property.

Example 3

We consider a population of N = 2M players with M ≥ 2. The players form the circular undirected graph Γ = (I, E⁰). The set of available networking levels is K = {0, e^1/4 −1, e−1} where e = exp(1) is the Euler number. Put b_ij(s_i, s_j) = 0 for {i,j} ∉ E and $b_{ij}(s_i,s_j)=\frac{1}{2}ln(1+s_i)\cdot ln(1+s_j)$ for {i,j} ∈ E. Then the pairwise interactions exhibit weak strategic complements rather than strategic substitutes.

With C_i = e⁻¹ for all i, we obtain a game G which has two symmetric equilibria, s⁰ = (0,…, 0) and s^● = (e − 1,…, e − 1).

Setting $C_i^{\prime }=e^{-1/4}/4<C_i$ for all i defines a game G′ which has three symmetric equilibria, s⁰, s^●, and s^●● = (e^1/4 − 1,…, e^1/4 − 1).

Thus, the example has actually several interesting features. First, there exists the equilibrium s⁰, an instance of mutual obstruction where nobody has an incentive to network if nobody else is networking. Next there exists the equilibrium s^● where everybody exerts maximum networking effort. Further, a cost reduction leads to the emergence of a third equilibrium, s^●● where everyone makes a positive but less than maximal effort. Regarding our original point, the conclusion of Propositions 4 and 5 obviously need not hold if the strategic substitutes assumption of the form (B) is violated.

The example satisfies assumptions (A) and (C). In addition, the games G and G′ are symmetric. As a consequence of Proposition 1, G and G′ have smallest and largest equilibria which are symmetric. s⁰ is the smallest equilibrium and s^● is the largest equilibrium in both games. Thus, the smallest and the largest equilibrium prove immune to a cost reduction. This observation is consistent with the claim that in response to a cost decrease, the smallest and the largest equilibrium will never decrease. Formally, we obtain a weak monotonicity result by applying an earlier result of Milgrom and Roberts [30]:

Proposition 6

Consider a family of networking games G^τ satisfying (A) and (C) which differ in the marginal cost parameters $\tau =(C_1,\dots ,C_N)\in {ℝ}_{++}^N$. Then the smallest and the largest equilibrium of G^τ are non-increasing functions of τ.

PROOF

Endow the parameter space ${ℝ}_{++}^N$ with the reverse ⊵ of its canonical partial order, that is for $\tau ,{\tau }^{\prime }\in {ℝ}_{++}^N$, τ ⊵ τ′ if and only if ${\tau }_i\le {\tau }_i^{\prime }$ for all i. Then the payoff functions given by (3.1) satisfy condition (A5) of Milgrom and Roberts [30]. (A) and (C) imply that each game G^τ is supermodular. Hence by Theorem 6 of Milgrom and Roberts, the smallest and the largest equilibrium of G^τ are non-decreasing in τ with respect to the reverse canonical partial order ⊵ of ${ℝ}_{++}^N$. Therefore, the assertion holds with respect to the canonical partial order ≥ of ${ℝ}_{++}^N$. ■

By Proposition 2, if in addition to satisfying (A) and (C), a networking game is a potential game, then the set of potential maximizers forms a nonempty sublattice of the set of equilibrium points. As a consequence of this added structure, there exist a smallest and a largest potential maximizer. Interestingly enough, the comparative statics à la Milgrom and Roberts for supermodular games extend to the smallest and largest potential maximizer. We choose a more abstract formulation in this instance than before. Let Θ be a nonempty subset of some Euclidean space ℝⁿ, n ∈ ℕ, with generic elements θ, θ′, and ϑ.

Proposition 7

Suppose that $G^{\theta }=(I,{(S_i)}_{i\in I},{(u_i^{\theta })}_{i\in I}),\theta \in \Theta$, is a collection of finite potential games with respective potentials P^θ, θ ∈ Θ. Further suppose that:

• For each i ∈ I, S_i is a finite subset of ℝ.

• For each i ∈ I and each θ ∈ Θ, $u_i^{\theta }$ satisfies increasing differences in (s_i, s_−i) ∈ S_i × S_−i.

• For each i ∈ I and each s_−i ∈ S_-i, the payoff function $u_i^{\theta }$ satisfies increasing differences in (s_i, θ) ∈ S_i × Θ.

Then the largest (smallest) potential maximizer for each game G^θ is weakly increasing in θ on Θ.

PROOF

Pick any s, s′ ∈ S with s ≥ s′ and any θ, ϑ ∈ Θ with θ ≥ ϑ. Define s(0), s(1),…, s(N) ∈ S as follows: $s(0)=s,s_i(k)=s_i^{\prime }\text{for}i,k\in I,i\le k$, and s_i(k) = s_i for i,k ∈ I, i > k. By construction, s(k) ≥ s(k + 1) for k = 0,1, 2,…, N − 1. Because G^θ and G^ϑ are potential games and the payoff function of each player i satisfies increasing differences on S_i × Θ, it is the case that s ≥ s′ and θ ≥ ϑ implies

$$\begin{array}{cc}{P}^{\theta }(s)-P^{\theta }(s^{\prime })& =\text{∑}_{i=1}^N(P^{\theta }(s(i-1))-P^{\theta }(s(i)))\\ & =\text{∑}_{i=1}^N(u_i^{\theta }(s(i-1))-u_i^{\theta }(s(i)))\\ & \ge \text{∑}_{i=1}^N(u_i^{\vartheta }(s(i-1))-u_i^{\vartheta }(s(i)))\\ & =\text{∑}_{i=1}^N(P^{\vartheta }(s(i-1))-P^{\vartheta }(s(i)))\\ \hfill & =P^{\vartheta }(s)-P^{\vartheta }(s^{\prime })\hfill \end{array}$$

This means that P^θ(s) satisfies increasing differences in (s,θ) on S × Θ. For each θ ∈ Θ, P^θ(s) is supermodular in s on S by assertion (α) of Proposition 2 and Remark (d) following Proposition 2. Then the correspondence S* : Θ ↠ S, θ ↦ arg max_s∈S P^θ(s) is increasing7 in θ ∈ Θ by Theorem 2.8.1 of Topkis [18].

Now consider θ, θ′ ∈ Θ with θ ≥ θ′ and pick any s ∈S*(θ) and s′ ∈ S* (θ′). Because S*(θ) ≥^p S* (θ′), sup_S{s, s′} ∈ S*(θ) and inf_S{s,s′} ∈ S*(θ′). Since S*(θ) and S*(θ′) are finite sublattices of S, sup_S S*(θ′) and sup_S S*(θ′) are the largest elements of S* (θ) and S*(θ′) respectively. Then s′ ≤ sup_S{s, s′} ≤sup_S S*(θ) and so sup_S S*(θ) is an upper bound for S*(θ′). But sup_S S*(θ′) is the least upper bound for S*(θ′), so sup_S S*(θ′) ≤ sup_S S*(θ) as asserted. By next comparing inf_S S*(θ) and inf_S S*(θ′), we reach a similar conclusion for the smallest elements of S*(θ) and S*(θ′), respectively. The proof is complete. ■

Example 4

Suppose that for some integer m > 1, Θ = {1,2,…, m}. Moreover, S_i = Θ for each i ∈ I and $u_i^{\theta }(s)=min\left\{\theta , s_1,\dots ,s_N\right\}$ for all i ∈ I, θ ∈ Θ, s ∈ S. Then the game has the potential P^θ(s) = min{θ, s₁,…, s_N}. For any θ ∈ Θ, the smallest potential maximizer is (θ,…, θ) and the largest potential maximizer is (m, …, m).

Note that the potential does not necessarily depend on θ even when each payoff function does. For instance, suppose that S_i = {1,…, m} for each i ∈ I, Θ ⊆ ℝ₊ and the payoff function is defined by $u_i^{\theta }(s)={min}_{i\in I}\left\{s_i\right\}+\theta$ for all i ∈I, θ ∈ Θ, s ∈ S. Then, for all θ ∈ Θ, P^θ(s) = min_i∈I{s_i}. Proposition 7 still applies: The set of potential maximizers is the singleton set {(m, m, …, m)} for each θ ∈ Θ.

Further note that the pairwise benefit function $b_{ij}(s_i,s_j)=\frac{1}{2}ln(1+s_i)\cdot ln(1+s_j)$ used in the first example of this section is just one from a rich family of functions of the multiplicative separable form f(s_i)f(s_j) and generalizations thereof, e.g., f(s_i)f(s_j)+g(s_i)g(s_j) with f,g ≥ 0, f′,g′ ≥ 0, f″,g″ ≤ 0, etc., which all present instances of increasing differences.

6. Two Linear Models

6.1. A Linear Model of Mutual Sympathy or Antipathy

Sympathy or antipathy among people need not be mutual, but often they are and here we assume that they are. We consider the special case of (3.2) with b_ij(s_i, s_j) = (s_i + s_j)·υ_ij. Let (I, E) be any undirected graph on I. If (iv) holds, then (i)–(iv) and, therefore, (I)–(III) hold and G is a potential game. Moreover, (A) and (B) hold. Hence with (iv), the assumptions of Propositions 1 and 2 are met.

Let us specialize further and postulate the mutual affinity condition (iv) and linear networking cost functions satisfying (C). Finally, we assume that players make binary choices, to network, s_i = 1, or not to network, s_i = 0. Accordingly, K = {0,1}.

To analyze the specific game G, let N_i be the set of player i′s neighbors and define W_i = Σ_j∈Ni υ_ij for i ∈ I. Each player i has weakly dominant strategies. Namely, the player's best responses are 1 if W_i − C_i > 0; 0 if W_i − C_i < 0; 0 and 1 if W_i = C_i.

A player's decision creates own payoff (W_i − C_i)s_i and the surplus (2W_i−C_i)s_i. Hence a player's best response is inefficient in two instances, if W_i = C_i and the player chooses s_i = 0 and if W_i < C_i < 2W_i. Therefore, inefficiencies always constitute under-investments. The aggregate functions P and W assume correspondingly simple forms:

$$P(s)=\text{∑}_i(W_i-C_i)s_i;W(s)=\text{∑}_i(2W_i-C_i)s_i$$

In particular, all equilibria are potential maximizers. Depending on model parameters and tie-breaking, equilibria may be efficient or inefficient.

Now mutual affinity allows for mutual lack of interest, υ_ij = υ_ji = 0 and mutual dislike, disadvantage, animosity, antipathy, enmity, or hostility, υ_ij = υ_ji < 0. In the beginning of the Introduction, we have presented an example of four players where each has two friends and one enemy. Obviously, affinities and adversities can give rise to a host of interesting social spill-overs, where a player is affected by affinities between other players. We confine ourselves to one more instructive example.

“The enemy of my enemy is my friend” usually means that if j is i′s enemy and k is j′s enemy, then i and k might form an alliance against j. Yet in the present situation, i may benefit from hostility between j and k in a different way: If i and j are enemies, υ_ij < 0, then i prefers that j is not networking. This is certainly the case if υ_jk < 0 for all k, that is if j has only enemies. For instance, let N = 3, υ₁₂ = υ₂₁ < 0, and υ₁₃ = 0. Then 1 prefers that 2 is not networking. This is guaranteed if W₂ = υ₂₃ + υ₂₁ < C₂. Since υ₂₁ < 0 the latter holds if 2 and 3 are enemies, υ₂₃ < 0, or not too close friends, 0 ≤ υ ₂₃ < |υ₂₁| + C₂.

6.2. A Linear Model with Variably Attractive Players

We consider networking games of the form (3.2) with (ii) which differ from games with pairwise symmetry. We postulate numbers numbers V₁,…, V_N such that

$$(\text{v}){\upsilon }_{ij}=V_j$$

If the V_i differ, then (iv) is violated and, as a rule, the pairwise interaction games G_ij do not have symmetric potentials. Consequently, Propositions 1 and 2 need not apply. In the sequel, we focus on a linear model which allows a systematic inquiry. This linear model is essentially identical with the one developed and analyzed in the previous subsection, with the crucial exception of condition (v):

Linear Model

We assume an undirected graph (I,E) such that b_ij(s_i,s_j) = (s_i + s_j)·V_j if {i,j} ∈ E and b_ij(s_i,s_j) = 0 if {i,j} ∉ E. We assume binary choices, K = {0,1}, and linear networking cost functions satisfying (C). Now let N_i be the set of player i′s neighbors and Z_i = |N_i| be the number of his neighbors. Since we always assume that nobody is isolated, Z_i ≥ 1. Further define W_i = Σ_j∈_Ni V_j. Then s_i = 1 is a best response for i iff W_i ≥ C_i and s_i = 0 is a best response for i iff W_i ≤ C_i. Moreover, G has the potential P(s) = Σ_i(W_i − C_i)s_i. The social welfare function W assumes the particular form W(s) = Σ_i(W_i + Z_iV_i− C_i)s_i. It follows that all equilibria are in weakly dominant strategies and potential maximizers. In general, the maximizers of P and W will not coincide. In fact, there can be under- or over-investment. Let us add two more observations.

First, “bad neighbors” may not only harm “good neighbors”, but can also harm each other through their networking efforts. For example, let N = 4, E = F, V₁ = V₂ = −1, V₃ = V₄ = 1, 0 < C_i < 1 for all i. Then the unique equilibrium is s = (1,1, 0, 0) with utilities u₁(s) = −C₁,u₂(s) = −C₂ and u₃(s) = u₄(s) = −2. Everybody would be better off at s⁰ = (0, 0,0, 0). But given any choices by 3 and 4, players 1 and 2 find themselves in a Prisoner's Dilemma. Incidentally, the efficient outcome would be t = (0, 0,1,1) with W(t) = 4 − (C₃ + C₄). Hence, the equilibrium s—which is in strictly dominant strategies and potential maximizing—exhibits over-investment by 1 and 2 and under-investment by 3 and 4.

Second, the particular networking game G has a potential, even though the games G_ij do not have symmetric potentials, thus violating the premise of Fact 1. Incidentally, a game G_ij does possess a potential β_ij given by β_ij(0,0) = 0, β_ij(0,1) = V_i, β_ij(1, 0) = V_j, β_ij(1, 1) = V_i + V_j. However, β_ij is asymmetric unless V_i = V_j.

7. Stochastic Stability

It turns out that potential maximizers in finite games are the stochastically stable states for a particular kind of stochastically perturbed best response dynamics. Therefore, any results obtained for potential maximizers also hold for those stochastically stable states. Our specific concept of stochastic stability of outcomes (joint strategies) in a finite N-player game

$$G=(I,{(S_i)}_{i\in I},{(u_i)}_{i\in I})$$

is based upon best response dynamics with logit perturbations. Throughout, we consider dynamics with asynchronous updating and persistent noise, with discrete time t = 0,1,… and states s ∈ S. Let q = (q₁,…, q_n) ≫ 0 be an n-dimensional probability vector. The recurrent game G is played once in each period. In each period t, one player, say i, is drawn with probability q_i > 0 from this population to adjust his strategy and does so according to a perturbed adaptive rule. The non-selected players repeat the strategies they have played in the previous period.

The perturbed adaptive rule is a logit rule: Suppose the current state is s = (s_j)_j∈I. In principle, the updating player i wants to play a best reply against s_−i = (s_j)_j≠i. But with some small probability, the player trembles and plays a non-best reply. If the player follows a logit rule, then for all t_i ∈ S_i, the probability that i chooses t_i in state s is given by

$$p_i^{t_i}(s)=\frac{exp\left[u_i(t_i,s_{-i})/\in \right]}{{\text{∑}}_{k_i}exp\left[u_i(k_i,s_{-i})/\in \right]}$$

(7.1)

where ϵ > 0 is a noise parameter. For given ϵ, two choices that yield the same payoff to i are equally likely. If one of them yields a higher payoff, it will be chosen with a higher probability. In particular, any best reply to s_−i is more likely to be chosen than a non-best reply. As ϵ → 0, the probability that a best reply is chosen goes to 1. For given ϵ > 0, one obtains a stationary Markov process on S with transition matrix M(ϵ). The matrix M(ϵ) has entries m_s,s′(ϵ) ∈ S × S with the following properties. If s and s′ differ in more than one component, then m_s,s′(ϵ)= 0. If s and s′ differ only in the ith coordinate and s′ = (t_i, s_−i), then $m_{s,s^{\prime }}(ϵ)=q_i\cdot p_i^{t_i}(s)$. If s = s′, then $m_{s,s}(ϵ)={\text{∑}}_{j\in I}{q}_j\cdot p_j^{s_j}(s)$. The process is irreducible and aperiodic, hence it is ergodic and has a unique stationary distribution, represented by a row probability vector μ(ϵ). Like in many prior studies of perturbed evolutionary games we want to determine the behavior of the system when ϵ → 0, that is when the noise becomes arbitrarily small. If the limit stationary distribution μ̃ = lim_ϵ→0 μ(ϵ) exists, we write S̃ for its support:

$$\tilde{S}$$

The profiles in S̃ will be referred to as stochastically stable states. These are the states in which the system stays most of the time when very little, but still some noise remains. Baron et al. [12] show that S̃ can be partitioned into minimal sets closed under asynchronous best replies. It turns out that the limit stationary distribution exists and the stochastically stable states are the maximizers of the potential, if the underlying game G has a potential:

$$\begin{array}{l}\text{If}G\text{has a potential}P,\text{then}\tilde{S}=S^{*}=arg{max}_{s\in S}P(s),\\ \tilde{S}\text{is a non}-\text{empty set of Nash equilibria},\\ \text{and all stochastically stable states have equal probability}.\end{array}\}$$

(7.2)

See Blume [7,8], Young [9], Baron et al. [10,12] for the key argument. We mentioned in the Introduction that two qualifications are warranted: First the coincidence of the set of potential maximizers and the set of stochastically stable states need not hold if the potential is not exact or updating is not asynchronous. Second, this is not to say that the study of stochastically stable states under logit perturbations has to be confined to games with exact potentials. See Alós-Ferrer and Netzer [11], Baron et al. [12], and Section 7 of Baron et al. [10].

As an immediate consequence of (7.2), we obtain:

Corollary 1

In Propositions 2 and 7 and elsewhere in Sections 3 to 6, S*, potential maximizer(s) and potential maximizing, respectively, can be replaced by S̃, stochastically stable state(s) and stochastically stable, respectively.

For instance, Lemma 1, Fact 1 and (7.2) apply to Example 3. There, it turns out that with a slight logit perturbation, the best response dynamics would stay most of the time in the equilibrium s^●, which is the unique stochastically state of the evolutionary model based on G or G′. In Example 2, case 1, all three equilibria are maximizers of the potential of P and, therefore, stochastically stable states. Consequently, under very small random perturbations, asymmetric outcomes are more likely (since they outnumber the symmetric one) than the symmetric equilibrium. Hence very likely, one observes that some players network more than others, although none of the players are distinguished as natural networkers.

Logit trembles have the appealing feature that mistake probabilities are state-dependent and the probability of making a specific mistake, that is of playing a specific non-best response, is inversely related to the opportunity cost of making the mistake.8 Furthermore, Mattsson and Weibull [31] and Baron et al. [10,12] derive a logit rule as the solution of a maximization problem involving a trade-off between the magnitude of trembles and control costs.

The investigation of logit perturbed best response dynamics for supermodular games with potentials and the associated set of stochastically stable states is one of the original contributions of the current paper. Dubey, Haimanko, and Zapechelnyuk [3] do not consider stochastic perturbations or “noise” and stochastic stability. To our knowledge only two earlier papers, Kandori and Rob [32] and Kaarboe and Tieman [33], combine stochastic stability and supermodularity in a general setting.9 These two papers focus on a class of global interaction games based on two-player and symmetric strict supermodular games. Players gradually adjust their behavior in taking a summary statistic into account. The adjustment process is perturbed by Bernoulli or uniform trembles or slight generalizations thereof. All authors obtain monotonicity results of best responses over the set of states and show that the limit sets of the unperturbed process correspond one-to-one with the set of (strict) Nash equilibria of the recurrent game. Consequently, the set of stochastically stable states is contained in the set of Nash equilibria. Hence supermodular games exposed to uniform trembles and potential games exposed to logit trembles both induce perturbed dynamics under which the stochastically stable states form a subset of the set of Nash equilibria. Unlike the present paper, the earlier literature does not examine the structure of the set of stochastically states and its variation in response to parametric changes.

8. Conclusions and Ramifications

Nonspecific networking means that an individual's networking effort establishes or strengthens links to a multitude of people. The individual cannot single out specific persons with whom she is going to form links. In the simplest case, the individual has a binary choice, to network or not to network. This particular case covers already a variety of interesting scenarios and phenomena. It encompasses scenarios with differential benefits across pairs of individuals, mutual versus non-mutual (positive or negative) affinities, leading for instance to second-order externalities such as the impact of an enemy of an enemy or to the co-existence of under-investment and over-investment in networking as exemplified in Section 6. Often, however, networking efforts are gradual and our model accommodates this possibility as well. Beyond expanding the descriptive scope of the model, the availability of several levels of networking effort makes the question of Section 5—how networking efforts respond to a change in networking costs—much more interesting. One conceivable generalization of our analysis, including the comparative statics, would assume multi-dimensional effort choices, like choosing software-hardware combinations.

The model also encompasses the formation of user networks, not dealt with in this paper. In that particular application, the player set I is interpreted as a finite population of users or adopters. Each player has to adopt exactly one technology or network good from the list K. The list K may consist of computer systems, word processors, internet providers, etc. The adopters of the same good constitute a user network. Baron et al. ([12], p. 574) consider the case of partial but imperfect compatibility of different technologies. Furthermore, two prominent classes of spatial games, both analyzed in detail in Baron et al. ([10], pp. 555-557) permit a novel interpretation as user network formation games. The first class consists of coordination games which can be reinterpreted as network formation games with perfect incompatibility of different technologies. The second class consists of minimum effort coordination games which allow an interpretation of network formation games with downward compatibility of technologies.

Supermodularity and increasing differences, utilized in some of our comparative statics, are cardinal properties. As Milgrom and Shannon [36] point out, comparative statics questions are inherently ordinal questions, and the conditions on objective functions and constraints necessary for comparative statics conclusions should possibly be ordinal. Indeed, Milgrom and Shannon [36] find such ordinal conditions for monotone comparative statics. They introduce and study quasi-supermodular functions and functions with the single crossing property. These functions generalize supermodular functions and functions with increasing differences and preserve the monotonicity conclusion for parametric optimization problems. A list of a wide variety of problems in economics and in noncooperative games presented by Milgrom and Shannon [36] makes a convincing case for the value added of their ordinal extension of complementarity conditions. In view of these results, one might ask whether Proposition 2 can be extended further by invoking such ordinal conditions. Precisely, if we assume that each b_ij satisfies the single crossing property on S_i × S_j, are we then able to show that the potential P is quasi-supermodular on S? Unfortunately, one cannot draw such a conclusion. The reason is that the generality of the single crossing property has its drawbacks: Namely, in the proof of Proposition 2 we make use of Corollary 2.6.1 in Topkis [18] which states that for a function defined on a finite product of totally ordered sets, pairwise supermodularity implies supermodularity. This crucial auxiliary result no longer holds when the single crossing property is substituted for the pairwise supermodularity property Shannon ([37], p. 220) demonstrates that the single crossing property in each pair of variables does not imply quasi-supermodularity in all variables.

Proposition 7 establishes a weak monotonicity result on the set of potential maximizers. It states that the largest (smallest) potential at a lower parameter value is smaller than the largest (smallest) potential maximizer at a higher parameter value. But this result does not assert that a given potential maximizer at a lower parameter value is smaller than any other potential maximizer at a higher parameter value. Echenique and Sabarwal [38, p. 309] give a condition on a pair of parameters θ,θ′ ∈ Θ, θ ≤ θ′, which implies sup S^N(θ) ≤ inf S^N(θ′) for the two equilibrium sets S^NE(θ) and S^NE(θ′). Since S*(θ) ⊆ S^N(θ) and S*(θ′) ⊆ S^N(θ′), their condition also implies supS*(θ) ≤ inf S*(θ′).

A further alternative could make the set of available efforts a (one- or multi-dimensional) interval or convex set and assume sufficient differentiability of the cost and benefit functions. As Brueckner [39] demonstrates in the context of specific networking, one arrives at some conclusions very elegantly, if such a continuous model is highly symmetry, but does not get very far otherwise. Most of our subcases and examples can be easily embedded into a larger continuous model. But again, while this might produce some eloquence and quickness of derivations in some cases, it would only render the analysis more complicated in others. An added complication stems from the fact that the concept of stochastic stability developed in the literature so far (based on logit or other perturbations) and employed in the present paper relies on a finite state space.

The idea that the strength or reliability of a link might depend on the efforts of both agents involved, is also central to the model of Brueckner [39].10 Similarly, Haller and Sarangi [41] and Baron et al. [42] consider the possibility that the reliability of a link between two agents depends on the efforts of both agents. Bloch and Dutta [43] consider the possibility that the strength of a link between two agents depends on the efforts of both agents. In Cabrales et al. [15], link intensity depends on the socialization or networking efforts of both players constituting the link. Moreover, their model exhibits nonspecific networking and productive investments with spill-overs across the network. Since we allow for negative affinity or attraction, some agents might not only abstain from networking but might take counter-measures against the networking attempts of others and be willing to incur costs in order to weaken or sever links. This eventuality suggests a further extension of the formal model.