1. Introduction
Economic analyses of markets with horizontally and vertically differentiated products have extensively examined collusion, cartel stability, and the effectiveness of antitrust interventions, emphasizing their dependence on factors such as product differentiation, cost asymmetries, and demand volatility (see
Feuerstein, 2005;
Marini, 2018, for surveys; see also
Motta, 2004).
1 These studies typically assume a two-sided dependency characterized by non-zero mutual cross-elasticities of demand (see, e.g.,
Varian, 1992, Chapter 16). In contrast, we focus on one-sided dependency, where the pricing of an independent seller affects the demand—and hence, the profit—of a dependent seller, while the reverse does not hold.
One-sided positive dependency occurs when a price reduction by the independent seller increases demand for the dependent seller’s product, while the reverse effect is negligible. This most likely occurs when the two goods are complementary in consumption. For example, in the market for printers and ink cartridges, a lower price of printers increases the demand for ink cartridges via increasing the demand for printers, yet a reduction in the price of ink cartridges would unlikely increase the demand for printers. Similarly, on markets for bicycles and helmets, lower prices of bicycles boost the demand for helmets, whereas the reverse effect is likely negligible.
In the case of one-sided negative dependence, a price cut by an independent seller reduces the demand of the dependent seller, whereas the same effect hardly works in the opposite direction. This asymmetry most likely occurs when the products are substitutes in consumption and are perceived by consumers as rather different in terms of quality or cultural characteristics. For instance, a price drop in luxury goods can reduce demand for cheaper alternatives, but the reverse is unlikely. Similarly, a reduction in the price of electric cars likely will negatively affect the demand for internal combustion engine vehicles, but the opposite is unlikely if the demand for electric vehicles is primarily driven by factors such as environmental concerns and fuel efficiency.
Due to the price externality, sellers may benefit from cooperating. For instance, they could form a cartel and share profits,
2 or they could merge. Rather than examining specific cooperation arrangements, we analyze stochastic cooperation with joint profit maximization and equal surplus sharing for an exogenously given probability of cooperation. In our view, there are several reasons to assume that cooperation among (non-)mutually dependent sellers is stochastic. First, implementing collusive behavior requires sellers to coordinate multiple aspects of their interaction, the success of which is inherently uncertain. Second, collusion may evade detection by antitrust authorities, particularly when mistakenly perceived as random fluctuations in volatile markets.
Specifically, we analytically explore a one-dimensional hybrid game class, in which the parameter
, with
, is the exogenously given probability of cooperation. In each game of this class, both sellers choose prices simultaneously. As in
Nash (
1953), these prices determine their endogenous threats, i.e., the conflict profits defining the surplus from cooperation—given by the maximal joint profit minus the sum of the conflict profits.
3 When setting prices, the sellers are aware of the cooperation probability,
, but cannot condition prices on whether or not there is cooperation. Therefore, they only react to the commonly known cooperation probability. In line with
Nash (
1953), we assume that sellers commit to the prices chosen before the stochastic uncertainty is resolved.
4We characterize the equilibrium prices and expected profits from stochastic cooperation. Specifically, we examine whether each seller’s expected profit increases monotonically with the probability of cooperation, given a level of one-sided dependency. Our main result shows that the independent seller earns higher expected profits when cooperation is more likely. In contrast, the dependent seller earns lower expected profits when the likelihood of cooperation is below a threshold that we explicitly characterize, and profits are higher thereafter. In contrast, the dependent seller’s expected profits decrease with the probability of cooperation when this probability is below a threshold that we explicitly identify, and increase once the probability exceeds this threshold. Despite the inherent asymmetry, due to the one-sided externality, this result seems unexpected: one might have guessed that both sellers would benefit from cooperation, earning higher expected profits as cooperation becomes more likely.
Our results are related to two features of the model. First, when cooperation occurs, sellers prefer a larger share of the joint profit. This share increases with the difference between their own conflict profit and the other seller’s conflict profit. Second, the independent seller can leverage the price externality when balancing the change in their conflict profit with that in their share of the joint profit. Given these features, it follows from an envelope argument that the independent seller’s expected profit raises monotonically with the probability of cooperation. The same argument shows that, when cooperation is certain not to occur, raising the probability of cooperation has no first-order effect on the independent seller’s conflict profit, but it reduces the dependent seller’s conflict profit. This negative impact offsets the positive effect of a higher likelihood of surplus sharing on the dependent seller’s expected profits. However, we also demonstrate that these effects reverse when is large enough.
This paper is organized as follows:
Section 2 introduces the model of stochastic cooperation;
Section 3 derives and analyzes the best responses and the equilibrium prices;
Section 4 derives the equilibrium expected payoffs and analyzes how they depend on the exogenous cooperation probability;
Section 5 analyzes graphically the equilibrium quantities;
Section 6 discusses some concluding remarks.
2. A Model of Stochastic Cooperation
Let denote the independent seller, to whom we also refer to as the “monopolist,” and denote the dependent seller. Furthermore, let denote the demand and the sale price of .
The (linear) demand functions are
and
. Here,
captures the sign and strength of the price externality: the demand of
D increases with
when
and decreases when
.
5 To avoid negative sales amounts, of course it will be ensured that
and
will hold. Moreover, to guarantee interior solutions to maximization problems below, we impose suitable restrictions on the parameters
and
, in addition to
. Specifically, we present the following assumptions.
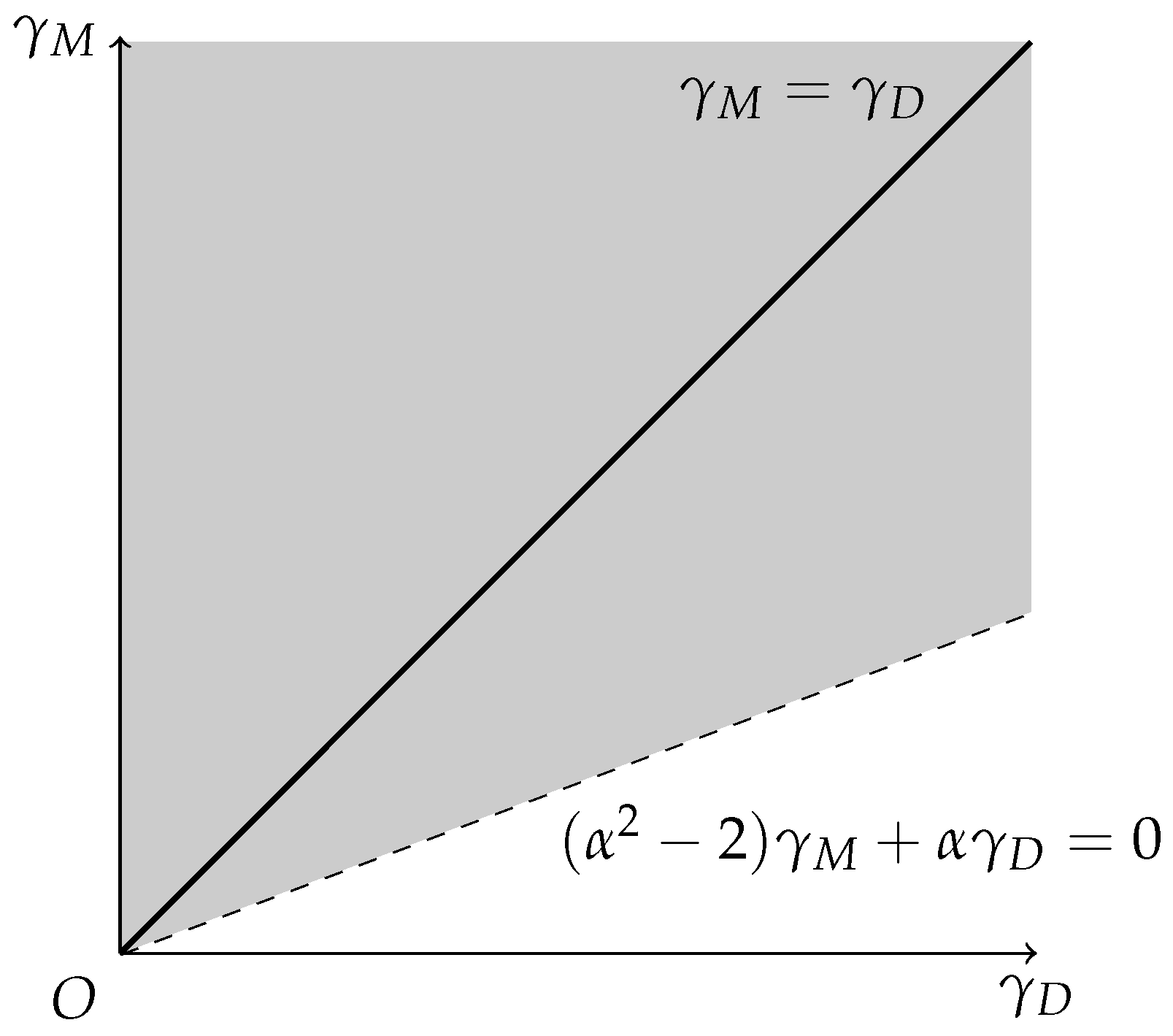
6Assumption 1. and .
Furthermore, for the sets
we assume the following:
Assumption 2. When , then must hold;
Assumption 3. When , then must hold.
We neglect production costs so that the profits of the sellers are
When cooperating, sellers equally share the surplus from cooperation, i.e., the difference between their maximal joint profit and the sum of both profits in (
1). When
denotes the solution to
the surplus from cooperation
is
The maximal joint profit
is attained at the prices
7
so that
It follows that
holds trivially when
, and it is due to Assumption 2 when
.
According to the terminology of bargaining with variable threats (
Nash, 1953), the profits in (
1) define the threat point, i.e., they are the conflict profits in the case, while the agreement profits are
As mentioned in the Introduction, we analyze the class of hybrid games that arise when sellers cooperate with an exogenously given probability
. In these games, the expected payoff of seller
M is
8
while the expected payoff of seller
D is equal to
The second lines in (
5) and (
6) express the expected payoffs as the sum of the conflict profit and half of the cooperation surplus, being weighted by the probability of cooperation. The third lines show how payoffs depend on
via a probability-weighted difference between each seller’s own conflict profit and that of the other.
3. Best Responses and Equilibrium Prices
The best responses
and
allow each seller to maximize their own expected payoff given the other seller’s price and are
9
When
, the best response of seller
M is
, which is independent of
because of the one-sided dependency, and the associated profit is
.
10 When
, the best response of seller
M depends on the sign of
: for
positive (negative), seller
M reduces (increases) its price relative to
, with the adjustment becoming more pronounced when the likelihood of cooperation increases. This follows because seller
M maximizes the expression
, given
. As a result, seller
M has to balance the reduction in their own monopoly profit against the reduction in demand and profit of seller
D via the price externality. Conversely, the best response of seller
D does not depend on
due to the one-sided dependency. This follows since
D maximizes
for a given
, which is equivalent to maximizing
, because
does not depend on
.
From (
7), one derives the equilibrium prices, which are denoted by
and
:
11Furthermore, from (
8), one derives the marginal effects of the change in
on the equilibrium prices as
12
Since
,
13 decreases (increases) with
when
(
). The intuition for this result is that a larger
increases the weight of the negative component of
D’s expected payoffs,
, while it decreases the weight of the positive component,
; see Equation (
5) above. Seller
M optimally adjusts
so that the reduction of
compensates
M in expectation for the reduction of
, and the sign of the externality determines whether this lets
marginally increase or decrease. Instead,
is negative regardless of the sign of
. The intuition for this is that, as
increases, seller
M adjusts
, thus decreasing the demand of seller
D, which in turn reduces
.
4. Expected Equilibrium Payoffs
Let
and
denote the conflict equilibrium profits. Moreover, let
denote the equilibrium surplus, which satisfies
14For seller
, let
denote the expected equilibrium payoff. Using the second expression in (
5) and (
6), direct computation yields
The total marginal effect of
on
is the sum of the direct effect when holding
and
—and thus the surplus—constant, and the indirect effect which accounts for the change in conflict profits and surplus due to changing
and
.
In order to characterize the indirect effects, one must take into account that profits vary with
via equilibrium prices. However, according to a standard envelope argument, one might expect the first-order effects to vanish. In fact,
and
satisfy the following first-order conditions for interior solutions:
Therefore, when
, the indirect effect (
12) is equal to
since
holds. From (
12) and (
15), one has
and, since
holds, the expected payoff of seller
M unambiguously increases with the cooperation probability, which also implies that
, i.e., the expected payoff is higher when cooperation is certain than when conflict is certain.
When
, the indirect effect in (
12) is equal to
Using (
14) once again, one has
and therefore,
So finally, (
12) and (
18) imply that
By evaluating the derivatives at the (interior) solution to the seller’s own profit maximization problem, one has that for seller
M, the first-order effect of the change in equilibrium prices is null due to the asymmetric price externality: changing
has no direct effect on
, and expected payoff maximization implies that the first-order effects of own pricing are zero for both sellers.
For seller
D, the situation is different: while the first-order effect of changing
is zero, the first-order effect of changing
is
. Since the first term in (
19) is positive and the second is negative when
(see (
11)), it may be that the expected payoff of seller
D decreases as the cooperation probability rises. To get an intuition for this result, while both sellers prefer a larger share of the maximum joint profit in case of cooperation, they rather seek a larger conflict profit if they do not. Each seller’s share in the case of cooperation depends positively on the difference between their own conflict profit and that of the other seller (see the third line in (
6)). Starting from
, an increase in the probability of cooperation has no first-order effect on seller
M’s conflict profit, while it has a negative first-order effect on seller
D’s conflict profit (see (
13) and (
17)). The negative effect on seller
D’s expected payoff, due to the smaller conflict profit, offsets the positive effect due to a larger likelihood of sharing the surplus from cooperation. However, from (
19), one might suppose that these effects could reverse as
rises, meaning that the expected payoff of seller
D eventually increases with the likelihood of cooperation. The next proposition confirms this intuition by identifying the threshold cooperation probability,
, below which
decreases as
rises, and above which it increases.
Proposition 1. For a given α, the equilibrium payoff of seller D, , decreases with β when and increases when , where Furthermore, for seller
D, it also holds that the expected payoff is higher when cooperation is certain than when conflict is certain, i.e., one has
15Let us finally discuss two possible modifications to our model. One idea is to avoid the assumption that surplus is shared equally among firms. While this is rather natural and focal, one can also assume unequal surplus sharing.
16 To this end, let
be the surplus share of seller
with
, so that the agreement profits (
4) are
and the expected profits (
5) and (
6)
for the two sellers can be presented as:
and
for seller
D. In this case, the equilibrium prices can be computed as in
Appendix B, setting
. Provided that
, so that prices are interior, the qualitative features of our analysis will be preserved.
Another possible modification is to explicitly account for production costs.
17 One approach is to assume that the marginal cost of production is constant and equal across sellers. In this case, the prices of sellers M and D would represent unit profit. With a suitable reinterpretation of the model’s parameters, the main qualitative results will remain unaffected.
5. A Graphical Analysis of the Equilibrium Quantities
In this section, we graphically simulate the equilibrium quantities as varies exogenously. To maintain consistency with the main analysis in the previous section, we assume equal surplus sharing. Moreover, to simplify the exposition and create noticeable visual effects, we also assume that and .
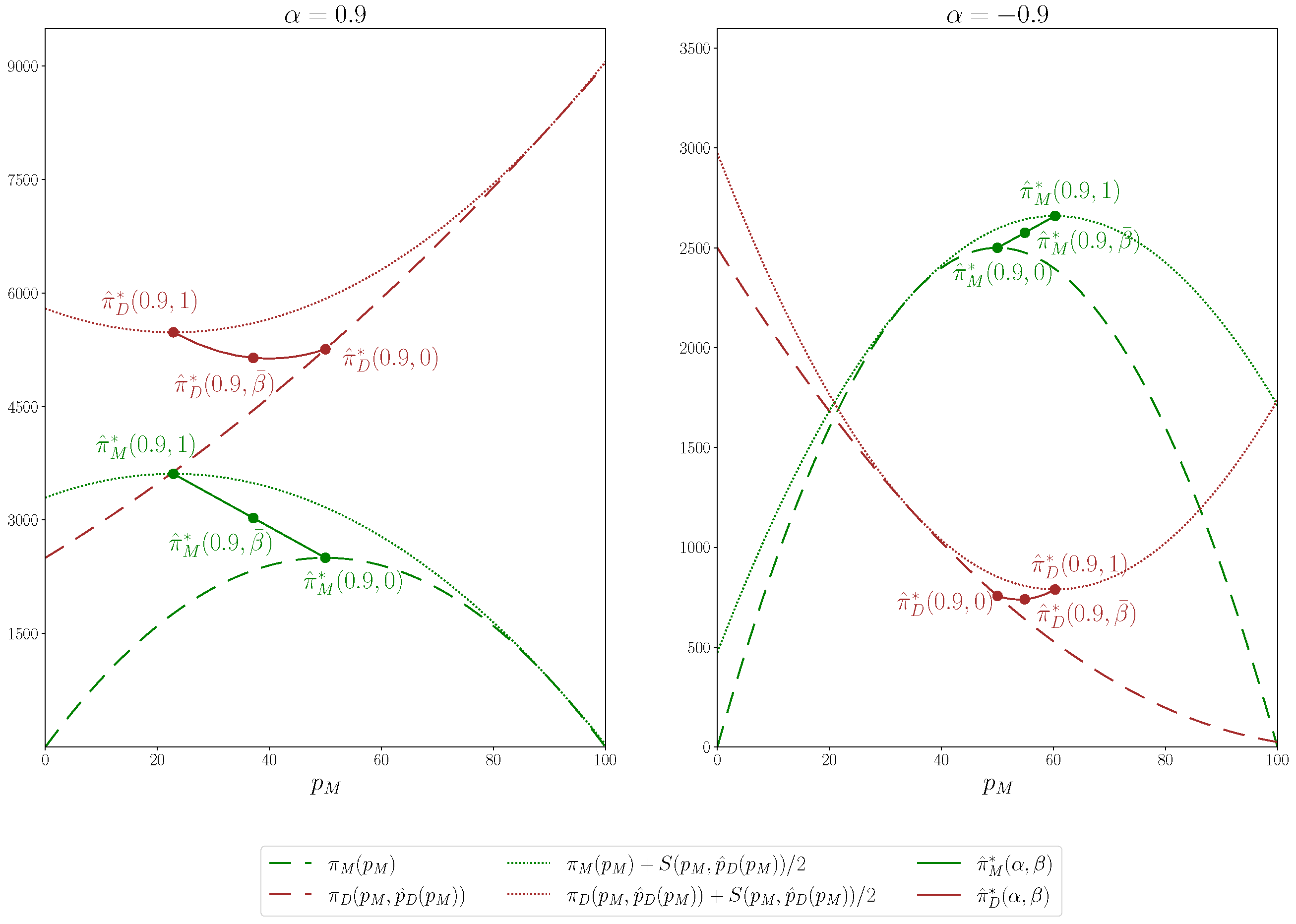
Figure 1, with
in the left panel and
in the right panel, plots agreement profits (dotted lines) and conflict profits (dashed lined) as
varies between 0 and
, and
is set according to
, as in (
7). In all cases, the green lines pertain to seller
M and the brown lines to seller
D. The solid lines represent the equilibrium expected payoffs
and
as
varies between 0 and 1. The three dots on these lines, moving leftward in the left panel and rightward in the right panel, correspond to
and
, respectively.
When
, the expected payoffs coincide with the conflict profits, and the equilibrium values coincide with the non-cooperative ones. As
increases, according to (
9) and (
10), seller
M and
D reduce their price when
, and they increase it when
. Furthermore, as shown in the figure, when
, the first-order effect on seller
M’s conflict profit is zero, while it is negative for seller
D. As
increases, the conflict profit curve of seller
D, which is initially steeper than that of seller
M, flattens, and the difference in the reduction of conflict profits shrinks. Initially, this allows seller
M to increase its own equilibrium expected payoff at seller
D’s expense. Subsequently, both sellers’ expected profits increase with the likelihood of cooperation.
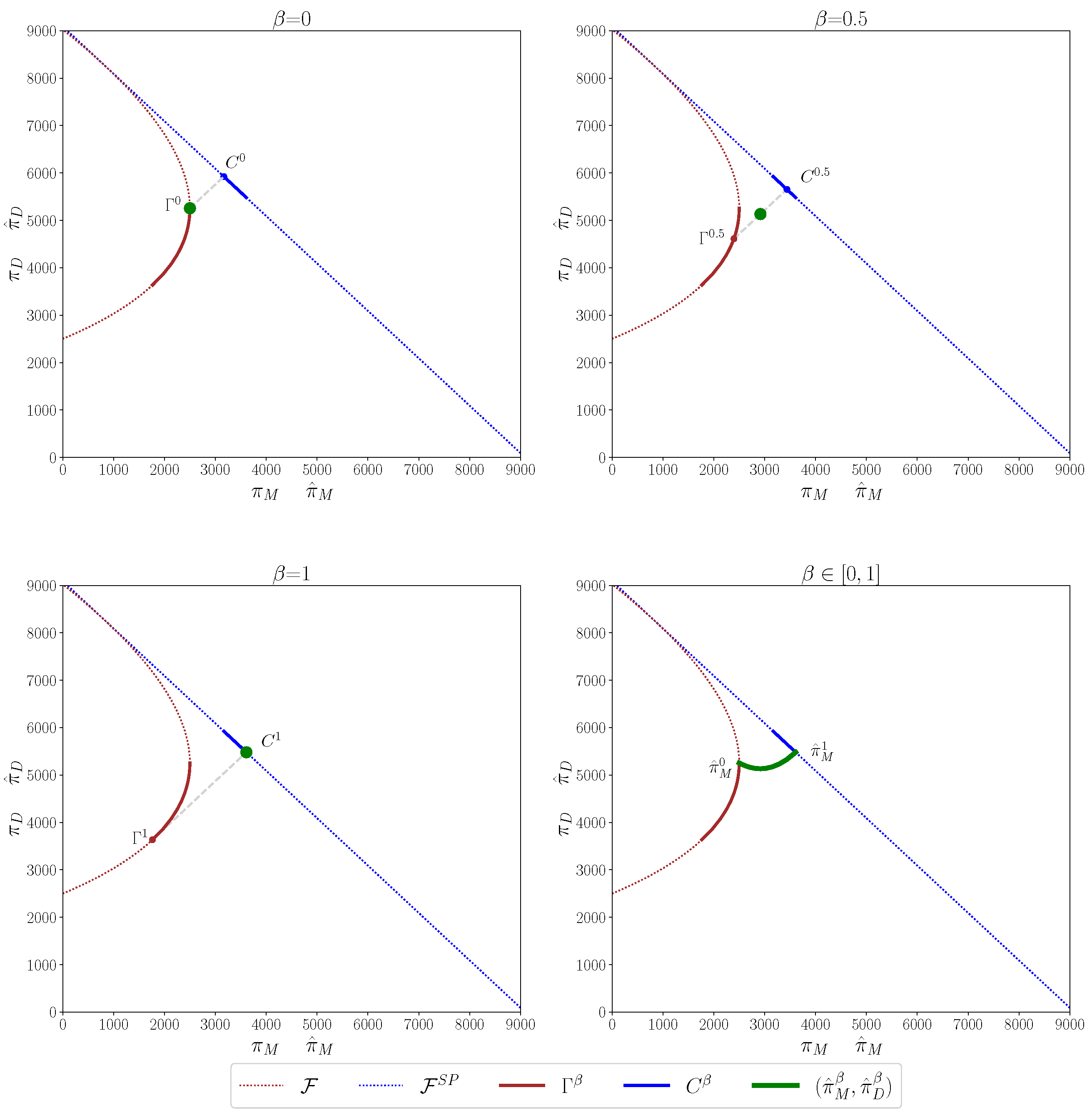
Figure 2 shows an alternative representation of profits and expected payoffs when
and
.
18 The dotted red line, referred to as
, is the conflict profit frontier, i.e., the locus of conflict profit combinations. The continuous section of this line shows the conflict profit combinations as
varies. Specifically, for a given
, the point denoted by
identifies the combination
. The dotted blue line, referred to as
, represents the combinations of profits that add up to
, which can be achieved via side payments among the sellers. The continuous section of this line shows the combinations of agreement profits as
varies. Specifically, for a given
, the point denoted by
identifies the combination
. Finally, in clockwise order, the green dots and line represent the combinations of sellers’ expected payoffs for
and 1, respectively, when
. The difference in how the expected payoffs of sellers
M and
D vary with
is also clearly apparent in this case.
6. Conclusions
Our analysis of the one-dimensional hybrid game class, parameterized by the exogenous probability of cooperation, shows that the dependent seller’s expected payoff falls below the non-cooperative payoff when the probability of cooperation is low enough. However, when the probability of cooperation is greater than a critical threshold, the dependent seller’s expected payoff exceeds the non-cooperative payoff and rises with the probability of cooperation. This non-monotonicity of the expected payoff highlights an asymmetry which could provide some insights for more extended analyses aiming at investigating the factors which determine the likelihood of cooperation. For example, while a low probability of cooperation may stem from volatile market conditions, it may also stem from dependent sellers boycotting the attempt to establish any system of coordination among sellers. Moreover, in case communication is necessary to support collusion (as for instance in
Aubert et al., 2006), the dependent firm can whistle-blow any attempt to promote cartelization by the monopolist.
19 Furthermore, substantially increasing the probability of cooperation more likely attracts scrutiny, provokes public discussion, and potentially leads to prosecution. In practice, the probability of cooperation—assumed here to be exogenously given—is likely shaped by efforts to establish, maintain, and, if necessary, conceal cooperative arrangements. Successful cooperation may even require sellers to disclose private information, creating an additional barrier to its initiation and reinforcement.
In such cases, the incentive to engage in cooperative behavior is weak, possibly deterring the dependent seller from participating in collusion attempts. A final implication of our analysis is that, within our framework, antitrust concerns may be attenuated. Since dependent sellers can incur losses from cooperation, such arrangements become less viable. When unanimity among sellers is required for cooperation, the non-monotonic incentives faced by dependent sellers further reduce the likelihood of collusive agreements in cases of one-sided dependencies between sellers.
Finally, we suggest two directions for future research: First, the analysis could be extended to consider the possibility that the cooperation probability is endogenously determined.
20 Second, the theoretical analysis could be complemented with an experimental analysis that investigates the behavioral implications of our model.