On Hurwicz Preferences in Psychological Games
Abstract
1. Introduction
2. Model and Equilibria
2.1. Hierarchies of Beliefs
2.2. Game and Equilibria
- (i)
- ;
- (ii)
- for every .
2.3. Summary Utility Functions
3. An Illustrative Example
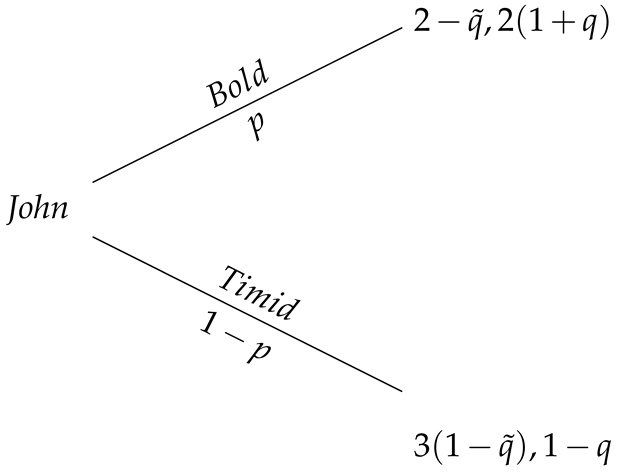
- -
- : John chooses to be ;
- -
- : John chooses to be ;
- -
- : John randomizes with probability .
- (i)
- If , then, for every , the α-PNE are: ;
- (ii)
- If , then:
- -
- for , the α-PNE are: ;
- -
- for , the α-PNE are: ;
- -
- for , the α-PNE are: ;
- -
- for , the unique α-PNE is: ;
- -
- for , the α-PNE are: ;
- -
- for , the α-PNE are: and every ;
- -
- for , the α-PNE are ;
- -
- for , the unique α-PNE is: ;
4. A Sensitivity Analysis
- (a)
- be a sequence of functions with ;
- (b)
- be a sequence of set-valued maps ;
- (c)
- be a sequence with ;
- (d)
- be the sequence of functions defined by the following:
4.1. Preliminary Definitions
4.2. The Stability Result
- (i)
- The sequence sequentially converges to the function ;9
- (ii)
- each function and function are continuous in ;
- (iii)
- the sequence converges to ;
- (iv)
- the sequence sequentially converges to the set-valued map . Suppose additionally that each and have compact and non-empty values for every .
4.3. A Remark on Equilibrium Selection
5. Existence of Equilibria: A Counterexample
- -
- for ,
- -
- for ,
- -
- for ,
- -
- for there are no PNE;
- -
- for there is only one PNE which is given by .
- (1)
- , where
- (2)
- , where
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Lemma 2
- (a)
- Denote with . If , the function decreases throughout the entire interval . If , decreases throughout the entire interval for , is constant on for , and increases on for . Moreover, for every , while if and only if .
- (b)
- Denote with . The function decreases throughout the entire interval for , is constant on for , and increases on for . Moreover, if and only if , while if and only if .
- (c)
- Denote with . If the function increases throughout the entire interval . If , the function decreases on for , is constant on for and increases throughout the entire interval if . Moreover, for every , while if and only if .
- -
- If , the function decreases on for , is constant for , and increases for .
- -
- If , the function decreases on for , is constant for , and increases for , where we have the following:
- (i)
- For ,Therefore, we obtain the following equilibria: , , and .
- (ii)
- For ,Therefore, we obtain the following equilibria: , , and .
- (iii)
- For ,Therefore, we obtain the following equilibria: , , and .
Appendix A.2. Proof of Lemma 3
- (a)
- Denote with . If , the function decreases throughout the entire interval . If , decreases on if , is constant on if , and increases on if . Moreover, if and only if , while if and only if .
- (b)
- Denote with ; the function decreases throughout the entire interval if , is constant on the interval if , and increases throughout the entire interval if .
- (c)
- Denote with . If , the function increases throughout the entire interval . If , the function decreases on for , is constant on for , and increases throughout the entire interval if . Moreover, if and only if , while if and only if .
- -
- If , the function decreases on for every .
- -
- If , then the function decreases on for , and is constant in for .
- -
- If , the function decreases on for , is constant on for , and increases on for .
- -
- If , the function decreases on for , is constant in for , and increases on for .
- -
- If , the function decreases on for , is constant on for , increases on for .
- -
- If , the function increases on for , and is constant for .
- -
- If , the function increases on for every .
- (i)
- For ,Therefore, we only have the following equilibrium: .
- (ii)
- For ,Therefore, we have the following equilibria: , , and . Note that for we obtain the following: .
- (iii)
- For ,In this case, we have an infinite number of equilibria: , , and every .
- (iv)
- For ,Therefore, we have three equilibria: , , and . Note that for , .
- (v)
- For ,Therefore, we have a unique equilibrium: .
Appendix A.3. Proof of Theorem 1
Appendix A.4. Proof of Lemma 4
- If , the function increases on p for , is constant for , decreasing for ;
- If , the function increases on p for , is constant for , decreasing for ;
- If , the function is constant on p since .
- Suppose ; in this case, we have thatTherefore, for every , we have the following:
- -
- If , then increases on and attains the maximum for .
- -
- If , then is constant on , increases on , and attains the maximum for .
- -
- If , then decreases on , increases on , and attains the maximum for .
- -
- If , then decreases on , increases on , and attains the maximum for and .
- -
- If , then decreases on , increases on , and attains the maximum for .
- -
- If , then decreases on , is constant on , and attains the maximum for .
- -
- If , then decreases on and attains the maximum for .
It follows that - Suppose ; in this case, we have thatTherefore, for every , we have the following:
- -
- If , then , increases on , and attains the maximum for .
- -
- If , then is constant on ; therefore, every is a maximum point.
- -
- If , then decreases on and attains the maximum for .
In this case, - Suppose ; in this case, we have thatTherefore, for every , we have the following:
- -
- If , then increases on and attains the maximum for .
- -
- If , then increases on and is constant on ; therefore, every is a maximum point.
- -
- If , then increases on , decreases in , and attains the maximum for .
- -
- If , then is constant on and decreases on ; therefore, every is a maximum point.
- -
- If , then decreases on and attains the maximum for .
In this case,
Appendix B
| John | |||
| Anne | |||
- -
- CASE , the function attains the maximum value 1 in the two maximum points , for every , i.e.,
- -
- CASE the function
- (a)
- strictly decreases on p for and attains the maximum for , soNote that
- (b)
- is constant on p for :
- (c)
- strictly increases on p for and attains no maximum points because the domain is not closed, but, in this case, we have the following:
| 1 | |
| 2 | Optimistic and intermediate attitudes actually have strong empirical support (see for example [21]). |
| 3 | See [7] for additional details on the topological and metric structure of the beliefs space. |
| 4 | |
| 5 | See the Introduction section in [5]. |
| 6 | Note that, lower and upper semi-continuous set-valued maps (or correspondences) are also often denoted in the literature, respectively, as lower and upper hemi-continuous set-valued maps. However, we follow the notation in the book [38]. |
| 7 | The game considered in Example 3.4 in [7] is different from the one presented in the present paper; however, ambiguous hierarchies of beliefs have the same structure. |
| 8 | For technical reasons, we consider the case where functions take values in . |
| 9 | The function is the one appearing in the construction of (see Equation (2)). |
| 10 | Note that, in this section, the value of , such that and are not defined, is studied separately. |
| 11 | In this section, with the abuse of notation, we denote with the classical utility function defined over the set of pure strategic profiles, and with the classical expected utility. |
| 12 | In this particular example, the belief correspondence depends only on p.This is the simplest model to show the mathematical property we look at. |
References
- Dow, J.; Werlang, S. Nash Equilibrium under Uncertainty: Breaking Down Backward Induction. J. Econ. Theory 1994, 64, 305–324. [Google Scholar] [CrossRef]
- Eichberger, J.; Kelsey, D. Non-Additive Beliefs and Strategic Equilibria. Games Econ. Behav. 2000, 30, 183–215. [Google Scholar] [CrossRef]
- Lehrer, E. Partially Specified Probabilities: Decisions and Games. Am. Econ. J. Microecon. 2012, 4, 70–100. [Google Scholar] [CrossRef][Green Version]
- Riedel, F.; Sass, L. Ellsberg Games. Theory Decis. 2013, 76, 1–41. [Google Scholar] [CrossRef]
- Battigalli, P.; Cerreia-Vioglio, S.; Maccheroni, F.; Marinacci, M. Self-confirming equilibrium and model uncertainty. Am. Econ. Rev. 2015, 105, 646–677. [Google Scholar] [CrossRef]
- De Marco, G.; Romaniello, M. Variational preferences and equilibria in games under ambiguous belief correspondences. Int. J. Approx. Reason. 2015, 60, 8–22. [Google Scholar] [CrossRef]
- De Marco, G.; Romaniello, M.; Roviello, A. Psychological Nash Equilibria under Ambiguity. Math. Soc. Sci. 2022, 120, 92–106. [Google Scholar] [CrossRef]
- Battigalli, P.; Dufwenberg, M. Dynamic psychological games. J. Econ. Theory 2009, 144, 1–35. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Battigalli, P.; Dufwenberg, M. Guilt in games. Am. Econ. Rev. 2007, 97, 170–176. [Google Scholar] [CrossRef]
- Attanasi, G.; Battigalli, P.; Nagel, R. Disclosure of belief-dependent preferences in the trust game. In Proceedings of the BQGT, Newport Beach, CA, USA, 14–16 May 2010; p. n.1. [Google Scholar]
- Attanasi, G.; Nagel, R. A survey of psychological games: Theoretical findings and experimental evidence. In Games, Rationality and Behavior. Essays on Behavioral Game Theory and Experiments; Innocenti, A., Sbriglia, P., Eds.; Palgrave McMillan: New York, NY, USA, 2008; pp. 204–232. [Google Scholar]
- Battigalli, P.; Dufwenberg, M. Belief-dependent motivations and psychological game theory. J. Econ. Lit. 2020, 60, 833–882. [Google Scholar] [CrossRef]
- Geanakoplos, J.; Pearce, D.; Stacchetti, E. Psychological games and sequential rationality. Games Econ. Behav. 1989, 1, 60–79. [Google Scholar] [CrossRef]
- Gilboa, I.; Schmeidler, D. Maxmin Expected Utility with a Non-Unique Prior. J. Math. Econ. 1989, 18, 141–153. [Google Scholar] [CrossRef]
- Hurwicz, L. Some specification problems and applications to econometric models. Econometrica 1951, 19, 343–344. [Google Scholar]
- Ghirardato, P.; Maccheroni, F.; Marinacci, M. Differentiating ambiguity and ambiguity attitude. J. Econ. Theory 2004, 118, 133–173. [Google Scholar] [CrossRef]
- Eichberger, J.; Grant, S.; Kelsey, D.; Koshevoy, G.A. The α-MEU model: A comment. J. Econ. Theory 2011, 146, 1684–1698. [Google Scholar] [CrossRef]
- Chateauneuf, A.; Ventura, C.; Vergopoulos, V. A simple characterization of the Hurwicz criterium under uncertainty. Rev. Écon. 2020, 71, 331–336. [Google Scholar] [CrossRef]
- Klibanoff, P.; Mukerji, S.; Seo, K.; Stanca, L. Foundations of ambiguity models under symmetry: α-MEU and smooth ambiguity. J. Econ. Theory 2022, 199, 105202. [Google Scholar] [CrossRef]
- Ivanov, A. Attitudes to ambiguity in one-shot normal-form games: An experimental study. Games Econ. Behav. 2011, 71, 366–394. [Google Scholar] [CrossRef]
- Jeleva, M.; Villeneuve, B. Insurance contracts with imprecise probabilities and adverse selection. Econ. Theory 2004, 23, 777–794. [Google Scholar] [CrossRef]
- Zapata, A.; Caraballo, M.A.; Monroy, L.; Mármol, A.M. Hurwicz’s criterion and the equilibria of duopoly models. Cent. Eur. J. Oper. Res. 2019, 27, 937–952. [Google Scholar] [CrossRef]
- Jaffray, J.; Jeleva, M. Information processing under imprecise risk with the Hurwicz criterion. In Proceedings of the 5th International Symposium on Imprecise Probability: Theories and Applications, Prague, Czech Republic, 16–19 July 2007. [Google Scholar]
- Dominiak, A.; Guerdjikova, A. Pessimism and optimism towards new discoveries. Theory Decis. 2021, 90, 321–370. [Google Scholar] [CrossRef]
- Yu, J. Essential equilibria of n-person noncooperative games. J. Math. Econ. 1999, 31, 361–372. [Google Scholar] [CrossRef]
- Carbonell-Nicolau, O. Essential equilibria in normal-form games. J. Econ. Theory 2010, 145, 421–431. [Google Scholar] [CrossRef]
- Scalzo, V. Continuity properties of the Nash equilibrium correspondence in a discontinuous setting. J. Math. Anal. Appl. 2019, 473, 1270–1279. [Google Scholar] [CrossRef]
- De Marco, G.; Romaniello, M. Beliefs Correspondences and Equilibria in Ambiguous Games. Int. J. Intell. Syst. 2012, 27, 86–107. [Google Scholar] [CrossRef]
- Walley, P. Towards a unified theory of imprecise probability. Int. J. Approx. Reason. 2000, 24, 125–148. [Google Scholar] [CrossRef]
- Eichberger, J.; Kelsey, D. Are the treasures of game theory ambiguous? Econ. Theory 2011, 48, 313–339. [Google Scholar] [CrossRef]
- Eichberger, J.; Kelsey, D. Optimism and pessimism in games. Int. Econ. Rev. 2014, 55, 483–505. [Google Scholar] [CrossRef]
- Denoeux, T. Decision-making with belief functions: A review. Int. J. Approx. Reason. 2019, 109, 87–110. [Google Scholar] [CrossRef]
- Petturiti, D.; Vantaggi, B. Modeling agent’s conditional preferences under objective ambiguity in Dempster-Shafer theory. Int. J. Approx. Reason. 2020, 119, 151–176. [Google Scholar] [CrossRef]
- Petturiti, D.; Vantaggi, B. Conditional decisions under objective and subjective ambiguity in Dempster-Shafer theory. Fuzzy Sets Syst. 2022, 447, 155–181. [Google Scholar] [CrossRef]
- Battigalli, P. Comportamento Razionale ed Euilibrio nei Giochi e Nelle Situazioni Strategiche. Unpublished Undergraduate Dissertation, Bocconi University, Milano, Italy, 1987. [Google Scholar]
- Fudenberg, D.; Levine, D.K. Self-confirming equilibrium. Econom. J. Econom. Soc. 1993, 61, 523–545. [Google Scholar] [CrossRef]
- Aubin, J.; Frankowska, H. Set Valued Analysis; Birkhauser: Boston, MA, USA, 1990. [Google Scholar]
- Lignola, M.; Morgan, J. Convergences of Marginal Functions with Dependent Constraints. Optimization 1992, 23, 189–213. [Google Scholar] [CrossRef]
- Van Damme, E. Stability and Perfection of Nash Equilibria; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Selten, R. Reexamination of the perfectness concept for equilibrium points in extensive games. Int. J. Game Theory 1975, 4, 24–55. [Google Scholar] [CrossRef]
| ∅ | ∅ | ∅ | ||||
| ∅ | ||||||
| ∅ |
| John | |||
| Anne | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Marco, G.; Romaniello, M.; Roviello, A. On Hurwicz Preferences in Psychological Games. Games 2024, 15, 27. https://doi.org/10.3390/g15040027
De Marco G, Romaniello M, Roviello A. On Hurwicz Preferences in Psychological Games. Games. 2024; 15(4):27. https://doi.org/10.3390/g15040027
Chicago/Turabian StyleDe Marco, Giuseppe, Maria Romaniello, and Alba Roviello. 2024. "On Hurwicz Preferences in Psychological Games" Games 15, no. 4: 27. https://doi.org/10.3390/g15040027
APA StyleDe Marco, G., Romaniello, M., & Roviello, A. (2024). On Hurwicz Preferences in Psychological Games. Games, 15(4), 27. https://doi.org/10.3390/g15040027






