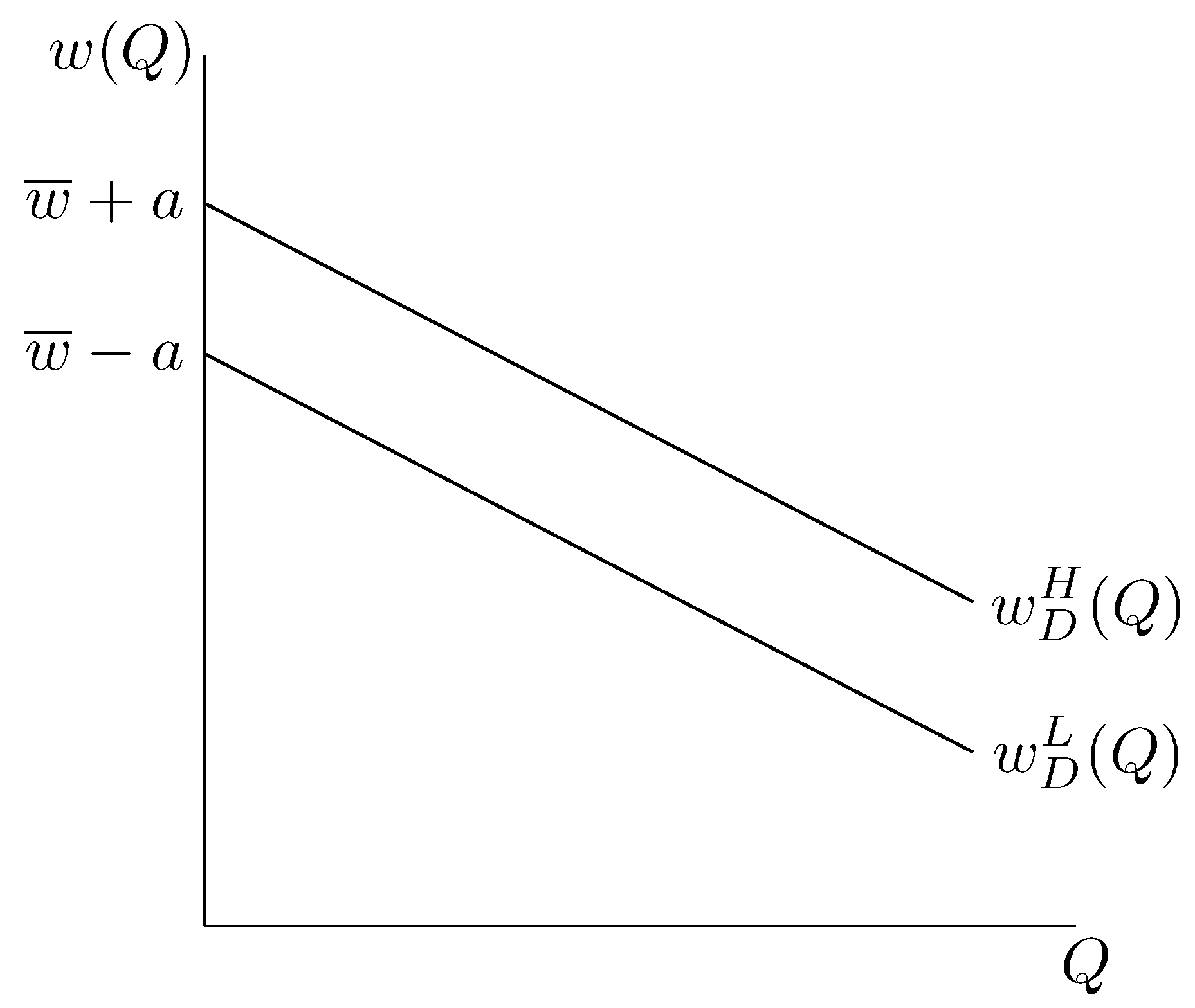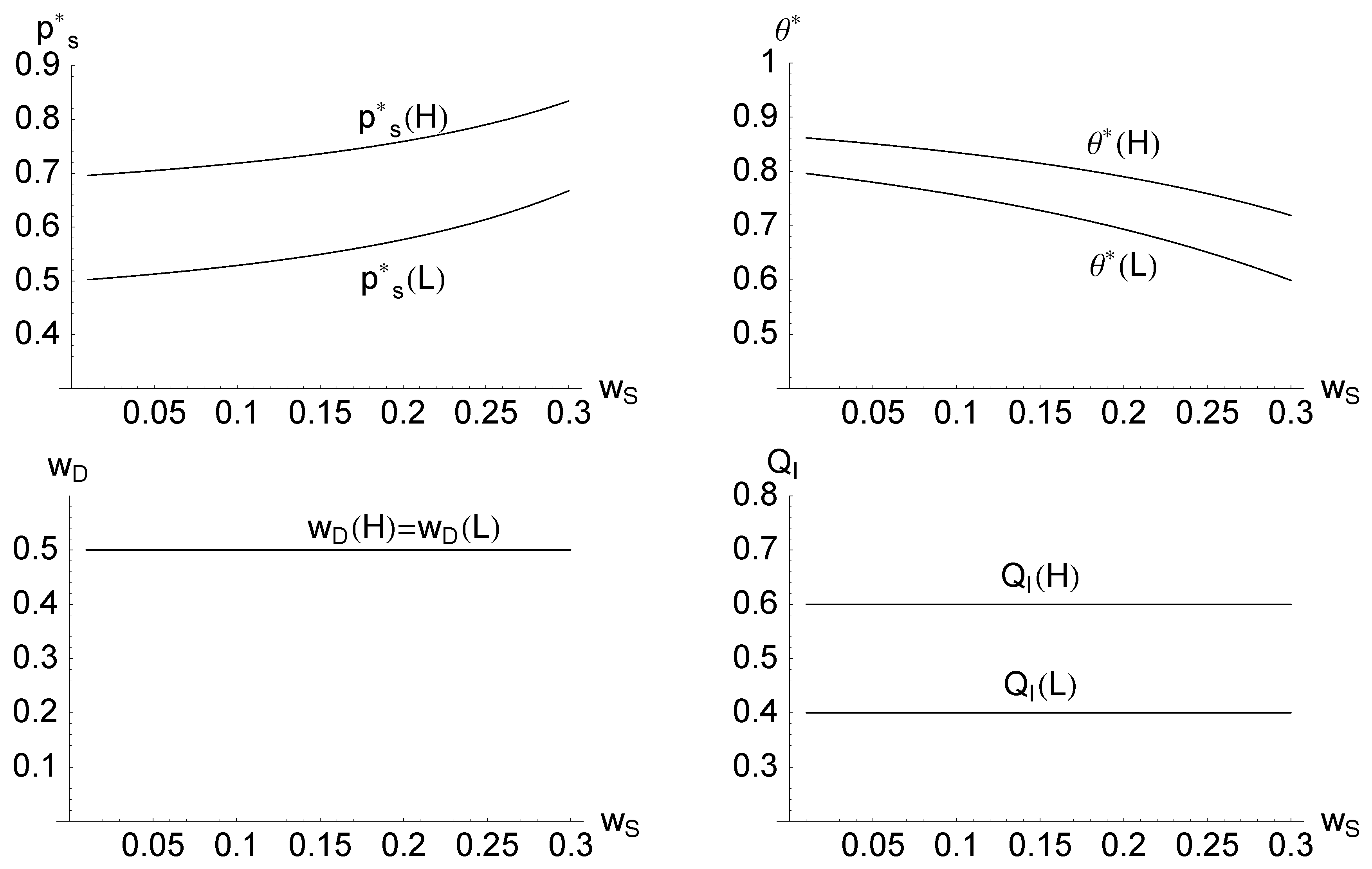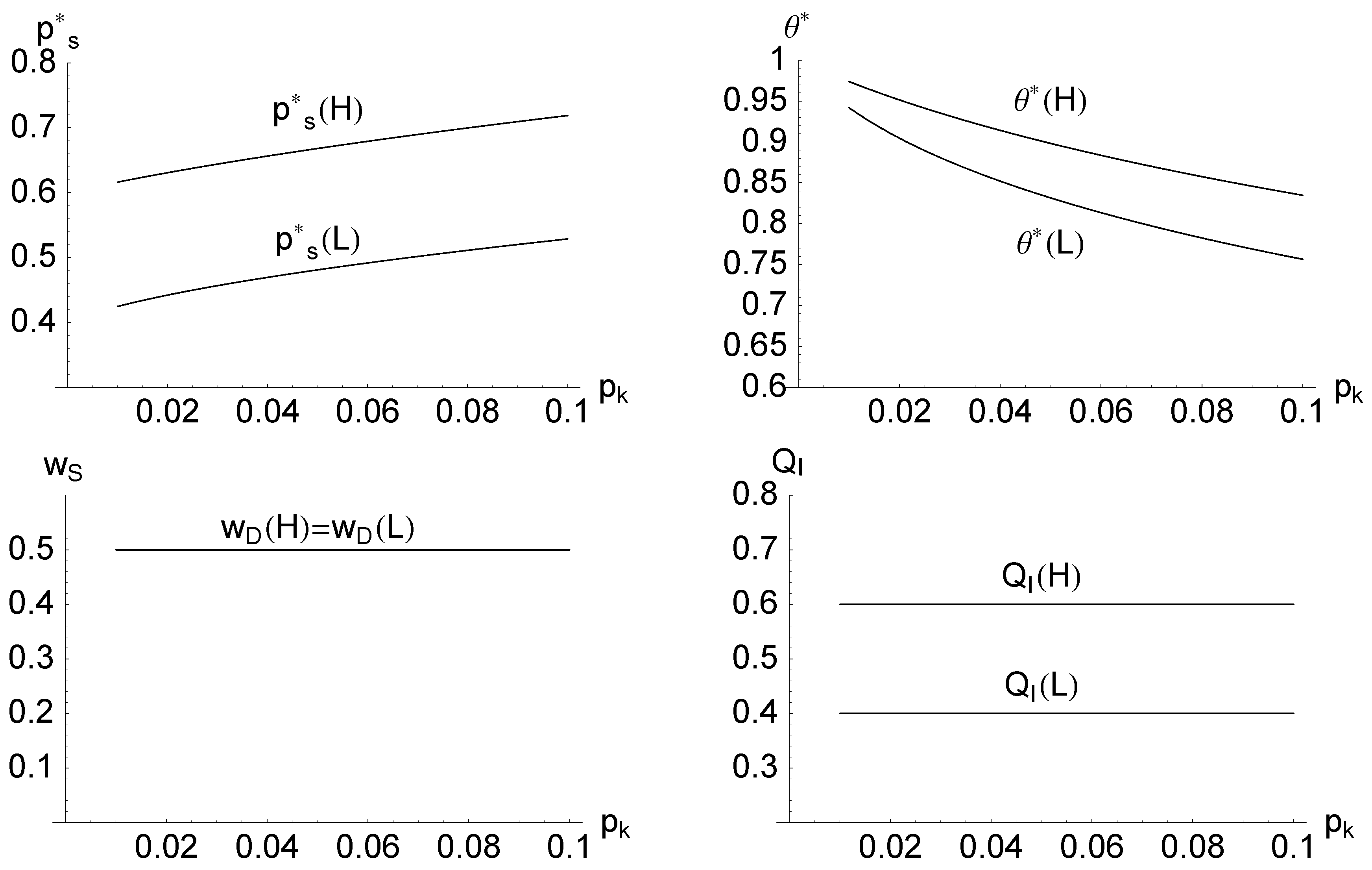Border Games: A Game Theoretic Model of Undocumented Immigration

Abstract

We consider a game-theoretic model of undocumented immigration with the aim of emphasizing the strategic interaction between the different forces affecting the issue. Specifically, we analyze the strategic interaction between firms in the destination country, native labor, the elected officials in the destination country, and the undocumented immigrants from the Source Country. We show that the impact of border enforcement is dampened because strategic interaction between the players will tend to mute any unilateral changes. We also study the effect of uncertainty in the labor market on migration issues and analyze the two cases where policymakers have to make their decisions before (ex-ante) or after (ex-post) the market state is realized.

1. Introduction

The issue of undocumented immigration, i.e., people residing in a nation without legal immigration status, has generated a great deal of public interest and was a major issue in recent elections in the United States and Europe. This is not surprising given their numbers, as there are an estimated more than ten million undocumented immigrants residing in the United States1, approximately one million residing in the United Kingdom, and about three times that number in the European Union and European Free Trade Association [2].

Although there is a body of economic literature that examines the impact of undocumented immigration, there is not a great deal that focuses on the decisions of the various actors involved. Further, the works tend to only focus on the decisions of the destination country, not involving actors from the source country. Ethier’s seminal work [3] was the first to model the decisions of governments, workers, and firms in the source country and those in the destination country. In particular, he considered domestic enforcement through imposing penalties on employers of illegal immigrants, with the economic effect of increasing the cost of hiring these workers. This domestic enforcement strategy is shown to complement border enforcement efforts in curtailing the demand for illegal immigrants. Bond and Chen [4] develop a two-country extension of Ethier’s model and consider the impact of capital mobility, comparing the effectiveness of employer sanctions with a wage tax on the employment of foreign workers. They demonstrate that the presence of enforcement costs makes this policy less efficient compared with implementing a wage tax instead. Moreover, when capital mobility is considered, their results show that foreign workers benefit from increased enforcement in their home country due to capital moving out of that country. Other studies, such as Kahana and Lecker [5], also only focus on the actions within the destination country by examining the use of foreign aid to increase the benefit to potential immigrants to staying in the source country. Angelucci [6] estimates the effect of United States border enforcement on the net flow of undocumented immigrants and finds that the inflow and outflow of illegal Mexican migration respond to changes in border enforcement. Angelucci shows that the marginal effect of enforcement is a positive function of enforcement for the inflow but a constant or decreasing one for the outflow. Faccini and Testa [7] examine quotas and lax enforcement as a way of implicitly allowing undocumented immigration, where the government maintains its political support by strategically adopting an immigration quota that appeals to the majority of voters while intentionally loosening its enforcement efforts on this quota. Similarly, Ruhs and Anderson [8] construct a model of semi-compliance where refugees and asylees who can legally reside in the United Kingdom but lack work permits still work. They consider the behavior of the migrants, employers, and government in the United Kingdom but not the behavior of potential immigrants in the Source Country as we do.2 In terms of the impact of undocumented immigration, Hillman and Weiss [11] examine the effects on traded and non-traded sectors within the destination country, and Borjas and Cassidy [12] investigate the wage penalty to undocumented immigration. It is worthwhile to note that similar models have been used to analyze the optimal quota setting problem for documented immigration [13,14].

Other works analyze immigration through the lens of political economy. Epstein and Weiss were the first to analyze immigration amnesties. Chau [15] developed an extension of Ethier’s [3] model of illegal immigration and showed the value of strategically granting amnesty to illegal workers to resolve the time inconsistency of employer sanctions and border enforcement efforts. Karlson and Katz [16] looked at the effect of amnesties for undocumented immigrants living in a destination country on future attempts at undocumented immigration.

Finally, in recent work, Hillman and Long [17] explore the political ramifications of immigration, particularly in terms of the potential support for allowing more immigrants. They suggest that workers may be inclined to support increased immigration because immigrants’ political views may align with theirs. However, our model is not concerned with future voter implications for undocumented immigrants since they cannot influence the political landscape due to their lack of documentation and therefore voting rights. In our model, we abstract away from political voting models and instead focus on the perspective of the elected official. The official aims to strike a balance between the preferences of native workers and employers who hire undocumented immigrants, using a straightforward weighted utility model.

In summary, in prior work, many economic models of undocumented immigration have been proposed (e.g., Ethier [3] and Chau [15]) to analyze the effect of various policies to curtail undocumented immigration. In all these works, the source country has been modeled exogenously, providing a constant flow of immigrant workers that only depends on the conditions of the source country. However, in reality, the source country families make choices endogenously given the current state of the enforcement levels and the destination country conditions. The objective of this paper is to close this gap in the literature by constructing a game-theoretic model that considers the strategic choices of all of the actors involved in undocumented immigration, including the destination country’s government, businesses, and workers, as well as the families in the source country. Our results in this paper indicate that modeling the strategic choice of source country family choices explicitly leads to strikingly different conclusions regarding the effect of source country economic factors on undocumented immigration.

Although the number of immigrants granted lawful permanent residence, admitted as temporary nonimmigrants, or granted asylum or refugee status is usually set by the legislature and chief executive of a nation, the number of undocumented immigrants is determined in a different manner. Their number will depend on both the number of people in a source country attempting to immigrate to a destination country as well as the enforcement efforts of the latter. In return, the number of people attempting to emigrate will depend on the wages in the source country and the destination country, as well as the chances of successfully crossing the border. Border enforcement, which will impact a potential undocumented immigrant’s probability of a successful attempt, depends on the resources the destination country is willing to commit to prevent undocumented immigration. The process of these players interacting in determining the level of successful undocumented immigration has not, to our knowledge, been modeled as such, and we add to our understanding of the process by creating a game-theoretic model of undocumented immigration.

The level of undocumented immigration can be thought of as having an initial equilibrium. Changes in the wage rate in the source country can influence the decision of potential immigrants to migrate, even without legal permission. This in turn might lead to workers in the destination country electing government officials who will put more resources into stricter border enforcement to prevent what they view as a substitute for their labor or for other reasons such as a fear of crime, a desire for laws to be followed, or a general dislike of those who are different from themselves3. In our model we use the term reduced wages to cover all types of disutility, both real and perceived, to destination country workers from undocumented immigration. On the other hand, business owners in the destination country might lobby for looser enforcement to enlarge the supply of workers. Our model shows that the responses of some of the players mitigate the effects of the initial move by another player. If wages decline in a source country, resulting in a rising number of migrants, the response in the destination country would be to increase border security, thus decreasing the probability of a successful attempt at undocumented immigration and a muted increase in the number of undocumented immigrants in the destination country.

The next section formulates the basic model with the players and their objectives. The third section fully develops the game theoretic model with simultaneous moves. The following section adds uncertainty to the model. The concluding section summarizes the model and applies it to an actual situation with a single source country and a single destination country.

2. Model

We focus exclusively on undocumented immigration. We assume that there are two nations: a destination country (DC) that undocumented workers attempt to migrate to and a source (SC) country from which they emigrate. Migrating workers are thought to be relatively unskilled, as those with skills could earn higher wages in their home country, and their education and credentials in the destination country might not be accepted, especially if they were undocumented. We assume that there is a strong demand for unskilled labor in the destination country and a much higher equilibrium wage for this type of labor there than in the source country4. In our model of the process, we assume the following players:

• Destination Country (DC) firms are trying to increase undocumented migration in order to increase the supply of labor and keep wages low.
• Destination Country (DC) workers are trying to decrease undocumented migration, thus limiting the supply of labor and keeping wages high.
• Elected officials in the Destination Country (DC) who wish to get re-elected and will balance the desires of firms for more workers, with resources to lobby and donate to election campaigns, and domestic workers/voters who desire fewer undocumented immigrants and higher wages.
• Families living in the Source Country (SC) who allocate their resources between a lower-wage job at home and a higher-wage job in the DC, but with a risky border crossing.

Destination Country (DC) firms are attempting to maximize profits, which are directly related to the supply of labor and inversely related to the wage rate. The firms will lobby and make political contributions to increase the level of immigrant labor. The DC government can respond by either increasing the quota of legal immigrants or adjusting the resources put into patrolling the border and allowing in more undocumented immigration [7]. The SC workers will balance the increased higher wages available in the destination country with both the probability of being apprehended and returned to their native land as well as the risk of injury or death from crossing the border. SC workers face a trade-off between the risk-free asset of not immigrating and a risky, dangerous, but potentially rewarding attempt to migrate5. After developing the model, we examine the impact of exogenous changes as well as uncertainty.

We assume there is a strong demand for unskilled labor in the destination country (DC), and the equilibrium wage for these jobs is much higher, thus creating an incentive for workers in the source country (SC) to migrate there. There is no legal immigration program for unskilled workers per se, and therefore the only option is undocumented migration across the border6.

We use a game-theoretic undocumented immigration model based on the conflicting interests of the four players:

• Source Country Families We assume families living in the source country send a proportion $\theta$ of their family’s labor force to attempt a border crossing and relocation to the destination country (DC). The workers trying to cross the border are faced with three outcomes: successfully making it to DC and finding a job with a probability $p_s$, being detected and sent back with a probability $p_b$, or dying or suffering an injury on the journey with a probability $p_k$ where:

  $$p_s+p_b+p_k=1$$

  (1)

As a result, the expected utility of the SC family that sends $\theta$ percent of its family’s labor force to the DC is given by:

$$u_{SF}=p_s{v}_S\left((1-\theta )w_S+\theta w_D\right)+p_b{v}_S\left((1-\theta )w_S+\theta \rho w_S\right)+p_k{v}_S\left((1-\theta )w_S\right)$$

(2)

where $w_S$ and $w_D$ denote the equilibrium wage in the unskilled labor market in the source and destination countries, respectively, and $v_S$ is the utility that the, source country workers derive from income, which is assumed to be proportional to the wages they receive7. We assume the utility function is concave with diminishing marginal utility and exhibits constant relative risk aversion (CRRA) with a coefficient of $\alpha$:

$$-\frac{w{v}_S^{″}\left(w\right)}{v_S^{\prime }\left(w\right)}=\alpha$$

(3)

The families choose $\theta$ to maximize their utilities. The discount factor $\rho$ is a constant modeling the lost wages due to unsuccessful attempts at crossing the border8. We adopt a stylized one-period model for undocumented immigration and assume all migrating members of one family travel together, and the outcome is the same for all. The model captures important characteristics of the border crossing scenario by modeling it as a decision problem of allocating resources between a risky asset (attempting a border crossing with three potential wage outcomes $\{w_D,\rho w_S,0\}$) and a risk-free asset (staying and working in the SC with a deterministic outcome of $\left\{w_S\right\}$). Source country families might also be concerned with the absence of democratic governance, breaches in the rule of law, the potential for conflict, human rights violations, and constraints on freedom of expression. We note that a depressed wage $w_S$ in the source country can be used in part to account for the dissatisfaction of source country families with their current political environment.

• Firms and Workers in the Destination Country (DC) The firms are interested in the availability of a pool of unskilled workers. We assume the firms can directly observe the number of undocumented immigrant workers who successfully enter the destination country, which is denoted by $Q_I$. The firms are interested in supporting a candidate for elected office who will enable a high number of undocumented immigrant workers9. The native workers in the destination country are interested in their average wage rate $w_D$ in this market and do not observe directly the number of immigrant workers. They base their support on their disposable income level, which is proportional to their wage. Although in some cases, the impact of immigrants on the wages of domestic workers is small10, if the workers in the destination country believe that unskilled immigrants will take their jobs and reduce their wages, this would be sufficient to support the election of government officials who will put more resources into border enforcement and restrict undocumented immigration.

• Elected Official The elected official is trying to maximize his chances of re-election. He is trying to balance the interests of the firms and corporations lobbying for a higher level of migration11 and the welfare of the native workers who are interested in higher wages. We assume the elected official’s utility function is of the quasi-linear form:

  $$u_{EO}=v_N\left(w_D\right)+\lambda Q_I$$

  (4)

The parameter $\lambda$ weighs the interest of the firms against the welfare of the native workers resulting from changes in the number of immigrants and $v_N$ is the utility that native workers derive from income. The elected official shapes the border security policy and determines the probability $p_s$ of successfully crossing the border12. There are multiple methods available to the EO to influence $p_S$ the probability of successfully crossing; these include building walls, increasing the use of drones, of boats, surveillance equipment, enforcement away from the border, deportation, as well as adjudications of asylum claims and detention.

The workers in the source country and the elected official choose $\theta$ and $p_s$ independently without observing each other’s choice in a simultaneous move game. Given a particular choice of $\theta$ and $p_s$, we assume the pool of workers in the source country is S, then the number of successful undocumented immigrants $Q_I$ is given by:

$$Q_I=S\theta p_s$$

(5)

the equilibrium wage in the destination country is determined by the demand for labor:

$$w_D=D_l^{-1}(Q_I+Q_N)=W_l(Q_I+Q_N).$$

(6)

where the $D_l$ and $W_l$ denote the demand and the inverse demand for labor, respectively (we assume $D_l^{\prime }<0,W_l^{\prime }<0$), and $Q_N$ is the number of native workers in the DC. The parameters $S,w_S,Q_N,\rho ,p_k,and\lambda$ are assumed to be exogenously specified. We can divide these parameters into two classes: (i) parameters entering the utility function of the elected official and the labor demand $\{\lambda ,S,Q_N\}$ (ii) parameters entering the utility function of only the SC Families $\{w_S,\rho ,p_k\}$.

The interests of the firms and the workers in the DC are implicit in the utility function of the elected official, who is trying to appeal to both firms and native workers in the destination country.

3. Simultaneous Move Game

In this section, we consider a simultaneous move game between the elected official and SC families. The elected official chooses $p_s$ through resources devoted to enforcement, and the source country (SC) families choose $\theta$ without directly observing each other’s actions. In real-world strategic interaction between elected officials and source country families, decisions and adjustments are made over a longer time horizon; nevertheless, we expect the Nash equilibrium of the simultaneous move game to prevail in this border interaction, as in this equilibrium, no player has an incentive to change their choice even if the choice of the other player is revealed.

In the following, we first derive the best response function for each player and solve these simultaneously to arrive at the Nash equilibrium.

Source Country Families (SF): We recall that the expected utility of a Source Country worker is given by:

$$\begin{array}{cc}\hfill u_{SF}(p_s,\theta ,p_k,w_D,w_S)& =p_s{v}_S\left((1-\theta )w_S+\theta w_D\right)+p_b{v}_S\left((1-\theta )w_S+\theta \rho w_S\right)\hfill \\ \hfill & \phantom{=}+p_k{v}_S\left((1-\theta )w_S\right)\hfill \end{array}$$

(7)

Note that the SC families do not consider the effect of their choice of $\theta$, the proportion of the family to send to the DC, on the DC wage level. We assume that undocumented immigrant workers originate from a large number of identical families, each solving the same decision problem given above. The families are faced with a problem of investment choice between a risky asset (attempted immigration) with three potential returns $(w_D,\rho w_S,0)$ and a risk-free asset (remaining in SC) with the deterministic return of $\left(w_S\right)$. Assuming an interior solution, $\theta >0$, the optimal portfolio allocation is given by the first-order condition:

$$\begin{array}{cc}\hfill \frac{\partial u_{SF}}{\partial \theta }& =p_s{v}_S^{\prime }\left((1-\theta )w_S+\theta w_D\right)(w_D-w_S)\hfill \\ \hfill & \phantom{=}-(1-p_s-p_k)v_S^{\prime }\left((1-\theta )w_S+\theta \rho w_S\right)(1-\rho )w_S-p_k{v}_S^{\prime }\left((1-\theta )w_S\right)w_S=0\hfill \end{array}$$

(8)

Equation (8) implicitly defines the best response function $f_{SF}$ of the SC families. The best response function $f_{SF}$ gives the optimal allocation $\theta$ of the family resources, given particular values for $p_s,p_k,w_D$ and $w_S$.

$${\theta }^{*}=f_{SF}(p_s,p_k,w_D,w_S)$$

(9)

Theorem 1.

If the utility function $v_S$ of the source country families is concave and differentiable, then the best response function $f_{SF}(p_s,p_k,w_D)$ satisfies:

$$\frac{\partial f_{SF}}{\partial p_s}>0,\frac{\partial f_{SF}}{\partial p_k}<0,$$

(10)

If the utility function $v_S$ of the SF exhibits constant relative risk aversion with a coefficient of $\alpha <1$ then the best response function also satisfies:

$$\frac{\partial f_{SF}}{\partial w_D}>0,\frac{\partial f_{SF}}{\partial w_S}<0$$

(11)

Proof. 

Total differentiation of Equation (8) with respect to the parameters of the model reveals the desired result. The details are given in Appendix A.1. □

Elected Official: In contrast to the SC families, the elected official accounts for the effect of border security actions on the labor market. With this assumption, the utility function for the elected official is given by:

$$\begin{array}{ccc}\hfill u_{EO}(p_s,\theta ,\lambda )& =& v_N\left(w(Q_N+S\theta p_s)\right)+\lambda S\theta p_s\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& =& {\tilde{v}}_N(Q_N+S\theta p_s)+\lambda S\theta p_s\hfill \end{array}$$

(13)

where ${\tilde{v}}_N$ is the composite function $v_N$ applied on w (i.e., ${\tilde{v}}_N=v_N\circ w$).

The optimal level of border security enforcement is determined by the first order condition

$$\frac{\partial u_{EO}}{\partial p_s}={\tilde{v}}_N^{\prime }(Q_N+S\theta p_s)S\theta +\lambda S\theta =0$$

(14)

Canceling

$${\tilde{v}}_N^{\prime }(Q_N+S\theta p_s)+\lambda =0$$

(15)

which leads to the following best response function for the elected official

$$p_s^{*}=f_{EO}(\theta ,\lambda )=\frac{{\tilde{v}}_N^{\prime -1}(-\lambda )-Q_N}{S\theta }$$

(16)

Theorem 2.

Assume the utility function of the destination country workers $v_D$ is concave and differentiable, then the best response function $f_{EO}(\theta ,\lambda )$ for the Elected Official satisfies:

$$\frac{\partial f_{EO}}{\partial \theta }<0,\frac{\partial f_{EO}}{\partial \lambda }>0$$

(17)

Proof. 

The total differentiation of Equation (15) with respect to the parameters of the model reveals the desired result. The details are given in Appendix A.2. □

Nash Equilibrium To obtain Nash equilibrium levels of ${\theta }^{*}(p_k,\lambda ,w_S)$ and $p_s^{*}(p_k,\lambda ,w_S)$, we solve the two best response functions:

$$\begin{array}{ccc}\hfill {\theta }^{*}& =& f_{SF}(p_s^{*},p_k,{\tilde{v}}_N(Q_N+S{\theta }^{*}{p}_s^{*}),w_S)\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill p_s^{*}& =& \frac{{\tilde{v}}_N^{\prime -1}(-\lambda )-Q_N}{S{\theta }^{*}}\hfill \end{array}$$

(19)

Theorem 3.

Assume the utility functions $v_D$ and $v_S$ of the DC workers and the SC families are differentiable and concave, with $v_S$ exhibiting constant relative risk aversion with a coefficient of $\alpha <1$, then the comparative statistics of the Nash equilibrium levels of $p_s^{*}$ and ${\theta }^{*}$ are given as below:

$$\frac{\partial p_s^{*}}{\partial p_k}>0,\frac{\partial p_s^{*}}{\partial w_S}>0,\frac{\partial {\theta }^{*}}{\partial p_k}<0,\frac{\partial {\theta }^{*}}{\partial w_S}<0,\frac{\partial p_s^{*}}{\partial \lambda }>0$$

(20)

Proof. 

First, we rearrange Equations (18) and (19) into homogeneous form with the variables $\theta ,p_s$ endogenously determined in the model based on the independent variables $p_k,w_s,\lambda$.

$$\begin{array}{cc}\hfill {\tilde{g}}_1(\theta ,p_s,p_k,w_s)& =g_1(\theta ,p_s,p_k,{\tilde{v}}_N(Q_N+S\theta p_s),w_S)=0\hfill \\ \hfill g_2(\theta ,p_s,\lambda )& =0\hfill \end{array}$$

Totally differentiating the matrix set of Equations (18) and (19) reveals the desired result. The detailed derivations are given in Appendix A.3. □

The focal result of our model is given by the following Theorem.

Theorem 4.

Assume the utility functions $v_D$ and $v_S$ of the DC workers and the SC families are differentiable and concave, and the inverse labor demand function is differentiable and convex. Then the equilibrium number of undocumented immigrant workers is an increasing function of λ.

$$Q_I^{*}=g\left(\lambda \right):={\tilde{v}}_N^{\prime -1}(-\lambda )-Q_N,{with g}^{\prime }\left(\lambda \right)>0$$

(21)

Proof. 

Rearranging the Nash equilibrium condition given in (19), we obtain the relationship between $\lambda$ and $Q_I^{*}$:

$$Q_I^{*}=S{p}_s^{*}{\theta }^{*}={\tilde{v}}_N^{\prime -1}(-\lambda )-Q_N$$

The monotonicity of the function $g\left(\lambda \right)$ follows from the inverse function theorem. The details are given in Appendix A.4. □

In other words, the equilibrium number of undocumented immigrant workers depends only on $\lambda$- the relative importance of the firms’ interest in the elected officials utility. Notably, the equilibrium number of undocumented immigrant workers is independent of the variables that only appear in the utility function of the SC families $\{p_k,w_S,\rho \}$. Therefore, policies aimed at controlling this undocumented immigration through these variables are destined to fail, because the strategic interaction between the SC families and the elected official cancels any changes introduced in these variables.

For example, if the probability of dying $p_k$ increases, perhaps due to unfavorable weather conditions in the border area, in equilibrium, the SC families decrease the proportion of their household they send to the DC. The elected official in DC, however, relaxes border enforcement, increasing $\theta$, resulting in a constant level of undocumented immigration workforce. Alternatively, if the wages $w_S$ of an SC family (for members remaining in the SC) decreases (Equation (7)), then in equilibrium, the SC families increase $\theta$, the proportion of household members they send to the DC. The elected official in DC, however, is predicted to tighten border enforcement, decreasing $p_s$ (the probability of successfully migrating as an undocumented person), resulting in a constant level of the undocumented workforce. We note that this observation coincides with Angelucci’s [6] finding that the inflow of immigrants increases with tighter border enforcement efforts while the outflow is constant or slightly decreasing between 1987 and 1996. For a more recent case, we look at the United States in the pre-pandemic period 2017–2019; we see that families in the source countries of Guatemala, Honduras, and El Salvador saw increased violence, reducing the compensated wage rate for those remaining in those nations. The result was a 76% increase in attempted undocumented border crossing into the United States, almost one-half a million attempts13, while the Department of Homeland Security estimated that the probability of successfully migrating, $p_s$, fell by almost two-thirds from 28.1% to 10.5%14. The result was that the estimated total unauthorized immigrant population in the United States rose by approximately 0.6%15 even with this substantial increase in the number of attempted unauthorized border crossings.

Discussion of Modeling Choices and Extensions

The above results do not depend on the particular wage preferences of the SC families, $v_S$, and the DC native workers, $v_N$, or the fact that the two players choose their actions simultaneously. They are also valid in a Stackelberg formulation of the game where the elected official moves first and commits to a particular value of $p_s$, followed by the SC families observing the elected official’s choice. We assume the source country’s wages are determined exogenously. An extension of the model can include the labor market equilibrium conditions in the source country as well; however, similar results could be obtained as long as the variations in $\theta$ are small compared with its equilibrium value. In addition, such a model will have to include multiple source and destination countries for completeness, deviating from our original aim of focusing on the dynamics of the destination country.

It is also conceivable that enforcing tighter border controls will come at a cost, which should be explicitly incorporated into the utility of the EO. We assume that the cost of border control enforcement increases with the number of immigrants that are being blocked at the border, which is given by $Q_B=S\theta (1-p_s)$. Therefore, a modified version of the utility of the EO can be formulated as:

$${\tilde{u}}_{EO}=v_N\left(w_D\right)+\lambda Q_I-C\left(Q_B\right)$$

(22)

Here, the function $C\left(Q_B\right)$ denotes the total cost of border controls that are blocking $Q_B=S\theta (1-p_s)$ source country workers who are trying to cross the border. As a larger number of source country workers that are being blocked, $Q_B$ will require a larger amount of resources, and we will have diminishing (or constant) returns to the resources spent on border controls; we have $C^{\prime }\left(Q_B\right)>0$ and $C^{″}\left(Q_B\right)\ge 0$. Under these mild regularity conditions, it is straightforward to show that Theorems 2 and 3 of the original model still hold true. However, the conclusions of Theorem 4 in general do not extend to this case, except for the important special case of the constant marginal cost.

To examine the relationship between the model parameters and the equilibrium number of undocumented workers $Q_I^{*}$, we consider the case of constant marginal cost of border enforcement $C^{\prime }\left(p_s\right)=-c$. Here c denotes the marginal cost of tightening border controls (equivalently the marginal cost of relaxing $p_s$; hence, a negative sign is built into the definition above). Furthermore, the following theorem extends our focal result given in Theorem 4 to the case of costly border controls:

Theorem 5.

Assume the utility functions $v_D$ and $v_S$ of the DC workers and the SC families are differentiable and concave, and the inverse labor demand function is differentiable and convex. Furthermore, assume the cost of enforcing border controls and blocking $Q_B$ source country workers is given by $C\left(Q_B\right)$, with $C^{\prime }\left(Q_B\right)>0$ and $C^{″}\left(Q_B\right)\ge 0$. Then we have the following comparative statistics for the equilibrium number of undocumented immigrants:

$$\frac{\partial Q_I^{*}}{\partial p_k}\le 0,\frac{\partial Q_I^{*}}{\partial w_S}\le 0$$

(23)

For both $p_k$ and $w_S$ the inequality is strict if and only if the border enforcement cost function exhibits diminishing returns to scale $C^{″}\left(Q_B\right)$.

Furthermore, if the marginal cost of border enforcement is constant, $C^{\prime }\left(Q_B\right)=c$, i.e., the marginal cost of blocking one extra attempted crossing by a source country worker is a constant c. Then, our focal result given in Theorem 4 extends to the case of costly border control enforcement.

$$\frac{\partial Q_I^{*}}{\partial p_k}=0,\frac{\partial Q_I^{*}}{\partial w_S}=0\frac{\partial Q_I^{*}}{\partial \lambda }>0\frac{\partial Q_I^{*}}{\partial c}>0$$

(24)

In other words, the equilibrium number of undocumented immigrant workers $Q_I^{*}$, increases with λ, the relative weight the EO puts on the interests of the DC firms, and the marginal cost of border enforcement c and is independent of the variables that only appear in the utility function of the SC families $\{p_k,w_s,\rho \}$.

Proof. 

The first-order condition of optimality is derived from the modified utility function for the EO given in (22) as:

$$\frac{\partial {\tilde{u}}_{EO}}{\partial p_s}={\tilde{v}}_N^{\prime }(Q_N+S\theta p_s)S\theta +\lambda S\theta +C^{\prime }\left(Q_B\right)S\theta =0$$

(25)

Next, we consider the partial derivative of the equilibrium number of undocumented workers $Q_I^{*}=S{p}_s^{*}{\theta }^{*}$, with respect to the model parameters $p_k$ and $w_s$.

$$\frac{\partial Q_I^{*}}{\partial p_k}=\frac{\partial p_s^{*}}{\partial p_k}S\theta +S{p}_s\frac{\partial {\theta }^{*}}{\partial p_k}\frac{\partial Q_I^{*}}{\partial w_S}=\frac{\partial p_s^{*}}{\partial w_S}S\theta +S{p}_s\frac{\partial {\theta }^{*}}{\partial w_S}$$

(26)

We observe that our focal result, that strategic interaction between the EO and the SF acts in a way that the number of undocumented workers is independent of the SC economic conditions and perils of border conditions, still holds for many important cases. First, an overwhelming portion of the border control enforcement costs are fixed costs, such as hiring and managing the agency in charge of border enforcement. Even if there are positive marginal costs of increasing efforts on the border, they can be approximated with a locally linear function for which the results still hold.

Totally differentiating the first-order condition for the SF (18) and the modified first-order condition for the EO (25), we get the desired results, with details given in Appendix A.5. Finally, when we assume a constant marginal cost of border enforcement, the first-order condition given in (25) reduces to:

$$\frac{\partial {\tilde{u}}_{EO}}{\partial p_s}={\tilde{v}}_N^{\prime }(Q_N+S\theta p_s)S\theta +\lambda S\theta +cS\theta =0$$

(27)

Rearranging the first order condition, we obtain the relationship between $\lambda$ and $Q_I^{*}$:

$$Q_I^{*}(\lambda ,c)=S{p}_s^{*}{\theta }^{*}={\tilde{v}}_N^{\prime -1}(-\lambda -c)-Q_N$$

We clearly observe that the equilibrium number of undocumented immigrants is just a function of the two model parameters $\lambda$ and c. The monotone increasing property of $Q_I^{*}$ with respect to $\lambda$ and c follows directly from the negative slope of the demand for labor. □

Finally, labor market conditions could change at a shorter timescale than the decisions that derive undocumented immigration. As a result, the elected official and the source country families have to make their decisions before the uncertainty in the labor market is resolved. In the next section, we will consider a specific example to illustrate the result and relax the assumption about the deterministic mapping between wages and the supply of undocumented immigrant workers by introducing uncertainty in the labor market.

4. Uncertainty in the Labor Market

In the previous section, we assumed that the elected official could perfectly foresee the effect of the quantity of undocumented immigrant workers on the wage level in the country. Here we introduce a simple uncertainty model for the labor market and introduce specific functional forms for the utility function of the DC workers and the SC families. We assume the labor market can be realized in one of the two states with equal probability; one state has a high wage in the DC unskilled market ($w_D\left(H\right)$) and the other has a lower wage ($w_D\left(L\right)$). The parameter a determines the wage difference between the two states for a given level of employment.

$$\begin{array}{ccc}\hfill W_D^H(Q_N+Q_I)& =& (\overline{w}+a)-(Q_N+Q_I)\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill W_D^L(Q_N+Q_I)& =& (\overline{w}-a)-(Q_N+Q_I)\hfill \end{array}$$

(29)

Figure 1 illustrates the uncertain demand model for labor. We also assume that both the SC and the DC workers’ wage preferences are represented by logarithmic utility functions $v_N\left(w\right)=v_S\left(w\right)=logw$.

First, we note that if both the elected official and the SC families choose their strategies after the labor market state is realized, the model of the previous section applies, and we obtain the equilibrium outcome in each state by plugging in the corresponding demand functions. In this case, the equilibrium is characterized by the strategy pairs $(p_s^{*}\left(H\right),{\theta }^{*}\left(H\right))$ and $(p_s^{*}\left(L\right),{\theta }^{*}\left(L\right))$. In general, we have the following results:

$$\begin{array}{ccc}\hfill p_s^{*}\left(H\right)& >& p_s^{*}\left(L\right)\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\theta }^{*}\left(H\right)& >& {\theta }^{*}\left(L\right)\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill Q_I^{*}\left(H\right)=S{p}_s^{*}\left(H\right){\theta }^{*}\left(H\right)& >& Q_I^{*}\left(L\right)=S{p}_s^{*}\left(L\right){\theta }^{*}\left(L\right)\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill w_D^{*}\left(H\right)& =& w_D^{*}\left(L\right)\hfill \end{array}$$

(33)

The equality in Equation (33) is a result of our assumption of the particular model of the labor market (linear labor demand with varying intercepts between the states). In general, we will have a weak dependence on the state ($w_D^{*}\left(H\right)\ge w_D^{*}\left(L\right)$). However, the main point is that the increase in wages in good times is depressed by increased undocumented immigration.

Plainly, favorable market conditions induce SC families to choose to send a higher percentage of their labor force over the border. Perhaps more surprisingly, favorable labor market conditions in the destination country also induce the elected official to relax border security because he is not under pressure to keep the wages of the DC workers high. Finally, the overall level of undocumented immigration is higher, keeping the realized wage level constant.

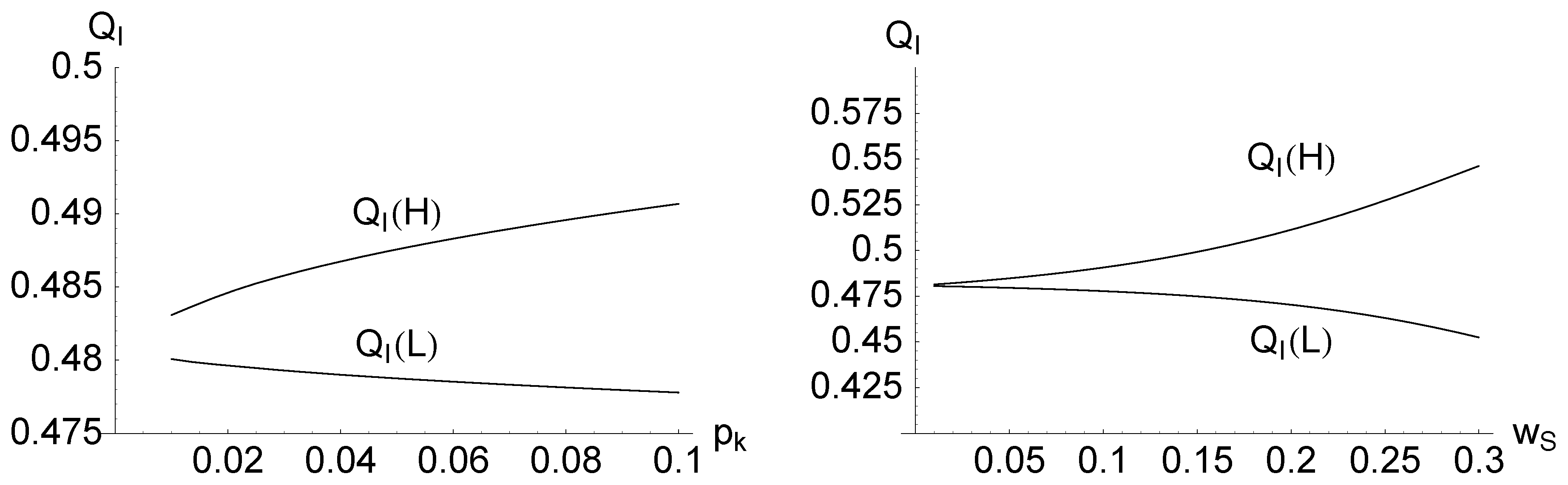
Figure 2 and Figure 3 illustrate the main results with a numeric example. First, while the equilibrium levels of $p_s$ and $\theta$ depend on exogenous variables, the wages and level of undocumented immigration is constant with respect to the variables that only affect the SC families, such as the probability of dying during an attempted border crossing and the wage level in the SC, $p_k$, and $w_S$. Second, for a given level of $w_S$ or $p_k$, favorable labor market conditions in the DC result in higher border crossing efforts by SC families and relaxed border security, resulting in higher undocumented immigration while keeping the wage level constant.

We conclude this section with an alternative game model for strategic interaction under uncertainty. In the following, we assume the elected official chooses the border security $p_s$ prior to learning the state of the labor market. This would be the case if the main instruments of border security are of a capital nature, such as building walls, remote sensors, etc. Further, it can take time to recruit and train new border control agents. As a result, the border security decision of the elected official can be viewed as constant over a long time horizon. We assume the SC families will adjust their trial efforts after the realization of the labor market state and will end up in one of the two equilibrium levels of effort $\theta \left(H\right)$ and $\theta \left(L\right)$. We are looking to find the Bayes-Nash equilibrium of this immigration game, i.e., the triple $p_s^{*},{\theta }^{*}\left(H\right),{\theta }^{*}\left(L\right)$ where:

$$\begin{array}{ccc}\hfill p_s^{*}& =& f_{EO}({\theta }^{*}\left(H\right),{\theta }^{*}\left(L\right),\lambda ,S,Q_N,a)\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\theta }^{*}\left(H\right)& =& f_{SF}(p{s}^{*},p_k,\rho ,w_S,w_D^{*}\left(H\right))\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\theta }^{*}\left(L\right)& =& f_{SF}(p{s}^{*},p_k,\rho ,w_S,w_D^{*}\left(L\right))\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill w_D^{*}\left(H\right)& =& W_D^H(Q_N+S{p}_s^{*}{\theta }^{*}\left(H\right))\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill w_D^{*}\left(L\right)& =& W_D^L(Q_N+S{p}_s^{*}{\theta }^{*}\left(L\right))\hfill \end{array}$$

(38)

Furthermore, the elected official is forced to choose a single effort level that is good for both states of labor demand. Figure 4 shows the results of a numerical example. We observe that under this assumption, the level of undocumented immigration is affected by exogenous variables such as the wage level in the source country $w_S$ and the probability of dying or being severely injured while attempting to cross the border $p_k$. At a high labor market demand state, the level of immigration increases with $p_k$ and $w_S$, and at a low market state, the level of immigration decreases with $p_k$ and $w_S$. The elected official is trying to choose the value of $p_s$ that will keep the level of immigration at an optimal level, balancing the interests of the firms and the DC workers. If the elected official has to make his decision before the labor market state is realized, the realized level of immigration will under- or over-shoot this target level depending on which labor market state takes place. Furthermore, the amount of over-under shoot is influenced by exogenous variables such as $w_S$ and $p_k$ amplifying the fluctuations in the labor market. In other words, the elected official is trying to keep the expected quantity of undocumented immigrants close to an optimal level, resulting in higher and lower levels of immigration than the target level in high- and low-demand states, respectively. We also note that in Figure 4, the gap between the target level and the realized level of undocumented immigration increases with $w_S$ and $p_k$. According to our model, these complex strategic interactions might lead to even seemingly paradoxical ex-post outcomes once the state of the labor market is realized. For example, an exogenous increase in the probability of dying $p_k$ leads to a decrease in the average level of undocumented immigration and relaxed border enforcement $p_s$ in equilibrium. However, as shown in Figure 4, in a high labor demand state, this will lead to an increase in the equilibrium number of undocumented immigrant workers, as the elected official is setting surveillance efforts $p_s$ before observing the labor market state and relaxing the surveillance efforts below the level necessary to counter the surge in $\theta$ observed in a high demand state.

5. Conclusions

Undocumented immigration is a multifaceted political issue, influenced by the conflicting interests of politicians, firms, and workers in the Destination Country (DC) and potential Source Country (SC) immigrants. In this paper, we considered an abstract game theoretic model with the aim of emphasizing the strategic interaction between the different forces affecting the issue. In particular, we have shown that exogenous changes affecting only some of the players might have effects of an unexpectedly small magnitude because strategic interaction between the players will tend to cancel any unilateral changes. Our model shows that if the wage rate in SC were to fall, the predicted result would be the attempted sending of more family members to DC as undocumented immigrants. Perhaps surprisingly, as our discussion of the situation in the Source Countries of Guatemala, Honduras, and El Salvador showed, the probability of a successful crossing would decrease as the elected officials in the United States, the Destination Country, tightened border enforcement because of the increase in attempted crossings. This would also be consistent with the recent events in Haiti and the Dominican Republic, where low wages and political instability in Haiti, the SC, have led to increasing immigration to the neighboring Dominican Republic. The response of the government of the Dominican Republic has been to deport Haitian immigrants, including those who had acquired birth-right citizenship there [25], thus reducing the probability of a permanent, successful migration. Further work remains to be completed to deal with the case of multiple destination countries or multiple source countries. We have also shown that undocumented immigration is actually beneficial in smoothing the fluctuations in the labor market as long as both parties are allowed to react to the changes in labor market conditions. The actions of the various parties result in stable wages, with the varying number of undocumented immigrants in the labor force stabilizing demand shocks.

In this work, we have focused on economic aspects of the undocumented immigration issue when we model source and destination country workers’ preferences; a potentially fruitful research direction would be to pair these with players with incentives that are politically motivated, such as asylum seekers from source countries and elected officials with median voter interests in the destination country.

Finally, in this study, we adopt a single-period model where the populations of destination and source country workers are assumed to be constant. In the long term, as the populations of native and undocumented workers change in relation to the overall economy, the wages and the political attitude towards undocumented immigrants will shift in the destination country. Our findings indicate that these adjustments will subsequently impact the percentage of source country workers attempting border crossings and the level of border enforcement chosen by elected officials. These strategic interplays will ultimately dictate the complex dynamics that govern the growth of undocumented immigrants. In future work, the insights derived from our work could be used to enrich the basic logistic growth models commonly used in the literature [26] to study the evolution of native and immigrant worker populations.