1. Introduction
Often, people like to shade the truth by being imprecise. A salesperson might say that he or she receives “few complaints” about an appliance he or she is trying to sell, even if three of the eight customers who bought that model in the past year had complained. A friend might explain his or her absence from a Sunday afternoon gathering he or she did not wish to attend by saying he or she had been “sick all weekend”, even if his or her temperature never went above 99.5 degrees Farenheit.
One characteristic of these vague utterances is that they are explicitly imprecise. This paper experimentally investigates how allowing players the option of sending explicitly imprecise messages instead of precise messages affects strategic information transmission in a standard cheap talk setting, similar to Crawford and Sobel [
1].
1 Counterintuitively, allowing imprecise messages improves communication—senders on average choose more informative messages, and receivers on average treat the messages as more informative.
An additional contribution of my paper is to explain why communication becomes more effective. In an experimental setting with rational, self-interested players, the kinds of messages available do not matter because in equilibrium, no messages convey any information [
1]. However, bounded rationality or honesty might cause players to communicate some information and to treat imprecise messages differently than equivalent precise messages. I find that both characteristics explain subject behavior but that bounded rationality is relatively more important.
In the experiment, the subjects communicate about a state
s, which is an integer between 1 and 5. The sender observes
s and chooses freely from a menu of English-language messages to send about it. In the base treatment, the menu consists of every message that specifies the state precisely, such as “The state is 3”. The rich language treatment adds three additional messages that specify an interval the state is within, either from 1 to 3, 2 to 4, or 3 to 5 (e.g., “The state is 1, 2, or 3”). After learning the message, the receiver then chooses an action
a. The receiver would like to choose
, while the sender would like him or her to choose
, so they play a partial common interest game [
4].
With either message space, with rational payoff-maximizing players, no Bayesian Nash equilibrium equilibrium exists in which m conveys any information about s, and as a result, a choices are independent of m. However, subjects in both treatments send messages that convey more information than optimal and are more trusting of messages than they should be.
This “overcommunication” finding is typical (e.g., Cai and Wang [
5] or Duffy et al. [
6]; see Blume et al. [
7] for a general overview). The prior experimental literature has alternately explained excess communication through preferences for truth-telling [
2,
8,
9,
10,
11,
12,
13,
14] or bounded rationality [
5,
15,
16,
17].
2Comparing their relative importance can be difficult, because from a money-maximizing perspective, honest behavior will seem unsophisticated. To compare them, I develop a model which teases out distinct implications of honesty and bounded rationality across my treatments. My model adapts the one-parameter Poisson cognitive hierarchy model in Camerer et al. [
18] to cheap talk and combines it with some players receiving a non-pecuniary benefit from truth-telling.
In structural non-equilibrium models such as cognitive hierarchy or level-
k models, players have a (typically incorrect) belief about how other players are acting and optimize given their beliefs.
3 Players vary in the sophistication of their beliefs. Level 0 (
) players act non-strategically—in this context, by either being truthful or by being completely credulous—while
players are defined inductively and believe all players are of lower levels. Due to the upward bias, for instance,
senders exaggerate
s by choosing
. If the
receivers think a few senders are
but most are
, they discount messages
by choosing
, but they think
are truthful and do not discount them. Following Camerer et al. [
18], I assume that the players’ levels have the Poisson distribution. Many qualitative aspects of my subjects’ behavior match this sort of reasoning.
Players vary in their honesty types in addition to their cognitive types. A player’s honesty type indicates how strong a preference for truth-telling he or she has and can be thought of as reduced-form behavior combining a variety of factors. Some subjects behave as if they dislike sending literal false messages (i.e., “lies”, following Sobel [
24]’s definition). This form of honesty is the most straightforward explanation for why senders’ message choices would be qualitatively different in the two treatments.
I am agnostic about the underlying reason my subjects behave in this way, though. Recent experiments show that in non-strategic settings, subjects seem to be motivated by honesty preferences that combine a direct cost of lying and a cost for being identified as a liar [
13,
14]. The dislike of sending literal false messages embodied in my model’s honesty types could stem from either of these explanations.
Players who care little about being honest, players who care moderately about being honest, and players who care strongly about being honest all should exhibit distinct behaviors in my experiment. The rich message treatment enables players to truthfully exaggerate, such as by sending the message “The state is 1, 2, or 3” when the state is really 1. All players believe that precise lies are more effective deceptions than truthful exaggerations, especially when the state is high. Like weakly honest players, moderately honest players in the base treatment should not send honest messages because the monetary loss from forgoing precise lies is too high. However, moderately honest players should engage extensively in truthful exaggeration in rich treatment. Finally, strongly honest players should be honest even when truthful exaggerations are not available in the base treatment.
Subject behavior across the treatments was more consistent with moderate honesty than strong honesty. Overall, 45% of the messages sent in the rich treatment were imprecise, and 57% of the imprecise messages were truthful. On the other hand, in the base treatment , only 15% of the messages were truthful.
I then estimate a simple structural model using maximum likelihood with two parameters of interest: , the average cognitive level of the subjects, and , the fraction (and subjects’ beliefs about the fraction) of moderately honest players. Most of the subjects in my experiment employed one or two levels of exaggeration or discounting (i.e., rounds of best-response reasoning). About a quarter of the subjects showed moderate preferences for honesty.
Despite the presence of honest players, when these estimates are used to calibrate my model, they imply that honesty plays a limited role in explaining why communication increases in rich language treatment. Just as important as honesty are two other factors. First, the model implies that precise messages are more informative in rich message treatment independent of honesty. In that treatment, senders of all honesty types often choose imprecise messages instead of precise ones if they observe a low state. Removing the most misleading lies from the pool of precise messages improves the accuracy of the precise messages. Second, I estimate that players are somewhat less sophisticated in their reasoning in the rich language treatment. The reduction in the average levels of reasoning seems likely to be driven by the increased complexity of strategic calculations in the rich language treatment. In the calibrated model, this reduction in sophistication manifests largely through increased receiver trust in the messages.
Several groups of experimental papers are closely related to this paper. My experimental setup in the base treatment mirrors Cai and Wang [
5] and Wang, Spezio, and Camerer [
15]. They explained the overcommunication in their experiments using level-
k but did not allow preferences for truth-telling in their models or investigate the impact of vagueness.
4, those choices caused the computer to randomize between states in an interval. The receivers always received a point message and were not informed that it was randomly chosen.
A second pair of experimental papers investigated how senders use vague or evasive language in simpler two-state strategic information transmission settings [
25,
26]. These found that deception through evasive messages such as feigning ignorance is less psychologically costly than deception through direct lies.
A third set of papers investigated information unraveling in voluntary disclosure games, in which the subjects were only able to send truthful messages. Benndorf et al. [
27] elicited a distribution of level-
k types in a disclosure game, finding substantial numbers of
,
, and
players. Jin et al. [
28] and Deversi et al. [
29] both used state spaces and payoff functions very similar to those in my experiment. Jin et al. [
28] found that senders disclose favorable information but withhold less favorable information, and receivers are insufficiently skeptical when information is not disclosed. Deversi et al. [
29] examined what occurs when senders can choose imprecise disclosures. They found that vagueness is profitably exploited by senders to take advantage of naive receivers, and information transmission is higher in their precise-only treatment. Hence, interestingly, my result that vagueness improves communication is reversed for disclosure games (see also Li and Schipper [
30] and Hagenbach and Perez-Richet [
31]). Unusually, Li and Schipper [
30] found that the subjects exhibited relatively high levels of sophistication in a disclosure game with imprecise messages.
Many other papers investigate the role of vague language in other forms of cheap talk games, including asymmetric coordination games with private information [
32], leader-follower public goods games [
33], delegation games [
34], cheating games [
35], three-player common interest context-dependent communication games [
36], and real-world communication about intentions on a TV game show [
37]. Like this paper, these papers found that subjects, given the choice, prefer imprecise messages to outright lies, and followers are too trusting of these messages. In some, vagueness is beneficial either because it can mask incentives that, if known, would make an attractive equilibrium strategically unsustainable [
32,
33], because it makes information more credible [
34], or because it enables more efficient communication of context-dependent information [
36].
Relative to these sets of papers, my contribution is to show that vagueness can have positive effects on communication in strategic information transmission contexts and offer an explanation for why it has positive effects.
5Section 2 describes my experiment, and
Section 3 provides descriptions and reduced-form analyses of subject behavior, focused on motivating my model.
Section 4 presents my model and its predictions, after which
Section 5 details my structural estimates. Finally,
Section 6 concludes the paper.
2. Experimental Design
My experimental design builds on those of Cai and Wang [
5] and Wang, Spezio, and Camerer [
15], which are discrete versions of the Crawford and Sobel [
1] cheap talk game. In each period, subjects were paired up, with one member of each pair being the sender and one being the receiver. A state of the world
was then randomly determined for each pair. Each state was equally likely. The sender then learned
s and chose
to send to the receiver. The message space
M—the set of possible messages—varied across treatments. Finally, the receiver learned
m and chose
.
The sender and receiver payoffs (in experimental units) were
The subjects were presented with payoff tables similar in format to
Table 1 below, although with neutral labels instead of “sender”, “receiver”, “action”, and “state”.
There were three treatments. In the base treatment, the sender could send only precise messages of the form “s is x” (i.e., the message space was ). In the rich language treatment, the sender could choose to send either precise messages or imprecise messages. Imprecise messages specified an interval of three numbers that s could be within, such as “s is 2, 3, or 4”, so the message space was .
Finally in a third treatment (the noise treatment), the sender observed
s imperfectly and could send precise messages or imprecise messages (
). Instead of observing
s, the sender observed
where
was equally likely to be any element of
and
s was equally likely to be any element of
. In practice, choices in the noise and rich treatments were indistinguishable, so I added the noise data to the rich data, setting
for noise observations.
6Three principles guided the construction of . First, having only a few additional messages made the choices easier for the subjects and simpler to analyze subsequently. Second, contiguous messages with intermediate precision of meaning suggest a natural interpretation of low, medium, and high. Third, the precise messages were uniformly distributed over the state space, and I chose to maintain that property for the imprecise messages.
Instructions for each treatment were handed out and read aloud at the start of that treatment. (
Appendix B contains the experimental instructions.) The experiment was conducted using z-Tree software [
42] at Clemson University in the fall of 2011. There were 42 subjects, 18 (42%) of whom were female. 24 (57%) subjects were first- or second-year college students, while 18 (43%) were third-year, fourth-year, or graduate students. The subjects were mostly College of Business and Behavioral Sciences undergraduates: 32 (76%) had majors in the business school, 4 (10%) had humanities majors, and 6 (14%) had science or engineering majors.
The subjects alternated roles and were randomly rematched each period in order to avoid repeated game effects. All subjects participated in all treatments, and the order of the treatments was randomized for each session.
7 In total, there were 268 rounds of the base treatment, 204 rounds of the vague treatment, and 220 rounds of the noise treatment (there were 4–6 rounds for each treatment). Note that a round yields one message choice observation and one action choice observation. Each experimental unit was worth USD 0.01. The average earnings were around USD 24, which included a USD 6 payment for showing up.
3. Results
Table 2 shows the state from which each message was sent, on average, along with the frequency of each message. Over half of messages in the base treatment were
, which led to that message not being especially informative, with
. Generally, the lower the message, the less likely it was to be chosen, and the stronger the signal it provided that
s was low. In the base treatment,
and
conveyed different information than the other messages: the distribution of
s, conditioned on
, was significantly differerent at the 10% level from that for
(two-tailed Mann–Whitney U test
), and the distribution for
was significantly different from
at the 1% level (MW
).
The rich treatment produces three related effects. First, higher messages become more accurate. For messages above , a precise message is a stronger signal that s is higher in the rich treatment than in the base treatment, while is 57% closer to its literal meaning (rich language versus base , MW ), and is 17% closer (rich language versus base , MW ). is also 43% closer to an expected than is the base treament (rich language versus base , MW ).
Second, almost half of the messages (45%) sent become imprecise, and imprecise messages are twice as likely as precise
. Imprecise messages are less likely to be sent from
but otherwise are employed about half the time in every state.
8 Such a high fraction of imprecise messages is inconsistent with many explanations of my subjects’ behavior. For example, the analysis in
Section 4 found that most variants of the level-
k models without honesty could predict that, at most, 20% of the messages would be imprecise, and those would predominantly be sent from
and
.
Third, the messages overall become less exaggerated. While 51% of the base treatment messages were , only 34% of the rich treatment messages were the highest possible. The difference was statistically significant (Fisher’s exact test ). The fraction of messages with an expected value of 4 (i.e., or ) doubled from 18% to 36% in the rich treatment (Fisher’s ). None of the other message frequencies were significantly different between the treatments when comparing all messages of the same expected value, except for , which went from 6% to 2% of the messages (Fisher’s ).
The receivers correctly treated the messages as informative, although many systematically misinterpreted them.
Table 3 shows both the average and optimal action choice for each message. The optimal action choice is the highest-payoff action choice given the true distribution of messages. On average, the chosen
a values were too high for both treatments but showed the “correct” comparative static of lower actions when receiving a lower message.
When comparing the responses in the rich treatment to the base treatment, the typical actions did not change much. With the exception of the responses to
, for which
increased from 3.47 to 3.79 (MW
), the hypothesis that the receivers’ responses to precise messages were the same across treatments could not be rejected. In addition, the responses to
were systematically higher than the responses to the precise treatment
(MW
). These patterns were consistent with the level-
k behavior, as
Section 4 explains.
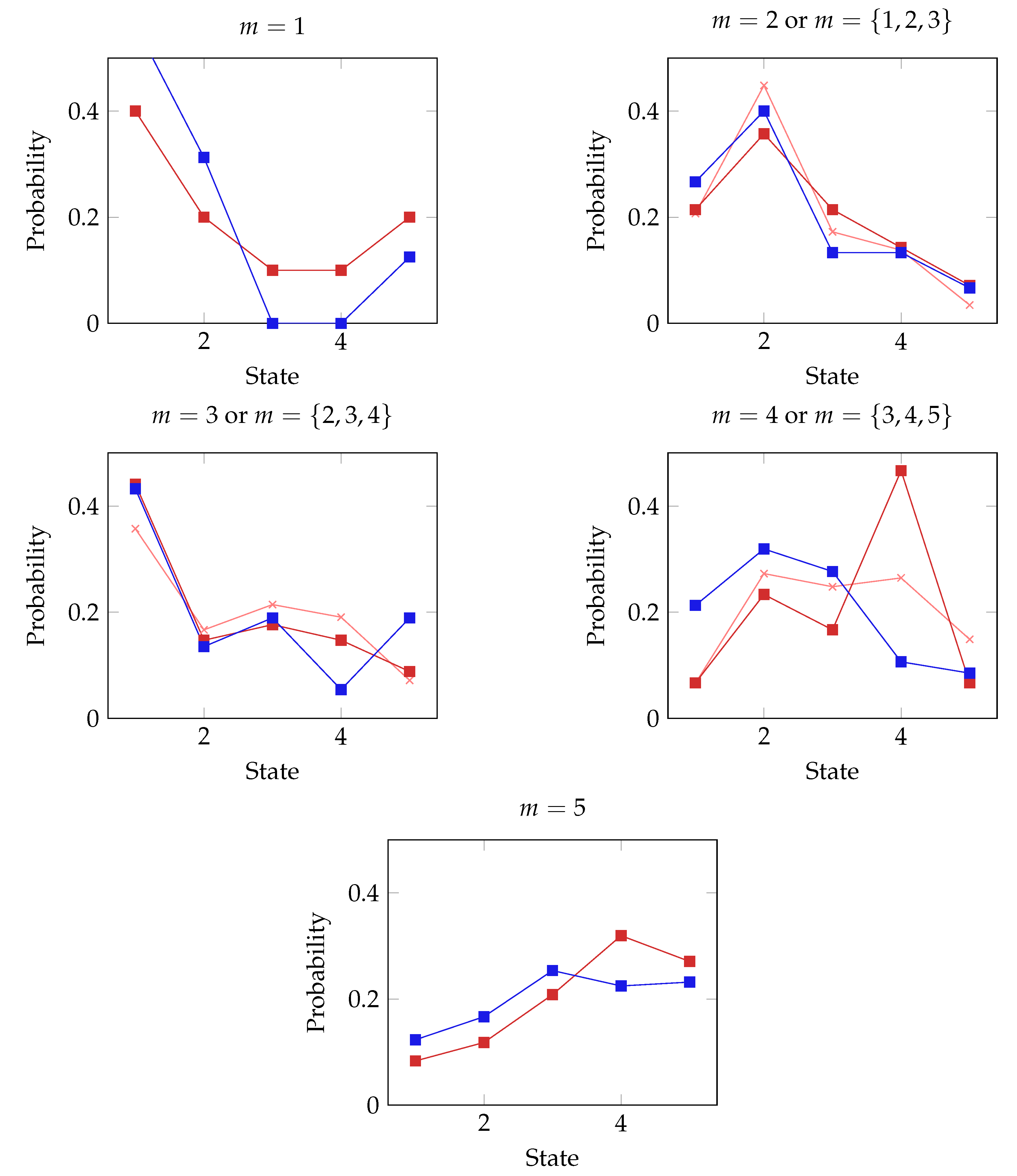
Figure 1 shows the full distribution of relative frequencies
for each message in the precise and rich treatments. For
and
, the most likely state from which the message was sent was the corresponding state
or
, while for
, with the exception of precise
in the rich treatment, the true state was
never the most likely. Consistent with the initial level-
k reasoning that sends
, messages
or
were most likely to have been sent from
in both treatments. In the base treatment, exaggerating by two units is common with
and
as well, but in the rich treatment, two-unit exaggerations were less typical.
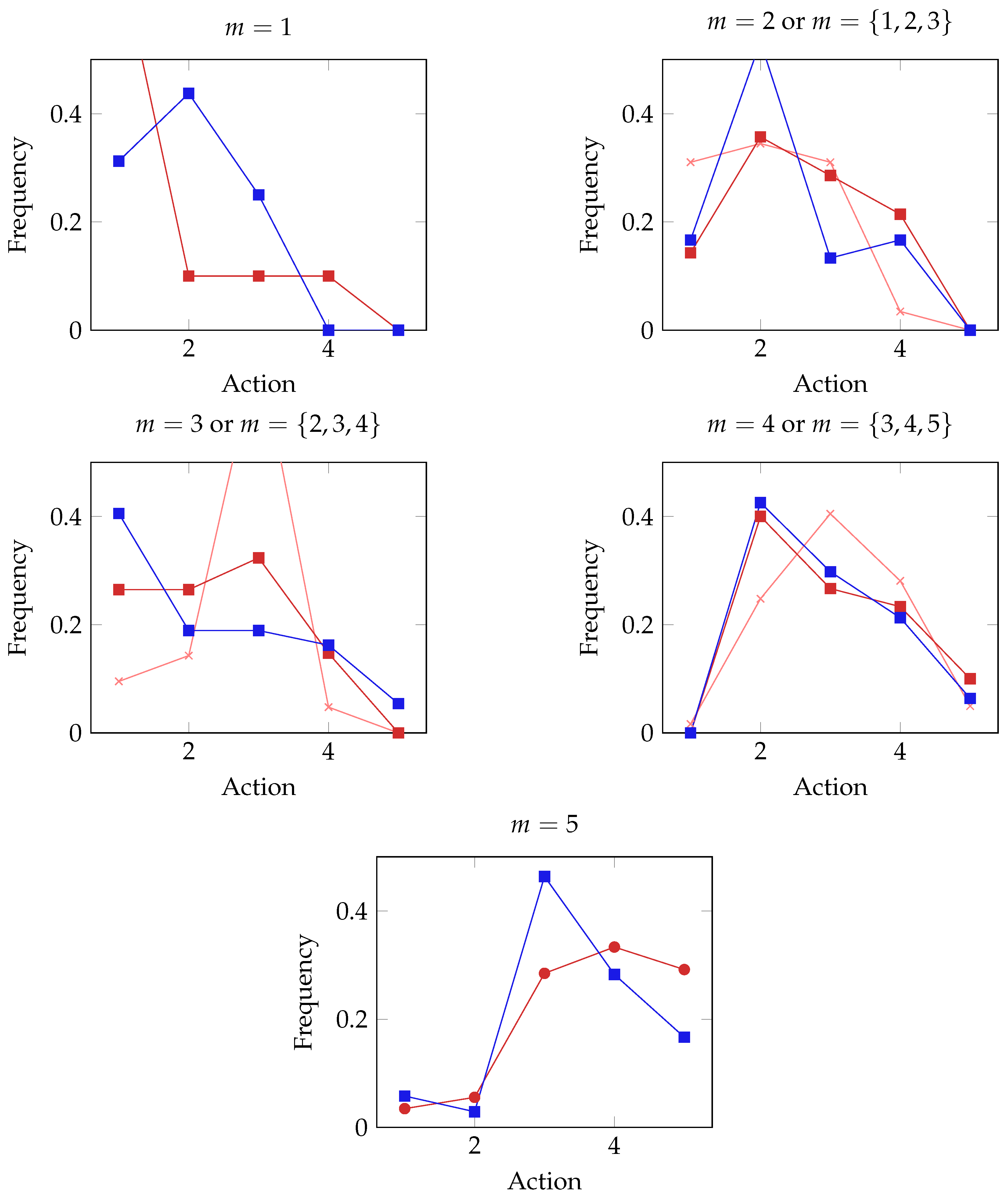
Next,
Figure 2 shows the frequency of each action for every message sent (
) in the base and rich treatments. Consistent with the level-
k predictions, there was widespread discounting of messages
by two units, such as choosing
in response to
. The discounting was less pronounced for
, imprecise messages, and
in the rich language treatment.
Figure 1 and
Figure 2 also show that the
m and
a choices were quite noisy in both treatments, with the exception of
in the base treatment,
for any
s, and generally
for all
s. This noisiness means that usually, the receivers would maximize utility by adjusting their action choices inward toward
(as in
Table 3).
While the number of subjects was too low to perform a detailed analysis of how different demographic characteristics affected communication choices, I did find a few differences in how the subjects behaved based on gender or college class year. The female subjects were less trusting of messages in the precise treatment than the male subjects, with a mean distance between the message they received and the action chosen of 1.39 versus 1.18 for the male subjects (MW ). Gender differences were not statistically significant at the 10% level in the vague treatment or for the messages sent. I also found that the first- and second-year college students sent much more accurate messages in the rich language treatment than the third-year, fourth-year, and graduate students. The average distance between the state and the message sent was 1.08 compared with 1.39 (MW ). Again, however, there were no other statistically significant differences in behavior either in the precise treatment or with the action choices.
Finally, there was no evidence that the players’ strategies changed during the sessions on aggregate. In particular, the fraction of imprecise messages was roughly constant in the early and late rounds, as was the share of truthful messages and the degree of discounting by receivers, ruling out sizeable learning effects.
4. Model
This section derives predictions about the subjects’ behavior using a cognitive hierarchy model, to which I add preferences for honesty. Cognitive hierarchy and level-
k models are structural nonequilibrium models of how players reason strategically. There is a hierarchy of discrete cognitive types, each with gradually more sophisticated beliefs about other players’ behavior. Because higher types use more iterations of best-response reasoning, senders of higher types exaggerate more and more due to their upward bias, while receivers of higher types discount the messages more and more. My model extends the applications of level-
k from Crawford [
21] and Cai and Wang [
5] to cheap talk by allowing heterogenous preferences for truth-telling on the part of the senders. A secondary difference is that I assume that
players best respond to a combination of behaviors of types lower than
k.
9The model has two purposes. First, it illustrates the broad differences in behavior one should expect between my treatments if the subjects are boundedly rational and some are honest. Second, the next section estimates the model structurally, taking into account that it is not likely that any subject perfectly complies with the predicted behavior of any type.
4.1. Definitions and Assumptions
Formally, players differ in their cognitive type, honesty level, and sender or receiver role. A player’s cognitive type determines his or her beliefs about how players in the other role behave. A level-k sender () has beliefs about the conditional probabilities induced by receiver behavior, and a level-k receiver () has beliefs about the conditional probabilities that he or she faces.
A player’s honesty type affects his or her relative utilities from sending dishonest or honest messages. All messages that are non-false according to their literal meaning are honest (i.e.,
m is honest if either
or
) and are dishonest otherwise. I discuss this assumption further in
Section 4.3. An honesty type
h acts as if sending a literally true message is worth giving up
h cents:
A receiver’s utility function is not affected by his or her honesty type. I assume that there is a finite set of honesty types, with every . The vector denotes the distribution of honest types, and I write to indicate the fraction of players with honesty type h. H and are common knowledge.
Level 0 cognitive types are non-strategic and primarily serve as conjectures about behavior by
players.
messages are truthful, and
messages are credulous.
10 Strategic
behavior is then defined inductively as responding optimally to beliefs about the other role’s behavior based on
behavior.
11 A level-
sender chooses for each state a (possibly) mixed strategy over messages
as a best response to that type’s beliefs
about receiver behavior. Likewise, a level-
receiver chooses
, which is a best response to his or her beliefs
about the sender’s behavior.
Definition 1. A type player sends every available honest message with equal probability. A type player chooses action if m is precise and if .
In the Poisson cognitive hierarchy model of Camerer, Ho, and Chong [
18], the frequency of level-
k behavior
follows the Poisson distribution, and the level-
k beliefs about the frequencies of type
players
are formed by normalizing
to sum up to one:
By definition, is the mean cognitive level in the population as well as the variance of the cognitive levels in the population.
Definition 2. For , a type player with honesty h has beliefs and chooses that followand a type player has beliefs and chooses that followwhere is calculated via Bayes’ rule. To operationalize Equation (
2), I assume that for cases in which the senders are indifferent between multiple
m, they randomize uniformly over their best messages.
It is helpful to think of honesty as falling into three levels: “weak” (
), “moderate” (
), and “strong” (
). These categories are based on the opportunity cost of being honest in different situations (i.e, the loss in pecuniary payoff for sending an
or
message versus the best non-honest message). In the base treatment,
and
believe that they can achieve
with
or remain honest and achieve
at a loss of
.
12 On the other hand, in the rich treatment, low-level senders perceive the opportunity cost of honesty to be either 25 or 32 for sending an imprecise message which is a truthful exaggeration. For instance, for
, when
,
has an opportunity cost of
.
In presenting the model’s predictions but
not estimating the model, I restrict attention to a set of parameters that encompasses most reasonable distributions of the types and for which the strategies of each type of player are largely constant. The restriction also limits the number of special cases that need to be described. Let the constant
.
c is proportional to the difference in payoff cost to the sender or receiver having an action choice 2 away from the player’s bliss point instead of 1 (i.e., a loss of
instead of a loss of 25). Let
be the share of players with honesty
.
13Definition 3. A standard type distribution
of players has frequencies of cognitive and honesty types that are distributed with This range is consistent with the estimates from other papers and with my preferred estimates. The restriction on asserts that roughly between 15% and 50% of my subjects are at least moderately honest which, again, is consistent with my estimates.
4.2. Predictions
Particular patterns of behavior for a role are usually common to pairs of cognitive types. best responds to , implying . That in turn implies and both effectively use one round of best responses, since both types believe all receivers are credulous. If is high enough that the players believe the players are uncommon, the and receivers act similarly as well. ’s best respond to a fraction of truthful messages and a fraction of single-level exaggerated messages, which are quite close to ’s beliefs for reasonable choices. Likewise, the and senders typically engage in two rounds of non-trival best-response reasoning, and so on.
Propositions 1–4, summarized in
Table 4,
Table 5 and
Table 6, characterize the behavior of senders and receivers drawn from a standard type distribution in my experiment. See
Appendix A for proofs.
Proposition 1. If the players have a standard type distribution, and no players are strongly honest, then the following is true for weakly honest senders and all receivers in the base treatment:
- (i)
and exaggerate one level if possible ();
- (ii)
and discount and by two units (), by one unit (), and or by zero units ();
- (iii)
and higher-level senders send the highest message except possibly when or (in which case and ); and
- (iv)
and higher-level receivers discount one unit (), by zero or one unit ( or ), and all other by two units (.
Moderately honest senders make identical choices to weakly honest senders, except that and choose .
Table 4 summarizes the types’ predicted behaviors in the base treatment. Proposition 1 predicts that
messages should be relatively rare, relatively truthful, and the receivers should trust them more. The truthfulness of the low messages does not stem from honesty. For
, many messages are exaggerations by two units, and the receivers discount them, often by two units. Finally, most of the messages are
.
In the base treatment, for players with , and would send . Then, if was low, and higher would discount it by the same amount as in Proposition 1 or by a smaller amount if was higher. That discounting makes honesty more costly to and higher, so unless there is a significant share of players with h significantly higher than 57, the behavior for the higher types becomes similar to that in Proposition 1. Thus, strong honesty would cause a sizeable share of honest messages and trusting action choices for as well as for for .
In the rich treatment, randomize between truthful precise and truthful imprecise messages. This leads to and with choosing imprecise messages , which exaggerate the state in a truthful way. In addition, weakly honest and send imprecise m deceptively () half the time in states and .
Both honest and non-honest level- senders employ imprecise messages, but exactly how they do so on depends whether they believe imprecise messages will be treated skeptically or credulously. Weakly honest level- senders often choose to masquerade as honest or naive types by sending imprecise messages but only when the state is low (). For example, for these senders, the message is an attractive deception in because they believe there is a good chance that , regardless of exactly how low-level senders use imprecise m.
Whether there is truthful exaggeration by moderately honest level- senders depends on what they believe receivers believe. If relatively few of the low-level imprecise messages are deceptive—which occurs either if is low enough or is high enough—then the and receivers are fairly trusting of imprecise messages and choose when they usually choose . Because of these a choices, moderately honest level- senders also send imprecise messages in states . In contrast, if a critical mass of non-deceptive messages is not available, low-level receivers are less trusting of imprecise messages, and these senders make use of imprecise messages in the same way as weakly honest senders because honesty is too costly.
Therefore, if imprecise messages are sent frequently from and , and and are trusted more than the corresponding precise messages, it cannot be the case that is high and is low. In order to generate the pattern of imprecise messages observed in the data, there must be higher-honesty senders sending imprecise messages from and as well.
Table 5 and
Table 6 organize the predictions of the following propositions describing behavior in the rich treatment.
Proposition 2. If players have a standard type distribution, then weakly honest players in the rich treatment choose identical strategies to those in Proposition 1 above, except for the following:
- (i)
and in states and send with probability ;
- (ii)
or higher-level senders in state send or ;
- (iii)
and senders in state may send .
Weakly honest senders do send imprecise messages but only in low states (). In contrast, senders who care more about honesty tend to send imprecise messages in every state except .
Proposition 3. If players have a standard type distribution, then moderately or strongly honest senders () in the rich treatment behave as in Proposition 2 above, except for the following:
- (i)
and truthfully exaggerate in and send and with equal probability;
- (ii)
truthfully exaggerate in , except possibly in ;
- (iii)
and truthfully exaggerate in and may also truthfully exaggerate in , , and .
While the senders change their behavior in the rich message treatment, the receivers’ predicted responses to precise messages do not change. However, receivers generally trust imprecise messages more than precise ones (e.g., sophisticated receivers choose , while they would choose ).
Proposition 4. If players have a standard type distribution, then in the rich treatment, receivers behave as in Proposition 1 above, except for the following:
- (i)
and do not discount imprecise messages ();
- (ii)
and higher discount imprecise messages by one unit (), except possibly discounting by two units ();
- (iii)
and higher do not discount precise ().
4.3. Model Discussion
Propositions 1–4 provide an explanation for why there is more communication in the rich treatment. Under a standard type distribution and, indeed, under most other type distributions, many player types who would send from in the base treatment instead send a different message in the rich treatment but continue to send from at the same rate. These messages therefore become more accurate in the rich treatment. Furthermore, the imprecise messages sent with are more accurate than the corresponding messages that would have been sent with . For instance, and higher send some from and , whereas and are usually sent from and with . The receivers do not change their responses much, but because they discount the common and the least, on average, they are more trusting of the messages they receive.
The model’s predictions match several patterns in the data. First, the model predicts that the sender’s behavior will be relatively more responsive than the receiver’s behavior to the rich message treatment. Precise messages and are predicted to become more accurate, since they are less likely to be sent from (Propositions 2 and 3). For many parameter values, the messages sent from are also predicted to often be imprecise. The receivers, on the other hand, are predicted to not change how they treat precise messages across the treatments (Proposition 4 (iii)) and to be somewhat more trusting of imprecise messages and than corresponding precise messages (Proposition 4 (i) and (ii)). Note that all of the comparative statics implicitly hold constant. However, is more complex, so might fall as well.
The form of honesty preferences in the model generates (1) receivers treating systematically differently than and (2) half of messages sent in the rich treatment being imprecise messages. Many alternative forms of honesty preference do not predict either. For instance, theories in which the senders care about the payoff disappointment experienced by the receiver, because and interpret and in the same way, would predict no systematic difference in how the senders used those messages. Likewise, there would be no systematic differences if the senders cared only about the de facto level of deception (i.e., , where E is the receivers’ expectation) instead of caring about deviating from the literal meaning of a message.
A major difference between the predicted and observed behavior is that the model predicts more skepticism about precise
than is observed.
senders and higher are predicted to play
. In part for this reason, I introduce noisy choice when estimating the model parameters.
14 5. Structural Estimates
In this section, I estimate the parameters of my model. Many papers have structurally estimated level-
k models before (e.g., Crawford and Iriberri [
43]), but to my knowledge, none have jointly estimated varying cognition levels and varying preferences. One goal for these estimates is to conduct a “horse race” between honesty and bounded rationality, but by using these estimates, I can also answer additional questions, such as how the different message spaces affect communication per se.
I assume that the subjects choose
a or
m, influenced by logistic errors of precision
and independent across rounds and treatments. These errors capture that level-
k reasoning is subject to error and unobserved utility shocks may occur, as well as any other sources of error. Hence, a level-
k sender or receiver chooses each
m or
a with a probability
where
is a level-
k sender’s beliefs,
is a level-
k receiver’s beliefs,
T is the treatment, and
h is a sender’s honesty type.
measures the noisiness of player choices. As
, each choice becomes equally likely, while as
, players best respond exactly according to their beliefs. For all
, the
players exactly follow the strategies specified in Definition 1.
For my preferred estimates, I restrict the honest types to either have (the “not honest” type) or (the “moderately honest” type), because it is hard to precisely identify the frequencies of more than two honesty types. I motivate this choice and discuss exactly what conclusions can be drawn about the distribution of honesty after presenting my base estimates.
Given a treatment
T, in which subject
i made
action choices
and
message
, the probability of
i’s observed choices for a given parameterization is
For a set of subjects
N, the log likehihood of their observed behavior in a set of treatments
is
I estimate the parameters by maximizing
and then derive confidence intervals through non-parametric bootstrapping.
15Column 1 of
Table 7 reports the parameter estimates for my entire dataset. The estimated mean steps of reasoning
was higher than that typical in the literature. However, given the definitions of
behavior for each role, the effective amounts of sophistication were similar. These estimates imply that 32% of the senders engaged in one iteration of strategic reasoning and 40% of the senders engaged in two iterations, while 16% of the receivers did not reason strategically (they were credulous). Additionally, 42% of the receivers engaged in one iteration of strategic reasoning, and 42% engaged in two or more iterations.
16 Cai and Wang [
5] and Wang et al. [
15] found comparable results. About 27% of the subjects had
or were believed to have
. Finally, the choices were noisy. For example, the estimated precision
implies that moderately honest types sent 10–20 percentage points fewer imprecise messages than they would without noise and that the weakly honest types sent 20 percentage points more imprecise messages than they would without noise.
The next columns report my model, estimated separately using the data from the rich treatment only (column 2) and the base treatment only (column 3). Reasoning was almost one level less sophisticated in the rich treatment than the base treatment, probably reflecting the greater difficulty of mental calculations involving . The choices were approximately as noisy. Not surprisingly, the confidence interval for in the base treatment was wide— could not easily be identified using choices over —but the estimates in model 3 were similar to those in the combined model (model 1).
The final two columns in
Table 7 report the model estimates using only the sender choice data (column 4) or receiver choice data (column 5). That the
estimates were even lower in model 5 than model 4 support the somewhat strange implication of my cognitive hierarchy model that receivers are less strategically sophisticated than senders (i.e., only
senders are naive, but
and
both act naively). If this assumption were inaccurate, one would expect the
estimate in model 5 to be higher than the estimate in model 4. It seems likely that the strategic reasoning that receivers must perform is more difficult than the strategic reasoning that senders must perform.
17The model pair of 2 and 3 and the pair of models 4 and 5 can be thought of as alternate models that relax one of the assumptions of my level-
k model. The combination of models 2 and 3 allows
and
to vary by treatment instead of forcing strategic sophistication to be constant. This treatment-varying specification (models 2 and 3) nests model 1 as a special case, and a likelihood ratio test comparing the null hypothesis (model 1) to the alternate (models 2 and 3) rejects the null at the 0.05 significance level (
,
). This is evidence of the systematic differences in the level and noisiness of reasoning between the two treatments.
18 A similar likelihood ratio test comparing the null hypothesis (model 1) to the alternate model with role-varying behavior (models 4 and 5) failed to reject the null hypothesis (
). Comparisons using the Bayesian Information Criterion, which assigns more importance to model parsimony, support the role- and treatment-invariant model (model 1) (
) over either the treatment-varying or role-varying model (
and
, respectively, for the combined models).
5.1. Honesty
The distribution of honesty was identified in two ways. First, the strength of the players’ preferences for honesty was identified through the qualitatively different behavior of weakly, moderately, and strongly honest senders. For instance, senders with moderate honesty should reliably and truthfully exaggerate in the rich treatment but not reliably send truthful messages in the precise treatment. Second, the fraction of players of a given honesty type (i.e.,
for a given
h) was identified through the magnitudes of honest behavior and through their indirect effect on how receivers and non-honest senders behave.
Section 4 described some of the identifying differences in greater detail. For instance, if
is low and
is high, the receivers should be relatively skeptical of imprecise
m, and the senders should send relatively few imprecise
m from states
and
.
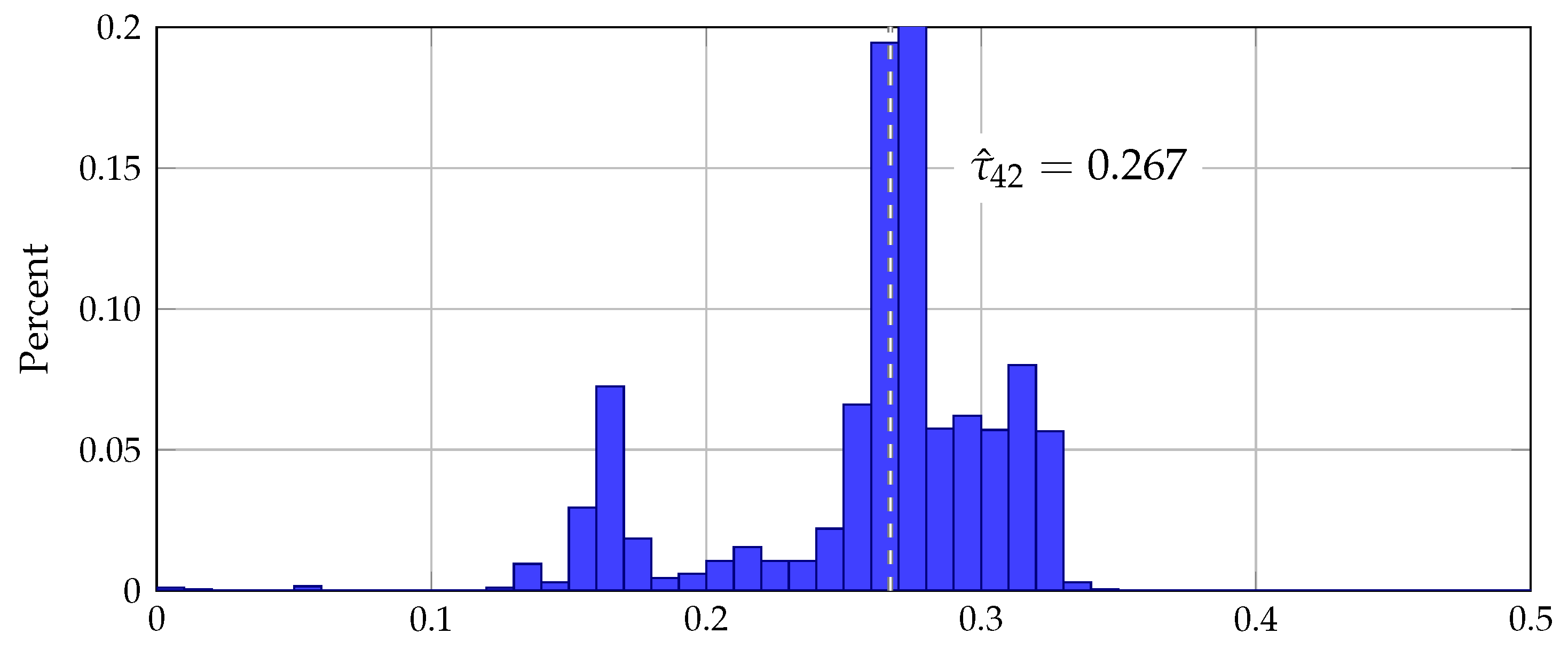
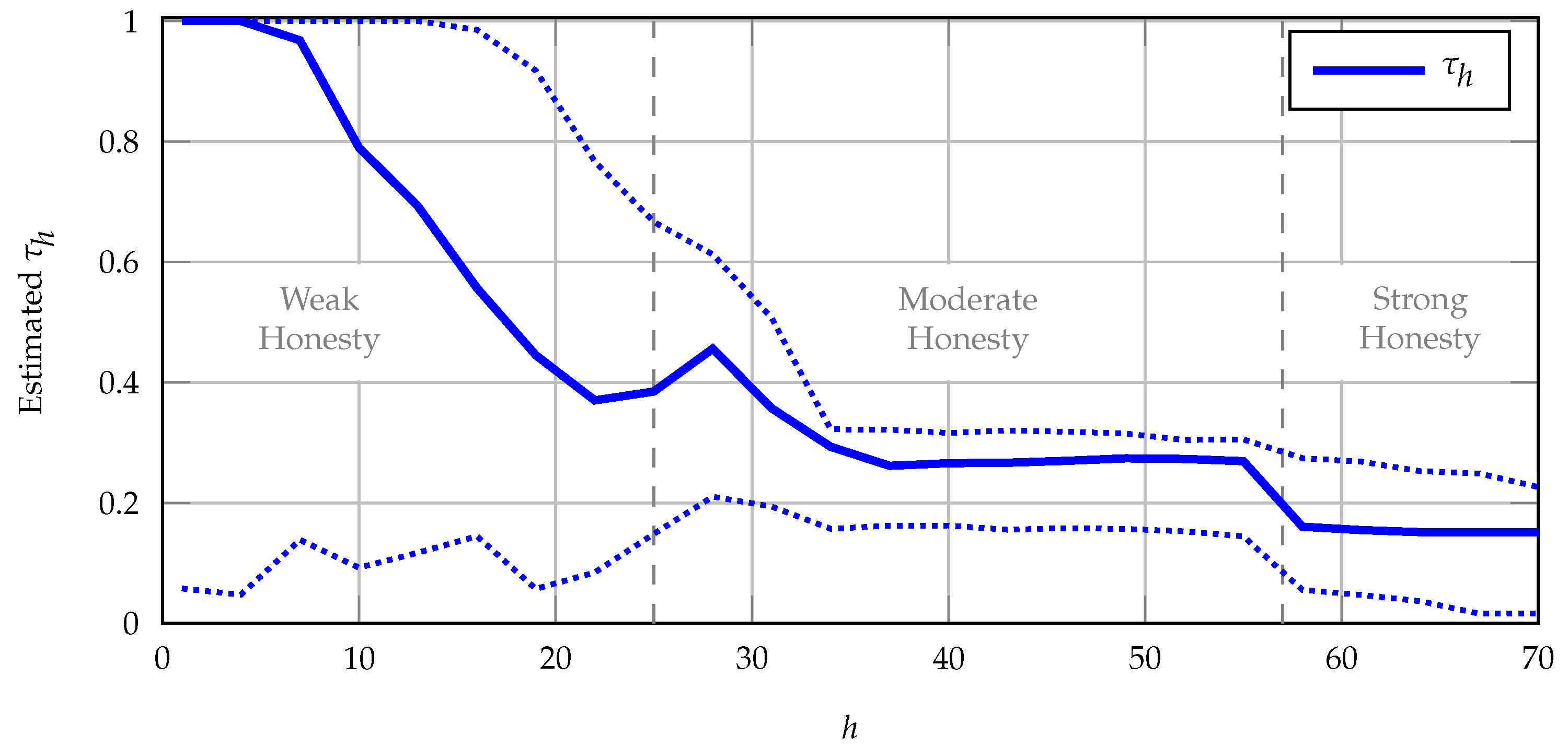
Figure 3 shows the distribution of
from the bootstrap for my preferred model. Most estimates are between
and
, although there is an almost invisible left tail for the lower estimates.
Unfortunately, the log-likelihood function was relatively flat with respect to the strength of honesty preferences within each of the
h intervals of not honest, moderately honest, and strongly honest.
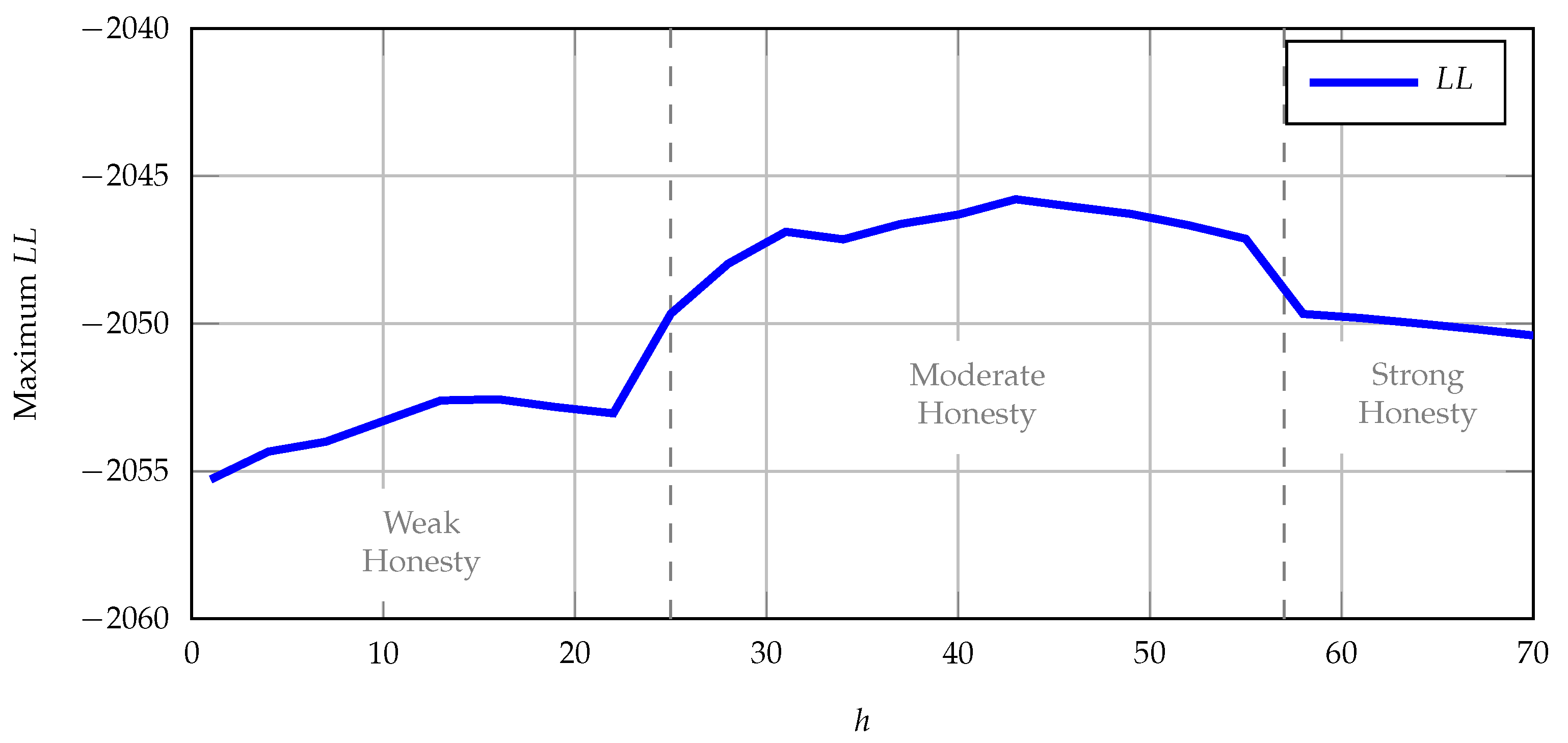
Figure 4 shows the maximum log-likelihoods from two-honesty-type models, where one type does not care about honesty and the other type is
h. Intuitively, for low honesty,
was estimated entirely from how it interacted with utility shocks in the message and action choice (Equations (
5) and (6)), while within each of the other
h intervals, the variation in behavior was small, so pinning down
h precisely was difficult. The
may have also been flat with respect to
h, because honesty has limited importance in my context. These problems also made it infeasible to estimate the frequencies of the honesty types in a richer model that contained two honest types
. Because the behavior is similar for any moderately or strongly honest type, the parameters
and
are colinear and cannot be estimated precisely.
Due to these difficulties, my approach is to assume that people are either fully self-interested or have a single degree of honesty
h. For each
h value,
Figure 5 shows the fraction of players estimated to be honest at this level and the 95% BCa confidence intervals. For any moderate honesty level, at least around 15% of players can be classified as honest with 95% confidence. I focus on
because the log-likelihood achieves its maximum at that value (see
Figure 4).
Despite the underlying identification problems, there is evidence that a substantial minority of subjects had at least moderate preferences for truth-telling and believed that other subjects did as well. While I am could not estimate the exact distribution of honesty in my subjects, I am able to show both that it was not extremely weak (all subjects having ) and that only a minority of the subjects had moderate or strong honesty preferences.
5.2. Why Vague Language Matters
Counterfactual comparisons using the structural model can also answer the question of why vague language improves communication. Communication might increase in the rich treatment either because it affects subjects’ decision processes in terms of reducing their sophistication or increasing choice noisiness, because the change in the message space opens up additional ways to communicate, which improves communication overall, or because honesty increases sender accuracy or receiver trust more under the more complex message space. To gauge these explanations’ relative importance, I hold some factors as fixed and evaluate how the predicted communication change as a single factor changed. For example, if strategic sophistication is fixed at the base treatment levels, and all players are assumed to be weakly honest, the predicted improvement in communication from adding imprecise messages to the message space is a measure of how important the change in the message space is according to my model.
To measure communication, I calculate the predicted mean distance between messages and states
to measure how informative the messages are and the predicted mean distance between actions and messages
to measure how trusting the action choices are.
19 Given a set of a parameters
,
, and
and a message space
M, the mean distance between the messages and actions is the distance between each
combination weighted by the predicted probability of observing that combination:
where
is the predicted probability that message
m is sent (obtained from Equation (
5)) and
is the predicted conditional probability (obtained from Equation (6)).
is defined similarly but with weights
instead of
.
Table 8 reports these measures for every combination of behavioral parameters and each message space. The rich language parameters are model 2’s: the MLE parameter estimated using only rich language treatment data. Rich honesty sets
, while rich rationality sets
and
. The base treatment parameters are those of model 3. Base honesty sets
, while base rationality sets
and
.
The first two rows compare the average distances in the base treatment data to the predicted average distances from calibrating the model with the parameter estimates from MLE using the base treatment data. The mean distance in the data was 1.52 in comparison with the predicted of 1.46, while for the receiver mean in the data, it was 1.30 in comparison with the predicted distance of 1.28. The calibrated model closely matches senders’ average exaggeration and receivers’ average skepticism.
The last two rows provide the same comparison for the rich language treatment. For the senders, the mean distance in the data was 1.22, while the model predicts a mean distance of 1.16. For the receivers, the mean distance was 0.98, while the model predicts a mean distance of 1.05.
The intermediate rows use alternative model calibrations to show which factors are important in the model for explaining the observed increases in communication. The three rows after the base treatment model each switch one factor from its value in the base treatment model to its value in the rich language treatment model. The next three rows then switch two factors from their values in the base treatment model to their values in the rich language treatment model. Factors that cause larger reductions in sender bias or receiver skepticism are more important in the model for explaining the increase in communication. To the extent that the model accurately captures aggregate behavior, these factors are likewise more important for explaining what caused the changes in subject behavior across the treatments.
For senders, the most important factor appeared to be the message space. Switching to a rich message space in the model but holding the behavioral parameters fixed at the base model values causes the mean to fall to 1.30 from 1.46, a larger effect than for switching any other single factor. Similarly, when two factors were switched, the cases that come closest to matching the predicted mean of 1.16 in the rich language treatment are the cases in which the message space and one behavioral parameter are switched to their values in the rich language model.
In my model and in my reduced form results, a rich message space improves sender accuracy because many senders shift from and to imprecise messages, making the high-m precise messages more accurate. This shift to imprecise messages, while most pronounced in the model for honest senders, occurred with all senders in low states.
For receivers, the most important factor appears to be the bounded rationality parameters of the mean steps of thinking and choice precision . Switching to the rich language model and parameter values but holding the message space and share of moderately honest players fixed at the base model values causes the predicted to fall to 1.08 from 1.28, a larger effect than for switching any other single factor. When two factors are switched, the cases that comes closest to matching the predicted of 1.05 in the rich language treatment are the cases in which the rationality parameters and one other parameter are switched to their values in the rich language model.
The increased cognitive complexity of strategic thinking in the rich message treatment made subjects worse at strategic reasoning, which manifests in the model estimates as a reduction in . Reducing makes the receivers more trusting, because the lower-level receivers engage in fewer rounds of iterated reasoning, which tends to mechanically increase receiver skepticism.
Interestingly, for the receivers, the model predicts that switching to the rich message space would cause a slight increase in the average receiver skepticism if honesty were not present. Switching to a rich message space in the model but holding the behavioral parameters fixed at the base model values causes the predicted to rise from 1.28 to 1.33, and likewise, switching to a rich message space in the model with the rich language model’s and and base model’s causes the predicted to rise from 1.08 to 1.14.
In summary, three factors explain the increase in communication produced by the rich treatment. The richer message space made the senders more accurate, while the increased difficulty of reasoning for made the receivers more trusting. The presence of honesty also reduced receiver skepticism when they were interpreting the messages.