Optimal Accuracy of Unbiased Tullock Contests with Two Heterogeneous Players
Abstract
:1. Introduction
2. Set-Up and Notation
- there is a unique Nash equilibrium, which is in pure strategies, if ,
- there is a unique Nash equilibrium, which is in semi-mixed strategies, if ,
- any Nash equilibrium is an all-pay auction equilibrium (i.e., it yields the same expected efforts, winning probabilities and expected payoffs as well as the same expected revenue for the contest designer as the unique equilibrium of the corresponding all-pay auction) in mixed strategies if ,
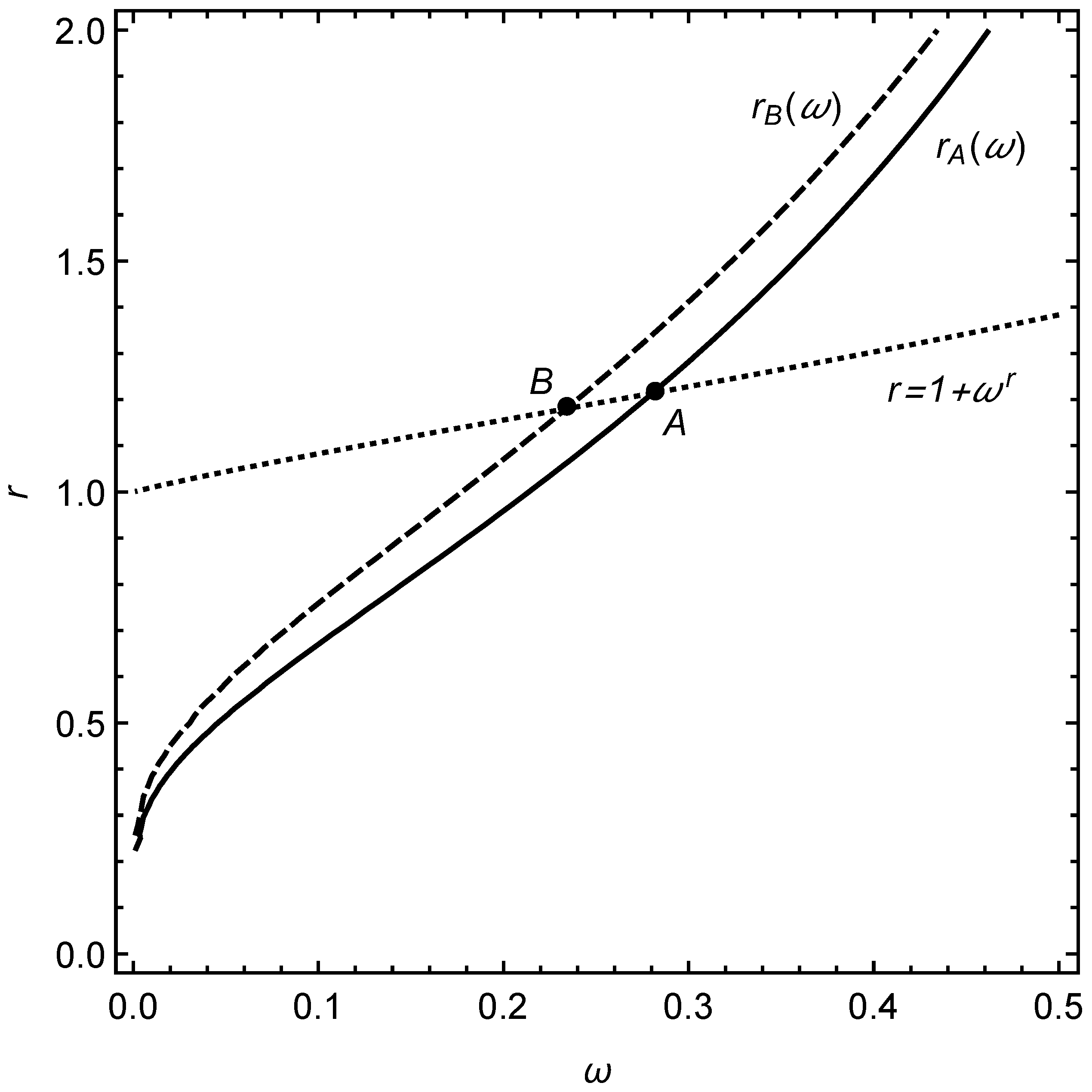
3. Maximization of Selection Quality
4. Effort Maximization
4.1. Maximization of Aggregate Effort
- (a)
- if ,
- (b)
- if .
4.2. Maximization of the Winner’s Expected Effort
- (a)
- if ,
- (b)
- if .
5. Conflicting Objectives
5.1. Tradeoff between Selection Quality and Minimum Effort
5.2. Tradeoff between Selection Quality and Maximum Effort
6. Conclusions
Funding
Conflicts of Interest
| 1 | In many countries (like France or Germany), the size of the jury depends on the importance of the case (amount in dispute, public interest, severeness) and increases from level to level of jurisdiction. Moreover, the legislator can adjust it according to the contemporary priorities: fore example, in 2012, France reduced the number of jurors from 9 to 6 for first instance proceedings and from 12 to 9 for appeal proceedings [1]. |
| 2 | Mastromarco and Runkel [2] provide an overview and suggest an alternative argument for the numerous rule changes in Formula One motor racing. |
| 3 | In October 2000, the International Table Tennis Federation replaced the older 38 mm (1.50 in) balls by 40 mm (1.57 in) balls to reduce the speed (and thus inherent noise) of the game [3]. |
| 4 | For example, the golden goal (sudden death)—a tie breaking rule by which the first team to score during extra-time was declared to be the winner—was introduced experimentally in 1993, used at the 1998 and 2002 FIFA World Cup tournaments, and abolished again in 2004 [4]. |
| 5 | Skaperdas [11] provides an axiomatic foundation for this type of contest success function. |
| 6 | |
| 7 | I used the software Mathematica to verify that for all . |
References
- Wikipedia: Jury. Available online: https://en.wikipedia.org/wiki/Jury (accessed on 18 March 2022).
- Mastromarco, C.; Runkel, M. Rule changes and competitive balance in Formula One motor racing. Appl. Econ. 2009, 41, 3003–3014. [Google Scholar] [CrossRef]
- Wikipedia: Table Tennis. Available online: https://en.wikipedia.org/wiki/Table_tennis (accessed on 18 March 2022).
- Wikipedia: Determining the Outcome of a Match (Association Football). Available online: https://en.wikipedia.org/wiki/Determining_the_Outcome_of_a_Match_(association_football) (accessed on 18 March 2022).
- Nti, K. Maximum efforts in contests with asymmetric valuations. Eur. J. Political Econ. 2004, 20, 1059–1066. [Google Scholar] [CrossRef]
- Alcalde, J.; Dahm, M. Rent seeking and rent dissipation: A neutrality result. J. Public Econ. 2010, 94, 1–7. [Google Scholar] [CrossRef]
- Wang, Z. The Optimal Accuracy Level in Asymmetric Contests. BE J. Theor. Econ. 2010, 10, 13. [Google Scholar] [CrossRef]
- Ewerhart, C. Revenue ranking of optimally biased contests: The case of two players. Econ. Lett. 2017, 157, 167–170. [Google Scholar] [CrossRef]
- Chowdhury, S.; Esteve-González, P.; Mukherjee, A. Heterogeneity, Leveling the Playing Field, and Affirmative Action in Contests; Munich Papers in Political Economy, Working Paper No. 6/2020; TUM: Munich, Germany, 2020. [Google Scholar] [CrossRef]
- Tullock, G. Efficient rent seeking. In Towards a Theory of the Rent-Seeking Society; Buchanan, J., Tollison, R., Tullock, G., Eds.; Texas A&M University Press: College Station, TX, USA, 1980; pp. 97–112. [Google Scholar]
- Skaperdas, S. Contest success functions. Econ. Theory 1996, 7, 283–290. [Google Scholar] [CrossRef]
- Epstein, G.; Mealem, Y.; Nitzan, S. Lotteries vs. all-pay auctions in fair and biased contests. Econ. Politics 2013, 25, 48–60. [Google Scholar] [CrossRef] [Green Version]
- Bruckner, D.; Sahm, M. Party Politics: A Contest Perspective; University of Bamberg: Bamberg, Germany, 2022; Unpublished Manuscript. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahm, M. Optimal Accuracy of Unbiased Tullock Contests with Two Heterogeneous Players. Games 2022, 13, 24. https://doi.org/10.3390/g13020024
Sahm M. Optimal Accuracy of Unbiased Tullock Contests with Two Heterogeneous Players. Games. 2022; 13(2):24. https://doi.org/10.3390/g13020024
Chicago/Turabian StyleSahm, Marco. 2022. "Optimal Accuracy of Unbiased Tullock Contests with Two Heterogeneous Players" Games 13, no. 2: 24. https://doi.org/10.3390/g13020024
APA StyleSahm, M. (2022). Optimal Accuracy of Unbiased Tullock Contests with Two Heterogeneous Players. Games, 13(2), 24. https://doi.org/10.3390/g13020024





