Abstract
In a two-period game, Player 1 produces zero-day exploits for immediate deployment or stockpiles for future deployment. In Period 2, Player 1 produces zero-day exploits for immediate deployment, supplemented by stockpiled zero-day exploits from Period 1. Player 2 defends in both periods. The article illuminates how players strike balances between how to exert efforts in the two periods, depending on asset valuations, asset growth, time discounting, and contest intensities, and when it is worthwhile for Player 1 to stockpile. Eighteen parameter values are altered to illustrate sensitivity. Player 1 stockpiles when its unit effort cost of developing zero-day capabilities is lower in Period 1 than in Period 2, in which case it may accept negative expected utility in Period 1 and when its zero-day appreciation factor of stockpiled zero-day exploits from Period 1 to Period 2 increases above one. When the contest intensity in Period 2 increases, the players compete more fiercely with each other in both periods, but the players only compete more fiercely in Period 1 if the contest intensity in Period 1 increases.
1. Introduction
1.1. Background
Zero-day attacks are becoming increasingly common. The most well-known attack, utilizing the Stuxnet worm to exploit four zero-day vulnerabilities, is probably the 2010 attack on the Natanz nuclear facility in Iran [1]. A so-called zero-day vulnerability means that a defender’s vulnerability in its computer system is known to the defender for zero days before it is discovered, most commonly through an attack. Zero-day attacks require resources and are challenging to produce. Once produced, the next challenge is whether to deploy them immediately or stockpile them for deployment at some suitable future point in time. Stockpiling can be useful for a player in providing security in the knowledge that threats posed by an opposing player can be ameliorated or eliminated. A more recent zero-day attack targeted Microsoft Windows in Eastern Europe in June 2019 [2]. The exploit abused a local privilege escalation vulnerability in Microsoft Windows pertaining to the NULL pointer dereference in the win32k.sys component (a NULL pointer dereference is an error causing a segmentation fault, which occurs when a program tries to read or write to memory with a NULL pointer). For other recent zero-day attacks, see PhishProtection [3].
1.2. Contribution
This article intends to capture the general aspects of this phenomenon, which are that a defender has an asset it seeks to defend, while the attacker seeks to attack the asset over two periods—by attacking and stockpiling in Period 1, and attacking and utilizing the stockpile in Period 2. A variety of reasons and justifications for stockpiling are illustrated. A two-player two-period game is analyzed. Player 1 is equipped with resources in Period 1, which can be utilized for producing zero-day exploits for immediate deployment in Period 1 or stockpiled for future deployment in Period 2. Player 2 defends against the attack in Period 1. Zero-day exploits may become more valuable if the stakes involved in their deployment increase, but this also entails the risk of becoming obsolete, e.g., if knowledge of their content leaks. We thus assume that Player 1′s stockpiled zero-day exploits may appreciate or depreciate in value from Period 1 to Period 2, i.e., the stockpiled zero-day exploits may become more or less valuable. Such changes in value may be due to technological, economic, or societal factors, market conditions, or the players’ preferences. In Period 2, Player 1 produces new zero-day exploits for immediate deployment in Period 2 and also deploys its stockpiled zero-day exploits. In Period 2, the defender defends against the attack, i.e., against both the zero-day exploits produced by Player 1 in Period 2 and the appreciated or depreciated zero-day exploits stockpiled from Period 1 to Period 2. The presence of Period 2 enables Player 1 to strike a balance between whether or not to stockpile in Period 1, and both players strike balances between how to exert efforts in both periods.
The research questions are how the attacking Player 1 allocates its resources between immediate zero-day attack in Period 1 and stockpiling for attack in Period 2, how the defender defends in both periods, and how the players’ strategic choices in both periods depend on the model characteristics, i.e., Player s available resources, the contest intensities in both periods, the zero-day appreciation factor from Period 1 to Period 2, and both players’ unit costs of effort, asset valuations, and time discount factors. Players in a cyberwar are always in a contest, regardless of the extent to which they understand the particulars of the contest, which justifies the use of the widely applied contest success function. The model in this article is applicable beyond zero-day vulnerabilities, assuming one attacking player and one defending player over two periods, where the attacking player can stockpile its capabilities from Period 1 to Period 2.
1.3. Literature
Aside from Hausken and Welburn [4] and, in part, Chen et al. [5], considered in Section 1.3.1, the literature has not directly considered the research questions in this article but has instead focused on various indirectly linked research questions, as shown in the subsequent subsections below. The literature on zero-day attacks is mostly concerned with detecting, mitigating, understanding, and simulating zero-day attacks. Most of the articles below have been identified by searching for the two words “zero-day” on the Web of Science database for the most recent years. Regarding zero-day vulnerabilities and their exploits, see Ablon and Bogart [6].
1.3.1. Game Theoretic Analyses
In earlier research, Hausken and Welburn [4] considered a one-period game theoretic model of zero-day cyber exploits, incorporating the benefit of stockpiling into the same period as when production and zero-day attack are determined. They found, for example, that decreasing Cobb Douglas output elasticity for a player’s stockpiling causes its attack to increase and its expected utility to eventually reach a maximum, while the opposing player’s expected utility reaches a minimum. Chen et al. [5] analyzed whether two countries should disclose or not disclose to the vendor the hardware/software vulnerabilities they discover in a repeated game. Disclosing may benefit the country if it gets exposed by the vulnerability. Not disclosing may benefit the country’s defense given that the other country does not discover the vulnerability and is exposed by it. They develop an algorithm and find that countries benefit from discovering vulnerabilities quickly and from incurring low costs of developing exploits.
1.3.2. Detection, Prioritization, Ranking, and Classification
Singh et al. [7] realized the challenge in defending against zero-day attacks. They proposed a framework for detection and prioritization based on likelihood by identifying the zero-day attack path and ranking the severity of the vulnerability. [8] developed a detection model for crypto-ransomware zero-day attacks. The model is based on an anomaly-based estimator, which suffers from high rates of false alarms, supplemented by behaviorally-based classifiers. Venkatraman and Alazab [9] reviewed existing visualization techniques for zero-day malware and designed a visualization using a similarity matrix method for classifying malware.
1.3.3. Detection and Identification by Applying Probability Theory and Statistics
Sun et al. [10] acknowledged the information asymmetry between attackers and defenders and applied Bayesian networks for identifying zero-day attack paths probabilistically; this is intended to be superior to targeting individual zero-day exploits. Parrend et al. [11] presented a framework for characterizing zero-day attacks and multistep attacks and relevant countermeasures. They applied rule-based and outlier-detection-based statistical solutions and machine learning, which detects behavioral anomalies and tracks event sequences. Singh et al. [12] proposed a hybrid layered architecture framework for real-time zero-day attack detection based on statistics, signatures, and behavior techniques.
1.3.4. Detection Applying Learning
Kim et al. [13] proposed a method to detect zero-day malware. The method generates fake malware and learns to distinguish it from real malware. A deep autoencoder extracts appropriate features and stabilizes the generative adversarial network training. Gupta and Rani [14] observed that zero-day malware grows exponentially in terms of volume, variety, and velocity. They proposed a big data framework with scalable architecture and machine learning for detection.
1.3.5. Mitigation, Robustness, Recovery, and Simulation
Sharma et al. [15] presented a consensus framework for mitigating zero-day attacks, incorporating context behavior, an alert message protocol, and critical data-sharing protocol for reliable communication. Haider et al. [16] applied data sets based on the Windows Operating System to evaluate the robustness of host-based intrusion detection systems to zero-day and stealth attacks. Tran et al. [17] implemented an epidemiological model to combat zero-day attacks. They proposed a dynamic recovery model to combat the simulated attack and minimize disruptions. Tidy et al. [18] simulate previous and hypothetical zero-day worm epidemiology scenarios, accounting for susceptible populous and stealth-like behavior on the dynamic, heterogeneous internet.
1.3.6. Filtering, Protocol Context, Honeypots, and Signatures
Chowdhury et al. [19] proposed a multilayer hybrid strategy for zero-day filtering of phishing emails by using training data collected during an earlier time span. Duessel et al. [20] incorporated protocol context into payload-based anomaly detection of zero-day attacks, integrating syntactic and sequential features of payloads, thus proceeding beyond analyzing plain byte sequences. Chamotra et al. [21] suggested baselining high-interaction honeypots, i.e., identifying and whitelisting legitimate system activities in the honeypot attack surface. Subsequently, captured zero-day attacks are mapped to the vulnerabilities exposed by the honeypot. Afek et al. [22] presented a tool for extracting zero-day signatures for high-volume attacks, intended to detect and stop unknown attacks.
1.3.7. Cyber Security
More generally, for cybersecurity, Baliga et al. [23] identified opportunities for cyber deterrence with detection and the potential to undermine deterrence. Edwards et al. [24] considered a game theoretic model of blame, with an attacker and a defender, involving attribution, attack tolerance, and peace stability. Welburn et al. [25] found that although a cybersecurity defender prefers not to signal truthfully, the defender can enhance deterrence through signaling, which has implications for cyber deterrence policies. Nagurney and Shukla [26] considered three models for cybersecurity investment involving noncooperation, the Nash bargaining theory with information sharing, and system optimization with cooperation.
1.3.8. Information Security
Within information security, game theoretic research has focused on data survivability versus security in information systems [27], substitution and interdependence [28,29,30], returns on information security investment [31,32], and information sharing to prevent attacks [33,34,35,36,37]. See Do et al. [38], Hausken and Levitin [39], and Roy et al. [40] for reviews on game theoretic cybersecurity research.
1.4. Article Organization
2. The Model
Consider two players in a simultaneous move two-period game.
2.1. Period 1
Assume that Player 1 in Period 1 gets cyber resources (e.g., capital, manpower, competence) from a national budget, which is allocated to develop zero-day exploits (zero-days, for short) deployed in Period 1 to exploit zero-day vulnerabilities for Player 2 at unit cost and develop zero-day exploits stockpiled for use in Period 2 at unit cost . The Nomenclature is shown before the reference list. Player 1′s upper constraint for resource allocation in Period 1 is
where is the actual amount of resources used by Player 1 in Period 1. Player 2 exerts defense effort in Period 1 at unit cost to defend its asset, which it values as and Player 1 values as . Figure 1 illustrates Period 1.
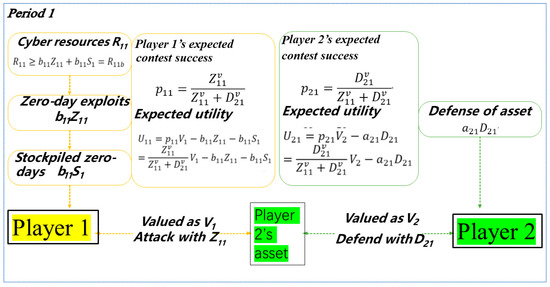
Figure 1.
Illustrating Period 1.
We apply the widely used ratio form contest success function [41], which is a plausible and widely used method for assessing two opposing players’ success. See Hausken and Levitin [42], Hausken [43], and Congleton et al. [44] for the use of the contest success function. In Period 1, Player 1′s expected contest success is and Player 2′s expected contest success is , i.e.,
where , , is the contest intensity in Period 1. Expected contest success is usually interpreted as a probability between 0 and 1. It can also be interpreted as a guaranteed fraction of an asset one competes to obtain, which presumes that the asset is divisible. When , the contest is egalitarian, and efforts do not matter. When , efforts matter proportionally. When , “winner-takes-all,” so that exerting slightly more effort than one’s opponent guarantees contest success. When , a disproportional advantage exists of investing less than one’s opponent. When , a disproportional advantage exists of investing more than one’s opponent. In Equation (2), the ratios have a sum of two efforts in the denominator and one of the efforts in the numerator. That gives a number between zero and one, which specifies contest success.
With these assumptions, Player ’s expected utility in Period 1 is
where Equations (1) and (2) have been inserted. Player 1′s two free-choice variables in Period 1 are and , constrained by Equation (1). Player 1 obtains no utility in Period 1 for allocating to stockpiling. Player 2′s one free-choice variable in Period 1 is , constrained by .
2.2. Period 2
Figure 2 illustrates Period 2.
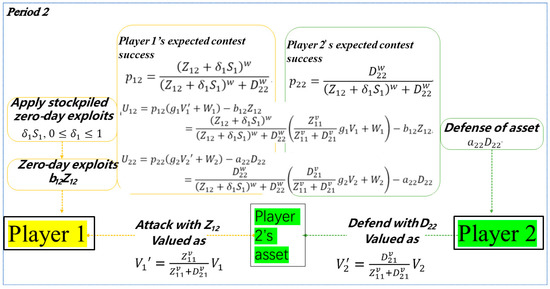
Figure 2.
Illustrating Period 2.
In Period 2, Player 1 applies its stockpiled zero-day exploits from Period 1, if it has stockpiled. Additionally, in Period 2, Player 1 exerts effort at unit cost to develop zero-day exploits, against which Player 2 exerts defense effort at unit cost . More specifically, assume that Player 1 in Period 2 applies its stockpiled zero-day exploits from Period 1, either keeping its same value with no appreciation if , appreciating in value if , or depreciating in value if . Appreciation of zero-day exploits over time occurs if technical, economic, or cultural circumstances change, making zero-day exploits more useful. In contrast, depreciation occurs if some aspects of the zero-day exploits leak or somehow becomes known or if technological or other developments make zero-day exploits less valuable over time. For example, increased competence may enable defenders against zero-day exploits to defend better, even though the nature of the zero-day exploit is unknown. 100% depreciation is expressed as .
Player 1 in Period 2 exerts effort at unit cost to develop zero-day exploits deployed in Period 2 to exploit zero-day vulnerabilities for Player 2. Player 2 exerts defense effort in Period 2 at unit cost to defend its asset, which it values as and Player 1 values as . In Period 2, Player 1′s expected contest success is and Player 2′s expected contest success is , i.e.,
where , , is the contest intensity in Period 2, with the same interpretation as for Period 1, and is determined by (1).
Assume that Player 2′s asset, valued as by Player , , grows with a growth factor from Period 1 to Period 2; , with an interpretation similar to that of for Player 1′s stockpiling . That is, an asset with value grows if , keeps its value if , and loses value if . Furthermore, assume that Player 2 in Period 2 gets injected with a new fresh asset valued as by Player , . With these assumptions, Player ’s expected utility in Period 2 is
Player 1′s one free-choice variable in Period 2 is , constrained by . Player 2′s one free-choice variable in Period 2 is , constrained by .
For the two-period game as a whole, with time discount factor , , Player ’s expected utility over the two periods is
The Max function is used for Player 1 since Player 1 will not use its entire budget if that causes negative expected utility .
3. Solving the Model
In Section 3.1.1, the game is solved with backward induction starting in Period 2. In Section 3.1.1, Period 1 is solved. Thereafter, various corner solutions have been determined. The 11 solutions in Table 1 have been identified for the game. All the solutions except Solution 9 have positive efforts and in Period 1, which is the nature of the ratio form contest success function in (2) and (3), with simultaneous moves in Period 1. That is, a player may decrease its effort arbitrarily close to zero, but not to zero. In Solution 9, Player 1 withdraws to avoid negative expected utility, i.e., to ensure .

Table 1.
Characteristics of the 11 solutions. and in Period 1 in all the solutions.
3.1. Solutions 1, 2, 3 (, , )
3.1.1. Solving Period 2
Differentiating Player ’s expected utility in (5) in Period 2 with respect to its one free-choice variable, i.e., for Player 1 and for Player 2, and equating it with zero, gives the first-order conditions
which are solved to yield
The second-order conditions are
which are satisfied as negative when
3.1.2. Solving Period 1
Inserting Equations (8) and (3) into Player ’s expected utility in Equation (6) over the two periods gives
which is rewritten as
which has three unknown variables: , and . Using (12), Player 1′s optimal stockpiling is
where according to (8) is the amount of stockpiling that causes zero effort for Player 1 in Period 2, and according to (1) is the maximum stockpiling permitted by Player 1′s budget constraint . Player 1 chooses the lowest of these two values since excessive stockpiling in Period 1, which cannot be utilized in Period 2, is not preferable, since Player 1 cannot exceed its budget constraint . We refer to in (13) when and as Solution 1. If , Player 1 does not stockpile in Period 1, i.e., , since its unit cost of stockpiling exceeds the product of Player 1′s unit cost of exerting effort in Period 2, Player 1′s time discount factor , and Player 1′s zero-day appreciation factor from Period 1 to Period 2. We refer to in (13) when and as Solution 2. Then, Player 1 chooses , optimally, and applies its remaining budget to stockpile .
Differentiating each player’s expected utility in (12) with respect to the two remaining free-choice variables, i.e., for Player 1 and for Player 2, and equating it with zero, gives the first-order conditions
which are cumbersome to analyze analytically. Hence, we solve (14) numerically for and and use (13) to determine , which are both inserted into (8) to determine the free-choice variables and in Period 2. We finally insert the result into (12) to determine the players’ expected utilities and over the two time periods.
3.1.3. Solution 3 ()
Inserting into (1) causes zero stockpiling, . Thus, Player 1 in Period 1 allocates all its resources to exploit zero-day vulnerabilities for Player 2 and has no resources to stockpile zero-day exploits for use in Period 2. The solution follows from solving the second first-order condition in (14) when and applying instead of the first first-order condition in (14).
3.2. Solutions 4–8 (, , )
When , Player 1 exerts no effort to develop zero-day capabilities in Period 2; instead, it relies on the stockpiling from Period 1 to attack Player 2. Solving Player 2′s first-order condition in (7) when gives
which is not analytically solvable for general (since appears multiplicatively under a root sign, appears as an exponent with two different bases, appears as an exponent under a root sign and without a root sign, and appears as an exponent under a root sign), but is, for conveniently solved to
Inserting , , and (3) into Player ’s expected utility in (6) gives
where follows from (16). Differentiating in (17) with respect to and equating with zero gives
The two remaining unknown variables and in (17) are determined by solving and together with (18) for Period 1.
3.2.1. Solution 4 (, )
When in (16), Player 2 is deterred from exerting effort in Period 2, i.e., . Then, Player 1 wins the Period 2 contest since . Inserting , and (3) into Player ’s expected utility in (6) gives
Differentiating (19) to determine the optimal efforts and for Players 1 and 2, respectively, and equating with 0 gives
which are solved to yield
The second-order conditions are
which are satisfied as negative when
To deter Player 2 in Period 2, Player 1 must choose sufficiently large stockpiling to make Player 2 indifferent between exerting and not exerting effort in Period 2. Inserting and into (3), that implies
where and in (17) are determined in (21).
3.2.2. Solution 5 (, )
The solution for , and in (17) and (24) presupposes that the budget constraint in (1) is not exceeded. If it is exceeded, Player 1 must decrease either the effort or the stockpiling that deters Player 2 in Period 2. Let us analyze the event that Player 1 chooses stockpiling to deter, as in (24), and uses the budget constraint in (1) to determine (which is then lower than the optimal with no budget constraint in (17)). Applying in (20), in (24), and the budget constraint in (1) gives the three equations
which are numerically solvable for , and .
3.2.3. Solutions 6–8 (, , )
If Player 1 chooses effort in Period 2 and Player 1′s budget constraint prevents sufficient stockpiling to deter Player 2 in Period 2, Player 2 will choose positive effort in Period 2. Then, (16) applies for and (17) applies for and . Solution 6 follows from solving in (17) together with in (18) and the budget constraint . Solution 7 follows from solving and in (17) together with the budget constraint . Solution 8, in which Player 1 does not utilize its entire budget , follows from solving and in (17) together with in (18). Solution 8 has not been demonstrated in practice. It is distinguished from Solutions 6 and 7 in that Player 1 does not utilize its entire budget , while still not deterring Player 2. It is also distinguished from Solutions 4 and 5, where Player 2 is indeed deterred, either by the player being superior (Solution 4) or by Player 1 utilizing its entire budget .
3.3. Solution 9 ()
Player 1′s budget constraint in (1) may prevent Player 1 from an optimal exertion of efforts. Hence, we require that Player 1 should always receive positive expected utility and otherwise assume that Player 1 chooses zero efforts in both periods and that Player 2 keeps its asset by exerting arbitrarily small defense efforts , where is arbitrarily small but strictly positive. Inserting into (3), (5) and (6), the players’ expected utilities are thus , , , .
3.4. Solution 10 (, )
A solution is possible, where the players are equally matched (equally advantaged) and Player 1 chooses Period 1 effort , which equals Player 2′s Period 1 effort . Furthermore, if the players are equally matched in Period 2 and exert equal and high Period 2 efforts , a solution can emerge where they both receive zero expected utilities since their efforts in both periods outweigh the benefits they receive from the asset values, i.e., .
3.5. Solution 11 ()
When Player 2 is deterred in Period 2, , and Player 1 does not stockpile in Period 1, , what remains for Period 1 is for Player 1 to choose effort and Player 2 to choose effort . In order to deter Player 2 in Period 1, so that Player 2 chooses zero effort , (19) for Player 2 implies
Equation (26) needs to be analyzed for each combination of parameter values to determine whether Player 1′s budget enables it to choose to deter Player 2 so that or whether deterrence is impossible. Solution 11 has not been demonstrated in practice. It is distinguished from Solutions 4 and 5, where Player 2 is also deterred, , in Period 2, but Player 1 stockpiles .
4. Illustrating the Solution
Figure 3 illustrates the solution, i.e., the efforts ,,,, stockpiling , the actual amount (dependent variable) of resources used by Player 1 in Period 1, and the expected utilities ,, , , , for Players 1 and 2 with the 16 benchmark parameter values , , , . We have chosen unitary parameter values whenever possible. We also plot as functions of and . In each of the 16 + 2 = 18 double panels, one parameter value varies, while the other parameter values are kept at their benchmarks. The upper part of each panel shows which solution is plotted for the various ranges along the horizontal axis. The benchmark solution (which is Solution 1) is , , , , , .
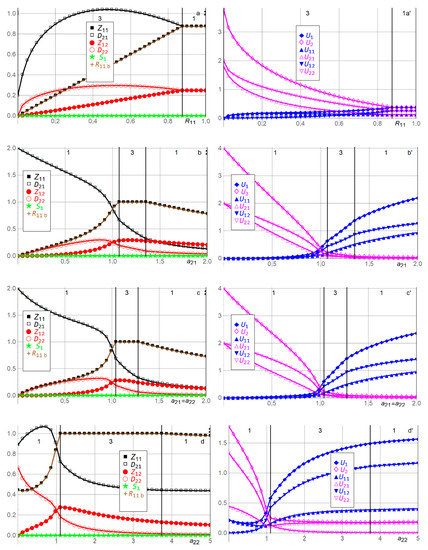
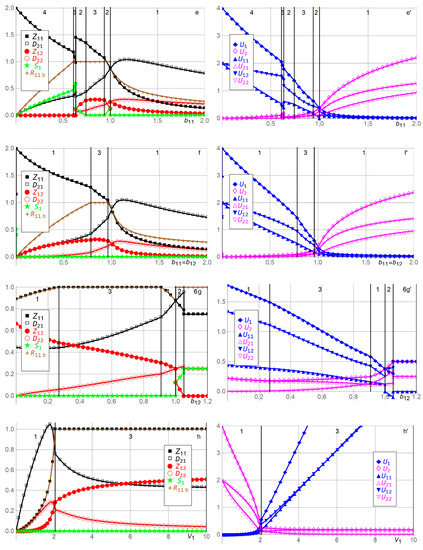
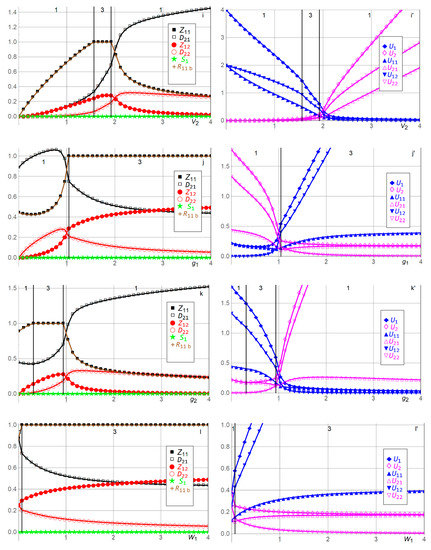
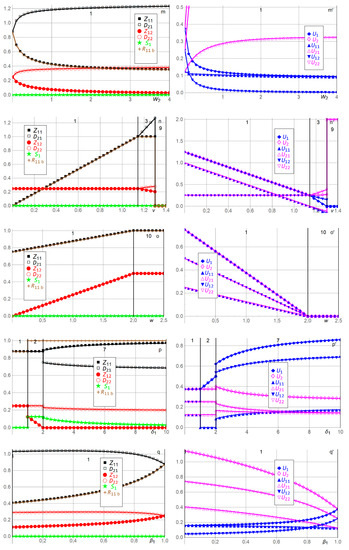
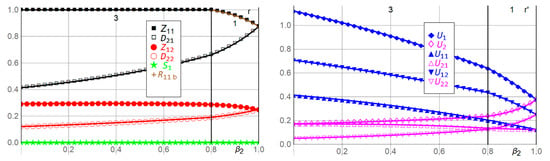
Figure 3.
Efforts , ,,, stockpiling , used resources , and expected utilities ,, ,, , for Players 1 and 2 as functions of , , , , relative to the benchmark parameter values , , , . See Table 2 and the text for an explanation of the 18 panels a,a’ to r,r’.
In Figure 3a,a’, when Player 1′s budget constraint exceeds the amount of resources used at benchmark , all variables remain at their benchmarks, as functions of , since Player 1 is not constrained in any way. In contrast, as decreases below , Player 1 is constrained in its effort , which decreases linearly to as decreases to . Player 2′s Period 1 defense effort is inverse U-shaped in since Player 1 first seeks to gain competitive advantage against Player 2 by competing more fiercely as decreases below . After reaches a maximum, it decreases as Player 2 becomes more advantaged and succeeds with lower effort due to Player 1′s decreasing budget . Hence, as decreases, Player 1′s expected utilities ,, decrease and Player 2′s expected utilities ,, increase.
In Figure 3b,b’, as Player 2′s unit effort cost of defense in Period 1 increases above , the disadvantaged Player 2′s efforts and in both periods and its expected utilities ,, decrease. Player 1′s efforts and in both periods are inverse U-shaped in . Initially, as increases above , Player 1 increases and to compete more successfully with Player 2. As increases further, Player 1 decreases its efforts and due to strength and being advantaged, as and are less needed to compete successfully with Player 2. As increases above , Player 1′s expected utilities ,, thus increase. For the range , Player 1 reaches its budget constraint due to competing fiercely with Player 2 (and being neither strongly advantaged nor strongly disadvantaged), causing maximum Period 1 effort , which depresses Player 1′s expected utility and increases Player 2′s expected utility slightly, relative to no budget constraint. In contrast, as decreases below , the advantaged Player 2 increases its Period 1 defense effort , while Player 1 decreases its efforts and in both periods. Player 2′s defense effort in period 2 is inverse U-shaped for the same reason as above. As approaches , less need exists for the advantaged Player 2 to exert effort in Period 2, and the asset fought over is less valuable since most of the value was distributes in Period 1. Hence, as decreases below , Player 2′s expected utilities ,, increase, and Player 1′s expected utilities ,, decrease. Player 1 does not stockpile since its efforts and are equally costly in both periods, its zero-day appreciation factor from Period 1 to Period 2 equals , and its time discount factor equals .
In Figure 3c,c’, Player 2′s unit defense costs are assumed equal in both periods. Player 1 is budget constrained when . Panel c,c’ is qualitatively similar to Panel b,b’. The main differences are that Player 2 becomes more disadvantaged when increases above and more advantaged when decreases below compared with Panel b,b’, where only varies. Hence, for example, when , the two inverse-U shapes for and are narrower in Panel c,c’ than in Panel d,d’.
In Figure 3d,d’, Player 2′s unit effort cost of defense in Period 2 varies, causing results qualitatively similar to Panels b,b’ and c,c’. The main differences are that Player 2 prefers being disadvantaged in Period 2, with high in Panel d,d’, rather than being disadvantaged in Period 1, with high in Panel b,b’, and that Player 2 prefers being advantaged in Period 1 with low in Panel b,b’ rather than being advantaged in Period 2 with high in Panel b,b’. That is, Player 2 prefers to be advantaged in the important Period 1. If Player 2 is to be disadvantaged, it prefers to be so in the less important Period 2, where a less valuable asset is at stake. Player 1 is budget-constrained when . The reason for the larger range of being budget-constrained (compared with Panels b,b’ and c,c’) is that when Player 1 is disadvantaged with a large unit effort cost in Period 2, which constrains its Period 2 effort , it becomes more important for Player 1 to compete as fiercely as possible with Player 2 in Period 1, utilizing the cheaper Period 1 effort .
In Figure 3e,e’, as Player 1′s unit effort cost of developing zero-day capabilities in Period 1 increases above , stockpiling continues not to occur in Solution 1 and exerting effort in Period 2 at unit cost is cheaper. Player 1′s efforts and in both periods decrease as increases since Player 1 becomes more disadvantaged, cannot justify the costly efforts, and receives lower expected utilities ,,. Player 2′s defense efforts and in the two periods are inverse U-shaped as increases above , which is common in such situations. That is, for intermediate above , the players are similarly advantaged and Player 2 exerts high efforts and . As increases, Player 2 becomes more advantaged and decreases and due to strength since high expected utilities ,, are obtained even with low efforts. As decreases, Player 2 becomes more disadvantaged and decreases and due to weakness, earning lower expected utilities ,,. In contrast, as decreases below , Player 1 stockpiles when the budget permits it and it is beneficial. More specifically, decreasing marginally below causes Player 1 to replace a maximum part of its Period 2 effort with stockpiling until its budget is reached, causing and to be discontinuous through and causing Solution 2. As decreases below , Solution 3 emerges. Player 1′s unit efforts cost is then so low that it chooses maximum Period 1 effort , as permitted by the budget , and zero stockpiling . This continues with increasing expected utilities ,, for Player 1 and decreasing expected utilities ,, for Player 2, until , where Solution 2 again emerges. The reason is that for , Player 1 is sufficiently advantaged compared with Player 2, does not need to increase its Period 1 effort further, and prefers instead to stockpile to become more competitive in Period 2. Hence, as decreases from to , Player 1′s Period 2 effort decreases as it is cost effectively replaced with stockpiling . As decreases below , Solution 5 emerges, where, interestingly, Player 1 stockpiles sufficiently with in Period 1 to deter Player 2 from defending in Period 2, i.e., . Player 1 exerts no effort in Period 2 (at unit cost ) since stockpiling at unit cost is more cost effective. To accomplish the substantial stockpiling required to deter Player 2 in Period 2, Player 1 must decrease its Period 1 effort substantially below its effort chosen when , as required by its budget constraint . As decreases below , within Solution 5, Player 1 can gradually afford to increase its Period 1 effort , enabling more successful competition with Player 2 in Period 1, and thus less stockpiling is required to deter Player 2 in Period 2. This process continues until , where Solution 4 emerges. In Solution 4, Player 1 is so superior that it does not need to utilize its entire budget . Its low unit effort cost in Period 1 enables it to stockpile sufficiently to deter Player 2 in Period 2 and to sufficiently avoid having to exert effort in Period 2, i.e., . Furthermore, as decreases below , Player 1 competes increasingly successfully through increasing effort with Player 2 in Period 1, which enables decreased stockpiling , increased expected utilities ,, for Player 1, and decreased expected utilities ,, for Player 2.
In Figure 3f,f’, Player 1′s unit effort costs of developing zero-day capabilities are assumed to be equal in both periods. Since Player 1′s zero-days do not appreciate, , and Player 1 does not discount time, , Player 1 does not need to stockpile, i.e., throughout. As increases above , the players’ Period 1 efforts and are qualitatively similar to Panel e,e’, i.e., decreasing for Player 1 and inverse U-shaped for Player 2. In Period 2, Player 1 is more disadvantaged in Panel f,f’ than in Panel e,e’ since its unit effort cost is higher (no longer ). Thus Player 1′s Period 2 effort decreases more quickly towards zero than in Panel e,e’, enabling the advantaged Player 2 to also decrease its Period 2 defense effort towards zero more quickly than in Panel e,e’. In contrast, as decreases below , Solution 2 with stockpiling does not arise as in Panel e,e’. Instead, Solution 1 continues to operate with increased Period 1 and Period 2 efforts and for Player 1 and decreased Period 1 and Period 2 efforts and for Player 2. This continues until when Player 1 reaches its budget constraint and Solution 3 emerges, as in Panel e,e’. Solution 3 is maintained, with increasing advantage for Player 1, until when Player 1 is so advantaged that it does not need to utilize its entire budget . Instead, Solution 1 emerges for , where all the four efforts , , , are positive since stockpiling does not occur, which would deter Player 2 in Period 2, as in Panel e,e’. As decreases, Player 1′s Period 1 effort increases since the unit effort cost decreases, while Player 1′s Period 2 effort decreases due to Player 1′s advantage and less of Player 2′s asset left to compete in Period 2.
In Figure 3g,g’, as Player 1′s unit effort cost of developing zero-day capabilities in Period 2 increases above to the disadvantage of Player 1, stockpiling emerges in Solution 2 since Player 1′s Period 2 effort becomes increasingly expensive and reaches when . As increases from to , Player 1 accepts negative expected utility in Period 1 in order to earn increasing positive expected utility in Period 2. As increases above , Player 1 exerts zero effort in Period 2, stockpiles optimally , and chooses its Period 1 effort in Solution 6 to satisfy the budget constraint . Player 1 thus offsets its increasing unit effort cost by stockpiling in Period 1. In contrast, as decreases below , stockpiling continues not to occur in Solution 1 since exerting effort in Period 2 at unit cost is cheaper. Player 1′s efforts and in both periods increase as decreases since Player 1 becomes more advantaged and receives higher expected utilities , ,. Player 2′s defense efforts and in the two periods decrease as decreases below since Player 2 becomes more disadvantaged and receives lower expected utilities , , . This continues until , when Player 1′s Period 1 effort at unit cost becomes too costly, Player 1 reaches its budget constraint and Solution 3 emerges. Solution 3 is maintained as decreases to , enabling Player 1 to increase its Period 2 effort and earn higher expected utilities ,,. Player 2′s defense efforts and in the two periods decrease as decreases below , earning lower expected utility . As decreases below , Player 1′s Period 2 effort becomes so high and cheap that Player 1 can rely on competing successfully with Player 2 in Period 2. Thus, Player 1 no longer needs to exert high Period 1 effort and no longer needs to apply its entire budget . Thus, Solution 1 re,emerges with higher expected utility to Player 1. Interestingly, Player 2 also receives higher expected utility as decreases towards since Player 1 still has the unit effort cost of its Period 1 effort , and, thus, to some extent, Player 2 competes somewhat successfully with Player 1 in Period 1.
In Figure 3h,h’, when Player 1′s valuation of Player 2′s asset increases above the benchmark , Player 1′s Period 1 effort increases rapidly from the benchmark and reaches the budget constraint when . That causes a transition from Solution 1 to Solution 3. As increases, Player 2′s Period 1 effort decreases, , determined numerically. That is, although Player 1′s valuation increases arbitrarily, Player 2′s valuation remains at the benchmark , causing Player 2 to compete to defend its asset in Period 1. In Period 2, this changes. As increases, Player 1 exerts increasing effort , , while Player 2 exerts decreasing effort , . As increases, Player 1 receives increasing expected utilities ,,, , while Player 2′s expected utility decreases, , . In contrast, as decreases below the benchmark , the results are qualitatively similar to Player 1′s budget decreasing below the benchmark in Panel a,a’. That is, Player 1 exerts lower efforts and and receives lower expected utilities ,,, while Player 2′s efforts are inverse U-shaped and it receives increasing expected utilities ,,.
In Figure 3i,i’, when Player 2′s valuation of its own asset increases above the benchmark , Player 2 exerts concavely increasing Period 1 defense effort for its more valuable asset, . Player 2′s Period 2 defense effort is inverse U-shaped, as it first competes more fiercely with Player 1 and eventually decreases due to being advantaged . Player 2′s expected utilities ,, thus increase, Player 1 responds by decreasing its efforts and in both periods, , receiving decreasing expected utilities ,,, . In contrast, as decreases below the benchmark , Player 1′s Period 1 effort increases rapidly from the benchmark and reaches the budget constraint when . That causes a transition from Solution 1 to Solution 3, but in the opposite direction compared with Panel h,h’. As decreases, Player 2′s Period 1 effort decreases convexly until , causing a transition back to Solution 1 since the advantaged Player 1 no longer needs to utilize its entire budget . Thus, Player 1′s Period 1 effort decreases. As decreases below the benchmark , Player 1′s Period 2 effort is inverse U-shaped, causing increasing expected utilities ,,, while both efforts and by Player 2 decrease, causing decreasing expected utilities ,,.
In Figure 3j,j’, when Player 1′s growth factor of asset from Period 1 to Period 2 increases above the benchmark , Player 1′s Period 1 effort increases rapidly from the benchmark , as in Panel h,h’, and reaches the budget constraint when . That causes a transition from Solution 1 to Solution 3. As increases, the results are qualitatively similar to increasing in Panel h,h’, since Player 1′s period 1 effort is locked to the budget constraint . The difference is that Player 1′s Period 1 expected utility does not approach infinity, since the growth factor is confined to Period 2, and, instead, approaches a constant concavely, . The other limit values are as in Panel h,h’, i.e., , , , , , . In contrast, as decreases below the benchmark , Player 1 decreases its Period 2 effort since the asset has less value in Period 2, receiving decreasing expected utility in Period 2. Both efforts and by Player 2 are inverse U-shaped, as in Panel h,h’, when the asset value decreases below the benchmark . Player 1′s Period 1 effort is slightly U-shaped since the asset still has value for Player 1 in Period 1. As decreases, Player 2′s expected utilities ,, increase, while Player 1′s expected utilities and are U-shaped. This latter remarkable result is caused by Player 1 focusing more explicitly on Period 1 when the growth factor is very low, while Player 2 focuses on both periods and strikes a balance between them.
In Figure 3k,k’, when Player 2′s growth factor of asset from Period 1 to Period 2 increases above the benchmark , Player 2′s Period 1 effort increases rapidly from the benchmark , as in Panel i,i’. Although growth does not manifest until Period 2, Player 2 competes fiercely in Period 1, knowing that what it can protect in Period 1 grows in Period 2. Thus, Player 2 exerts concavely increasing Period 1 defense effort , . As increases, the results are qualitatively similar to increasing in Panel i,i’. The difference is that Player 2′s Period 1 expected utility does not approach infinity, since the growth factor is confined to Period 2. Instead, it is inverse U-shaped and approaches zero, . The other limit values are as in Panel i,i’, i.e., , . In contrast, as decreases below the benchmark , Player 2′s Period 1 effort is slightly U-shaped since the asset still has value for Player 2 in Period 1. Solution 3 arises when . Player 2 decreases its Period 2 effort since the asset has less value in Period 2, receiving decreasing expected utility in Period 2. Both efforts and by Player 1 are inverse U-shaped, as in Panel i,i’, when the asset value decreases below the benchmark . As decreases, Player 1′s expected utilities ,, increase, while Player 2′s expected utilities and are U-shaped. This latter remarkable result is caused by Player 2 focusing more explicitly on Period 1, when the growth factor is very low, while Player 1 focuses on both periods and strikes a balance between them.
In Figure 3l,l’, when Player 1′s valuation of Player 2′s asset acquired in Period 2 increases above the benchmark , Player 1′s Period 1 effort quickly increases to its budget constraint , causing transition from Solution 1 to Solution 3 when . Player 1′s Period 1 expected utility is thus constrained, increasing concavely to . Player 1′s Period 2 effort increases concavely, , and its expected utilities and increase without bounds,. In contrast, Player 2′s defense efforts and in the two periods and its expected utilities and decrease convexly, , , , . Player 2′s Period 1 expected utility increases concavely, , since Player 1 is budget-constrained in Period 1 and strongly focuses instead on Period 2 as increases.
In Figure 3m,m’, when Player 2′s valuation of its own asset acquired in Period 2 increases above the benchmark , Player 2′s Period 1 defense effort and expected utility increase concavely, , . Player 1′s Period 1 effort and expected utilities and decrease concavely, , . Player 2′s Period 2 defense effort also increases concavely, , and Player 2′s expected utilities and increase without bounds, . Player 1′s Period 2 effort and expected utility decrease convexly, .
In Figure 3n,n’, when the contest intensity in Period 1 increases above the benchmark , the players compete more fiercely with each other in Period 1, receiving decreasing expected utilities ,,, until Player 1 reaches its budget constraint when . When , which gives a transition from Solution 1 to Solution 3, Player 2 competes even more fiercely with increasing Period 1 defense effort while accepting negative Period 1 expected utility . Player 1′s Period 1 expected utility is even more negative. When , the advantaged Player 2 exerts slightly increasing Period 2 effort , while Player 1 exerts decreasing effort . That continues until , when Player 1 starts to receive negative expected utility over the two periods, which is unacceptable for Player 1. Hence Solution 9 emerges, where Player 1 withdraws from both periods and receives zero expected utilities . When , Player 2 exerts a arbitrarily small positive effort and keeps its asset, i.e.,, where is arbitrarily small but positive, and receives expected utilities , . In contrast, as decreases below the benchmark , both players exert lower Period 1 efforts and and eventually zero effort at the limit for an egalitarian contest , where efforts do not matter. Concomitantly, both players’ expected utilities ,,, increase. The players’ Period 2 efforts and expected utilities are constant at .
In Figure 3o,o’, when the contest intensity in Period 2 increases from (egalitarian contest) through to the benchmark and to , the players’ Period 2 efforts and increase from through , and to . Simultaneously, the players’ Period 1 efforts and increase from when (no egalitarian contest in Period 1), through the benchmark , and to when . These increases in the efforts , ,, depress the players’ expected utilities ,,,,,, all of which decrease after reaching when . When , causing transition from Solution 1 to Solution 10, we assume that the players choose the equilibrium, where they both exert the efforts and and receive zero expected utilities . Increasing the Period 2 contest intensity is quite costly for equally matched (equally advantaged) players.
In Figure 3p,p’, when Player 1′s zero-day appreciation factor of stockpiled zero-day exploits from Period 1 to Period 2 increases above the benchmark , causing transition from Solution 1 to Solution 2 in Table 1, Player 1 immediately utilizes its entire Period 1 budget , allocating to stockpiling, to the Period 1 attack, and to the Period 2 attack. Hence, Player 1 cuts the Period 2 attack in half, from the benchmark to , utilizing stockpiling from Period 1 instead as increases above . As increases above , Player 1 keeps its stockpiling at , as permitted by its budget constraint , but decreases its Period 2 attack linearly since stockpiling at gets multiplied with the increasing (see in (5)). Player 1′s expected utilities and increase, while its Period 1 expected utility is zero, , since its stockpiling gives a cost in Period 1 and a benefit in Period 2. Player 2′s expected utilities ,, remain at their benchmarks when since Player 1′s allocation from to is all that happens when . As increases above , Player 1′s Period 2 attack decreases to , as it gets entirely replaced by stockpiling . That causes transition from Solution 2 to Solution 7 in Table 1. As increases above , Player 1 decreases its stockpiling , , which continues to impact Period 2 due to in (5). That enables Player 1 to increase its Period 1 attack , within its budget , . Thus, Player 2 decreases its defense in both periods, , . Thus, Player 1′s expected utilities ,, increase concavely, , , , while Player 2′s expected utilities ,, decrease convexly, , , . In contrast, when is less than 1, i.e., , which means depreciation, then Player 1 refrains from stockpiling, . Hence, all variables are constant at their benchmark values as functions of when .
In Figure 3q,q’, as Player 1′s time discount factor decreases below the benchmark , so that Player 1 assigns less weight to the future Period 2, Player 1 exerts decreasing efforts and in both periods, receiving decreasing expected utilities and but increasing expected utility in Period 1, which is more important than Period 2 for Player 1, while Player 2 assigns equal importance to both periods. As decreases, Player 2 exerts increasing defense efforts and in both periods, which eventually decrease slightly, causing inverse U-shapes as approaches . As decreases, Player 2 becomes more competitive due to weighing both periods equally and receiving increasing expected utilities ,,. When , Player 1 assigns less weight to Period 2 than Period 1, causing zero stockpiling .
In Figure 3r,r’, as Player 2′s time discount factor decreases below the benchmark , so that Player 2 assigns less weight to the future Period 2, Player 2 exerts decreasing defense efforts and in both periods, receiving decreasing expected utilities and but increasing expected utility in Period 1, which is more important than Period 2 for Player 2, while Player 1 assigns equal importance to both periods. As decreases, Player 1 exerts increasing efforts and in both periods, becoming more competitive due to weighing both periods equally and receiving increasing expected utilities ,,. As decreases below , Player 1 reaches its budget constraint, which constricts its Period 1 effort , causing a transition from Solution 1 to Solution 3.
5. Discussion
Table 2 presents the key findings from Section 4, including the three situations where Player 1 stockpiles in Panels e,e’, g,g’, and p,p’.

Table 2.
Key findings from Section 4, including the three situations where Player 1 stockpiles in Panels e,e’, g,g’, and p,p’.
6. Conclusions
The article presents a two-player two-period game between players producing zero-day exploits for immediate deployment in Period 1 or stockpiles for future deployment in Period 2. In Period 2, Player 1 produces zero-day exploits for immediate deployment, supplemented by stockpiled zero-day exploits from Period 1. Player 2 defends its asset against the attack in both periods. The analysis implies 11 solutions, where Player 1 may or may not stockpile, may or may not utilize its entire budget, may or may not attack in Period 2, and may or may not deter Player 2 from defending in Period 2. Relative to a benchmark solution with no stockpiling, 18 parameter values are altered to understand the nature of the zero-day phenomenon over two periods. Both players strike balances between how to exert efforts over the two periods, while Player 1 additionally decides whether to stockpile.
Player 1 may stockpile in three situations. First, as Player 1′s unit effort cost of developing zero-day capabilities in Period 1 decreases below that of Period 2, it may exploit the Period 1 advantage for stockpiling and deployment in Period 2. Second, when Player 1′s unit effort cost of developing zero-day capabilities in Period 2 increases above that of Period 1, it may similarly exploit the Period 1 advantage for stockpiling, potentially even accepting negative expected utility in Period 1 in order to benefit from subsequent deployment in Period 2. Third, when Player 1′s zero-day appreciation factor of stockpiled zero-day exploits from Period 1 to Period 2 increases above one, it stockpiles for utilization in Period 2 until no additional Period 2 attack is required.
When the contest intensity in Period 1 increases, the players compete more fiercely with each other in Period 1, receiving decreasing expected utilities, until Player 1 reaches its budget constraint. Thereafter, Player 2 competes more fiercely, and both players receive negative Period 1 expected utilities. This continues until Player 1 receives negative expected utility over both periods, causing it to withdraw, while Player 2 keeps its asset. When the contest intensity in Period 2 increases, all efforts increase until both players receive zero expected utilities, assuming that they are equally advantaged.
If a player’s time discount factor decreases, the player exerts lower efforts in both periods and receives lower expected utilities except in Period 1. The other player exerts higher efforts overall. The model confirms many intuitive results. For example, a player exerts more effort if it is cheaper, if it values the asset more, if the asset has a higher growth factor, and if the asset added in Period 2 is more valuable. If a player’s unit effort costs increase (decrease) equally as much in both periods, the player becomes more disadvantaged (advantaged) than if the unit effort cost in only one period increases (decreases). The phenomenon of inversely U-shaped efforts is documented extensively. Typically, a player competes most fiercely when equally advantaged compared with the other player and decreases its efforts due to cost-effectiveness when too advantaged (due to superiority) or too disadvantaged (due to inferiority).
Future research should include more players, outside interference from governments and nongovernment bodies, regulation, and supervision and account for technological developments of the various aspects of zero-day exploits. The parameter values should be estimated by considering zero-day attacks that have occurred. Empirical support should be provided from contemporary and historical records. More complexity and more than two time periods may also be incorporated.
Author Contributions
All authors of this article contributed to idea generation, conceptual design, analysis, and writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank two anonymous reviewers and the editor of this journal for useful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Parameters | |
| Player s cyber resources in Period 1, | |
| Player 2′s unit effort cost of defense in Period , , | |
| Player 1′s unit effort cost of developing zero-day capabilities in Period , , | |
| Player ’s valuation of Player 2′s asset, | |
| Growth factor of asset from Period 1 to Period 2, | |
| Player ’s valuation of Player 2′s asset acquired in Period 2, | |
| Contest intensity in Period 1, | |
| Contest intensity in Period 2, | |
| Player 1′s zero-day appreciation factor of stockpiled zero-day exploits from Period 1 to Period 2, | |
| Player ’s time discount factor, | |
| Strategic Choice Variables | |
| Player 1′s effort to develop zero-day capabilities in Period 1, | |
| Player 2′s defense effort in Period 1, | |
| Player 1′s effort to develop zero-day capabilities in Period 2, | |
| Player 2′s defense effort in Period 2, | |
| Dependent Variables | |
| Player 1′s stockpiling of zero-day exploits in Period 1 for use in Period 2, | |
| Player ’s expected contest success in Period , , | |
| Player ’s expected utility in Period , | |
| Player ’s expected utility over both time periods, | |
| The actual amount of resources used by Player 1 in Period 1 | |
References
- Nakashima, E.; Warrick, J. Stuxnet Was Work of U.S. and Israeli Experts, Officials Say. 2012. Available online: https://cyber-peace.org/wp-content/uploads/2013/06/Stuxnet-was-work-of-U.S.pdf (accessed on 16 December 2020).
- Cherepanov, A. Windows Zero-Day CVE-2019-1132 Exploited in Targeted Attacks. 2019. Available online: https://www.welivesecurity.com/2019/07/10/windows-zero-day-cve-2019-1132-exploit/ (accessed on 14 December 2020).
- PhishProtection. Recent Zero-Day Attacks: Top Examples and How to Prevent It. 2020. Available online: https://www.phishprotection.com/content/zero-day-protection/recent-zero-day-attacks/ (accessed on 14 December 2020).
- Hausken, K.; Welburn, J.W. Attack and Defense Strategies in Cyber War Involving Production and Stockpiling of Zero-Day Cyber Exploits. Inf. Syst. Front. 2020, 1–12. [Google Scholar] [CrossRef]
- Chen, H.; Han, Q.; Jajodia, S.; Lindelauf, R.; Subrahmanian, V.S.; Xiong, Y. Disclose or Exploit? A Game-Theoretic Approach to Strategic Decision Making in Cyber-Warfare. IEEE Syst. J. 2020, 14, 3779–3790. [Google Scholar] [CrossRef]
- Ablon, L.; Bogart, A. Zero Days, Thousands of Nights: The Life and Times of Zero-Day Vulnerabilities and Their Exploits; RAND Corporation: Santa Monica, CA, USA, 2017. [Google Scholar]
- Singh, U.K.; Joshi, C.; Kanellopoulos, D. A Framework for Zero-Day Vulnerabilities Detection and Prioritization. J. Inf. Secur. Appl. 2019, 46, 164–172. [Google Scholar] [CrossRef]
- Al-Rimy, B.A.S.; Maarof, M.A.; Prasetyo, Y.A.; Shaid, S.Z.M.; Ariffin, A.F.M.; Malaysia, S.K.C. Zero-Day Aware Decision Fusion-Based Model for Crypto-Ransomware Early Detection. Int. J. Integr. Eng. 2018, 10, 82–88. [Google Scholar] [CrossRef]
- Venkatraman, S.; Alazab, M. Use of Data Visualisation for Zero-Day Malware Detection. Secur. Commun. Netw. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Sun, X.y.; Dai, J.; Liu, P.; Singhal, A.; Yen, J. Using Bayesian Networks for Probabilistic Identification of Zero-Day Attack Paths. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2506–2521. [Google Scholar] [CrossRef]
- Parrend, P.; Navarro, J.; Guigou, F.; Deruyver, A.; Collet, P. Foundations and Applications of Artificial Intelligence for Zero-Day and Multi-Step Attack Detection. EURASIP J. Inf. Secur. 2018, 2018, 4. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, P.K.; Moon, S.Y.; Park, J.H. A Hybrid Layered Architecture for Detection and Analysis of Network Based Zero-Day Attack. Comput. Commun. 2017, 106, 100–106. [Google Scholar] [CrossRef]
- Kim, J.Y.; Bu, S.J.; Cho, S.B. Zero-Day Malware Detection Using Transferred Generative Adversarial Networks Based on Deep Autoencoders. Inf. Sci. 2018, 460, 83–102. [Google Scholar] [CrossRef]
- Gupta, D.; Rani, R. Big Data Framework for Zero-Day Malware Detection. Cybern. Syst. 2018, 49, 103–121. [Google Scholar] [CrossRef]
- Sharma, V.; Lee, K.; Kwon, S.; Kim, J.; Park, H.; Yim, K.; Lee, S.Y. A Consensus Framework for Reliability and Mitigation of Zero-Day Attacks in IoT. Secur. Commun. Networks 2017, 2017, 1–24. [Google Scholar] [CrossRef]
- Haider, W.; Creech, G.; Xie, Y.; Hu, J.K. Windows Based Data Sets for Evaluation of Robustness of Host Based Intrusion Detection Systems (IDS) to Zero-Day and Stealth Attacks. Future Internet 2016, 8, 29. [Google Scholar] [CrossRef]
- Tran, H.; Campos-Nanez, E.; Fomin, P.; Wasek, J. Cyber Resilience Recovery Model to Combat Zero-Day Malware Attacks. Comput. Secur. 2016, 61, 19–31. [Google Scholar] [CrossRef]
- Tidy, L.; Woodhead, S.; Wetherall, J. Simulation of Zero-Day Worm Epidemiology in the Dynamic, Heterogeneous Internet. J. Def. Model. Simul. Appl. Methodol. Technol. 2015, 12, 123–138. [Google Scholar] [CrossRef]
- Chowdhury, M.U.; Abawajy, J.H.; Kelarev, A.V.; Hochin, T. Multilayer Hybrid Strategy for Phishing Email Zero-Day Filtering. Concurr. Comput. Pract. Exp. 2017, 29, e3929. [Google Scholar] [CrossRef]
- Duessel, P.; Gehl, C.; Flegel, U.; Dietrich, S.; Meier, M. Detecting Zero-Day Attacks Using Context-Aware Anomaly Detection at the Application-Layer. Int. J. Inf. Secur. 2017, 16, 475–490. [Google Scholar] [CrossRef]
- Chamotra, S.; Sehgal, R.K.; Misra, R.S. Honeypot Baselining for Zero Day Attack Detection. Int. J. Inf. Secur. Priv. 2017, 11, 63–74. [Google Scholar] [CrossRef]
- Afek, Y.; Bremler-Barr, A.; Feibish, S.L. Zero-Day Signature Extraction for High-Volume Attacks. IEEE/ACM Trans. Netw. 2019, 27, 691–706. [Google Scholar] [CrossRef]
- Baliga, S.; De Mesquita, E.B.; Wolitzky, A. Deterrence with Imperfect Attribution. Am. Political Sci. Rev. 2020, 114, 1155–1178. [Google Scholar] [CrossRef]
- Edwards, B.; Furnas, A.; Forrest, S.; Axelrod, R. Strategic aspects of cyberattack, attribution, and blame. Proc. Natl. Acad. Sci. USA 2017, 114, 2825–2830. [Google Scholar] [CrossRef] [PubMed]
- Welburn, J.W.; Grana, J.; Schwindt, K. Cyber Deterrence or: How We Learned to Stop Worrying and Love the Signal; RAND Corporation: Santa Monica, CA, USA, 2019. [Google Scholar]
- Nagurney, A.; Shukla, S. Multifirm models of cybersecurity investment competition vs. cooperation and network vulnerability. Eur. J. Oper. Res. 2017, 260, 588–600. [Google Scholar] [CrossRef]
- Levitin, G.; Hausken, K.; Taboada, H.A.; Coit, D.W. Data Survivability vs. Security in Information Systems. Reliab. Eng. Syst. Saf. 2012, 100, 19–27. [Google Scholar] [CrossRef]
- Enders, W.; Sandler, T. What Do We Know About the Substitution Effect in Transnational Terrorism? In Researching Terrorism: Trends, Achievements, Failures; Silke, A., Ilardi, G., Eds.; Frank Cass: Ilfords, UK, 2003. [Google Scholar]
- Hausken, K. Income, Interdependence, and Substitution Effects Affecting Incentives for Security Investment. J. Account. Public Policy 2006, 25, 629–665. [Google Scholar] [CrossRef]
- Lakdawalla, D.N.; Zanjani, G. Insurance, Self-Protection, and the Economics of Terrorism. J. Public Econ. 2005, 89, 1891–1905. [Google Scholar]
- Hausken, K. Returns to Information Security Investment: The Effect of Alternative Information Security Breach Functions on Optimal Investment and Sensitivity to Vulnerability. Inf. Syst. Front. 2006, 8, 338–349. [Google Scholar] [CrossRef]
- Hausken, K. Returns to Information Security Investment: Endogenizing the Expected Loss. Inf. Syst. Front. 2014, 16, 329–336. [Google Scholar] [CrossRef]
- Hausken, K. Information Sharing Among Firms and Cyber Attacks. J. Account. Public Policy 2007, 26, 639–688. [Google Scholar] [CrossRef]
- Hausken, K. A Strategic Analysis of Information Sharing Among Cyber Attackers. J. Inf. Syst. Technol. Manag. 2015, 12, 245–270. [Google Scholar] [CrossRef]
- Hausken, K. Information Sharing Among Cyber Hackers in Successive Attacks. Int. Game Theory Rev. 2017, 19, 33. [Google Scholar] [CrossRef]
- Hausken, K. Security Investment, Hacking, and Information Sharing between Firms and between Hackers. Games 2017, 8, 23. [Google Scholar] [CrossRef]
- Hausken, K. Proactivity and Retroactivity of Firms and Information Sharing of Hackers. Int. Game Theory Rev. 2018, 20, 1750030. [Google Scholar] [CrossRef]
- Do, C.T.; Tran, N.H.; Hong, C.; Kamhoua, C.A.; Kwiat, K.A.; Blasch, E.; Ren, S.; Pissinou, N.; Iyengar, S.S. Game theory for cyber security and privacy. ACM Comput. Surv. 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Hausken, K.; Levitin, G. Review of Systems Defense and Attack Models. Int. J. Perform. Eng. 2012, 8, 355–366. [Google Scholar] [CrossRef]
- Roy, S.; Ellis, C.; Shiva, S.; Dasgupta, D.; Shandilya, V.; Wu, Q. A survey of game theory as applied to network security. In Proceedings of the 2010 43rd Hawaii International Conference on System Sciences, Honolulu, HI, USA, 5–8 January 2010; pp. 1–10. [Google Scholar]
- Tullock, G. Efficient Rent-Seeking. In Toward a Theory of the Rent-Seeking Society; Buchanan, J.M., Tollison, R.D., Tullock, G., Eds.; Texas A&M University Press: College Station, TX, USA, 1980; pp. 97–112. [Google Scholar]
- Hausken, K.; Levitin, G. Efficiency of Even Separation of Parallel Elements with Variable Contest Intensity. Risk Anal. 2008, 28, 1477–1486. [Google Scholar] [CrossRef] [PubMed]
- Hausken, K. Additive Multi-Effort Contests. Theory Decis. 2020, 89, 203–248. [Google Scholar] [CrossRef]
- Congleton, R.D.; Hillman, A.L.; Konrad, K.A. 40 Years of Research on Rent Seeking—Applications: Rent Seeking in Practice; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).