1. Introduction
Pollution mitigation and adaptation are two major policies commonly used by governments to reduce the environmental damage. Spending on mitigation and adaptation is enormous. Indeed, the total global economic cost of mitigating climate change is estimated to be €200–350 billion per year by 2030 [
1]. Accurate assessment of effective environmental policies and actions has been a subject of intensive research for the last forty years. It includes analytic models [
2,
3,
4,
5] and computer simulation methods, known as the integrated assessment models [
6,
7,
8]. This paper contributes to analytic modeling of adaptation and mitigation activities in the competitive world. Analytic models lead to better understanding of observed environmental changes and predicting consequences of human impact on the environment. They also stimulate the improvement of computer simulation models. However, a systematic analytic theory of adaptation and mitigation is to be developed.
A short survey below demonstrates a growing number of related analytic models with scattered underlying assumptions and fragile links among various models and their outcomes. The modeling tools often reflect the analytic expertise of their authors. The adaptation–mitigation models can be deterministic or stochastic, static, or dynamic, in continuous or discrete time (including two- or three-stage versions). Because of analytic complexity, all models make simplifying assumptions about production, pollution, mitigation, and adaptation [
5,
6,
9,
10,
11,
12]. Corresponding optimization problems can involve one or several objectives, and one or many players [
13]. Some adaptation–mitigation models consider one country and neglect the international dimension of environmental protection [
5,
12,
14,
15,
16,
17]. The optimization models with several players reflect the international context of the environmental protection and lead to static or dynamic games. Multi-country models usually restrict their analysis to a symmetric case of identical countries [
18,
19,
20,
21,
22,
23,
24].
Here, we focus on a rigorous analysis of optimal adaptation and mitigation. To reduce modeling complexity, some analytic games with adaptation do not involve a separate mitigation variable and use the emission reduction caused by environmental damage as a proxy for mitigation effort [
10,
12,
16,
22,
25]. Such concept of mitigation is costless, so, the related models cannot compare adaptation and mitigation investments. Two-stage dynamic game [
9] analyzes both adaptation and mitigation but ignores endogenous production. A two-country static game of [
10] considers endogenous production, pollution, and adaptation, but oversimplifies mitigation as a reduced emission. The multi-country model of [
22] significantly generalizes the game [
10] by adding cross-country differences in adaptation costs but it also does not include a separate mitigation cost. Papers [
12,
16] consider dynamic optimization with uncertain damage, though over-simply mitigation. The models [
5,
12,
15,
16,
26] rigorously analyze mitigation and adaptation actions in one country ignoring international aspect of the problem. A static game of [
27] and a dynamic game of [
28] include separate endogenous mitigation variable, nevertheless, do not consider adaptation. Paper [
11] analyzes a static game of
n countries with pollution and adaptation but does not explicitly include mitigation.
A separate group of studies focuses on the formation and stability of possible coalitions in environmental protection, see [
11,
18,
23,
24] and the references therein. The impact of strategic commitment in a model with
n symmetric countries, including adaptation and mitigation, is evaluated in [
11,
18]. Two-stage coalition formation model of [
23] employs a general static game of
n identical countries with separate endogenous mitigation and adaptation variables. The authors show that adaption can lead to larger stable coalitions and higher global welfare (compared to the only mitigation case), but they do not estimate related adaptation and mitigation investments.
Different modeling assumptions about payoff functions, pollution disutility/damage, and mitigation and adaptation effectiveness are used in [
29,
30,
31,
32,
33,
34,
35,
36,
37,
38] to explore economic, agricultural, welfare, political, and regional aspects of strategic interactions among pollution, mitigation, and adaptation.
The novelty of the present paper relative to the existing literature is to analyze and compare a country’s strategic investments in mitigation and adaptation in the competitive world. Estimating the optimal mix of adaptation and mitigation efforts has tremendous policy implications [
5,
20]. We introduce a multi–country model with separate mitigation and adaptation investment controls and systematically analyze its competitive and cooperative cases, focusing on analytic solutions for the optimal emission, adaptation, and mitigation. The constructed nonlinear model follows natural economic assumptions and is not restricted to linear-quadratic cases. In general, it is not easy to find analytic solutions to non-quadratic games. For clarity, we employ the static game framework to obtain closed-form solutions, useful for policy analysis. Dynamic models of [
20,
39] with endogenous production, emission, mitigation, and adaptation are conceptually close to the present paper though they differ in modeling assumptions and are restricted to two regions.
The paper is organized as follows.
Section 2 formulates optimization problems for competitive and cooperative scenarios.
Section 3 provides a comparative analysis of the competitive (Nash equilibrium) and cooperative solutions, focusing on their dependence on the number of countries and country’s productivity.
Section 4 discusses obtained outcomes and their policy implications and concludes.
3. Results: Comparative Analysis
In this section, we investigate and compare analytic properties of the competitive game (4) and cooperative problem (5). In our analysis, we emphasize the dynamics of competitive and cooperative strategies when the number of countries is large. To demonstrate our technique, let us start with the simplest case.
Special case k = 0, a = 0 (no adaptation and no mitigation). Then, the game (4) becomes
and does not include mitigation and adaptation controls
yi and
zi. The only control in Equation (9) is the pollution level
xi that also defines the economic output (1). Differentiating (9) in
xi, setting the derivative to zero, and using the symmetry assumption (6), we obtain the Nash equilibrium solution of the game (4) as
By Theorem 1, the cooperative solution is
It is easy to see that the pollution is higher:
, and the payoff is smaller in the competitive game (4) than in the cooperative case:
By Equations (11) and (14), the cooperative payoff
FC
is always positive, but the competitive payoff
FN > 0 only when
n(1 −
η) < 2. Thus, the concave utility
η > 0 is required for a positive Nash payoff at
n > 1. A similar condition on model parameters appears in [
18] to guarantee that each player’s decision is interior in equilibrium.
Next, we explore the properties of competitive and cooperative strategies in models with mitigation, adaptation, and both controls. We compare competitive and cooperation strategies in the terms of pollution, adaptation, and mitigation. We also analyze how those strategies depend on the key model parameters, the number n of countries and their stage of development, represented by the production cleanness factor A.
3.1. Model with Mitigation
The competitive game (4) with mitigation is presented as follows:
Differentiating Equation (15) in
yi and
xi and setting derivatives to zero, we obtain the explicit formulas for Nash equilibrium solution:
and the related payoff
By Theorem 1, the solution of the related cooperative problem (5) is
Here and thereafter, the notation z(v) ~ f(v) describes asymptotic behavior of the function z(v) when v is large and means that
Theorem 2. Let k < (η + 1)/2. Then, in both competitive game (15) and its cooperative case, the optimal emission x, mitigation y, and payoff F increase when A and/or η increase, but decrease when n and/or B increase. The mitigation /pollution ratio increases and is convex when A increases: The global emission in the competitive case X = nx ~decreases in n at k < ηand increases at η < k < (η + 1)/2. At k → (η + 1)/2, the optimal x→∞ and y→∞.
Proof. Follows from formulas (16)–(21). □
The game (13) and related cooperative problem have no finite solution at k ≥ (η + 1)/2.
By Equations (16) and (19), the optimal mitigation y is positive in both competitive and cooperative scenarios, but it is small and much smaller than emission, x << y, for weak economies with A << 1. The optimal emission (17) of an individual country is always larger in the presence of mitigation than with no mitigation in both competitive and social optimum scenarios. However, it is not so for the competitive optimal payoff (18). By Theorem 2, the relation between the mitigation effectiveness parameter k and risk aversion η essentially affects both optimal competitive and cooperative strategies. The sign of k − η determines whether the global pollution increases or decreases when the number n of countries becomes larger. The optimal emission, mitigation, and payoffs are finite at 0 < k < (η + 1)/2, but they increase indefinitely when k → (η + 1)/2. At k ≥ (η + 1)/2, mitigation is so effective that the optimal output Axiyik in Equation (1) grows faster than the mitigation cost yi, which leads to the infinite output and pollution.
3.2. Model with Adaptation
With adaptation, the competitive and cooperative strategies become richer, but the analytic complexity increases. For clarity, let us first consider the problems (4) and (5), with adaptation but without mitigation. Then, the competitive game (4) becomes
Theorem 3. Letthen the Nash equilibrium solution of the competitive game (23) is:where v, 1 ≤ v < ∞, is the unique solution of the nonlinear equationwith If a < acr, then the optimal adaptation ZN = 0 and is determined by Equation (10).
Proof. Setting the partial derivatives of
in Equation (23) with respect to
xi and
zi to zero, we obtain the following system of two nonlinear equations in
xi and
zi:
Since the countries are identical, their competitive strategy is the same:
xi =
x,
zi =
z,
I = 1, …,
n, and the system of Equations (29) and (30) becomes
Formulas (25) follow from Equations (31) and (32) after expressing them via the new auxiliary variable
v =
. Excluding
x from the system of Equations (31) and (32), we obtain one nonlinear Equation (26) in
v. To analyze the existence and uniqueness of its solution, let us rewrite Equation (26) as
where
and
σ is defined by (27).
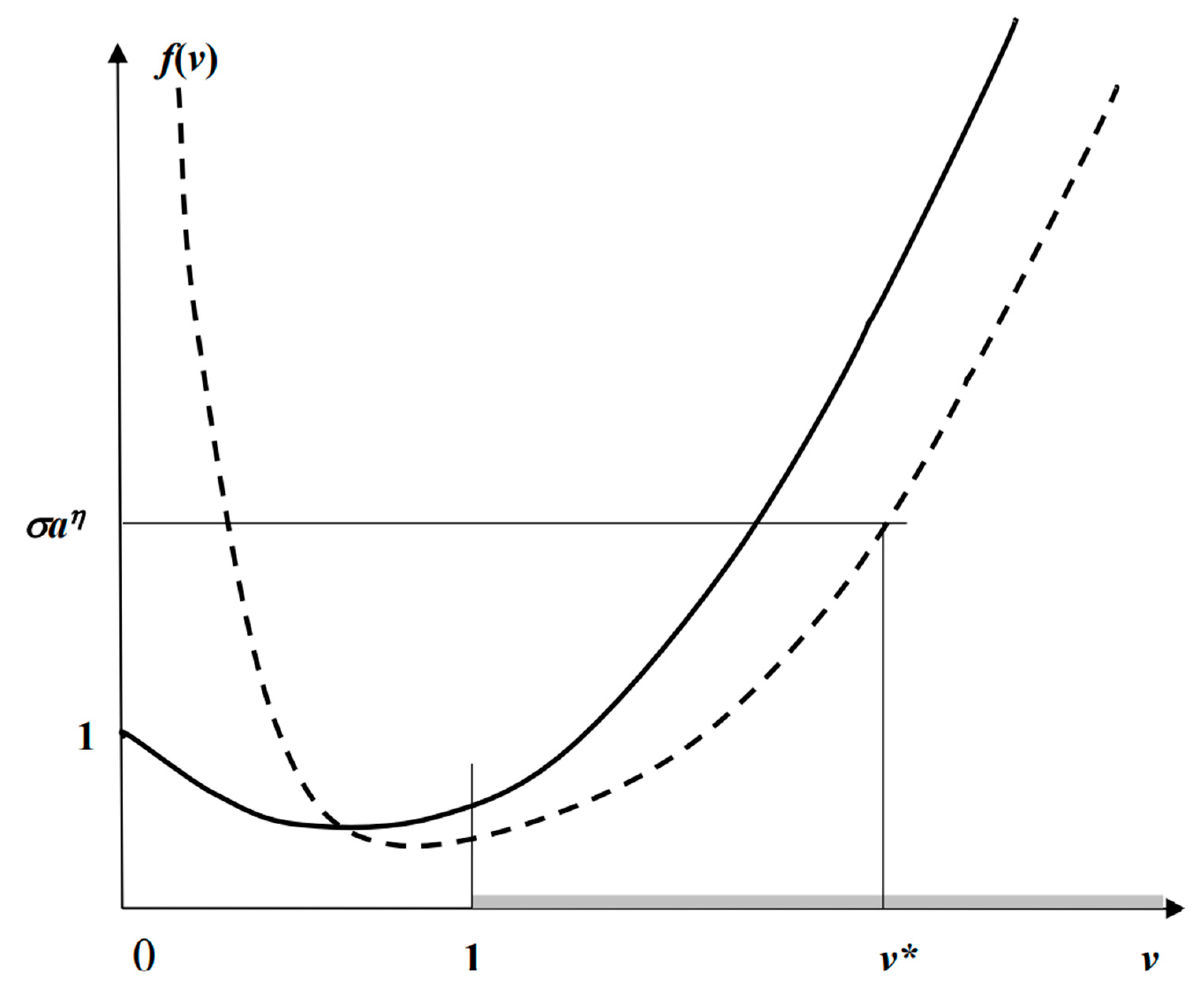
A typical shape of the function
f(
v) is shown with the solid line in
Figure 1. Because of the constraint
zi ≥ 0 in Equation (23), we are interested in the solution
v of the Equation (33) only in the interval [1, ∞). It is easy to see that there is no solution
v ≥ 1 if the right-hand side
σ of Equation (33) is small. Let
acr denote the smallest critical value of the parameter
a when a solution
v ≥ 1 exists.
To find acr, let = 0, then v = 1 and in Equation (25). Therefore, acr is determined from Equations (26) and (27) as Equation (24).
The payoff (28) is obtained combining Equations (23) and (29). Next, we find the derivative f′(v) and obtain that f′(v) > 0 at v ≥ 1 at natural conditions. Therefore, the solution v to the nonlinear Equation (33) is unique in the interval [1, ∞).
If 0 < a < acrN, then the optimal zN = 0 is a corner solution in [0, ∞), while xN coincides with Equation (10). As expected, the resulting payoff (28) in this case is the same as (11).
The Theorem is proven. □
By Theorem 3, the economy must be productive enough to engage into adaptation activities. The critical value acr positively depends on the climate vulnerability B and residual damage D. Thus, the larger B and D are, the more economically powerful a country should be to profitably engage in adaptation.
Using Theorems 1 and 3, the cooperative solution is
At
where
vc is the unique solution of the nonlinear equation over [1,∞):
while
and
xc is given by Equation (12) at
. The cooperative payoff is:
The adaptation threshold aC is larger in the cooperative scenario: aC > acr.
The behavior of optimal solutions (25)–(27) and (34)–(37) at large values of parameters n and A is summarized in the below statement.
Corollary 1. Letin the competitive game (23). Then, the following relations hold for optimal adaptation and emission controls: In the cooperative case, if, then: Proof. The proof is based on the analysis of the nonlinear Equation (33). The condition
means
>> 1. In Equation (33), if
f(
v) is large, then
v is also large:
v >> 1, because of specific form of the function
f. Next,
when
v >> 1.
Substituting Equation (40) to the formulas (25), we obtain (38). The asymptotic estimate (39) for the cooperative case is obtained analogously. The Corollary is proven. □
Corollary 1 implies that the optimal adaptation in a competitive case is asymptotically greater for a larger n >> 1. Theorem 4 extends this result for any number n > 1.
Theorem 4. Let σ > 1 in the competitive game (23). Then, the adaptation zN increases and pollution xN decreases when n increases. For n >> 1, Both emission xN and adaptation zN increase when A increases, in both competitive and cooperative cases. For A >> 1, Proof. We consider the case of an increasing
n first. Let us assume that
f(
v) in the Equation (33) is a function of two variables
v and
n:
Let us give some increments ∆
v and ∆
n to
v and
n. Then, by the Implicit Function theorem,
and by Equation (43),
Next, as shown in the proof of Theorem 3, because σ > 1 and v >1. So, ∆v > 0 at ∆n > 0 by Equation (44), and, therefore, both v and are larger when n is larger.
At σ >> 1, the solution v of Equation (43) is also large: v >> 1. Next, the asymptotic estimates (41) and (42) for zN, xN, and E follow directly from Equations (38) and (39).
The proof of the case of increasing A is analogous. The Theorem is proven. □
By Theorem 4, the presence of adaptation does not affect the asymptotic growth of pollution. In particular, the global pollution E always increases when the number of competing countries becomes larger (in the absence of mitigation).
3.3. Model with Mitigation and Adaptation
Now, we explore the games (4) and (5) with both adaptation and mitigation controls and analyze how the number of countries affects environmental policies, in particular, the optimal ratio between mitigation and adaptation. In the case of two countries, this issue is studied in [
20].
Theorem 5. Let k < (η + 1)/2. If a > acr,then the Nash equilibrium solution of the competitive game (4) is:where v, 1 ≤ v < ∞, is the unique solution to the nonlinear equationand σ is given by Equation (27). At k → (η + 1)/2, the optimal emission xN → ∞ and yN → ∞. The game (4) has no finite solution at k ≥ (η + 1)/2.
If 0 < a < acr, then the optimal adaptation zN = 0, while pollution xN and mitigation yN are given by Equations (16) and (17). The payoff is Proof. Setting the partial derivatives of
in Equation (4) with respect to
xi,
yi, and
zi equal to zero and taking the symmetry condition (6) into consideration, we obtain the following system of three nonlinear equations
with respect to three unknowns
xi =
x,
yi =
y,
zi =
z,
I = 1, …,
n. In the new variable
v = 1 +
az, this system is reduced to one nonlinear Equation (47) in
v. Let us rewrite Equation (47) as
where
The nonlinear function
f(
v) is shown in
Figure 1 with a dashed line. Its behavior differs from the function (33) from Theorem 1 at small
v but is qualitatively similar over the interval
v∈[1, ∞). As before, we are interested in solutions
v > 1 because of the constraint
z ≥ 0. Again, it is easy to see that no solution
v > 1 exists if the RHS of Equation (52) is small enough. Let
acr denote the smallest critical value of the parameter of
a when the solution
v ≥ 1 exists. To find
acr, let
ZN = 0, then
v = 1,
ZN = 0 by Equation (46), and
. Substituting those values to (47), we obtain the formula (45) for
acr.
Next, let us analyze the asymptotic of f(v) at large v. By Equation (53), f(v)~v1−2k+η, so at k < (η + 1)/2, and at k > (η + 1)/2. Therefore, the Equation (52) is guaranteed to have a solution 1 ≤ v < ∞ only at k < (η + 1)/2. Similarly to Equation (33), the first derivative f′(v) is positive at v ≥ 1 at natural conditions. Hence, the solution to the Equation (52) is unique if it exists. The payoff (48) is obtained from Equations (3) and (46).
If 0 < a < acr, then the optimal zN = 0 is a corner solution in [0, ∞), while the optimal xN and yN coincide with (19) and (20). The payoff (48) is the same as (18).
The theorem is proven. □
Again, a solution to the cooperative problem (5) is obtained using Theorem 1. Namely, if
a > acr, where
Then
where
vC, 1 ≤
vC < ∞, is a unique solution of the nonlinear equation
If a < acr, then zC
= 0, while xC and yC are found in Equations
(19) and (20).
The cooperative payoff is
The solutions (46) and (47) and (54) and (55) depend on six given model parameters: risk aversion η, mitigation efficiency k, adaptation efficiency a, productivity A, climate change vulnerability B, and the number of countries n. Analysis of these dependencies leads to interesting outcomes with relevant policy implications. Analogously to Theorem 4 and Corollary 1, we establish the following result.
Corollary 2. Let k < (η + 1)/2 in the competitive game (4). Then, the optimal emission xN is smaller and mitigation yN is larger for a larger n. For n >> 1,i.e., the adaptation zN increases in n atand decreases otherwise. The optimal ratio between adaptation and mitigation The global emissionis smaller for larger n at k > η and larger at k < η.
The optimal emission, adaptation, and mitigation efforts are larger in both competitive (4) and cooperative (5) games for a larger A. At A >> 1,and the optimal ratio between adaptation and mitigation decreases with A as Proof. The first step is to obtain an asymptotic estimate (for large
n) for the solution
v of nonlinear Equation (47). Using the same technique as in Corollary 1, we obtain the estimate
for the solution
v of Equation (47) when
f(
v) is large. The formula (61) is similar to (52) but includes the additional parameter
k. Nevertheless, fixing all parameters in Equation (61) except for
n, we obtain the asymptotic estimate
v ~
. Next, substituting this estimate to Equation (46), we obtain the asymptotic estimates (57) for
xN,
yN,
zN and, subsequently, (58).
The asymptotic estimates (59) and (60) for the case of large and increasing A are obtained analogously.
The Corollary is proven. □
Theorem 5 and Corollary 2 generalizes outcomes of
Section 3.1 and
Section 3.2. First of all, the global emission
E in the competitive case is smaller for a larger number
n of countries when the mitigation technology is efficient (at
k >
η) and is larger at
k <
η. Second, the adaptation in both competitive (4) and cooperative games (5) is positive only above a certain adaptation efficiency threshold. This threshold depends on the country’s ratio between its vulnerability
B, non-avoided damage
D, and the productivity
A of the economy. A similar result was obtained for one country case in [
5,
26] and for a dynamic two-country model in [
20]. Theorem 5 extends this result to the multi-country case. Now, one can see how this result depends on the number
n of symmetric countries. In particular, by Equations (58) and (60), the optimal ratio
yN/
zN between mitigation and adaptation in the competitive strategy is smaller when more countries are involved in the game, and is larger when the country’s productivity becomes larger.
A new outcome is that the adaptation investment zN in competitive strategy is larger in absolute units for a larger number n if the mitigation effectiveness k is weak: k < η/2. At more effective mitigation: , the adaptation becomes less relevant and decreases with n. If mitigation becomes even more effective: k ≥ (η + 1)/2, then the optimal output grows faster than the mitigation cost and leads to infinite output (as it was in the model (13) with mitigation only).
4. Discussion and Conclusions
Many recent publications [
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
42,
43,
44,
45,
46] explore various economic, political, financial, welfare, and regional aspects of strategic interplay between mitigation and adaptation. The majority of related papers tend to favor mitigation versus adaptation for various relevant (and not-so-relevant) reasons. The most convincing pitch of [
38] states that adaptation always represents a significant loss of global welfare and, as such, should be zero. The present paper adds a new argument to this discussion. Namely, as opposed to the mitigation efficiency parameter
k, the adaptation efficiency
a does not appear in the growth rates for the optimal emission and output in both competitive and cooperative strategies. This implies that mitigation leads to a higher payoff than adaptation and, therefore, adaptation
plays a secondary role compared to mitigation in a crowded (large
n) and/or highly efficient (large
A) symmetric world. Indeed, mitigation addresses the causes of environmental contamination, while adaptation reduces related damages, but does not decrease the contamination itself.
At the same time, our analysis reveals that the
presence of mitigation increases the effectiveness of adaptation. Indeed, the output, emission, adaptation, and mitigation efforts (in both competition and cooperation) increase with the country’s productivity, and this increase is
faster with a more effective mitigation. This outcome analytically confirms the recent simulation result of the integrated assessment model AD-MERGE [
8] that using both adaptation and mitigation is more effective than using just one. In other words, there is a synergy between adaptation and mitigation, even in the one-country case.
The optimal pollution and output of an individual country are always larger in the presence of mitigation than with no mitigation in both competitive and social optimum scenarios. However, the competitive optimal welfare (payoff) evolution depends on the efficiency of mitigation. All of those levels can only increase further when the adaptation is added.
As the primary strategy, the mitigation determines whether the collective action dilemma worsen when the number n of players (countries) increases. Namely, the answer depends on the relation between mitigation efficiency k and the utility function parameter η (consumer risk aversion). The global emission in the competitive world is larger for a larger number of countries when k < η and smaller at k > η.
Despite being a public good, mitigation is the only strategy that can alleviate the environmental pollution problem. The optimal adaptation activity is also subjected to the mitigation efficiency. If the mitigation is effective, then the adaptation effort decreases with n. When the mitigation is weak, then adaptation investment in competition is larger in absolute units for a bigger n. The optimal ratio between mitigation and adaptation investments in the competitive case decreases when the country’s productivity is larger and increases when more countries are involved in the game.
In both competitive and cooperative cases, the adaptation is positive starting at a certain critical level of a country’s productivity/harmfulness ratio. Adaptation in the cooperative case starts later and is smaller than in competition. As shown above, the optimal environmental policy for weak economies (with small productivity
A) involves a minimal mitigation effort and no adaptation. In reality, poorer countries are more affected by global environmental problems, but they simply cannot pay for those efforts. A nonlinear game of two asymmetric regions, north and south, developed in [
22], addresses this inequality issue. Incorporating such asymmetries in a multi-country environmental game is an important direction for further research.