Learning (Not) to Evade Taxes
Abstract
1. Introduction
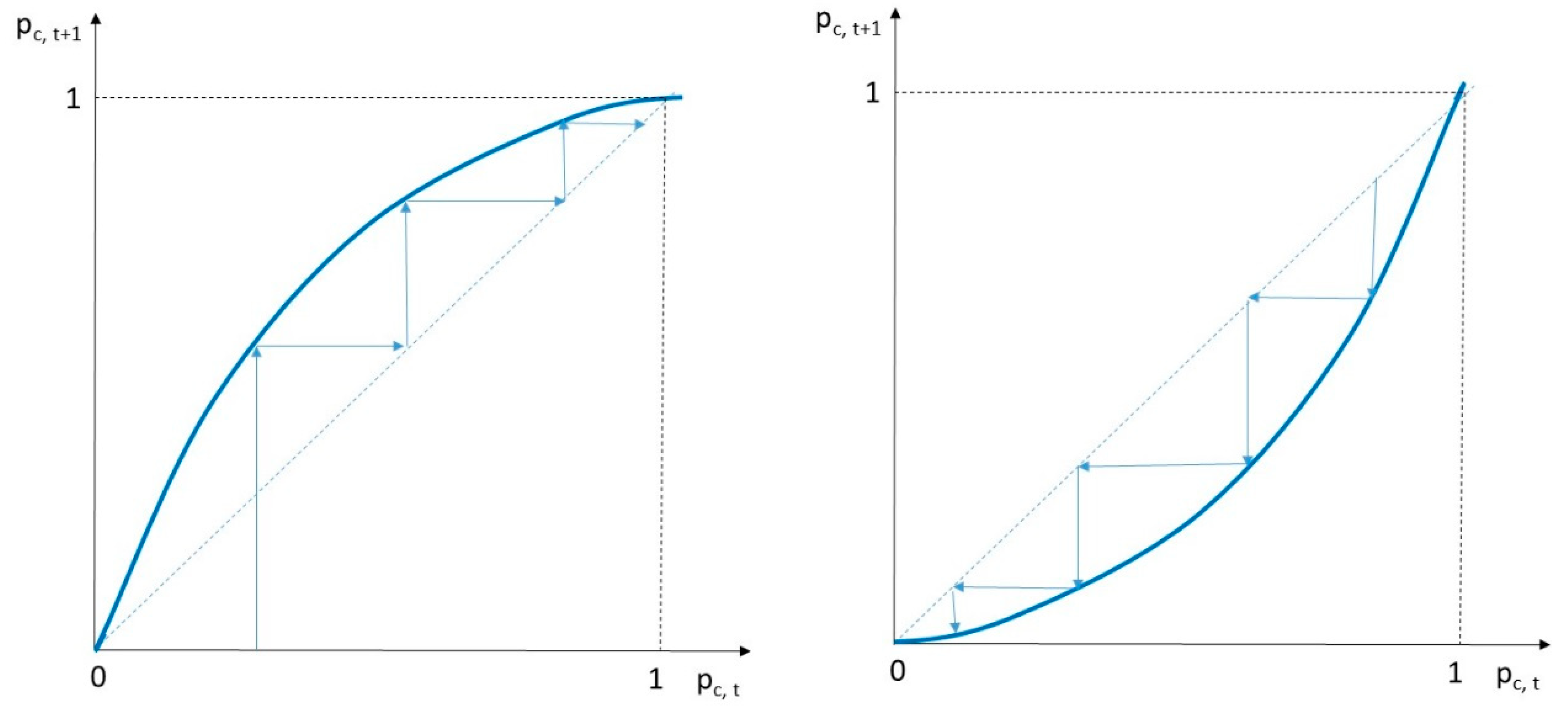
2. A Deterministic Approach to Tax Experiment Learning
- Y: income (exogenously fixed);
- T(Y): tax tariff;
- Td,t: tax due on the basis of the declared income with Td ≤ T(Y);
- t: time;
- : probability of a tax audit (detection probability of tax evasion), 0 < < 1;
- F(Td): penalty in the case of detected tax evasion, F(Td) > 1;
- pc: degree of tax compliance, pc = Td/T(Y);
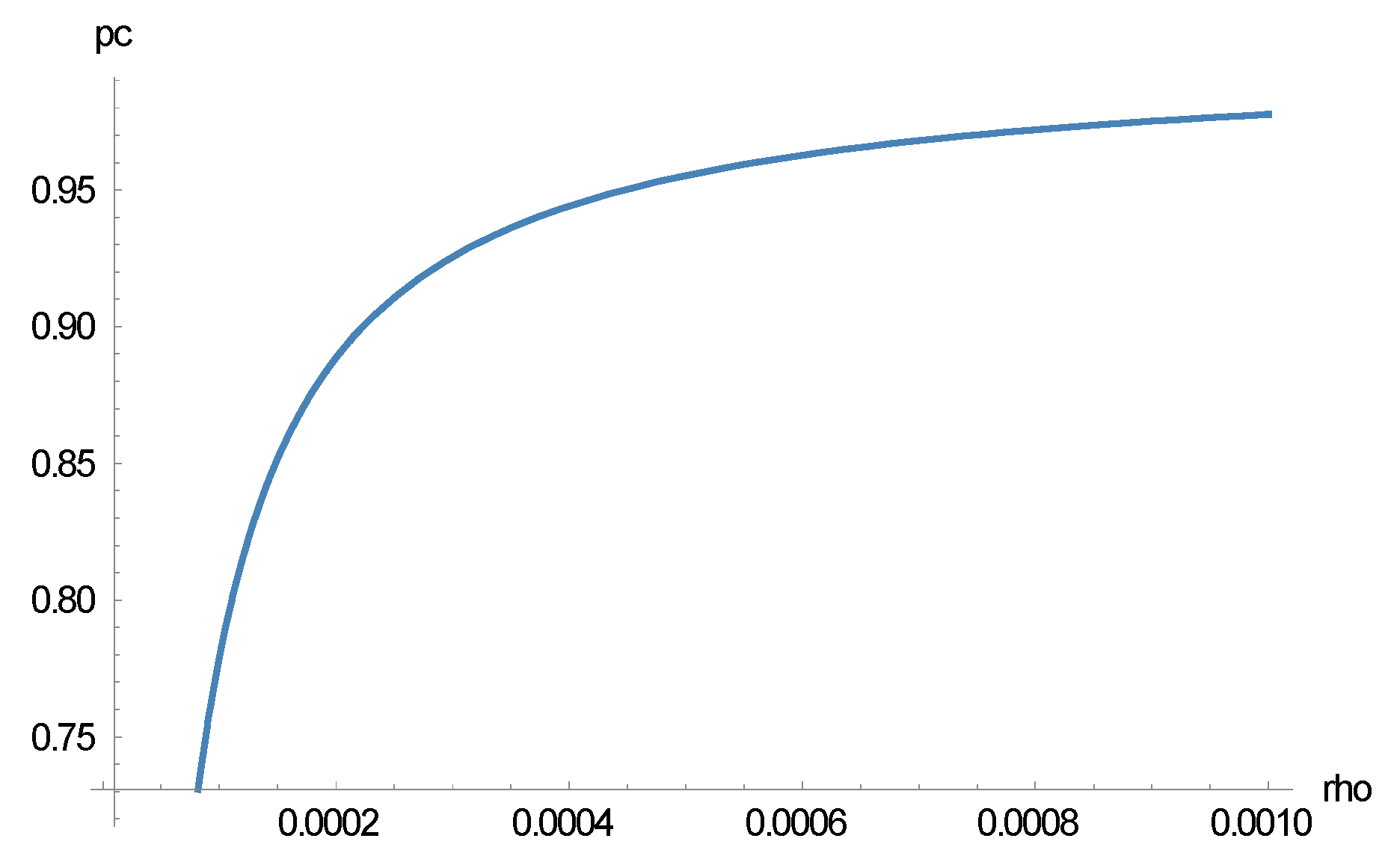
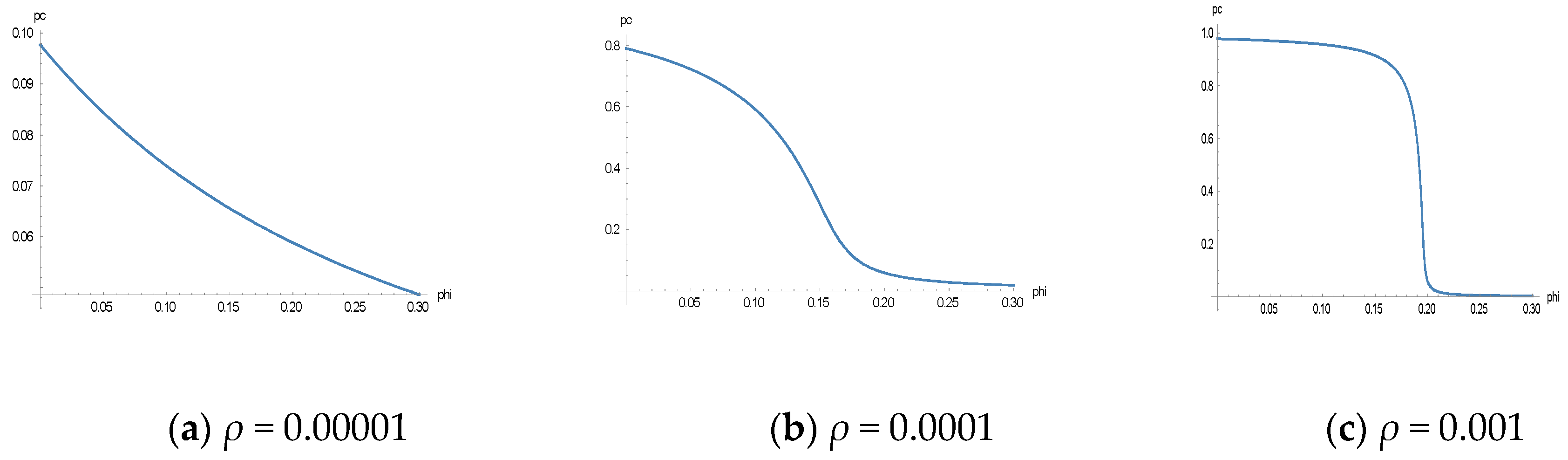
3. Stochastic Learning in Tax Experiments
3.1. Theoretical Analysis
3.2. Simulations
- The most likely compliance probabilities (or propensities) in tax compliance experiments are zero and unity, deterministically, as well as with trembling hand stochasticity;
- Linear approximations of utility functions, in combination with aspiration levels and learning rates, may suffice to explain the experiments’ results.
- “Trembling hands” and learning are seemingly important elements for the explanation of the results of the experiments.
- “Trembling hand” effects cannot be detected with deterministic approaches. The key new insight from the stochastic model is that it captures and explains erratic and idiosyncratic behavioral effects. This implies that participants may not behave irrationally, but only with “trembling hands”.
- Unobservable variables, represented in the above model by the learning rate and the aspiration level, are relevant ingredients in a theory of experimental behavior of human subjects.
4. Empirical Analysis
4.1. Descriptive Analysis
4.2. Econometric Analysis
4.3. Robustness Check
4.4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Allingham, M.G.; Sandmo, A. Income tax evasion: A theoretical analysis. J. Public Econ. 1972, 1, 323–338. [Google Scholar] [CrossRef]
- Yitzhaki, S. Income tax evasion: A theoretical analysis. J. Public Econ. 1974, 3, 201–202. [Google Scholar] [CrossRef]
- Torgler, B. Speaking to theorists and searching for facts: Tax morale and tax compliance in experiments. J. Econ. Surv. 2002, 16, 657–683. [Google Scholar] [CrossRef]
- Mascagni, G. From the lab to the field: A review of tax experiments. J. Econ. Surv. 2018, 32, 273–301. [Google Scholar] [CrossRef]
- Hashimzade, N.; Myles, G.D.; Tran-Nam, B. Applications of behavioral economics to tax evasion. J. Econ. Surv. 2013, 27, 941–977. [Google Scholar]
- Luttmer, E.F.P.; Singhal, M. Tax morale. J. Econ. Perspect. 2014, 28, 149–168. [Google Scholar] [CrossRef]
- Pickhardt, M.; Prinz, A. Behavioral dynamics of tax evasion. A survey. J. Econ. Psychol. 2014, 40, 1–19. [Google Scholar] [CrossRef]
- Slemrod, J. Tax Compliance and Enforcement. NBER 2018. [Google Scholar] [CrossRef]
- Ariely, D. The (Honest) Truth about Dishonesty; HarperCollins: New York, NY, USA, 2012. [Google Scholar]
- Mazar, N.; Amir, O.; Ariely, D. The dishonesty of honest people: A theory of self-concept maintenance. J. Marketing Res. 2008, 45, 633–644. [Google Scholar] [CrossRef]
- Cross, J.G. A stochastic learning model of economic behavior. Q. J. Econ. 1973, 87, 239–266. [Google Scholar] [CrossRef]
- Börgers, T.; Sarin, R. Learning through reinforcement and the replicator dynamics. J. Econ. Theory 1997, 77, 1–14. [Google Scholar] [CrossRef]
- Erev, I.; Roth, A.E. Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Goeree, J.; Holt, C.A. Stochastic game theory: For playing games, not just for doing theory. PNAS 1999, 96, 10564–10567. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K. The Theory of Learning in Games; MIT Press: Cambridge, UK, 1998. [Google Scholar]
- Fudenberg, D.; Levine, D.K. Whither game theory? Towards a theory of learning in games. J. Econ. Perspect. 2016, 30, 151–169. [Google Scholar] [CrossRef]
- Neiman, T.; Loewenstein, Y. Reinforcement learning in professional basketball players. Nat. Commun. 2011, 2, 569. [Google Scholar] [CrossRef]
- Spanknebel, M.; Pawelzik, K. Dynamics of human cooperation in economic games. Available online: https://arxiv.org/abs/1508.05288 (accessed on 27 September 2019).
- Vale, R. A model for tax evasion with some realistic properties. Available online: https://arxiv.org/pdf/1508.02476.pdf (accessed on 27 September 2019).
- Soliman, A.; Jones, P.; Cullis, J. Learning in experiments: Dynamic intraction of policy variables designed to deter tax evasion. J. Econ. Psychol. 2014, 40, 175–186. [Google Scholar] [CrossRef]
- Kastlunger, B.; Kirchler, E.; Mittone, L.; Pitters, J. Sequences of audits, tax compliance, and taxpaying strategies. J. Econ. Psychol. 2009, 30, 405–418. [Google Scholar] [CrossRef]
- DeBacker, J.; Heim, B.T.; Tran, A.; Yuskavage, A. Once bitten, twice shy? The lasting impact of enforcement on tax compliance. J. Law Econ. 2018, 61, 1–35. [Google Scholar] [CrossRef]
- Kogler, C.; Mittone, L.; Kirchler, E. Delayed feedback on tax audits affects compliance and fairness perceptions. J. Econ. Behav. Organ. 2016, 124, 81–87. [Google Scholar] [CrossRef]
- Muehlbacher, S.; Mittone, L.; Kastlunger, B.; Kirchler, E. Uncertainty resolution in tax experiments: Why waiting for an audit increases compliance. J. Socio-Econ. 2012, 41, 289–291. [Google Scholar] [CrossRef]
- Gangl, K.; Torgler, B.; Kirchler, E.; Hofmann, E. Effects of supervision on tax compliance: Evidence from a field experiment in Austria. Econ. Lett. 2014, 123, 378–382. [Google Scholar] [CrossRef]
- Mittone, L.; Saredi, V. Commitment to tax compliance: Timing effects on willingness to evade. J. Econ. Psychol. 2016, 53, 99–117. [Google Scholar] [CrossRef]
- Mittone, L. Dynamic behaviour in tax evasion: An experimental approach. J. Socio-Econ. 2006, 35, 813–835. [Google Scholar] [CrossRef]
- Maciejovsky, B.; Kirchler, E.; Schwarzenberger, H. Misperception of chance and loss repair: On the dynamics of tax compliance. J. Econ. Psychol. 2007, 28, 678–691. [Google Scholar] [CrossRef]
- Kirchler, E.; Hoelzl, E.; Wahl, I. Enforced versus voluntary tax compliance: The „slippery slope“ framework. J. Econ. Psychol. 2008, 29, 210–225. [Google Scholar] [CrossRef]
- Prinz, A.; Muehlbacher, S.; Kirchler, E. The slippery slope framework on tax compliance: An attempt to formalization. J. Econ. Psychol. 2014, 40, 20–34. [Google Scholar] [CrossRef]
- Kastlunger, B.; Muehlbacher, S.; Kirchler, E.; Mittone, L. What goes around comes around? Experimental evidence of the effect of rewards on tax compliance. Public Financ. Rev. 2011, 39, 150–167. [Google Scholar] [CrossRef]
- Krauskopf, T.; Prinz, A. Methods to reanalyze tax compliance experiments: Monte Carlo simulations and decision time analysis. Public Financ. Rev. 2011, 39, 168–188. [Google Scholar] [CrossRef]
- Srinivasan, T.N. Tax evasion: A model. J. Public Econ. 1973, 2, 339–346. [Google Scholar] [CrossRef]
- Güth, W. Satisficing and (un)bounded rationality—A formal definition and its experimental validity. J. Econ. Behav. Organ. 2010, 73, 308–316. [Google Scholar] [CrossRef]
- Selten, R. Re-examination of the perfectness concept for equilibrium points in extensive games. Int. J. Game Theory 1975, 4, 25–55. [Google Scholar] [CrossRef]
- Jetschke, G. Mathematik der Selbstorganisation; VEB Deutscher Verlag der Wissenschaften: Berlin, Germany, 1989. [Google Scholar]
- Pontryagin, L.; Andronov, A.; Vitt, A. On the statistical treatment of dynamical systems. In Noise in Nonlinear Dynamical Systems. Vol. 1: Theory of Continuous Fokker-Planck Systems; Moss, F., McClintock, P.V.E., Eds.; Cambridge University Press: Cambridge, UK, 1989; pp. 329–348. [Google Scholar]
- Pfister, R.; Schwarz, K.A.; Janczyk, M.; Dale, R.; Freeman, J.B. Good things peak in pairs: A note on the bimodality coefficient. Front. Psychol. 2013, 4, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Freeman, J.B.; Dale, R. Assessing bimodality to detect the presence of a dual cognitive process. Behav. Res. Methods 2013, 45, 83–97. [Google Scholar] [CrossRef]
- Mead, N.L.; Baumeister, R.F.; Gino, F.; Schweitzer, M.E.; Ariely, D. Too tired to tell the truth: Self-control resource depletion and dishonesty. J. Exp. Soc. Psychol. 2009, 45, 594–597. [Google Scholar] [CrossRef]
- Wu, S.; Peng, M.; Mei, H.; Shang, X. Unwilling but not unable to control: Ego depletion increases effortful dishonesty with material rewards. Scand. J. Psychol. 2019, 60, 189–194. [Google Scholar] [CrossRef] [PubMed]
- Shteingart, H.; Loewenstein, Y. Reinforcement learning and human behavior. Curr. Opin. Neurobiol. 2014, 25, 93–98. [Google Scholar] [CrossRef] [PubMed]
- Engel, C.; Rand, D.G. What does “clean” really mean? The implicit framing of decontextualized experiments. Econ. Lett. 2014, 122, 386–389. [Google Scholar] [CrossRef]
- Zizzo, D.J. Experimenter demand effects in economic experiments. Exp. Econ. 2010, 13, 75–98. [Google Scholar] [CrossRef]
| 1 |
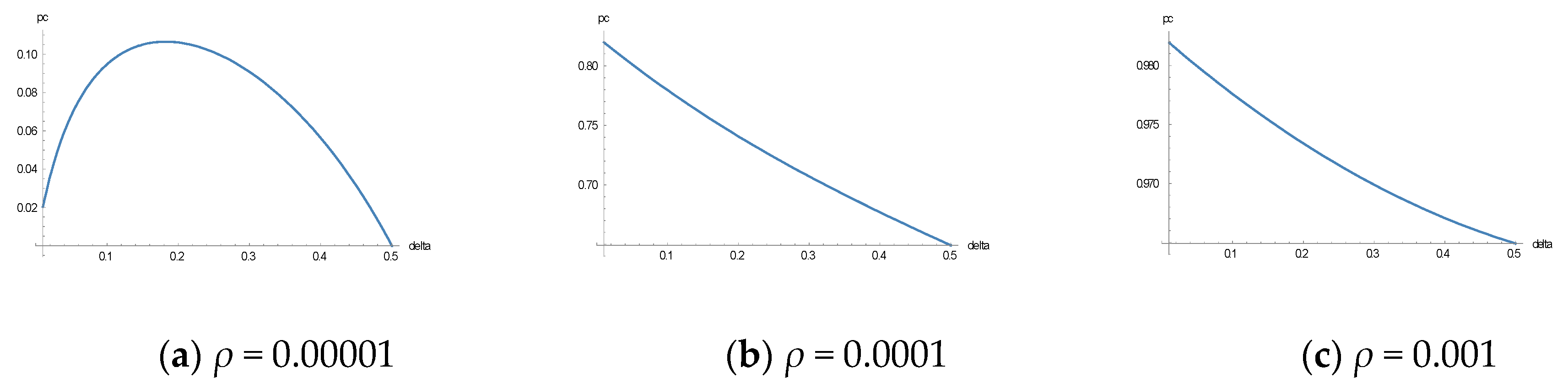
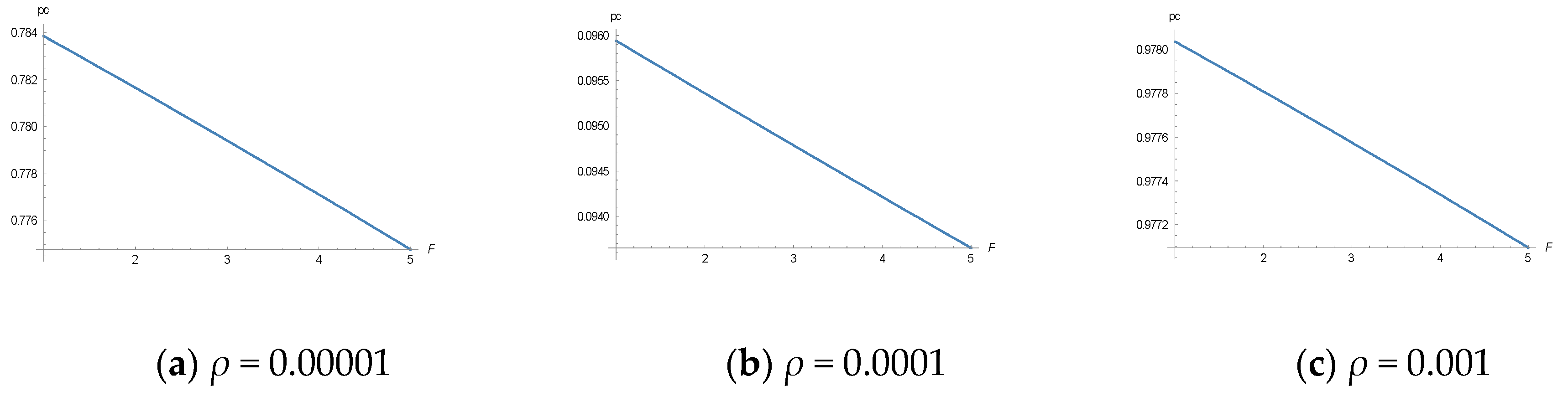
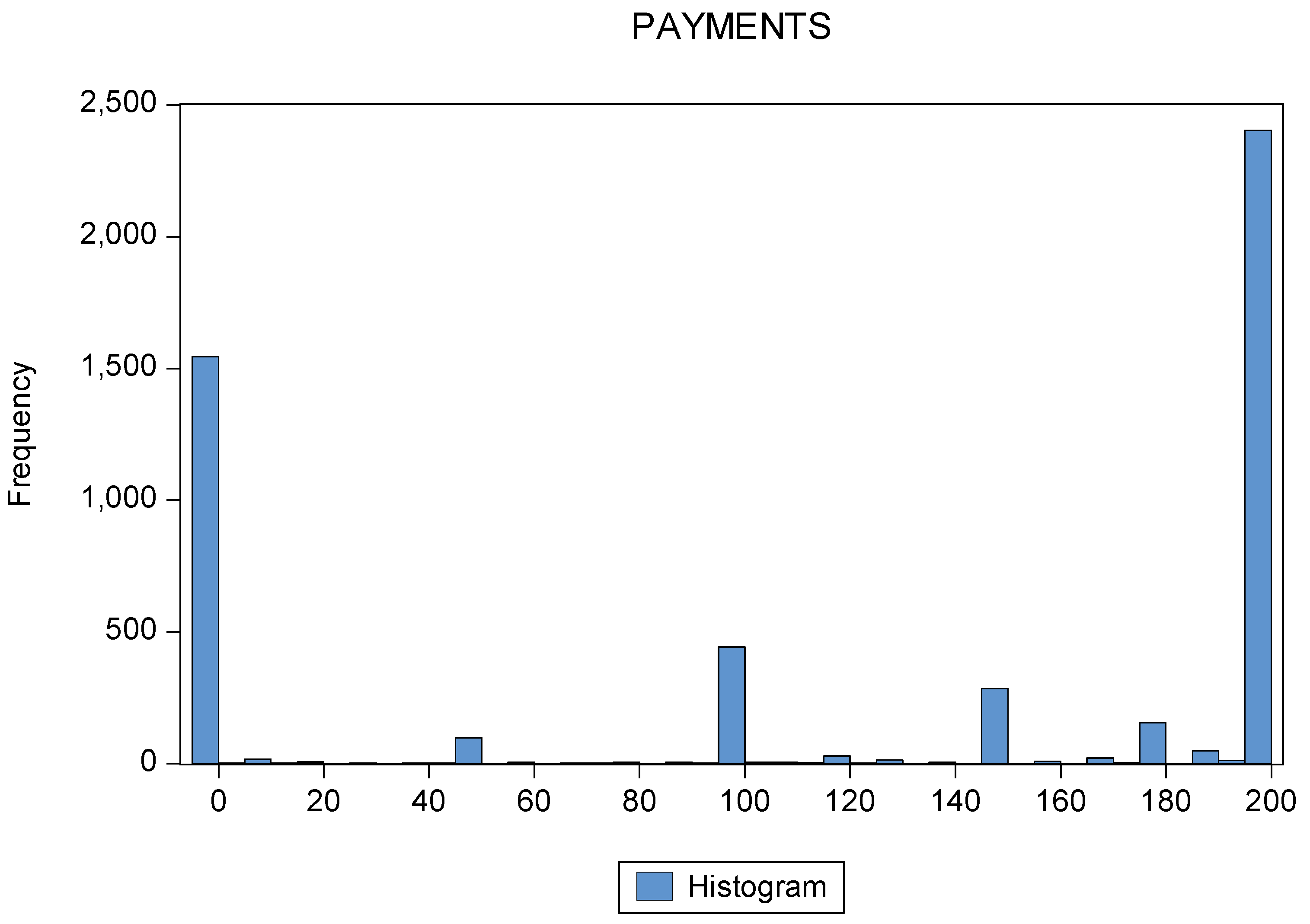
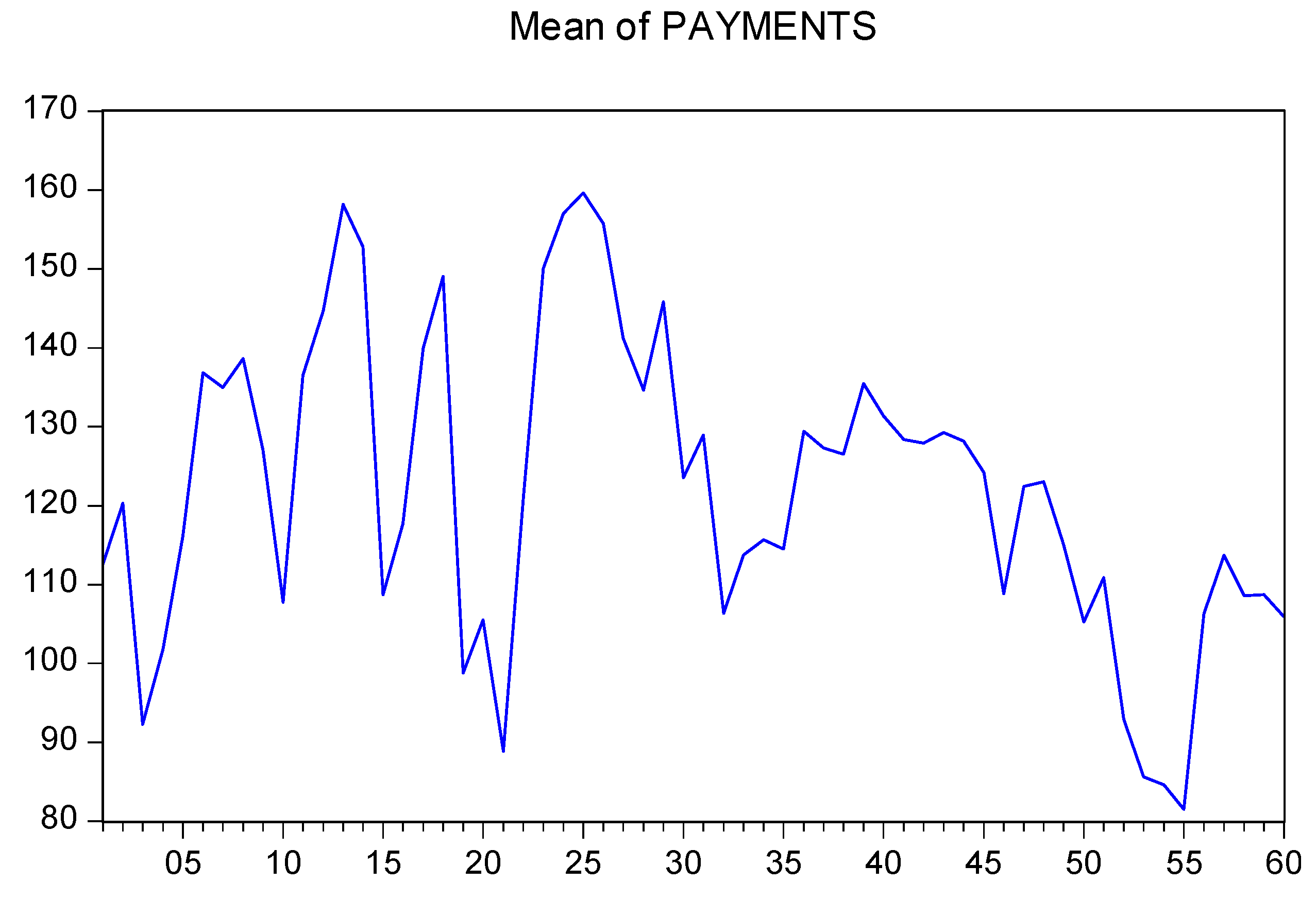
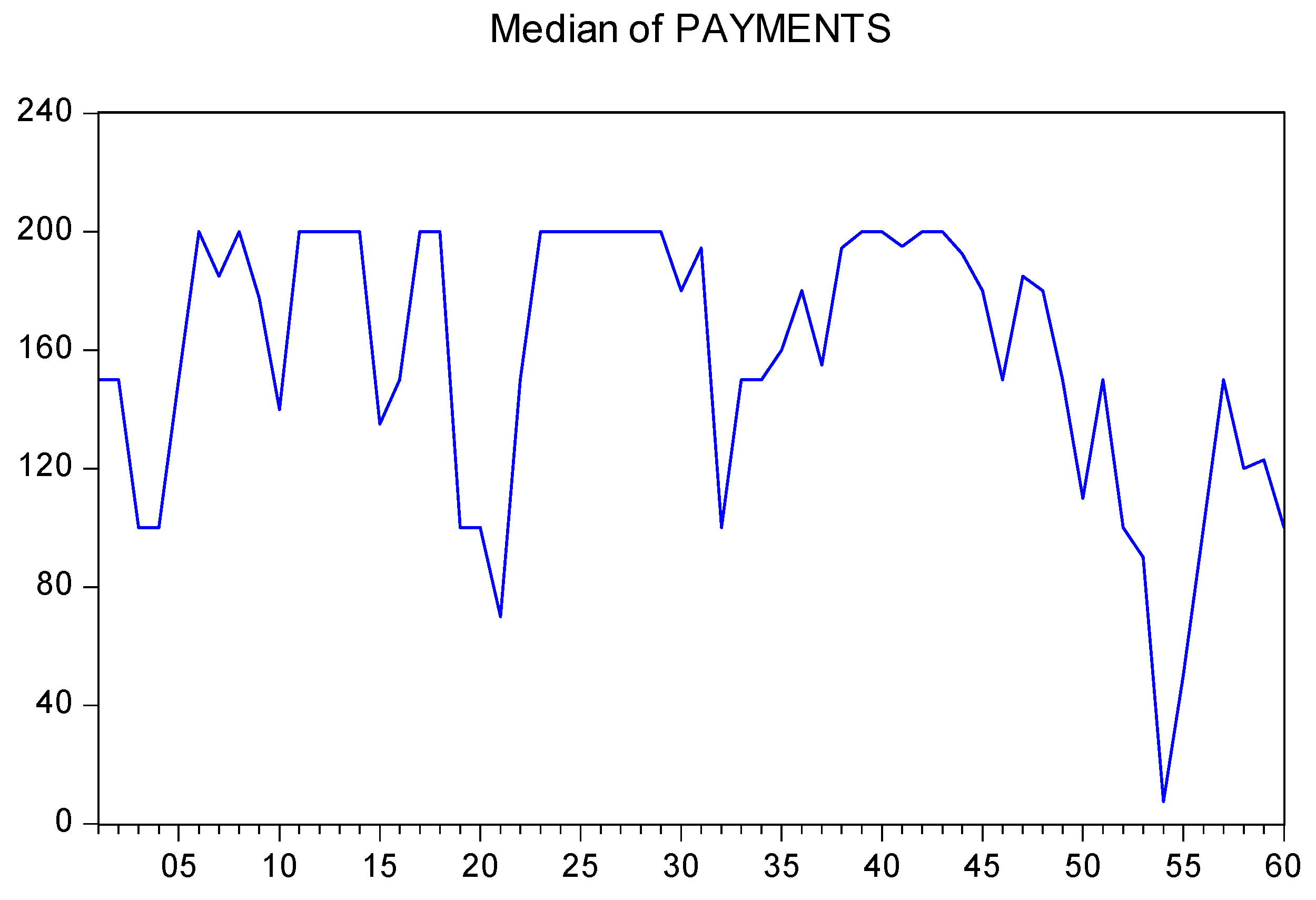
| Treatment | Mean Payment | Median Payment | Standard Deviation |
|---|---|---|---|
| No reward | 124.96 | 150.00 | 82.44 |
| Reward = 200 | 103.72 | 105.00 | 92.97 |
| Reward = 400 | 139.57 | 200.00 | 84.19 |
| Treatment 1 | Treatment 2 | Treatment 3 | ||||
|---|---|---|---|---|---|---|
| Variable | Coefficient | t-Statistic | Coefficient | t-Statistic | Coefficient | t-Statistic |
| Constant | 134.46 *** | 41.58 | 112.40 *** | 31.95 | 155.58 *** | 49.09 |
| Trend | −0.32 *** | −3.41 | −0.29 *** | −2.86 | −0.54 *** | −5.86 |
| Adjusted R2 | 0.29 | 0.34 | 0.43 | |||
| F-Statistic | 25.50 *** | 31.84 *** | 46.85 *** | |||
| Observations | 1800 | 1800 | 1560 | |||
| Variable | Coefficient | t-Statistic |
|---|---|---|
| Constant | 89.81 *** | 8.52 |
| Trend | −0.38 *** | −5.56 |
| Age | 1.29 *** | 2.87 |
| Sex (female) | 30.63 *** | 11.63 |
| Treatment = 2 | −11.01 *** | −3.50 |
| Treatment = 3 | 16.87 *** | 5.47 |
| Adjusted R2 | 0.06 | |
| F-Statistic | 66.19 *** | |
| Observations | 5100 |
| Treatment 1 | Treatment 2 | Treatment 3 | All Participants | |||||
|---|---|---|---|---|---|---|---|---|
| Rounds | Trend | t-Statistics | Trend | t-Statistics | Trend | t-Statistics | Trend | t-Statistics |
| 1–20 | −0.065 | −0.13 | 0.733 | 1.38 | 1.508 *** | 3.39 | 0.689 ** | 2.37 |
| 21–40 | 0.059 | 0.12 | −0.685 | −1.35 | −1.220 *** | −2.64 | −0.587 ** | −2.09 |
| 41–60 | −2.36 *** | −5.25 | −0.698 | −1.37 | −1.964 *** | −4.43 | −1.661 *** | −6.09 |
| Treatment 1 | Treatment 2 | Treatment 3 | ||||
|---|---|---|---|---|---|---|
| Variable | Coefficient | t-Statistic | Coefficient | t-Statistic | Coefficient | t-Statistic |
| Constant | 148.09 *** | 39.95 | 120.42 *** | 29.42 | 166.31 *** | 45.47 |
| Round = 3 | −53.76 *** | −4.16 | −38.17 *** | −2.68 | −60.93 *** | −4.78 |
| Round = 4 | −33.84 *** | −2.63 | −31.39 ** | −2.21 | −58.24 *** | −4.58 |
| Round = 8 | −9.21 | -0.72 | 12.76 | 0.90 | −7.86 | −0.62 |
| Round = 10 | −39.54 *** | −3.10 | −34.00 ** | −2.41 | −17.10 | −1.36 |
| Round =15 | −43.62 *** | −3.44 | −15.06 | −1.08 | −21.34 * | −1.71 |
| Round = 19 | −56.79 *** | −4.50 | −29.91 ** | −2.15 | −14.04 | −1.13 |
| Round = 21 | −62.79 *** | −4.98 | −35.34 ** | −2.54 | −29.81 ** | −2.40 |
| Round = 32 | −28.87 ** | −2.30 | −12.68 | −0.92 | −15.60 | −1.26 |
| Round = 52 | −26.40 ** | −2.08 | −14.60 | −1.04 | −21.41 * | −1.71 |
| Trend | −0.58 *** | −5.65 | −0.45 *** | −3.98 | −0.77 *** | −7.52 |
| Adjusted R2 | 0.32 | 0.35 | 0.45 | |||
| F-Statistic | 22.60 *** | 25.50 *** | 37.26 *** | |||
| Observations | 1800 | 1800 | ||||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prinz, A. Learning (Not) to Evade Taxes. Games 2019, 10, 38. https://doi.org/10.3390/g10040038
Prinz A. Learning (Not) to Evade Taxes. Games. 2019; 10(4):38. https://doi.org/10.3390/g10040038
Chicago/Turabian StylePrinz, Aloys. 2019. "Learning (Not) to Evade Taxes" Games 10, no. 4: 38. https://doi.org/10.3390/g10040038
APA StylePrinz, A. (2019). Learning (Not) to Evade Taxes. Games, 10(4), 38. https://doi.org/10.3390/g10040038





