A COVID-19 Epidemic Model Predicting the Effectiveness of Vaccination in the US
Abstract
:1. Introduction
2. Materials and Methods
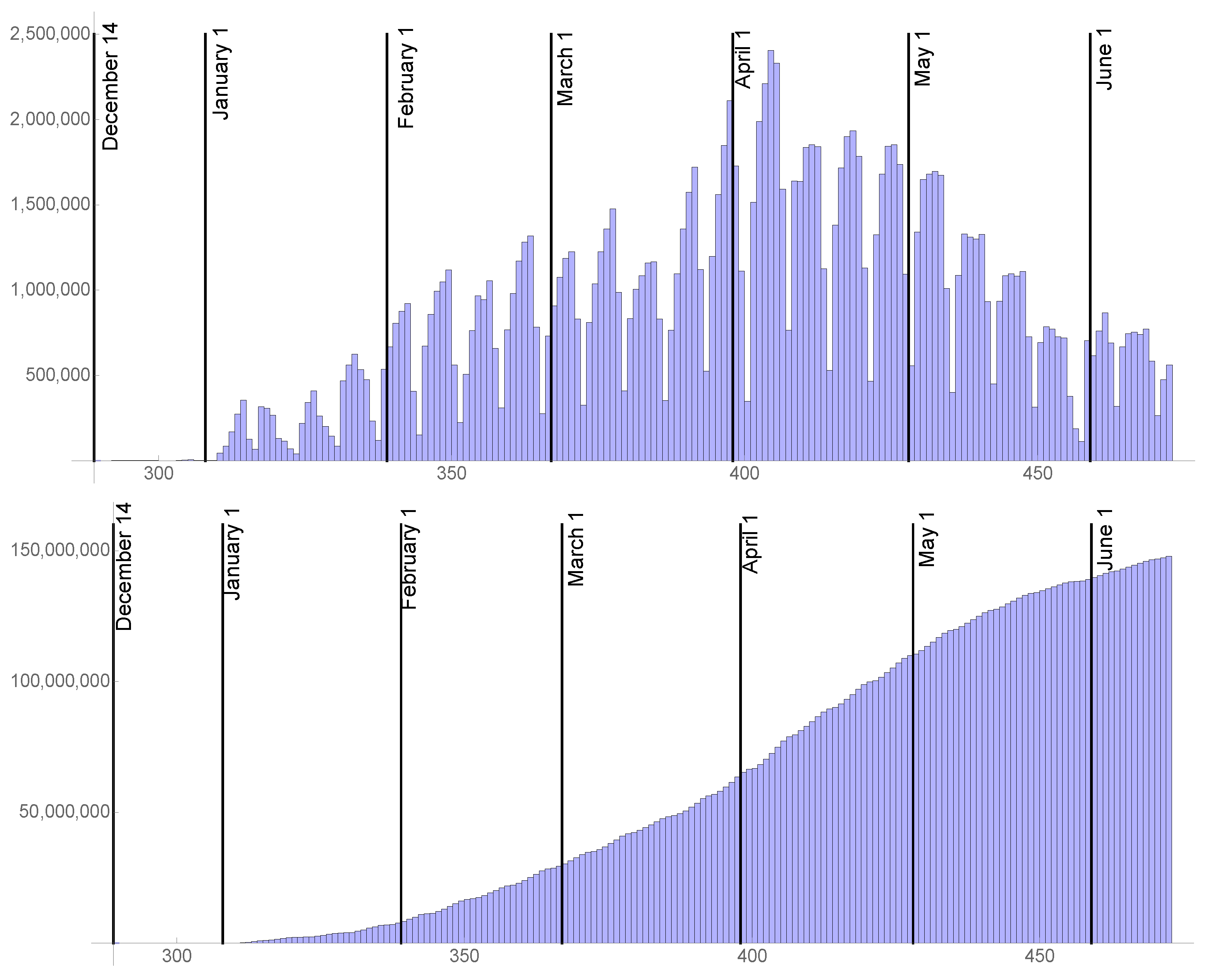
2.1. The Transmission Rate before the Last Day of Daily Reported Cases
2.2. The Transmission Rate after the Last Day of Daily Reported Cases
2.3. The Rates of Transition from Asymptomatic Infection to Symptomatic Infection
2.4. The Rate of Vaccination
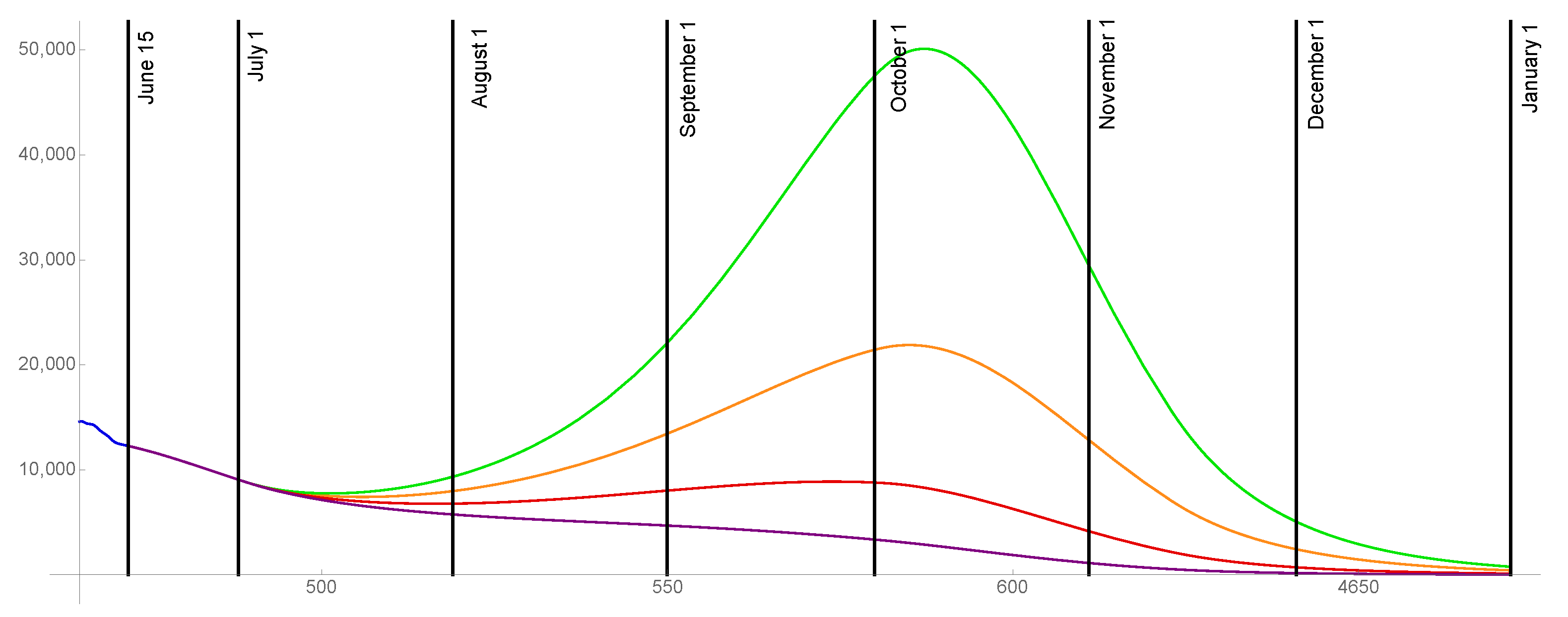
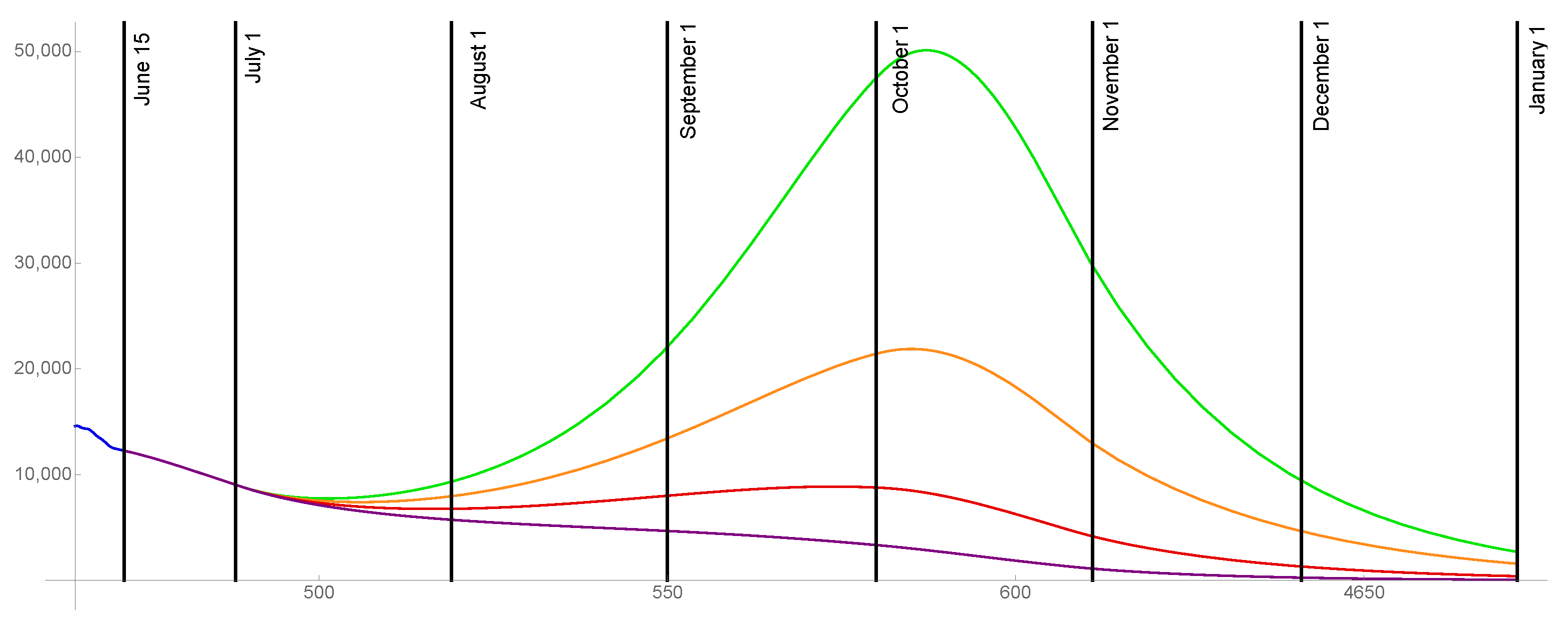
3. Results
3.1. of the Population Becomes Fully Vaccinated
3.2. of the Population Becomes Fully Vaccinated
3.3. of the Population Becomes Fully Vaccinated
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aldila, D.; Samiadji, B.; Simorangkir, G.; Khosnaw, S.; Shahzad, M. Impact of early detection and vaccination strategy in COVID-19 eradication program in Jakarta, Indonesia. BMC Res. Notes 2021, 14, 132. [Google Scholar] [CrossRef]
- Angulo, M.; Castanos, F.; Moreno-Morton, R.; Velasco-Hernandez, J.; Moreno, J. A simple criterion to design optimal non-pharmaceutical interventions for mitigating epidemic outbreaks. R. Soc. Int. 2021, 18, 20200803. [Google Scholar] [CrossRef]
- Arino, J.; Portet, S. A simple model for COVID-19. Infect. Dis. Model. 2021, 5, 309–315. [Google Scholar] [CrossRef]
- Ayoub, H.; Chemaitelly, H.; Mikhail, M.; Kanaani, Z.; Kuwari, E.; Butt, A.; Coyle, P.; Jeremijenko, A.; Kaleeckal, A.; Latif, A.; et al. Epidemiological impact of prioritising SARS-CoV-2 vaccination by antibody status: Mathematical modelling analyses. BMJ Inner. 2021, 7, 327–336. [Google Scholar] [CrossRef]
- Betti, M.; Hefferman, J. A simple model for fitting mild, severe, and known cases during an epidemic with an application to the current SARS-CoV-2 pandemic. Infect. Dis. Model. 2021, 5, 313–323. [Google Scholar] [CrossRef]
- Bonanca, P.; Angelillo, I.; Villani, A.; Biasci, P.; Scotti, S.; Russo, R.; Maio, T.; Vitali Rosati, G.; Barretta, M.; Bozzola, E.; et al. Maintain and increase vaccination coverage in children, adolescents, adults and elderly people: Let’s avoid adding epidemics to the pandemic: Appeal from the Board of the Vaccination Calendar for Life in Italy: Maintain and increase coverage also by re-organizing vaccination services and reassuring the population. Vaccine 2021, 39, 1187–1189. [Google Scholar] [CrossRef]
- Bracis, C.; Burns, E.; Moore, M.; Swan, D.; Reeves, D.; Schiffer, J.; Dimitrov, D. Widespread testing, case isolation and contact tracing may allow safe school reopening with continued moderate physical distancing: A modeling analysis of King County, WA data. Infect. Dis. Model. 2021, 6, 24–35. [Google Scholar] [CrossRef]
- Britton, T.; Ball, F.; Trapman, P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science 2020, 369, 846–849. [Google Scholar] [CrossRef]
- Bubar, K.; Reinholt, K.; Kessler, S.; Lipsitch, M.; Cobey, S.; Grad, Y.; Larremore, D. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science 2021, 371, 916–921. [Google Scholar] [CrossRef] [PubMed]
- Byambasuren, O.; Cardona, M.; Bell, K.; Clark, J.; McLaws, M.-L.; Glasziou, P. Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: Systematic review and meta-analysis. Off. J. Assoc. Med. Microbiol. Infect. Dis. Can. 2020, 5, 223–234. [Google Scholar] [CrossRef]
- Byrne, A.; McEvoy, D.; Collins, A.; Hunt, K.; Casey, M.; Barber, A.; Butler, F.; Griffin, J.; Lane, E.; McAloon, C.; et al. Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open 2020, 10, e039856. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, J.; Kim, J.E.; Choi, H.; Lee, C. Vaccination prioritization strategies for COVID-19 in Korea: A mathematical modeling approach. Int. J. Environ. Res. Public Health 2021, 18, 4240. [Google Scholar] [CrossRef]
- Contreras, S.; Priesemann, V. Risking further COVID-19 waves despite vaccination. Lancet Infect. Dis. 2021. [Google Scholar] [CrossRef]
- Das, P.; Upadhyay, R.; Misra, A.; Rihan, F.; Das, P.; Ghosh, D. Mathematical model of COVID-19 with comorbidity and controlling using non-pharmaceutical interventions and vaccination. Nonlinear Dyn. 2021. [Google Scholar] [CrossRef]
- Dashtbali, M.; Mirzaie, M. A compartmental model that predicts the effect of social distancing and vaccination on controlling COVID-19. Sci. Rep. 2021, 11, 8191. [Google Scholar] [CrossRef] [PubMed]
- Dean, N.; Pastore, Y.; Piontti, A.; Madewell, Z.; Cummings, D.; Hitchings, M.; Joshi, K.; Kahn, R.; Vespignani, A.; Halloran, M.; et al. Ensemble forecast modeling for the design of COVID-19 vaccine efficacy trials. Vaccine 2020, 38, 7213–7216. [Google Scholar] [CrossRef] [PubMed]
- De la Sen, M.; Ibeas, A. On an SE(Is)(Ih)AR epidemic model with combined vaccination and antiviral controls for COVID-19 pandemic. Adv. Differ. Equ. 2021, 92. [Google Scholar] [CrossRef]
- Demongeot, J.; Griette, Q.; Magal, P. SI epidemic model applied to COVID-19 data in mainland China. R. Soc. Open Sci. 2021, 7, 21878. [Google Scholar] [CrossRef]
- Eikenberry, S.; Muncuso, M.; Iboi, E.; Phan, T.; Eikenberry, K.; Kuang, Y.; Kostelich, E.; Gummel, A. To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 2021, 5, 293–308. [Google Scholar] [CrossRef]
- Elhia, M.; Chokri, K.; Alkama, M. Optimal control and free optimal time problem for a COVID-19 model with saturated vaccination function. Commun. Math. Biol. Neurosci. 2021, 5. [Google Scholar] [CrossRef]
- Firth, J.; Hellewell, J.; Klepac, P.; Kissler, S.; CMMID COVID-19 Working Group; Kucharski, A.; Spurgin, L. Using a real-world network to model localized covid-19 control strategies. Nat. Med. 2020, 26, 1616–1622. [Google Scholar] [CrossRef] [PubMed]
- Fontanet, A.; Cauchemez, S. COVID-19 herd immunity: Where are we? Nat. Rev. Immunol. 2020, 20, 583–584. [Google Scholar] [CrossRef] [PubMed]
- Forien, R.; Pang, G.; Pardoux, E. Estimating the state of the COVID-19 epidemic in France using a model with memory. R. Soc. Open Sci. 2021. [Google Scholar] [CrossRef]
- Foy, B.; Wahl, B.; Mehta, K.; Shet, A.; Menon, G.; Britto, C. Comparing COVID-19 vaccine allocation strategies in India: A mathematical modelling study. Int. J. Infect. Dis. 2021, 103, 431–438. [Google Scholar] [CrossRef]
- Gokbulut, N.; Kuymakamzade, B.; Sanlidag, T.; Hincal, E. Mathematical modelling of Covid-19 with the effect of vaccine. AIP Conf. Proc. 2021, 2325, 020065. [Google Scholar] [CrossRef]
- Goldstein, J.; Cassidy, T.; Wachter, K. Vaccinating the oldest against COVID-19 saves both the most lives and most years of life. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef] [PubMed]
- Griette, Q.; Magal, P. Clarifying predictions for COVID-19 from testing data: The example of New-York State. Infect. Dis. Model. 2021, 6, 273–283. [Google Scholar] [CrossRef]
- Griette, Q.; Liu, Z.; Magal, P.; Thompson, R. Real-Time Prediction of the End of an Epidemic Wave: COVID-19 in China as a Case-Study; Semantic Scholar: Seattle, WA, USA, 2020. [Google Scholar]
- Gumel, A.; Ibio, E.; Ngonghala, C.; Elbas, E. A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations. Infect. Dis. Model. 2021, 6, 148–168. [Google Scholar] [CrossRef]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.; Jarvis, C.; Russell, T.; Munday, J.; Kucharski, A.; Edmunds, W.; Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group; et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, E488–E496. [Google Scholar] [CrossRef] [Green Version]
- Huo, X.; Chen, J.; Ruan, S. Estimating asymptomatic, undetected and total cases for the COVID-19 outbreak in Wuhan: A mathematical modeling study. Bmc Infect Dis. 2021, 21. [Google Scholar] [CrossRef]
- Huo, X.; Sun, X.; Bragazzi, N.; Wu, J. Effectiveness and feasibility of convalescent blood transfusion to reduce COVID-19 fatality ratio. R. Soc. Open Sci. 2021, 8. [Google Scholar] [CrossRef] [PubMed]
- Iboi, E.; Ngonghala, C.; Gumel, A. Will an imperfect vaccine curtail the COVID-19 pandemic in the US? Infect. Dis. Model. 2021, 5, 510–524. [Google Scholar] [CrossRef]
- IHME COVID-19 Forecasting Team; Reiner, R.; Barber, R.; Collins, J.; Zheng, P.; Adolph, C.; Albright, J.; Antony, C.; Aravkin, A.; Bachmeier, S.; et al. Modeling COVID-19 scenarios for the United States. Nat. Med. 2021, 27, 94–105. [Google Scholar] [CrossRef]
- Inayaturohmat, F.; Zikkah, R.; Supriatna, A.; Anggriani, N. Mathematical model of COVID-19 transmission in the presence of waning immunity. J. Phys. Conf. Ser. 2021, 1722, 012038. [Google Scholar] [CrossRef]
- Jackson, L.; Anderson, E.; Rouphael, N.; Roberts, P.; Makhene, M.; Coler, R.; McCullough, M.; Chappell, J.; Denison, M.; Stevens, L.; et al. An mRNA Vaccine against SARS-CoV-2—Preliminary Report. N. Engl. J. Med. 2021, 383, 1920–1931. [Google Scholar] [CrossRef]
- Jentsch, P.; Anand, M.; Bauch, C. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: A mathematical modelling study. Lancet Infect. Dis. 2021. [Google Scholar] [CrossRef]
- Jewell, N.; Lewnard, J.; Jewell, B. Predictive mathematical models of the COVID-19 pandemic: Underlying principles and value of projections. JAMA 2020, 323, 1893–1894. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.; Quandelacy, T.; Kada, S.; Prasad, P.; Steele, M.; Brooks, J.; Slayton, R.; Biggerstaff, M.; Butler, J. SARS-CoV-2 Transmission From People Without COVID-19 Symptoms. JAMA Netw. Open 2021, 4. [Google Scholar] [CrossRef]
- Kalyan, D.; Kumar, G.; Reddy, K.; Lakshminarayand, K. Sensitivity and elasticity analysis of novel corona virus transmission model: A mathematical approach. Sens. Int. 2021, 2, 100088. [Google Scholar] [CrossRef]
- Keeling, M.; Hill, E.; Gorsich, E.; Penman, B.; Guyver-Fletcher, G.; Holmes, A.; Leng, T.; McKimm, H.; Tamborrino, M.; Dyson, L.; et al. Predictions of COVID-19 dynamics in the UK: Short-term forecasting and analysis of potential exit strategies. PLoS Comp. Biol. 2021, 17. [Google Scholar] [CrossRef]
- Kucharski, A.; Russell, T.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R. Early dynamics of transmission and control of covid-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Lauer, S.; Grantz, K.; Bi, Q.; Jones, F.; Zheng, Q.; Meredith, H.; Azman, A.; Reich, N.; Lesser, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Libotte, G.; Lobato, F.; Platt, G.; Neto, A. Determination of an optimal control strategy for vaccine administration in COVID-19 pandemic treatment. Comput. Meth. Prog. Biol. 2020, 196, 105664. [Google Scholar] [CrossRef]
- Lipsitch, M.; Dean, N. Understanding COVID-19 vaccine efficacy. Science 2020, 370, 763–765. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding unreported cases in the 2019 -n Cov epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Mod. 2021, 5, 323–337. [Google Scholar] [CrossRef]
- Magal, P.; Webb, G. The parameter identification problem for SIR epidemic models: Identifying unreported cases. J. Math. Biol. 2018, 77, 1629–1648. [Google Scholar] [CrossRef]
- Makhoul, M.; Chemaitelly, H.; Ayoub, H.; Seedat, S.; Abu-Raddad, L. Epidemiological Differences in the Impact of COVID-19 Vaccination in the United States and China. Vaccines 2021, 9, 223. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.; Khatua, A.; Adak, S.; Kar, T. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Rodriguez, D.; Gonzalez-Parra, G.; Villanueva, R.-J. Analysis of key factors of a SARS-CoV-2 vaccination program: A mathematical modeling approach. Epidemiologia 2021, 2, 12. [Google Scholar] [CrossRef]
- Matrajt, L.; Halloran, M.; Antia, M. Successes and failures of the live-attenuated influenza vaccine: Can we do better? Clin. Infect. Dis. 2020, 70, 1029–1037. [Google Scholar] [CrossRef] [Green Version]
- Matrajt, L.; Eaton, J.; Leung, T.; Brown, E. Vaccine optimization for COVID-19: Who to vaccinate first? Sci. Adv. 2020, 7. [Google Scholar] [CrossRef]
- McDonnell, A.; Van Exan, R.; Lloyd, S.; Subramanian, L.; Chalkidou, K.; La Porta, A.; Li, J.; Maiza, E.; Reader, D.; Rosenberg, J.; et al. COVID-19 Vaccine Predictions: Using Mathematical Modelling and Expert Opinions to Estimate Timelines and Probabilities of Success of COVID-19 Vaccines; Center for Global Development: Washington, DC, USA, 2020. [Google Scholar]
- Mizumoto, K.; Chowell, G. Transmission potential of the novel coronavirus (COVID-19) onboard the diamond Princess Cruises Ship, 2020. Infect. Dis. Mod. 2021, 5, 264–270. [Google Scholar] [CrossRef]
- Moghadas, S.; Fitzpatrick, M.; Sah, P.; Pandey, A.; Shoukat, A.; Singer, B.; Galvani, A. The implications of silent transmissin for the control of COVID-19 outbreaks. Proc. Natl. Acad. Sci. USA 2020, 117, 17513–17515. [Google Scholar] [CrossRef] [PubMed]
- Moore, S.; Hill, E.; Dyson, L.; Tildesley, M.; Keeling, M. Modelling optimal vaccination strategy for SARS-CoV-2 in the UK. PLoS Comput. Biol. 2021. [Google Scholar] [CrossRef]
- Moore, S.; Hill, E.; Tildesley, M.; Dyson, L.; Keeling, M. Vaccination and non-pharmaceutical interventions for COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2021. [Google Scholar] [CrossRef]
- Olivares, A.; Steffetti, E. Uncertainty quantification of a mathematical model of COVID-19 transmission dynamics with mass vaccination strategy. Chaos Solitons Fractals 2021, 146. [Google Scholar] [CrossRef]
- Ng, V.; Fazil, A.; Waddell, L.; Turgeon, P.; Otten, A.; Ogden, N. Modelling the impact of shutdowns on resurging SARS-CoV-2 transmission in Canada. R. Soc. Open Sci. 2021. [Google Scholar] [CrossRef]
- Ngonghala, C.; Iboi, E.; Eikenberry, S.; Scotch, M.; MacIntyre, C.; Bonds, M.; Gumel, A. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel coronavirus. Math. Biosci. 2020, 9, 108364. [Google Scholar] [CrossRef]
- Ngonghala, C.; Iboi, E.; Gumel, A. Could masks curtail the post-lockdown resurgence of covid-19 in the US? Math. Biosci. 2020, 329, 108452. [Google Scholar] [CrossRef]
- Noh, J.; Danuser, G. Estimation of the fraction of COVID-19 infected people in U.S. states and countries worldwide. PLoS ONE 2021, 16. [Google Scholar] [CrossRef]
- Paget, J.; Caini, S.; Cowling, B.; Esposito, S.; Falsey, A.; Gentile, A.; Kynci, J.; Macintyre, C.; Pitman, R.; Lina, B. The impact of influenza vaccination on the COVID-19 pandemic? Evidence and lessons for public health policies. Vaccine 2021, 38, 6485–6486. [Google Scholar] [CrossRef]
- Paltiel, A.; Schwartz, J.; Zheng, A.; Walensky, R. Clinical outcomes of a COVID-19 vaccine: Implementation over efficacy. Health Aff. 2021, 40. [Google Scholar] [CrossRef]
- Peak, C.; Kahn, R.; Grad, H.; Childs, L.; Li, R.; Lipstich, M.; Buckee, C. Individual quarantine versus active monitoring of contacts for the mitigation of COVID-19: A modelling study. Lancet Infect. Dis. 2020, 20, 1025–1033. [Google Scholar] [CrossRef]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, M.; Yan, P.; Chowell, G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Mod. 2021, 5, 256–263. [Google Scholar] [CrossRef] [PubMed]
- Saldana, F.; Fiores-Arguedas, H.; Camacho-Gutierrez, J.; Barradas, I. Modeling the transmission dynamics and the impact of the control interventions for the COVID-19 epidemic outbreak. Math. Biosci. Eng. 2020, 17, 4165–4183. [Google Scholar] [CrossRef]
- Saldana, F.; Velasco-Hernandez, J. The trade-off between mobility and vaccination for COVID-19 control: A metapopulation modelling approach. R. Soc. Open Sci. 2021, 8, 202240. [Google Scholar] [CrossRef]
- Shim, E.; Tariq, A.; Choi, W.; Lee, Y.; Chowell, G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 2020, 93, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Shim, E. Optimal allocation of the limited COVID-19 vaccine supply in South Korea. J. Clin. Med. 2021, 10, 591. [Google Scholar] [CrossRef]
- Sung-Mok, J.; Akira, E.; Ryo, K.; Hiroshi, N. Projecting a second wave of COVID-19 in Japan with variable interventions in high-risk settings. R. Soc. Open Sci. 2021. [Google Scholar] [CrossRef]
- Tang, B.; Bragazzi, N.; Li, Q.; Tang, S.; Xiao, Y.; Wu, J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect. Dis. Mod. 2021, 5, 248–255. [Google Scholar] [CrossRef]
- Tariq, A.; Lee, L.; Roosa, K.; Blumberg, S.; Yan, P.; Ma, S.; Chowell, G. Real-time monitoring the transmission potential of COVID-19 in Singapore. BMC Med. 2020, 18, 1–14. [Google Scholar] [CrossRef]
- Thunstrom, L.; Ashworth, M.; Newbold, S. Hesitancy towards a COVID-19 vaccine and prospects for herd immunity. Psychology 2020. [Google Scholar] [CrossRef]
- Thurmer, S.; Klimek, P.; Hanel, R. A network-based explanation of why most covid-19 infection curves are linear. Proc. Natl. Acad. Sci. USA 2020, 117, 22684–22689. [Google Scholar] [CrossRef]
- Usherwood, T.; LaJoie, Z.; Srivastava, V. A model and predictions for COVID-19 considering population behavior and vaccination. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef]
- Wang, Z.; Muecksch, F.; Schaefer-Babajew, D.; Finkin, S.; Viant, C.; Gaebler, C.; Hoffman, H.; Barnes, C.; Cipolla, M.; Ramos, V.; et al. Naturally enhanced neutralising breadth against SARS-CoV-2 one year after infection. Nature 2021. [Google Scholar] [CrossRef]
- Webb, G. A COVID-19 epidemic model predicting the effectiveness of vaccination. Math. Appl. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Wilder, B.; Champignon, M.; Killian, J.; Ou, H.-C.; Mate, A.; Jabbari, S.; Perrault, A.; Desai, A.; Taube, M.; Majumder, M. Modelling between-population variation in COVID-19 dynamics in Hubei, Lombardy, and New York City. Proc. Natl. Acad. Sci. USA 2020, 117, 25904–25910. [Google Scholar] [CrossRef]
- Xue, L.; Jing, S.; Miller, J.; Sun, W.; Li, H.; Estrada-Franco, J.; Hyman, J.; Zhu, H. A data-driven network model for the emerging covid-19 epidemics in Wuhan, Toronto and Italy. Math. Biosci. 2020, 326, 108391. [Google Scholar] [CrossRef] [PubMed]








| Vaccinated | ||||
|---|---|---|---|---|
| = 14,768,000 | = 17,985,000 | = 19,771,000 | = 20,570,000 | |
| 3,768,000 | 2,068,000 | 1,155,000 | 745,000 | |
| = 20,971,000 | = 26,023,000 | = 28,821,000 | = 29,954,000 | |
| 3,967,000 | 2,171,000 | 1,184,000 | 750,000 | |
| = 10,147 | ||||
| = 25,486,000 | = 33,142,000 | = 37,926,000 | = 34,712,000 | |
| 4,788,000 | 2,624,000 | 1,310,000 | 774,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Webb, G. A COVID-19 Epidemic Model Predicting the Effectiveness of Vaccination in the US. Infect. Dis. Rep. 2021, 13, 654-667. https://doi.org/10.3390/idr13030062
Webb G. A COVID-19 Epidemic Model Predicting the Effectiveness of Vaccination in the US. Infectious Disease Reports. 2021; 13(3):654-667. https://doi.org/10.3390/idr13030062
Chicago/Turabian StyleWebb, Glenn. 2021. "A COVID-19 Epidemic Model Predicting the Effectiveness of Vaccination in the US" Infectious Disease Reports 13, no. 3: 654-667. https://doi.org/10.3390/idr13030062
APA StyleWebb, G. (2021). A COVID-19 Epidemic Model Predicting the Effectiveness of Vaccination in the US. Infectious Disease Reports, 13(3), 654-667. https://doi.org/10.3390/idr13030062





