Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Nonparametric Methods
Abstract
1. Introduction
2. Methods
2.1. Observational Data
2.2. Mathematical and Statistical Modelling
2.2.1. Asymptotic and Instantaneous Fatality–Case Ratios
- Delay asymptotic fatality–case ratio:
- Delay instantaneous fatality–case ratio:
2.2.2. Diagnosis-to-Death Duration via Maximum Correlation between Deaths and Time-Delayed Cases
2.2.3. Generation Time via Delay-Time Autocorrelation of Cases and Deaths
2.2.4. Piecewise Exponential Growth and the Basic Reproduction Number
3. Results
3.1. Fatality–Case Ratios Worldwide and for Eight Selected Countries
3.2. Diagnosis-to-Death Duration for Germany
3.3. Diagnosis-to-Death Duration for the Eight Selected Countries
3.4. Negative Correlation of the Fatality-to-Case Ratio with the Number of Cases
3.5. Estimating Generation Time
3.6. Time-Dependent Infection Rate and the Effective Reproduction Number
3.7. Per Capita Growth Rate as an Alternative for the Reproduction Number
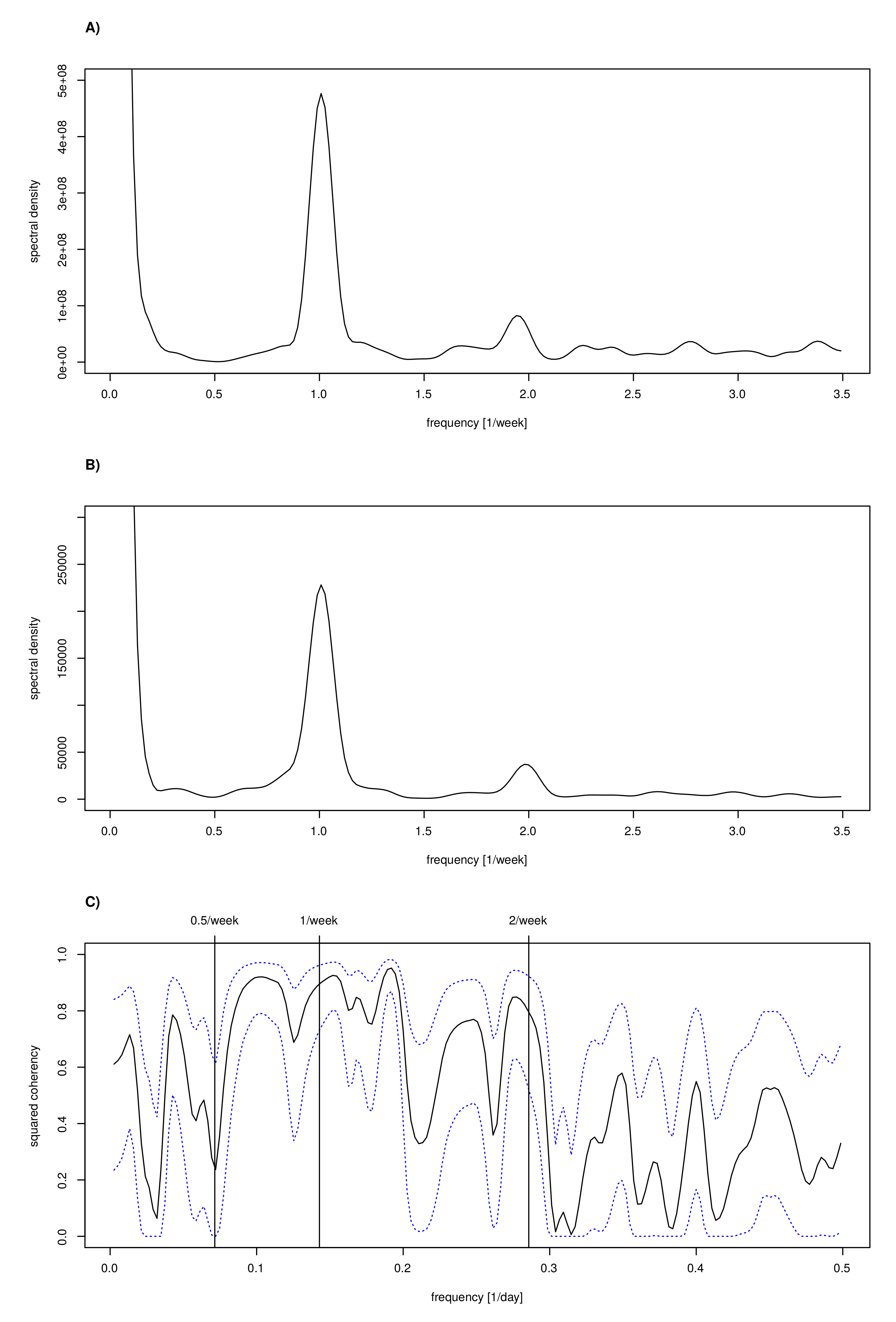
3.8. Spectral Analysis to Confirm Periods
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFCR | Asymptotic Fatality–Case Ratio |
| Generation time | Average time between two consecutive infections |
| IFCR | Instantaneous Fatality–Case Ratio |
| Basic Reproduction Number, number of secondary infections emerging | |
| from an index case in a fully susceptible population | |
| Serial interval | Average time between the onset of symptoms of two consecutive |
| infections, often used as an approximation to the generation time | |
| SIR/SEIR | Susceptible-(exposed)-infected-removed epidemiological |
| compartment models | |
| Time-to-death duration | Average time between the registrations of new cases and the |
| corresponding registrations of deaths, if applicable. |
References
- Brainard, J. Scientists are drowning in COVID-19 papers. Can new tools keep them afloat? Science 2020, 13. [Google Scholar] [CrossRef]
- Bramstedt, K.A. The carnage of substandard research during the COVID-19 pandemic: A call for quality. J. Med. Ethics 2020, 46, 803–807. [Google Scholar] [CrossRef] [PubMed]
- Jahedi, S.; Yorke, J. When the best pandemic models are the simplest. Biology 2020, 9, 353. [Google Scholar] [CrossRef] [PubMed]
- Dietz, K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res. 1993, 2, 23–41. [Google Scholar] [CrossRef] [PubMed]
- Heesterbeek, J.A.P.; Dietz, K. The concept of R0 in epidemic theory. Stat. Neerl. 1996, 50, 89–110. [Google Scholar] [CrossRef]
- Böhmer, M.M.; Buchholz, U.; Corman, V.M.; Hoch, M.; Katz, K.; Marosevic, D.V.; Böhm, S.; Woudenberg, T.; Ackermann, N.; Konrad, R.; et al. Investigation of a COVID-19 outbreak in Germany resulting from a single travel-associated primary case: A case series. Lancet Infect. Dis. 2020, 20, 920–928. [Google Scholar] [CrossRef]
- Nishiura, H. Correcting the actual reproduction number: A simple method to estimate R(0) from early epidemic growth data. Int. J. Environ. Res. Public Health 2010, 7, 291–302. [Google Scholar] [CrossRef]
- Khailaie, S.; Mitra, T.; Bandyopadhyay, A.; Schips, M.; Mascheroni, P.; Vanella, P.; Lange, B.; Binder, S.; Meyer-Hermann, M. Development of the reproduction number from coronavirus SARS-CoV-2 case data in Germany and implications for political measures. BMC Med. 2020, 19, 1–16. [Google Scholar] [CrossRef]
- JHU CSSE. COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. github.com Repository. 2020. Available online: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series (accessed on 18 March 2021).
- Krispin, R.; Byrnes, J. Coronavirus: The 2019 Novel Coronavirus COVID-19 (2019-nCoV) Dataset; R Package Version 0.3.21.; 2021. Available online: https://cran.r-project.org/web/packages/coronavirus/index.html (accessed on 18 March 2021).
- ECDC. Download Today’s Data on the Geographic Distribution of COVID-19 Cases Worldwide. European Centre for Disease Prevention and Control. Covid-19 Database. 2020. Available online: https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide (accessed on 18 March 2021).
- Robert Koch-Institut; Bundesamt für Kartographie und Geodäsie. CSV-Datei mit den aktuellen Covid-19 Infektionen pro Tag (Zeitreihe). 2020. Available online: https://www.arcgis.com/home/item.html?id=f10774f1c63e40168479a1feb6c7ca74 (accessed on 18 March 2021).
- Häussler, B. Pandemie-Meldewesen: Deutschland im Corona-Blindflug. ÄrzteZeitung 2021. Available online: https://www.aerztezeitung.de/Politik/Deutschland-im-Corona-Blindflug-416280.html (accessed on 18 March 2021).
- OECD. Testing for COVID-19: A way to lift confinement restrictions. In Organisation for Economic Co-operation and Development (OECD); Online; OECD: Paris, France, 2020; Available online: https://www.oecd.org/coronavirus/policy-responses/testing-for-covid-19-a-way-to-lift-confinement-restrictions-89756248/ (accessed on 18 March 2021).
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef]
- Streeck, H.; Schulte, B.; Kuemmerer, B.; Richter, E.; Hoeller, T.; Fuhrmann, C.; Bartok, E.; Dolscheid, R.; Berger, M.; Wessendorf, L.; et al. Infection fatality rate of SARS-CoV-2 infection in a German community with a super-spreading event. medRxiv 2020. [Google Scholar] [CrossRef]
- Maier, B.F.; Brockmann, D. Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science 2020, 368, 742–746. [Google Scholar] [CrossRef] [PubMed]
- Nazarimehr, F.; Pham, V.; Kapitaniak, T. Prediction of bifurcations by varying critical parameters of COVID-19. Nonlinear. Dyn. 2020, 101, 1681–1692. [Google Scholar] [CrossRef]
- Taghvaei, A.; Georgiou, T.T.; Norton, L.; Tannenbaum, A.R. Fractional SIR Epidemiological Models. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Volpert, V.; Banerjee, M.; d’Onofrio, A.; Lipniacki, T.; Petrovskii, S.; Tran, V.C. Coronavirus-Scientific insights and societal aspects. Math. Model. Nat. Phenom. 2020, 15, E2. [Google Scholar] [CrossRef]
- Sadeghi, M.; Greene, J.M.; Sontag, E.D. Universal Features of Epidemic Models Under Social Distancing Guidelines. bioRxiv 2020. [Google Scholar] [CrossRef]
- Bendavid, E.; Mulaney, B.; Sood, N.; Shah, S.; Ling, E.; Bromley-Dulfano, R.; Lai, C.; Weissberg, Z.; Saavedra-Walker, R.; Tedrow, J.; et al. COVID-19 Antibody Seroprevalence in Santa Clara County, California. medRxiv 2020. [Google Scholar] [CrossRef]
- Diebner, H.H.; Timmesfeld, N. Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Non-parametric Methods. Preprints 2020, 2020090628. [Google Scholar] [CrossRef]
- Steiger, J. Tests for comparing elements of a correlation matrix. Psychol. Bull. 1980, 87, 245–251. [Google Scholar] [CrossRef]
- Diebner, H.H.; Kather, A.; Roeder, I.; de With, K. Mathematical Basis for the Assessment of Antibiotic Resistance and Administrative Counter-Strategies. PLoS ONE 2020, 15, e0238692. [Google Scholar] [CrossRef]
- Ruck, D.J.; Bentley, R.A.; Borycz, J. Early warning of vulnerable counties in a pandemic using socio-economic variables. Econ. Hum. Biol. 2021, 41, 100988. [Google Scholar] [CrossRef]
- Griffin, J.; Casey, M.; Collins, Á.; Hunt, K.; McEvoy, D.; Byrne, A.; McAloon, C.; Barber, A.; Lane, E.A.; More, S. Rapid review of available evidence on the serial interval and generation time of COVID-19. BMJ Open 2020, 10, e040263. [Google Scholar] [CrossRef]
- Dowd, J.B.; Andriano, L.; Brazel, D.M.; Rotondi, V.; Block, P.; Ding, X.; Liu, Y.; Mills, M.C. Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 9696–9698. [Google Scholar] [CrossRef]
- Loy, A.; Follett, L.; Hofmann, H. Variations of Q–Q Plots: The Power of Our Eyes! Am. Stat. 2016, 70, 202–214. [Google Scholar] [CrossRef]
- Robert-Koch-Institut. RKI–Robert-Koch-Institut, Germany. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/nCoV_node.html (accessed on 4 February 2021).
- Bundesamt für Gesundheit. BAG–Bundesamt für Gesundheit, Switzerland. Available online: https://www.bag.admin.ch/bag/de/home/krankheiten/ausbrueche-epidemien-pandemien/aktuelle-ausbrueche-epidemien/novel-cov/testen.html (accessed on 4 February 2021).
- Adenubi, O.; Adebowale, O.; Oloye, A.; Bankole, N.; Adesokan, H.; Fadipe, O.; Ayo-Ajayi, P.; Akinloye, A. Level of Knowledge, Attitude and Perception About COVID-19 Pandemic and Infection Control: A Cross-Sectional Study Among Veterinarians in Nigeria. Preprints 2020, 2020070337. [Google Scholar] [CrossRef]
- Bundesamt, S. Sterbefallzahlen und Übersterblichkeit. Available online: www.destatis.de/DE/Themen/Querschnitt/Corona/Gesellschaft/bevoelkerung-sterbefaelle.html (accessed on 18 March 2021).
- EuroMomo. Bulletin, Week 38. Available online: www.euromomo.eu (accessed on 18 March 2021).
- Czuber, E. Der Mittelwert eines Quotienten. J. Die Reine Angew. Math. 1920, 1920, 175–179. [Google Scholar] [CrossRef]
- Ganan-Calvo, A.M.; Ramos, J.A.H. The fractal time growth of COVID-19 pandemic: An accurate self-similar model, and urgent conclusions. arXiv 2020, arXiv:2003.14284. [Google Scholar]
- Qeadan, F.; Honda, T.; Gren, L.H.; Dailey-Provost, J.; Benson, L.S.; VanDerslice, J.A.; Porucznik, C.A.; Waters, A.B.; Lacey, S.; Shoaf, K. Naive Forecast for COVID-19 in Utah Based on the South Korea and Italy Models-the Fluctuation between Two Extremes. Int. J. Environ. Res. Public Health 2020, 17, 2750. [Google Scholar] [CrossRef]
- Samadder, S.; Ghosh, K. Analysis of Self-Similarity, Memory and Variation in Growth Rate of COVID-19 Cases in Some Major Impacted Countries. J. Phys. Conf. Ser. 2021, 1797, 012010. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A General Model for the Origin of Allometric Scaling Laws in Biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Diebner, H.H.; Zerjatke, T.; Griehl, M.; Roeder, I. Metabolism is the tie: The Bertalanffy-type cancer growth model as common denominator of various modelling approaches. Biosystems 2018, 167, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Blasius, B. Power-law distribution in the number of confirmed COVID-19 cases. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 093123. [Google Scholar] [CrossRef]
- Mikut, R.; Mühlpfordt, T.; Reischl, M.; Hagenmeyer, V. Schätzung einer zeitabhängigen Reproduktionszahl R für Daten mit einer wöchentlichen Periodizität am Beispiel von SARS-CoV-2-Infektionen und COVID-19; Technical Report; 46.12.01; LK 01; Karlsruher Institut für Technologie (KIT): Karlsruhe, Germany, 2020. [Google Scholar] [CrossRef]
- He, X.; Lau, E.H.Y.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef]









| Delay | Corr | p | p_adj |
|---|---|---|---|
| 0 | 0.965 | 0.000 | 0.000 |
| 1 | 0.969 | 0.000 | 0.000 |
| 2 | 0.972 | 0.000 | 0.000 |
| 3 | 0.976 | 0.000 | 0.000 |
| 4 | 0.979 | 0.000 | 0.000 |
| 5 | 0.982 | 0.000 | 0.000 |
| 6 | 0.984 | 0.000 | 0.000 |
| 7 | 0.986 | 0.000 | 0.000 |
| 8 | 0.989 | 0.000 | 0.000 |
| 9 | 0.990 | 0.007 | 0.112 |
| 10 | 0.992 | 0.085 | 1.000 |
| 11 | 0.993 | 0.416 | 1.000 |
| 12 | 0.993 | 0.839 | 1.000 |
| 13 | 0.993 | 1.000 | 1.000 |
| 14 | 0.993 | 0.855 | 1.000 |
| 15 | 0.993 | 0.506 | 1.000 |
| Delay | Corr | p | p_adj |
|---|---|---|---|
| 0 | 0.711 | 0.065 | 0.087 |
| 1 | 0.588 | 0.000 | 0.000 |
| 2 | 0.526 | 0.000 | 0.000 |
| 3 | 0.478 | 0.000 | 0.000 |
| 4 | 0.525 | 0.000 | 0.000 |
| 5 | 0.659 | 0.002 | 0.004 |
| 6 | 0.735 | 0.234 | 0.288 |
| 7 | 0.743 | 0.335 | 0.383 |
| 8 | 0.666 | 0.003 | 0.005 |
| 9 | 0.571 | 0.000 | 0.000 |
| 10 | 0.545 | 0.000 | 0.000 |
| 11 | 0.571 | 0.000 | 0.000 |
| 12 | 0.704 | 0.045 | 0.065 |
| 13 | 0.775 | 1.000 | 1.000 |
| 14 | 0.768 | 0.826 | 0.881 |
| 15 | 0.693 | 0.023 | 0.037 |
| IT | DE | |
|---|---|---|
| (Intercept) | 0.158 | 0.054 |
| 1000 cases | ||
| time (months) | ||
| cases:time | ||
| R | ||
| Adj. R | ||
| Num. obs. | 303 | 307 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diebner, H.H.; Timmesfeld, N. Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Nonparametric Methods. Infect. Dis. Rep. 2021, 13, 302-328. https://doi.org/10.3390/idr13020031
Diebner HH, Timmesfeld N. Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Nonparametric Methods. Infectious Disease Reports. 2021; 13(2):302-328. https://doi.org/10.3390/idr13020031
Chicago/Turabian StyleDiebner, Hans H., and Nina Timmesfeld. 2021. "Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Nonparametric Methods" Infectious Disease Reports 13, no. 2: 302-328. https://doi.org/10.3390/idr13020031
APA StyleDiebner, H. H., & Timmesfeld, N. (2021). Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Nonparametric Methods. Infectious Disease Reports, 13(2), 302-328. https://doi.org/10.3390/idr13020031







