Geographic Ontologies, Gazetteers and Multilingualism

Abstract

Different languages imply different visions of space, so that terminologies are different in geographic ontologies. In addition to their geometric shapes, geographic features have names, sometimes different in diverse languages. In addition, the role of gazetteers, as dictionaries of place names (toponyms), is to maintain relations between place names and location. The scope of geographic information retrieval is to search for geographic information not against a database, but against the whole Internet: but the Internet stores information in different languages, and it is of paramount importance not to remain stuck to a unique language. In this paper, our first step is to clarify the links between geographic objects as computer representations of geographic features, ontologies and gazetteers designed in various languages. Then, we propose some inference rules for matching not only types, but also relations in geographic ontologies with the assistance of gazetteers.

1. Introduction

Generally speaking, ontologies play a double role in information technologies as a key structure for both database interoperability and information retrieval. In geographic information science, any request against the Internet is enriched not only by using ontologies, but also gazetteers, which can be loosely defined as dictionaries of place names or toponyms. Imagine somebody looking for information about the Italian city of Venice on the Internet. If he only speaks English, only English documents will be retrieved, whereas many documents are written in other languages, Italian in this case.

One of the key problems we are facing is that the majority of ontologies are developed in English with English concepts. Additionally, ontologies developed in other languages regroup not only different terminologies, but also different organizations of the content. In short, one has to consider two networks with totally different structures. Then, how does one match them?

Indeed, in several applications, such as cross-border environmental planning, for instance along the Rhine river, several countries must be involved with different languages, so different documents and different ontologies. Beyond the interoperability framework [1], multilingualism in ontologies is a great challenge. Secondly, multilingualism must be the base of the fusion of different documents retrieved on the Internet.

Consider two countries and their governments. One can have a king and another an elected president. Afterwards, one can have 10 ministers and several sub-ministers, whereas another has 50 ministers. When there is a delegation of three ministers visiting another country, since all of them have no identical titles and responsibilities, usually they say they meet their counterparts. The same observation can be made when considering two ontologies, each written with a different language: there are practically never strict equivalences, but rather homologies.

Remember that ontologies can be defined as shared conceptualization in which several experts do agree [2]. For translations, since there are no authorities able to claim exact or good translations, we can assert that we must consider shared translations of concepts. The same consideration can be extended to place names. Let us call homology the relationship between similar concepts and similar toponyms in two different languages.

Often, specialists or experts mastering both languages are asked to translate geographic ontologies manually. However, this can also be done automatically by using gazetteers, or, specifically, geometric characteristics and toponyms, in order to match geographic concepts. In other words, the main contribution of this paper is to use geographic properties to match multilingual ontological concepts via gazetteers.

In this paper, after having examined the specificities of geographic ontologies, we will study toponyms and gazetteers. Finally, some inference rules of translating geographic concepts based on geographic properties of toponyms will be given.

2. Geographic Ontologies

In general, an ontology specifies a vocabulary of concepts together with some indication of their meanings [2,3]. As discussed in [4], the term “ontology” is used nowadays by information scientists, in a non-philosophical sense, to assist in the task of specifying and clarifying the concepts employed in given domains, above all by formalizing them within the framework of some formal theory with a well-understood logical (syntactic and semantic) structure. From a computational point of view, an ontology can be seen as a network of concepts linked essentially by the following relations:

• “is a” (females and males are subtypes or subclasses of human being);
• “has a” (a paper has one or several authors);
• “part of” (a finger is a part of a hand).

In the seminal paper of Jones et al. [5], the main differences of geographic ontology are explicated. First, they advocated for the integration of topological relations into geographic queries based on ontology. Then, [6] proposed integrating topological relations into ontologies.

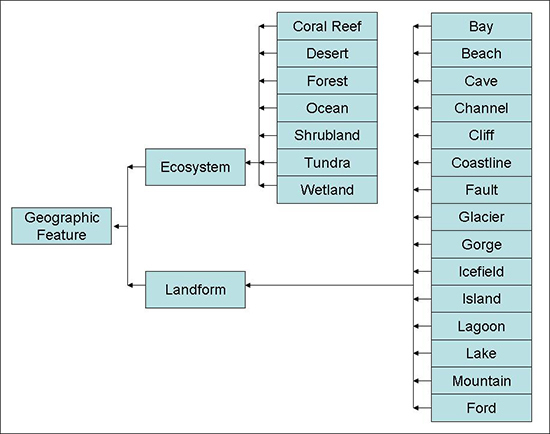
2.1. Geographic Features, Types and Languages

However, the specificity of geographic ontology does not lie only in geographic features (as illustrated in Figure 1) [7]. It lies overall in their geometry and in their spatial relationships [8]. Usually, Egenhofer [9,10] or Region Connection Calculus (RCC) [11] relations (Figure 2) are fully integrated into the definitions of geographic features.

Figure 1. Example of the beginning of a geographic ontology with only “is-a” relationships.

Figure 1. Example of the beginning of a geographic ontology with only “is-a” relationships.

Figure 2. Egenhofer topological relations [9].

Figure 2. Egenhofer topological relations [9].

See Figure 3 and Figure 4 for examples of geographic objects linked with topological relations, the first for the whole planet, and the second for administrative subdivisions of a country. Concerning administrative subdivisions [4], here are a set of remarks:

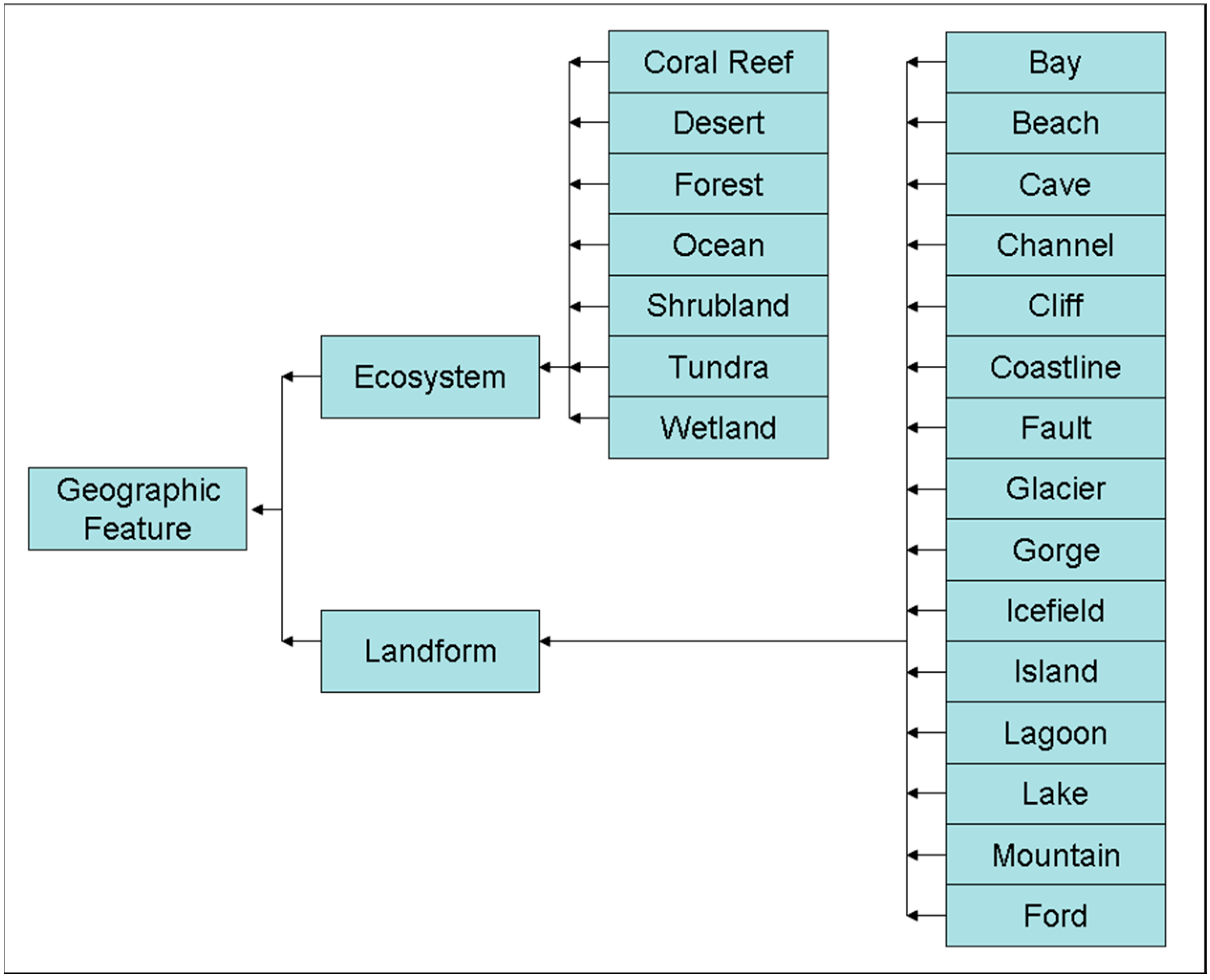
• Generally, they form an administrative tessellation (as defined by administrative laws of the concerned countries) and often a hierarchical tessellation (in which a zone of the first level can be decomposed into a second level tessellation (example: in the U.S., country, states, counties);
• However, this tessellation is often disrupted, because of the existence of external territories with special statuses; see, for instance, territories, such as Guam, Northern Mariana Islands, Puerto Rico and the Virgin Islands for the United States;
• Even if types are the same, they do not have the same meaning; compare, for instance, a Canadian province, such as “British Columbia”, and an Italian province (provincia in Italian) for which the size, statuses, prerogatives and governance are very different.

As a consequence, for structuring geographic ontologies, let us notice that:

• the so-called administrative tessellations are often not strictly mathematical tessellations due to measurement errors and sliver polygons;
• and the spatial relationships could always be generalized or mutated due to scale effects (See [12] for more details); for instance, a road running along the seashore can have a “disjoint” relation or a “touches” relation according to the scale.

Figure 3. Example of ontology-based on spatial relations.

Figure 3. Example of ontology-based on spatial relations.

Figure 4. Example of administrative subdivisions with spatial relations.

Figure 4. Example of administrative subdivisions with spatial relations.

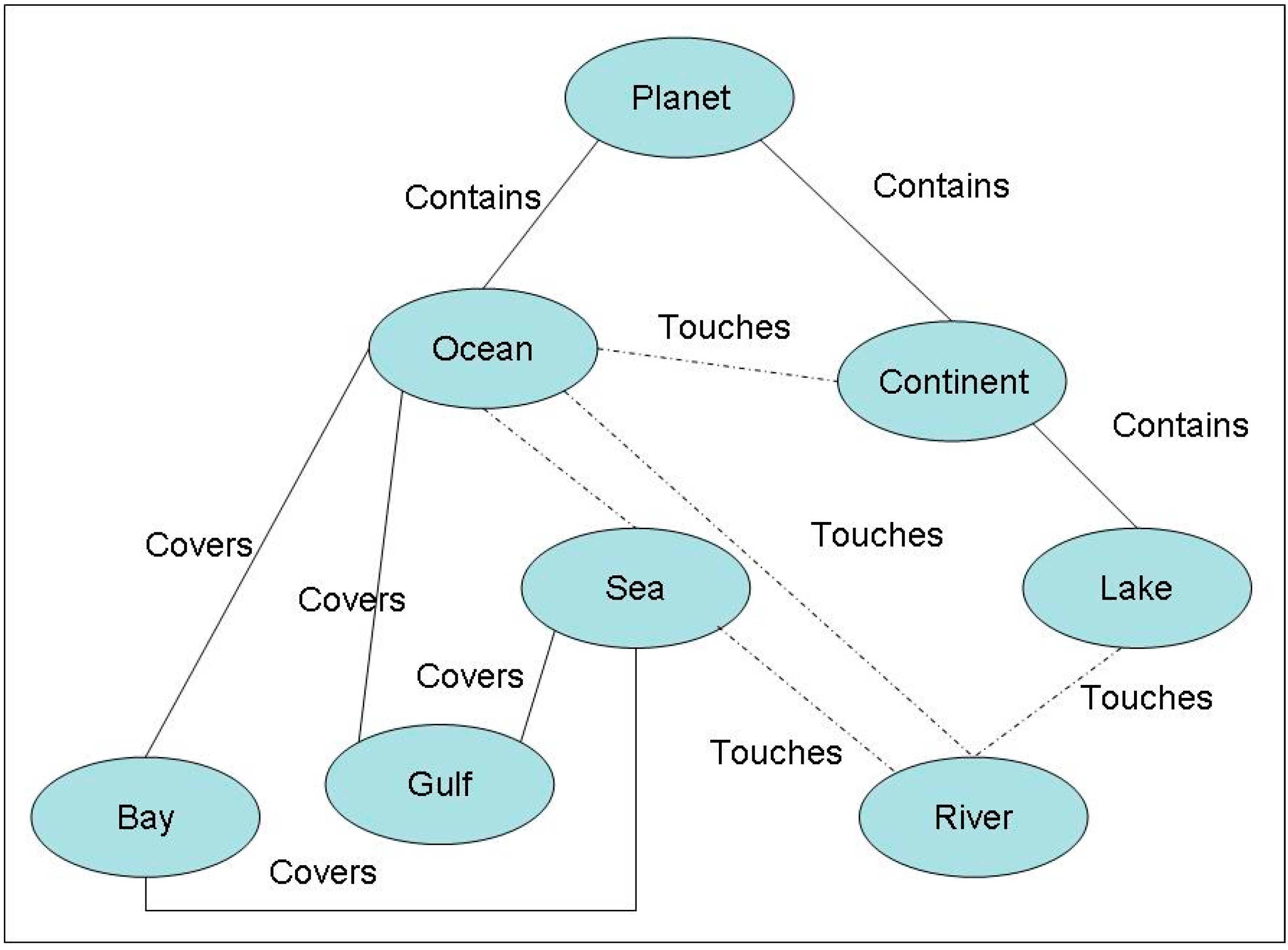
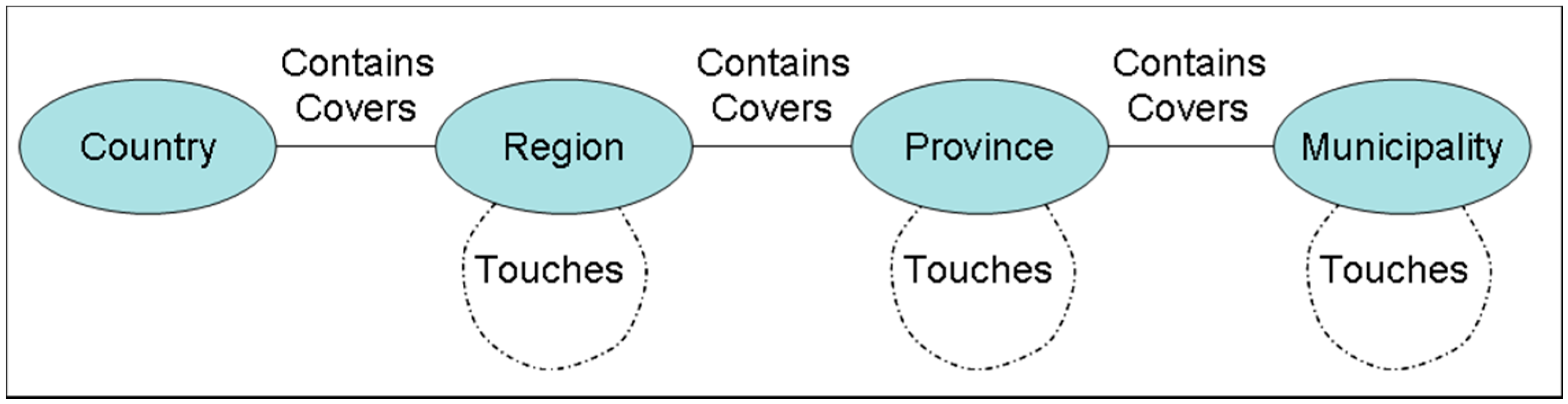
2.2. Ontological Categories and Languages

The objective of the Towntology project [8,13] was to design ontologies for urban planning. A COST group was created with people coming from different countries. Since concepts were different in different languages, the preliminary question was “do we design either separate mono-lingual ontologies or a unique ontology in English, including everything, and deriving other ontologies in various languages?” There was no clear-cut answer, so the output was two-fold: some subgroups constructed urban ontologies in their own vernacular languages, whereas others in English.

The well-known English term “bank” represents both a riverside and a financial institution. In other words, the first meaning will be translated in French and Spanish, respectively, as “rive”, “ribera” and the second by “banque” and “banco”.

Let us examine a special case: In the French language, the word “quai” defines a wharf, an embankment, a train platform or a street along a river. In Spanish, especially in Barcelona, “rambla” is a ravine or a special kind of broad avenue. In Venice, “rioterà” is a special type of pedestrian lane, whereas other denominations are used, such as salizada, sottoportego, ramo, fondamenta, campiello, corte, calle, riva, etc. As far as I know, those terms have no equivalent in English.

Matching two ontologies is a very complex task [14] in which semantic and structural aspects are involved together with some indicators to qualify the degree of quality or the confidence of the matching.

However, matching ontologies in different languages is a more complex task [15]. Indeed, the authors proposed using translation techniques as an intermediate step to translate the conceptual labels within an ontology. This approach essentially removes the natural language barrier in the mapping environment and enables the application of monolingual ontology mapping tools. They show that the key to this translation-based approach to cross-lingual ontology mapping is selecting an appropriate ontology label translation in a given mapping context with some confidence structure.

However, in the case of matching geographic ontology, the geometric characteristics of geographic features must be taken into account. For instance, a river, a city, a road, an island or any kind of feature have very different geometric structures that can help matching.

3. About Geographic Names and Gazetteers

By definition, a gazetteer is a directory of toponyms [16,17]. However, now, more and more gazetteers are becoming complex databases. Since they increasingly include other attributes of the named features, they tend to become toponym ontologies [18,19].

3.1. What Is beneath a Name?

Beneath a geographic name, various objects or features can exist. On the Earth, few points have names, perhaps only the North and South Poles, and only a few lines, such as the Equator, Tropic of Cancer, Tropic of Capricorn, Greenwich Meridian, Polar Circle, etc. The majority of names are given to areas, since even rivers are areas or may be modeled as lines or ribbons [18]. As previously mentioned, they must be considered as simply connected (with islands and holes), and they can be replaced by their centroids for some operations. In some geographic databases, for instance, the geographic object named “Italy” can include Vaticano and San Marino, whereas those places do not belong officially to the country named Italy.

3.2. Generalities

Indeed, in addition to a pure list of place names, it is necessary to locate them with accuracy and to assign them some features or geographic objects. Moreover, a place can have different names in different languages and different periods of time. Let us first examine a few well-known examples:

• “Mississippi” can be the name of a river or of a state.
• The city, “Venice”, Italy, is also known as “Venezia”, “Venise”, “Venedig”, respectively, in Italian, French and German.
• The local name of the Greek city of “Athens” is “Αθήνα”; read [a’θina].
• “Istanbul” was known as “Byzantium” and “Constantinople” in the past.
• The modern city of Rome is much bigger than in Romulus’s time.
• There are two Georgias, one in the United States and another one in Caucasia.
• The toponym “Milano” can correspond to the city of Milano or the province of Milano.
• The river “Danube” crosses several European countries; practically in each country, it has a different name, “Donau” in Germany and Austria, “Dunaj” in Slovakia, “Duna” in Hungary, “Dunav” in Croatia and Serbia, “Dunav” and “Дунав” in Bulgaria, “Dunărea” in Romania and in Moldova and “Dunaj” and Дунай” in the Ukraine. It is also called “Danubio” in Italian and Spanish, “Tonava” in Finnish and “Δούναβης” in Greek. Moreover, its name is feminine in German and masculine in some other languages.
• Sometimes, names of places can be also names of something else; for instance “Washington” can also refer to George Washington or anybody with this first name or last name.
• In the U.K., there are several rivers named Avon.
• Some place names are formed of two or several words; for instance, “New Orleans”, “Los Angeles”, “Antigua and Barbuda”, “Trinidad and Tobago”, “Great Britain”, “Northern Ireland”, “Tierra del Fuego”, “El Puente de Alcántara”, etc.
• Some very long names can have simplifications; the well-known Welsh town “Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch” is often simplified to “Llanfair PG” or “Llanfairpwll”.
• Some abbreviations can be common, such as “L.A.” for “Los Angeles”, whereas its name at its inception was “El Pueblo de Nuestra Señora la Reina de los Angeles del Rio de la Porciúncula”;
• Peking became Beijing after a change of transcription to the Roman alphabet; but the capital of China has not modified its name in Chinese.
• In some languages, grammatical gender is important, so that place names can be feminine or masculine; for instance, in French, Italian and Spanish, names such as “Japan”, “Brazil” and “Portugal” are masculine, whereas “Argentina”, “Bolivia” and “Tunisia” are feminine.
• In addition, as the great majority of toponyms are singular, some can be plural, like “The Alps”; but for “The Netherlands”, the situation is more complex: plural in French (Les Pays-Bas), in Italian (I Paesi Bassi) and in Spanish (Los Países Bajos), whereas singular and plural are both acceptable in English (The Netherlands are, The Netherlands is);
• Some places have nicknames; e.g., Dixieland, Big Apple, City of the Lights, etc.
• Do not forget that in some languages, toponyms can have declensions, for instance for the Rhine River in German (der Rhein, des Rheins, etc.).

Consider now the toponym “Granada”: there are places in practically all Spanish-speaking countries bearing this name:

• a small country located in the Caribbean Islands;
• in Spain, a city capital of the eponymous province, a few other places located in Barcelona and Huelva provinces and a river in the Vizcaya province;
• in Colombia, three cities with this toponym;
• in the U.S., cities in California, Colorado, Kansas, Minnesota, Mississippi, etc.;
• in Mexico, a city in Yucatán;
• in Nicaragua, a city capital of the eponymous department;
• in Peru, a district.

As a consequence, there is a very complex many-to-many relationship between places and place names (Figure 5).

Figure 5. Very complex many-to-many relations link places and their names.

Figure 5. Very complex many-to-many relations link places and their names.

Among place names, there are street names together with the number in the street (civic number); these are not so easy to handle. This is very important, not only for the automatic processing of postal addresses, but also for all applications connected to an emergency. The Urban and Regional Information Systems Association (URISA) association has organized many conferences on the topic (see [19]). The specificities of street names are as follows:

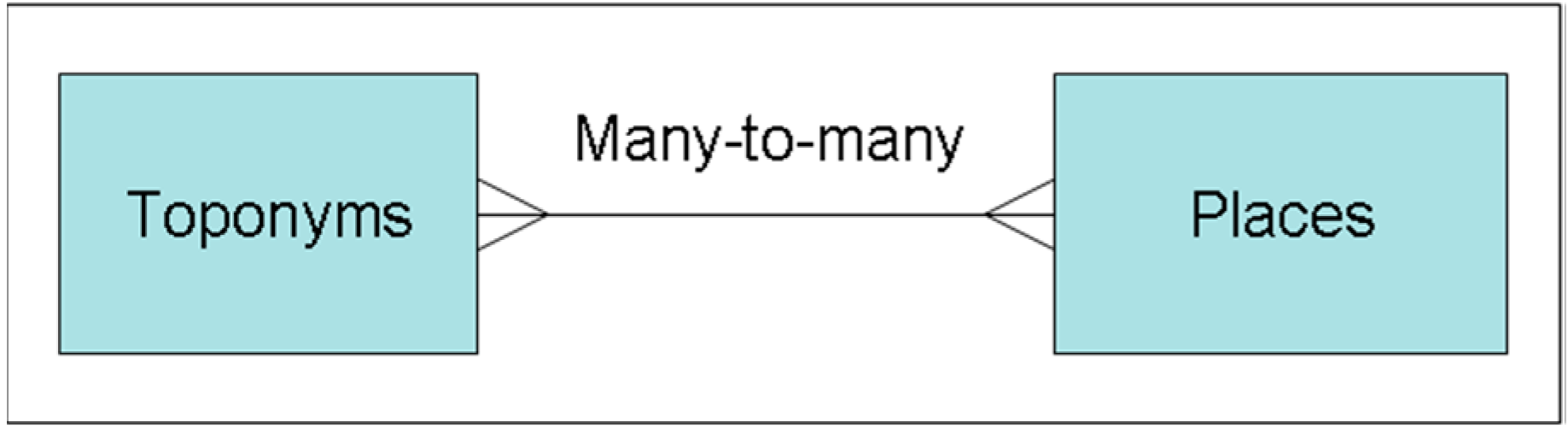
• some streets comprise a few dozens of yards, whereas others several miles;
• in some human settlements, streets have no names;
• sometimes, there are variations about the way to write some street names; for instance “3rd Street”, “Third Street”, “Third St”; the words “avenues” and “boulevards” are commonly simplified into “Ave” and “Blvd” or “Bd”;
• in some countries, the equivalent of the words “street”, “avenue”, etc., are usually removed;
• in some places, streets can have several names; for instance, in New York City, “Sixth Avenue” is also known as “Avenue of the Americas”;

As a main consequence, the name of a place cannot be a unique ID from a computing point of view. In order to clarify, let us give a few definitions:

• toponym is the general name of a geographic feature;
• endonym is a local name in the official language of the country or in a well-established language occurring in that area where the feature is located; there may be several toponyms in countries with different official languages (Brussel in Flemish, Bruxelles in French);
• exonym is a name in languages other than the official languages; for instance Brussels in English;
• archeonym is a name that existed in the past: for instance, Byzantium for Istanbul;
• hyperonym and hyponym are the names of places with a hierarchy; hyponym is the opposite of hyperonym; for instance, Europe is a hyperonym of France, whereas France is a hyponym of Europe;
• meronym is a name of a part of a place without a hierarchy; sometimes the expression partonym is used; for instance “Adriatic Sea” is a meronym of the Mediterranean Sea;
• hydronym is a name of a waterbody;
• oronym is a name for a hill or a mountain;

Figure 6 gives the essential elements of a gazetteer, the names, the features, the dates and everything regarding geometry and georeferencing according to [20].

In addition, places, such as airports, can have several names. Sometimes, their International Air Transport Association (IATA) [21] codes are used: the well-known New York airport, John F. Kennedy International Airport, is often referred to as JFK airport. Zip codes or postcodes can also be considered as toponyms. However, the definition of postcodes differs according to country: In some cases, one postcode can correspond to a few houses, and in others some hundred thousand inhabitants.

Figure 6. Essential elements of a toponym, after Jakir et al. (2011) [20].

Figure 6. Essential elements of a toponym, after Jakir et al. (2011) [20].

To conclude this section, in an automatic system for searching geographic information in the web (often known as GIR, geographic information retrieval), a preliminary phase of disambiguation is necessary, since the name can correspond to something that is not geographic (Figure 7).

Let us define as a literal a string of characters (perhaps including blank spaces, hyphens and numbers): this literal may be a toponym, the name of a person (Washington) or something else (China and porcelain). Toponyms can be described as literals.

Figure 7. Disambiguation of literals to extract toponyms. GIR, geographic information retrieval.

Figure 7. Disambiguation of literals to extract toponyms. GIR, geographic information retrieval.

3.3. Examples

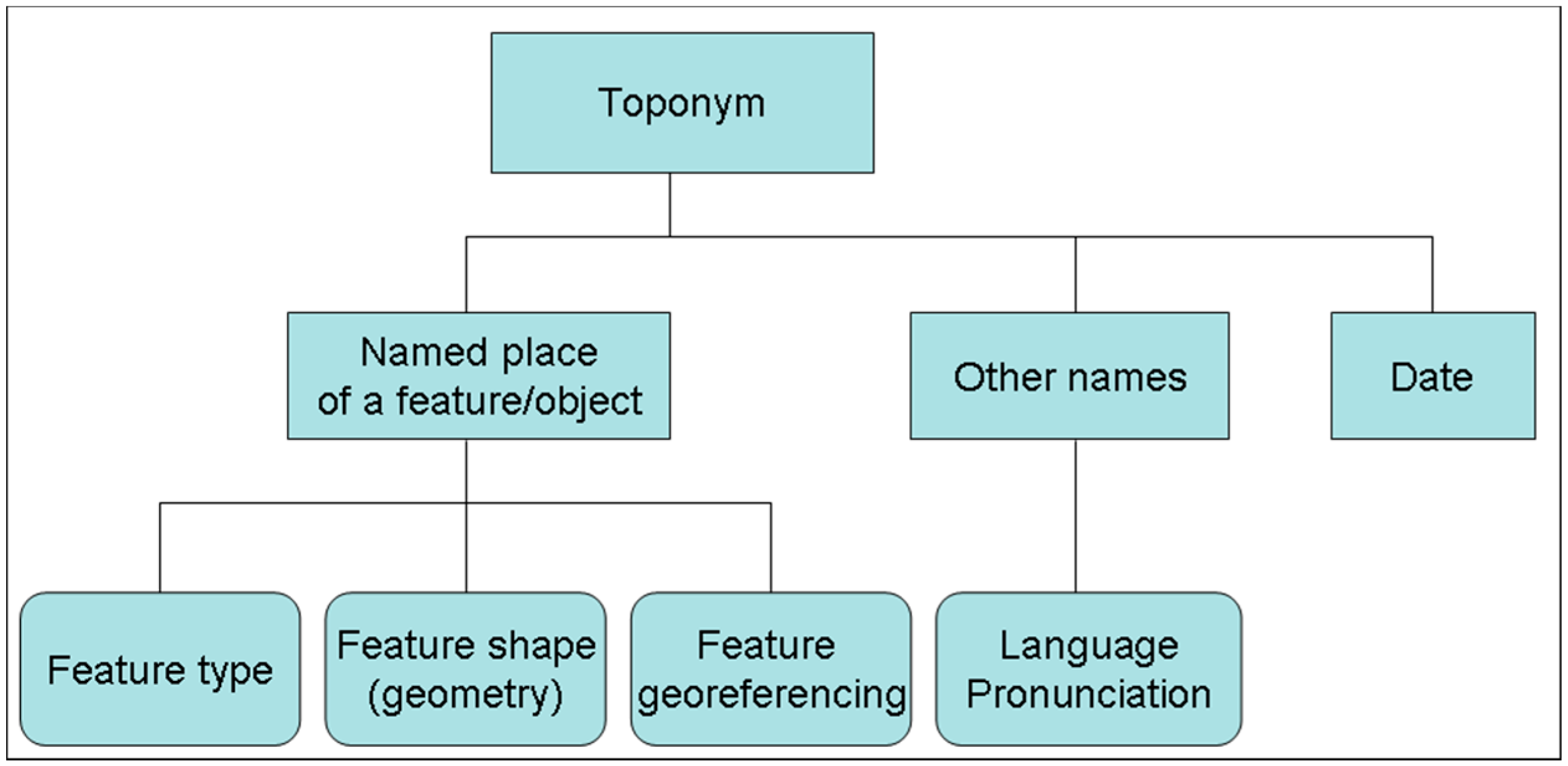
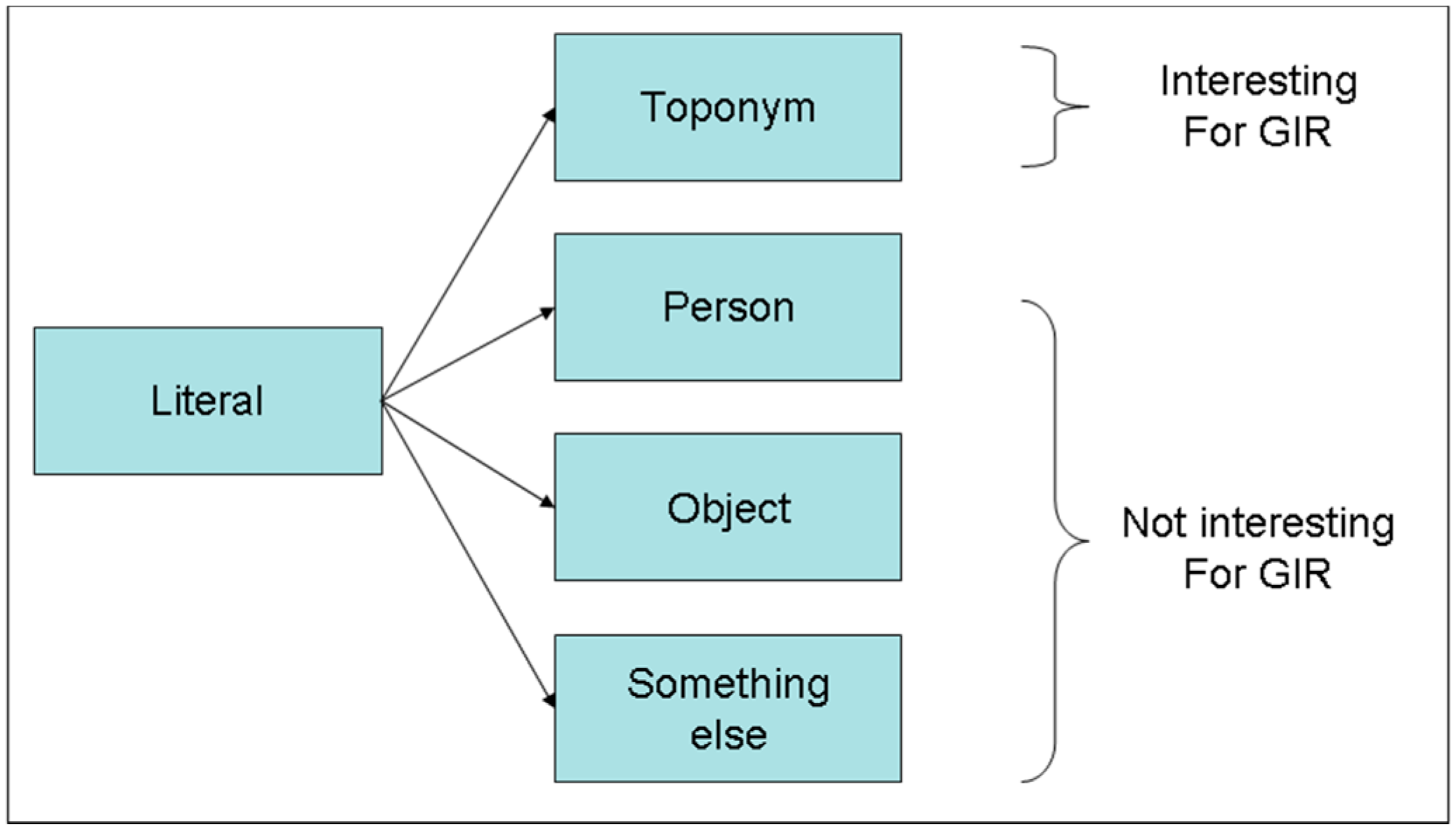
Generally speaking, a gazetteer is designed for a specific activity, for instance to help post offices, to assist the history of a region, etc. As a consequence, several gazetteers can have different structures. Let us examine a few examples.

3.3.1. Simple Gazetteer

A simple gazetteer consists of a list of place names and equivalence relationships between them, such as:

“U.S.A.” ≡ “United States of America”

Therefore, the database tables are as follows

• Placenames (ID, toponym);
• Equivalence (ID1, ID2).

3.3.2. Gazetteer as an Index for a Map (Street Directory)

The starting point is a map of a certain region with a precise objective and scale with a visual vocabulary presented in the legend. In this case, the map is usually split into a crossword-like grid in which squares are located by letters and numbers identified by CW-location (CW for Crossword). For instance “Main Street” goes from B3 to C7. The directory can have the following forms.

• Location1 (street-name, CWbeginning-location, CWending-location)

In addition, an alternative could be with street names with the names of the other streets, which are at the beginning and at the end.

• Location2 (street-name, beginning-street-name, ending-street-name)

3.3.3. Gazetteer for a Local Post-Office

For the post-office, the gazetteer can have the previous forms, but in addition, it can also include several important monuments, administrations and enterprises that can be stored:

• Urban-feature (name, street-address)

3.3.4. Gazetteer for Hydrology

Here, there are only names of rivers, lakes, seas, etc. Important relations are for tributaries and possible estuaries with the sea in which id, id1 and id2 are computer object identifiers or access-keys.

• Hydronym (id, onto-type, geometry)
• Endonym (id, hydronym)
• Exonym (id, language, hydronym)
• Tributary (id1, id2, location)
• Estuary (id1, id2, location)
• Meronym (id1, id2).

3.3.5. Gazetteer for the History of a Place

Here, we essentially deal with ancient names. Let us start with the actual toponyms.

• Placename (id, onto-type, geometry, beginning-date)
• Archeonym (id, language, toponym, geometry, beginning-date, ending-date)
• Exonym (id, language, toponym).

3.3.6. Gazetteer Covering Several Actual Countries, for Instance Europe

• Placename (id, onto-type, geometry, beginning-date)
• Exonym (id, language, toponym)
• Hydronym (id, onto-type, geometry)
• Endonym (id, hydronym)
• Exonym (id, language, hydronym)
• Meronym (id1, id2).

3.4. Existing Systems

Concerning ontologies and gazetteers, several systems exist. Let us rapidly present two of them, GeoNames [22] and GeoSPARQL [23] (See Section 3.4.2).

3.4.1. GeoNames

The GeoNames [22] database contains over 10,000,000 geographical names corresponding to over 7,500,000 unique features. All features are categorized into one out of nine feature classes and further subcategorized into one out of 645 feature codes. Beyond names of places in various languages, the data stored include latitude, longitude, elevation, population, administrative subdivisions and postal codes. Among spatial relationships, GeoNames utilizes a special way to model hierarchical tessellations:

• Children, i.e., the list of administrative divisions (first relative sublevel);
• Hierarchy, i.e., the list of toponyms higher up in the hierarchy of a place name;
• Neighbors, i.e., the list of all neighbors for a country or administrative division;
• Contains, i.e., the list of all features within the feature;
• Siblings, i.e., the list of all siblings of a toponym at the same level.

For instance, here is an excerpt of the description of Sicily in which the tag <ToponymName> corresponds to endonym and <name> to exonym):

• <geoname>
• <toponymName>Sicilia</toponymName>
• <name>Sicily</name>
• <lat>37.75</lat><lng>14.25</lng>
• <geonameId>2523119</geonameId>
• <countryCode>IT</countryCode>
• <countryName>Italy</countryName>
• <numberOfChildren>9</numberOfChildren>
• </geoname>

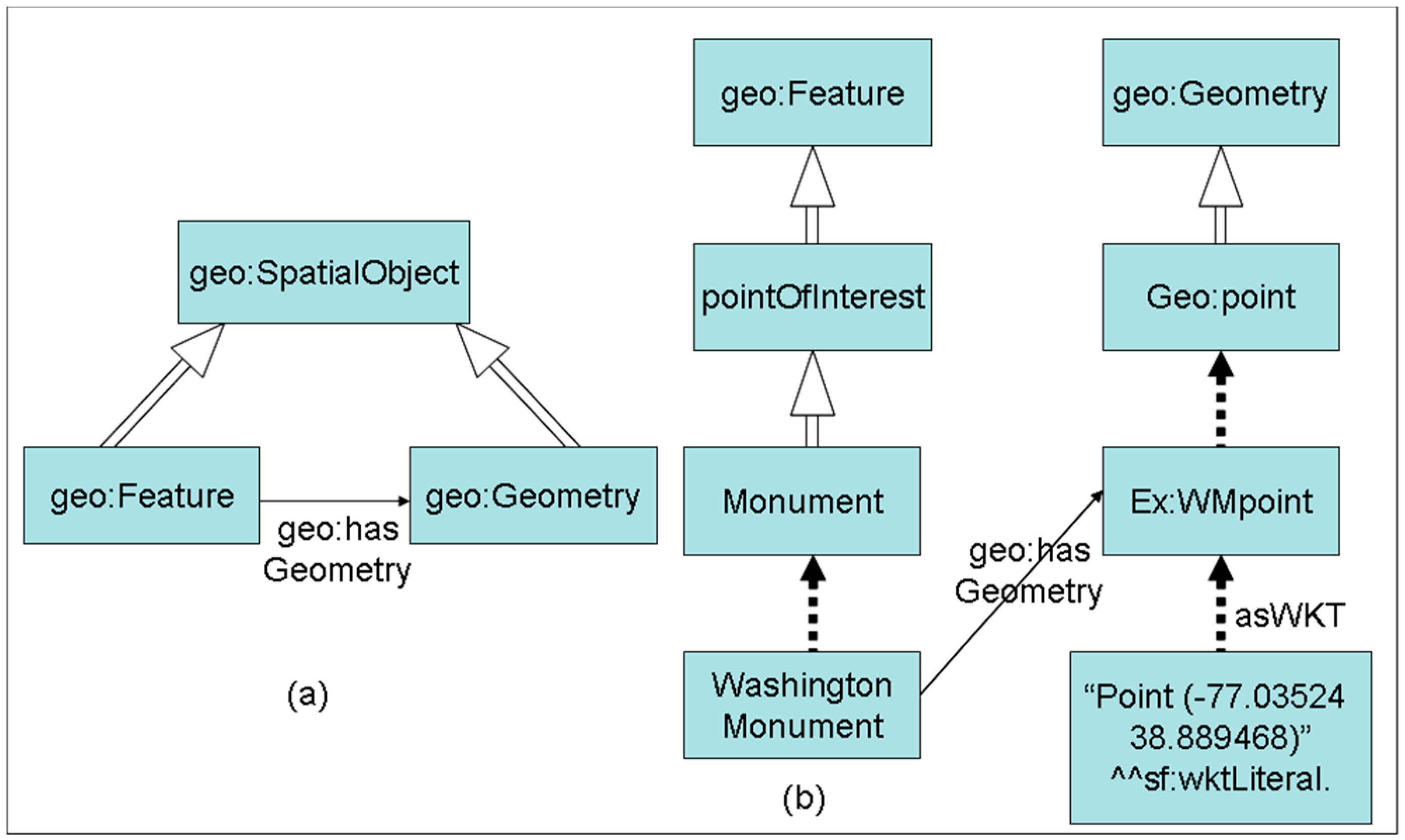
3.4.2. GeoSPARQL

GeoSPARQL [23] is a standard for the representation and querying of geospatially-linked data for the Semantic Web from the Open Geospatial Consortium (OGC) [24]. It can be seen as an extension of SPARQL [25]. The definition of a small ontology based on well-understood OGC standards is intended to provide a standardized exchange basis for geospatial Resource Description Framework (RDF) [26] data, which can support both quantitative and qualitative spatial reasoning and querying with the SPARQL database query language.

However, with SPARQL, some simple geographic queries, i.e., without geometric information and spatial relationships, can be launched. For instance: “What are all of the country capitals in Africa?”

• PREFIX abc: <http://example.com/exampleOntology#>
• SELECT ?capital ?country
• WHERE {
• ?x abc:cityname ?capital ;
• abc:isCapitalOf ?y .
• ?y abc:countryname ?country ;
• abc:isInContinent abc:Africa.
• }

However, with GeoSPARQL, not only geometric attributes (shapes), but also Egenhofer/RCC topological relations can be invoked.

In addition, the following functions are integrated: distance, buffer, convex hull, intersection, union, difference, etc. The general structure and an example are given in Figure 8, in which WKT means “well known text” as defined by OGC. To get the Washington Monument, one has to write a small filter as a minimum bounding rectangle (MBR) as exemplified in the GeoSPARQL user guide (by using an MBR, the search space is reduced not to run the query against the whole database):

• PREFIX geo: <http://www.opengis.net/ont/geosparql#>
• PREFIX geof: <http://www.opengis.net/def/function/geosparql/>
• PREFIX sf: <http://www.opengis.net/ont/sf#>
• PREFIX ex: <http://example.org/PointOfInterest#>
• SELECT ?a
• WHERE {
• ?a geo:hasGeometry
• ?ageo .
• ?ageo geo:asWKT
• ?alit
• FILTER( geof:sfWithin(?alit, “Polygon((-77.089005 38.913574,-77.029953 38.913574,-77.029953 38.886321,-77.089005 38.886321,-77.089005 38.913574))”^^sf:wktLiteral)) }

For instance, a query for getting the airports near London is as follows:

• PREFIX co: <http://www.geonames.org/countries/#>
• PREFIX xsd: <http://www.w3.org/2001/XMLSchema#>
• PREFIX geo: <http://www.w3.org/2003/01/geo/wgs84_pos#>
• SELECT ?link ?name ?lat ?lon
• WHERE {
• ?link gs:within(51.139725 -0.895386 51.833232 0.645447) .
• ?link gn:name ?name .
• ?link gn:featureCode gn:S.AIRP .
• ?link geo:lat ?lat .
• ?link geo:long ?lon }

Figure 8. Example of describing geographic entities in GeoSPARQL [23]. (a) Generic structure; (b) example for a monument.

Figure 8. Example of describing geographic entities in GeoSPARQL [23]. (a) Generic structure; (b) example for a monument.

If somebody is looking for all land parcels with some type of commercial zoning that touches some arterial street, the query is the following:

• SELECT ?parcel ?hwy
• WHERE { ?parcel rdf:type :Commercial .
• ?parcel rdf:type ogc:GeometryObject .
• ?hwy rdf:type :Arterial_Street .
• ?hwy rdf:type ogc:GeometryObject .
• ?parcel ogc:touches ?hwy }

Now that the notions of gazetteers and geographic ontologies in multiple languages are clarified, let us work with those elements to enrich them.

4. Inference Rules for Matching Geographic Ontologies in Different Languages

In this section, we will consider neither temporal aspects nor street addresses. First, the conceptual framework will be given and will be followed by a few inference rules.

4.1. Conceptual Framework

Let us consider a geographic knowledge base consisting of geographic objects and relations. Any geographic object will be defined with two parts, a geometric one and a linguistic one, which will depend on languages. However, before explicating them, let us define homology relations.

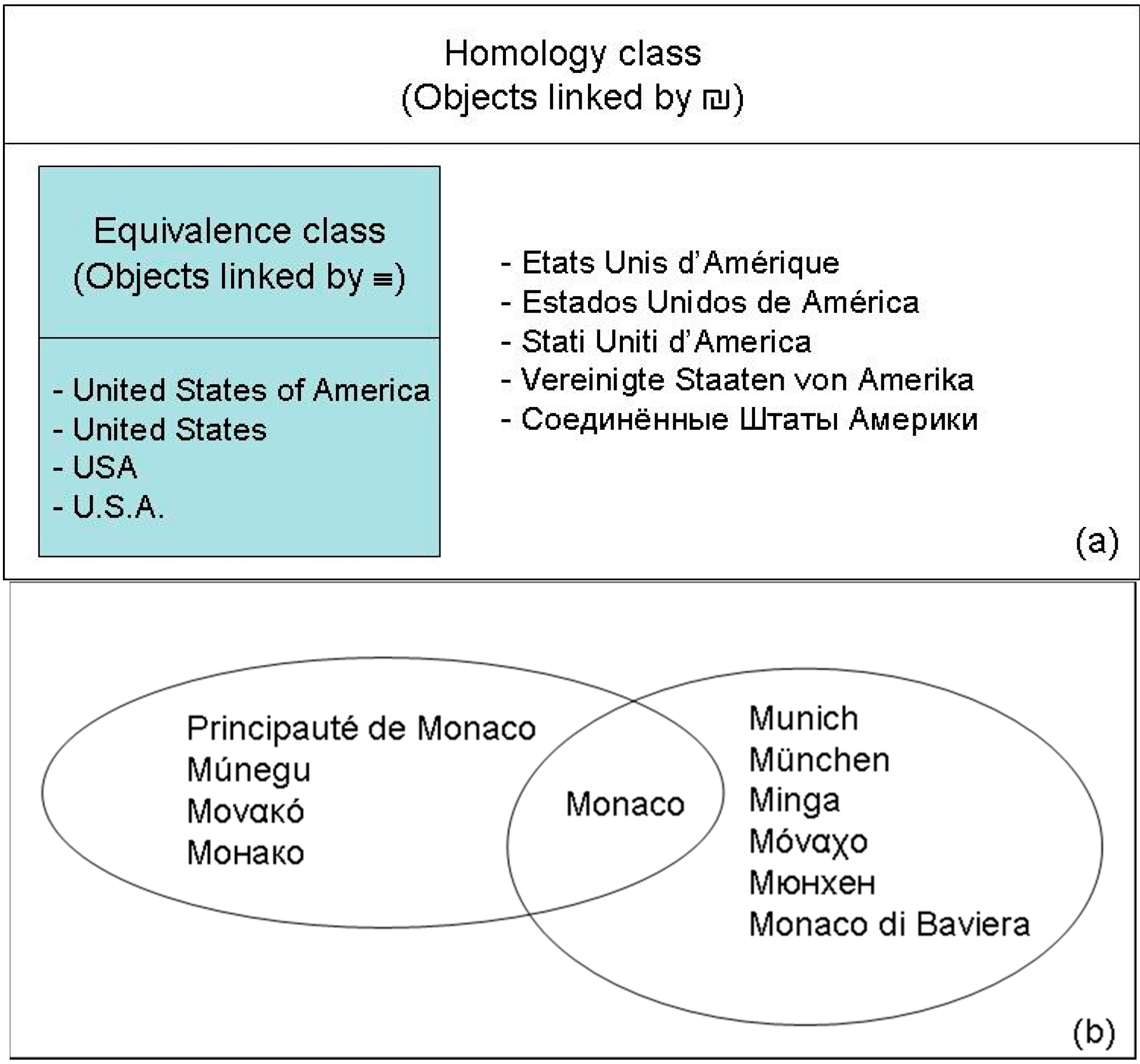
4.1.1. Homology Relations

Between two objects, A and B, a homology relation is a relation that is reflexive and symmetric. Let us denote ₪ as this relation, so that A ₪ B. Therefore, both A ₪ A and B ₪ A hold. Remark that an equivalence relation (≡) is a homology relation, which is also transitive.

When we want to compare two geographic objects, we need to ascertain whether the geometric shapes (taking measurement errors into account) are similar or not. For that purpose, the ideal will be to create an equivalence relation, that is to say, reflexive, symmetric and transitive. However, due to the previous remarks, one can mention that transitivity is not every time verified. Therefore, let us consider geometric homology relations (denoted as ₪_G).

For crisp geographic objects (A and B), the boundaries are well known and agreed upon, but there are practically always measurement discrepancies. In this case, to match them, we can compare their geometric shapes (Figure 9) and their locations, for instance, by their centroids. By definition, two geographic objects, A and B, are considered as geometrically homologous iff:

$$\begin{gathered} Geom(A) {₪}_{\text{G}} Geom(B) \\ \iff (\frac{2\times Area(A\otimes B)}{(Area(A\cup B)+Area(A\cap B)}\le \text{ε}1)\wedge Dist(Centroid(A),Centroid(B))<\text{ε}2) \end{gathered}$$

(1)

In this expression, remember that the symbol ⊗ is called “symmetric difference” and is defined as follows a ⊗ b = (a∩¬b) ∪ (¬a∩b).

Figure 9. Two homologous geometric descriptions of the same geographic object.

Figure 9. Two homologous geometric descriptions of the same geographic object.

For natural objects, this is more complex. When it is for islands, we can apply the previous method for matching them. However, in other cases, this is more difficult, because sometimes, boundaries are indeterminate, especially for mountains and deserts. Comparing two representations of the Rocky Mountains based on geometry is not so easy, because two experts can give two different boundaries to the mountains.

Regarding toponyms, equivalence relations can be created, for instance by writing “U.S.A.”≡”United States of America”. By extension, an equivalence class can be defined. However, for the translation of toponyms (Venice, Venezia, etc.), there is no systematic way to define them, and there is no authority to define them, except dictionaries. In other words, we are dealing with traditional translations agreed upon by many people. As a consequence, we can define a toponymic homology relation, such as ₪_T, so that we can write Venezia ₪_T Venice. A homology class can be made by regrouping all of the agreed upon translations of a toponym. See Figure 10a,b.

For types, similar remarks can be made, and another homology relation can be defined to link types and their counterparts other languages.

To alleviate the notation, we will use the symbol ₪ without subscript throughout this text.

Figure 10. (a) Emphasizing the differences between equivalence and homology for toponyms; (b) example of a toponym (Monaco) belonging to two homology classes.

Figure 10. (a) Emphasizing the differences between equivalence and homology for toponyms; (b) example of a toponym (Monaco) belonging to two homology classes.

4.1.2. Geographic Objects

The geographic objects (representing features) will be defined as follows:

Og = (GeoID, Geom, Toponym, Type)

in which:

• GeoID corresponds to the object identifier; this identifier is only used internally and will generally not be known by users;
• Geom corresponds to the geometry of the objects;
• Toponym corresponds to the name of the geographic object in the concerned language; in addition, this will be the main user’s identifier as listed in a monolingual gazetteer;
• Type corresponds to the type of this object as defined in an ontology.

4.1.3. Relations

In addition to classical ontological relations (“is_a”, “has_a”, “part_of”), geographic ontologies include topological relations, as illustrated in Figure 2. There are several ways to encode this knowledge. The first is to use GeoID, so that we can write:

GeoID₁ RelationX GeoID₂

As this is very good for internal use, it is not very convenient for users who prefer toponyms. However, as mentioned above, when using toponyms, some problems occur due to the existence of ambiguities about location. Suppose we use “Mississippi”; do we mean the state or the river?

4.1.4. Geometry

As is well known [27], there are various ways to define the shape of a feature, essentially depending on the accuracy of the device used for measuring it. For instance, the same state can be represented as a polygon of either 500 or 1000 points. As a consequence, in two databases or knowledge bases, the geographic objects describing the same geographic feature can have two different geometric descriptions.

4.1.5. Languages

ISO 639 is a set of international standards that lists short codes for language names (See [28]). The following is a complete list of three-letter codes defined in part two (ISO 639-2) of the standard, including the corresponding two-letter (ISO 639-1) codes where they exist. In this paper, we will use the three-letter codes as the prefix (ENG for English, FRE for French, ITA for Italian, SPA for Spanish, GER for German, GRE for Greek, RUS for Russian, ARA for Arabic, etc.). Therefore, for the city of Venice, we can distinguish various exonyms: ITA.Venezia, SPA.Venecia, FRE.Venise, ENG.Venice, GER.Venedig, POL.Wenecja, GRE.Bενετία, RUS.Bенеция, ARA.البندقية (transliterated into Al Bundukiyya or Al Bondokia), etc.

In a more general form, let Λ = {λ₁, λ₂, λ₃, … λ_l: l ∈ N} define the set of human languages. Therefore, we can denote λ.Topo as any toponym Topo in the λ language.

When alphabets are different, sometimes it is necessary to make a transliteration. Let us denote Transliteration as a function transforming a text written in one alphabet into a text in a second alphabet according to rules.

Text₂ = Transliteration (λ, Text₁)

4.1.6. Toponyms and Located Toponyms

One can define a homology relationship for toponyms. For instance, the various cities in the word Sevilla are also called Séville in French and أشبيليّة (transliterated into Ishbiliyya) in the Arabic language:

Sevilla ₪ Séville

Sevilla ₪ أشبيليّة

Indeed, this relation is not an equivalence relation, because transitivity does not hold everywhere. Indeed, consider the Principality of Monaco (also called Múnegu in the Monégasque language, as given in Figure 10b). Therefore:

Monaco ₪ Múnegu

However, in the Italian language, the German city of Munich (München, in German) is also called Monaco. Therefore, we can write:

Monaco ₪ Munich

It is obvious that “Munich” and “Múnegu” have nothing in common except their names in Italian. In this case, when necessary to disambiguate, Italians say “Monaco di Baviera” and “Principato di Monaco”. In the U.S., when speaking about a place named Washington, generally it is followed by the name of the state.

Regarding the multiplicity of languages, in some cases, it is important to get the endonym of a place. As previously mentioned, sometimes there are several possible endonyms: in this case, one will prefer the name as used by local people in a well-established language. For instance, in Canada, the French toponym “Québec” will be the endonym of the English toponym “Quebec”. Therefore, let Endonym denote a function transforming any toponym into its corresponding exonym. For example:

Venezia = Endonym (Venice)

Back to the example of Granada, in order to disambiguate those homonyms, a solution is to use a hyperonym, for instance the name of the country as a topological prefix ⊃ in which A ⊃ B can be read “A contains B”, “B inside A” or A is the hyperonym of B. Therefore, we can write ES ⊃ Granada, US ⊃ California ⊃ Granada, US ⊃ Kansas ⊃ Granada, MX ⊃ Granada, etc., in which MX stands for Mexico, ES for Spain. Let us call them located toponyms. As a consequence, if there is no ambiguity, we can define relationships in another mode:

LocTopo₁ RelationX LocTopo₂

As the previous solution is interesting to distinguish designated human settlements or administrative subdivisions, it cannot be used directly to disambiguate natural features, such as rivers, mountains, etc., which can spread over several cities, provinces, regions and even countries. Indeed US ⊃ Mississippi can relate to both the state and the river.

Let us define Earth as a toponym with its homologous “planet”, “our planet”, etc. Any located toponym can derive from Earth by a sort of inclusion path. For instance:

• ENG.Earth ⊃ “Pacific Ocean”
• ENG. Earth ⊃ America ⊃ “North America” ⊃ California ⊃ Granada
• ENG.Earth ⊃ America ⊃ “North America” ⊃ “Lake Erie”.

For the path description of Hawaii, there are two possibilities:

• country inclusion: ENG.Earth ⊃ “U.S.A.” ⊃ Hawaii;
• location inclusion: ENG.Earth ⊃ “Pacific Ocean” ⊃ Hawaii.

4.1.7. Matching Two Geographic Ontologies in Different Languages

In this paper, we will examine two geographic ontologies respectively designed in different languages (Ω₁ and Ω₂), for instance one in English and one in Spanish. Since concepts can be different or differently organized, how does one match them?

From a mathematical point of view, we have two graphs in which nodes correspond to concepts and edges to relations. Matching ontologies means that:

• types will be linked by homology relations;
• and ontological relations will also be linked via homology relations.

4.1.8. Homologous Geographic Objects

Two geographic objects sharing homologous geometries, homologous toponyms and homologous types are said to be homologous (Og₁ ₪ Og₂). In this case, they can be regrouped to form a single object having linguistic descriptions in two different languages. However, the newly-created object must have a unique geometric description. Several solutions can be given:

• adopt the more recent geographic description
• adopt the more accurate
• or create a mix of both.

By extension, several linguistic descriptions can be considered for the same object.

4.1.9. Geographic Knowledge Base

To sum up what was previously said, a geographic knowledge base, GKB, will be defined as follows:

GKB = (Terr, λ, Ω, OG, Γ, R)

with OG = {Og₁, Og₂, … Og_m: m ∈N}

in which Terr defines a territory, such as Terr INSIDE Earth, O_G is a set of geographic objects (see Section 4.1.2), a Γ gazetteer, Ω an ontology and R a set of relationships between geographic objects. Remember that when considering Terr as the whole Earth, several Egenhofer planar relations do not hold anymore due to its rotundity [29]. In this paper, a strong assumption is that a gazetteer and an ontology are designed in only one language (λ). The gazetteer will consist of two things, a list of toponyms and a list R_Γ of relationships between them:

Γ = (λ, To, R_Γ)

To = {Toponym₁, Toponym₂, Toponym₃, …. Toponym_t: t ∈ N}

in which λ is a language, Toponym₁ and Toponym₂ are Toponyms and R_Γ a set of relationships among toponyms:

Concerning the ontology, it has a similar structure:

Ω = (λ, Ty, R_Ω)

Ty = {Type₁, Type₂, Type₃, …. Type_s: s ∈ N}

in which Type₁ and Type₂ are Types and R_Ω a set of relationships among types, including the following relations, more precisely in the λ language:

• the three classical ontological relations, is_a, i.e., the “is-a” relation, has_a, i.e., the “has-a” relation and part_of, i.e., the “part-of” relation;
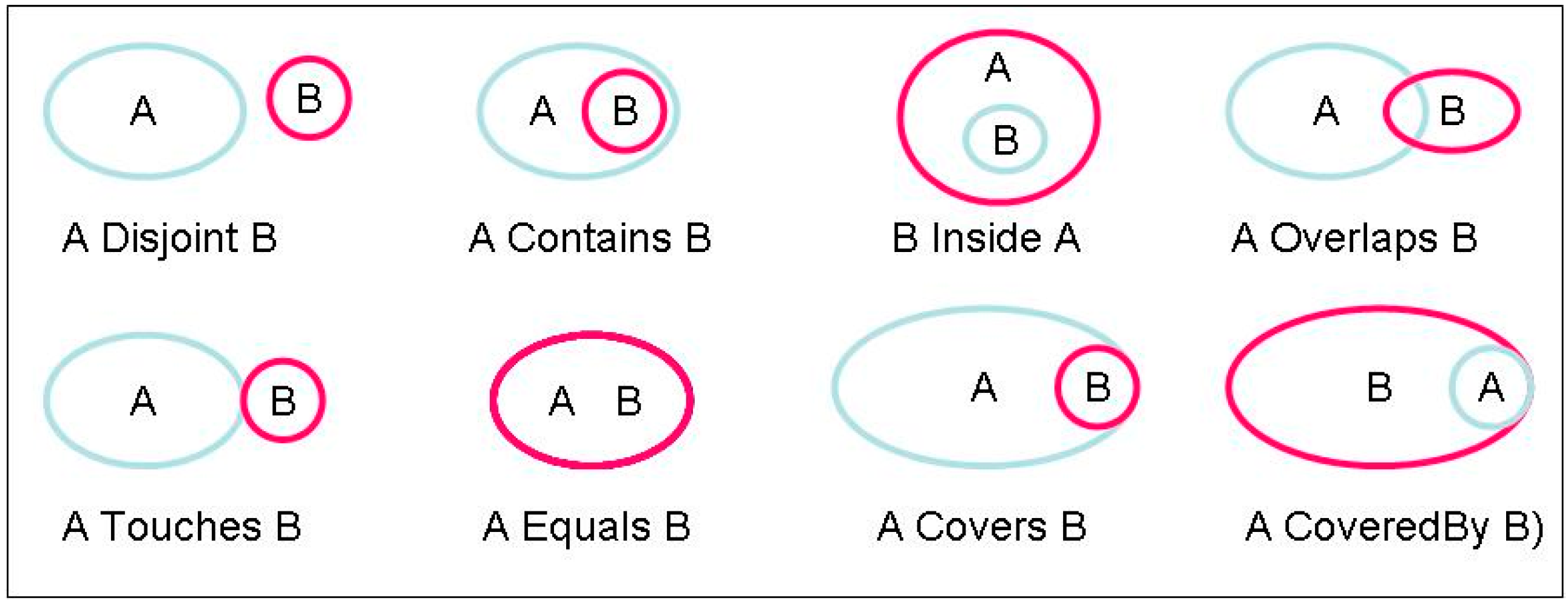
• the eight Egenhofer topological relations (see Figure 2) are, respectively, Disjoint, Contains, Inside, Overlaps, Touches, Equals, Covers and CoveredBy;
• and possibly other additional relations.

4.2. Geographic Rules

Based on the previous formalism, let us explain and write a few rules involving gazetteers and ontologies. Consider two geographic knowledge bases, each one developed with a different language. Suppose it is possible to transform them into the following structures:

GKB₁ = (Terr₁, λ₁, Ω₁, OG₁, Γ₁, R₁)

GKB₂ = (Terr₂, λ₂, Ω₂, OG₂, Γ₂, R₂)

in which languages, ontologies, gazetteers geographic objects and relationships are different (λ₁ ≠ λ₂, Ω₁ ≠ Ω₂, Γ₁ ≠ Γ₂). However, in addition, the territories are supposed to have some parts in common; otherwise, there is no way to compare or to match them. However, in this case, there is an additional interesting problem, which is outside the scope of this paper, which is the fusion of two geographic knowledge bases.

4.2.1. Inferring Geometry

Suppose we have the description of two geographic objects each in one knowledge base, and suppose that one of the objects has an unknown geometry (noted null). If their toponyms and types are homologous, we can infer that those objects are homologous. In addition, we can transfer the geometry (Figure 11). Formally, we have:

∀Og₁ ∈ GKB₁, ∀Og₂ ∈ GKB₂, ∀ λ₁, λ₂∈ Λ: λ₁ ≠ λ₂
∧(Og₁. λ₁.Toponym₁ ₪ Og₂. λ₂.Toponym₂)
∧(Og₁. λ₁.Type₁ ₪ Og₂. λ₂.Type₂)
∧(Og₂.Geom₂ = null)
⇒
(Og₁ ₪ Og₂)

(Rule 1)

In the case of ambiguities, for instance to decide among the possible rivers named Avon in the U.K., a solution can be to ask the user to help situate approximately within, for instance, a minimum bounding rectangle MBR. By doing so, the research space can be reduced until there is no ambiguity.

∀Og₁ ∈ GKB₁, ∀Og₂ ∈ GKB₂, ∀ λ₁, λ₂∈ Λ: λ₁ ≠ λ₂
∧(Og₁. λ₁.Toponym₁ ₪ Og₂. λ₂.Toponym₂)
∧(Og₁. λ₁.Type₁ ₪ Og₂. λ₂.Type₂)
∧(Og₁.Geom₁ INSIDE (MBR)
∧(Og₂.Geom₂ = null)
⇒
(Og₁ ₪ Og₂)

(Rule 1bis)

Therefore it implys also (Og₁.Geom₁ ₪ Og₂.Geom₂). To reinforce the validity of the last relationship (Og₁.Geom₁ ₪ Og₂.Geom₂), since one of the starting value was originally unknown (Og₂.Geom₂ = null), the best solution is to copy the geometric value in order to give (Og₂.Geom₂ = Og₁.Geom₁). Another possibility is to regroup both objects into a single one, so having two linguistic descriptions: in this case, the schema of the knowledge base must be modified accordingly.

Figure 11. Example illustrating Rule 1.

Figure 11. Example illustrating Rule 1.

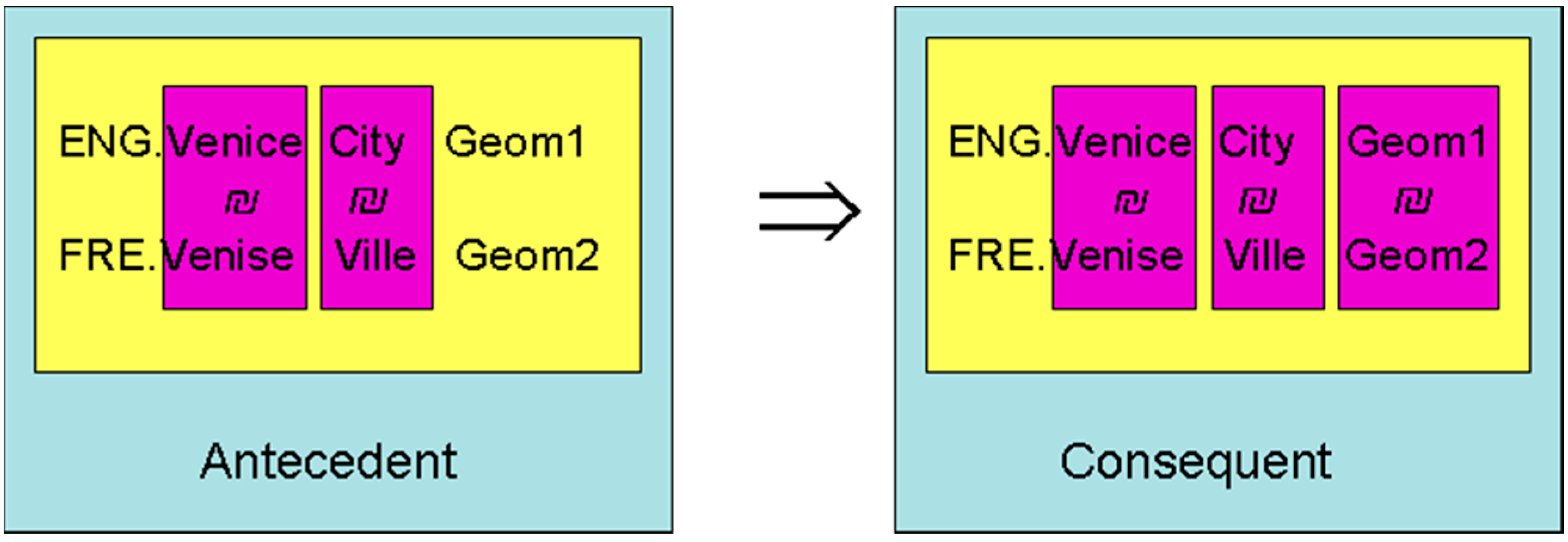
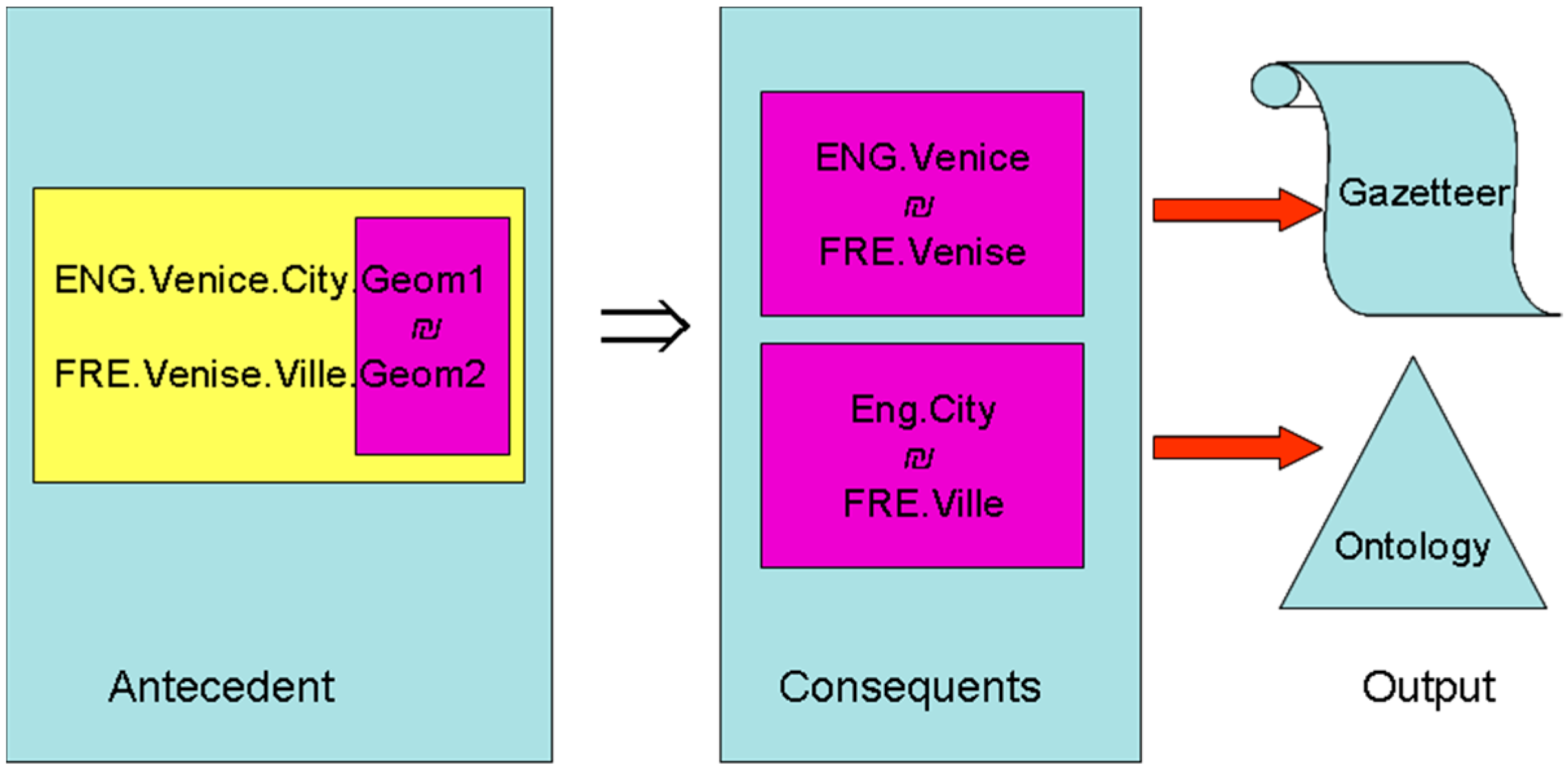
4.2.2. From Homologous Geometry to Homologous Objects

Consider now two objects having homologous geometries; we can infer that (See Figure 12):

-

their toponyms are homologous;

-

their types are homologous;

-

and so, the geographic objects are homologous.

Formally, we can write:

∀Og₁ ∈ GKB₁, ∀Og₂ ∈ GKB₂: Og₁.Geom₁ ₪ Og₂.Geom₂
⇒(Og₁.Toponym₁ ₪ Og₂.Toponym₂)
∨(Og₁.Type₁ ₪ Og₂Type₂)
∨(Og₁ ₪ Og₂)

(Rule 2)

As a consequence, by applying this rule, we generate correspondences in both gazetteers, and we provide a translation of two types in both ontologies.

Suppose you are in Finland, Spanish-speaking and facing the lake, Sääksjärvi: you will say in Spanish “Lago Sääksjärvi”. In the case where a toponym is unknown, say Toponym₂, without loss of generality, i.e., Toponym₂ ∉ Γ₂, the missing toponym can be forced to be the endonym of the other: so:

Toponym₂ = Endonym (Toponym₁)

When the alphabets are different, some transliteration is needed into the λ₂ language, so that:

Toponym₂ = Transliteration (λ₂, Endonym (Toponym₁)).

Figure 12. Example illustrating the Rule 2.

Figure 12. Example illustrating the Rule 2.

4.2.3. Inferring Ontological Relations

Suppose now that, in addition, we have topological relationships in both gazetteers. Therefore, the knowledge bases are now constituted as follows, in which ρ₁ and ρ₂ stand for any type of ontological relationship:

GKB₁ = {Og₁, ρ₁} and GKB₂ = {Og₂, ρ₂}

with:

ρ₁ = GeoID₁₁ R₁ GeoID₁₂ and ρ₂ = GeoID₂₁ R₂ GeoID₂₂

If two couples of homologous objects have relationships between them, then their relations are homologous (see Figure 13 for an example).

Figure 13. Example of Rule 3 for inferring homology between two relations in which “Mereo” means a meronym relation.

Figure 13. Example of Rule 3 for inferring homology between two relations in which “Mereo” means a meronym relation.

Formally, we can write:

∀Og₁₁, Og₁₂, R₁ ∈ GKB₁, ∀Og₂₁, Og₂₂, R₂ ∈ GKB₂:
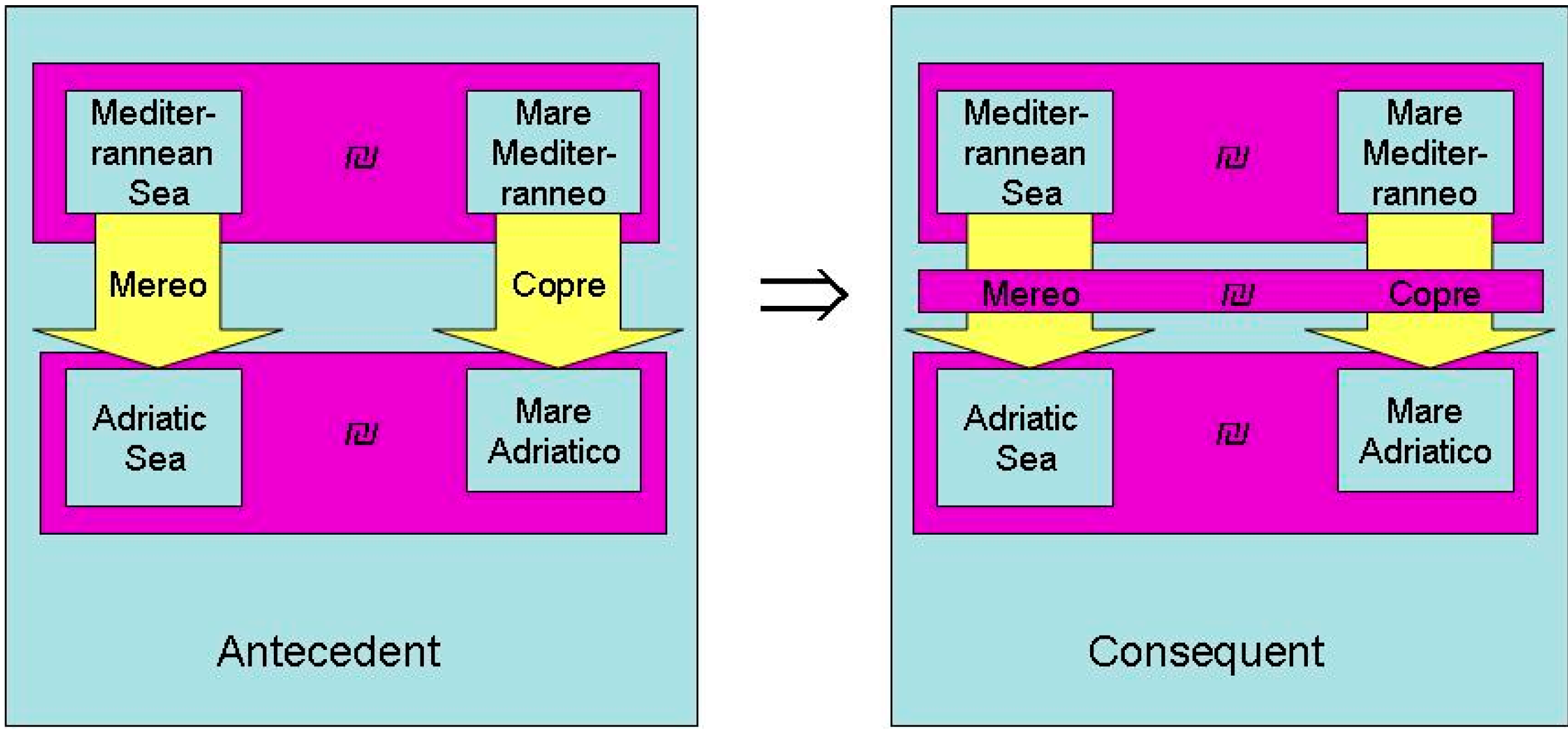
(Og₁₁ ₪ Og₂₁) ∧ (Og₁₂ ₪ Og₂₂)
(Og₁₁ R₁ Og₁₂) ∧ (Og₂₁ R₂ Og₂₂)
⇒(R₁ ₪ R₂)

An interesting case is when the relation name is unknown in one knowledge base, for instance, say R₂. In this case, there are several solutions:

• to confer the same name, but in this case, it is not correct in the second language;
• or to ask an expert to propose a solution for the translation of this name.

Perhaps, some other rules can be written, so as to match geographic objects, their geometric shapes, their place names and types in different languages.

5. Conclusions

This paper tries to establish the connections between geographic objects, ontologies and gazetteers in multilingual contexts. We have established some inference rules in order to match concepts between two geographic ontologies, each of them written with a different language. We have shown that gazetteers can be used in the foundation of this matching, not only for concepts, but also for relations between concepts. Several inference rules were described, but certainly some others can be designed.

One of the main assumption was that time was not involved. This can be a prospect to extend this framework in order to take temporal aspects into account. Among the difficulties, remember that toponyms and, more precisely, archeonyms can evolve, but the overall geographic descriptions of old features remain unknown or is very difficult to estimate: what were exactly the coordinates of Roma as created by Romulus?

This paper can also be seen as a first step towards the fusion of several geographic knowledge bases written in different languages.

Another perspective is to include non-spatial attributes, as they are very common in GIS. Due to this, the geographic knowledge base can be enriched by knowledge extracted by spatial data mining.