Abstract
This article presents and explains a methodology based on cryptanalytic and reverse engineering techniques that can be employed to quickly recover information from encrypted files generated by malware. The objective of the methodology is to minimize the effort with static and dynamic analysis, by using cryptanalysis and related knowledge as much as possible. In order to illustrate how it works, we present three case studies, taken from a big Brazilian company that was victimized by directed attacks focused on stealing information from a special purpose hardware they use in their environment.
1. Introduction
Malware nowadays has frequently been playing a major role in directed attacks, in order to disrupt services or steal sensitive information. Examples of these include Stuxnet [1] and Flame [2], which targeted Iran’s nuclear facilities and Middle Eastern countries, respectively. The complexity of the techniques that have been used by each new breed of malware to infect, spread, and take advantage of the compromised systems has been progressively increasing. For instance, Stuxnet injected code on programmable logic controllers of industrial control systems, while Flame improved Steven’s cryptanalytic attack on MD5 [3] collisions [4], in order to trick Microsoft Windows Update component to accept it as a valid software patch.
In this article, we introduce and discuss a methodology for retrieving information from encrypted files generated by malware, containing the victim’s stolen information. In order to validate the effectiveness of the proposed process, we applied it to three different breeds of malware, much less sophisticated than Stuxnet and Flame, that were built to attack a big Brazilian company. They acted intercepting all the traffic between a specialized hardware and servers and storing the captured data in an encrypted way, before sending the results to the criminals. In this scenario, we were hired by the victim to discover exactly which information had leaked, but without being provided any access to the compromised environment. The only things available for our analysis were the data files and the malware binaries collected by the client, during the incident response process.
After talking to the team that took the initial measures to treat the case, we realized they had the knowledge to perform a dynamic and static analysis on the malicious code, but lacked the necessary cryptographic skills to understand the algorithms each malware used for “protecting” the stolen data. This is where the main contribution of this article lies: we provide a thorough explanation of all the techniques we employed to retrieve the original information, without spending much time with reverse engineering the binaries. Therefore we hope this text can help other people do the same work as ours as part of their security incident handling processes.
The rest of this article is organized as follows. In Section 2, we introduce and discuss our methodology. Section 3 presents the case studies, and, for each one of them, we give general information about the malware and its output, explain the sequence of steps taken to break the encrypted file, according to the methodology, and conclude with a description of the cipher and the cryptographic key used. Section 4 describes related work and compares it to this one. Opportunities for automation are discussed in Section 5, while conclusions are finally drawn in Section 6. It is important to note that, due to the sensitivity of the information being dealt, we used fake sample files, instead of the real ones, in order to illustrate the discussed techniques.
2. The Proposed Methodology
The proposed methodology, whose steps are depicted in Figure 1, starts by the analysis of the file containing the encrypted stolen information. This can be accomplished by simply opening it in a hexadecimal editor, in order to check if it is a text file or if there are patterns that could indicate the use of an encoding mechanism, such as Base64, Radix-64, or two-digit ASCII code. Whenever one gets a positive response for this verification, one should proceed with the data decoding. This step should be repetitively executed until one cannot identify an output containing encoded information. Additionally, one should verify whether compression is used or not and unpack the data if necessary.
In order to test whether a classic (or weak) cryptographic algorithm is used, one can measure the level of redundancy of the data, by trying to compress it. One shall remember that the output of a strong encryption mechanism should look like something random, which implies that compression should result in a slightly bigger file, instead of a smaller one. The reasoning behind this is that compression is based on few elements being more frequent than others, which should not occur in a random stream, considering a sample of reasonable size, since each element tends to appear approximately the same number of times. Another simple technique to check this consists in making a histogram of the file contents and look for an uneven distribution of the byte values.
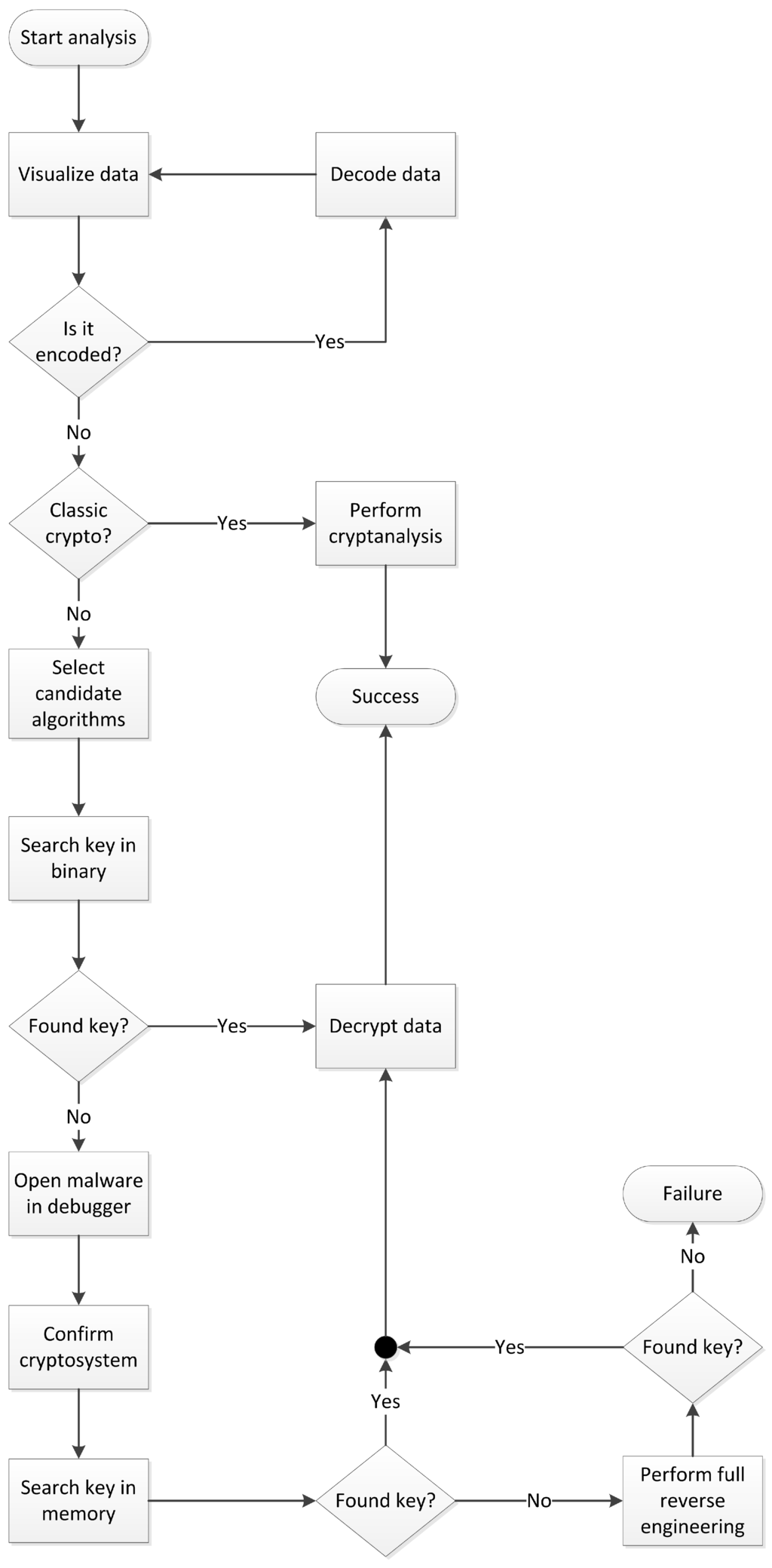
Figure 1.
Methodology for retrieving information from malware encrypted output files.
There are several techniques that can be employed to perform the cryptanalysis of a classic algorithm. For simple substitution ciphers, one can employ frequency analysis [5], which is based on the following facts: (1) frequencies of plaintext symbols are preserved in the ciphertext; (2) each language has a characteristic frequency distribution of symbols. Considering these facts, the idea consists simply in substituting symbols in one alphabet for another according to similar frequencies. Transposition ciphers can also be broken using language statistics, but those related to the frequency of digrams and trigrams. In case of polyalphabetic mechanisms, one can employ Kasiski’s method [5], which takes into consideration that a repeated sequence of symbols renders the same ciphertext when encrypted with the same key positions. This observation helps in finding the key length k, which is enough to reduce the original problem to the cryptanalysis of k mono-alphabetic ciphers. Alternatively, the period of the polyalphabetic cipher can be found by using the index of coincidence [6], which measures the relative frequency of symbols in the ciphertext.
Normally, it should not be possible to pinpoint the encryption algorithm that was used to generate a given ciphertext. However, one can at least try to infer some information related to the class of cipher used by inspecting the encrypted data. For instance, if one identifies that the messages have a fixed length of 2048 bits, it is reasonable to consider that an asymmetric cipher was used, especially the RSA cryptosystem [7], which commonly uses such a key size. On the other hand, if the size of messages varies and is multiple of 128 bits, one can suppose a 128-bit block cipher is being used. Finally, if one detects a variable message size that is not multiple of a common block size, a stream cipher might be a possible candidate. Note that it is important to know which algorithm we are facing, in order to correctly search the key and to be able to perform the decryption at the final step.
The initial approach concerning key search in malware binary consists in looking for textual information contained in it. Clearly, it is a vulnerability to embed sensitive information, such as keys, in the source code, but even malware writers quite frequently do that [8]. If this test is unsuccessful, however, one can try Shamir’s algorithm [9], which considers the entropy of a securely generated key. The idea is to scan the whole binary, through a fixed size window, in search of the region that contains the most quantity of different byte values. In fact, this is far from being a formal method for measuring entropy, but it is enough for our purposes.
If at this point, one has not found the key yet, it will be necessary to perform, at least, basic malware analysis. As usual it is advisable to use a confined and virtual environment, although there is malware that might not unpack inside a virtual machine, as a protection mechanism against reverse engineering. In order to confirm or discover the employed cryptosystem, one can look for known structures that might be used by the candidate algorithms. For instance, DES [10] implementations normally define two matrices, PC1 and PC2, for use in the key scheduling process. Once one of those data structures is found, it is possible to locate the key through the code that references that data. If we take AES [11] as another example, one can search for the forward or inverse S-Boxes matrices definitions, which will likely be in place. Additionally, it is possible to use Shamir’s algorithm again, but this time to scan the memory allocated to the process.
If, in the worst scenario, none of the aforementioned techniques work, it will be necessary to perform a full reverse engineering of the malware. The success in this case is going to depend on the countermeasures employed by the malware to avoid being reversed. Examples of techniques that might hinder the analysis include code obfuscation, detection of virtual machines, code encryption, detection of debuggers, and anti-disassemblers methods, just to name a few [12].
3. Case Studies
In this section, we present a few case studies originated from the application of our methodology to Brazilian malware used in directed attacks.
3.1. First Malware
The malware covered in this section employs only classical cryptography and for this reason it is enough to analyze the output file only, in order to retrieve the original information.
3.1.1. Description of the Malware and the Encrypted File
The malware is stored in a file named “systen.exe”, which is identified as a generic malicious code by 34 out of the 45 antiviruses run in the site VirusTotal [13]. According to PEiD [14], it was written in Microsoft Visual Basic 5.0/6.0 [15] and no packer is used for code protection. A sample of the encrypted file it generates is shown in Figure 2, loaded in the GHex utility. An important thing to see there is the repetition of the string “robin@hoo”.
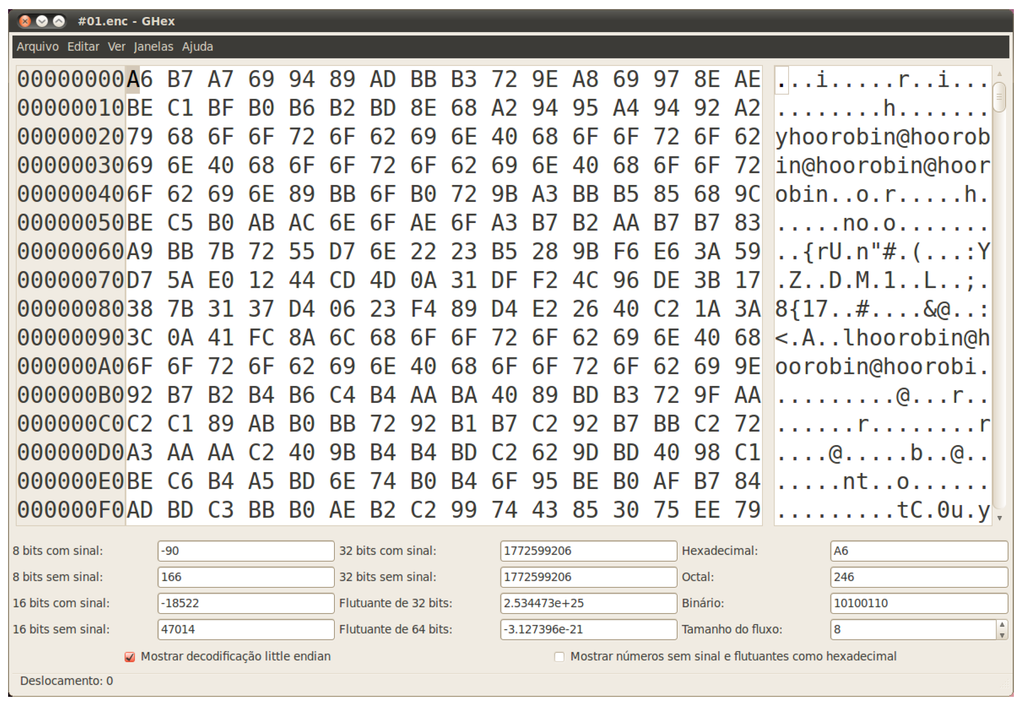
Figure 2.
Encrypted file #1 sample.
3.1.2. Analysis of the Encrypted File
As already mentioned, one of the premises of a strong encryption algorithm is that its output should look random, that is, one should not be able to find any patterns on it whatsoever. This very basic rule is not satisfied by the encrypted file of this section, which can be easily verified by the repetition of the string “robin@hoo”. The issue can also be graphically detected by the histogram illustrated in Figure 3, which clearly shows a non-uniform distribution, with values concentrated between 80 and 180.
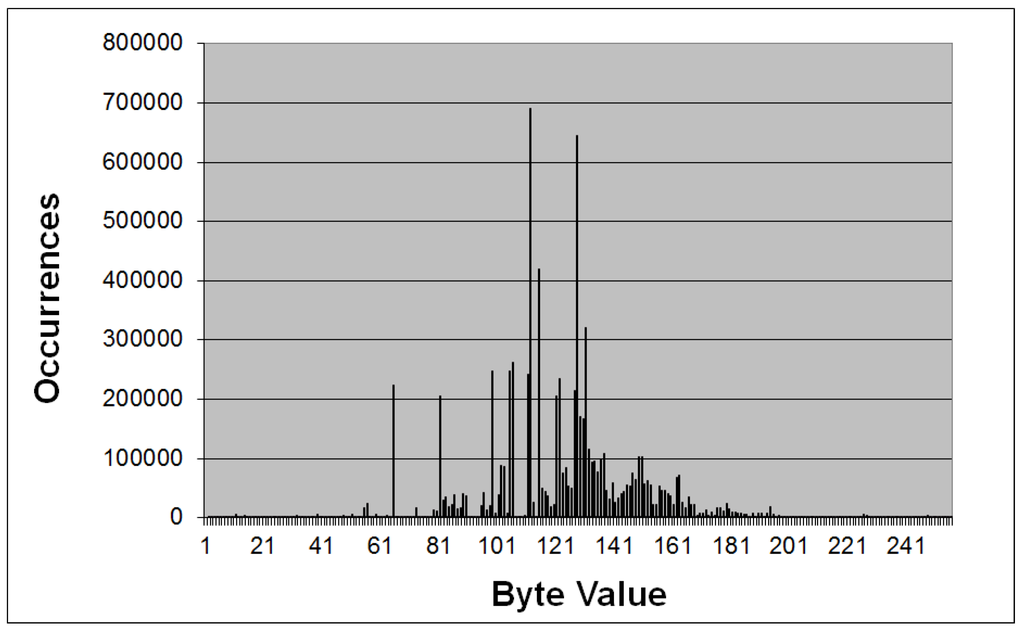
Figure 3.
Histogram of byte values for the encrypted file #1.
The next step in the analysis consists in identifying the distance between each occurrence of “robin@hoo”, which happens to be exactly the size of the string, i.e., nine. Another important fact to be noted here is that the position it appears the first time is apart from the beginning of the file a number of bytes, that is multiple of the string length. This implies that, in case “robin@hoo” is related to the cryptographic key, it might be first used from the initial byte.
From this point, one can formulate two main hypotheses:
- Hypothesis #1: a constant number is added to each byte modulo 256 and a given string is repeated several times in the plaintext, resulting in the occurrences of the string “robin@hoo”. Although this is not likely, it should be tested, by simply trying every one of the 256 possible keys, and checking if a meaningful message pops out from the process. As expected this test fails and does not solve the problem.
- Hypothesis #2: a Vigenère cipher [5] over an alphabet of 256 elements and a period that equals 9 is used by the malware. Of course, in this scenario, the candidate key is the aforementioned string, which is probably being added to a sequence of null bytes present in the original message. Testing this theory results in the text shown in Figure 4, in which the beginning of words seems to be incorrectly decrypted. Taking a closer look to the wrong letters, under the light of the ASCII code, one can see that the distance to the expected values is always thirty-two, implying this amount should be subtracted from every single byte of the candidate key. The final and successful result can be seen in Figure 5.
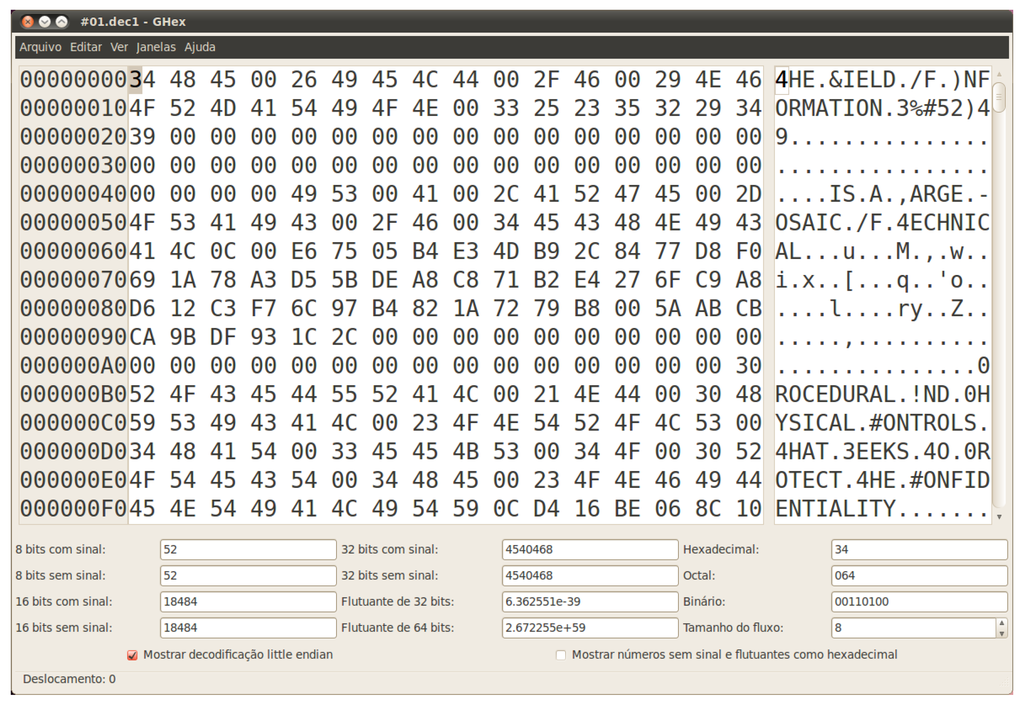
Figure 4.
First attempt to decrypt file #1.
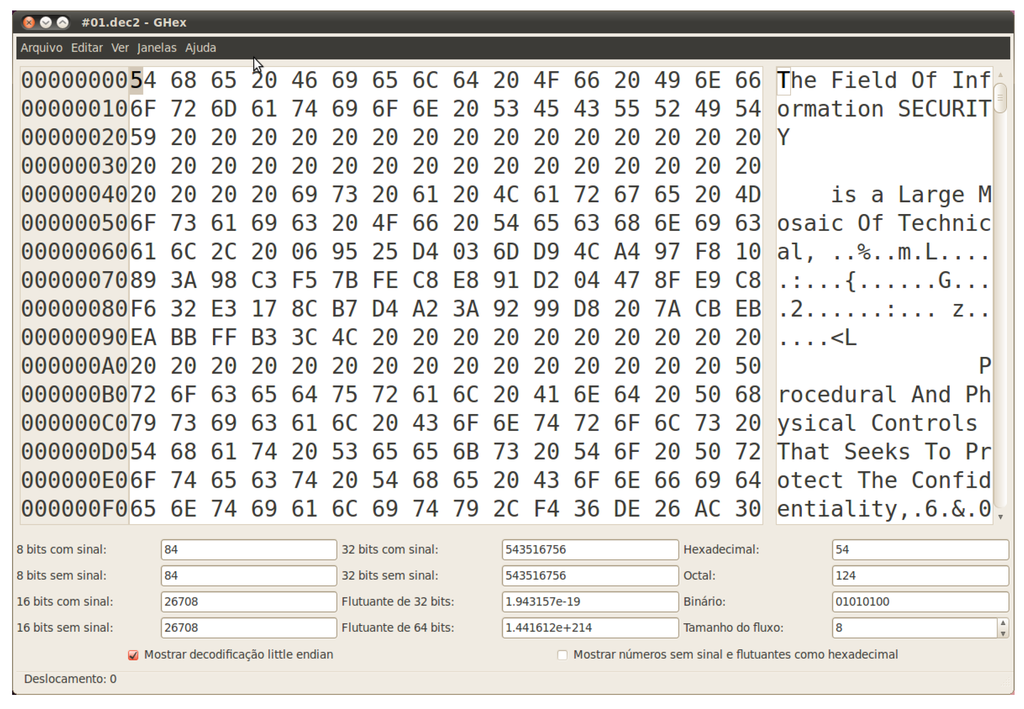
Figure 5.
Second and final attempt to decrypt file #1.
3.1.3. Summary of the Analysis
Figure 6 summarizes the analysis of file #1, highlighting the methodology’s steps that were executed.
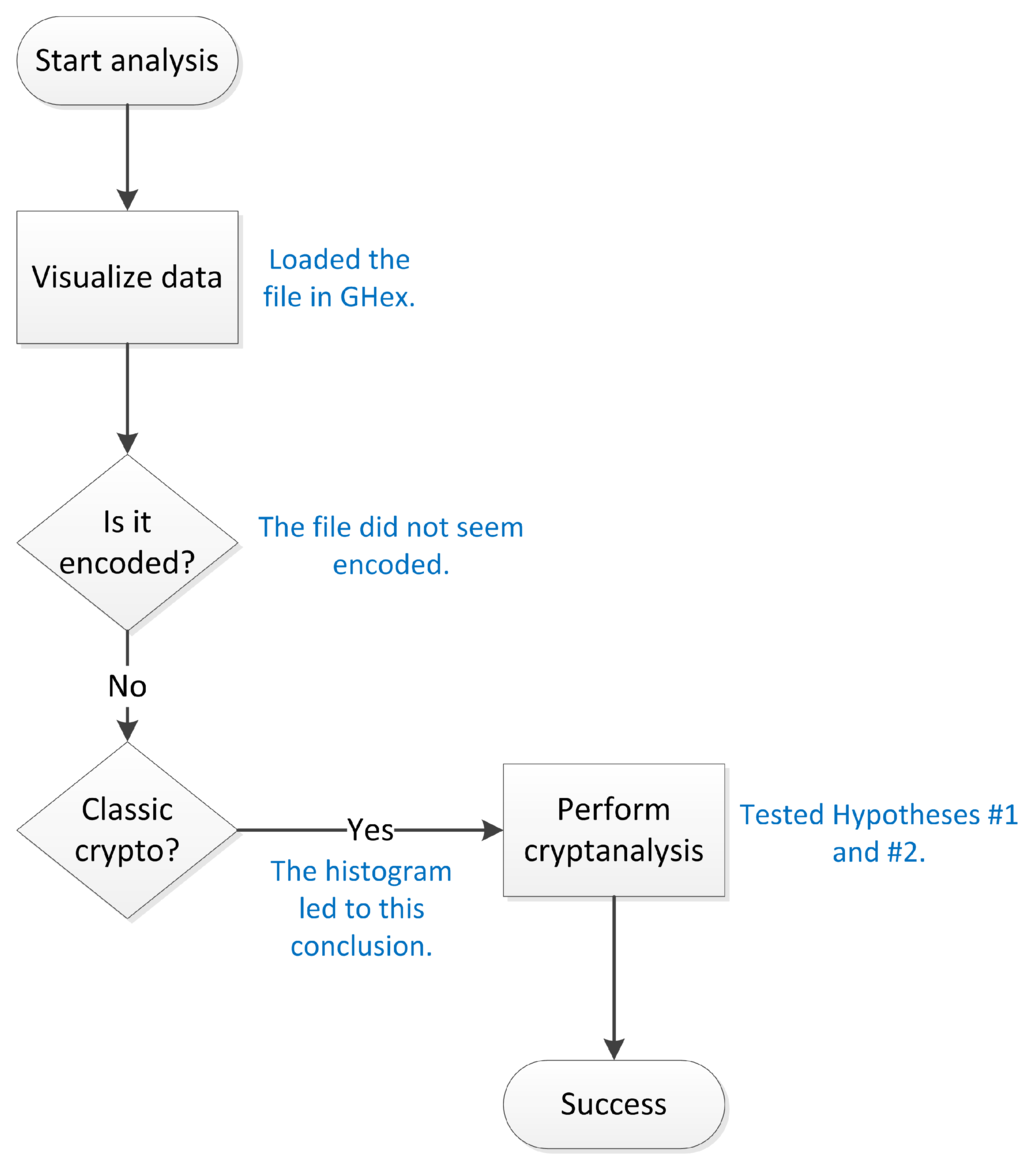
Figure 6.
Summary of the analysis of file #1.
3.1.4. Description of the Cipher and the Key
The cipher and cryptographic key used by the malware can be described as follows:
- Alphabet of definition:
- Plaintext:
- Ciphertext:
- Key: (ROBIN HOO)
- Encryption function:
- Decryption function:
3.2. Second Malware
The second malware we are going to analyze is cryptographically similar to the previous one, since it employs the same encryption algorithm, but with a larger key. In terms of functionality, besides capturing special purpose hardware information, it also monitors and records everything the user types. Finally, it exfiltrates the stolen information by sending them to free e-mail accounts the criminal owns.
3.2.1. Description of the Malware and the Encrypted File
The malware is composed of two files, “cftmon.exe” and “scvhost.exe”, which are identified as generic malicious code, respectively, by 27 out of 44 and 30 out of 45 antiviruses run in the site VirusTotal. According to PEiD, both of them were written in Microsoft Visual Basic 5.0/6.0 and no packer is used for code protection. A sample of the encrypted information obtained from the criminal’s e-mail account can be seen in Figure 7.

Figure 7.
Encrypted file #2 sample.
3.2.2. Analysis of the Encrypted File
One can easily see from Figure 7 that each block starts with a prefix (C1@, C3@, K@) and that some kind of encoding scheme is being used in the rest of each entry. Considering there are only digits and letters from A to F, it is reasonable to expect that every pair of symbols corresponds to a hexadecimal representation of an octet. The result obtained by decoding the first block of the message is illustrated in Figure 8, from which it is possible to note the absence of any printable characters. As the next step one can draw the histogram of the decoded information, but over more blocks from the original file, resulting in the distribution shown in Figure 9. This resembles the histogram in Figure 3 with respect to the uneven distribution, and thus it might indicate a mono- or poly-alphabetic cipher.
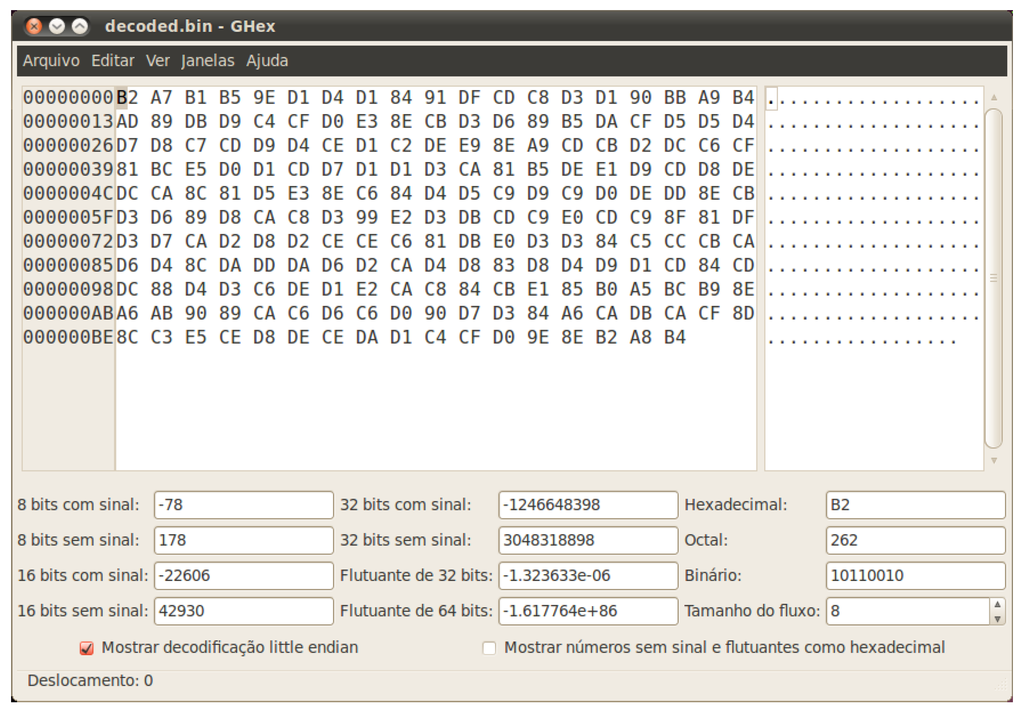
Figure 8.
Result of decoding the first block of file #2.
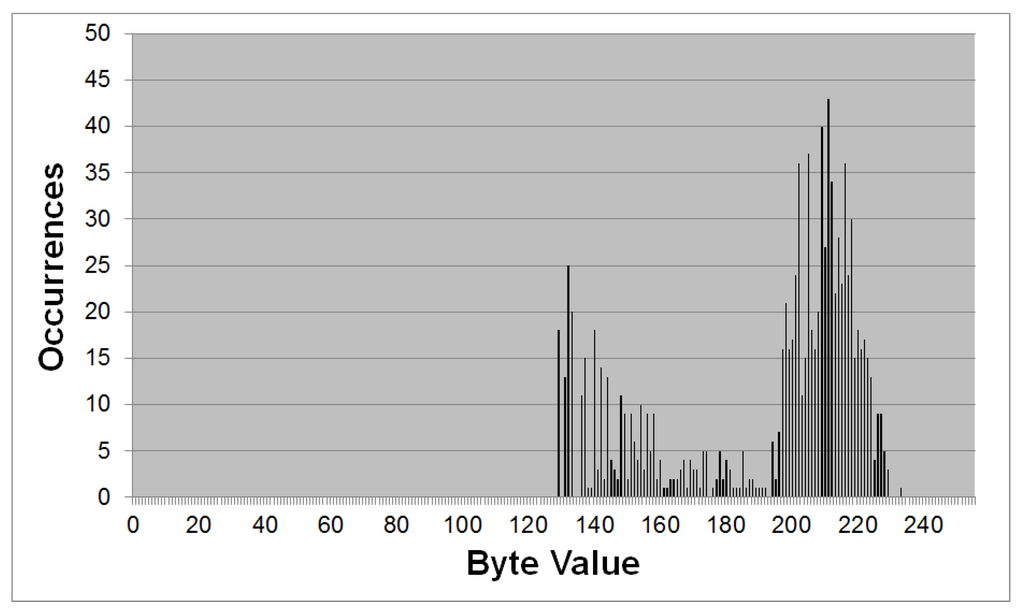
Figure 9.
Histogram of byte values for the encrypted file #2.
Trying to add every value from 0 to 255, modulo 255, i.e., all possible keys of an 8-bit shift cipher, does not recover any plaintext from the decoded information at all. This result means we tested for the wrong algorithm and then we should proceed to other monoalphabetic and polyalphabetic encryption mechanisms. Before trying to perform a frequency analysis or to apply Kasiski’s method, however, it is worth looking for interesting strings that may be contained in the malware binaries. For that matter, it is advisable to consider several encodings, such as ASCII, Unicode and UTF, for example, having the endianness of the platform in mind. The utility strings can help with this task, with the options below:
- strings cftmon.exe
- strings -e l cftmon.exe
- strings scvhost.exe
- strings -e l scvhost.exe
The last command reveals an interesting string, the anagram “ecalpneddih”, marked by the red rectangle in Figure 10. That could very well be the key for a Vigenère cipher, like in the previous case, and that hypothesis can be confirmed by being able to successfully decrypt the original information with it. Since the provided files contain intercalated messages originated from several compromised hosts, one needs a method to detect the current key position for each origin. Our solution to this problem is to align the key according to language statistics of the decrypted information, i.e., we should check whether the result is meaningful or not in the victim’s mother language.
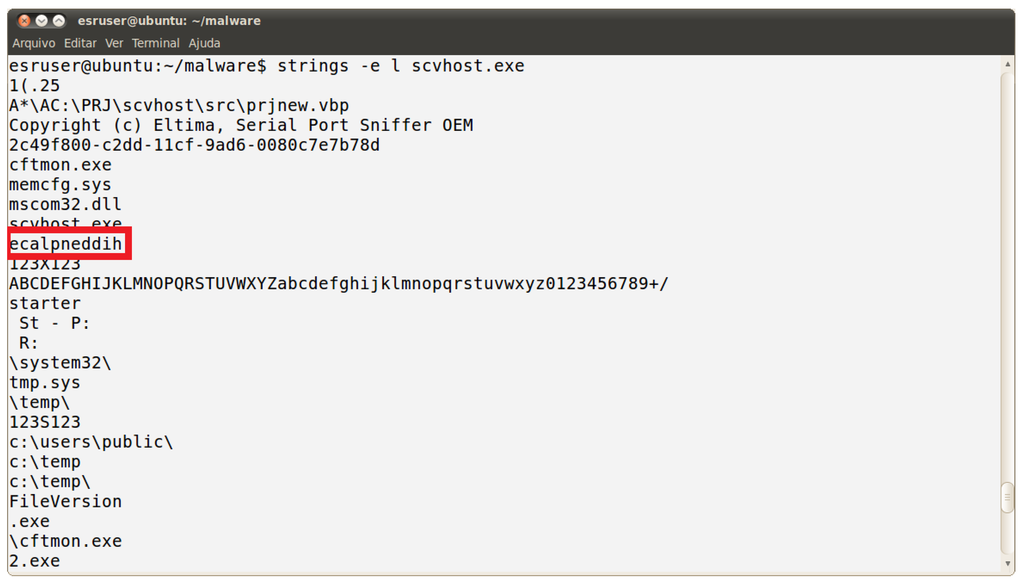
Figure 10.
Strings contained in scvhost.exe.
3.2.3. Summary of the Analysis
Figure 11 summarizes the analysis of file #2, highlighting the methodology’s steps that were executed.
3.2.4. Description of the Cipher and the Key
The cipher and cryptographic key used by the malware can be described as follows:
- Alphabet of definition:
- Plaintext:
- Ciphertext:
- Key: (ecalpneddih)
- Encryption function:
- Decryption function:

Figure 11.
Summary of the analysis of file #2.
3.3. Third Malware
The last malware is the most interesting of the three, because it uses a reasonably modern encryption algorithm, requiring deeper analysis and creativity in order to quickly find the key.
3.3.1. Description of the Malware and the Encrypted File
The malware is stored in a file named “portsys.exe”, which is identified as a generic malicious code by 38 out of the 46 antiviruses run in the site VirusTotal. According to PEiD, it was written in Borland Delphi 6.0 [16], a common language used in the creation of Brazilian malware, and no packer is used for code protection. A sample of the encrypted file it generates is shown in Figure 12.
As mentioned before, this is not a real output file from the malware and neither can it be decrypted with the key we will find in the analysis. The only purpose of it is to illustrate the initial steps of the cryptanalysis process.
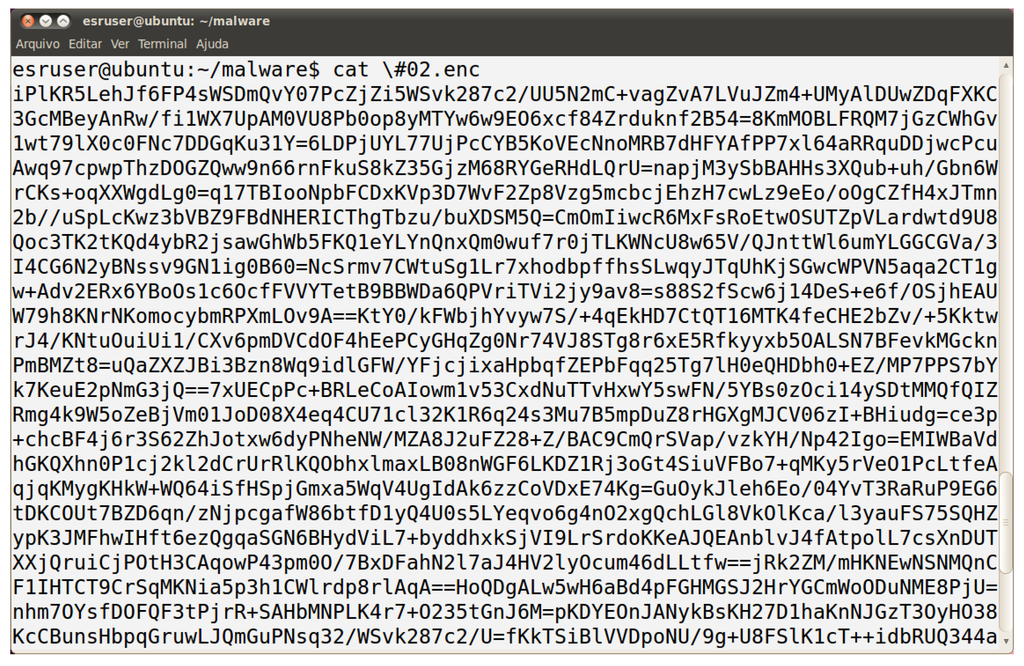
Figure 12.
Encrypted file #3 sample.
3.3.2. Analysis of the Encrypted File
From Figure 12, one can easily see that the file is Base64 encoded. Trying to decode it gives us the result illustrated in Figure 13. At first sight, it seems the decoded file is very entropic, meaning a not so weak encryption algorithm was used. In order to confirm or reject the supposition, one can estimate the randomness of the file, by checking the compression rate that can be achieved. When running the decoded file through gzip, one actually gets an increase in its size, implying that classical cryptosystems can be discarded.
The next step therefore requires one to discover if an asymmetric or symmetric encryption algorithm was used, and, in the latter case, if it is a stream or a block cipher. Public-key schemes are not likely to be employed, due to a bigger code size and because they are not suitable for large inputs. Stream ciphers, on the other hand, are generally not secure when different messages are protected under the same key, because one can simply xor two distinct encrypted texts to cancel the keystream and perform a statistical analysis on the result [5]. Of course this is not common knowledge and actually one can find this vulnerable use of cryptography on the wild. However, considering that one has far more implementations of block ciphers than stream ciphers, we should try the former first.
In order to proceed, one needs to find the cipher block size so as to narrow the list of possible algorithms. One way to do that is to analyze the Base64 encoded file, determine the boundaries between messages, and then check their sizes. One should remember that Base64 encodes three octets into four Base64 characters. Therefore, when the input size is multiple of three, it is not possible to detect where a message ends. For example, “new”, “man”, and “newman” are encoded as “bmV3”, “bWFu”, and “bmV3bWFu”, respectively. Observe that, in the last case, it is not possible to affirm if the original text consists of a single word or not.
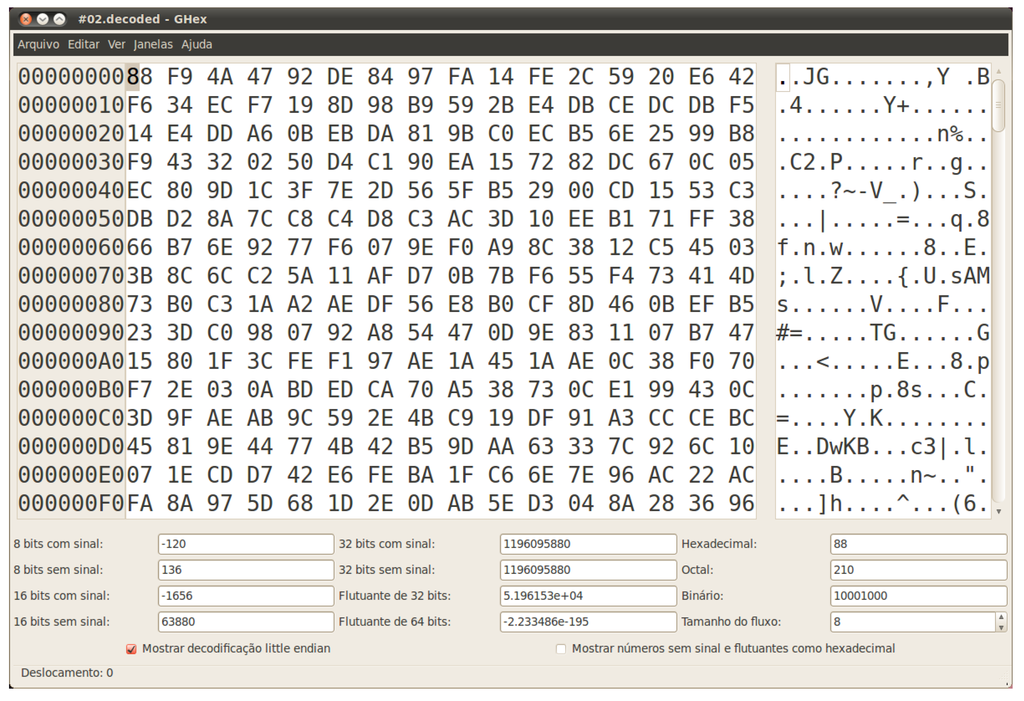
Figure 13.
Result of Base64 decoding the file #3.
One straight strategy that can be adopted to circumvent that problem consists in looking for messages whose size is not multiple of three. In this situation, the last input block can have one or two octets, resulting in the padding illustrated in Figure 14. Searching the file for the padding character (“=”) will help us find message boundaries and consequently infer the cipher block size. One such desired occurrence can be seen in Figure 15.
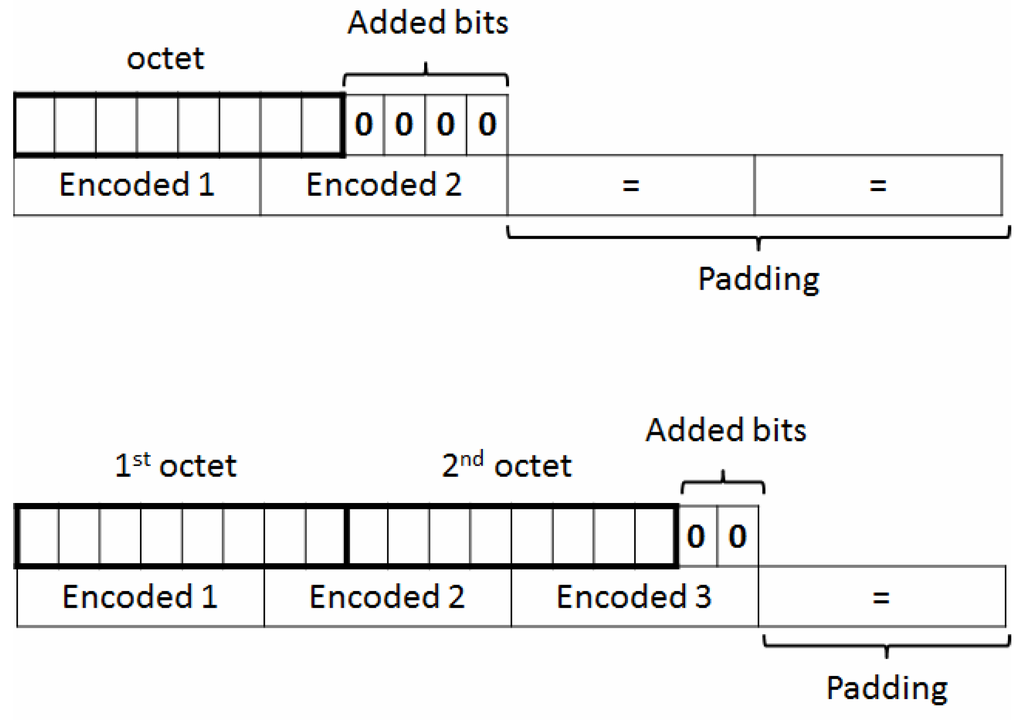
Figure 14.
Base64 padding process.
Observe that, in the example, the delimited message contains 56 Base64 characters, of which the last four comprise a padded input block of length one. Since each four Base64 characters correspond to three input octets, we conclude that the message size is 40 bytes: we need to subtract 4 from 56, due to the padding block, multiply the result, 52, by , which gives us 39 octets, and finally add 1 back, which is related to the last block.

Figure 15.
Message boundaries.
Most modern block ciphers, such as AES [11], employs a 128-bit or larger block size (192 or 256-bit). Legacy encryption algorithms, such as DES, on the other hand, use a 64-bit block size. Given 40 bytes is not multiple of 16 (128 bits), 24 (192 bits), neither 32 (256 bits), we can assume that the malware does not use any modern algorithm, and therefore we should focus our work on 64-bit block ciphers. The (not exhaustive) list of candidate cryptosystems is presented below:
- DES—acronym for Data Encryption Standard, the first commercial-grade encryption algorithm with open specification;
- Triple DES with 2 keys—consists in successively applying DES three times with the first key being equal to the third and different from the second one [17];
- Triple DES with 3 keys—consists in successively applying DES three times with the keys being pairwise different [17];
- FEAL—the acronym for Fast Data Encipherment Algorithm, a block cipher proposed by Shimizu and Miyaguchi [18] that uses a 64-bit key to generate a 256-bit key;
- IDEA—block cipher created by Lai and Massey [19] that uses a 128-bit key;
- SAFER K-64— the acronym for Secure And Fast Encryption Routine with a Key of length 64 bits, a byte-oriented block cipher proposed by Massey [20];
- RC5—created by Rivest [21] and designed to be fast, both in hardware and software, having a variable number of rounds and variable-length cryptographic key, and to be adaptable to architectures with different word sizes;
- Loki—cipher created by Pieprzyk et al. [22] that employs a 64-bit key;
- Blowfish—this cipher was created by Schneier [23] and can use key lengths up to 448 bits; and
- KATAN64—one of the members of a family of hardware oriented block ciphers, all using 80-bit keys, created by Cannière et al. [24].
To the best of the author’s experience, among the enumerated algorithms, the most commonly used are DES, Triple DES, and Blowfish. They will hence be our first choice.
In order to help in the identification of the algorithm used, we can search for strings related to the candidates in the malware binary. Thus, one should try “encrypt”, “crypto”, “cipher”, “des”, “bf”, and “blowfish”, to name just a few examples. The results of this step, shown in Figure 16, give us an important hint (“LbCipher”). Searching this word in Google, we find out that it is a library for Borland Delphi, which implements the algorithms DES, Triple DES, and Blowfish.
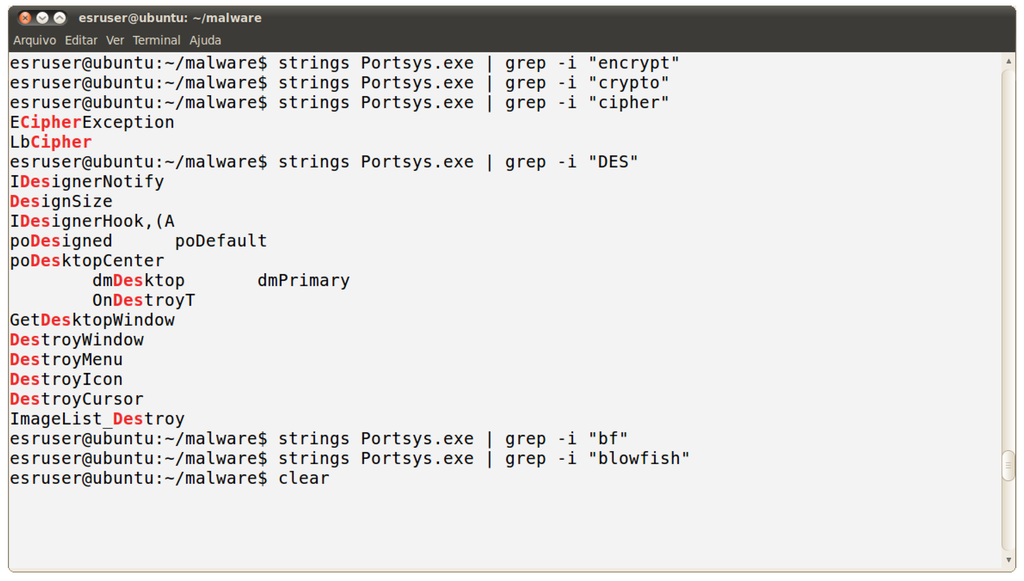
Figure 16.
Search results of common words.
Although we have been capable of narrowing the list of candidate algorithms, obviously that is not enough to decrypt the malware output files and we still need to identify the exact cryptosystem and key. Starting with DES, we have the following basic facts: DES is a block cipher based on a 16-round Feistel network, using a 64-bit key of which only 56 of them are effective, due to parity bits. Sixteen 48-bit round sub-keys are derived from the original cryptographic key by a scheduling algorithm, which uses two tables, PC1 and PC2, for bit selection. These tables are illustrated in Figure 17.
Even though DES uses other structures in tabular form, such as the initial and final permutations (IP and IP), for example, the interest in PC1 and PC2 lies in the fact that the key scheduling algorithm is the only point in the whole algorithm where the key is referenced. Therefore, if we are able to find them inside the malware binary, besides confirming the use of this cipher, we can, as a side effect, easily locate the code that manipulates the key.
Just to evidence that we are in the right track, we can check the presence of PC1 and PC2 in the source code of LbCipher, which can be obtained from the Internet. As expected, those two tables are declared as arrays in the library, as shown in Figure 18. It is important to note that, since the first position in the array is zero, all the values of Figure 17 are subtracted by one. Hence, when searching the binary for those data structures, this fact needs to be taken into consideration. Another comment regarding the excerpt in Figure 18 is that knowing how much times the procedure InitEncryptDES is called in the program allows us to pinpoint if DES or Triple DES is used, based on the information summarized in Table 1.
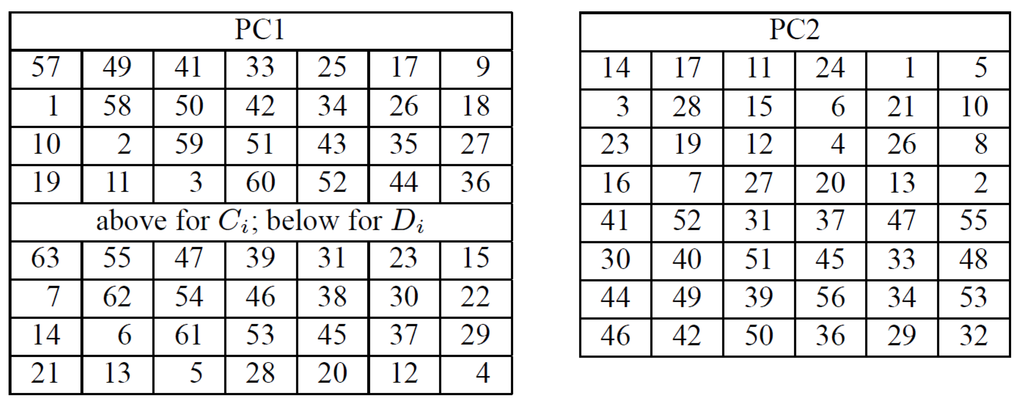
Figure 17.
DES key schedule bit selections. Extracted from [5].
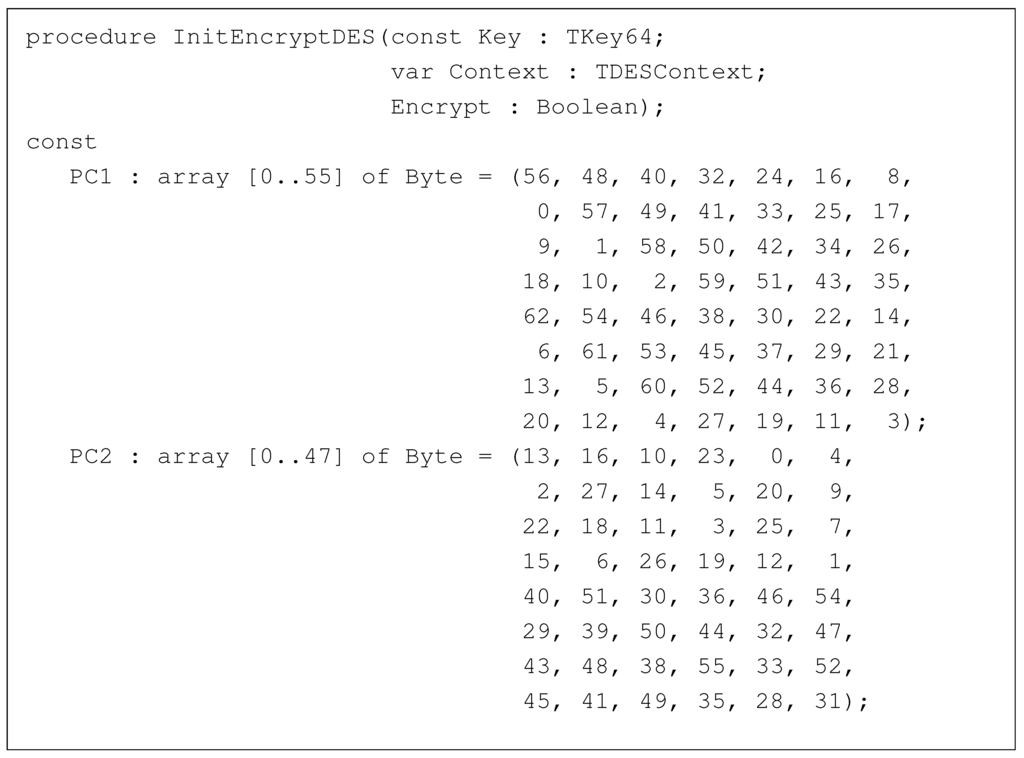
Figure 18.
Excerpt from LbCipher.pas highlighting PC1 and PC2 matrices.
All the information collected so far can guide our next steps, beginning with loading the malware in a debugger, such as OllyDbg [25], and finding PC1, as illustrated in Figure 19. It suffices to enter just a few bytes of the table, represented as hexadecimal characters. The result of this search is shown in Figure 20, marked with a red rectangle.

Table 1.
Number of calls to InitEncryptDES from each procedure within LbCipher.
| Procedure name | Number of calls |
|---|---|
| Plain DES | 1 |
| InitEncryptTripleDES | 4 |
| InitEncryptTripleDES3Key | 6 |
| ShrinkDESKey | 2 |
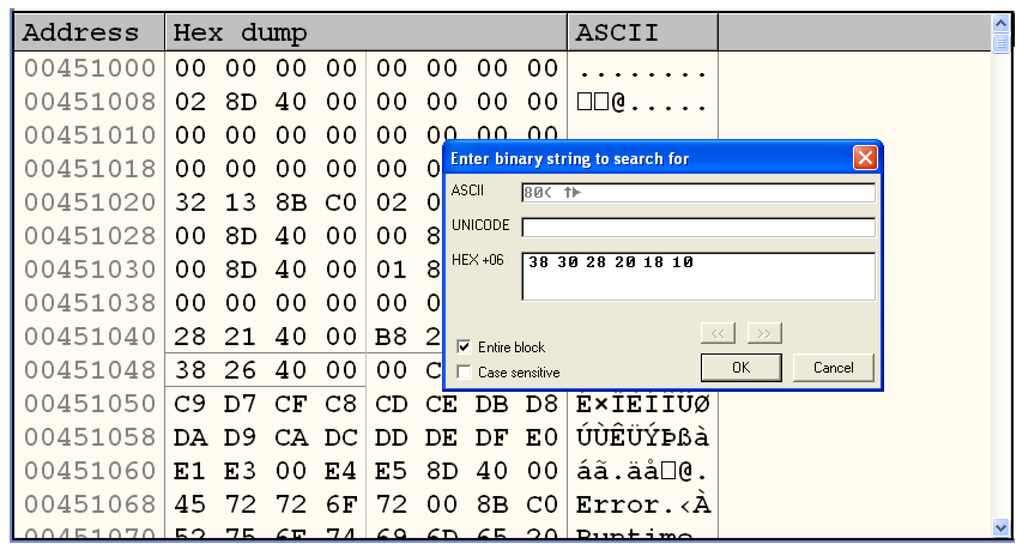
Figure 19.
Malware loaded in OllyDbg and search for PC1.
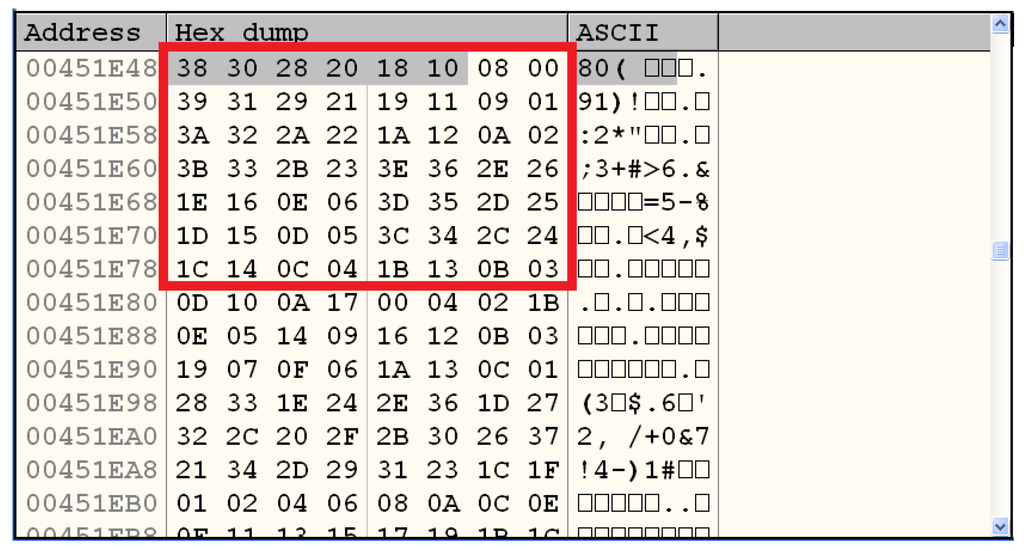
Figure 20.
PC1 contained in the data section of the malware binary.
In order to find references to PC1 in the code section, we can select the first byte of the data structure and press Ctrl+R in OllyDbg (Figure 21). Since there is only one point in the malware binary that accesses the bit selection matrix, we conclude that the procedure InitEncryptedDES is called a single time, implying, by inspecting LbCipher source code, that a plain DES is used, probably, in ECB mode.
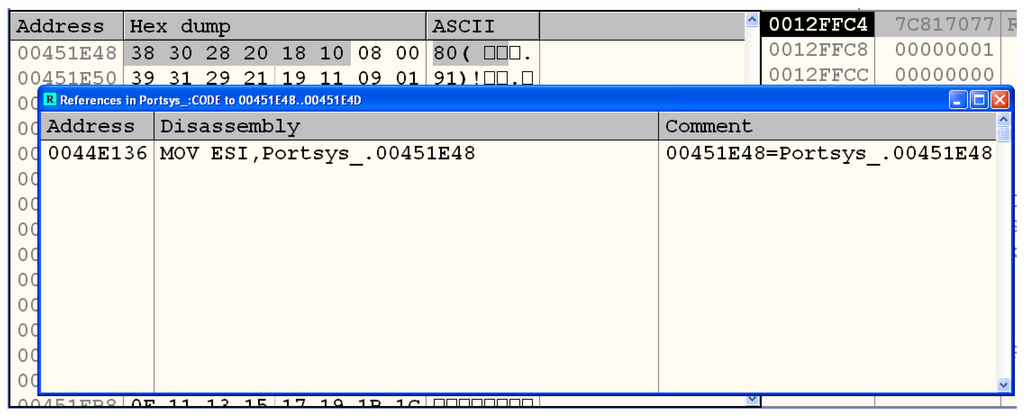
Figure 21.
Instruction in code section that references PC1.
Following the address 0x0044e136 leads us to the code of the procedure InitEncryptDES, as seen in Figure 22, whose entry point is at address 0x0044e11c. The initial instructions are responsible for saving the current values of a few registers, which will be used by the routine, whilst the MOVs that follow copy the arguments passed in the procedure invocation to the stack. We are interested in the value of the parameter Key, which is defined as an array of eight bytes, in LbCipher.pas, by the following code:
TKey64 = array[0..7] of Byte;
Considering a 32-bit architecture, the key cannot be passed through a register, so the address of where it is stored in memory is provided instead. We can see in Figure 22 that the registers CL, EDX, and EAX carry the arguments to the procedure call. In order to know the register that we should look at, we need to consider Delphi’s calling convention, which takes the parameters from left to right as explained below:
- 1st parameter—EAX register;
- 2nd parameter—EDX register;
- 3rd parameter—ECX register;
- Remaining parameters—stack;
Since Key is the first parameter, its value is passed in the EAX register. Now, we only need to run the malware to one of the initial instructions of InitEncryptDES and follow the address contained in the aforementioned register to find the key and conclude our work. These steps are represented by Figure 23, Figure 24 and Figure 25, which show that the key is stored at the address 0x00453c04 and has the value 0xc24fa010744eb153.
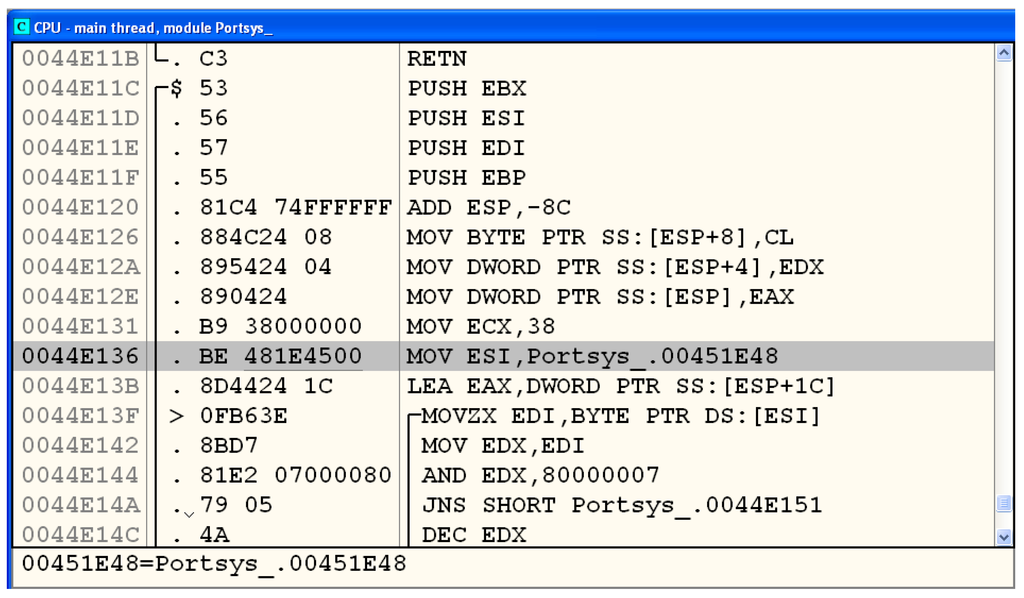
Figure 22.
Code of procedure InitEncryptDES.
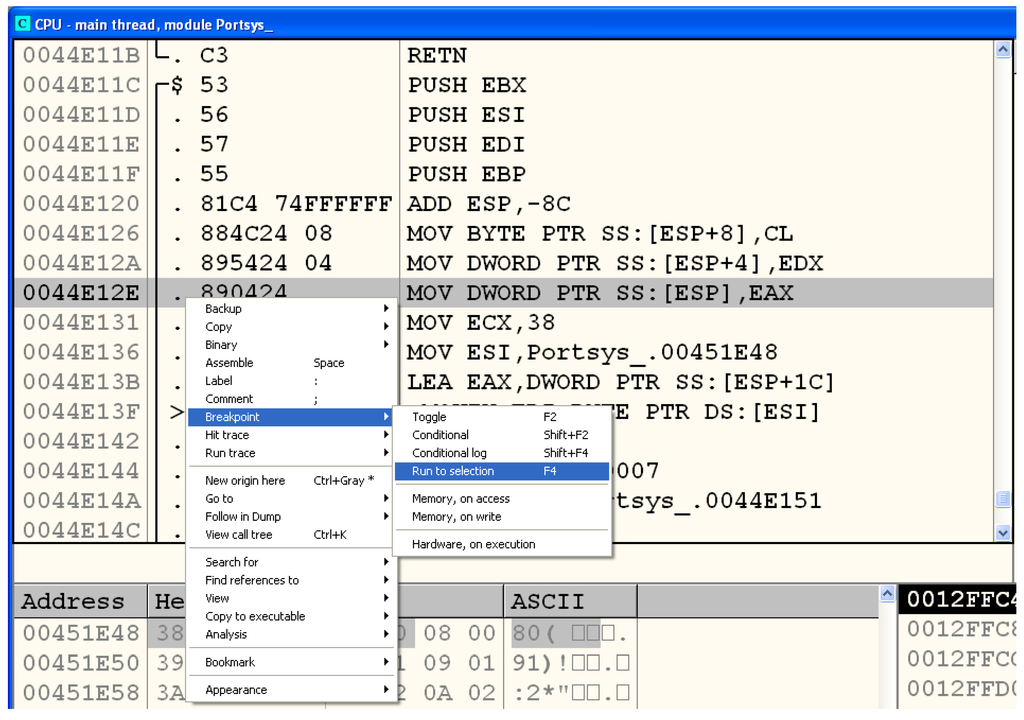
Figure 23.
Running the malware to the selected instruction.
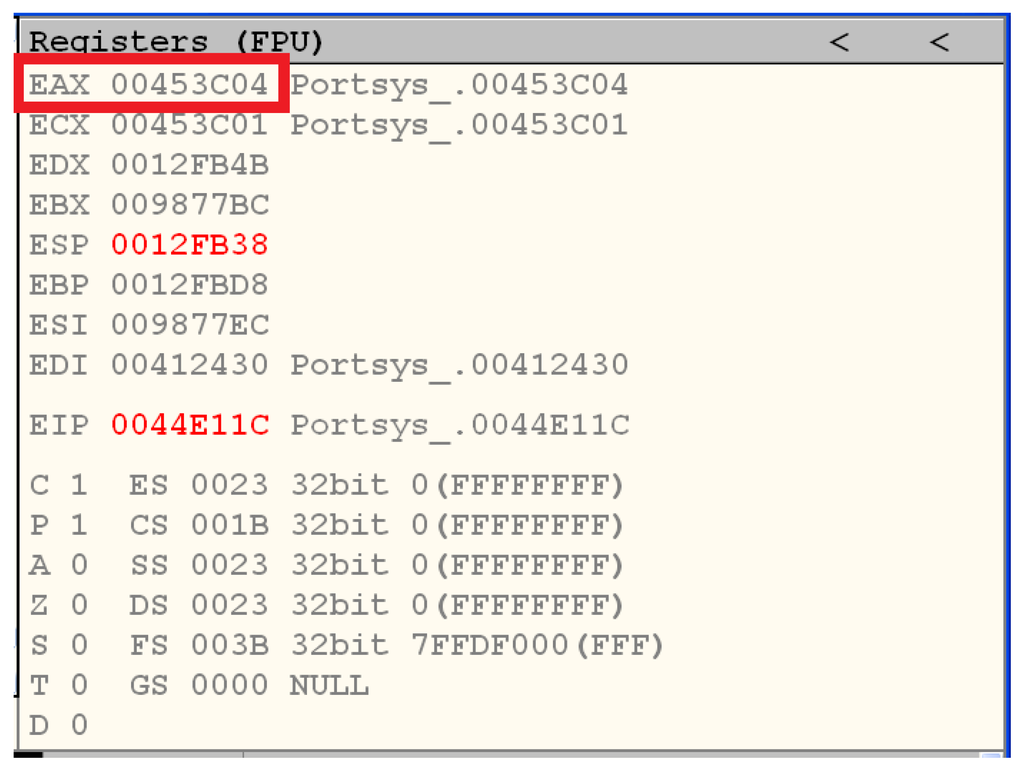
Figure 24.
Address where the key is stored in memory.
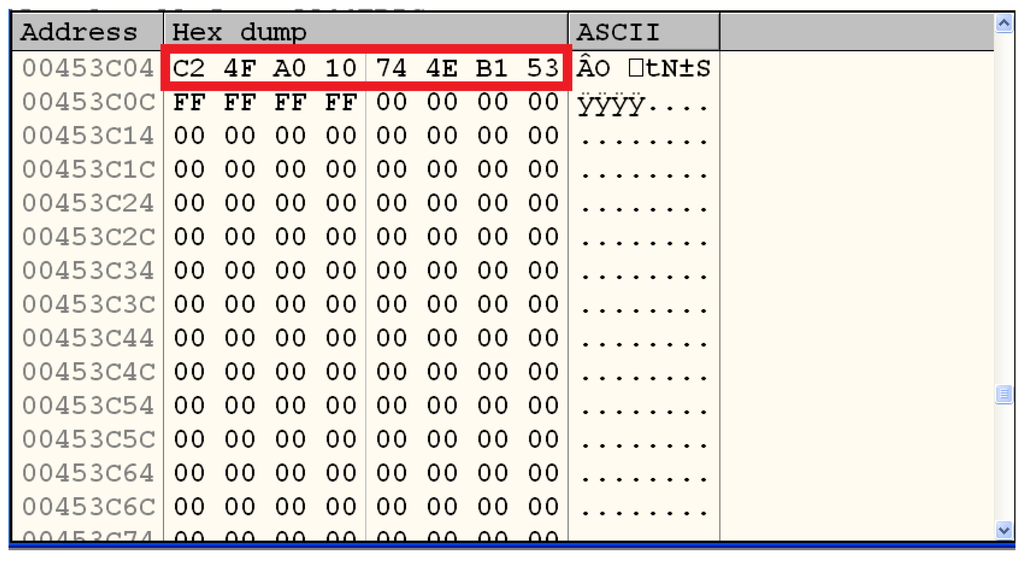
Figure 25.
Value of the DES key used.
3.3.3. Summary of the Analysis
Figure 26 summarizes the analysis of file #3, highlighting the methodology’s steps that were executed.
3.3.4. Description of the Cipher and the Key
The cipher and the cryptographic key used by the malware can be described as follows:
- Encryption algorithm: DES
- Mode of operation: ECB
- Key:
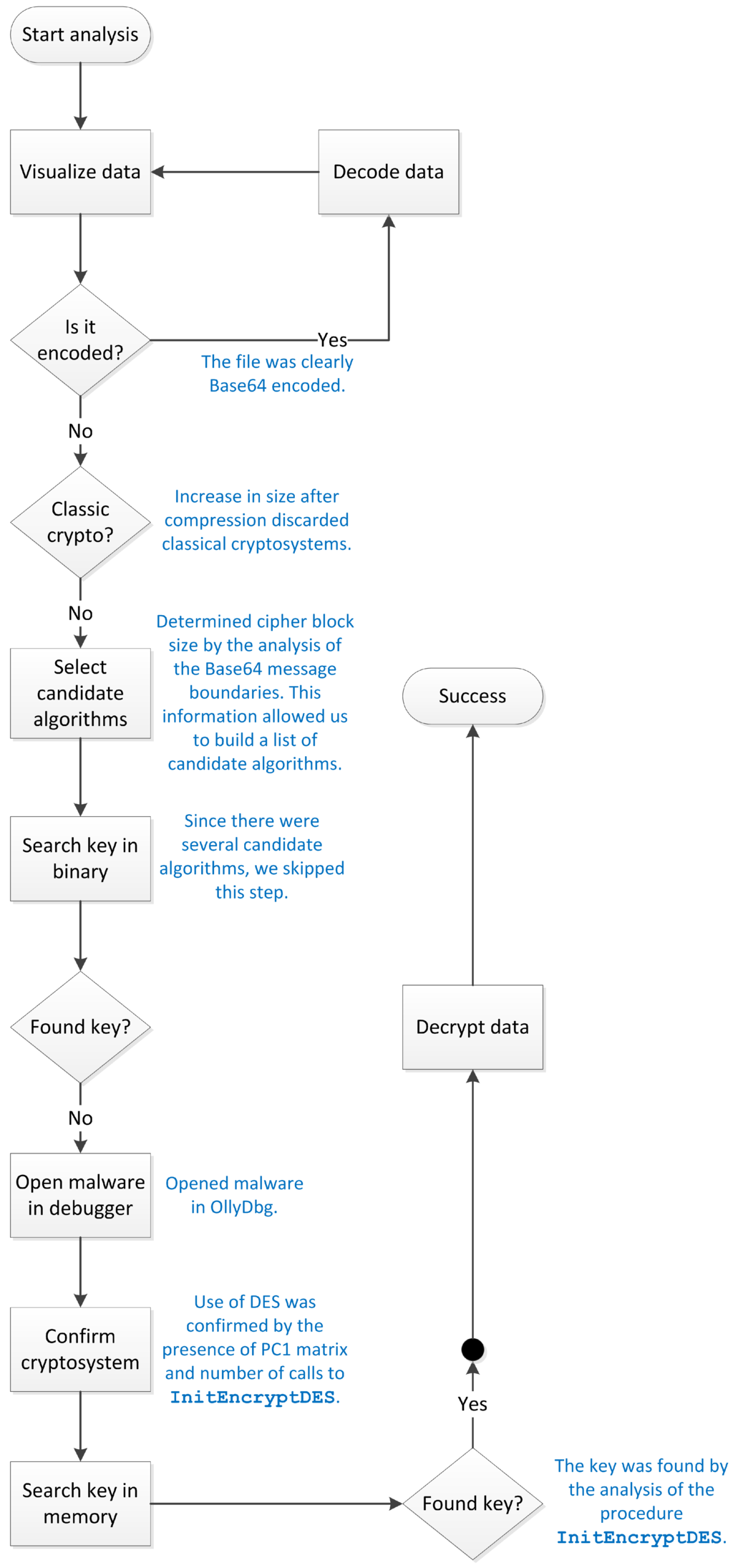
Figure 26.
Summary of the analysis of file #3.
4. Related Work
In this section, we describe related work and compare it with our methodology, which addresses the problem of decrypting malware output files in a general way as opposed to what is found in the literature that often targets the automatic detection of cryptographic algorithms and related parameters, employing static or dynamic methods. This means these techniques and tools can be used in specific steps of our methodology and therefore it is valuable to know them.
Wang et al. introduce in [26] a system called ReFormat, which can be used to automatically reverse engineer encrypted messages that are part of known or unknown protocols. This tool needs to dynamically instrument the target program, in order to collect a trace of the instructions that operate over encrypted data. The main assumption of their approach is that most of the instructions of a decryption routine perform arithmetic and bitwise operations. Therefore, by analyzing the rate of these instructions in the execution trace, one can pinpoint the code that implements cryptographic algorithms, and, the memory region containing the decrypted message. Limitations of ReFormat include the inability to work with obfuscated programs and the ones that decrypt messages in several steps.
The tool created by Caballero et al. [27], called Dispatcher, also focuses on automatic protocol reverse engineering, extending Wang’s aforementioned paper. The first improvement of their work over the latter consists in identifying in a program every piece of code that implements cryptographic operations, by removing the assumption that decryption and consumption processes must be completely linear. In order to flag those regions, the tool considers functions of at least 20 instructions, which present a ratio between the number of arithmetic and bitwise instructions over the total that is greater than 0.55. Other enhancement presented by Dispatcher is the ability to identify buffers containing plaintext used by both encryption and decryption processes. The evaluation of these techniques were performed over a Mega-D botnet [28] execution traces and an Apache HTTPS session, resulting in successful identification of all cryptographic routines.
Another dynamic analysis method for identifying cryptographic primitives is presented by Gröbert et al. in [29]. In the first stage, their technique uses the dynamic binary instrumentation framework Pin [30] to collect an execution trace of the target program, including memory addresses manipulated by it. After that, three heuristics are employed in order to pinpoint cryptographic code inside the trace: (i) Chains—compares sequences of instructions, no matter the operands, against a database of signatures created from open source cryptosystem implementations; (ii) Mnemonic-Const—extends the Chains heuristic by also taking into consideration typical constants that are used with the instructions in those reference implementations; and (iii) Verifier—based on possible key, k, plaintext, m, and ciphertext, c, obtained from the memory reconstruction mechanism they describe, uses a reference implementation of the candidate algorithm to test if it is possible to get c by encrypting m with k.
An interesting solution that works with obfuscated programs as well as unprotected ones is described by Calvet et al. in [31]. They propose a tool called Aligot, also based on Pin framework, which is able to identify several symmetric cryptosystems, such as MD5 and AES. As usual in dynamic analysis, Aligot starts collecting an execution trace of the target program, from which it detects loops, assuming that they contain the cryptographic operations, and I/O parameters resulting from the use of cryptography. Finally, the extracted values are compared with reference implementations of cryptosystems, by verifying if the same output can be calculated from the candidate inputs. According to the authors, they were able to successfully apply Aligot against code protected by the ASProtect packer [32] and several obfuscated malware, such as the Storm worm [33].
The major drawback of dynamic analysis rests in the fact that the cryptographic code of the target program must be executed, in order to allow the building of the execution trace. This would not be possible in our case studies, since we were not able to run the malicious codes in the live environment containing the specialized hardware they target. In all cases, the absence of these devices makes the cryptographic implementation of each malware not triggered, therefore avoiding the collection of necessary information for automatic analysis.
In order to conclude this section, we would like to list a few tools that use static analysis to identify cryptographic algorithms and show how they perform in our case studies:
- Draft Crypto Analyzer (DRACA) [34]—it is an old command line tool, written by Ilya Levin and Fyodor Yarochkin, that can identify some block ciphers and hash functions;
- Krypto Analyzer (KANAL) [35]—it is a plugin for PEiD that is able to identify cryptographic algorithms and related constants, functions, and libraries;
- Signsrch [36]—it is a signature based tool, created by Luigi Auriemma, that can be used to identify compression, cryptographic, and multimedia algorithms. The signature database is frequently updated and contains thousands of items;
- SnD Crypto Scanner [37]—this tool, created by Loki, works as a plugin for OllyDbg and searches for cryptographic signatures.
The results of running the above tools to identify the cryptographic algorithms in the scope of this article are presented in Table 2. Note that none of them could detect the Vigenère cipher and that there were several false positives for the third sample.

Table 2.
Detection results for the samples of this article.
| Tool | File #1 | File #2 | File #3 |
|---|---|---|---|
| Methodology | Vigenère | Vigenère | DES |
| DRACA | - | - | DES |
| KANAL | - | - | Base64, Blowfish, DES |
| Signsrch | - | - | Base64, Blowfish, Haval [38], DES, DESX [39] |
| SnD Crypto Scanner | - | Base64 | Base64, DESX |
5. Automation
In order to help with the steps of the methodology, we created several ad-hoc scripts and programs that we have been using in consulting services in the scope of this article. We intend in the near future to pack all of them as a toolkit, to extend the provided functionalities, and to distribute it as an open source software. Below we list what can be automatically performed:
- Decoding—detecting several encoding schemes and decoding the input are simple tasks that can be grouped in a single utility. One should consider, at least, the following schemes: ASCII, Unicode, UTF, EBCDIC, and hexadecimal representation;
- Cryptanalysis of classical algorithms—one can implement automatic frequency analysis, Kasiski’s method, and index of coincidence, giving the user the possibility to define the alphabet to be used in the process. In order to check the success or failure of the operation, one should compare the statistics of the output against the one expected for the original information. Normally, this can be accomplished with high success and low false positive rates;
- Identification of cryptosystems—cryptosystems can be identified by searching the malware binary or process memory for data structures that might be used by specific algorithms. For instance, for Data Encryption Standard, one should search for PC1 and PC2 matrices; for Advanced Encryption Standard, forward or inverse S-Boxes matrices; for Camellia [40], the key generation constants; and so on. Several times, this process leads to the cryptographic key as well, as a nice collateral effect. This type of functionality is best implemented as a plugin for debugger software, such as OllyDbg and IDA Pro [41], and examples can be found in Section 4;
- Key search—it is not uncommon for malware authors (actually, software developers in general) to use weak cryptographic keys, even when strong algorithms are employed. In order to find keys in such a situation, one should have a dictionary of common keys, words, and patterns, and use it to search the malware binary and process memory. Sometimes, this can save a lot of time, as we showed in the analysis of the second malware. For strongly generated keys, the recommendation is to use Shamir’s algorithm [9], using a window size according to the encryption mechanism identified in the previous step. The key search method should be implemented as a plugin for debugger software, together with the cryptosystem identification functionality.
6. Conclusions
We presented in this article a methodology for recovering, with the least effort possible, information from encrypted files generated by malware. In order to fulfill that objective, most of the techniques used are based on cryptanalysis, instead of static and dynamic reverse engineering. The steps of the methodology were illustrated by three case studies taken from a Big Brazilian company, which was victimized by directed attacks targeting a special purpose hardware they have in their environment.
It should be mentioned, however, that if cryptography is properly used in scenarios such as the ones presented here, there is no way to succeed without being able to perform a memory dump of the live environment. One example would be a malware that generates session keys for encrypting the stolen data and that sends it together, protected by a public key cryptosystem. Supposing the only person that knows the corresponding private key is the criminal, there is not much one can do to retrieve the original information. That would require the unlikely task of breaking a well known asymmetric cryptosystem, in order to first recover the data encryption key.
Unfortunately, we are not able to provide any statistics about how often the malware addressed in this paper can be found in the wild. Anyways, it is our hope that this work can be helpful for those people victimized by them.
Acknowledgements
The author would like to thank the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper and CPqD for the financial support.
References
- Falliere, N.; Murchu, L.O.; Chien, E. W32.Stuxnet Dossier-Version 1.4; Symantec Security Response Technical Report; Symantec: Mountain View, CA, USA, 2011. [Google Scholar]
- sKyWIper (a.k.a. Flame a.k.a. Flamer): A Complex Malware for Targeted Attacks; Technical Report for Laboratory of Cryptography and System Security (CrySyS Lab): Budapest, Hungary, 2012.
- Rivest, R.L. RFC 1321–The MD5 Message-Digest Algorithm; MIT Laboratory for Computer Science and RSA Data Security, Inc.: Bedford, MA, USA, 1992. [Google Scholar]
- Stevens, M.; Lenstra, A.; Wegger, B. Chosen-prefix collisions for MD5 and colliding X.509 certificates for different identities. Lect. Notes Comput. Sci. 2007, 4515, 1–22. [Google Scholar]
- Menezes, A.; van Oorschot, P.; Vanstone, S. Handbook of Applied Cryptography, 5th ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Friedman, W.F. The Index of Coincidence and Its Applications in Cryptology; Department of Ciphers Publ 22, Riverbank Laboratories: Geneva, IL, USA, 1922. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Sikorski, M.; Honig, A. Practical Malware Analysis: The Hands-On Guide to Dissecting Malicious Software, 1st ed.; No Starch Press: San Francisco, CA, USA, 2012. [Google Scholar]
- Shamir, A.; van Someren, N. Playing “hide and seek” with stored keys. Lect. Notes Comput. Sci. 1999, 1648, 118–124. [Google Scholar]
- Data Encryption Standard (DES); FIPS Pub 46-3; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999.
- Advanced Encryption Standard (AES); FIPS Pub 197; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001.
- Eilam, E. Reversing: Secrets of Reverse Engineering; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- VirusTotal. Available online: https://www.virustotal.com/en/ (accessed on 16 April 2013).
- PE iDentifier. Available online: http://www.peid.info (accessed on 16 April 2013).
- Zimmerman, M.W. Microsoft Visual Basic 6.0: Programmer’s Guide; Microsoft Press: Redmond, WA, USA, 1998. [Google Scholar]
- Pacheco, X. Borland Delphi 6 Developer’s Guide; Sams: Indianapolis, IN, USA, 2001. [Google Scholar]
- Barker, W.C.; Barker, E. Recommendation for the Triple Data Encryption Algorithm (TDEA) Block Cipher; NIST SP 800-67, Revision 1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012. [Google Scholar]
- Shimizu, A.; Miyaguchi, S. Fast data encipherment algorithm FEAL. Lect. Notes Comput. Sci. 1988, 304, 267–278. [Google Scholar]
- Lai, X.; Massey, J.L. A proposal for a new block encryption standard. Lect. Notes Comput. Sci. 2006, 473, 389–404. [Google Scholar]
- Massey, J.L. SAFER K-64: A byte-oriented block-ciphering algorithm. Lect. Notes Comput. Sci. 1994, 809, 1–17. [Google Scholar]
- Rivest, R.L. The RC5 encryption algorithm. Lect. Notes Comput. Sci. 1995, 1008, 86–96. [Google Scholar]
- Brown, L.; Pieprzyk, J.; Seberry, J. LOKI–A cryptographic primitive for authentication and secrecy applications. Lect. Notes Comput. Sci. 1990, 453, 229–236. [Google Scholar]
- Schneier, B. Description of a new variable-length key, 64-bit block cipher (Blowfish). Lect. Notes Comput. Sci. 1994, 809, 191–204. [Google Scholar]
- Cannière, C.; Dunkelman, O.; Knezevic, M. KATAN and KTANTAN—A family of small and efficient hardware-oriented block ciphers. Lect. Notes Comput. Sci. 2009, 5747, 272–288. [Google Scholar]
- OllyDbg. Available online: http://www.ollydbg.de/ (accessed on 16 April 2013).
- Wang, Z.; Jiang, X.; Cui, W.; Wang, X.; Grace, M. ReFormat: Automatic reverse engineering of encrypted messages. Lect. Notes Comput. Sci. 2009, 5789, 200–215. [Google Scholar]
- Caballero, J.; Poosankam, P.; Kreibich, C. Dispatcher: Enabling Active Botnet Infiltration Using Automatic Protocol Reverse-Engineering. In Proceedings of the 2009 ACM Conference on Computer and Communications Security, Sydney, Australia, 10–12 March 2009.
- Cho, C.Y.; Caballero, J.; Grier, C.; Paxson, V.; Song, D. Insights from the Inside: A View of Botnet Management from Infiltration. In Proceedings of the 3rd USENIX Workshop on Large-Scale Exploits and Emergent Threats, San Jose, CA, USA, 27 April 2010.
- Gröbert, F.; Willems, C.; Holz, T. Automated identification of cryptographic primitives in binary programs. Lect. Notes Comput. Sci. 2011, 6961, 41–60. [Google Scholar]
- Luk, C.; Cohn, R.S.; Muth, R.; Patil, H.; Klauser, A.; Lowney, P.G.; Wallace, S.; Reddi, V.J.; Hazelwood, K.M. Pin: Building Customized Program Analysis Tools with Dynamic Instrumentation. In Proceedings of the ACM SIGPLAN 2005 Conference on Programming Language Design and Implementation, Chicago, IL, USA, 12–15 June 2005.
- Calvet, J.; Fernandez, J.M.; Marion, J. Aligot: Cryptographic Function Identification in Obfuscated Binary Programs. In Proceedings of the ACM Conference on Computer and Communications Security, CCS ’12, Seoul, Korea, 2–4 May 2012.
- ASProtect. Available online: http://www.aspack.com/asprotect.html (accessed on 16 April 2013).
- Holz, T.; Steiner, M.; Dahl, F.; Biersack, E.; Freiling, F.C. Measurements and Mitigation of Peer-to-Peer-Based Botnets: A Case Study on Storm Worm. In Proceedings of the First USENIX Workshop on Large-Scale Exploits and Emergent Threats, San Francisco, CA, USA, 15 April 2008.
- Levin, I.; Yarochkin, F. Draft Crypto Analyzer (DRACA). Available online: http://www.literatecode.com/draca (accessed on 16 April 2013).
- Krypto Analyzer (KANAL). Available online: http://www.peid.info (accessed on 16 April 2013).
- Auriemma, L. Signsrch. Available online: http://aluigi.altervista.org/mytoolz.htm (accessed on 16 April 2013).
- Loki. SnD Crypto Scanner. Available online: http://www.woodmann.com/collaborative/tools/index.php/SnD_Crypto_Scanner_(Olly/Immunity_Plugin) (accessed on 16 April 2013).
- Zheng, Y.; Pieprzyk, J.; Seberry, J. HAVAL—A One-way hashing algorithm with variable length of output. Lect. Notes Comput. Sci. 1993, 718, 81–104. [Google Scholar]
- Kilian, J.; Rogaway, P. How to protect DES against exhaustive key search (an analysis of DESX). J. Cryptol. 2001, 14, 17–35. [Google Scholar] [CrossRef]
- Aoki, K.; Ichikawa, T.; Kanda, M.; Matsui, M.; Moriai, S.; Nakajima, J.; Tokita, T. Specification of Camellia–a 128-bit Block Cipher; Technical Report for Nippon Telegraph and Telephone Corporation: Osaka, Japan, 2000. [Google Scholar]
- IDA. Available online: https://www.hex-rays.com/products/ida/index.shtml (accessed on 16 April 2013).
© 2013 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).