Computational and Energy Costs of Cryptographic Algorithms on Handheld Devices
Abstract
: Networks are evolving toward a ubiquitous model in which heterogeneous devices are interconnected. Cryptographic algorithms are required for developing security solutions that protect network activity. However, the computational and energy limitations of network devices jeopardize the actual implementation of such mechanisms. In this paper, we perform a wide analysis on the expenses of launching symmetric and asymmetric cryptographic algorithms, hash chain functions, elliptic curves cryptography and pairing based cryptography on personal agendas, and compare them with the costs of basic operating system functions. Results show that although cryptographic power costs are high and such operations shall be restricted in time, they are not the main limiting factor of the autonomy of a device.1. Introduction
The technological cost reduction of network devices has lead to the expansion of personal portable computers and the appearance of new types of networks. Heterogeneous ubiquitous networks formed by small and constrained devices are actively researched or already in use, and security mechanisms have to be provided to protect them from malicious attacks. The main nature of ubiquitous networks (providing easy network interconnections anytime and anywhere) makes the introduction of measures to ensure the correct operation of the protocols is very necessary at all layers; from networking operations (routing and network management) to collaborative enforcing protocols or privacy protecting mechanisms. Therefore, it is important to know the real cost of cryptography in small devices and design client protocols that suit this context.
Some research works have studied the performance of cryptographic algorithms in small and constrained devices as Personal Digital Assistants (PDAs). However, none of them provides a global view of the impact of cryptographic techniques in the system, nor can be inferred since tests do not share any common ground. Some works focus on a few types of cryptosystems [1–4], while others only analyze the utilization of some particular resources [5,6]. Specifically, the work of Potlapally et al. [5] is one of the most interesting because it covers symmetric and asymmetric cryptography (including elliptic curve algorithms), and hash algorithms. However, it only deals with energy consumption.
In this paper we present a study of different cryptographic techniques in embedded devices based on ARM architectures, measuring the computational ability to process cryptographic functions and the battery power consumption. We are interested in a broad vision of the problem, how security affects the autonomy and functioning of a device with the goal to design efficient secure communication protocols. The primary security needs of network protocols are to provide authenticity and integrity. Thus, we center our study on block ciphers (because MACs can be constructed from block ciphers), hash functions, and public key digital signature algorithms.
We conducted benchmarking tests for the most used algorithms nowadays and the ones recommended by international organizations and projects (NIST, NESSIE, CRYPTREC). The chosen block cipher algorithms are Data Encryption Standard (DES), Triple DES (3DES) and Advanced Encryption Standard (AES). The tested hash functions are Message Digest 5 (MD5), Secure Hash Algorithm 1 (SHA-1) and Secure Hash Algorithm 2 (SHA-2). In public key cryptography, we have tested Rivest Shamir Adleman (RSA), Digital Signature Algorithm (DSA), Elliptic Curve Digital Signature Algorithm (ECDSA) and emerging algorithms based on pairings (Boneh-Lynn-Shacham (BLS) and Boneh-Boyen (BB)). We have used the procedures of OpenSSL-0.98d C library to program the tests, except for the pairing schemes, in which we have used the PBC_sig-0.0.2 library from Stanford University.
The rest of the paper is organized as follows. We first describe the testing environment and measurement system. Then, in Section 3, we present the basic costs of the system and the performance of chosen cryptosystems. Finally, in Section 4 we summarize the most relevant results.
2. Testing Environment
Benchmarks tests were launched on two actual PDAs, a Compaq iPAQ3970 and an HP Hx2790. HP Hx2790 is more powerful than the other so that we can generalize how further technology improvements can modulate the results. Compaq iPAQ3970 uses an Intel XScale PXA250 processor at 400 MHz. It runs Linux Familiar operating system. On the other hand, HP Hx2790 uses an Intel XScale PXA270 processor at 624 MHz. It runs Windows Mobile operating system. Specifications of both platforms are detailed in Table 1.
Tests were conducted with the support of a PC, a DELL-DCNE with a 2.8 GHz Intel processor and 512 MB of RAM, and which runs Ubuntu Linux. Tests and required libraries have been built in the PC using cross-compilers (see Table 2) and have been installed and launched on the PDA through a serial port connection. Security-related libraries can be downloaded from KISON Research Group web page: http://kison.uoc.edu.
The performance study has evaluated two aspects of different PDA processes: temporal cost and consumed energy. Time delays have been measured through the implementation of temporal monitors in test applications. We have used the function times of the C Standard Library to control the elapsed CPU time for every process. The energy costs have been estimated from the battery status information provided by the battery drivers. In particular, in the Linux Familiar operating system, we have used the asic driver for the management of the battery which outputs status information in the system file /prov/asic/battery. In Windows Mobile we have used the GetSystemPowerStatusEx2 function from the Windows MSDN library that retrieves information of the battery status.
3. Benchmark Results
In this section we present benchmark test results for various PDA functions. On one hand we measured the basic power costs of the PDA, i.e., network interface, screen and basic operating system functions. On the other hand, we analyzed the temporal and energy costs of the main algorithms of different cryptographic systems. In the following, we first present a comparison of the basic power costs with the average expenses of executing diverse cryptographic systems. Afterwards, we detail the benchmark of each cryptosystem.
3.1. Basic Costs
The cost of the basic operating system functions was measured with the default operation system applications on, the serial port connectivity enabled, all network interfaces disabled, and without running any end-user application. Then, we evaluated the screen consumption by switching on the display and computing the introduced overhead. Eventually, we analyzed the network interface costs (we only evaluated these costs for the Hx2790 device, since our iPAQ3970 is not equipped with this interface).
Figure 1 shows the results.
The most contributing factor in the basic power costs is the wireless network interface. The network card consumption in idle state and configured with a transmission power of 15 dBm (∼32 mW) and a sensitivity of –80 dBm is 792.68 mW. When using the communication channel, data transmission costs 10.40 μJ per byte, while the reception is 3.48 μJ per byte. Transmitting requires more energy than receiving, but the difference is not so significant bearing in mind that both processes have associated an intrinsic idle state cost. Network idle costs are critical and a main concern for ubiquitous networks.
The next contributor to basic power costs is the screen, which is usually switched on if the user is working with the PDA. In iPAQ3970, the use of the screen at maximum luminescence costs 406.58 mW, while in Hx2790 this power is 501.06 mW. This cost can be reduced if the screen brightness is set at low levels. The consumption rate is linearly proportional to the glow.
Finally, the basic operating system functions use up 375.64 mW in iPAQ3970, and 213.28 mW in Hx2790. The differences between the two devices are due to the processor, operating system, and battery.
The exposed results show that the power overhead for executing cryptographic algorithms is higher in the newest and fastest PDA: Hx2790. Nevertheless, this does not mean that this machine is less efficient for cryptography, as we will see in next sections. Hx2790 can better exploit its resources when necessary so that operations are fast.
Moreover, we studied whether the battery charge affects the performance of a device, and we confirmed that it does. The process time to execute an algorithm when the battery drain is at 25% is the same that in full charge. Still, the instant current increases and so also the total spent energy. In average, the costs induced when the battery is at 25% are around 16% higher.
3.2. Symmetric Cryptography
We initiate the analysis of security performance in a PDA with the simplest cryptographic operations: symmetric ciphers and hash functions. Benchmark tests were conducted using eight different plaintexts of size 20 B, 1 KB, 10 KB, 100 KB, 250 KB, 500 KB, 750 KB and 1 MB. For each plaintext file the test was repeated from 500 times for big files, up to 50,000 for small ones, with the aim that the uncertainty of the results is less than 0.01%.
Regarding symmetric cryptography, we analyzed the resources employed by DES, 3DES and AES to encrypt and decrypt a file using the Electronic Code Book (ECB) cipher mode, in which each plaintext block is encrypted in turn with the block cipher. ECB is the easiest of the cipher modes because there are no dependencies between ciphered blocks. We take this mode for our analysis as a reference point, because of its simplicity and its widespread use.
Since in ECB the plaintext is cut in blocks of a predefined size and these blocks are sequentially encrypted by the processor, we have modelled the consumed energy and time of symmetric encryption with a linear equation: Consum = a · x + b, where Consum is the consumed energy or time, x is the size in KB of the plaintext. So, there exists a constant component b associated to the load of the program and the key setup phase, and an incremental one a that is proportional to the size of the input.
The key setup phase is common to all block ciphers and it is performed before the encryption/decryption. This phase consists in expanding the input key in order to derive a distinct and cryptographically strong key. Then, the ciphering proceeds through a repeated sequence of mathematical computations over input blocks of data. The results demonstrate the model is correct because obtained regression lines present a determination coefficient r2 above 99.9%.
Table 3 shows temporal costs of symmetric cryptographic algorithms (encryption and decryption) for both iPAQ3970 and Hx2790 platforms. It expresses the linear regression for each tested algorithm in function of the input-text size x in KB, and besides, it compares the performance rate between the two devices.
Results are better in the Hx2790 device, which is faster. While the clock frequency of the Hx2790 is 1.56 times faster than the one of iPAQ3970, cryptographic performance has improved more than threefold. This is because not only the core processor speed is greater but also is the system bus, and what is more, the processor has an internal memory for optimizing the performance. Furthermore, the increase of performance when using a faster PDA is demonstrated to be greater for AES algorithms than for DES or 3DES. The implementation of AES can take profit of the major resources of a device.
In any case, we notice that AES algorithms perform much better than DES and 3DES in both ARM processors. The required time to cipher or decipher a DES file is even worse than the time required for doing it using AES with keys of 256 bits, and the security level of this last one is stronger. Nowadays DES algorithm is considered weak, not because it is vulnerable to security flaws, but because the keys are so small that they may be discovered by brute force attacks.
From the time cost expressions, it is remarkable that the required initialization time for DES and 3DES algorithms is greater than that of AES (in fact, in Hx2790 the initialization cost of most of the algorithms is is smaller than 1 μs, and so, depreciable). This means that AES is not only the best algorithm for ciphering large documents, but also for small ones. For example, in Hx2790, to cipher 1 KB of information takes around 270 ns using DES, 745 ns using 3DES, 152 ns using AES-128, and 204 ns using AES-256. Regarding 3DES, we evaluated the 3DES-EDE variant, which involves two DES encryptions and a DES decryption using three DES keys (168 bits in total). The results give evidence that 3DES is three times slower than DES.
In the same way that temporal costs, Table 4 summarizes the energy costs of the selected block cipher algorithms. We have seen in Section 3.1 that the required power to execute cryptographic functions in Hx2790 is almost twice as large as in iPAQ3970. However, since Hx2790 runs block cipher algorithms four times faster that the other, the total consumed energy is the half. Thus, we can conclude that Hx2790 is more efficient.
One issue of AES is that decryption does not perform exactly the same steps than encryption, and so, the code is partially different. In [7], Razvi et al. model the computational operations involved in the AES encryption scheme and make a theoretical evaluation of its expected consumed energy. They estimate the number of computational operations for deciphering an AES message is three times greater than the operations for ciphering. Since the energy consumption is also related to the number of processor cycles which are used in the computation of basic operations, they calculate the decryption process spends nearly three times more energy than encryption.
Actually, depending on the implementation, AES encryption and decryption differences can be more significant in one sense or another. In OpenSSL, AES is accelerated via a 10 KB lookup table implementation. The OpenSSL compilation for Linux Familiar takes full profit of this design and the effect is that a decryption process in the iPAQ3970 is even faster than encryption (20% faster). In the same way, the consumed energy is in general lower, except when using small input files (up to 100 KB). Yet, in the Windows mobile platform the results are not quite the same. The throughput of the encryption and decryption operations in the Hx2790 is more or less the same for both cases. As for the energy, the encryption better results are very significant, but the differences between ciphering and deciphering keep coming down as the size of the input text grows. This means that deciphering has some complex operations that do not depend on the size of the input text and that become dissolved with the rest of computations as the size of the ciphertext grows. The differences in AES encryption and decryption processes lead to slightly different results in throughput and energy consumption. Nevertheless, data presented in Tables 3 and 4, and the following Figure 2, is the average of both operations.
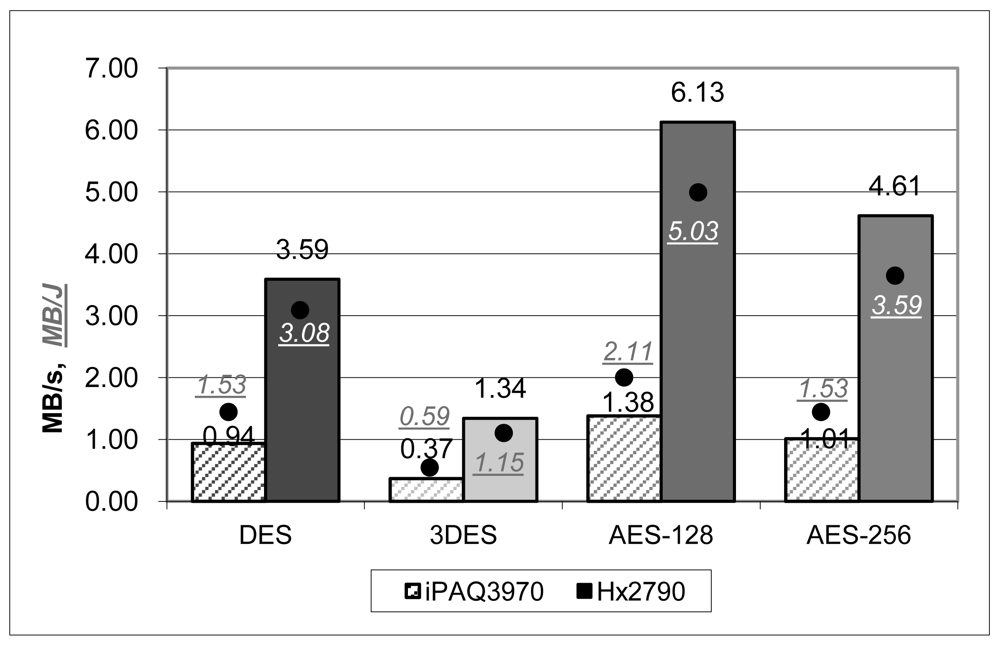
Figure 2 makes a comparison of the quantity of data that can be ciphered in a second of time and with a Joule of energy. Temporal results can be compared with that obtained by other implementations and tests:
In [3], authors launched some benchmarking tests in two PDAs of similar characteristics than ours: an iPAQ4150 with a PXA255 XScale CPU at 400 MHz, and a Dell Axim x30 with a PXA270 XScale CPU at 640 MHz. The throughput for AES-256 working in ECB cipher mode is 98KB/s in iPAQ4150, and 149.5 KB/s in Axim x30.
Tests in [2] were executed in an iPAQ4700 with a PXA270 XScale CPU at 624 MHz. They evaluated the throughput for AES-256 working in ECB cipher mode, and the result is 1382.7 KB/s.
In [1] the performance of block ciphers in a PDA with a StrongARM SA-1100 processor at 200 MHz was evaluated. This device is slower than the rest ones presented here; however, the result for AES-128 working in ECB cipher mode is very good, 1470.5 KB/s.
Our AES results (AES-256: 1035.29 KB/s in iPAQ3970 and 4724.55 KB/s in Hx2790) are much better than [2,3], which use similar hardware. We impute the differences with [3] to the way of implementing the algorithms. They wrote the tests in C# using Microsoft .NET programming framework. We programmed them in plain C, using the well-tested OpenSSL libraries. On the other hand, Ramachandran et al. [2] also coded the tests in C. However, we outperformed their results a little. This is because they tested the cipher with very small input data (128 bits) so we cannot really compare the results; the operational costs of the initialization are not amortized if working with small input files.
Finally, we compare the results with [1], that used an optimized self implementation library of AES. Our results are worse bearing in mind we use faster processors, so the implementation of OpenSSL can be clearly optimized.
Regarding energy results, they are in accordance with other studies, like [5], in the sense that AES-128 is about a 60% more efficient than DES, and 3DES, as expected, is three times more consuming than DES. However, values differ substantially depending on the device and implementation. For example, Hager et al. [3] report that the iPAQ4150 (similar to our iPAQ3970) has an outcome of 0.37 MB/J for AES-256, while we measured 1.53 MB/J. On the other hand, Großschäßdl, et al. [1] use a StrongARM SA-1100 processor at 200 MHz with, as we have seen before, has an excellent temporal performance. In this case the expended energy is also high comparing with our results, since it states an outcome for AES-128 of 0.04 MB/J while ours is 2.11 MB/J in iPAQ3970. Finally, Potlapally et al. [5], using a similar device to [1] (a StrongARM SA-1110 at 206 MHz) have an outcome of 2.12 MB/J.
3.3. Hashing Algorithms
We conducted benchmark tests for hash functions. A hash function is a one-way collision resistant function that compresses an arbitrarily large message into some information of fixed length. The construction of a hash function consists of two elements: a compression function that maps a fixed length input to a fixed length output, and a domain extender, that allows us to apply the compression function to inputs of variable sizes. Compression functions are usually designed using block ciphers. On the other hand, most hash functions have a domain extender that is constructed using an iterative structure, which is based on Merkle-Damgård hash construction. Since hash algorithms work in data blocks of fixed size, we assume temporal and energetic costs have a linear dependency with the input message size. Results confirm this assumption and also that the initialization phase of the algorithm is negligible.
Figure 3 shows a comparison of the quantity of data that can be hashed in a second of time and with a Joule of energy. The tested hash functions are MD5, SHA-1 and SHA-2. MD5 and SHA-1 are the most widely used hash functions nowadays. However, they are vulnerable to some attacks ([8,9]) and National Institute of Standards and Technology (NIST) is recommending to replace them with the family of SHA-2 functions. From SHA-2 family, we have tested in particular SHA-256, SHA-384 and SHA-512.
The faster device, Hx2790, clearly outperforms the other and, as in the symmetric cryptography case, the improvements are greater in the temporal domain than in the energetic one. The algorithms of the SHA-2 family are the ones which benefits more of a faster processor, with differences between Hx2790 and IPAQ 3970 greater than fivefold. Compared with symmetric algorithms results, the simpler hash functions (MD5, SHA-1) are at least two times faster, while the behaviour of SHA-2 functions is similar to the AES cryptosystems.
For each device, the energy cost relation between all the algorithms is quite similar to what happened in temporal costs. However, the main difference is that MD5 and SHA-1 are more energy efficient in iPAQ3970 than in Hx2790. This is because these algorithms are simple and can be executed with the same number of instructions in both devices, and executing an instruction requires less energy in iPAQ3970 than in Hx2790.
3.4. Key Generation Algorithms
The evaluated public key algorithms are RSA, DSA, Elliptic Curve Cryptography (ECC) and Pairings.
We have evaluated RSA and DSA using keys of 512, 1,024 and 2,048 bits. We have set the public exponent of RSA keys to 3 because it provides better performance in signature verifications; this exponent is usually used in constrained environments where a lot of verifications have to take place. The results using other exponents do not differ a lot, signature generations are more efficient and verifications are not so much, but overall, the general performance of the algorithm is quite the same.
For the case of ECC, we have tested the algorithm using three curves, secp112r1, secp160r1, and secp224r1. All curves are over a prime field and their parameters are chosen verifiable at random. The length of the field order of each curve is: 112 bits for the secp112r1, 160 bits for the secp160r1 and 224 bits for the secp224r1.
Regarding Pairings, we have analyzed key generation algorithms for two digital signature schemes: BLS signatures from [10], and BB signatures from [11]. We have generated the pairing using type A curves as defined in [12] which are the fastest and most efficient. The prime order of cyclic groups G1 and G2 is 160 bits, and the elements of the groups take 512 bits to represent.
Table 5 shows key sizes of different cryptographic systems for equivalent security levels. Values are from the European Network of Excellence for Cryptology (ECRYPT) [13], which are very similar to the ones issued by other organizations like NIST in [14].
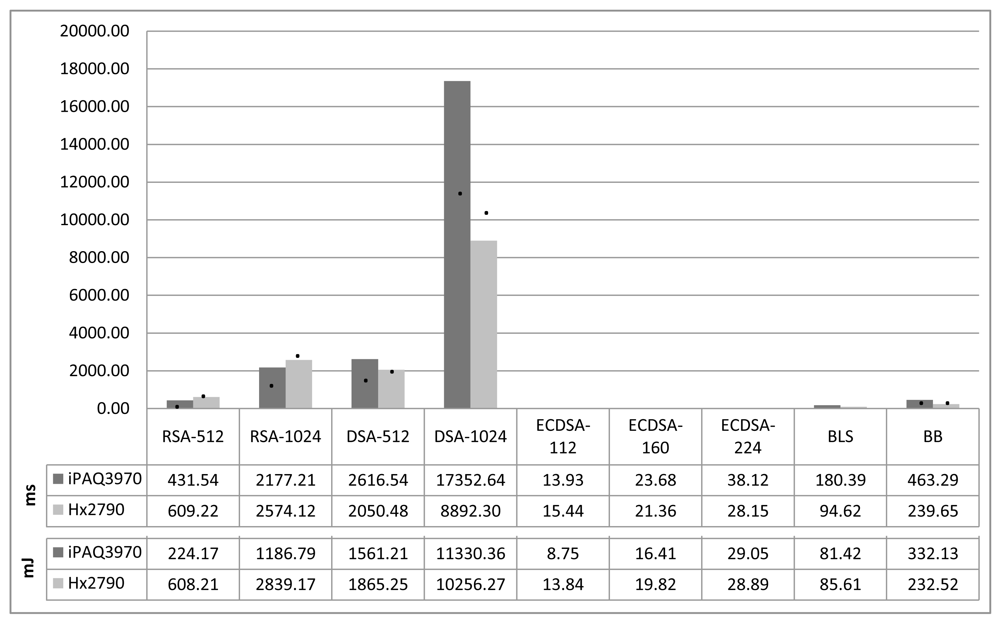
Figure 4 shows the temporal and energy costs of asymmetric key generation in our testing devices. The generation of ECC keys is by far the fastest algorithm, followed by pairing key generation. Moreover, the generation of 1024-bit DSA keys is nearly unacceptable by PDA devices, with execution times that greatly surpass 5 seconds, which is a lot. Nevertheless, in systems that do not require to renew cryptographic keys in short time periods, key generation has to be run only once and so, time performance is not really significant. What matters is the performance of working with those keys, that is, digital signature algorithms that we will see next.
RSA and DSA key generation involves primality testing, which is an expensive operation. Besides, prime tests are probabilistic, which means that the execution times are not always the same and occasionally can be very long. The required time to find proper primes increases polynomially with the size of the searched prime. Figure 4 shows average values. The generation of a 512-bit RSA key requires finding two prime numbers of 256 bits, and the generation of a 512-bit DSA key requires a prime number of 512 bits. This last operation is more expensive than RSA's because of the size of the prime, and so, it takes more time. On the other hand, we also note that the increment of time delay due to the complexity increase of some operations (i.e., the size of the key), is even more significant when using slower microprocessors. The generation of 2048-bit RSA and DSA keys is too resource consuming for the devices under test and can not be assured that the generation will end successfully. So, results are not provided in the figure.
The performance for ECC key generation is very good as it only involves one scalar point multiplication; that is, it multiplies a scalar k (a large integer) and a point P on an elliptic curve. All in all, the scalar multiplication is the most time consuming operation in ECC scheme. This operation can be performed on an elliptic curve group by adding point P k – 1 times to itself. The difference between the computational effectiveness of ECC over RSA and DSA is obvious and it gets more notorious as the required security strength increases and so the length of the keys.
Finally, the key generation in pairing based schemes is also quite efficient because it is based on modular exponentiations over a prime field. The key generation for BLS only requires one exponentiation, and the one for BB signature requires two exponentiations, and one bilinear pairing. The results show that key generation in BB is about three times greater than in BLS.
Several papers (i.e., [15–18]) have made comparisons between ECC, RSA and DSA, finding ECC to be significantly faster than others, although the magnitude of the difference varies. DSA is the slowest of them.
Regarding energy costs, Potlapally et al. [5] studied the energy consumption of symmetric and asymmetric cryptography using a StrongARM SA-1110 processor at 206 MHz. The results they obtained for AES are similar to ours in the iPAQ3970. However, the results of asymmetric key generation algorithms are quite different. They report the RSA-1024 key generation to consume 270.13 mJ, the DSA-1024 to be 293.20 mJ and ECDSA keys in a field the order of which has 163 bits to be 226.65 mJ. Our results also identify ECDSA as the most energy efficient algorithm and DSA the least; yet, the values and ratios between our results and theirs differ.
Potlapally et al. [5] also benchmarked the signature generation and verification operations, as we will comment in Section 3.5. Using their results it can be concluded that RSA and DSA signatures generation are energetically more expensive than key generation, but this is not consistent with the fact that key generation processes are more complex. Thus, we consider in this case Potlapally results for key generation algorithms cannot be generalized, and we assert our values.
3.5. Digital Signature Algorithms
We have evaluated the digital signature algorithms RSA, DSA, ECDSA, BLS and BB using the keys generated in previous Section 3.4. The following results do not include hashing operations, except for the BB case where the hashing is intrinsically embedded in the signature and verification process. Thus, for the RSA case, signing is equivalent to deciphering, and verifying is equivalent to ciphering.
3.5.1. Temporal Costs
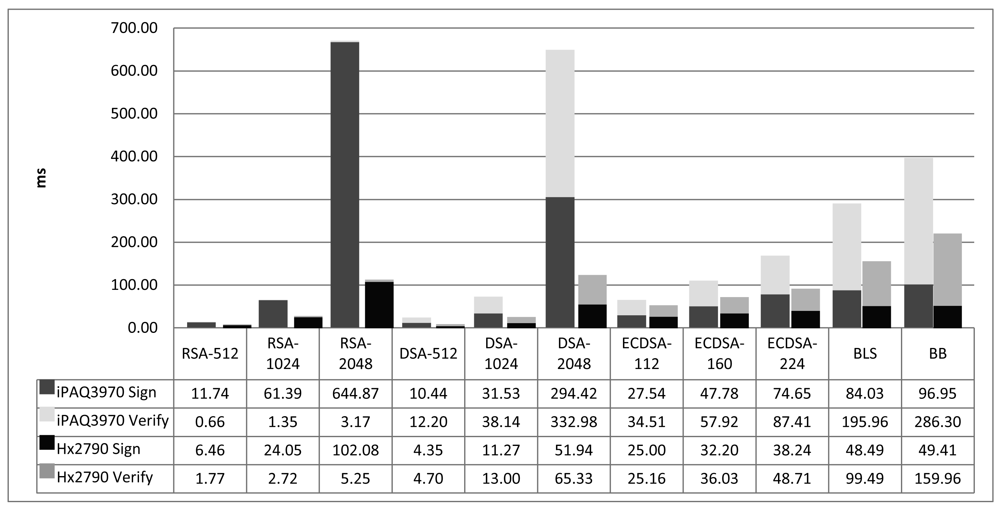
Figure 5 shows the temporal costs of digital signature algorithms in our two testing platforms. The graphic evidences that the best performance in small handheld devices is from RSA and DSA. The average time of signature generation and verification is more or less the same for the two algorithms, however, RSA has best results in verification, while DSA is faster in signature generation. For this reason, RSA is well suited for systems that require only few signature generations but thousands of signature verifications. Depending on the application, RSA or DSA will fit better.
ECDSA key generation algorithm was the best of all key generation candidates, but Figure 5 demonstrates that it is not so efficient for signature operations in small order fields. Yet, a signature generated with ECDSA is half the size the length of the field order, which is much shorter than the signatures generated with RSA keys of an equivalent security level, and so are the certificates. Thus, when working in this security level, an evaluation of the amount of operations and data transmissions involved in a security protocol is required to conclude which is the best algorithm to use for each particular case.
Furthermore, ECDSA performs better than RSA and DSA when incrementing the security level. In average, RSA operations using 512 bit keys are about 4 times faster than using 1,024 bits keys. In DSA this ratio is around 3. Besides, this ratio increases when the length of the RSA and DSA keys gets longer. In contrast, the ratio for ECDSA keys of 112 and 160 bits is less than twofold and shrinks when increasing the security level.
Finally, the temporal costs of pairing based signatures are quite high compared with the others. The advantages of these schemes are for one hand that the signatures are very short, so their transmission is quite easy. The other is that they support multisignature and batch signature verification schemes that can reduce the overhead and provide competitive time results.
Moreover, pairing based operations can be optimized in hardware implementations thus reducing the overhead of BLS and BB signatures. The pbl_sig library we are using implements Tate pairing calculations based on Miller's algorithm, from [19]. However, [20] states pairings based on modified Duursam-Lee algorithm ([21]) are nearly 65% faster, and hardware implementations are about 95% more efficient. The development of short signature schemes using these algorithms could get performances better than ECC.
There are some other research works that have studied the performance of digital signature algorithms in constrained devices. [4] makes a comparison on a sharp Zaurus SL-5500G with a SA-1110 Strong ARM CPU at 206 MHz. They obtained execution times for OpenSSL of RSA, with results for RSA-512 signature generation of 13.7 ms, and verification 1.3 ms. The results for RSA-1024 signature generation were 78.0 ms, and 4.3 ms for verification. These results are clearly coherent with ours, that in the iPAQ3970 at 400 MHz get an RSA-512 signature with 11.74 ms, a verification with 0.66 ms, and an RSA-1024 signature with 61.39 ms and the verification with 1.35 ms.
On the other hand, they also launched ECDSA benchmarks with a self implementation library of ECC that uses general elliptic curves over binary fields. They state their library is on average 5 times faster than OpenSSL. Results for 163-bits ECDSA were 5.7 ms for signature generation, and 17.9 ms for signature verification. These results are clearly better that those we obtained with OpenSSL 0.98 d libraries. In an iPAQ3970 device, we get for a ECDSA-160 signature generation 47.78 ms, and the signature verification takes 57.92 ms.
Gupta et al. [22] are the authors of the ECC support to OpenSSL 0.9.6 b and performed some tests to compare the results of their library with RSA. They obtained the execution times for ECDSA and RSA signature operations on a PDA with a SA-1110 Strong ARM CPU at 206 MHz. According to their observations, RSA-1024 signature generation lasts 32.1 ms, and verification takes 1.7 ms. The results for 163-bits ECDSA were 6.8 ms for signing and 13 ms for verifying. Their results are better than ours, but coherent.
Table 6 shows the throughput in MB/s of the analyzed algorithms in an Hx2790 device (iPAQ3970 presents the same shape with poorer performance). Here, all required computations to perform a signature and a verification over a message are considered.
RSA, DSA and ECDSA use the SHA-1 hash algorithm (costs described in Section 3.3).
BLS signatures use a hash algorithm over bilinear maps and a compression-decompression algorithm. The time required to execute this hash algorithm is (105.08 + 0.03 · x) ms, with x the size of the input message in KB. Besides, the compression or decompression algorithm takes 5.98 ms.
In BB short signatures the hash of the message is embedded in the signature process.
The column labelled with a Δ shows the performance increase of the algorithm as the length in KB of the message becomes bigger. Thus BB, which is the algorithm with a highest Δ in the signing operation, is the most efficient algorithm for signing large documents (from tens KB) with a performance of 20.24 MB /s for files of 1 M. Contrary, for signing small documents, the fastest algorithm is DSA-512. The fastest algorithm for performing a signature validation is RSA-512 regardless the size of the document.
Comparing with the throughput of symmetric algorithms (see Figure 2), results show that a cryptographic operation on big data files over 400 KB can be more efficient using asymmetric algorithms than symmetric ones.
3.5.2. Energy Costs
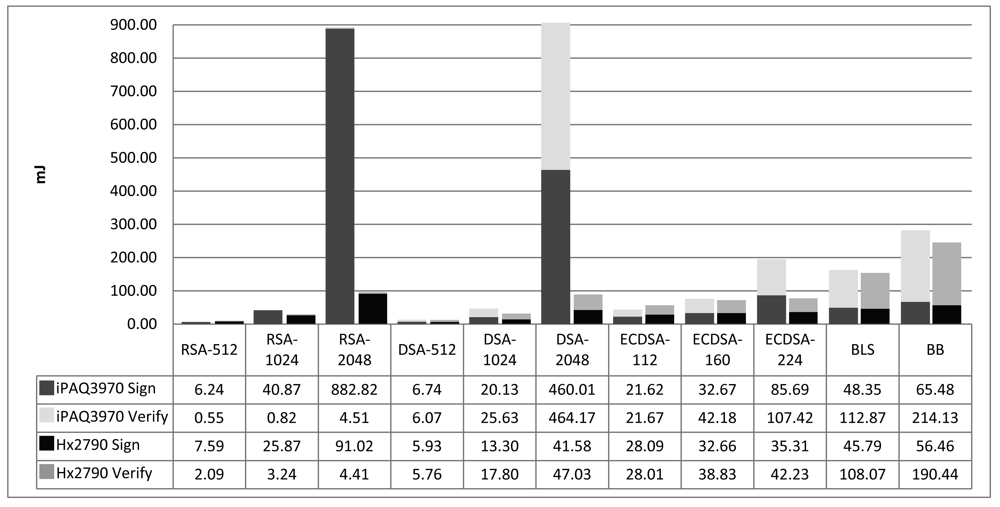
Figure 6 shows the energy costs of digital signature algorithms. The form of the graphic is the same as Figure 5 of temporal costs. We have measured the average consumed power induced by asymmetric cryptography operations and it is about 10% lower than that of symmetric cryptography. Thus, we conclude that the processor is not working so intensive. A study on how to better fit the code for ARM processors and improve the performance of asymmetric cryptography on PDAs can be successful, although it is out of the scope of this work.
Results of other studies are coherent with ours in the sense that the relationship between the performances of the algorithms in each device is quite similar to what we have obtained in our target PDAs. However, in absolute values, results are very different due to the use of different processors. Potlapally et al. [5], using a StrongARM SA-1110 processor at 206 MHz, get: 546.5 mJ for RSA-1024 signature generation and 15.97 mJ for verification; 313.6 mJ for DSA-1024 signature generation and 338.02 mJ for verification; and 134.2 mJ for ECDSA signature generation and 196.23 mJ for verification. The only significant difference with our measurement is in ECDSA, where [5] get comparatively better results because they use a different elliptic curve over a binary field.
Table 7 shows the expense of energy in MB/J of the analyzed signature algorithms. All the computations required to perform a signature and a verification over a message are included in the depicted graphics. The energy cost associated with the hash algorithm used in BLS is (165.81 + 0.03 · x) mJ, and the compression algorithm is 9.81 mJ.
The most efficient signature algorithm is the BB short signature, closely followed by DSA and RSA algorithms using keys of 512 bits. The least energy-consuming verification algorithms are RSA using keys of 512 and 1,024 bits.
Comparing with the energy costs of symmetric algorithms (see Figure 2) asymmetric cryptography is more expensive. In iPAQ3970 it is better working with asymmetric algorithms if input data is above 200 KB, while in the Hx2790 it should be above 400 KB.
4. Conclusions
In this paper we have analyzed the performance of different cryptographic algorithms in PDAs and we have compared it with device's basic costs: operating system, screen, and network interface. This study provides evidence to determine the amount of overhead that a security protocol can introduce in a system.
The conclusions are the following:
The best symmetric algorithm for ARM processors, both regarding time and energy costs, is AES. The throughput of AES-256 is around 25% smaller than AES-128. Both are more efficient than DES. Besides, AES has a greater security level than DES or 3DES.
Hash algorithms present a similar throughput as symmetric algorithms. MD5 is the fastest of them, although it presents some collisions and its use is not recommended.
In public key cryptography, key generation is in general very complex and demanding. DSA presents the worst results, while ECC has very good performance.
The results of digital signature functions are quite different depending on the algorithm. RSA-512 is the most efficient, nearly followed by DSA-512. In the next security level RSA-1204 is the lightest of all, with a performance around 75% slower than RSA-512. This difference is more pronounced in slower processors. It is also remarkable that RSA is very light especially in verifications. The average cost of signing and verifying in DSA-1024 and ECDSA-112 is quite similar than that of RSA-1024, however they have better results in signature generation. In the top security level, the best algorithm is by far ECDSA-224.
The global costs of signing and verifying a message involve the expenses of hash operations or some compression algorithms. In this sense, it is remarkable that BB pairing based signatures are more efficient (above all in time) than the others when working with medium and large files.
The drain on the battery sets the energy expenses of the device. The consumption of running cryptographic algorithms when the batteries are low charged is around 16% higher than when they are full.
The use of cryptographic algorithms in network protocols, specially multi-hop protocols, introduces an important overhead due to the network interface costs during waiting times. The problem is not so in computationally cryptographic costs, but the total protocol completion time that involves notorious energy consumption. Thus, security protocols shall be designed to reduce delay times as much as possible, for example applying appropriate scheduling techniques [23].
The main contribution of this paper is that it presents a benchmark of a wide range of algorithms and a consistent comparison between them. Results can be used to estimate the costs of network security protocols, design them appropriately and evaluate them.


| Parameters | iPAQ3970 | Hx2790 |
|---|---|---|
| CPU | Intel XScale PXA250 400 MHz | Intel XScale PXA270 624 MHz |
| Screen | 3,8″ TFT (240 × 320) | 3,5″ TFT (240 × 320) |
| OS | LinuxFam. 0.8.4 (k 2.4.19) | Microsoft WinMobile 5.0 |
| Flash ROM | 48 MB | 320 MB |
| SDRAM | 64 MB | 64 MB |
| SRAM | – | 256 KB |
| Cache | 64 KB | 64 KB |
| System bus | 100 MHz | 208 MHz |
| Battery | 1,400 mAh Lithium Ion | 1,440 mAh Lithium Ion |
| WiFi card (11 Mbps) | – | Power = 15 dBm Sensitivity < –80 dBm |
| iPAQ3970 (Linux Familiar) | Hx2790 (Windows Mobile) | |
|---|---|---|
| Cross-compiler | arm-linux | arm-wince-cegcc |
| GMP libs | lib-gmp-4.2.1-arm-linux | lib-gmp-4.2.1-arm-wince |
| PBC libs | lib-pbc-0.4.7-arm-linux | lib-pbc-0.4.7-arm-wince |
| PBC_sig libs | lib-pbc_sig-0.0.2.arm-linux | lib-pbc_sig-0.0.2-arm-wince |
| Time (ms) | |||
|---|---|---|---|
| iPAQ3970 | Hx2790 | Ratio | |
| DES (64) | 0.24 + 1.04x | 0.27x | 3.83 |
| 3DES (192) | 0.90 + 2.66x | 0.02 + 0.73x | 3.66 |
| AES (128) | 0.02 + 0.71x | 0.16x | 4.44 |
| AES (256) | 0.03 + 0.97x | 0.21x | 4.56 |
| Energy (mJ) | |||
|---|---|---|---|
| iPAQ3970 | Hx2790 | Ratio | |
| DES (64) | 0.35 + 0.64x | 0.01 + 0.32x | 2.01 |
| 3DES (192) | 0.56 + 1.66x | 0.03 + 0.85x | 1.95 |
| AES (128) | 0.07 + 0.46x | 0.19x | 2.38 |
| AES (256) | 0.07 + 0.64.x | 0.27x | 2.35 |
| Equivalent symmetric key | Asymmetric key | |
|---|---|---|
| ECC | RSA | |
| 48 | 96 | 480 |
| 56 | 112 | 640 |
| 80 | 160 | 1248 |
| 112 | 224 | 2048 |
| 128 | 256 | 3248 |
| 256 | 512 | 15424 |
| Sign | Verify | |||||
|---|---|---|---|---|---|---|
| Δ | MB/s (files 1 K) | MB/s (files 1 M) | Δ | MB/s (files 1 K) | MB/s (files 1 M) | |
| RSA-512 | 1.33 · 10−2 | 1.50 · 10−1 | 13.73 | 1.38 · 10−2 | 5.33 · 10−1 | 14.67 |
| RSA-1024 | 1.08 · 10−2 | 4.05 · 10−2 | 11.06 | 1.38 · 10−2 | 3.51 · 10−1 | 14.47 |
| RSA-2048 | 5.79 · 10−3 | 9.56 · 10−3 | 5.94 | 1.35 · 10−2 | 1.84 · 10−1 | 13.96 |
| DSA-512 | 1.36 · 10−2 | 2.22 · 10−1 | 14.14 | 1.36 · 10−2 | 2.05 · 10−1 | 14.07 |
| DSA-1024 | 1.25 · 10−2 | 8.62 · 10−2 | 12.88 | 1.22 · 10−2 | 7.47 · 10−2 | 12.60 |
| DSA-2048 | 8.24 · 10−3 | 1.88 · 10−2 | 8.45 | 7.41 · 10−3 | 1.49 · 10−2 | 7.59 |
| ECDSA-112 | 1.07 · 10−2 | 3.90 · 10−2 | 10.94 | 1.06 · 10−2 | 3.87 · 10−2 | 10.92 |
| ECDSA-160 | 9.89 · 10−3 | 3.03 · 10−2 | 10.14 | 9.52 · 10−3 | 2.71 · 10−2 | 9.76 |
| ECDSA-224 | 9.32 · 10−3 | 2.55 · 10−2 | 9.56 | 8.47 · 10−3 | 2.00 · 10−2 | 8.69 |
| BLS | 4.81 · 10−3 | 5.90 · 10−3 | 4.92 | 3.84 · 10−3 | 4.51 · 10−3 | 3.94 |
| BB | 1.98 · 10−2 | 1.98 · 10−2 | 20.24 | 6.11 · 10−3 | 6.11 · 10−3 | 6.25 |
| Sign | Verify | |||||
|---|---|---|---|---|---|---|
| Δ | MB/J (files 1 K) | MB/J (files 1 M) | Δ | MB/J (files 1 K) | MB/J (files 1 M) | |
| RSA-512 | 1.05 · 10−2 | 1.27 · 10−1 | 10.87 | 1.09 · 10−2 | 4.52 · 10−1 | 11.56 |
| RSA-1024 | 8.82 ·10−3 | 3.76 · 10−2 | 9.06 | 1.09 · 10−2 | 2.95 · 10−1 | 11.40 |
| RSA-2048 | 5.56 · 10−3 | 1.07 · 10−2 | 5.70 | 1.08 · 10−2 | 2.18 ·10−1 | 11.25 |
| DSA-512 | 1.07 · 10−2 | 1.63 · 10−1 | 11.07 | 1.07 · 10−2 | 1.67 · 10−1 | 11.09 |
| DSA-1024 | 9.93 · 10−3 | 7.30 · 10−2 | 10.23 | 9.51 · 10−3 | 5.46 · 10−2 | 9.78 |
| DSA-2048 | 7.73 · 10−3 | 2.34 · 10−2 | 7.93 | 7.41 · 10−3 | 2.07 · 10−2 | 7.61 |
| ECDSA-112 | 8.65 · 10−3 | 3.47 · 10−2 | 8.89 | 8.66 · 10−3 | 3.48 · 10−2 | 8.89 |
| ECDSA-160 | 8.32 · 10−3 | 2.98 · 10−2 | 8.54 | 7.90 · 10−3 | 2.51 · 10−2 | 8.11 |
| ECDSA-224 | 8.14 · 10−3 | 2.76 · 10−2 | 8.35 | 7.69 · 10−3 | 2.31 · 10−2 | 7.89 |
| BLS | 3.81 · 10−3 | 4.41 · 10−3 | 3.90 | 3.07 · 10−3 | 3.44 · 10−3 | 3.14 |
| BB | 1.73 · 10−2 | 1.73 · 10−2 | 17.71 | 5.13 · 10−3 | 5.13 · 10−3 | 5.25 |
Acknowledgments
This work is partially supported by the Spanish Ministry of Science and Innovation and the FEDER funds under the grants TSI-020100-2009-374 SAT2, TSI2007-65406-C03-03 E-AEGIS and CONSOLIDER CSD2007-00004 ARES.
References and Notes
- Großschädl, J.; Tillich, S.; Rechberger, C.; Hofmann, M.; Medwed, M. Energy evaluation of software implementations of block ciphers under memory constraints. Proceedings of Design, Automation and Test in Europe (DATE) Conference, Nice France, 16–20 April 2007; pp. 1110–1115.
- Ramachandran, A.; Zhou, Z.; Huang, D. Computing Cryptographic Algorithms in Portable and Embedded Devices. Proceedings of IEEE International Conference on Portable Information Devices (PORTABLE), Orlando, FL, USA, 25–29 May 2007; pp. 1–7.
- Hager, C.; Midkiff, S.; Park, J.; Martin, T. Performance and energy efficiency of block ciphers in personal digital assistants. Proceedings of IEEE International Conference on Pervasive Computing and Communications (PerCom), Kauai Island, HI, USA, 8–12 March 2005; pp. 127–136.
- Westhoff, D.; Lamparter, B.; Paar, C.; Weimerskirch, A. On digital signatures in ad hoc networks. J. Eur. Trans. Telecom. 2005, 16, 411–425. [Google Scholar]
- Potlapally, N.; Ravi, S.; Raghunathan, A.; Jha, N. A study of the energy consumption characteristics of cryptographic algorithms and security protocols. Trans. Mobile Comput. 2006, 5, 128–143. [Google Scholar]
- Branovic, I.; Giorgi, R.; Martinelli, E. Memory Performance of Public-Key cryptography Methods in Mobile Environments. Proceedings of ACM SIGARCH Workshop on MEmory Performance: DEaling with Applications, Systems and Architecture (MEDEA), New Orleans, LA, USA, 27 September– 1 October 2003; pp. 24–31.
- Razvi Doomun, M.; Sunjiv Soyjaudah, K.; Bundhoo, D. Energy consumption and computational analysis of rijndael-AES. Proceedings of International Conference in Central Asia on Internet, Tashkent, Uzbekistan, 26–28 September 2007; pp. 1–6.
- Wang, X.; Yin, Y.L.; Yu, H. Finding Collisions in the Full SHA-1. Proceedings of CRYPTO: 25th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2005; pp. 17–36.
- Wang, X.; Yu, H. How to Break MD5 and Other Hash Functions. Proceedings of EUROCRYPT: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; pp. 19–35.
- Boneh, D.; Lynn, B.; Shacham, H. Short Signatures from the Weil Pairing. J. Cryptol. 2004, 17, 297–319. [Google Scholar]
- Boneh, D.; Boyen, X. Short Signatures Without Random Oracles and the SDH Assumption in Bilinear Groups. J. Cryptol. 2008, 21, 149–177. [Google Scholar]
- Lynn, B. On the Implementation of Pairing-Based Cryptosystems. Ph.D. Thesis, Standford University, Palo Alto, CA, USA, June 2007. [Google Scholar]
- Babbage, S.; Catalano, D.; Cid, C.; Weger, B.; Dunkelman, O.; Gehrmann, C.; Granboulan, L.; Guneysu, T.; Lange, T.; Lenstra, A.; Mitchell, C.; Naslund, M.; Nguyen, P.; Paar, C.; Paterson, K.; Pelzl, J.; Pornin, T.; Preneel, B.; Rechberger, C.; Rijmen, V.; Robshaw, M.; Rupp, A.; Schlaffer, M.; Vaudenay, S.; Vercauteren, D.; Ward, M. Yearly Report on Algorithms and Keysizes (2009-2010); D.SPA.13; ICT-2007-216676; ECRYPT II Network of Excellence: Leuven, Belgium; March; 2010. [Google Scholar]
- Barker, E.; Barker, W.; Burr, W.; Polk, W.; Smid, M. NIST, Recommendation for Key Management, Part 1: General (Revised); Technical Report; Special Publication 800-57; US National Institute for Standards and Technology: Gaithersburg, MD, USA; March; 2007. [Google Scholar]
- Wiener, M.J.; Handschuh, H.; Paillier, P.; Rivest, R.L.; Biham, E.; Knudsen, L.R. Performance Comparison of Public-Key Cryptosystems, SmartCard Crypto-Coprocessors for Public-Key Cryptography, Chaffing and Winnowing: Confidentiality without Encryption, DES, Triple-DES and AES. CryptoBytes 1998, 4, 1–3. [Google Scholar]
- Endrodi, C. Efficiency Analysis and Comparison of Public Key Algorithms; Technical Report; SEARCH Laboratory: Budapest, Hungary, 2002. [Google Scholar]
- Jansma, N.; Arrendondo, B. Performance Comparison of Elliptic Curve and RSA Digital Signatures; Technical Report; University of Michigan: Ann Arbor, MI, USA, 2004. [Google Scholar]
- Cronin, E.; Jamin, S.; Malkin, T.; McDaniel, P. On the performance, feasibility, and use of forward-secure signatures. Proceedings of ACM Conference on Computer and Communication Security, Washington, DC, USA, 27–30 October 2003; pp. 131–144.
- Miller, V.S. The Weil Pairing, and its Efficient Calculation. J. Cryptol. 2004, 17, 235–261. [Google Scholar]
- Zhao, M.; Smith, S.W.; Nicol, D.M. Aggregated path authentication for efficient BGP security. Proceedings of ACM Conference on Computer and Communication Security, Alexandria, VA, USA, 7–11 November 2005; pp. 128–138.
- Barreto, P.S. A note on efficient computation of cube roots in characteristic 3, Report 2004/305; Cryptology ePrint Archive. 2004. Available online: http://eprint.iacr.org/2004/305/ (accessed on 31 January 2011).
- Gupta, V.; Gupta, S.; Chang, S.; Stebila, D. Performance analysis of elliptic curve cryptography for SSL. Proceedings of ACM Workshop on Wireless Security (WiSe), Atlanta, GA, USA, 28 September 2002; pp. 87–94.
- Lee, J.; Bahk, S. Energy efficient scheduling for downlink elastic traffic in wireless networks. Wirel. Comm. Mobile Comput. 2010, 10, 932–941. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Rifà-Pous, H.; Herrera-Joancomartí, J. Computational and Energy Costs of Cryptographic Algorithms on Handheld Devices. Future Internet 2011, 3, 31-48. https://doi.org/10.3390/fi3010031
Rifà-Pous H, Herrera-Joancomartí J. Computational and Energy Costs of Cryptographic Algorithms on Handheld Devices. Future Internet. 2011; 3(1):31-48. https://doi.org/10.3390/fi3010031
Chicago/Turabian StyleRifà-Pous, Helena, and Jordi Herrera-Joancomartí. 2011. "Computational and Energy Costs of Cryptographic Algorithms on Handheld Devices" Future Internet 3, no. 1: 31-48. https://doi.org/10.3390/fi3010031
APA StyleRifà-Pous, H., & Herrera-Joancomartí, J. (2011). Computational and Energy Costs of Cryptographic Algorithms on Handheld Devices. Future Internet, 3(1), 31-48. https://doi.org/10.3390/fi3010031





