Modelling Large-Scale Group Decision-Making Through Grouping with Large Language Models

Abstract

The growing ubiquity of digital platforms has enabled unprecedented participation in large-scale group decision-making processes. Nevertheless, integrating subjective linguistically expressed opinions into structured decision protocols remains a significant challenge. This paper presents a novel framework that leverages the semantic and affective capabilities of large language models to support large-scale group decision-making tasks by extracting and quantifying experts’ communicative traits—specifically clarity and trust—from natural language input. Based on these traits, participants are clustered into behavioural groups, each of which is assigned a representative preference structure and a weight reflecting its internal cohesion and communicative quality. A sentiment-informed consensus mechanism then aggregates these group-level matrices to form a collective decision outcome. The method enhances scalability and interpretability while preserving the richness of human expression. The results suggest that incorporating behavioural dimensions into large-scale group decision-making via large language models fosters fairer, more balanced, and semantically grounded decisions, offering a promising avenue for next-generation decision-support systems.

1. Introduction

In contemporary society, group decision-making constitutes a foundational element of collective dynamics. The profound transformations brought about by globalisation and the pervasive influence of social media have redefined the frameworks through which deliberative processes unfold [1]. The near-universal accessibility of the internet has democratised participation, enabling a wider and more diverse population to contribute to decision-making mechanisms [2]. Concurrently, the exponential increase in the volume and complexity of information presents substantial challenges for effective analysis and governance. To address these intricacies, the field has witnessed the emergence of a specialised domain referred to as large-scale group decision-making (LSGDM) [3,4,5,6], which seeks to manage decision processes involving a vast number of participants. Over recent years, LSGDM has garnered significant scholarly attention, reflecting its growing importance in both theoretical inquiry and practical applications [7].

Social networks have become an environment for carrying out LSGDM methods because people from different parts of the world can express their opinions on a topic without having to travel [8,9]. When people communicate using social networks, they often express their ideas using natural language [10]. Natural Language Processing (NLP) is a line of research that has become relevant in this area since it allows experts to provide inputs in a form closer to natural communication [11].

Nevertheless, using natural language and social networks to create an LSGDM method presents several challenges. Firstly, the unstructured nature of natural language makes it difficult to extract meaningful preferences. Secondly, the volume of information in LSGDM processes far exceeds that of classical GDM, demanding more efficient methods for processing and analysis. To address these challenges, recent advances in NLP, particularly the use of large language models (LLMs), offer a promising solution [12]. These models are capable of interpreting and summarising expert opinions expressed in natural language, providing structured data for decision-making processes.

In this paper, we propose an LSGDM method designed to handle these challenges. Our method uses an LLM to process the comments made by experts during discussions, extracting relevant preferences and behavioural features. Additionally, we apply a variable selection process to eliminate irrelevant information, reducing complexity and optimising performance [13]. To efficiently manage the large volume of data, grouping techniques are applied to group similar experts and opinions [7,14,15,16].

There are several existing approaches for grouping experts in LSGDM contexts [17,18]. In our method, once expert inputs are processed by the LLM, we classify experts based on behavioural and linguistic cues extracted from their contributions. Each group of experts is assigned a representative preference relation and a weighting factor based on characteristics such as consistency, expressiveness, or assertiveness [19].

To achieve consensus, our method introduces an optimised process that focuses on inter-group comparison rather than exhaustive expert-to-expert comparison. This significantly reduces computational cost while maintaining the robustness of the final decision.

This study introduces a novel behavioural framework for large-scale group decision-making (LSGDM) that departs from the conventional models in several key ways:

• It leverages large language models (LLMs) to extract behavioural signals—specifically clarity and trust—from unstructured expert commentary.
• It uses these communicative features to group experts based not only on their stated preferences but also on how those preferences are articulated.
• It introduces a weighted aggregation mechanism in which the influence of each group is modulated by its internal cohesion and communicative quality, measured through intra-group consensus and sentiment scores.
• It demonstrates, through comparative analysis, that this behaviourally informed approach maintains decision quality while enhancing interpretability and fairness, especially in heterogeneous expert panels.

Unlike the existing methods, which treat preference statements as isolated context-free inputs, our framework integrates linguistic tone and rhetorical expression as fundamental dimensions of group reasoning. This represents a conceptual shift from strictly preference-based models to a sentiment-aware and interaction-sensitive paradigm for consensus modelling in LSGDM contexts.

While preference aggregation is a core component of LSGDM, our approach introduces a behavioural dimension by modelling how preferences are expressed, not just what they are. This distinction becomes crucial in large, diverse expert groups where communication quality varies significantly. Grouping based on clarity and trust allows the model to attenuate the influence of unclear or disruptive discourse and amplify contributions that are constructive and coherent, leading to more interpretable and socially robust decisions. These communicative traits can directly impact consensus building, especially in open, unmoderated, or asynchronous environments, such as online platforms or crowdsourcing settings.

The structure of this document is as follows. Section 2 presents the fundamental concepts related to LSGDM and group decision-making processes. Section 3 details the stages of the proposed method, describing the system based on sentiment analysis integrated with an LSGDM approach. Section 4 provides an illustrative example demonstrating the application of the proposed method. In Section 5, a comparative analysis is conducted to highlight the strengths and limitations of the proposed system in relation to existing approaches in the current literature. Finally, Section 6 provides the concluding remarks.

2. Preliminaries

This section introduces the foundational ideas required to understand the method proposed in this work. Section 2.1 reviews recent advances in computational language understanding, focusing on LLMs and how they can be leveraged to map textual contributions into rich semantic and affective representations. Section 2.2 then presents the core concepts behind LSGDM problems (see Figure 1).

2.1. Contextual Language Understanding with Large Language Models

Human communication is inherently nuanced, imprecise, and context-dependent. Computers, on the other hand, reason over numerical structures. Bridging this gap has traditionally required NLP techniques capable of converting free text into machine-readable data. Early approaches relied on sparse vector models such as bag-of-words (BoW) [20,21]; however, recent work shows that transformer-based LLMs provide far richer representations [22,23].

In our framework, each expert’s contribution to the debate is first encoded by a pretrained LLM (e.g., BERT or GPT-3) that produces a contextual embedding $\mathbf{h}\in {\mathbb{R}}^d$ for the entire utterance [24,25]. These continuous vectors capture syntax, semantics, and pragmatic signals—including affect—without the need for manual feature engineering. A lightweight classifier, fine-tuned on annotated dialogue data, then infers two affective dimensions that are critical for LSGDM processes: trust and clarity. This allows the decision-support system to quantify sentiment with sentence-level granularity while preserving linguistic subtleties that BoW cannot model. While other behavioural dimensions—such as influence, engagement, or persuasiveness—could potentially affect consensus formation, we selected clarity and trust due to their foundational communicative role and their operational reliability. Clarity ensures intelligibility and transparency of discourse, which facilitates semantic alignment across participants. Trust promotes respectful and constructive interaction, which is essential to mitigate conflict and foster cooperation. Furthermore, these two dimensions are semantically stable and can be robustly identified by transformer-based LLMs across different contexts, whereas other dimensions are more context-sensitive and harder to quantify without task-specific supervision. This makes clarity and trust especially suitable for scalable domain-independent group decision-making frameworks.

The recent literature shows a growing interest in the application of LLMs to process expert-generated content in various domains. For example, [26] introduces a neural architecture for e-commerce that combines lexical resources with deep learning modules to enhance textual interpretation. Ref. [27] proposes a transformer-based model tailored to social media that captures syntactic and semantic subtleties. Ref. [28] presents a hybrid model integrating neural embeddings with blockchain to improve the traceability and classification of textual input. These approaches reflect a transition from traditional sentiment-driven pipelines to more sophisticated and holistic treatments of natural language based on LLMs.

2.2. Group Decision-Making

Large-scale group decision-making refers to contexts in which a high number of individuals, typically referred to as experts, are involved in a collective decision process [29,30]. Let us define a group of m experts, denoted by E, who must evaluate a set of n possible alternatives, X, using individual preference structures $P_s$ for $s=1,\dots ,m$.

Numerous strategies for representing expert preferences have been developed [31], among which preference relations are one of the most commonly adopted formats [32,33]. This work follows the preference relation model as it facilitates the comparison of alternatives and supports the assessment of internal consistency. The preferences are expressed through a function ${\mu }_s:X\times X\to [0,1]$, which reflects the degree to which one alternative is preferred over another. The resulting matrix $P_s=(p_s^{ij};i\ne j=1,\dots ,n)$ is of size $n\times n$, where each entry $p_s^{ij}={\mu }_s(x_i,x_j)$ captures the pairwise comparison between alternatives $x_i$ and $x_j$.

The methodology proposed in this work follows a structured process divided into distinct phases, which are outlined as follows:

• Expression of preferences: Experts engage in preliminary discussions to exchange viewpoints on the alternatives under consideration. Following this deliberation phase, each expert provides their individual preferences through a preference relation matrix [33].
• Consensus evaluation: The level of agreement among experts is assessed by calculating a consensus degree, which measures the alignment of opinions [34,35]. A consensus threshold $\alpha \in [0,1]$ is defined, indicating the minimum acceptable consensus level [36]. If this threshold is not met, experts are prompted to revise their evaluations. This iteration can occur for a predefined number of rounds [29], after which a final decision is made regardless of the consensus achieved [37].
• Aggregation of preferences: To generate a unified representation of the collective opinion, the individual matrices are aggregated into a collective preference matrix $C_G$. This step relies on the use of aggregation functions to combine the diverse evaluations [32].
• Deriving the final ranking: The collective matrix $C_G$ is then employed to compute a ranking of the alternatives. This can be achieved through various dominance-based techniques, including the quantifier-guided dominance degree (QGDD) [38].

Recent research has proposed numerous models and strategies to address LSGDM challenges. For example, in [39], a decision-making approach incorporates trust propagation and conflict resolution within a social network structure. The method in [5] identifies opinion leaders using grouping techniques and a k-core decomposition strategy. A two-stage method introduced in [6] enhances consensus in multi-attribute decision settings. Meanwhile, Ref. [40] explores hesitant fuzzy preference relations to model uncertainty in expert judgments. The model in [41] addresses non-cooperative behaviour through rationality-based adjustments, and [42] integrates probabilistic terms to handle imprecise inputs from decision-makers.

In contrast with previous approaches that relied on sentiment analysis techniques or bag-of-words models to extract meaning from expert opinions, this work proposes the integration of an LLM to support the reasoning process behind preference elicitation. The LLM interprets natural language justifications provided by experts, helping to refine their preferences and ensuring they align with the context and objectives of the decision problem. This advanced linguistic capability allows for a more robust, semantic-aware interpretation of human input, enhancing the quality and adaptability of the decision-making process.

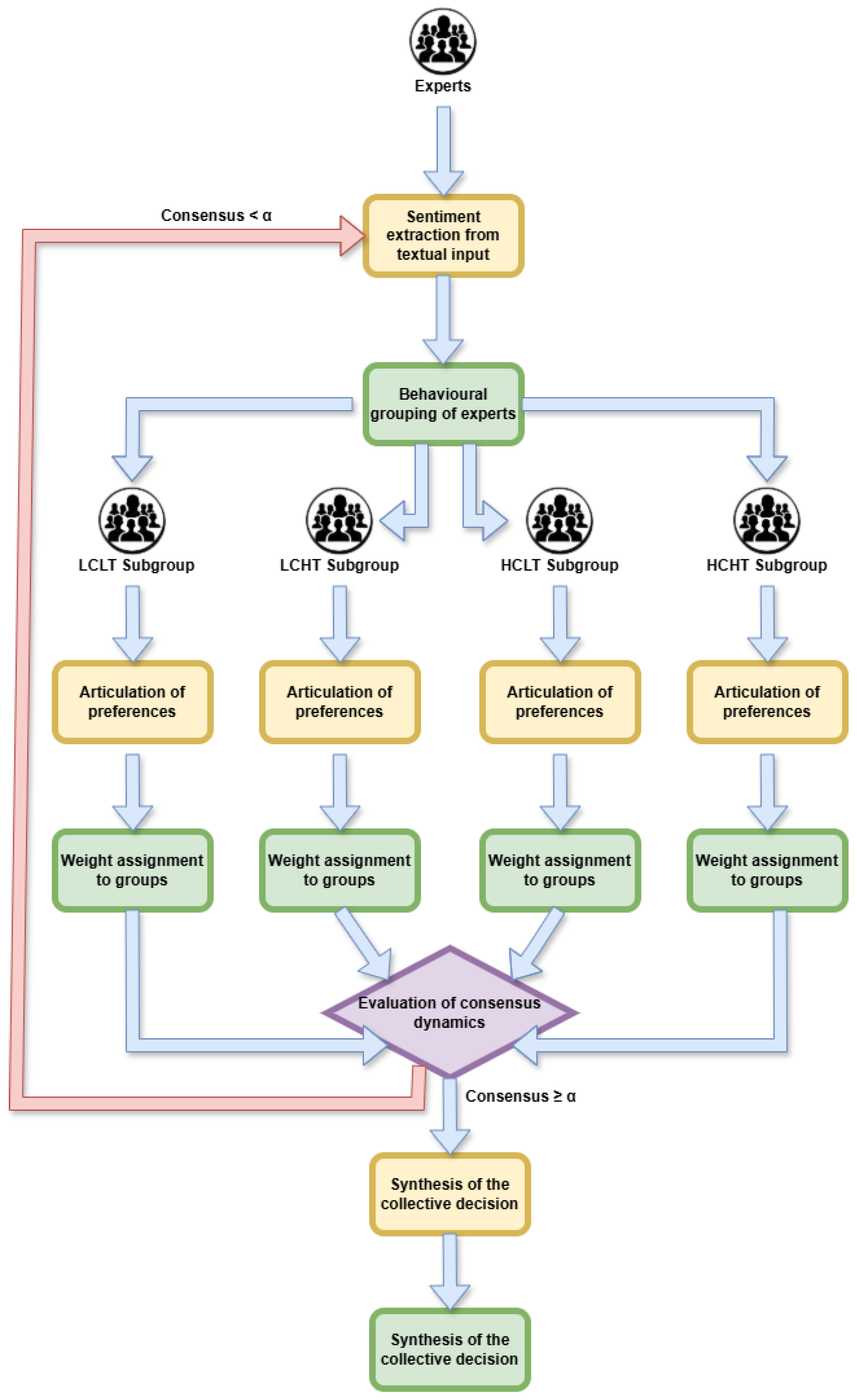
3. Method: Modelling LSGDM Through Grouping with LLM

This section introduces a novel framework designed to address LSGDM problems by incorporating a sentiment-aware classification of experts. The approach capitalises on recent advances in natural language understanding to assess two specific communicative traits: clarity—defined as the intelligibility, structure, and transparency of language—and trust—understood as the degree of constructive, respectful, and receptive interaction exhibited in expert discourse. By leveraging these dimensions, the method structures deliberation not merely around preferences but around the expressive quality of expert engagement. 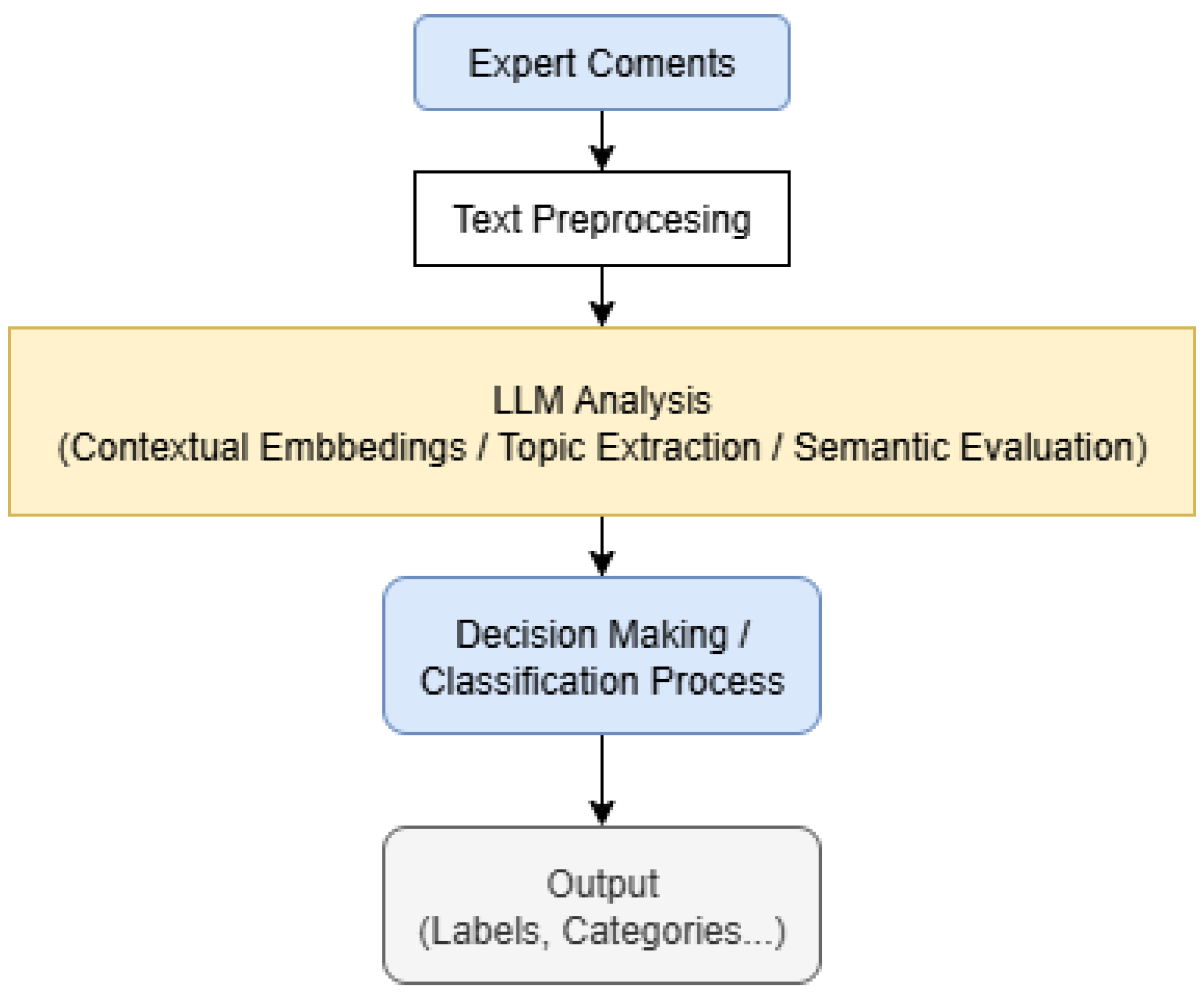The full process unfolds through the following stages (see Figure 2):

• Sentiment extraction from textual input: Expert comments provided during the discussion phase are subjected to semantic analysis using transformer-based language models. Each contribution is quantitatively evaluated to determine the speaker’s average clarity and trust scores, thus enabling behavioural profiling of all participants grounded in their communicative expression.
• Behavioural grouping of experts: Experts are then partitioned into four distinct behavioural profiles based on their previously computed sentiment scores. The resulting groups—combinations of high/low clarity and trust—allow for a segmentation of the decision space that accounts for both cognitive and interpersonal aspects of interaction.
• Articulation of preferences: After completing the discussion, each expert is asked to provide their judgments regarding the set of alternatives. These judgments are encoded using fuzzy preference relations, allowing for nuanced and non-binary evaluations that better reflect real-world reasoning.
• Derivation of intra-group preference structures: Within each sentiment-based group, individual preferences are aggregated to construct a group-level preference matrix. At this stage, each expert contributes equally, ensuring internal fairness within behavioural categories.
• Weight assignment to groups: To modulate the influence of each group in the final decision, weights are assigned on the basis of four factors: internal consensus, number of members, average clarity, and average trust. This composite weighting scheme ensures that groups characterised by cohesion and constructive discourse exert proportionally greater influence.
• Evaluation of consensus dynamics: Both intra-group and inter-group agreement levels are examined to assess the overall harmony or polarisation in the collective decision-making environment. This diagnostic step provides insights into the nature of dissent or alignment across the behavioural spectrum of experts.
• Synthesis of the collective decision: The final preference relation is obtained by integrating the group-level matrices using the corresponding weights.
• Creating the Ranking of Alternatives: The decision-making process concludes with the application of aggregation techniques, such as QGDD [38], to derive a ranking of the alternatives that encapsulates both individual judgments and behavioural quality.

To substantiate the scalability of the proposed framework, we provide an asymptotic analysis of the computational effort required by its principal components. Let m represent the number of experts, k the average number of comments per expert, and n the number of decision alternatives. The sentiment extraction stage requires each comment to be processed by a transformer-based language model to generate clarity and trust scores. Assuming an average comment length of L tokens and constant-time inference per token, the overall complexity can be expressed as $O(m·k·L)$. Since L remains bounded in practical settings, this stage exhibits linear growth with respect to the number of comments. The behavioural grouping step partitions experts into four clusters based on two scalar attributes, clarity and trust. Using a threshold-based approach, this operation is performed in $O\left(m\right)$ time. Even if more advanced clustering methods (such as k-means) are employed, the cost remains $O(m·i)$, where i is the number of iterations, typically a small constant. Finally, preference aggregation and weighting involve constructing intra-group preference matrices at a cost of $O(m·n^2)$ and synthesising the global collective matrix in $O(g·n^2)$, where g is the number of behavioural groups ($g=4$ in this case).

3.1. Sentiment Extraction from Textual Input

In the initial phase of the proposed framework, the core objective is to extract quantifiable sentiment indicators from the textual contributions of experts. Consider a set of N experts $E=\{e_1,e_2,\dots ,e_N\}$, where each expert $e_i$ produces a sequence of comments $C_i=\{c_{i1},c_{i2},\dots ,c_{i{M}_i}\}$, with $M_i$ representing the number of comments submitted by expert i. Each comment $c_{ij}$ is a natural language text segment encapsulating the expert’s opinion or argument.

To transform these qualitative inputs into a structured quantitative form, we apply a sophisticated language model $\mathcal{M}$ based on transformer architectures, trained to assess communicative attributes. Specifically, $\mathcal{M}$ computes two distinct sentiment scores per comment: clarity $s_{ij}^{\mathrm{clarity}}$ and trust $s_{ij}^{\mathrm{trust}}$, both normalised within the unit interval $[0,1]$. In our approach, the sentiment analysis model extracts two communicative dimensions from expert comments: clarity and trust.

Clarity is defined as the degree to which a comment exhibits linguistic structure, coherence, and intelligibility. It reflects how well the speaker’s intent and reasoning are conveyed in natural language.

Trust, as used in this work, is operationally defined as the degree to which a comment is perceived as constructive, respectful, and receptive to others’ viewpoints. While classical definitions of trust often imply an asymmetric two-way relationship between agents, our model focuses on the textual expression of trustworthy intent as inferred from linguistic tone. This formulation enables sentence-level estimation and circumvents the need for explicit dyadic modelling.

To ensure reproducibility, we report the exact prompt formulations used in the LLM-based evaluation. For each expert comment, the model was queried with the following zero-shot prompts:

• Clarity prompt: “On a scale from 0 to 1, how clear, structured, and easy to follow is the following comment?”
• Trust prompt: “On a scale from 0 to 1, how constructive, respectful, and receptive is the tone of the following comment?”

These scores were then normalised and averaged per expert, yielding a behavioural profile ${\mathbf{S}}_i=[S_i^{\mathrm{clarity}},S_i^{\mathrm{trust}}]$ used in the clustering process. We note that this model of trust prioritises communicative disposition over interpersonal dependency, which aligns with recent discourse-level sentiment frameworks.

$$\mathcal{M}:c_{ij}\mapsto \left(s_{ij}^{\mathrm{clarity}},s_{ij}^{\mathrm{trust}}\right),s_{ij}^{\mathrm{clarity}},s_{ij}^{\mathrm{trust}}\in [0,1]$$

(1)

This mapping can be formally represented as a vector-valued function:

$${\mathbf{s}}_{ij}=\left[\begin{array}{c}{s}_{ij}^{\mathrm{clarity}}\\ s_{ij}^{\mathrm{trust}}\end{array}\right]$$

(2)

The individual sentiment vectors ${\mathbf{s}}_{ij}$ are aggregated at the expert level to define an expert-specific sentiment profile vector ${\mathbf{S}}_i$, which summarises the overall behavioural tendencies of expert $e_i$:

$${\mathbf{S}}_i={\displaystyle \frac{1}{M_i}}\sum _{j=1}^{M_i}{\mathbf{s}}_{ij}=\left[\begin{array}{c}{S}_i^{\mathrm{clarity}}\\ S_i^{\mathrm{trust}}\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{1}{M_i}}\sum _{j=1}^{M_i}{s}_{ij}^{\mathrm{clarity}}\\ {\displaystyle \frac{1}{M_i}}\sum _{j=1}^{M_i}{s}_{ij}^{\mathrm{trust}}\end{array}\right]$$

(3)

This averaging process effectively smooths the fluctuations in individual comment sentiment scores and yields a robust estimate of the expert’s communication style across the entire discussion.

In matrix notation, if we define the sentiment matrices for all comments by expert $e_i$ as

$${\mathbf{S}}_i=\left[\begin{array}{cccc}{s}_{i1}^{\mathrm{clarity}}& s_{i2}^{\mathrm{clarity}}& \dots & s_{i{M}_i}^{\mathrm{clarity}}\\ s_{i1}^{\mathrm{trust}}& s_{i2}^{\mathrm{trust}}& \dots & s_{i{M}_i}^{\mathrm{trust}}\end{array}\right]$$

(4)

then the expert profile vector is computed by

$${\mathbf{S}}_i={\mathbf{S}}_i·{\displaystyle \frac{\mathbf{1}}{M_i}}$$

(5)

where $\mathbf{1}\in {\mathbb{R}}^{M_i\times 1}$ is a column vector of ones, and the dot denotes matrix multiplication.

It is important to highlight that the transformer model $\mathcal{M}$ leverages deep contextual embeddings and attention mechanisms to capture subtle nuances in language, allowing the system to discern not only explicit sentiment but also implicit cues related to clarity and trustworthiness.

The resultant vectors ${\mathbf{S}}_i$ for all experts form the basis for the subsequent behavioural grouping step, where experts are grouped according to similarity in their communicative profiles. This step ensures that the decision-making process is informed not merely by stated preferences but also by the qualitative nature of expert interactions.

Thus, this phase constitutes a foundational transformation from unstructured textual data to structured sentiment-informed expert profiles, enabling a richer and more interpretable group decision-making framework. It is important to acknowledge that, in this study, we did not perform an empirical validation of the LLM-generated sentiment scores against human annotations. The clarity and trust scores are derived from prompt-based evaluations using an instruction-tuned transformer model, selected for its demonstrated performance in discourse-level tasks. While this approach ensures scalability and domain flexibility, future work should include controlled annotation studies and inter-rater agreement analyses to benchmark the model’s outputs against expert human judgment. Such validation would enhance the methodological robustness and interpretability of the behavioural grouping mechanism. While other behavioural traits such as emotional tone, assertiveness, or engagement could be considered for analysis, we limited the grouping mechanism to clarity and trust due to their semantic generality, task-independence, and interpretability. These dimensions are robustly inferred from natural language using transformer-based models and directly impact deliberative quality, which makes them particularly suitable for large-scale domain-independent decision frameworks.

3.2. Articulation of Preferences

Upon completion of the textual deliberations and the exchange of arguments among the experts, each participant is requested to articulate their preferences over the set of decision alternatives. This process translates subjective judgments into a formal structure that can be mathematically processed.

Experts are not required to provide exact fuzzy numbers. Instead, each expert expresses their pairwise preferences among alternatives using a predefined ordinal linguistic scale (e.g., “equally preferred”, “moderately preferred”, “strongly preferred”, etc.). These qualitative judgements are then mapped to fuzzy numerical values in the $[0,1]$ interval using a calibrated transformation function, consistent with standard practices in LSGDM literature.

Let $E=\{e_1,e_2,\dots ,e_m\}$ denote the set of m experts and $X=\{x_1,x_2,\dots ,x_n\}$ represent the set of n alternatives under consideration. Each expert $e_s\in E$ expresses their preference via a fuzzy preference relation $P_s$, defined as the matrix

$$P_s=\left(p_s^{ij}\right)\mathrm{for}i,j=1,\dots ,n,i\ne j,$$

(6)

where the element $p_s^{ij}\in [0,1]$ quantifies the degree to which expert $e_s$ prefers alternative $x_i$ over $x_j$.

The interpretation of the preference values follows the conventional fuzzy preference semantics:

$$p_s^{ij}\left\{\begin{array}{cc}>0.5,\hfill & \mathrm{indicates}\mathrm{that}{x}_i\mathrm{is}\mathrm{preferred}\mathrm{to}{x}_j\mathrm{by}\mathrm{expert}{e}_s,\hfill \\ =0.5,\hfill & \mathrm{indicates}\mathrm{indifference}\mathrm{between}{x}_i\mathrm{and}{x}_j,\hfill \\ <0.5,\hfill & \mathrm{indicates}\mathrm{that}{x}_j\mathrm{is}\mathrm{preferred}\mathrm{to}{x}_i.\hfill \end{array}\right.$$

(7)

Note that the diagonal elements $p_s^{ii}$ are conventionally set to $0.5$, reflecting indifference of an alternative with itself:

$$p_s^{ii}=0.5,\forall i=1,\dots ,n.$$

(8)

This fuzzy relational representation enables experts to express graded preferences rather than strict binary choices, thereby capturing nuanced judgments that more closely approximate real decision-making processes.

The set of preference matrices $\{P_1,P_2,\dots ,P_m\}$ collected from all experts forms the foundational data for the subsequent aggregation and analysis steps. Furthermore, the sentiment scores extracted previously (clarity and trust) will be employed to contextualise and weight these preference relations according to the behavioural profiles of the experts.

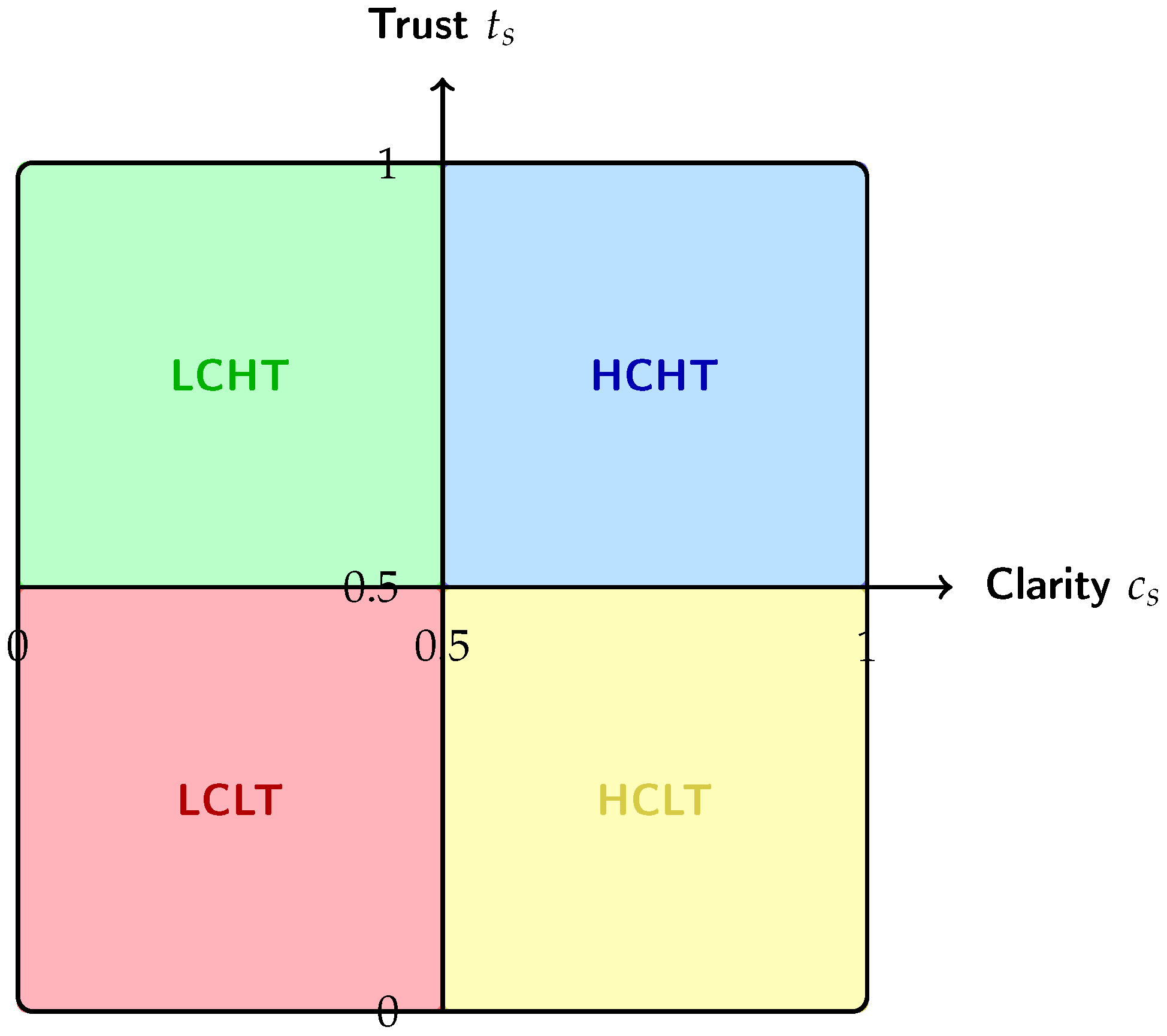
3.3. Behavioural Grouping of Experts

In this phase, experts are segmented into distinct clusters according to their measured degrees in two critical communicative dimensions: clarity and trust. These dimensions serve as proxies for behavioural tendencies, capturing, respectively, the transparency and coherence of the expert’s discourse, and the constructive, respectful nature of their interaction [43].

By crossing these two continuous scales, four unique behavioural archetypes arise:

• Low Clarity–Low Trust (LCLT): Experts whose contributions are unclear and exhibit low levels of respectful or constructive engagement.
• Low Clarity–High Trust (LCHT): Experts with less clear discourse but who maintain a constructive and trustworthy interaction style.
• High Clarity–Low Trust (HCLT): Experts whose communication is clear but may lack trustworthiness, potentially reflecting blunt or overly critical attitudes.
• High Clarity–High Trust (HCHT): Experts who express their opinions both clearly and with a high degree of trustworthiness, facilitating constructive deliberation.

Formally, let us denote the clarity and trust scores for expert $e_s$ as $c_s$ and $t_s$, respectively, both ranging within a normalised scale: $c_s,t_s\in [0,1]$. The thresholds defining the partition boundaries for these dimensions are set as $l_c=0.5,l_t=0.5$, dividing the score space into quadrants corresponding to the behavioural clusters. Accordingly, the cluster assignment function is defined as (see Figure 3)

$$\mathrm{Cluster}\left(e_s\right)=\left\{\begin{array}{cc}\mathrm{LCLT},\hfill & c_s<l_c,t_s<l_t,\hfill \\ \mathrm{LCHT},\hfill & c_s<l_c,t_s\ge l_t,\hfill \\ \mathrm{HCLT},\hfill & c_s\ge l_c,t_s<l_t,\hfill \\ \mathrm{HCHT},\hfill & c_s\ge l_c,t_s\ge l_t.\hfill \end{array}\right.$$

(9)

Subsequently, the analysis is applied to the comments produced by each expert. Let $e_j$ be an expert who has made $M_j$ comments $\{c_{j1},c_{j2},\dots ,c_{j{M}_j}\}$. For each comment $c_{ji}$, the language model $\mathcal{M}$ computes a clarity score $s_{ji}^{\mathrm{clarity}}$ and a trust score $s_{ji}^{\mathrm{trust}}$, both in the interval $[0,1]$.

For each expert $e_j$, two score vectors are constructed:

$${\mathbf{s}}_j^{\mathrm{clarity}}=\left\{s_{j1}^{\mathrm{clarity}},s_{j2}^{\mathrm{clarity}},\dots ,s_{j{M}_j}^{\mathrm{clarity}}\right\},$$

(10)

$${\mathbf{s}}_j^{\mathrm{trust}}=\left\{s_{j1}^{\mathrm{trust}},s_{j2}^{\mathrm{trust}},\dots ,s_{j{M}_j}^{\mathrm{trust}}\right\}.$$

(11)

Then, the average clarity and trust scores for expert $e_j$ are calculated as

$${\overline{s}}_j^{\mathrm{clarity}}={\displaystyle \frac{1}{M_j}}\sum _{i=1}^{M_j}{s}_{ji}^{\mathrm{clarity}},$$

(12)

$${\overline{s}}_j^{\mathrm{trust}}={\displaystyle \frac{1}{M_j}}\sum _{i=1}^{M_j}{s}_{ji}^{\mathrm{trust}}.$$

(13)

Using the thresholds $l_c$ and $l_t$ defined in the clustering phase, expert $e_j$ is assigned to a behavioural group according to

$$\mathrm{Cluster}\left(e_j\right)=\left\{\begin{array}{cc}\mathrm{LCLT},\hfill & {\overline{s}}_j^{\mathrm{clarity}}<l_c,{\overline{s}}_j^{\mathrm{trust}}<l_t,\hfill \\ \mathrm{LCHT},\hfill & {\overline{s}}_j^{\mathrm{clarity}}<l_c,{\overline{s}}_j^{\mathrm{trust}}\ge l_t,\hfill \\ \mathrm{HCLT},\hfill & {\overline{s}}_j^{\mathrm{clarity}}\ge l_c,{\overline{s}}_j^{\mathrm{trust}}<l_t,\hfill \\ \mathrm{HCHT},\hfill & {\overline{s}}_j^{\mathrm{clarity}}\ge l_c,{\overline{s}}_j^{\mathrm{trust}}\ge l_t.\hfill \end{array}\right.$$

(14)

This classification enables a nuanced weighting of expert inputs in the aggregation process, taking into account both their evaluative judgments and the qualitative nature of their communication style. It is important to note that the current implementation employs fixed mid-point thresholds $\left(0.5\right)$ for both clarity and trust, reflecting the natural semantic boundary between low and high values in the normalised $[0,1]$ scale. This choice ensures balanced group distributions and interpretability. However, the framework is designed to be modular, and the thresholds can be adjusted or derived from the data. Alternative approaches—such as k-means clustering, Gaussian mixture models, or quantile-based segmentation—can be adopted to dynamically determine group boundaries based on the statistical properties of the sentiment distributions. This flexibility allows the method to be adapted to different contexts while preserving behavioural interpretability.

3.4. Derivation of Intra-Group Preference Structures

Once experts have been classified into behavioural groups according to their clarity and trust scores, the next step consists of deriving a preference matrix for each group. This process synthesises the individual evaluations within each behavioural cluster, creating an intra-group preference structure that reflects both the judgments and the communicative traits of its members.

Let $\mathcal{G}=\{\mathrm{LCLT},\mathrm{LCHT},\mathrm{HCLT},\mathrm{HCHT}\}$ be the set of behavioural groups derived in Section 3.4. Each group $G\in \mathcal{G}$ contains a subset of experts $U_G\subseteq E$ whose communicative profiles—measured in terms of clarity and trust—are similar. For each expert $e_s\in U_G$, let $P_s$ denote their fuzzy preference relation, following the representation introduced in Section 3.3.

To derive the intra-group preference relation $P_G$, the individual matrices $P_s$ are aggregated using the arithmetic mean, with equal weight assigned to all experts in the group. This yields the following formulation for each pair of alternatives $(i,j)$:

$$p_G^{ij}={\displaystyle \frac{1}{|U_G|}}\sum _{e_s\in U_G}{p}_s^{ij},\forall i,j=1,\dots ,n,i\ne j$$

(15)

and the diagonal entries are set as usual:

$$p_G^{ii}=0.5,\forall i=1,\dots ,n$$

(16)

The resulting group-level preference matrix $P_G$ captures the central tendencies within each communicative group. Since the members of a group are behaviourally similar in their clarity and trust levels, the aggregation also benefits from internal consistency. These matrices will be used in the next stage (Section 3.6) to construct a behaviourally weighted global preference relation.

3.5. Weight Assignment to Groups

Once the intra-group preference structures have been established (see Section 3.4), we proceed to compute the weight of each behavioural group in order to synthesise a global collective preference relation. These weights reflect both the distribution of experts across the groups and the communicative quality of their interactions. To obtain the group weights, we define a weighting scheme based on three key factors:

• The proportion of experts assigned to the group (membership rate).
• The average clarity and trust score of the group.
• The internal consensus among members of the group.

Let $\mathcal{G}=\{\mathrm{LCLT},\mathrm{LCHT},\mathrm{HCLT},\mathrm{HCHT}\}$ denote the set of behavioural groups. For a group $G\in \mathcal{G}$, let $U_G$ represent the set of experts assigned to that group, and let $|U_G|$ be the number of experts in the group. Let $m=\left|E\right|$ be the total number of experts.

The relative size of the group is calculated as

$$t_G={\displaystyle \frac{|U_G|}{m}}$$

(17)

Let $s_e^{\mathrm{clarity}}$ and $s_e^{\mathrm{trust}}$ denote the average clarity and trust scores, respectively, of expert $e\in U_G$ (as computed in Section 3.1). Then, the average clarity and trust for group G are

$${\overline{C}}_G={\displaystyle \frac{1}{|U_G|}}\sum _{e\in U_G}|s_e^{\mathrm{clarity}}|,{\overline{T}}_G={\displaystyle \frac{1}{|U_G|}}\sum _{e\in U_G}\left|s_e^{\mathrm{trust}}\right|$$

(18)

Let $P_i$ and $P_j$ be the fuzzy preference matrices of any two experts $e_i,e_j\in U_G$. The consensus between them is defined using a normalised distance function:

$$\mathrm{dis}(P_i,P_j)=1-{\displaystyle \frac{\sqrt{{\sum }_{\delta =1}^n{\sum }_{\begin{array}{c}z=1\\ \delta \ne z\end{array}}^n{\left(p_i^{\delta z}-p_j^{\delta z}\right)}^2}}{n(n-1)}}$$

(19)

The average consensus within the group is computed as

$${\mathrm{Cons}}_G={\displaystyle \frac{2}{|U_G{|}^2+\left|U_G\right|}}\sum _{i=1}^{|U_G|-1}\sum _{j=i+1}^{|U_G|}\mathrm{dis}(P_i,P_j)$$

(20)

Combining the above elements, the unnormalised weight for group G is given by

$$w_G=\sqrt[4]{t_G·{\overline{C}}_G·{\overline{T}}_G·{\mathrm{Cons}}_G}$$

(21)

Finally, the weights are normalised to ensure they sum to one:

$$W_G={\displaystyle \frac{w_G}{{\sum }_{G^{\prime }\in \mathcal{G}}{w}_{G^{\prime }}}}$$

(22)

These normalised weights $W_G$ capture the relative importance of each behavioural group in the aggregation process. Groups with higher communicative quality (as reflected in clarity and trust) and greater internal consensus will have a stronger influence on the final collective preference relation.

To facilitate interpretation, it is useful to consider the conceptual meaning of each term in the weighting formula. The parameter $t_G$ represents the relative size of the behavioural group, while ${\overline{C}}_G$ and ${\overline{T}}_G$ correspond to its average clarity and trust scores, respectively. The term $Con{s}_G$ captures intra-group consensus and thus reflects the internal coherence of evaluations. The combined expression integrates these dimensions multiplicatively to ensure that groups with greater size, communicative quality, and agreement exert proportionally more influence on the final aggregation.

3.6. Evaluation of Consensus Dynamics

The consolidation of a collective decision within a multi-agent system is contingent upon the presence of a sufficient degree of alignment across divergent behavioural groups. In the proposed framework, the evaluation of consensus dynamics serves as a critical checkpoint, ensuring that the integration of intra-group preferences into a final collective decision is grounded in inter-group concordance rather than procedural aggregation alone.

This process is conceptually structured into two sequential stages. First, a formal quantification of the consensus degree among the distinct behavioural groups is performed. Second, this empirical value is contrasted with a predefined consensus threshold, denoted $\alpha \in [0,1]$, which operationalises the minimal acceptable standard for agreement prior to decision ratification [44].

Let $\mathcal{G}=\{\mathrm{LCLT},\mathrm{LCHT},\mathrm{HCLT},\mathrm{HCHT}\}$ denote the set of behavioural archetypes identified through clarity–trust profiling. For each group $G\in \mathcal{G}$, let $C_G$ represent the intra-group preference matrix derived in Section 3.5. These matrices are constructed via intra-cluster aggregation and capture the representative attitudinal disposition of the group toward the decision alternatives.

To evaluate inter-group consensus, we invoke the distance metric previously defined in Equation (19), now applied to the aggregated matrices $C_{G_i}$ and $C_{G_j}$. The overall consensus score is calculated as the mean pairwise proximity between all distinct group matrices:

$$\mathrm{Consensus}={\displaystyle \frac{2}{\left|\mathcal{G}\right|\left(\right|\mathcal{G}|-1)}}\sum _{\begin{array}{c}{G}_i,G_j\in \mathcal{G}\\ G_i<G_j\end{array}}\mathrm{dis}(C_{G_i},C_{G_j})$$

(23)

Given that $\left|\mathcal{G}\right|=4$, this simplifies to

$$\mathrm{Consensus}={\displaystyle \frac{2}{12}}\sum _{i=1}^3\sum _{j=i+1}^4\mathrm{dis}(C_{G_i},C_{G_j})$$

(24)

where $\mathrm{dis}(·,·)$ denotes the normalised Euclidean divergence between preference matrices.

This metric captures the structural alignment of aggregated preferences across behavioural segments. Should the resulting consensus score satisfy $\mathrm{Consensus}\ge \alpha$, it is inferred that the behavioural groups exhibit sufficient coherence to proceed with the derivation of the final collective preference relation and the corresponding ranking of alternatives.

Conversely, if the consensus falls below the required threshold, the system initiates a feedback-driven deliberation protocol. This mechanism seeks to foster convergence by encouraging inter-group dialogue and the reconsideration of evaluative stances. Additionally, experts whose communicative behaviour impedes consensus—particularly those manifesting persistently low clarity or trust metrics—may be prompted to adjust their rhetorical approach to facilitate mutual understanding.

To prevent indefinite deliberative cycles, an upper bound $R\in \mathbb{N}$ is imposed on the number of consensus iterations, consistent with best practices in dynamic consensus models [45]. If, after R rounds, the consensus score remains below $\alpha$, the decision-support system proceeds to synthesise the global preference relation using the most recent intra-group matrices and their corresponding behavioural weights, thereby ensuring procedural closure and decision tractability.

3.7. Calculating the Collective Preference Relation

Upon construction of the intra-group preference matrices $C_G$ for each behavioural cluster $G\in \mathcal{G}=\{\mathrm{LCLT},\mathrm{LCHT},\mathrm{HCLT},\mathrm{HCHT}\}$ and the derivation of their corresponding behavioural weights $W_G$ (as outlined in Section 3.6), it becomes possible to synthesise a global collective preference relation, denoted $C_{\mathrm{Global}}$.

This matrix encapsulates the evaluative consensus of the entire expert panel, integrating both individual judgments and the qualitative communication characteristics embedded in group formation. To perform the aggregation, we adopt a weighted arithmetic mean across the group-level matrices [46,47]. Formally, the collective preference matrix is defined as

$$p_{C_{\mathrm{Global}}}^{ij}=\sum _{G\in \mathcal{G}}{W}_G·p_G^{ij}\forall i,j=1,\dots ,n,i\ne j$$

(25)

where $p_G^{ij}$ represents the pairwise preference value between alternatives $x_i$ and $x_j$ within group G, and $W_G$ is the normalised behavioural weight assigned to group G.

This procedure ensures that the final preference matrix $C_{\mathrm{Global}}$ is not merely a numerical fusion of evaluations but a sentiment-informed synthesis that acknowledges the deliberative and rhetorical profiles of the decision participants.

3.8. Creating the Ranking of Alternatives

Once the global collective preference relation $C_{\mathrm{Global}}$ has been established (as defined in Equation (25)), the final stage of the decision-making process involves determining a prioritised list of alternatives that best reflect the consensus preferences of the expert panel.

To this end, we adopt the quantifier-guided dominance degree (QGDD), a well-established operator in fuzzy decision-making frameworks [38,48]. This operator assesses the relative dominance of each alternative over the remaining ones based on the aggregated preference values.

Formally, for each alternative $x_j\in X=\{x_1,x_2,\dots ,x_n\}$, its QGDD score is defined as

$$QGD{D}_j={\displaystyle \frac{1}{n-1}}\sum _{\begin{array}{c}s=1\\ s\ne j\end{array}}^n{p}_{C_{\mathrm{Global}}}^{js}$$

(26)

where $p_{C_{\mathrm{Global}}}^{js}$ represents the degree to which alternative $x_j$ is preferred over alternative $x_s$ in the collective preference matrix.

The QGDD value encapsulates the average strength of an alternative in dominating others, thus serving as a scalar representation of its overall support within the group. Higher QGDD values indicate stronger collective endorsement.

The final ranking of alternatives is then obtained by sorting the set X in descending order of their corresponding QGDD scores:

$$\mathrm{Rank}\left(X\right)={\mathrm{sort}}_{\mathrm{desc}}\left({\left\{QGD{D}_j\right\}}_{j=1}^n\right)$$

(27)

This ranking reflects the collective evaluative landscape, filtered through the lens of behavioural group weighting and sentiment-aware aggregation. By relying exclusively on QGDD, the method emphasises dominance as the primary mechanism for selecting the most preferred alternatives in large-scale group decision contexts.

3.9. Computational Cost Comparison: With vs. Without Grouping

To support the methodological rigour of the proposed approach, we present a formal comparison of the computational complexity between the grouping-based model and a baseline scenario where all expert preferences are aggregated directly without sentiment-based clustering.

Let m be the number of experts, n the number of alternatives, k the average number of comments per expert, L the average comment length in tokens, and g the number of behavioural groups (typically $g=4$, as defined in Section 3.3).

Without Grouping

In the non-grouped case:

• Sentiment analysis: Not performed. Cost: $\mathcal{O}\left(1\right)$.
• Preference aggregation: Aggregating m fuzzy preference matrices into a single matrix: $\mathcal{O}(m·n^2)$.
• Consensus evaluation: Optional or trivial since there are no intra-/inter-group layers. However, if full consensus evaluation between individual experts is required, this would involve $O(m^2·n^2)$ complexity due to the $m·(m-1)/2$ pairwise comparisons of fuzzy preference matrices. This becomes significant in large-scale scenarios and is one of the motivations for reducing the consensus space via behavioural grouping.

Total complexity: $\mathcal{O}(m·n^2)$.

With Grouping (Proposed Method)

• Sentiment extraction: Each of the $m·k$ comments is analysed by an LLM, with per-token inference cost: $\mathcal{O}(m·k·L)$.
• Grouping: Sentiment vectors clustered into $g=4$ groups: $\mathcal{O}\left(m\right)$ (threshold-based).
• Intra-group aggregation: $\mathcal{O}(m·n^2)$ (same as non-grouped).
• Group weighting: Involves consensus measures among m matrices: $\mathcal{O}(m^2·n^2)$ in the worst case, but reduced to $\mathcal{O}(g·n^2)$ due to grouping.
• Final aggregation: Combine g group matrices into global consensus: $\mathcal{O}(g·n^2)$.

Total complexity:

$$\mathcal{O}(m·k·L+m·n^2+g·n^2)$$

Since $g\ll m$ and L is bounded, the dominant term is $\mathcal{O}(m·k·L+m·n^2)$, which remains scalable.

While the grouped model introduces additional overhead due to sentiment analysis, it reduces the cost of consensus measurement by avoiding $m^2$ pairwise comparisons. Therefore, in scenarios with large m, the proposed approach is computationally competitive, particularly when k is moderate and grouping stabilises consensus formation. In contrast to non-grouped approaches that may require $O\left(m^2\right)$ comparisons for consensus computation, our method reduces this to $O\left(g^2\right)$ comparisons among aggregated group matrices, yielding significant computational savings while preserving decision robustness.

4. Case Study

To illustrate the proposed method, this section presents a case study involving a simulated group decision-making process among 20 domain experts focused on strategic priorities in digital policy. The expert panel is constructed to reflect a range of communicative behaviours. Each expert contributes a set of 10 text-based comments, crafted to display variation in clarity and interpersonal tone, either by manual generation based on typical discourse patterns or by adapting examples from real-world consultation settings. While the present case study is simulated, it is constructed using representative behavioural profiles and discourse examples inspired by real consultation settings. As future work, we aim to conduct an empirical evaluation of the proposed method with real expert panels in order to assess its practical applicability and behavioural validity.

The model is prompted to score each utterance in terms of two behavioural dimensions: clarity, understood as linguistic structure and coherence, and trust, interpreted as constructive, respectful engagement. The resulting scores are averaged per expert and used to classify participants into four behavioural groups. After the deliberation phase, each expert submits a fuzzy preference matrix over a set of four digital policy alternatives. The expert panel is denoted as $E=\{e_1,e_2,\dots ,e_{20}\}$. The context involves advising a national digital agency on the most appropriate public investment measures to improve the digital infrastructure and governance of the country.

The set of alternatives under consideration is defined as $X=\{x_1,x_2,x_3,x_4\}$, where

• $x_1$: increase investment in cybersecurity systems.
• $x_2$: expand broadband infrastructure in rural areas.
• $x_3$: promote digital literacy and education programs.
• $x_4$: develop AI governance frameworks and regulations.

Each expert contributes a set of 10 textual comments during a moderated online discussion phase. These texts can range in length from a brief statement to an extended argument. The use of the term “text” is intended to generalise across this variability. If an expert provides fewer than 14 comments, the remaining entries are considered neutral placeholders—i.e., empty texts—to maintain uniformity in the sentiment aggregation process. This ensures that each expert’s behavioural profile (clarity and trust) can be computed on a comparable basis. For sentiment analysis, we employed a state-of-the-art instruction-tuned large language model capable of interpreting natural language comments through zero-shot prompt-based scoring. Each expert comment was evaluated by prompting the model with structured questions designed to yield scalar ratings for clarity (e.g., coherence, structure, and intelligibility) and trust (e.g., respectfulness and constructiveness). These scores were normalised within the [0, 1] range and averaged per expert to produce behavioural profiles.

Following the textual contribution phase, each comment is processed through a transformer-based sentiment analysis model, which assigns a pair of scores for clarity and trust. Based on these scores, each expert is classified into one of four behavioural groups:

• high clarity–high trust (HCHT);
• high clarity–low trust (HCLT);
• low clarity–high trust (LCHT);
• low clarity–low trust (LCLT).

This behavioural classification enables the construction of intra-group preference matrices, followed by the weighting and aggregation steps described in Section 3.1. The goal is to derive a sentiment-aware collective preference structure that reflects not only the experts’ evaluations of the alternatives but also the communicative quality of their participation.

Examples of comments include

• “That proposal completely ignores rural communities.” (low trust–moderate clarity);
• “I strongly support expanding broadband; it’s essential.” (high trust–high clarity);
• “Your idea lacks a long-term perspective.” (low trust–high clarity);
• “Great point about inclusion; very well argued.” (high trust–high clarity).

After the discussion phase, each expert submits a fuzzy preference relation $P_s$ over the four alternatives. Some representative matrices include

$$P_1=\left(\begin{array}{cccc}-& 0.4& 0.0& 0.5\\ 0.6& -& 0.4& 0.7\\ 1.0& 0.6& -& 0.9\\ 0.5& 0.3& 0.2& -\end{array}\right)P_6=\left(\begin{array}{cccc}-& 0.8& 0.1& 0.9\\ 0.2& -& 0.3& 0.8\\ 0.9& 0.7& -& 0.8\\ 0.1& 0.2& 0.2& -\end{array}\right)$$

Following the sentiment extraction phase described in Section 3.3, each expert is assigned to one of four behavioural groups based on their average clarity and trust scores:

• $G_{LCLT}$: low clarity–low trust;
• $G_{LCHT}$: low clarity–high trust;
• $G_{HCLT}$: high clarity–low trust;
• $G_{HCHT}$: high clarity–high trust.

The resulting distribution of experts and corresponding behavioural metrics are shown in

Table 1. Group composition and behavioural metrics.

Group	#Experts	Avg. Clarity	Avg. Trust	Intra-Group Consensus
$G_{LCLT}$	5	0.17	0.22	0.69
$G_{LCHT}$	4	0.20	0.79	0.76
$G_{HCLT}$	6	0.88	0.26	0.56
$G_{HCHT}$	5	0.91	0.84	0.68

.

Each group’s internal preferences are then aggregated using the arithmetic mean to obtain intra-group preference matrices. For instance,

$$C_{G_{LCLT}}=\left(\begin{array}{cccc}-& 0.41& 0.29& 0.53\\ 0.59& -& 0.34& 0.59\\ 0.71& 0.66& -& 0.82\\ 0.47& 0.41& 0.18& -\end{array}\right)C_{G_{LCHT}}=\left(\begin{array}{cccc}-& 0.43& 0.25& 0.53\\ 0.57& -& 0.22& 0.49\\ 0.75& 0.78& -& 0.55\\ 0.47& 0.51& 0.45& -\end{array}\right)$$

$$C_{G_{HCLT}}=\left(\begin{array}{cccc}-& 0.54& 0.29& 0.52\\ 0.46& -& 0.32& 0.45\\ 0.71& 0.68& -& 0.82\\ 0.48& 0.55& 0.18& -\end{array}\right)C_{G_{HCHT}}=\left(\begin{array}{cccc}-& 0.49& 0.35& 0.48\\ 0.51& -& 0.22& 0.48\\ 0.65& 0.78& -& 0.66\\ 0.52& 0.52& 0.34& -\end{array}\right)$$

The group weights are calculated according to Equation (22), combining the size of the group, average clarity, average trust, and intra-group consensus. The results are presented in

Table 2. Group weights based on behavioural profiles.

Group	Normalised Weight
$G_{LCLT}$	0.1647
$G_{LCHT}$	0.2288
$G_{HCLT}$	0.2574
$G_{HCHT}$	0.3490

.

For example, consider the group $G_{HCHT}$ with size proportion $t_G=0.25$, average clarity ${\overline{C}}_G=0.91$, trust ${\overline{T}}_G=0.84$, and consensus $Con{s}_G=0.68$. Applying Equation (21), the unnormalised weight is computed as $w_G=\sqrt[4]{(0.25·0.91·0.84·0.68)}\approx 0.395.$ Following normalisation across all groups (Equation (22)), this yields a final weight of approximately $0.349$, consistent with the value reported in Table 2.

To ensure that the aggregation reflects a reasonable level of agreement across behavioural groups, the inter-group consensus is calculated using the distance metric defined in Equation (24).

Table 3. Inter-group consensus metrics.

Group Pair	Consensus Score
$G_{LCLT}$, $G_{LCHT}$	0.9629
$G_{LCLT}$, $G_{HCLT}$	0.9773
$G_{LCLT}$, $G_{HCHT}$	0.9700
$G_{LCHT}$, $G_{HCLT}$	0.9631
$G_{LCHT}$, $G_{HCHT}$	0.9802
$G_{HCLT}$, $G_{HCHT}$	0.9752
Average	0.9714

reports the pairwise consensus values:

Since the average consensus value exceeds the threshold $\alpha =0.85$, the process proceeds without further deliberation. The final collective preference matrix is obtained using Equation (25):

$$C_{Global}=\left(\begin{array}{cccc}-& 0.4760& 0.3018& 0.5100\\ 0.5240& -& 0.2655& 0.4927\\ 0.6982& 0.7345& -& 0.7024\\ 0.4900& 0.5073& 0.2976& -\end{array}\right)$$

Finally, the ranking of alternatives is derived using the QGDD operator (Equation (26)). The resulting values are shown in

Table 4. QGDD values using the collective preference relation $C_G$.

Alternative	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$
QGDD	0.4293	0.4274	0.7117	0.4316

.

Finally, we employ Trillo’s Theorem [49] to verify the internal consistency and coherence of the group decision-making outcome. This theorem establishes that, if a unique alternative appears at the top of the aggregated ranking obtained through the Quantified Group Decision Degree (QGDD), and the variance of individual preferences is low for that alternative, then the result can be considered both valid and consensual.

By sorting the alternatives in descending order of QGDD, the resulting ranking is

$$\mathbf{Ranking}:\{x_3,x_4,x_1,x_2\}$$

According to the theorem, the clear prominence of $x_3$ at the top of the list—combined with its low preference dispersion—confirms the robustness and legitimacy of the group decision, and also reveals a bias among the experts in favour of $x_3$: promoting digital literacy and inclusion programs.

Comparative Scenario Without Grouping

To assess the added value of the behavioural grouping process, we conducted a comparative evaluation using the same expert preference matrices but omitting the sentiment-based clustering stage. In this baseline scenario, all individual fuzzy preference matrices were directly aggregated using an unweighted arithmetic mean:

$$p_{ij}^{\mathrm{direct}}={\displaystyle \frac{1}{m}}\sum _{s=1}^m{p}_{ij}^s$$

(28)

This yielded the following collective preference matrix:

$$C_{\mathrm{direct}}=\left(\begin{array}{cccc}-& 0.4650& 0.3112& 0.4995\\ 0.5350& -& 0.2693& 0.4910\\ 0.6888& 0.7307& -& 0.7051\\ 0.5005& 0.5090& 0.2949& -\end{array}\right)$$

The QGDD scores for the alternatives were as follows (see

Table 5. QGDD scores for the non-grouped scenario.

Alternative	QGDD
$x_1$	0.4252
$x_2$	0.4317
$x_3$	0.7082
$x_4$	0.4348

):

The resulting ranking was

$$\mathbf{Ranking} \mathbf{\left(}\mathbf{no}\mathbf{grouping}\mathbf{\right)}\mathbf{:} \mathbf{\{}{\mathbf{x}}_{\mathbf{3}}\mathbf{,}{\mathbf{x}}_{\mathbf{4}}\mathbf{,}{\mathbf{x}}_{\mathbf{2}}\mathbf{,}{\mathbf{x}}_{\mathbf{1}}\mathbf{\}}$$

While the top alternative ($x_3$) remains unchanged, the scores for $x_2$ and $x_4$ are closer, and the influence of communicative behaviour is no longer present. This illustrates how grouping and behavioural weighting enhance the interpretability and robustness of the final decision, particularly when preferences are heterogeneous or conflicting. Without grouping, high-clarity or high-trust contributions exert no additional influence, which may obscure the quality and credibility of the consensus. The grouped model also showed greater stability under weight perturbation, suggesting its suitability for environments with variable communication behaviour or uncertain participant quality.

5. Discussion

This study proposes a novel perspective on LSGDM by incorporating behavioural signals derived from expert discourse. Rather than relying solely on declared preferences, the model interprets how opinions are expressed, particularly in terms of clarity and trust, which are quantified as core behavioural indicators during expert grouping. Central to this approach is the use of LLMs, whose contextual understanding enables the extraction of nuanced communicative patterns often invisible to traditional techniques.

The practical motivation behind sentiment-informed grouping lies in its ability to manage heterogeneity in deliberative quality. In traditional LSGDM, all preference inputs are treated equally regardless of whether they come from vague, incoherent, or aggressive contributors. By introducing clarity and trust as communicative weights, the method promotes interpretability and fairness, rewarding constructive participation. This is particularly useful in large-scale panels where it is infeasible to manually moderate or validate each input. Our case study demonstrates that such behavioural weighting leads to consistent decisions even under expert diversity. Although further empirical validation is planned, the results already suggest the framework’s robustness and potential utility.

While the proposed framework assumes that expert discourse is generated in good faith, real-world environments may present noisy or even adversarial contributions. For instance, actors could deliberately manipulate linguistic cues to secure membership in high-weight groups (e.g., by artificially inflating clarity or trust markers) or to degrade consensus quality. Such vulnerabilities warrant careful consideration. Potential mitigation strategies include the integration of anomaly detection mechanisms to identify behavioural profiles that deviate significantly from normative patterns, the use of regularisation techniques to limit the impact of outlier groups on global aggregation, and cross-validation of sentiment-derived features with historical participation records. Future work should also explore adversarial robustness benchmarks and stress-testing scenarios to ensure that sentiment-aware consensus models maintain integrity under strategic manipulation.

The contribution of NLP, and specifically LLMs, is foundational. The formation of expert groups is driven by linguistic features, and the weighting mechanism used to modulate group influence depends directly on these behavioural indicators. Without this semantic layer, the model would be incapable of capturing the affective and interpersonal dynamics that are crucial to realistic consensus formation. The structure of the weighting formula reflects this as it integrates discourse-derived metrics in a way that would be infeasible through classical methods. A key innovation lies in repositioning expert commentary from a peripheral role to a central mechanism of influence. The deliberative exchange is no longer a preliminary step but a functional component of the system itself. As a result, not only the content but also the form of expression becomes relevant, affecting how opinions are grouped and weighted.

This framework points toward a new generation of decision-support systems—those that do not merely quantify preferences but interpret discourse as a core input. Future work may explore how such models can adapt to evolving conversation dynamics in real time, further bridging the gap between natural communication and structured collective reasoning.

The proposed approach offers several key advantages that reinforce its suitability for complex large-scale decision-making environments:

• Sentiment-based expert classification: Through LLM-driven sentiment analysis, the method evaluates the emotional tone and assertiveness of expert comments, enabling the identification of behavioural profiles. Experts are grouped accordingly, improving interpretability and reducing the complexity of consensus formation.
• Linguistic-informed weight adjustment: The influence of each group is adjusted based on the tone of its members’ discourse. Groups marked by respectful and constructive communication receive higher weights, fostering fairer influence allocation and promoting collaborative engagement.
• Scalability to large expert panels: As consensus is computed within behavioural groups, the model avoids exhaustive pairwise comparisons. This design ensures efficiency and adaptability regardless of the number of participants involved.

The application of sentiment analysis in LSGDM has attracted increasing attention in research. Nonetheless, studies addressing the integration of multidimensional behavioural factors within flexible and dynamic decision-making frameworks remain scarce. The approach proposed herein distinguishes itself by classifying experts according to the affective qualities of their textual inputs, specifically measuring both positivity and aggressiveness through advanced LLMs. This contrasts with prior work such as [50], which relies on unidimensional positivity scoring of words to categorise comments before group decision-making. Similarly, while [51,52] develop consensus models that emphasise structural preference aggregation and predefined cooperation parameters in the social and financial domains, our methodology derives behavioural insights directly from the discourse of experts, embedding sentiment analysis as a key component of consensus formation. Moreover, although [28] employs sentiment analysis within group decision contexts, it is limited to a single emotional dimension, whereas our model’s multidimensional sentiment framework facilitates more granular expert grouping and more accurate weight adjustments reflective of communicative dynamics. Finally, building on the work of [53], which utilises sentiment grouping focused on positivity, our method extends this paradigm by incorporating aggressiveness as an additional critical dimension, thus enhancing the behavioural modelling capabilities and enabling a dual-purpose use of sentiment metrics for grouping and dynamic weighting, ultimately promoting a more equitable and precise group decision-making process. In contrast with prior sentiment-aware GDM approaches—such as [50], which relies on simple positivity scoring, or [28], which uses static emotional dimensions—our method introduces a dual-purpose sentiment extraction mechanism that informs both expert grouping and group influence weighting. Furthermore, while models such as [39,41] incorporate behavioural factors like trust or non-cooperation, they often require predefined structures or rule-based mechanisms. By contrast, our model derives behavioural insights directly from discourse using large-scale language models, enabling richer context-sensitive interpretation of interactional tone. This comparison underscores the novelty of our approach as a flexible LLM-driven framework for behavioural modelling in group decision-making.

To evaluate the robustness of the collective ranking to fluctuations in behavioural weights, we performed a perturbation analysis in which each group weight was adjusted by $\pm 10\%$, followed by renormalisation to preserve a total sum of 1. The resulting changes in the quantifier-guided dominance degree (QGDD) scores revealed minimal variation: the top-ranked alternative ($x_3$ in our case study) consistently retained its position, while the remaining alternatives exhibited shifts in ranking of at most one position. These findings suggest that the proposed aggregation framework demonstrates satisfactory stability under moderate deviations in behavioural weighting. Nevertheless, scenarios involving extreme imbalance or adversarial manipulation of weights could lead to ranking volatility. Future research should formalise sensitivity indices and develop weight-regularisation strategies to guarantee decision resilience under such conditions.

A notable limitation of the present framework is its reliance on a single transformer-based LLM for sentiment extraction and behavioural profiling. While this design choice ensures computational efficiency and methodological simplicity, it also exposes the system to potential biases and performance limitations inherent to a specific model. Future work should explore ensemble-based approaches or the integration of multiple LLMs trained on heterogeneous corpora. Such strategies could improve robustness by reducing model-specific variance and enhancing generalisability across domains and linguistic contexts. Additionally, incorporating confidence calibration and inter-model agreement metrics would allow for more reliable behavioural assessments, ultimately strengthening the fairness and interpretability of the consensus-building process.

6. Conclusions

This study introduces an innovative framework for LSGDM that incorporates the computational modelling of expert behaviour—specifically the latent dimensions of aggressiveness and attitudinal polarity—into the decision-making architecture. Contemporary approaches to GDM have traditionally prioritised preference aggregation and consensus measurement while largely neglecting the rich behavioural signals embedded in the deliberative discourse. Such omissions risk oversimplifying the social dynamics that underpin collective decisions, particularly in settings marked by heterogeneity of opinion and interaction style.

Our proposed methodology departs from conventional lexicon-based sentiment analysis by employing advanced LLMs capable of capturing nuanced pragmatic and affective features in textual communication.

The case study presented in this work illustrates the potential of using large language models (LLMs) to infer behavioural signals—such as clarity and trust—from expert discourse and to incorporate them into the consensus-building process. However, we acknowledge that the current implementation remains exploratory and serves primarily as a conceptual and methodological proof of principle.

While the proposed framework offers a promising integration of behavioural modelling and decision theory, further empirical validation is required to confirm its applicability across diverse real-world contexts. In particular, systematic evaluations, comparative benchmarks, and real-user deployments will be necessary to substantiate the benefits suggested by this preliminary study.

An important limitation of the current framework lies in the potential bias of the LLM-based sentiment analysis. Since large language models are trained on data that may reflect cultural, linguistic, or social biases, the clarity and trust scores assigned to expert comments could be influenced by stylistic or regional variations. While we implemented prompt standardisation and score normalisation to reduce variance, further work is needed to ensure fairness and robustness across diverse populations. Future extensions of this method should incorporate bias detection protocols, multilingual fairness benchmarks, and culturally adaptive calibration strategies to enhance the reliability of behavioural assessments.

This integration of behavioural modelling with decision theory opens promising avenues for further inquiry. Notably, future work could focus on constructing a standardised cross-domain behavioural corpus enriched through LLM-based annotation, which would serve as a benchmark for evaluating interpersonal dynamics in deliberative contexts. Such a resource would enhance the generalizability of behavioural GDM models and support the development of more ethically grounded, socially aware decision-support systems.