An Explainable Machine Learning Approach for IoT-Supported Shaft Power Estimation and Performance Analysis for Marine Vessels
Abstract
1. Introduction
1.1. Problem Statement—Motivation
1.2. Literature Review
| Research Topic | Methods | Number of Vessels | Dataset Timespan | Vessel Types | Citation |
|---|---|---|---|---|---|
| Power Prediction | NL-PCR, NL-PLSR, ANN | 2 | [6] | ||
| XGBoost, ANN, SVR | Chemical tanker, PCTC vessel | [7] | |||
| LR, DT, KNN, ANN, RF | 5 | Container ships (8700 TEU capacity) | [8] | ||
| SVR | 1 | 7 months | Bulk cargo ship (200,000 tons) | [9] | |
| ANN | 2 | 8 years | Car-carrying vessels | [10] | |
| LR | [11] | ||||
| ENN, ANN | [12] | ||||
| ANN | [13] | ||||
| MLR, DT, KNN, ANN, RF | [8] | ||||
| RNN, CNN | 719 days | [14] | |||
| MLP, CNN | [16] | ||||
| RF | 16 months | general cargo ship | [15] | ||
| Fuel Consumption | White, Black, Gray Box Models | 1 | Handymax chemical/product tanker | [17] | |
| ANN | 1 | Pogoria ship | [18] | ||
| LASSO | 97 | 3.5 years | Container ships | [19] | |
| MLR | bulk carriers | [20] | |||
| HR, LGBM | [21] | ||||
| MLR, RR, LASSO, SVR | [22] | ||||
| ANN, GPR | [23] | ||||
| ANN, MLR | 6 months | 13,000 TEU class container | [24] | ||
| ANN | [25] | ||||
| SVR, RF, ET, ANN | [26] | ||||
| Resistance Prediction | RT, SVR, ANN | Three types of Sailboats | [27] | ||
| ANN | [28] | ||||
| Speed Prediction | LR, RT GP, SVR | 1 | Domestic ferry (“M/S Smyril”) | [29] | |
| Deep Learning models | 2 | 1.5 years | Handymax chemical/product tankers | [30] | |
| Emissions’ Prediction | ANN | 1 | 6 days | Harbour vessel | [31] |
| Path Planning | A* Algorithm | [32] | |||
| Event Detection | ANN | [33] | |||
| Monitoring | GB, RF, ANN, LR | [34] | |||
| RF, KNN, ET, GBM, LR, SVM | Various vessels | [37] | |||
| Ridge, LASSO | 1 | Ferry vessel | [35] | ||
| SVM | [36] |
1.3. Contribution
- Development of a data-driven framework: Leveraging 36 months of sensor data from nine (9) Very Large Crude Carriers (VLCCs), the study develops and evaluates a comprehensive machine learning framework for shaft power prediction.
- Comparison of diverse ML models: Multiple models—including k-NN, SVM, Decision Trees, Random Forest, XGBoost, LightGBM, and neural networks—are rigorously compared using , standard deviation, and confidence intervals.
- Integration of Explainable AI: SHapley Additive exPlanations (SHAP) are employed to interpret model predictions, identifying the key features.
2. Methods and Materials
2.1. Dataset Description
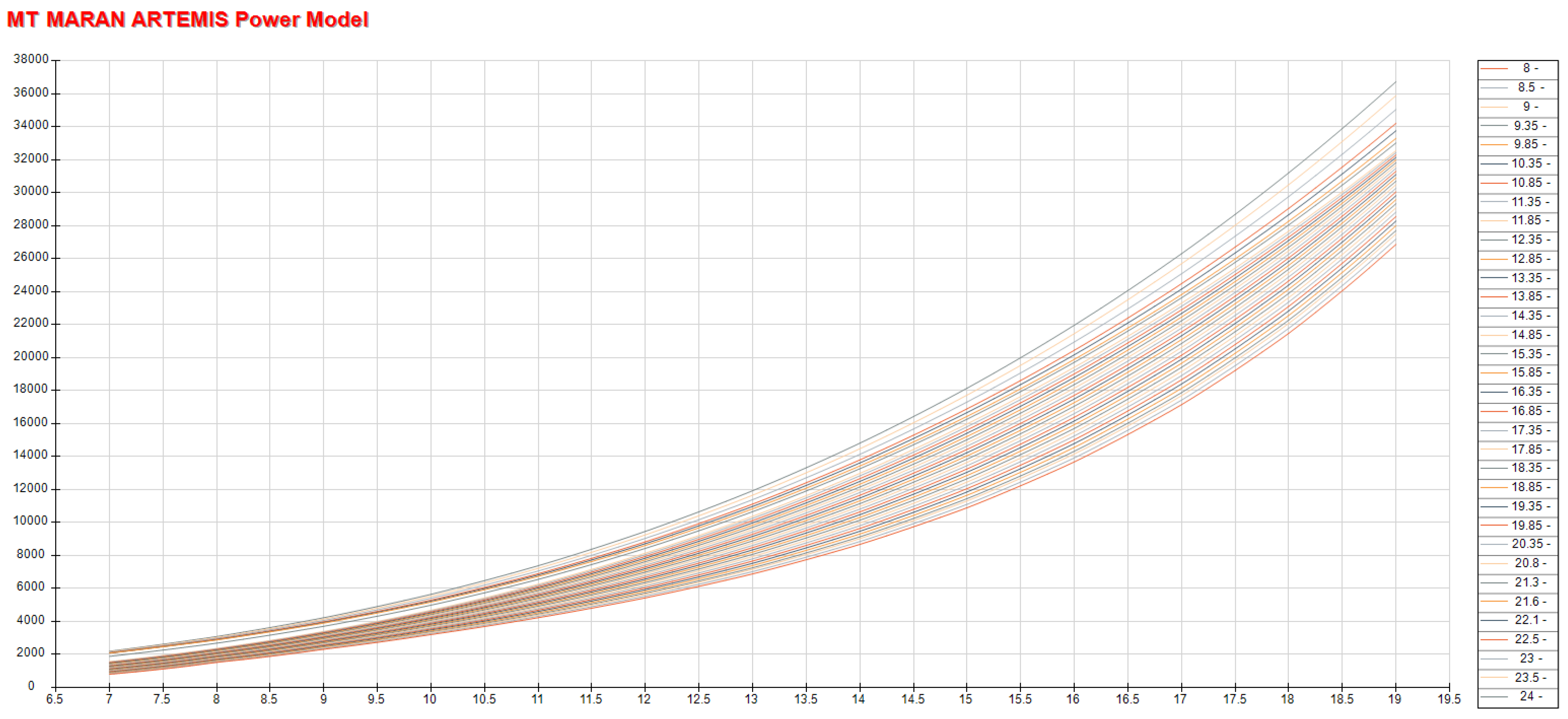
2.2. Baseline Ship Performance Model
2.3. Mathematical Formulation
2.4. Statistical Machine Learning Models and SHAP Method
2.4.1. The knn
2.4.2. Support Vector Machines
- The Gaussian kernel which is defined as .
- The polynomial kernels which are defined as .
- The sigmoid kernel which is defined as .
2.4.3. Neural Networks
2.4.4. Decision Trees (DTs)
2.4.5. Random Forest
2.4.6. XGBoost and LightGBM
2.4.7. SHapley Additive exPlanations
2.5. The Hyperparameter Combinations
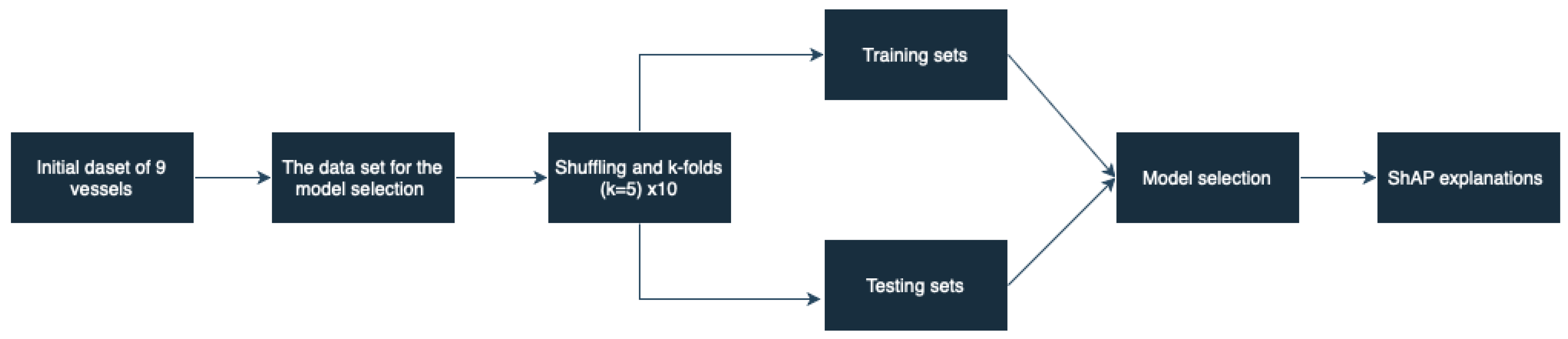
2.6. Methodological Workflow
3. Results
3.1. Model Selection Results
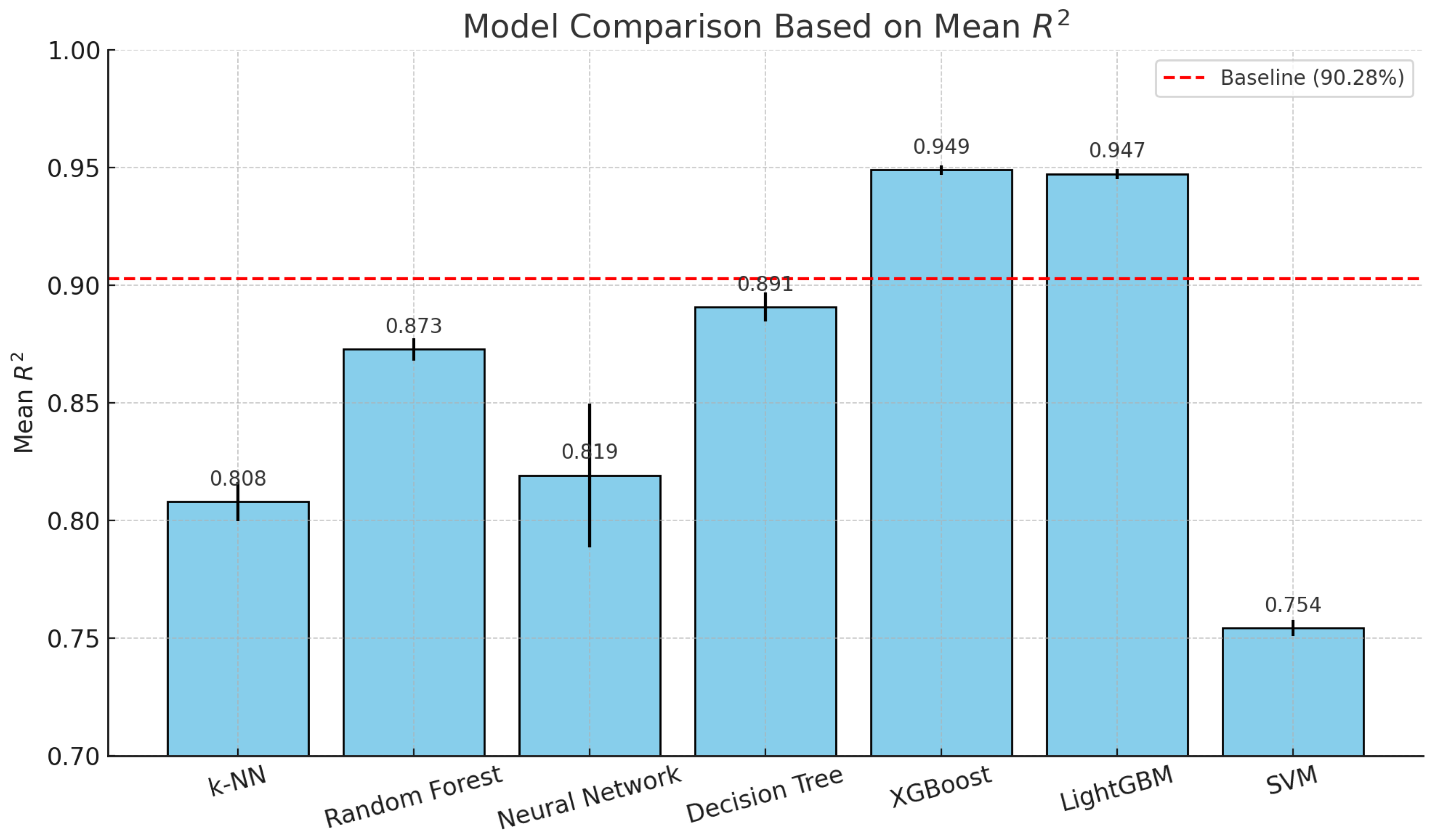
- k-NN achieved a mean of 0.8081, which is lower than the baseline.
- Random Forest achieved a mean of 0.8728, which is lower than the baseline.
- Neural networks achieved a mean of 0.8193, which is lower than the baseline.
- Decision Tree achieved a mean of 0.8909, which is slightly lower than the baseline.
- XGBoost achieved a mean of 0.9490, which is higher than the baseline, indicating better performance.
- LightGBM achieved a mean of 0.9474, which is also higher than the baseline, indicating better performance.
- SVM achieved a mean of 0.7544, which is lower than the baseline.
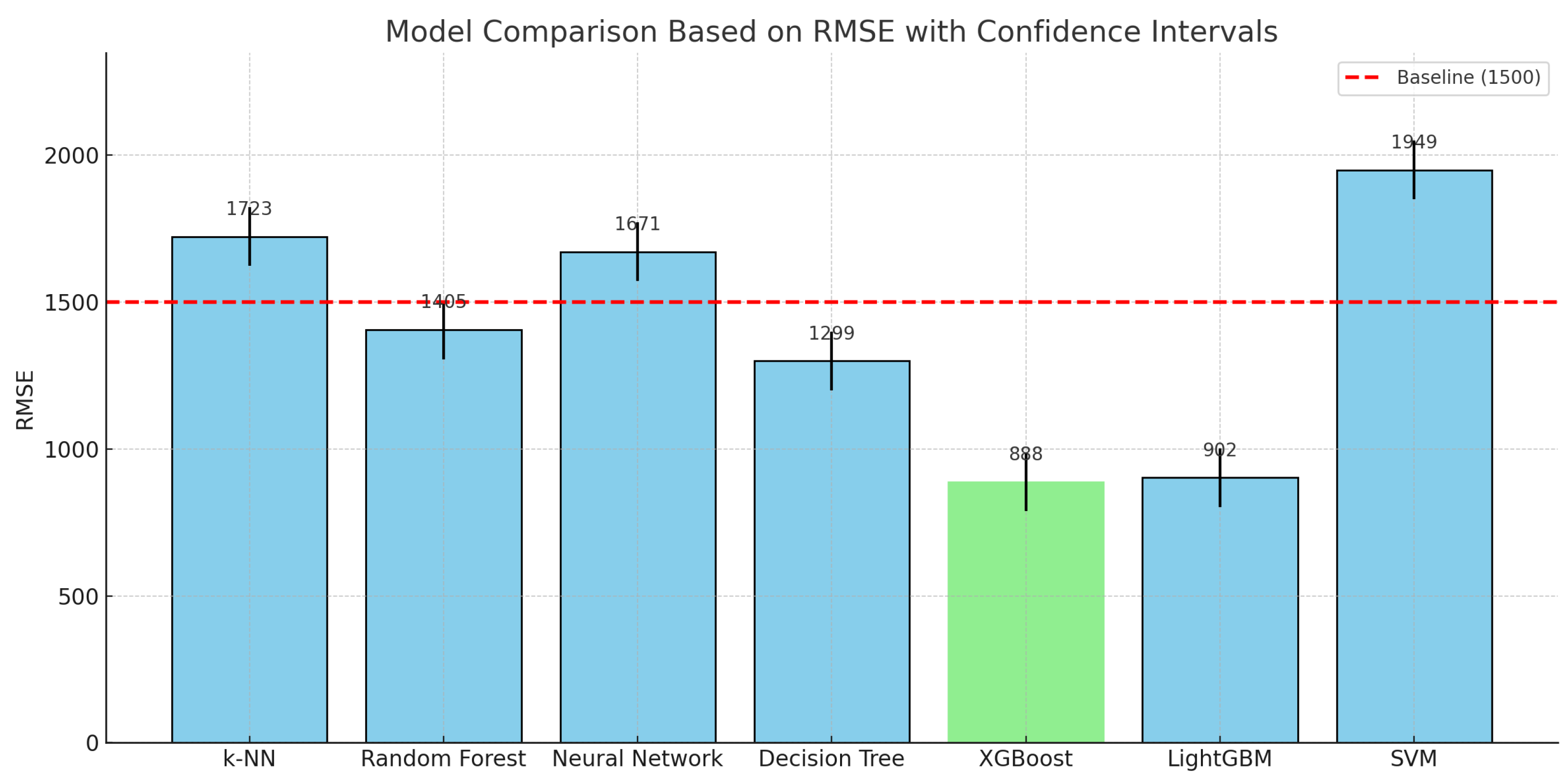
- XGBoost achieved the lowest RMSE of 888.30, indicating the highest accuracy in absolute prediction error.
- LightGBM closely followed with an RMSE of 902.17, also showing excellent performance.
- Decision Tree achieved an RMSE of 1299.57, outperforming more complex models like k-NN and neural networks.
- Random Forest achieved a high RMSE of 1405.59.
- Neural networks and k-NN showed higher RMSE values of 1671.12 and 1723.41, respectively.
- SVM had the highest RMSE of 1949.73, indicating the weakest performance in this context.
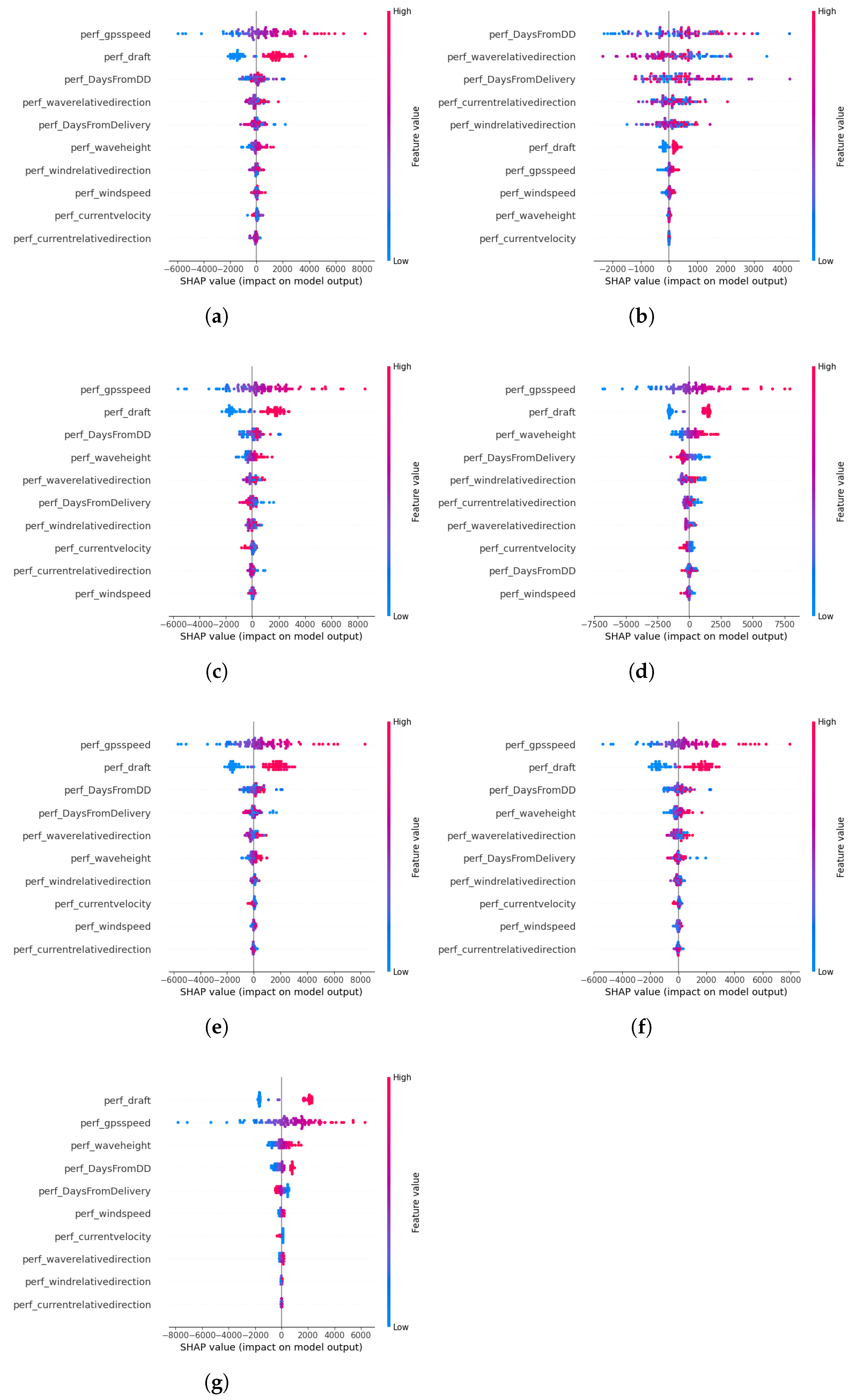
3.2. SHAP Explanations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CNN | Convolutional Neural Network |
| DT | Decision Tree |
| ENN | Ensemble Neural Network |
| ET | Extra Tree |
| GPR | Gaussian Process Regression |
| GTBM | Gradient Tree Boosting Machine |
| IoT | Internet of Things |
| knn | K Nearest Neighbours |
| LGBM | Light Gradient Boosting Machine |
| LR | Linear Regression |
| MLP | Multi-layer Perceptron |
| MLR | Multiple Linear Regression |
| NL-PCR | non-linear Principal Component Regression |
| NL-PLSR | non-linear Partial Least Squares Regression |
| NOAA | National Oceanic and Atmospheric Administration |
| RF | Random Forest |
| RNN | Recurrent Neural Network |
| RR | Ridge Regression |
| RT | Regression Tree |
| SGDs | Sustainable Development Goals |
| SHAP | SHapley Additive exPlanations |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| VLCCs | Very Large Crude Carriers |
References
- Lee, B.X.; Kjaerulf, F.; Turner, S.; Cohen, L.; Donnelly, P.D.; Muggah, R.; Davis, R.; Realini, A.; Kieselbach, B.; MacGregor, L.S.; et al. Transforming Our World: Implementing the 2030 Agenda Through Sustainable Development Goal Indicators. J. Public Health Policy 2016, 37, 13–31. [Google Scholar] [CrossRef]
- Wang, X.; Yuen, K.F.; Wong, Y.D.; Li, K.X. How can the maritime industry meet Sustainable Development Goals? An analysis of sustainability reports from the social entrepreneurship perspective. Transp. Res. Part D Transp. Environ. 2020, 78, 102173. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Vujanović, M. Greenhouse gas emissions reduction potential by using antifouling coatings in a maritime transport industry. J. Clean. Prod. 2021, 295, 126428. [Google Scholar] [CrossRef]
- Huang, J.; Duan, X. A comprehensive review of emission reduction technologies for marine transportation. J. Renew. Sustain. Energy 2023, 15, 032702. [Google Scholar] [CrossRef]
- Morobé, C. 3 Examples of How Improved Ship Performance Modelling Can Save Fuel. White Paper, Torqua AI, 2022. Available online: https://toqua.ai/whitepapers/3-examples-of-how-improved-ship-performance-modelling-can-save-fuel (accessed on 1 June 2025).
- Gupta, P.; Rasheed, A.; Steen, S. Ship performance monitoring using machine-learning. Ocean Eng. 2022, 254, 111094. [Google Scholar] [CrossRef]
- Lang, X.; Wu, D.; Mao, W. Comparison of supervised machine learning methods to predict ship propulsion power at sea. Ocean Eng. 2022, 245, 110387. [Google Scholar] [CrossRef]
- Laurie, A.; Anderlini, E.; Dietz, J.; Thomas, G. Machine learning for shaft power prediction and analysis of fouling related performance deterioration. Ocean Eng. 2021, 234, 108886. [Google Scholar] [CrossRef]
- Kim, D.; Lee, S.; Lee, J. Data-Driven Prediction of Vessel Propulsion Power Using Support Vector Regression with Onboard Measurement and Ocean Data. Sensors 2020, 20, 1588. [Google Scholar] [CrossRef]
- Kriezis, A.C.; Sapsis, T.; Chryssostomidis, C. Predicting Ship Power Using Machine Learning Methods. In Proceedings of the SNAME Maritime Convention, Houston, TX, USA, 29 September 2022; p. D031S017R005. [Google Scholar] [CrossRef]
- Kim, H.S.; Roh, M.I. Interpretable, data-driven models for predicting shaft power, fuel consumption, and speed considering the effects of hull fouling and weather conditions. Int. J. Nav. Archit. Ocean Eng. 2024, 16, 100592. [Google Scholar] [CrossRef]
- Radonjic, A.; Vukadinovic, K. Application of ensemble neural networks to prediction of towboat shaft power. J. Mar. Sci. Technol. 2015, 20, 64–80. [Google Scholar] [CrossRef]
- Parkes, A.; Sobey, A.; Hudson, D. Physics-based shaft power prediction for large merchant ships using neural networks. Ocean Eng. 2018, 166, 92–104. [Google Scholar] [CrossRef]
- Sun, L.; Liu, T.; Xie, Y.; Zhang, D.; Xia, X. Real-time power prediction approach for turbine using deep learning techniques. Energy 2021, 233, 121130. [Google Scholar] [CrossRef]
- Kim, D.; Handayani, M.P.; Lee, S.; Lee, J. Feature Attribution Analysis to Quantify the Impact of Oceanographic and Maneuverability Factors on Vessel Shaft Power Using Explainable Tree-Based Model. Sensors 2023, 23, 1072. [Google Scholar] [CrossRef]
- Kim, Y.C.; Kim, K.S.; Yeon, S.; Lee, Y.Y.; Kim, G.D.; Kim, M. Power Prediction Method for Ships Using Data Regression Models. J. Mar. Sci. Eng. 2023, 11, 1961. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Baldi, F.; Anguita, D. Vessels fuel consumption forecast and trim optimisation: A data analytics perspective. Ocean Eng. 2017, 130, 351–370. [Google Scholar] [CrossRef]
- Tarelko, W.; Rudzki, K. Applying artificial neural networks for modelling ship speed and fuel consumption. Neural Comput. Appl. 2020, 32, 17379–17395. [Google Scholar] [CrossRef]
- Wang, S.; Ji, B.; Zhao, J.; Liu, W.; Xu, T. Predicting ship fuel consumption based on LASSO regression. Transp. Res. Part D Transp. Environ. 2018, 65, 817–824. [Google Scholar] [CrossRef]
- Hajli, K.; Rönnqvist, M.; Dadouchi, C.; Audy, J.F.; Cordeau, J.F.; Warya, G.; Ngo, T. A fuel consumption prediction model for ships based on historical voyages and meteorological data. J. Mar. Eng. Technol. 2024, 23, 439–450. [Google Scholar] [CrossRef]
- Le, T.T.; Sharma, P.; Pham, N.D.K.; Le, D.T.N.; Van Vang Le, S.M.O.; Rowinski, L.; Tran, V.D. Development of comprehensive models for precise prognostics of ship fuel consumption. J. Mar. Eng. Technol. 2024, 23, 451–465. [Google Scholar] [CrossRef]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine learning approach to ship fuel consumption: A case of container vessel. Transp. Res. Part D Transp. Environ. 2020, 84, 102389. [Google Scholar] [CrossRef]
- Hu, Z.; Jin, Y.; Hu, Q.; Sen, S.; Zhou, T.; Osman, M.T. Prediction of fuel consumption for enroute ship based on machine learning. IEEE Access 2019, 7, 119497–119505. [Google Scholar] [CrossRef]
- Kim, Y.R.; Jung, M.; Park, J.B. Development of a fuel consumption prediction model based on machine learning using ship in-service data. J. Mar. Sci. Eng. 2021, 9, 137. [Google Scholar] [CrossRef]
- Moreira, L.; Vettor, R.; Guedes Soares, C. Neural network approach for predicting ship speed and fuel consumption. J. Mar. Sci. Eng. 2021, 9, 119. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I.; Theotokatos, G. Machine learning models for predicting ship main engine Fuel Oil Consumption: A comparative study. Ocean Eng. 2019, 188, 106282. [Google Scholar] [CrossRef]
- Fahrnholz, S.F.; Caprace, J.D. A machine learning approach to improve sailboat resistance prediction. Ocean Eng. 2022, 257, 111642. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, M.; Zhou, L.; Garme, K.; Burman, M. A machine learning-based method for prediction of ship performance in ice: Part I. ice resistance. Mar. Struct. 2022, 83, 103181. [Google Scholar] [CrossRef]
- Bassam, A.M.; Phillips, A.B.; Turnock, S.R.; Wilson, P.A. Ship speed prediction based on machine learning for efficient shipping operation. Ocean Eng. 2022, 245, 110449. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Baldi, F.; Cipollini, F.; Atlar, M.; Savio, S. Data-driven ship digital twin for estimating the speed loss caused by the marine fouling. Ocean Eng. 2019, 186, 106063. [Google Scholar] [CrossRef]
- Chen, Z.S.; Lam, J.S.L.; Xiao, Z. Prediction of harbour vessel emissions based on machine learning approach. Transp. Res. Part D Transp. Environ. 2024, 131, 104214. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Zissis, D.; Xidias, E.K.; Lekkas, D. A cloud based architecture capable of perceiving and predicting multiple vessel behaviour. Appl. Soft Comput. 2015, 35, 652–661. [Google Scholar] [CrossRef]
- Aizpurua, J.I.; Knutsen, K.E.; Heimdal, M.; Vanem, E. Integrated machine learning and probabilistic degradation approach for vessel electric motor prognostics. Ocean Eng. 2023, 275, 114153. [Google Scholar] [CrossRef]
- Soner, O.; Akyuz, E.; Celik, M. Statistical modelling of ship operational performance monitoring problem. J. Mar. Sci. Technol. 2019, 24, 543–552. [Google Scholar] [CrossRef]
- Lee, Y.E.; Kim, B.K.; Bae, J.H.; Kim, K.C. Misalignment detection of a rotating machine shaft using a support vector machine learning algorithm. Int. J. Precis. Eng. Manuf. 2021, 22, 409–416. [Google Scholar] [CrossRef]
- Panagiotakopoulos, T.; Filippopoulos, I.; Filippopoulos, C.; Filippopoulos, E.; Lajic, Z.; Violaris, A.; Chytas, S.P.; Kiouvrekis, Y. Vessel’s trim optimization using IoT data and machine learning models. In Proceedings of the 2022 13th International Conference on Information, Intelligence, Systems and Applications (IISA), Rhodes, Greece, 18–20 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Filippopoulos, I.; Stamoulis, G. Collecting and using vessel’s live data from on board equipment using “Internet of Vessels (IoV) platform” (May 2017). In Proceedings of the 2017 South Eastern European Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Rhodes, Greece, 24–26 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Filippopoulos, I.; Stamoulis, G.; Sovolakis, I. Transferring Structured Data and applying business processes in remote Vessel’s environments using the “InfoNet” Platform. In Proceedings of the 2018 South-Eastern European Design Automation, Computer Engineering, Computer Networks and Society Media Conference (SEEDA-CECNSM), Rhodes, Greece, 24–26 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Filippopoulos, I.; Panagiotakopoulos, T.; Skiadas, C.; Triantafyllou, S.M.; Violaris, A.; Kiouvrekis, Y. Live Vessels’ Monitoring using Geographic Information and Internet of Things. In Proceedings of the 13th International Conference on Information, Intelligence, Systems and Applications, IISA 2022, Corfy, Greece, 18–20 July 2022. [Google Scholar]
- Kreitner, J. Heave, pitch, and resistance of ships in a seaway. Trans. R. Inst. Nav. Archit. 1939, 87. [Google Scholar]
- ISO 15016:2015; Ships and Marine Technology—Guidelines for the Assessment of Speed and Power Performance by Analysis of Speed Trial Data. The International Organization for Standardization: Geneva, Switzerland, 2015. Available online: https://www.iso.org/standard/61902.html (accessed on 1 June 2025).
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, New York, NY, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
| Measured Feature | Unit of Measurement | |
|---|---|---|
| Operational Conditions | GPS Speed | knots |
| Draft | meters | |
| Days from Delivery | days | |
| Days from Dry Dock | days | |
| Environmental Conditions | Wave Height | meters |
| Wave Relative Direction | degrees | |
| Wind Speed | knots | |
| Wind Relative Direction | degrees | |
| Current Velocity | meters per second | |
| Current Relative Direction | degrees | |
| Sea Temperature | Celsius | |
| Sea Depth | meters | |
| Target Variable | Shaft Power | kilo watts |
| Model | Hyperparameters |
|---|---|
| Neural Networks (NNs) | - Activation: tanh, ReLU - Hidden layer size: 5, 10, 20, 50 - Learning rate: 0.01, 0.1, 0.2 - Solver: adam |
| Random Forests (RF) | - Number of estimators: 50, 100, 200 - Criterion: squared error, absolute error and Friedman MSE - Max depth: 10 |
| k-Nearest Neighbors (KNN) | - p: 1, 1.5, 2, 3 - Number of neighbours: 5, 10, 25, 50, 100, 150 - Weights: uniform, distance |
| XGBoost | - Lambda: 1, 10 - Number of estimators: 100, 300, 500 - Learning rate: 0.01, 0.05 - Max depth: 5, 10, 20 |
| LightGBM | - Number of leaves: 31, 50, 100 - Number of estimators: 100, 300, 500 - Learning rate: 0.01, 0.1, 0.2 - Max depth: 5, 10, 20 |
| Support Vector Machines (SVMs) | - Kernel: linear - C: 0.1, 1 - Epsilon: 0.01, 0.1 |
| Decision Trees (DTs) | - Min samples: 2, 5, 10, 20, 50 |
| Model | Mean | Std. Dev. | 95% CI |
|---|---|---|---|
| k-NN | 0.8081 | 0.0041 | [0.8074, 0.8089] |
| Random Forest | 0.8728 | 0.0024 | [0.87275, 0.87285] |
| Neural Network | 0.8193 | 0.0153 | [0.8190, 0.8196] |
| Decision Tree | 0.8909 | 0.0031 | [0.8905, 0.8912] |
| XGBoost | 0.9490 | 0.00093 | [0.9488, 0.9492] |
| LightGBM | 0.9474 | 0.0011 | [0.9469, 0.9478] |
| SVM | 0.7544 | 0.0017 | [0.7541, 0.7547] |
| Model | RMSE | |
|---|---|---|
| k-NN | 0.8081 | 1723.41291 |
| RF | 0.8728 | 1405.59474 |
| NN | 0.8193 | 1671.11765 |
| DT | 0.8909 | 1299.57351 |
| XGBoost | 0.9490 | 888.29617 |
| LightGBM | 0.9474 | 902.16747 |
| SVM | 0.7544 | 1949.72586 |
| Model | Train (s) | Test (s) |
|---|---|---|
| k-NN | 0.1394 | 0.4714 |
| RF | 9.4640 | 0.0818 |
| NN | 24.0860 | 0.0656 |
| DT | 1.1772 | 0.0068 |
| XGBoost | 49.5807 | 0.2582 |
| LightGBM | 0.1927 | 0.0200 |
| SVM | 3642.6518 | 39.0189 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiouvrekis, Y.; Gkirtzou, K.; Zikas, S.; Kalatzis, D.; Panagiotakopoulos, T.; Lajic, Z.; Papathanasiou, D.; Filippopoulos, I. An Explainable Machine Learning Approach for IoT-Supported Shaft Power Estimation and Performance Analysis for Marine Vessels. Future Internet 2025, 17, 264. https://doi.org/10.3390/fi17060264
Kiouvrekis Y, Gkirtzou K, Zikas S, Kalatzis D, Panagiotakopoulos T, Lajic Z, Papathanasiou D, Filippopoulos I. An Explainable Machine Learning Approach for IoT-Supported Shaft Power Estimation and Performance Analysis for Marine Vessels. Future Internet. 2025; 17(6):264. https://doi.org/10.3390/fi17060264
Chicago/Turabian StyleKiouvrekis, Yiannis, Katerina Gkirtzou, Sotiris Zikas, Dimitris Kalatzis, Theodor Panagiotakopoulos, Zoran Lajic, Dimitris Papathanasiou, and Ioannis Filippopoulos. 2025. "An Explainable Machine Learning Approach for IoT-Supported Shaft Power Estimation and Performance Analysis for Marine Vessels" Future Internet 17, no. 6: 264. https://doi.org/10.3390/fi17060264
APA StyleKiouvrekis, Y., Gkirtzou, K., Zikas, S., Kalatzis, D., Panagiotakopoulos, T., Lajic, Z., Papathanasiou, D., & Filippopoulos, I. (2025). An Explainable Machine Learning Approach for IoT-Supported Shaft Power Estimation and Performance Analysis for Marine Vessels. Future Internet, 17(6), 264. https://doi.org/10.3390/fi17060264







