Exact and Approximation Algorithms for Task Offloading with Service Caching and Dependency in Mobile Edge Computing

Abstract

With the continuous development of the Internet of Things (IoT) and communication technologies, the demand for low latency in practical applications is becoming increasingly significant. Mobile edge computing, as a promising computational model, is receiving growing attention. However, most existing studies fail to consider two critical factors: task dependency and service caching. Additionally, the majority of proposed solutions are not related to the optimal solution. We investigate the task offloading problem in mobile edge computing. Considering the requirements of applications for service caching and task dependency, we define an optimization problem to minimize the delay under the constraint of maximum completion cost and present a $(1+ϵ)$-approximation algorithm and an exact algorithm. Specifically, the offloading scheme is determined based on the relationships between tasks as well as the cost and delay incurred by data transmission and task execution. Simulation results demonstrate that in all cases, the offloading schemes obtained by our algorithm consistently outperform other algorithms. Moreover, the approximation ratio to the optimal solution from the approximation algorithm is validated to be less than $(1+ϵ)$, and the exact algorithm consistently produces the optimal solution.

1. Introduction

Although the CPU of mobile devices is constantly being updated and iterated, and their computational capabilities are gradually improving, the processing power of mobile devices still appears to be insufficient, especially when compared to the explosive growth of data. This is due to limitations such as battery capacity and computational resources. With the continuous development of the Internet of Things (IoT) and communication technologies, there are an increasing number of computationally intensive and latency-sensitive applications, like image processing and machine learning, or those requiring real-time processing, such as augmented reality (AR) and autonomous driving, which are particularly challenging for mobile devices to handle [1,2]. Although cloud servers have powerful processing capabilities, running resource-intensive applications requires significant time for data transmission, resulting in unpredictable communication delays [3,4,5]. The emergence of mobile edge computing (MEC) addresses the shortcomings of both cloud and mobile devices, offering great potential in solving the task offloading problem [6,7,8,9,10].

Although [11,12,13,14] propose new computational models in MEC, it still faces numerous challenges. Taking object and pose recognition as an example, a typical object and pose recognition application requires several steps: feature extraction, object model matching, pose estimation, clustering, and classification [15]. When devising offloading strategies for these tasks, there are two factors that we need to consider.

The first factor is whether the device has cached the necessary services for task execution. This is one of the key issues in the development of future 6G technology [16,17]. Service caching not only enhances network reliability, adaptability, and bandwidth utilization, but also, by caching the required services on the execution node, effectively supports offloading strategies, thereby improving the performance of the algorithm [18]. However, most research on service caching focuses on the issue of service placement [2,19,20], which incurs higher costs and time compared to task transmission and execution [20]. For instance, a machine learning model requires a large amount of data for training, and if we wanted to migrate this service to another execution node, it would take a considerable amount of time. This is not desirable for delay-sensitive applications. Therefore, like in [10], we assume that the service is already placed on the execution node. We focus on the impact of service caching on the offloading strategy.

The second factor is whether there is dependency among tasks. For instance, the pose estimation task can only be executed after the object model matching task. Each subtask requires the result of its parent task to continue execution, and different offloading strategies directly affect real-time performance. Traditional coarse-grained scheduling only considers operations at the application level [21], which makes it unable to address the complex and diverse demands of current applications. Although most current studies take this into account, they either rank subtasks based on delay constraints and execute each subtask sequentially [22,23,24,25], or use heuristic algorithms to solve such problems [26,27,28,29]. This results in certain limitations and makes it difficult to ensure performance guarantees.

Therefore, service caching and task dependency both impact the performance and feasibility of offloading strategies. When considering task offloading, if service caching is considered without considering the dependency between tasks, the offloading strategy may fail to execute [10]. Conversely, if only task dependency is considered, significant time may be spent caching services for the offloading strategy, which affects the performance of the algorithm. Meanwhile, both service caching and task dependency significantly influence the integration of MEC and future 6G technologies. Considering service caching leverages the user-proximity feature of MEC to meet the high-bandwidth, high-data-rate, and low-latency requirements of 6G, thereby promoting the convergence of communication, computation, and caching (3C) [16]. On the other hand, incorporating task dependency facilitates the integration of AI technologies, such as object and pose recognition applications, with MEC, further enhancing the role and applicability of MEC in the 6G era [17]. Although many current studies take both factors into account, their approaches are either based on deep learning or solved through heuristic algorithms [10,19,30,31], which cannot guarantee that the offloading strategy obtained is the optimal solution or close to the optimal solution, and they lack strong performance guarantees.

To overcome these constraints, effectively solve the offloading problem, and ensure the optimality of the offloading schemes, we propose both a polynomial-time approximation algorithm and an exact algorithm. These algorithms are improved based on dynamic programming (DP) and the Bellman–Ford algorithm, respectively. We summarize the main contributions as follows.

• We define the delay-minimization problem under task dependency, service caching, and the maximum completion cost constraint, and prove its NP-hardness. Due to dependency, the delay and cost of task offloading are related to all the predecessor nodes. However, many existing studies fail to take this into account, which is of practical importance for delay-sensitive applications.
• We then propose a $(1+ϵ)$-approximation algorithm to solve the aforementioned problem, and derive its time complexity as $O(d_{in}{N}^{\prime }{M^{\prime }}^2{\displaystyle \frac{L}{ϵ}}(\log \log (UB/LB)+1))$, where L denotes the depth of the task graph, $d_{in}$ denotes the maximum indegree of the task graph, $M^{\prime }$ is the number of execution devices, $N^{\prime }$ is the number of tasks, and $LB$ and $UB$ represent the lower and upper bounds of the delay, respectively. In this paper, our approximation algorithm enables each task to make its offloading decision based on local information during execution, without the need to consider global decisions. Moreover, it provides worst-case performance guarantees, which aligns well with the characteristics of the distributed structure of MEC.
• We propose an exact algorithm that can obtain the optimal solution to the aforementioned problem. Although its time complexity is theoretically exponential, in practice, the running time is much smaller than the theoretical value when solving real-world problems.
• We finally evaluate the proposed algorithm using a random task model and a real task model, then compare it with the FixDoc algorithm [19], the Hermes algorithm [32], and a brute force algorithm. The simulation results validate the approximation ratio $(1+ϵ)$ and the superiority of the obtained offloading scheme of our algorithm over the other algorithms.

The rest of this paper is organized as follows. Section 2 summarizes the related work. In Section 3, we model the problem and prove its complexity. Section 4 presents the polynomial-time approximation algorithm. Section 5 introduces the exact algorithm. In Section 6, we conduct experiments and discuss the proposed algorithms. Finally, Section 7 concludes the paper.

2. Related Works

An increasing number of applications require low latency and low costs, such as autonomous driving, facial recognition, and AR. MEC, as a new computing model, is gaining more and more attention.

Yang et al. [11] combined an intelligent reflecting surface (IRS) with the MEC model and considered an IRS-aided multi-device MEC system, where each IoT device follows a binary offloading policy to minimize the total energy consumption of the IoT devices. Liu et al. [12] proposed a novel STAR-RIS-assisted MEC system that extends the coverage range of wireless access points (APs) from half-space to full-space. Chen et al. [13] discussed the problem of computational task offloading and resource allocation in remote areas lacking ground communication infrastructure through an air–ground integrated MEC system. Qin et al. [14] introduced a new user-centric mobile edge computing (UCMEC) model that addresses the issues of resource allocation imbalance and network interference in traditional MEC architectures. Although the above studies have made improvements to task offloading in traditional MEC systems, they do not consider two crucial constraints in task offloading: task dependency and service caching.

With the increasing complexity of applications, edge servers are constrained by limited resources and cannot cache all task services [2,20]. Research on service caching mainly focuses on the joint optimization of service placement and task offloading. However, compared to task execution and offloading, service placement and updates often incur higher costs and time, negatively affecting system stability [20]. Moreover, due to the uncertainty of tasks and delay sensitivity, offloading schemes may cause congestion at certain execution nodes, significantly impacting the required offloading time [33]. Based on these factors, Farhadi [20] proposed a task offloading scheme that decouples the time scales of task offloading and service deployment. Their method introduces a joint optimization framework for task offloading and service deployment under multiple constraints.

However, the above-mentioned problem does not take into account the dependency between tasks. With the continuous development of applications, the vast majority of applications consist of sets of interdependent tasks, making the offloading of dependent tasks essential [15,19]. Arabnejad et al. [22] addressed the cost minimization problem of dependent tasks under delay constraints in cloud environments. They set sub-delay constraints for each subtask based on the delay constraints and ranked them. Then, a heuristic ProLiS algorithm and a metaheuristic L-ACO algorithm were proposed to solve this problem. Lou et al. [23] applied the aforementioned task ranking method to the MEC environment and proposed a two-stage heuristic algorithm to obtain the cost-minimized offloading scheme. Wang et al. [26] focused on reducing delay and improving resource utilization for dependent tasks. To address this problem, they designed a Nash Equilibrium-based Joint Task Scheduling and Offloading Strategy (N-JSU). Hosny et al. [27] proposed a method based on an Enhanced Genetic Algorithm (EMGA), which considers task dependencies while optimizing multiple objectives. Cai et al. [28] combine the prioritized queue strategy with a joint delay-quality dependence model, then transform the task assignment process into a tree search problem and solve it using a heuristic tree-based algorithm. However, they only consider task dependencies while neglecting service caching, limiting the applicability to real-world applications.

In fact, the tasks of applications now not only need to determine the execution order based on their dependencies, but each subtask also requires specific services to be executed. Therefore, it is crucial to simultaneously consider both factors for task offloading. Liu et al. [19] proposed a DP-based heuristic algorithm targeting task-completion-time minimization. Zhao et al. [10] addressed the limitations of computational resources in mobile devices and proposed a convex optimization-based approach to solve this problem. Zhao et al. [30] proposed a dynamic caching-assisted task offloading scheme (CachOf), which combines collaborative computing of edge servers and dynamic resource allocation strategies. They then applied deep reinforcement learning (DRL) methods to optimize the task offloading strategy. Li et al. [31] proposed a method based on the multi-objective artificial bee colony algorithm (MOTOCP) to maximize cache hit rate and minimize service delay. The method gradually improves the algorithm’s performance by balancing multiple objectives through Pareto optimality. However, the aforementioned methods are either based on deep learning or heuristic algorithms. The former cannot guarantee an offloading solution within polynomial time, while the latter cannot guarantee that each offloading solution obtained will be optimal or near-optimal.

In most practical applications, tasks are often dependent on specific services for execution. Additionally, many tasks require low-latency performance. Due to the distance to the server, transmission delay inevitably tends to be relatively high. In the context of approximate algorithms for wireless networks, Tan et al. [34,35] considered the sum-rate maximization problem by Perron-Frobenius theory. They focused on finding approximately optimal solutions by studying the solutions to two related problems: the signal-to-interference-plus-noise ratio (SINR) approximation power control (SAPC) problem and the max–min weighted SINR problem. For the SAPC problem, the authors proposed an asynchronous iterative algorithm, while for the max–min weighted SINR problem, they developed a fast, two-timescale algorithm and derived a synchronous algorithm. However, the approximation ratio in their work depends on the parameters of the problem instances, and the problem model they consider differs significantly from ours. For the use of approximation algorithms in the task offloading problem, Zhang et al. [36] considered the energy minimization problem under latency constraints with linear task dependency, and proposed the Lagrangian Relaxation Based Aggregated Cost algorithm to obtain both optimal and approximate solutions to the constrained optimization problem. However, unlike our approach, they did not provide a clear approximation ratio. Zhou et al. [37], aiming to jointly optimize the tradeoff between latency and energy in a multi-server MEC system, proposed an approximation algorithm based on the Markov approximation framework to solve the proposed problem. Additionally, Younis et al. [38] introduced an energy–latency-aware task offloading and approximation computation problem. They decomposed the original problem into three subproblems and used duality techniques and convex optimization to obtain an approximate solution. Although both of these studies proposed approximation algorithms to address the task offloading problem, their approximation ratios are dependent on the objective values of the problem. In contrast, by setting the value of $ϵ$, we can guarantee a constant approximation ratio of (1 + $ϵ$) for each case, which provides a better approximation guarantee in our research. To the best of our knowledge, only Hermes [32] has proposed a polynomial-time approximation algorithm to address the delay-minimization problem under a cost constraint. The approximation ratio of this algorithm is also (1 + $ϵ$), which is the same as ours. However, their approach does not take into account constraints related to service caching, which may lead to situations where offloading solutions are not feasible.

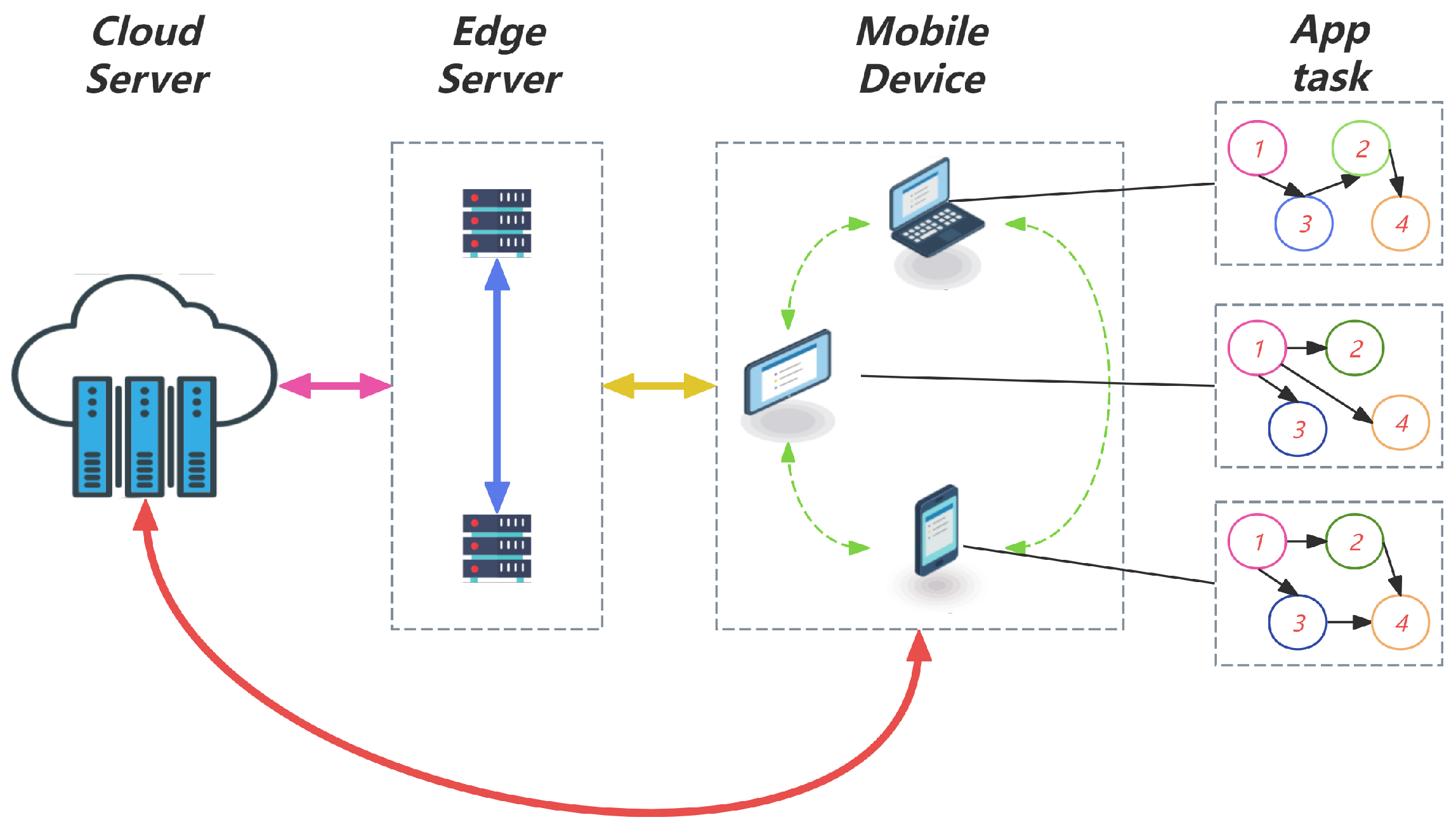
3. System Model and Problem Formulation

3.1. System Model

We consider a model comprising a set of mobile devices, a set of edge nodes, and a cloud node. As shown in Figure 1, each node in every layer can communicate not only with nodes within the same layer but also with any node in other layers. The cloud node possesses robust processing capabilities, featuring minimal processing delay and the capacity to cache all services. However, it incurs higher processing costs and is located at a considerable distance from both mobile devices and edge nodes, resulting in increased transmission delay and cost. In contrast, mobile devices exhibit the lowest processing capabilities among the three entities and are only capable of caching a limited number of services. Nonetheless, mobile devices have the advantage of minimal transmission delay and the lowest transmission costs when communicating with each other. We consider a set of execution nodes, including cloud nodes, edge nodes, and mobile devices. Let $M_v=\{m_1,m_2,\dots ,m_{M^{\prime }}\}$ denote the set of execution nodes that satisfy the service cache requirements for task v.

We consider an application that must be completed within a maximum cost T. The application consists of multiple interdependent tasks, and these dependencies can be modeled as a directed acyclic graph (DAG) $G=(V,E)$, where V represents the set of tasks, and E represents the set of edges used to represent the dependency relationships between tasks. An edge $(i,j)\in E$ indicates that the output data of task i will serve as the input data for task j, meaning task j can only be executed after task i is completed and the data is transmitted. Our delay and cost calculation models are based on [9,19,39]. Next, we provide a detailed introduction to the processing and communication models.

(1) Processing model: We assume that execution node v has cached the services required by task j and can process multiple tasks simultaneously, so the time to process task j on execution node v is solely composed of the computation time. Specifically, the time and cost to process task j on execution node v are

$$T_j^v={\displaystyle \frac{L_j}{f_v}},T_j^v=p_v·T_j^v$$

(1)

respectively, where $L_j=S_j·C_v$ [11] represents the computational workload of task j, with $S_j$ denoting the data size of task j and $C_v$ representing the number of CPU cycles required by execution node v to process 1 bit of data. $f_v$ denotes the CPU frequency of execution node v, where the CPU frequency of servers is generally higher than that of mobile devices. $p_v$ represents the computational cost per unit time for execution node v, which is an approximation in this paper [39].

(2) Communication model: The communication time between execution nodes includes both the task data upload and the result download durations. Following [9], we assume uplink/downlink channel reciprocity and denote the channel gain for transmitting the output data of task i from execution node k to execution node v as the input data of task j by $h_{ij}^{kv}=A_d·{\left({\displaystyle \frac{3\times {10}^8}{4\pi f_c{d}_{kv}}}\right)}^{d_e}$, where $A_d=4.11$ denotes the antenna gain, $f_c=915\mathrm{MHz}$ denotes the carrier frequency, $d_e=26$ denotes the path loss exponent, and $d_{kv}$ denotes the distance between execution nodes k and v. We assume that the channel gain does not change during the transmission of tasks i and j. The uplink and downlink rates for transmitting the output data of task i from execution node k to execution node v as the input data of task j are given by $R_{ij}^{kv}=B·{\log }_2\left(1+{\displaystyle \frac{c{h}_{ij}^{kv}}{{\sigma }^2}}\right)$ and ${\tilde{R}}_{ij}^{kv}=\tilde{B}·{\log }_2\left(1+{\displaystyle \frac{c{h}_{ij}^{kv}}{{\tilde{\sigma }}^2}}\right)$, respectively, where B and $\tilde{B}$ denote uplink and downlink the communication bandwidth, respectively; $c=0.935$ watt denotes the communication cost per unit time, which is an approximation [39,40]; and ${\sigma }^2$ and ${\tilde{\sigma }}^2$ denote uplink and downlink the noise power, respectively. For simplicity, we assume equal noise power without loss of generality. Therefore, the communication time and cost for transmitting the output data of task i from execution node k to execution node v as the input data of task j can be expressed as follows:

$$T_{ij}^{kv}={\displaystyle \frac{O_i}{R_{ij}^{kv}}}+{\displaystyle \frac{I_j}{{\tilde{R}}_{ij}^{kv}}},C_{ij}^{kv}=c·T_{ij}^{kv}$$

(2)

where $O_i$ is the output data of task i and $I_j$ is the input data of task j, since during communication, the output of task i is used as the input for task j, thus $O_i$ = $I_j$.

We assume that an application must begin and end on the same execution node. To satisfy this requirement in task modeling, we insert two virtual nodes (task s and task t) into the directed acyclic graph. These virtual nodes correspond to tasks with zero execution time and cost. Specifically, task s is added to the local device to initiate the application, and task t is added to the local device to collect the results at the end of execution. We use $V^{\prime }$ to represent the task set before the insertion of the virtual nodes. Consequently, the total number of tasks can be expressed as

$$N^{\prime }=\left|V^{\prime }\right|+2.$$

Figure 2 illustrates an example of an offloading scheme that considers both service caching and task dependency, which consists of three execution nodes. Execution node $m_2$ caches the functionality of task 1, and execution node $m_3$ caches the functionalities of tasks 2 and 3. The application task set is initiated by execution node $m_1$. Specifically, virtual nodes are offloaded to $m_1$. However, since neither $m_1$ nor $m_3$ caches the functionality of task 1, task 1 is offloaded to $m_2$. Similarly, tasks 2 and 3 are offloaded to $m_3$. In this example, $m_1$ and $m_2$ represent mobile devices, while $m_3$ represents an edge node. The cloud node is not considered in this case.

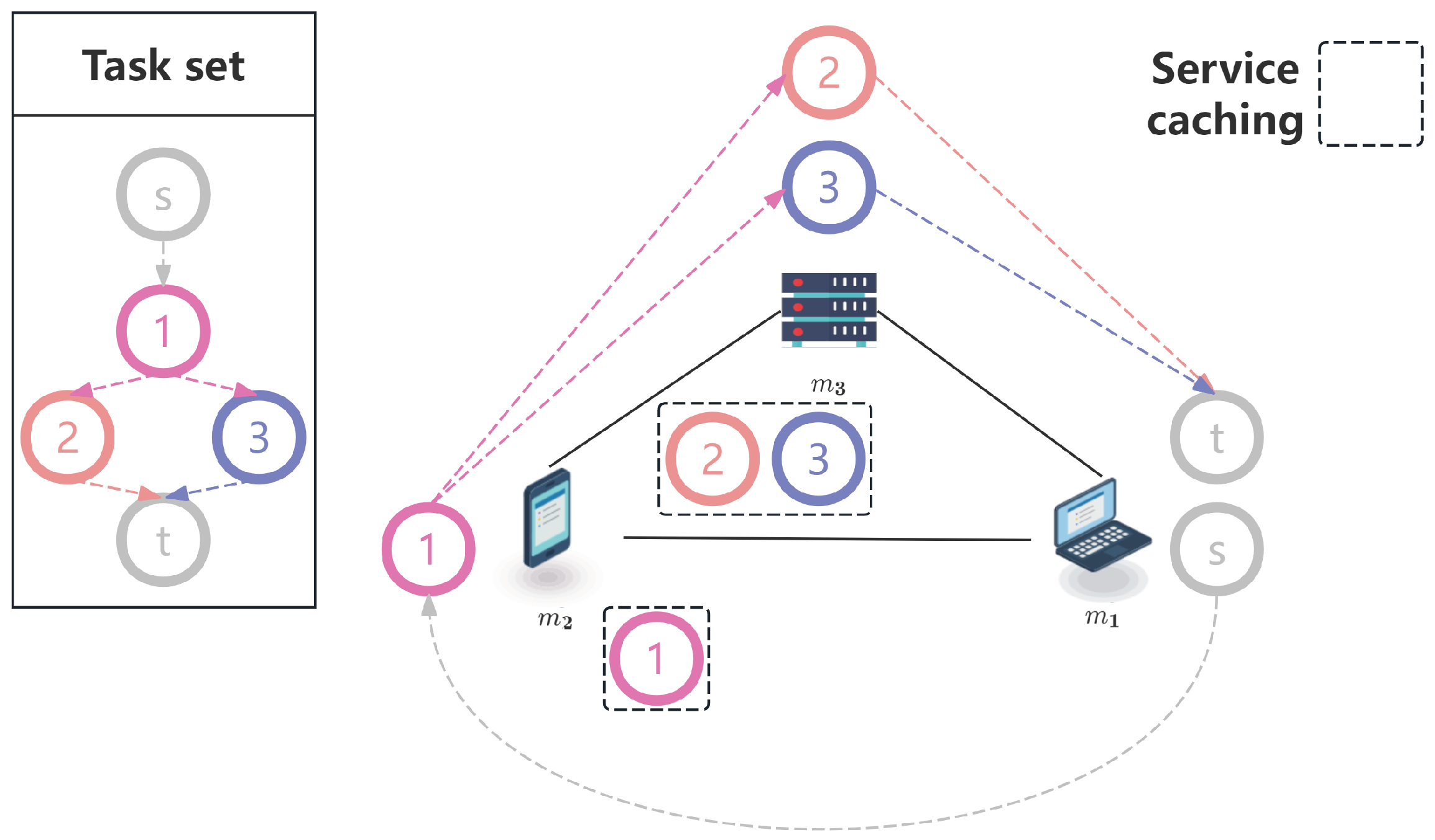
3.2. Problem Formulation

Our objective is to determine a task offloading scheme x that minimizes the total delay while satisfying the cost constraint, considering a network with task dependencies and service caching.

$$C(j,x)=C_j^{x_j}+\sum _{i\in \mathcal{C}\left(j\right)}\left[C(i,x)+C_{ij}^{x_i{x}_j}\right].$$

(3)

$C(j,x)$ represents the cost of completing task j in offloading scheme x. $x_j$ denotes the device selected for offloading task j. The set $C\left(j\right)$ represents the set of predecessor nodes of node j. $C_j^{x_j}$ represents the processing cost incurred by server $x_j$ for handling task j. Additionally, $C_{ij}^{x_i{x}_j}$ denotes the communication cost between server $x_i$, which offloads task i, and server $x_j$, which offloads task j. As described in the above equation, the total cost of completing task j is the sum of the costs of completing all its predecessor tasks, the data transmission cost, and the execution cost of task j.

$$T(j,x)=\underset{i\in \mathcal{C}\left(j\right)}{max}\left[T(i,x)+T_{ij}^{x_i{x}_j}\right]+T_j^{x_j}.$$

(4)

$T(j,x)$ represents the time required to complete task j in offloading scheme x. $T_j^{x_j}$ represents the processing delay incurred by server $x_j$ for handling task j. Additionally, $T_{ij}^{x_i{x}_j}$ denotes the communication delay between server $x_i$, which offloads task i, and server $x_j$, which offloads task j. Task i can only be executed after data has been transmitted from all its predecessor nodes, and its execution time is determined by the slowest predecessor node.

$$P:\underset{x\in {\left[M_v\right]}^V}{min}T\left(V,x\right)$$

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.C(N^{\prime },x)& \le T,\hfill \\ \hfill |x_i|-|x_j|& \ge 0,\forall x_i,x_j\in x,\forall (i,j)\in E\hfill \end{array}$$

In this context, $C(N^{\prime },x)$ and $T(V,x)$ are defined in (3) and (4), respectively. Here, $M_v=\{m_1,m_2,\dots ,m_{M^{\prime }}\}$ denote the set of execution nodes that satisfy the service cache requirements for task v, V represents the set of all tasks, $N^{\prime }$ denotes the last task in the sequence, and T represents the cost constraint. The first constraint indicates that the cost incurred when completing the virtual task t should not exceed the cost limit. The second constraint ensures that the successor tasks can only be offloaded once the predecessor tasks have been completed.

Theorem 1. 

P is NP-hard.

Proof. 

In a serial task graph where service caching and data transmission are not considered, we transform the binary partition problem of P into a 0–1 knapsack problem. Since the 0–1 knapsack problem is NP-hard, problem P is at least NP-hard as well [32].

We rewrite a special case of the original problem P as problem $P^{\prime }$, where $C_i^0=0$. $C_i^1$ and $T_i^1$ represent the cost and delay required to complete task i, respectively.

$$P\prime :\underset{x_i\in \{0,1\}}{min}\sum _{i=1}^{N^{\prime }}\left[(1-x_i)T_i^0+x_i{T}_i^1\right]$$

$$\mathrm{s}.\mathrm{t}.\sum _{i=1}^{N^{\prime }}{x}_i{C}_i^1\le T$$

By setting $T_i^0=0$, $T_i^1=-v_i$, and $C_i^1=w_i$, problem $P^{\prime }$ can be transformed into problem Q, which corresponds to the 0-1 knapsack problem.

$$Q:\underset{x_i\in \{0,1\}}{max}\sum _{i=1}^{N^{\prime }}{x}_i{v}_i$$

$$\mathrm{s}.\mathrm{t}.\sum _{i=1}^{N^{\prime }}{x}_i{w}_i\le T$$

If we solve $P^{\prime }$, we can also solve Q. Since $P^{\prime }$, as a special case of the original problem P, is NP-hard, it follows that the original problem P is also NP-hard.    □

4. Approximation Algorithm

In this section, we propose an approximation algorithm and provide a proof of its approximation ratio and time complexity.

4.1. Upper and Lower Bounds of Delay

Before describing the approximation algorithm, we first need to determine the upper and lower bounds of the delay, as shown in Algorithm 1. We assume that the task set is initiated by device a.

From line 1 to line 2, we initialize the lower and upper bounds of the delay for all tasks on different servers to infinity (since it is not feasible to set the value to infinity in practice, we substitute it with ${10}^6$ or a larger value), and set the lower bound of the virtual task s at device a to be 0. From line 3 to line 7, based on the task order in List I, we calculate the upper and lower bounds of the delay for each task on the execution node that satisfies its service requirements. This calculation is performed using a greedy approach, without considering the cost constraint. List I represents the task order obtained through a topological sorting algorithm, such as the Kahn algorithm, ensuring that all task dependencies are respected. Finally, at line 8, $UB$ and $LB$ are obtained as the delay bounds.

Algorithm 1 FULC($G(V,E)$, List I)

1: Initialize $T_{\min }(v,m)\leftarrow \infty$, $T_{\max }(v,m)\leftarrow 0$, $v\in V,m\in M$. 2: Set $T_{\min }(s,a)\leftarrow 0$. 3: for $j\in V\setminus \left\{s\right\}$ in List I do 4:     for $m\in M_j$ do 5:        $T_{\min }(j,m)\leftarrow T_j^m+\underset{x_i\in M_i}{min}\underset{i\in \mathcal{C}\left(j\right)}{max}\left[T(i,x_i)+T_{ij}^{x_{i}m}\right].$        $T_{\max }(j,m)\leftarrow T_j^m+\underset{x_i\in M_i}{max}\underset{i\in \mathcal{C}\left(j\right)}{max}\left[T(i,x_i)+T_{ij}^{x_{i}m}\right].$ 6:     end for 7: end for 8: $LB\leftarrow T_{\min }(t,a)$, $UB\leftarrow T_{\max }(t,a)$.

4.2. Polynomial-Time Approximation Algorithm

We use $C(i,j,k)$ to represent the minimum completion cost of task i on device j under a maximum consumption delay of k. The optimal strategy is derived by solving all subproblems for $i\in \left[V\right]$ and $j\in \left[M_i\right]$ of this problem.

We do not solve all subproblems for $k\in [1,UB]$, but instead discretize the delay values.

$$q_S\left(x\right)=k,(k-1)S<x\le kS,S={\displaystyle \frac{LBϵ}{L+1}}.$$

(5)

L denotes the depth of task graph (the greatest number of nodes contained within a single path). If all subproblems of a given problem have already been solved, the problem can be described as follows:

$$k_{\mathrm{add}}=q_S\left(T_j^m+T_{ij}^{x_{i}m}\right),k-k_{\mathrm{add}}>=0.$$

(6)

$$\begin{array}{c}\hfill C_{\mathrm{new}}(j,m,k)=C_j^m+\underset{x_i\in M_i}{min}\sum _{i\in \mathcal{C}\left(j\right)}\left[C_{ij}^{x_{i}m}+C(i,x_i,k-\underset{i\in \mathcal{C}\left(j\right)}{max}{k}_{\mathrm{add}})\right].\end{array}$$

(7)

$k_{\mathrm{add}}$ represents the quantized value of transmission delay and execution delay. Equation (7) calculates the minimum cost that satisfies the maximum consumption delay k based on all feasible solutions, where $\underset{i\in \mathcal{C}\left(j\right)}{max}{k}_{\mathrm{add}}$ represents the slowest predecessor node in each feasible solution. Since the cost function (7) is additive, this implies that the minimum cost to complete task j on device m only depends on the sum of the costs of completing all its predecessor tasks and the data transmission cost. Furthermore, since all predecessor tasks of task j are independent of each other, this means that each predecessor task can be completed independently on different devices, and the data transmission process is also independent. As a result, the minimum value of the sum of the costs of completing all its predecessor tasks and the data transmission cost can be transformed into the sum of the minimum completion cost for each predecessor task and the corresponding transmission cost from that task i to task j. Therefore, we can transform (7) into (8) while ensuring that the quality of the solution remains unchanged. At the same time, the solution space is reduced from $M^{\prime p}$ to $p{M}^{\prime }$, where p denotes the number of predecessor tasks for task j, and $M^{\prime }$ is the number of execution devices for task j.

$$\begin{array}{c}\hfill C_{\mathrm{new}}(j,m,k)=C_j^m+\sum _{i\in \mathcal{C}\left(j\right)}\underset{x_i\in M_i}{min}\left[C_{ij}^{x_{i}m}+C(i,x_i,k-\underset{i\in \mathcal{C}\left(j\right)}{max}{k}_{\mathrm{add}})\right].\end{array}$$

(8)

After solving all subproblems of $C(i,j,k)$, all the data needs to be aggregated to the local device a. Therefore, the original problem can be transformed into the following form:

$$mink\mathrm{s}.\mathrm{t}.C\left(t,a,k\right)\le T$$

We propose an approximation algorithm to solve the task offloading problem, as shown in Algorithm 2. In lines 1 to 2, we initialize the minimum cost of all tasks when the maximum consumption delay is 0 to infinity, and set the virtual task s to have a minimum cost of 0 at the maximum consumption delay of 0, with the quantized value of $UB$ being $U{B}^{\prime }$. From lines 3 to 16, we compute the minimum cost for each task on the execution node that satisfies its service requirements, based on DP [41], under the constraint that the maximum consumption delay does not exceed k. If a feasible solution with a delay constraint is found before k exceeds $U{B}^{\prime }$, we return the corresponding offloading scheme. Otherwise, we return FAIL.

Algorithm 2 PTA($G(V,E)$, $M_v$, $UB$, $LB$, T, $ϵ$, List I)

1: Initialize $S\leftarrow {\displaystyle \frac{LBϵ}{L+1}}$, $C(v,m,0)\leftarrow \infty$ for all nodes $v\in V,m\in M_v$.   2: Set $C(s,a,0)\leftarrow 0$, $U^{\prime }\leftarrow ⌊{\displaystyle \frac{UB}{S}}⌋+L+1$.   3: for $k=1,2,\dots ,U^{\prime }$ do   4:     for $j\in V$ in List I do   5:         for $m\in M_j$ do   6:             $C(j,m,k)\leftarrow C(j,m,k-1)$.             Compute $k_{\mathrm{add}}$, $C_{\mathrm{new}}(j,m,k)$ according to (6) and (8).   7:             if $C_{\mathrm{new}}(j,m,k)<C(j,m,k)$ then   8:                 $C(j,m,k)\leftarrow C_{\mathrm{new}}(j,m,k)$.   9:                 if $C(t,a,k)\le T$ then 10:                    return the corresponding plan and delay. 11:                end if 12:            end if 13:         end for 14:      end for 15: end for 16: return FAIL.

Lemma 1. 

Let x represent any offloading scheme, and let $\tilde{d}\left(x\right)$ denote the quantized delay value of the offloading scheme x. The delay of the offloading scheme x satisfies $d\left(x\right)\le \tilde{d}\left(x\right)S\le d\left(x\right)+(L+1)S$.

Proof. 

The proof is presented in Appendix A.    □

However, since Algorithm 2 does not guarantee polynomial-time complexity, we present an approximate testing process of $UB$ and $LB$ (Algorithm 3), which iteratively invokes Algorithm 2 to reduce the gap between $UB$ and $LB$ as well as the quantization step size, thereby reducing the overall time complexity to guarantee polynomial-time complexity.

Algorithm 3 TUL($G(V,E)$, $UB$, $LB$, T, $ϵ$, List I)

1: Set $B_L\leftarrow LB$, $B_U\leftarrow {\displaystyle \frac{UB}{1+ϵ}}$.   2: while ${\displaystyle \frac{B_U}{B_L}}>2$ do   3:     $B\leftarrow \sqrt{B_U\times B_L}$.   4:     if $PTA$($G(V,E)$, $M_v$, B, B, T, $ϵ$, List I) returns FAIL then   5:         Test$(ϵ,B)$ = Yes, $B_L\leftarrow B$.   6:     else   7:          Test$(ϵ,B)$ = No, $B_U\leftarrow B$.   8:     end if   9:  end while 10: return PTA($G(V,E)$, $M_v$, $(1+ϵ)B_U$, $B_L$, T, $ϵ$, List I).

Lemma 2. 

If Test(ϵ,B) = Yes, when $PTA$($G(V,E)$, $M_v$, B, B, T, ϵ, List I) returns FAIL, then $d^{*}>B$; otherwise, $d^{*}<(1+ϵ)B$, where $d^{*}$ represents the delay of the optimal solution.

Proof. 

The proof is presented in Appendix B.    □

Theorem 2. 

Given valid bounds $0<LB\le d^{*}\le UB$, by Lemma 1 and Lemma 2 we can obtain a $(1+ϵ)$-approximate result in $O(d_{in}{N}^{\prime }{M^{\prime }}^2{\displaystyle \frac{L}{ϵ}}(\log \log (UB/LB)+1))$ time.

Proof. 

From Algorithm 2, each DP procedure solves $N^{\prime }{M}^{\prime }{U}^{\prime }$ subproblems [32]. Let $d_{in}$ denote the maximum indegree of the task graph. For solving each subproblem in equation 8, there can be up to $d_{in}$ minimization problems across $M^{\prime }$ devices. Consequently, the overall complexity of the procedure in Algorithm 3 can be bounded by

$$O\left(d_{in}{N}^{\prime }{M^{\prime }}^2{U}^{\prime }\right)=O\left(d_{in}{N}^{\prime }{M^{\prime }}^{2}L·{\displaystyle \frac{UB}{LBϵ}}+d_{in}{N}^{\prime }{M^{\prime }}^{2}L\right).$$

If $UB\ge LB$, and $ϵ\le 1$, then

$$O\left(d_{in}{N}^{\prime }{M^{\prime }}^2{U}^{\prime }\right)=O\left(d_{in}{N}^{\prime }{M^{\prime }}^{2}L·{\displaystyle \frac{UB}{LBϵ}}\right).$$

In Algorithm 1, we first compute the maximum delay $UB$ and minimum delay $LB$ for the problem without cost constraints, which serve as valid bounds. By Lemma 2, $\mathrm{Test}(ϵ,B)$ is an effective process for reducing the dynamic range. Lines 4 to 8 in Algorithm 3 ensure that, at each iteration, $B_L$ is a valid lower bound and $(1+ϵ)B_U$ is a valid upper bound. In Algorithm 3, binary search is used to search for the boundary within the range of $log{B}_L$ to $log{B}_U$ until the condition $B_U/B_L\le 2$ is satisfied. During the iterative process, $log(B_U/B_L)$ decreases to either $log\left(\sqrt{B_U{B}_L}/B_L\right)$ or $log\left(B_U/\sqrt{B_U{B}_L}\right)$. Since $log\left(\sqrt{B_U{B}_L}/B_L\right)=log\left(B_U/\sqrt{B_U{B}_L}\right)={\displaystyle \frac{1}{2}}log\left(B_U/B_L\right)$, the dynamic range is halved after each iteration. Therefore, the binary search requires $\log \log (UB/LB)$ calls to Algorithm 2. The complexity of lines 4 to 8 in Algorithm 3 is $O(d_{in}{N}^{\prime }{M^{\prime }}^2{\displaystyle \frac{L}{ϵ}}\log \log (UB/LB))$. Since $UB/LB=(1+ϵ)B_U/B_L=O\left(1\right)$ in line 10 of Algorithm 3, the complexity of line 10 in Algorithm 3 is $O(d_{in}{N}^{\prime }{M^{\prime }}^2{\displaystyle \frac{L}{ϵ}})$. Therefore, the total complexity is $O(d_{in}{N}^{\prime }{M^{\prime }}^2{\displaystyle \frac{L}{ϵ}}(\log \log (UB/LB)+1))$.

According to Lemma 1, we assume x is the offloading scheme obtained by Algorithm 2, and $x^{*}$ is the optimal offloading scheme. we can deduce that Algorithm 2 can produce an offloading scheme x satisfying

$$d\left(x\right)\le \tilde{d}\left(x\right)S\le \tilde{d}\left(x^{*}\right)S\le d\left(x^{*}\right)+(L+1)S=d\left(x^{*}\right)+LBϵ\le d^{*}(1+ϵ).$$

  □

5. Exact Algorithm

In this section, we introduce the exact algorithm and prove its time complexity. Note that the exact algorithm in this paper is primarily used for comparison with approximation algorithms, and it also performs well in certain scenarios.

5.1. Label Structure

For each task in the task set, a label set $L_v$, where $v\in V$, needs to be stored. Each label in this label set can be represented as $L_{\{v,m,h\}}=\{f^{\mathrm{delay}}\left(x\right),f^{\mathrm{cost}}\left(x\right),h_p,m_p\}$, where $f^{\mathrm{delay}}\left(x\right)$ and $f^{\mathrm{cost}}\left(x\right)$ denote the delay and cost consumed by the offloading scheme x for completing task v. $h_p$ is the length index, representing the position of the label on the y-axis in Figure 3. The maximum value of $h_p$ is H. $m_p$ is the execution node index, representing the position of the label on the x-axis in Figure 3, used to distinguish the offloading scenarios of individual tasks on different execution nodes.

5.2. Dominance Test

We use x and y to represent the two labels. The operator ⊙ represents the dominance test. By $x\odot y$, we calculate the non-dominated set $\{x,y\}$ based on the delay and cost performance of x and y.

We use $(=,=)$ to denote the situation where $x\left(\mathrm{delay}\right)=y\left(\mathrm{delay}\right)$ and $x\left(\mathrm{cost}\right)=y\left(\mathrm{cost}\right)$, and similar notation is used for other cases. The $(=,=)$ case implies two equivalent offloading schemes. During our computation, we only need to store the minimal complete set, so we can randomly select either x or y for storage. However, if we want to store the maximal complete set, since x and y represent different offloading schemes but have the same indicators, both should be stored, i.e., $\{x,y\}$ should be saved. In all other cases, the dominance relationship is clear. $x\odot y=\{x,y\}$ means that x and y do not dominate each other; $x\odot y=\left\{x\right\}$ means that y is dominated by x, and vice versa.

5.3. Exact Algorithm

A Bellman–Ford framework-based exact algorithm (Algorithm 4) is essentially a label correction (LC) algorithm [42,43] based on an improved version of the Bellman–Ford algorithm. In lines 1 to 2, we first initialize all label sets as empty. The outer loop runs for $N^{\prime }-1$ iterations, which is similar to the classic Bellman–Ford algorithm. From lines 3 to 18, we iterate over all tasks according to List I. For each task, we generate all offloading schemes by combining the label sets of all predecessor nodes, and then calculate new labels based on these offloading schemes. Afterward, we perform a dominated test (DT) on the new labels with those having the same execution node index. If the newly generated label is not dominated by any other label, it returns false. We remove the labels dominated by the new label and insert the new label into the label set; otherwise, we discard the new label. In simple terms, during each iteration, the Pareto frontier is stored for the label set of each node on each server based on the DT table in

Table 1. Dominance test.

⊙	$x^{\mathrm{delay}}>y^{\mathrm{delay}}$	$x^{\mathrm{delay}}<y^{\mathrm{delay}}$	$x^{\mathrm{delay}}=y^{\mathrm{delay}}$
$x^{\mathrm{cost}}>y^{\mathrm{cost}}$	$\left\{y\right\}$	$\{x,y\}$	$\left\{y\right\}$
$x^{\mathrm{cost}}<y^{\mathrm{cost}}$	$\{x,y\}$	$\left\{x\right\}$	$\left\{x\right\}$
$x^{\mathrm{cost}}=y^{\mathrm{cost}}$	$\left\{y\right\}$	$\left\{x\right\}$	$\{x\mid y\}$

. Finally, in line 19, we find the offloading scheme that satisfies the cost constraint and minimizes the delay in the label set of the virtual node t, which serves as the optimal solution.

As shown in Figure 3, the labels $\{1,4\}$ and $\{2,3\}$ are retained because they are non-dominated. However, if a new label $\{3,3\}$ arrives at the same execution node as labels $\{1,4\}$ and $\{2,3\}$, it cannot be added to the set $L_v$, as $\{3,3\}$ is dominated by $\{2,3\}$. On the other hand, if the new label is $\{2,2\}$, it will be added to the set $L_v$ and the label $\{2,3\}$ will be removed. Moreover, since the x-axis in Figure 3 represents different execution nodes, even though the labels $\{2,4\}$ and $\{3,3\}$ are dominated by the labels $\{1,4\}$ and $\{2,3\}$, respectively, they can still be added to the set $L_v$.

Algorithm 4 BFF($G(V,E)$, $M_v$, T, List I)

1: Initialize $L_{j,M_j,h}\leftarrow Ø$ for all $j\in V,$ for any $h\in [1,H]$.   2: Set $L_{s,a,1}\leftarrow \{0,0,1,a\}$.   3: for $q=1$ to $N^{\prime }-1$ do   4:     for $j\in V$ in List I do   5:         for $m\in M_j$ do   6:             $k\leftarrow$ All permutations of $L_i$, $i\in \mathrm{C}\left(j\right)$.   7:             $L_{\mathrm{new}}\leftarrow \{f^{\mathrm{delay}}\left(k\right),f^{\mathrm{cost}}\left(k\right),h^{*},m\}$.   8:             if $DT(L_{\mathrm{new}}\odot L_{j,m,\ast })=false$ then   9:                 for $h\in [1,H]$ do 10:                   if $L_{\mathrm{new}}\odot L_{j,m,h}=L_{\mathrm{new}}$ then 11:                       $L_{j,m,h}\leftarrow Ø$. 12:                   end if 13:                end for 14:                $L_{j,m}\leftarrow L_{j,m}\cup L_{\mathrm{new}}$. 15:            end if 16:        end for 17:     end for 18: end for 19: The optimal solution is the label value in $L_t$ that satisfies the cost constraint T and minimizes the delay.

Theorem 3. 

The maximum time complexity of BFF is $N^{\prime 2}{M}^{\prime }{\left(H{M}_{max}\right)}^{d_{in}}$.

Proof. 

The outermost loop runs $N^{\prime }-1$ times, where $N^{\prime }$ denotes the total number of tasks. In each iteration of this loop, every task and server is traversed. Therefore, there are $N^{\prime }{M}^{\prime }$ operations to find the new label set. Since each new label set is derived by permuting the label sets stored in all predecessor nodes, and each node’s label set contains at most $H{M}_{\max }$ labels, where $M_{\max }$ denotes the maximum value of $M^{\prime }$, the new label set can have at most ${\left(H{M}_{\max }\right)}^{d_{\mathrm{in}}}$ labels. Thus, the maximum time complexity is $N^{\prime 2}{M}^{\prime }{\left(H{M}_{\max }\right)}^{d_{in}}$. □

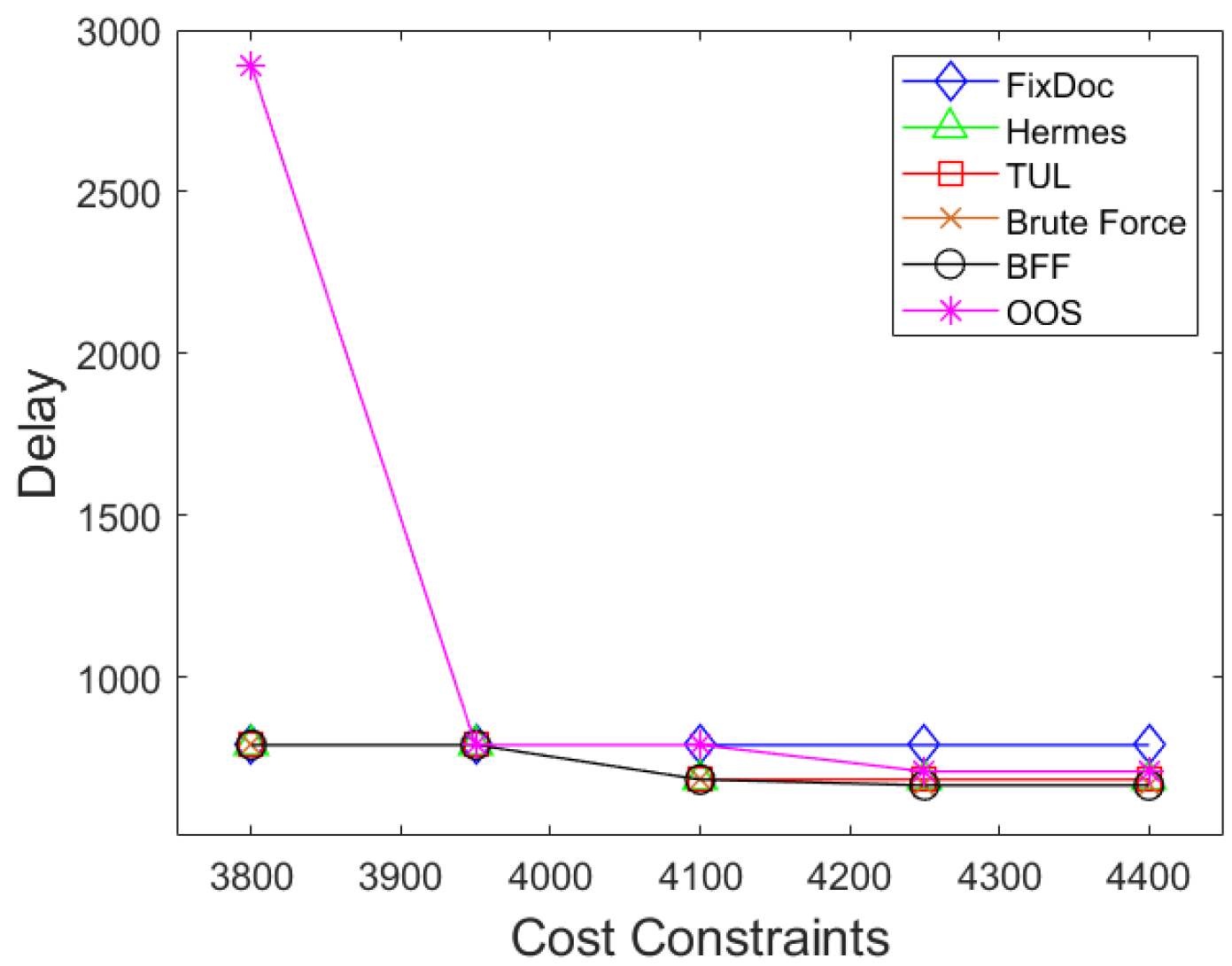
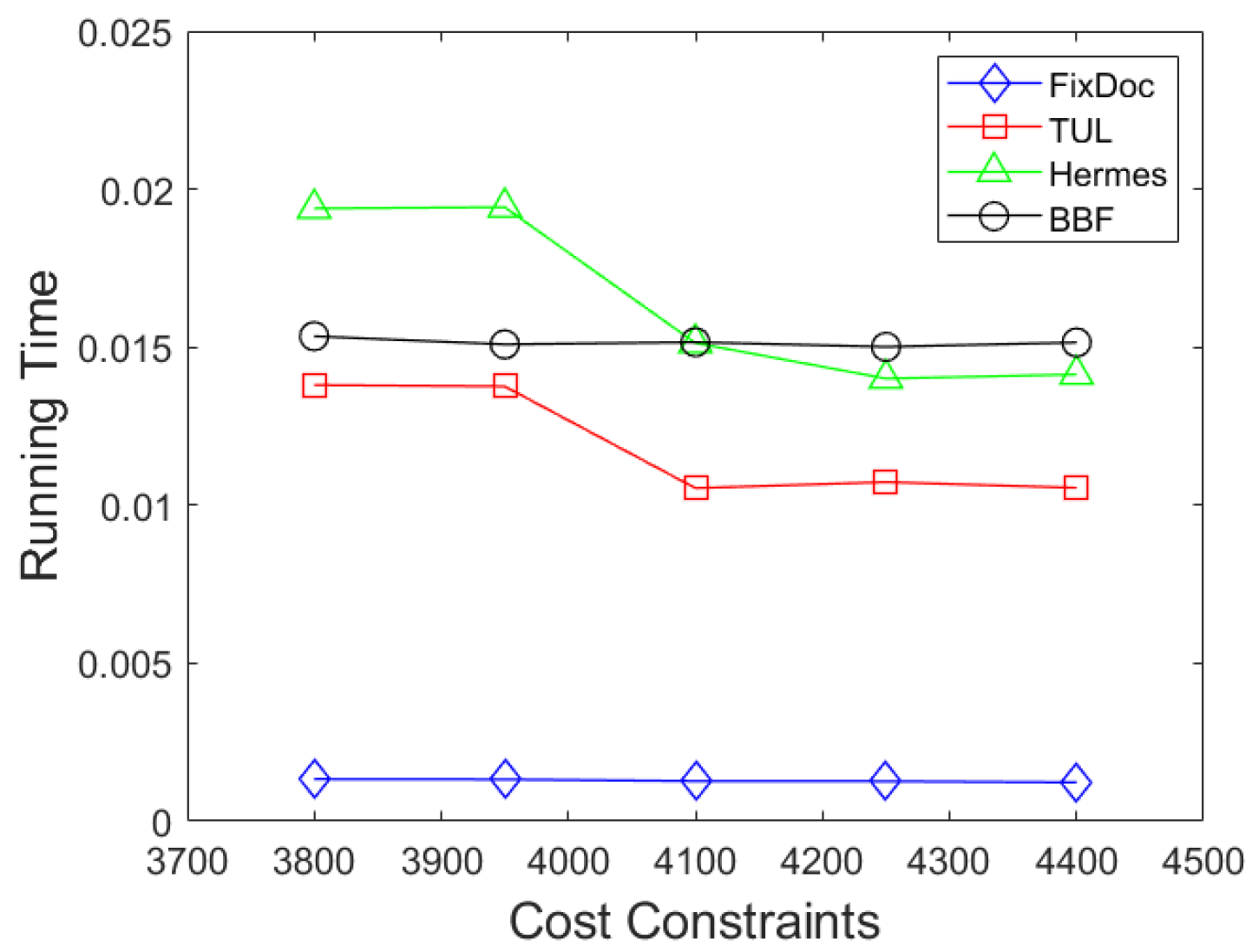
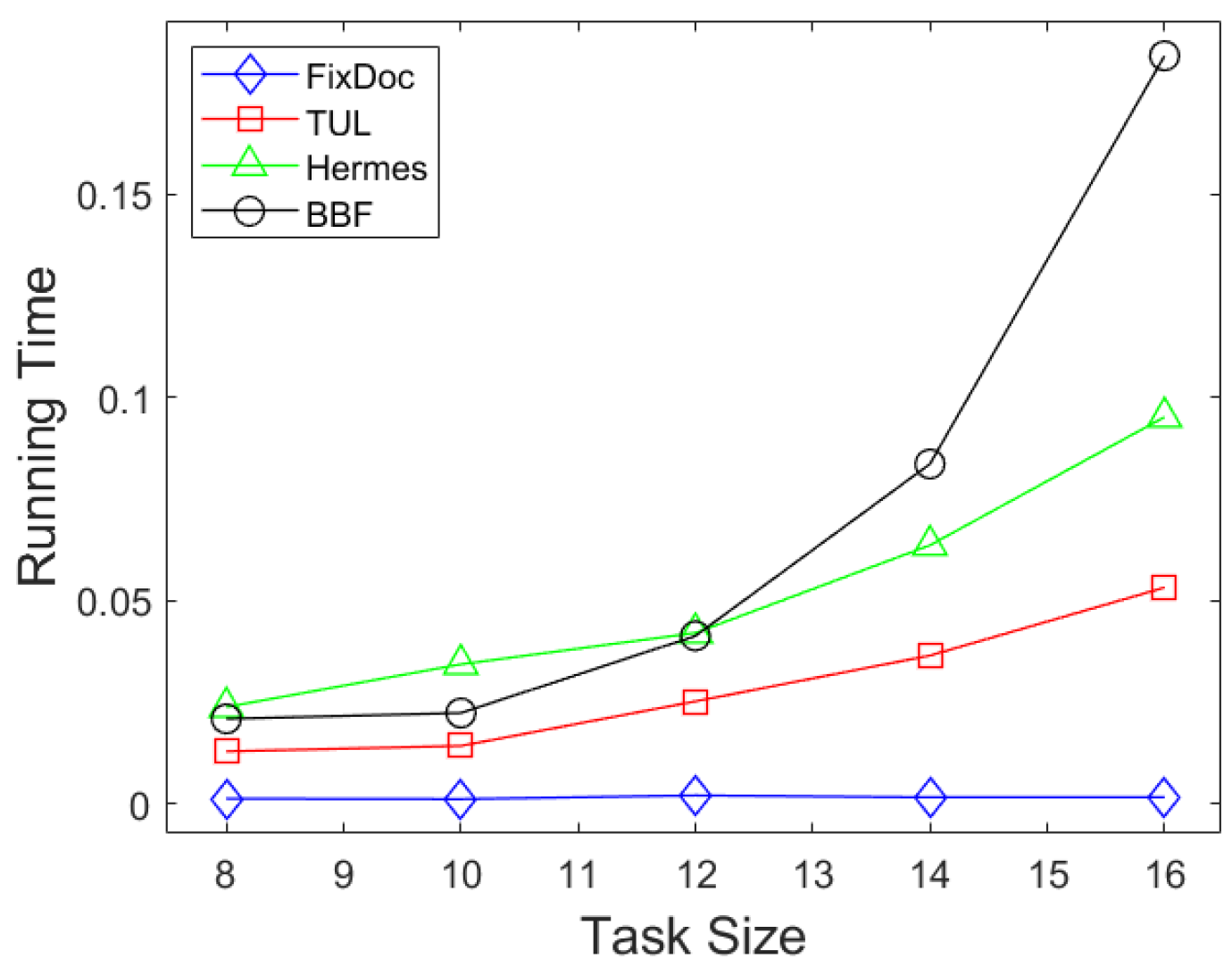
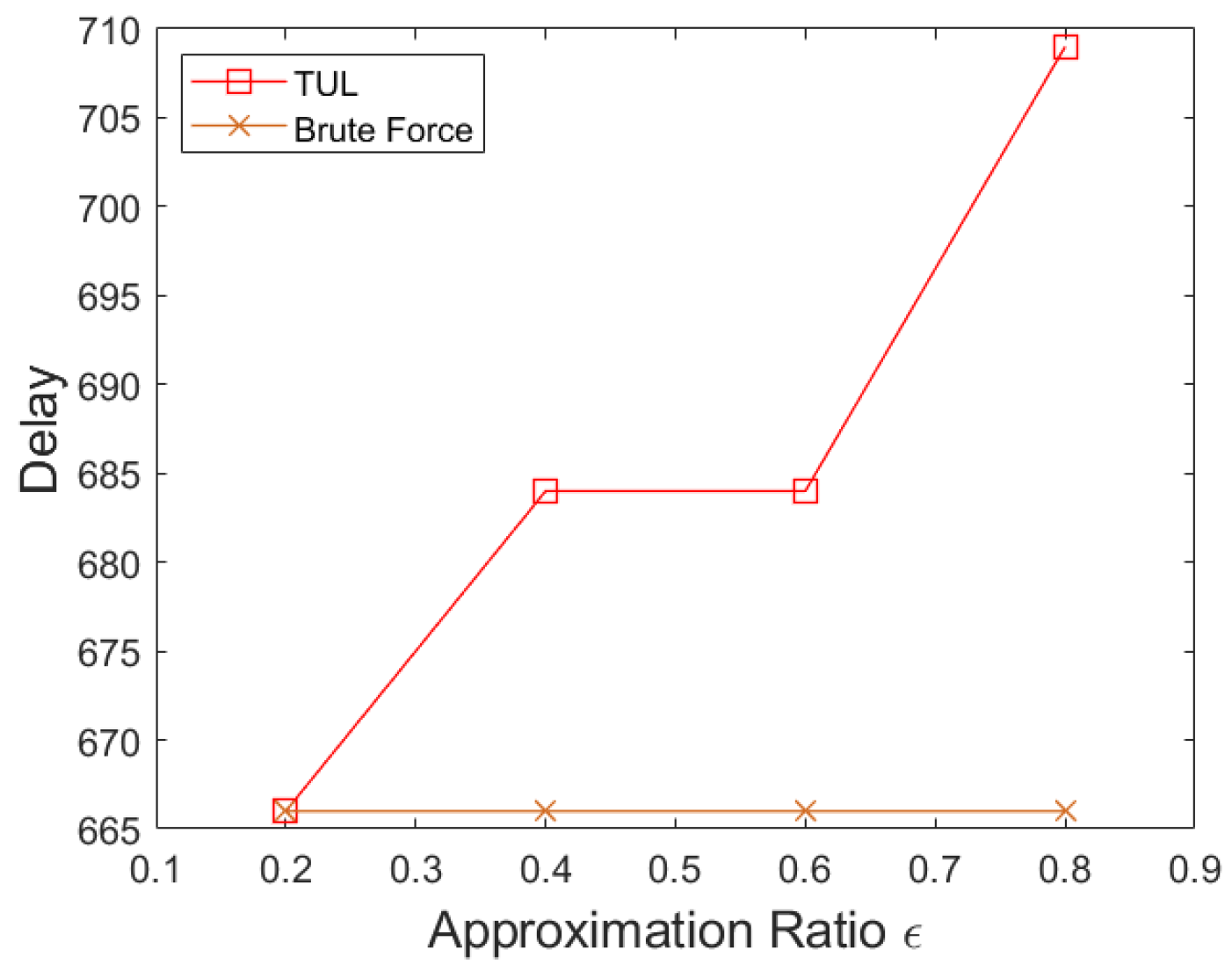
6. Simulation Results

6.1. Simulation Environment and Settings

The simulation was performed on an average computer with Intel i7-13700H (Intel Corporation: Santa Clara, CA, USA) at 2.40 GHz and 16 GB RAM. All the considered algorithms were implemented in MATLAB 2023b. In our simulation, there are seven mobile devices, three edge servers, and one cloud server. We set $ϵ=0.4$, $c=0.935$ watt, $P=0.944$ watt, $S_n=[4,80]$ Mb, $O_j=I_j=[0.1,2]$ Mb, $C_C=C_{EN}={\displaystyle \frac{1}{2}}{C}_{EC}=50$ cycles/bit, and $f_C=2f_{EN}=10f_{EC}$, where C, $EN$, and $EC$ denote the cloud server, edge server, and mobile device, respectively. Additionally, we set $B=\tilde{B}={10}^6$ Hz, ${\sigma }^2={\tilde{\sigma }}^2={10}^{-10}$ watt, and $f_{EN}=10$ GHz [9]. The processing cost for the mobile device is denoted as P, while the processing cost at the edge server is between 4 watt, and at the cloud server is 10 watt [39]. To better reflect the distance differences between different execution nodes, we set the distance between mobile devices to be 30 m, the distance between mobile devices and edge servers to be 100 m, the distance between edge servers to be 150 m, and the distances from mobile devices and edge servers to the cloud server to be 500 m and 400 m, respectively. Current research methods are predominantly based on deep learning or solved through heuristic algorithms [10,30,31], which cannot guarantee finding an approximate or optimal solution. Therefore, we do not compare our method with them. To evaluate the performance of the proposed algorithm, we compare it with the following methods:

• Offloading only to servers (OOS): The BFF algorithm offloads tasks only to edge and cloud servers. If the final offloading scheme fails to meet the cost constraints, a significant amount of time will need to be spent on the local device to cache the services required to execute these tasks. Note that the BFF algorithm in this paper is primarily used for comparison with approximation algorithms, and it also performs well in certain scenarios.
• FixDoc [19]: The algorithm is presented as Algorithm 1 in [19]. It is a task offloading method based on DP, which is the earliest proposed method in the problem we are considering. We use this algorithm to derive the task offloading strategy that minimizes the cost while satisfying the cost constraint.
• Hermes [32]: A polynomial-time approximation algorithm used to solve the delay-minimization problem under the cost constraint. To ensure fairness, we impose a constraint of service caching on the original algorithm.
• Brute force: This algorithm enumerates all possible offloading strategies to obtain the optimal solution.

6.2. Simulation Results

In Figure 4 and Figure 5, we compare the effect of cost constraints on the delay values and running time. Similar to [10], we generate a DAG for the structure of the real world, that is, the Gaussian elimination (GE) algorithm [44], and the dimension of the given graph is 4. For each task, the total number of mobile devices and edge servers corresponding to the service is cached as [2, 3]. Since the time complexity of OOS is identical to that of BFF, and its performance is inferior, while the brute force algorithm yields the same results as BFF but with significantly longer running times, we exclude OOS and the brute force algorithm from the comparison based on running time. As the cost constraint increases, the delay values of the offloading solutions generated by various algorithms progressively decrease. When the cost constraint is very small, the solutions obtained by OOS perform the worst. This is due to the high server cost, which causes all feasible solutions to violate the cost constraint. As a result, the algorithm is forced to spend a considerable amount of time performing local caching in order to execute the tasks. On the other hand, both TUL and Hermes consistently achieve a $(1+ϵ)$-approximation solution. As the cost constraint is relaxed, the running times of these algorithms decrease. However, the running time of TUL is significantly smaller than that of Hermes. In contrast, BFF computes all possible solutions based on the DT table for each experiment and then selects the optimal solution that satisfies the cost constraint. As a result, the running time of BFF does not change as the cost constraint is relaxed. In all cases, the solutions obtained by BFF are identical to the optimal solution. When the cost constraint is very small, the running time of BFF is slightly smaller than that of Hermes. Although the time complexity of BFF is theoretically exponential, in practical applications, the number of labels retained during each task iteration tends to be relatively small, making the algorithm more efficient in real-world scenarios.

Figure 6 and Figure 7 describe the effect of task size on delay values and running time when the cost constraint is set to a tiny value. The task mapping is derived from a randomly generated DAG diagram. For each task, the total number of mobile devices and edge servers corresponding to the service is cached as [2, 3]. Due to the long running time of the brute force algorithm and the fact that its results are identical to those of BFF, it is not included in this experiment. Given that the time complexity of OOS matches that of BFF, but its empirical performance is inferior, we exclude OOS from the running time comparison. As the number of tasks grows, the delay values of the offloading solutions derived from different algorithms generally increase. Among them, OOS consistently shows the poorest performance, with the highest delay values across all task sets. On the other hand, FixDoc demonstrates the fastest running time as it solely utilizes DP to compute the minimum completion cost of task offloading. However, the solutions it provides result in relatively high delay values. Both TUL and Hermes are able to consistently provide a $(1+ϵ)$-approximation solution, regardless of the task set being used. However, TUL stands out by achieving this with a significantly smaller running time compared to Hermes, which makes TUL more efficient in terms of execution speed. In contrast, BFF produces solutions with the lowest delay values, indicating that it optimizes delay performance better than the other algorithms. Its running time is obviously smaller than that of Hermes when the task quantity is low, but as the task set continues to grow, the difference in running time between it and TUL becomes increasingly large.

Figure 8 and Figure 9 provide a detailed illustration of how the approximation ratio $ϵ$ influences the performance of the TUL algorithm. We used the same experimental setup as in Figure 4 and Figure 5, with the cost constraint set to be very small. From the experimental findings, it is evident that as the approximation ratio $ϵ$ gradually increases, the delay values of the offloading solutions produced by TUL also tend to increase. Meanwhile, the running time of TUL decreases. Additionally, the running time of TUL is significantly smaller than that of the brute force algorithm. However, it is important to note that, even with the increase in $ϵ$, the delay values of these solutions never exceed the bound of $(1+ϵ)$ times the optimal solution. This behavior highlights the effectiveness of TUL in maintaining a close approximation to the optimal solution.

In

Table 2. Effect of task quantity, the number of execution nodes, and the value of $ϵ$ on the delay of the two algorithms.

	$N^{\prime }=7,M^{\prime }=2$	$N^{\prime }=7,M^{\prime }=8$	$N^{\prime }=12,M^{\prime }=2$	$N^{\prime }=12,M^{\prime }=8$	$N^{\prime }=17,M^{\prime }=2$	$N^{\prime }=17,M^{\prime }=8$
BFF	763	335	1345	510	1326	765
TUL($\epsilon =0.2$)	763	335	1345	510	1326	765
TUL($\epsilon =0.5$)	763	367	1345	510	1326	813
TUL($\epsilon =0.8$)	763	335	1533	591	1326	861

and

Table 3. Effect of task quantity, the number of execution nodes, and the value of $ϵ$ on the running time of the two algorithms.

	$N^{\prime }=7,M^{\prime }=2$	$N^{\prime }=7,M^{\prime }=8$	$N^{\prime }=12,M^{\prime }=2$	$N^{\prime }=12,M^{\prime }=8$	$N^{\prime }=17,M^{\prime }=2$	$N^{\prime }=17,M^{\prime }=8$
BFF	0.02	53.73	0.05	94.42	0.12	140.48
TUL($\epsilon =0.2$)	0.07	4.13	0.14	6.08	0.29	17.54
TUL($\epsilon =0.5$)	0.02	1.03	0.02	1.39	0.07	2.84
TUL($\epsilon =0.8$)	0.007	0.51	0.01	0.79	0.04	1.58

, we compare the effects of the number of tasks, the number of execution nodes, and the value of $ϵ$ on the two algorithms to analyze their approximation ratio, time complexity, and overall differences. In this experiment, the task mapping is derived from a randomly generated DAG diagram. to represent the task dependency structures. From the results, it is observed that when the number of tasks, $N^{\prime }$, increases while keeping other parameters constant, the delay and running time of each algorithm increase. However, due to the random generation of DAG, increasing the number of tasks may increase the width of the DAG rather than its depth, which sometimes results in a smaller delay value despite a larger number of tasks. When the number of execution nodes, $M^{\prime }$, increases while keeping other parameters constant, the delay and running time of each algorithm decrease. This is because the increased number of execution nodes leads to a larger set of feasible solutions, thereby improving the chances of finding better solutions. When the values of $N^{\prime }$, $M^{\prime }$, and $ϵ$ are small, the running times and results of TUL and BFF show little difference. Since the time complexity of TUL and BFF are linearly related to $N^{\prime }$ and $N^{\prime 2}$, respectively, the running time difference between TUL and BFF is not significant when the number of tasks increases. However, as the number of execution nodes increases, the running time difference between BFF and TUL becomes much more significant. This is because the running time of BFF is proportional to $M^{\prime d_{in}}$, while the running time of TUL is proportional to $M^{\prime 2}$. In a DAG, the maximum indegree, $d_{in}$, is usually greater than 2, so the running time of BFF increases much more significantly with $M^{\prime }$ than that of TUL. Additionally, we observe that when $ϵ$ decreases, TUL’s running time difference becomes more pronounced with increases in tasks and execution nodes. This is because the running time of TUL is inversely proportional to $ϵ$, so for the same changes in the number of tasks and execution nodes, smaller values of $ϵ$ result in larger variations in running time. Furthermore, when the value of $ϵ$ decreases while keeping other parameters constant, TUL typically produces more accurate results but at the cost of longer running times. Although there are cases where a larger $ϵ$ yields better results, TUL guarantees a (1 + $ϵ$)-approximate solution. Regardless of the value of $ϵ$, TUL will never exceed the optimal solution by more than a factor of (1 + $ϵ$), further validating the truth of TUL’s approximation ratio.

7. Conclusions

In this paper, we propose a delay-minimization task offloading problem that takes into account task dependencies, service caching, and the maximum completion cost. Unlike traditional MEC, we add peripheral mobile devices to the offload to make it more realistic. Furthermore, we design a $(1+ϵ)$-approximation algorithm and exact algorithm to solve this problem. The simulation results demonstrate that our approximation algorithm indeed achieves the approximation ratio $(1+ϵ)$, and outperforms other algorithms related to this problem. The exact algorithm consistently produces the optimal solution.