Multi-Criteria Genetic Algorithm for Optimizing Distributed Computing Systems in Neural Network Synthesis
Abstract
1. Introduction
- Custom mathematical models for evaluating both performance and availability metrics of DCS nodes, enabling precise matching between computational tasks and resource profiles.
- A multi-objective optimization scheme that leverages Pareto-front analysis to jointly optimize energy consumption, computational latency, and system reliability—parameters that are rarely optimized in combination in the related literature.
- A GA-based decision-support system, which does not merely optimize ANN hyperparameters but also orchestrates resource allocation strategies across distributed nodes, adapting in real time to system feedback and load conditions.
2. Related Works
| Reference | Focus | Applied Model | Results | Limitations |
|---|---|---|---|---|
| [21] | Multi-criterion optimization for distribution networks in supply chains | GA integrated with Analytic Hierarchy Process (AHP) | Enhanced decision-making with better balance between cost, efficiency, and service levels. | May require extensive computational resources for large-scale problems. |
| [23] | Job scheduling in computational Grids considering multiple criteria | AGA and AGA with Overhead (AGAwO) | Superior performance across multiple criteria for energy efficiency and security. | High computational demands; overhead considerations for real-time applications. |
| [25] | Electrical distribution system optimization using Pareto fronts | GA with AHP and TOPSIS for decision-making | Effective multi-objective optimization with scalable applications to microgrids and larger networks. | Results dependent on the selection of criteria weighting and operator tuning. |
| [27] | Planning of distributed energy systems with multi-criteria evaluation | -constraint optimization with AHP and Gray Relation Analysis | Comprehensive framework integrating optimization and evaluation for diverse scenarios. | Complex model setup; reliance on accurate input data for optimization. |
| [29] | Optimization of distributed energy systems in commercial buildings | GA | Identified optimal strategies for energy and CO2 reductions, tailored by building types. | Context-specific findings may not generalize to non-commercial settings. |
| [30] | Logistics performance evaluation using MCDM techniques | GA for criteria weighting | More accurate logistics rankings and frequent evaluations with GA outperforming traditional methods. | Limited to the Logistics Performance Index framework; model effectiveness depends on input data quality. |
| [31] | Framework for Distributed Multi-Energy Systems (DMES) | GA with Maximum Rectangle Method | Enhanced DMES performance with tailored operation strategies like Following Electrical Load (FEL). | Performance influenced by load uncertainties and market conditions. |
| [32] | Hybrid energy system for electricity and desalination | GA and ANN | Improved efficiencies and reduced costs; path to sustainable energy and water production. | System performance depends on optimal parameter selection and operational stability. |
3. Problem Statement
3.1. Multicriteria Optimization of ANN Structure
3.2. Parallel GA for ANN Structure Synthesis
4. Materials and Methods
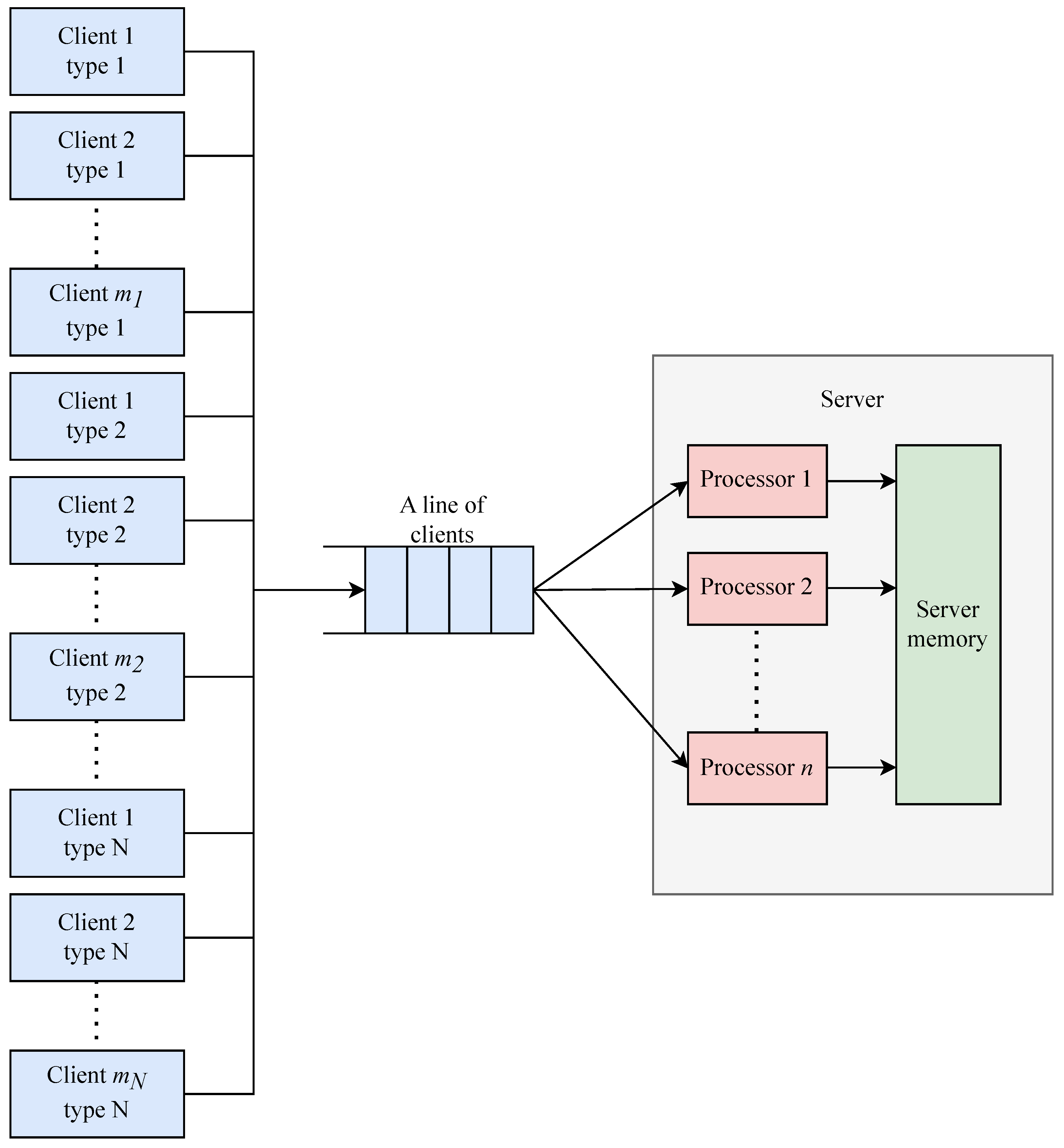
4.1. Performance Model for Heterogeneous Client–Server Networks
- : no requests in the system, all n servers idle.
- : one request from type-1 clients is being served on one processor, with no queue.
- : one request from type-N clients is in service, with no queue.
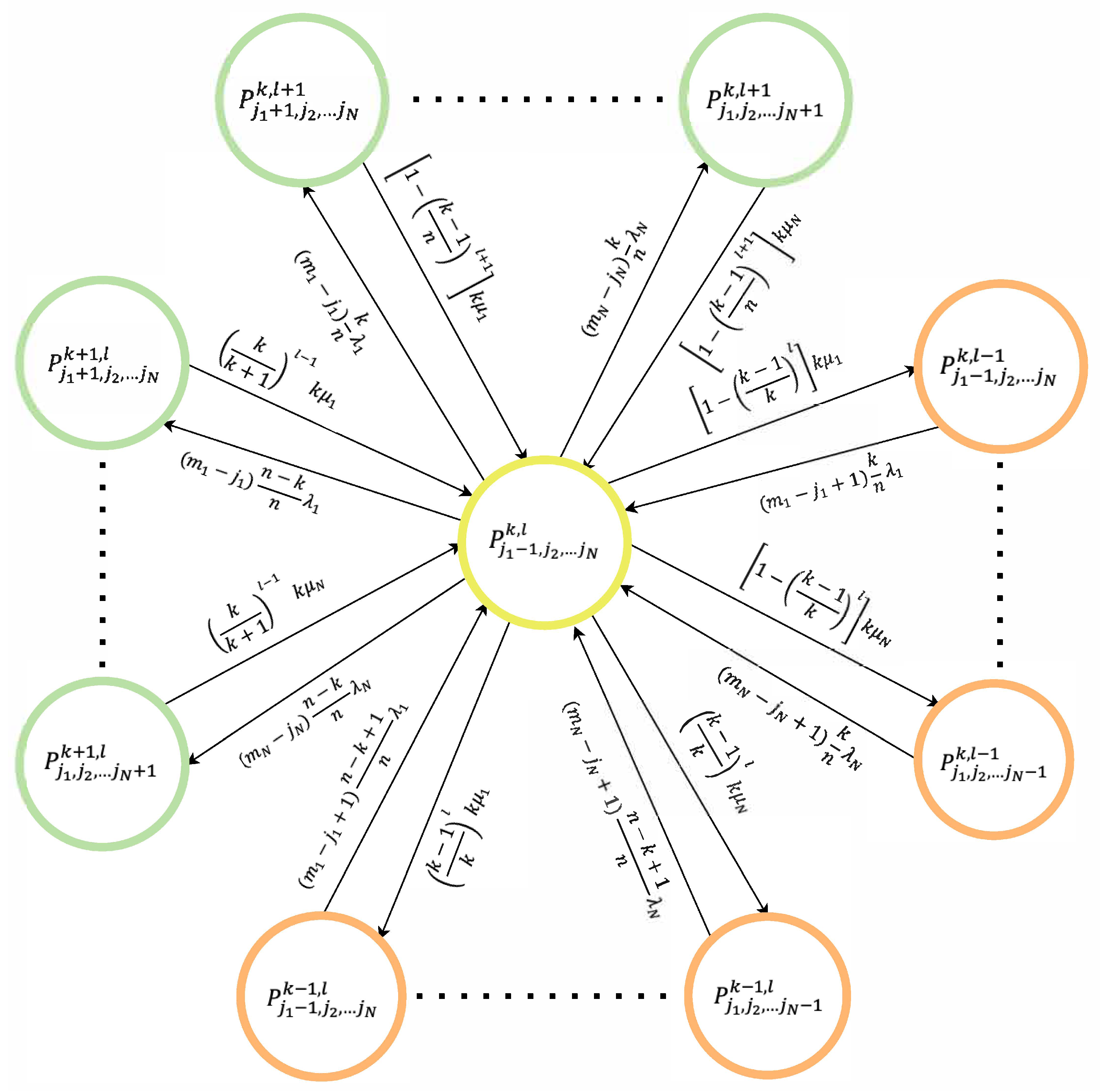
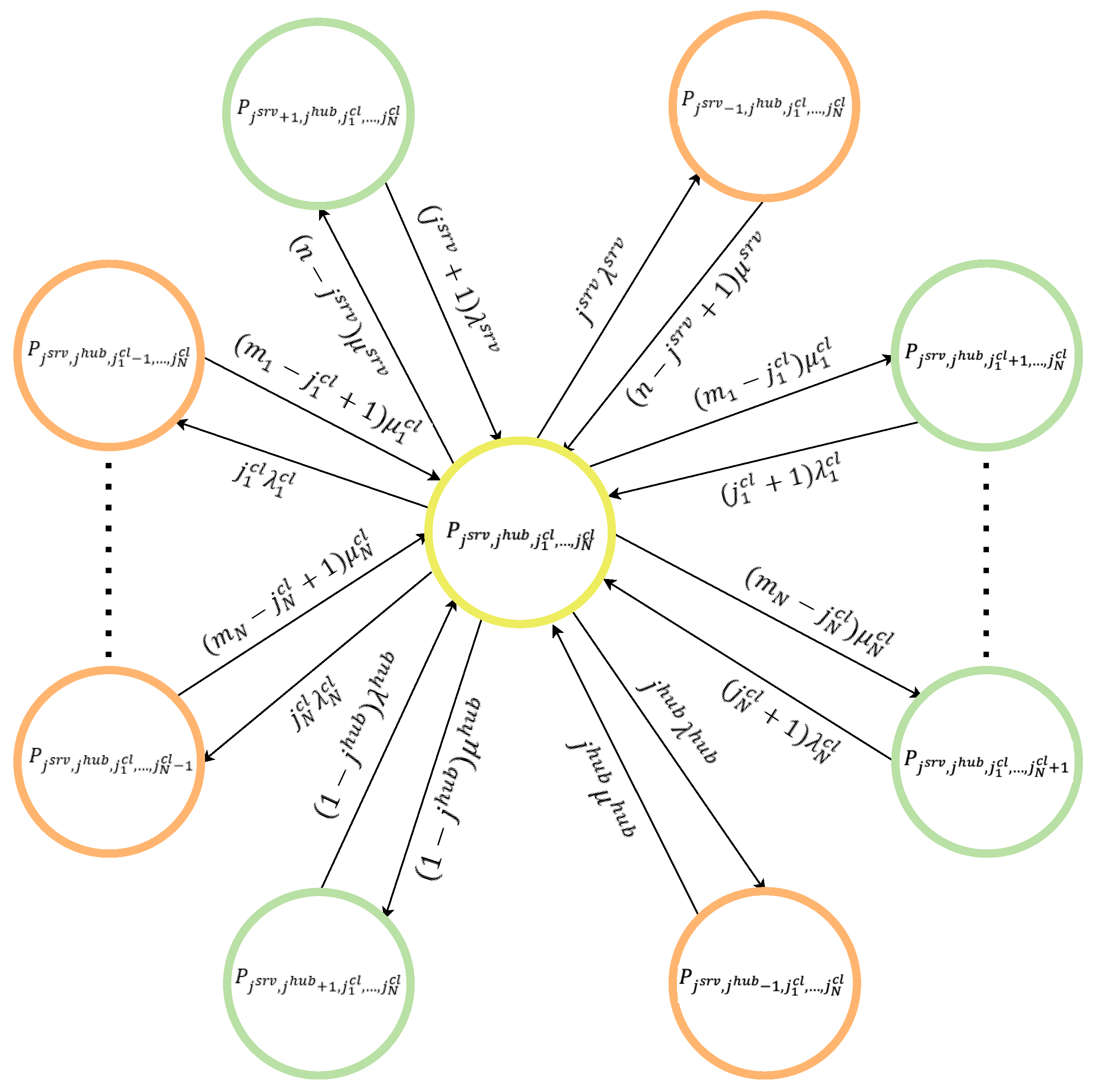
4.2. Reliability Assessment Model for Radial Type Distributed Client–Server Architecture CN
- —failure rate of client nodes of type i, ;
- —the failure rate of the server processors;
- —the failure rate of the concentrator.
- — recovery intensity of client nodes of the i-th type ();
- — the intensity of server processor recovery;
- —the recovery intensity of the hub.
- : No servers, no hub, and no clients are available; all elements are down and undergoing restoration, halting computation.
- : Exactly one server processor is functional while the remaining processors, the hub, and all clients are failed and being repaired; computation is suspended.
- : Only the central hub is up, with every server processor and client node failed and in repair; no processing occurs.
- or : A single client of type 1 (or type N) is operational, while its peers, the hub, and all servers are down and repairing; computational tasks remain paused.
- : A subset of server processors and clients of each type i are working, with the hub and the other components in failed-repair mode; processing is not active.
- : The active group includes servers, the hub, and clients of each class, while the rest are under repair; computation proceeds.
- : The entire network—n server processors, the hub, and all clients of each type—is up and executing tasks.
4.3. Setting the Problem of Selecting an Effective Configuration of a Computer Network
- N: Total distinct client categories;
- : Quantity of clients in category i ();
- n: Number of identical server CPUs;
- : Computational throughput of a type-i client (in FLOPS);
- : Processing capability of each server CPU (in FLOPS);
- : Data transfer rate between type-i clients and the server (bits/s);
- : Failure rate for client nodes of type i ();
- : Failure rate of a server CPU;
- : Failure rate of the network hub;
- : Repair rate of type-i client nodes ();
- : Repair rate of server CPUs;
- : Repair rate of the network hub;
- P: Chosen performance metric;
- C: Cost metric, context-dependent;
- : Achieved availability of the heterogeneous CN;
- : Target (maximum allowable) availability level;
- , : Upper and lower bounds on the number of server CPUs;
- , : Upper and lower bounds on count of client nodes in category i ().
4.4. Methods for Solving Multi-Criteria Optimization Problems
- Reduce the gap between the discovered non-dominated front and the true Pareto boundary.
- Provide a diverse set of solutions, ensuring a wide range of options.
- Maximize the positive effects derived from the non-dominated front, highlighting unattainable values for each criterion within the results.
- Assigning fitness and selecting candidates to achieve a Pareto-optimal set.
- Population dispersion by introducing diversity-preserving operations to avoid early convergence and ensure an evenly spread non-dominated set.
4.5. FFGA Method
- Input: (population).
- Output: F (suitability values).
- For each , calculate its rank:where denotes the cardinality of the set.
- Sort the population according to rank . Each is assigned a raw fitness by interpolating from the best () to the worst individual () using linear ranking [79].
- Calculate suitability values by averaging the raw suitability values among individuals with identical rank (suitability equalization in the target space).
5. Results
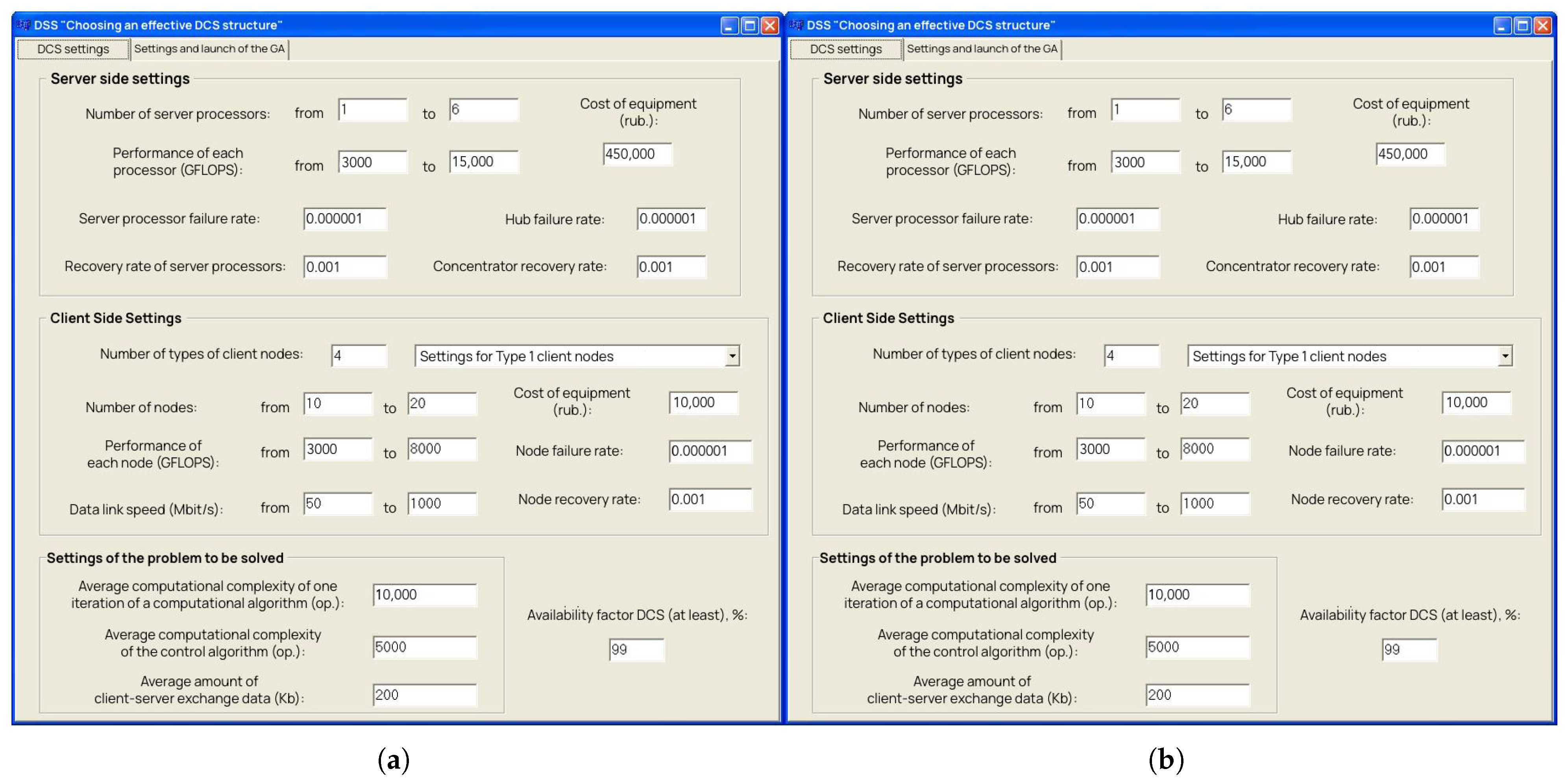
5.1. Automated DSS for Efficient Distributed CN Selection
5.2. Efficient Configuration Selection for Heterogeneous CNs
6. Discussion
6.1. Limitations
6.2. Decision Criteria for Applying the Proposed Approach
6.3. Future Work
7. Conclusions
- The total hardware cost of the FFGA-optimized configuration is 250 kUSD.
- The performance is 1220.745 TFLOPS;
- The availability factor is 99.03%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nižetić, S.; Šolić, P.; Gonzalez-De, D.L.d.I.; Patrono, L. Internet of Things (IoT): Opportunities, issues and challenges towards a smart and sustainable future. J. Clean. Prod. 2020, 274, 122877. [Google Scholar] [CrossRef]
- Pandiyan, P.; Saravanan, S.; Usha, K.; Kannadasan, R.; Alsharif, M.H.; Kim, M.K. Technological advancements toward smart energy management in smart cities. Energy Rep. 2023, 10, 648–677. [Google Scholar] [CrossRef]
- Lee, C.C.; Yuan, Z.; Wang, Q. How does information and communication technology affect energy security? International evidence. Energy Econ. 2022, 109, 105969. [Google Scholar] [CrossRef]
- Hussain, F.; Hussain, R.; Anpalagan, A.; Benslimane, A. A new block-based reinforcement learning approach for distributed resource allocation in clustered IoT networks. IEEE Trans. Veh. Technol. 2020, 69, 2891–2904. [Google Scholar] [CrossRef]
- Hussain, F.; Hassan, S.A.; Hussain, R.; Hossain, E. Machine learning for resource management in cellular and IoT networks: Potentials, current solutions, and open challenges. IEEE Commun. Surv. Tutor. 2020, 22, 1251–1275. [Google Scholar] [CrossRef]
- Górriz, J.M.; Ramírez, J.; Ortiz, A.; Martinez-Murcia, F.J.; Segovia, F.; Suckling, J.; Leming, M.; Zhang, Y.D.; Álvarez-Sánchez, J.R.; Bologna, G.; et al. Artificial intelligence within the interplay between natural and artificial computation: Advances in data science, trends and applications. Neurocomputing 2020, 410, 237–270. [Google Scholar] [CrossRef]
- Maier, H.R.; Galelli, S.; Razavi, S.; Castelletti, A.; Rizzoli, A.; Athanasiadis, I.N.; Sànchez-Marrè, M.; Acutis, M.; Wu, W.; Humphrey, G.B. Exploding the myths: An introduction to artificial neural networks for prediction and forecasting. Environ. Model. Softw. 2023, 167, 105776. [Google Scholar] [CrossRef]
- Chowdhury, A.M.M.; Imtiaz, M.H. Contactless Fingerprint Recognition Using Deep Learning—A Systematic Review. J. Cybersecur. Priv. 2022, 2, 714–730. [Google Scholar] [CrossRef]
- Lu, S.; Chai, H.; Sahoo, A.; Phung, B.T. Condition Monitoring Based on Partial Discharge Diagnostics Using Machine Learning Methods: A Comprehensive State-of-the-Art Review. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1861–1888. [Google Scholar] [CrossRef]
- Surenther, I.; Sridhar, K.; Roberts, M.K. Enhancing data transmission efficiency in wireless sensor networks through machine learning-enabled energy optimization: A grouping model approach. Ain Shams Eng. J. 2024, 15, 102644. [Google Scholar] [CrossRef]
- Cruz, Y.J.; Villalonga, A.; Castaño, F.; Rivas, M.; Haber, R.E. Automated Machine Learning Methodology for Optimizing Production Processes in Small and Medium-sized Enterprises. Oper. Res. Perspect. 2024, 12, 100308. [Google Scholar] [CrossRef]
- Champa-Bujaico, E.; Díez-Pascual, A.M.; Redondo, A.L.; Garcia-Diaz, P. Optimization of mechanical properties of multiscale hybrid polymer nanocomposites: A combination of experimental and machine learning techniques. Compos. Part B Eng. 2024, 269, 111099. [Google Scholar] [CrossRef]
- Guerrero, L.E.; Castillo, L.F.; Arango-Lopez, J.; Moreira, F. A systematic review of integrated information theory: A perspective from artificial intelligence and the cognitive sciences. Neural Comput. Appl. 2023, 37, 7575–7607. [Google Scholar] [CrossRef]
- Ito, T.; Yang, G.R.; Laurent, P.; Schultz, D.H.; Cole, M.W. Constructing neural network models from brain data reveals representational transformations linked to adaptive behavior. Nat. Commun. 2022, 13, 673. [Google Scholar] [CrossRef] [PubMed]
- Jalali Khalil Abadi, Z.; Mansouri, N.; Javidi, M.M. Deep reinforcement learning-based scheduling in distributed systems: A critical review. Knowl. Inf. Syst. 2024, 66, 5709–5782. [Google Scholar] [CrossRef]
- Donta, P.K.; Murturi, I.; Casamayor Pujol, V.; Sedlak, B.; Dustdar, S. Exploring the potential of distributed computing continuum systems. Computers 2023, 12, 198. [Google Scholar] [CrossRef]
- Ünal, H.T.; Başçiftçi, F. Evolutionary design of neural network architectures: A review of three decades of research. Artif. Intell. Rev. 2022, 55, 1723–1802. [Google Scholar] [CrossRef]
- Alghamdi, M.I. Optimization of load balancing and task scheduling in cloud computing environments using artificial neural networks-based binary particle swarm optimization (BPSO). Sustainability 2022, 14, 11982. [Google Scholar] [CrossRef]
- Aron, R.; Abraham, A. Resource scheduling methods for cloud computing environment: The role of meta-heuristics and artificial intelligence. Eng. Appl. Artif. Intell. 2022, 116, 105345. [Google Scholar] [CrossRef]
- Sharma, N.; Garg, P.; Sonal. Ant colony based optimization model for QoS-Based task scheduling in cloud computing environment. Meas. Sens. 2022, 24, 100531. [Google Scholar] [CrossRef]
- Chan, F.; Chung, S.H. Multi-criteria genetic optimization for distribution network problems. Int. J. Adv. Manuf. Technol. 2004, 24, 517–532. [Google Scholar] [CrossRef]
- Ho, W. Integrated analytic hierarchy process and its applications—A literature review. Eur. J. Oper. Res. 2008, 186, 211–228. [Google Scholar] [CrossRef]
- Gkoutioudi, K.; Karatza, H.D. A simulation study of multi-criteria scheduling in grid based on genetic algorithms. In Proceedings of the 2012 IEEE 10th International Symposium on Parallel and Distributed Processing with Applications, Leganes, Spain, 10–13 July 2012; pp. 317–324. [Google Scholar]
- Gkoutioudi, K.Z.; Karatza, H.D. Multi-criteria job scheduling in grid using an accelerated genetic algorithm. J. Grid Comput. 2012, 10, 311–323. [Google Scholar] [CrossRef]
- Mazza, A.; Chicco, G.; Russo, A. Optimal multi-objective distribution system reconfiguration with multi criteria decision making-based solution ranking and enhanced genetic operators. Int. J. Electr. Power Energy Syst. 2014, 54, 255–267. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Jing, R.; Zhu, X.; Zhu, Z.; Wang, W.; Meng, C.; Shah, N.; Li, N.; Zhao, Y. A multi-objective optimization and multi-criteria evaluation integrated framework for distributed energy system optimal planning. Energy Convers. Manag. 2018, 166, 445–462. [Google Scholar] [CrossRef]
- Hamdi, A.; Merghache, S.M. Application of artificial neural networks (ANN) and gray relational analysis (GRA) to modeling and optimization of the material ratio curve parameters when turning hard steel. Int. J. Adv. Manuf. Technol. 2023, 124, 3657–3670. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, G.; Wu, W.; Liao, S. Genetic algorithm-based operation strategy optimization and multi-criteria evaluation of distributed energy system for commercial buildings. Energy Convers. Manag. 2020, 226, 113529. [Google Scholar] [CrossRef]
- Gürler, H.E.; Özçalıcı, M.; Pamucar, D. Determining criteria weights with genetic algorithms for multi-criteria decision making methods: The case of logistics performance index rankings of European Union countries. Socio-Econ. Plan. Sci. 2024, 91, 101758. [Google Scholar] [CrossRef]
- Wang, J.; Ren, X.; Li, T.; Zhao, Q.; Dai, H.; Guo, Y.; Yan, J. Multi-objective optimization and multi-criteria evaluation framework for the design of distributed multi-energy system: A case study in industrial park. J. Build. Eng. 2024, 88, 109138. [Google Scholar] [CrossRef]
- Hai, T.; Almujibah, H.; Mostafa, L.; Kumar, J.; Van Thuong, T.; Farhang, B.; Mahmoud, M.H.; El-Shafai, W. Innovative clean hybrid energy system driven by flame-assisted SOFC: Multi-criteria optimization with ANN and genetic algorithm. Int. J. Hydrogen Energy 2024, 63, 193–206. [Google Scholar] [CrossRef]
- Hussien, A.G.; Bouaouda, A.; Alzaqebah, A.; Kumar, S.; Hu, G.; Jia, H. An in-depth survey of the artificial gorilla troops optimizer: Outcomes, variations, and applications. Artif. Intell. Rev. 2024, 57, 246. [Google Scholar] [CrossRef]
- Qiao, Y.; Yin, J.; Wang, W.; Duarte, F.; Yang, J.; Ratti, C. Survey of deep learning for autonomous surface vehicles in marine environments. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3678–3701. [Google Scholar] [CrossRef]
- Taubert, O.; Weiel, M.; Coquelin, D.; Farshian, A.; Debus, C.; Schug, A.; Streit, A.; Götz, M. Massively parallel genetic optimization through asynchronous propagation of populations. In Proceedings of the International Conference on High Performance Computing, Hamburg, Germany, 21–25 May 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 106–124. [Google Scholar]
- Haritha, K.; Shailesh, S.; Judy, M.; Ravichandran, K.; Krishankumar, R.; Gandomi, A.H. A novel neural network model with distributed evolutionary approach for big data classification. Sci. Rep. 2023, 13, 11052. [Google Scholar] [CrossRef]
- Capel, M.I.; Salguero-Hidalgo, A.; Holgado-Terriza, J.A. Parallel PSO for Efficient Neural Network Training Using GPGPU and Apache Spark in Edge Computing Sets. Algorithms 2024, 17, 378. [Google Scholar] [CrossRef]
- Xu, H.; Deng, Q.; Zhang, Z.; Lin, S. A hybrid differential evolution particle swarm optimization algorithm based on dynamic strategies. Sci. Rep. 2025, 15, 4518. [Google Scholar] [CrossRef]
- Sahu, A.; Davis, K. Inter-domain fusion for enhanced intrusion detection in power systems: An evidence theoretic and meta-heuristic approach. Sensors 2022, 22, 2100. [Google Scholar] [CrossRef] [PubMed]
- Baioletti, M.; Di Bari, G.; Milani, A.; Poggioni, V. Differential evolution for neural networks optimization. Mathematics 2020, 8, 69. [Google Scholar] [CrossRef]
- Tang, B.; Xiang, K.; Pang, M. An integrated particle swarm optimization approach hybridizing a new self-adaptive particle swarm optimization with a modified differential evolution. Neural Comput. Appl. 2020, 32, 4849–4883. [Google Scholar] [CrossRef]
- Giordano, M.; Doshi, R.; Lu, Q.; Murmann, B. TinyForge: A Design Space Exploration to Advance Energy and Silicon Area Trade-offs in tinyML Compute Architectures with Custom Latch Arrays. In Proceedings of the 29th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, La Jolla, CA, USA, 27 April 2024–1 May 2024; Volume 3, pp. 1033–1047. [Google Scholar]
- Faraji Googerdchi, K.; Asadi, S.; Jafari, S.M. Customer churn modeling in telecommunication using a novel multi-objective evolutionary clustering-based ensemble learning. PLoS ONE 2024, 19, e0303881. [Google Scholar] [CrossRef]
- Shao, Y.; Lin, J.W.; Srivastava, G.; Guo, D.; Zhang, H.; Yi, H.; Jolfaei, A. Multi-Objective Neural Evolutionary Algorithm for Combinatorial Optimization Problems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 2133–2143. [Google Scholar] [CrossRef]
- Zgurovsky, M.; Sineglazov, V.; Chumachenko, E. Artificial Intelligence Systems Based on Hybrid Neural Networks; Springer: Cham, Switzerland, 2023; p. 512. [Google Scholar]
- Aspray, W. John von Neumann and the Origins of Modern Computing; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Harada, T.; Alba, E. Parallel genetic algorithms: A useful survey. ACM Comput. Surv. (CSUR) 2020, 53, 1–39. [Google Scholar] [CrossRef]
- Vie, A.; Kleinnijenhuis, A.; Farmer, D. Qualities, challenges and future of genetic algorithms: A literature review. arXiv 2021, arXiv:2011.05277. [Google Scholar]
- Soufan, O.; Kleftogiannis, D.; Kalnis, P.; Bajic, V. DWFS: A Wrapper Feature Selection Tool Based on a Parallel Genetic Algorithm. PLoS ONE 2015, 10, e0117988. [Google Scholar] [CrossRef]
- Knysh, D.; Kureichik, V. Parallel genetic algorithms: A survey and problem state of the art. J. Comput. Syst. Sci. Int. 2010, 49, 579–589. [Google Scholar] [CrossRef]
- Kazimipour, B.; Li, X.; Qin, A. A review of population initialization techniques for evolutionary algorithms. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014. [Google Scholar] [CrossRef]
- Rigatti, S. Random Forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep learning with tensorflow: A review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
- Chen, T.; Li, M.; Li, Y.; Lin, M.; Wang, N.; Wang, M.; Zhang, Z. Mxnet: A flexible and efficient machine learning library for heterogeneous distributed systems. arXiv 2015, arXiv:1512.01274. [Google Scholar]
- Xu, Y.; Lee, H.; Chen, D.; Hechtman, B.; Huang, Y.; Joshi, R.; Chen, Z. GSPMD: General and scalable parallelization for ML computation graphs. arXiv 2021, arXiv:2105.04663. [Google Scholar]
- Syan, C.; Ramsoobag, G. Maintenance Applications of Multi-Criteria Optimization: A Review. Reliab. Eng. Syst. Saf. 2019, 190, 106520. [Google Scholar] [CrossRef]
- Rece, L.; Vlase, S.; Ciuiu, D.; Neculoiu, G.; Mocanu, S.; Modrea, A. Queueing Theory-Based Mathematical Models Applied to Enterprise Organization and Industrial Production Optimization. Mathematics 2022, 10, 2520. [Google Scholar] [CrossRef]
- Furber, S. Large-scale neuromorphic computing systems. J. Neural Eng. 2016, 13, 051001. [Google Scholar] [CrossRef]
- Xiao, Y.; Nazarian, S.; Bogdan, P. Self-Optimizing and Self-Programming Computing Systems: A Combined Compiler, Complex Networks, and Machine Learning Approach. IEEE Trans. Very Large Scale Integr. Syst. 2019, 27, 1416–1427. [Google Scholar] [CrossRef]
- Martínez, V.; Berzal, F.; Cubero, J.C. A Survey of Link Prediction in Complex Networks. ACM Comput. Surv. 2017, 49, 1–33. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; Rostamizadeh, A.; Gonina, E.; Ben-tzur, J.; Hardt, M.; Recht, B.; Talwalkar, A. A System for Massively Parallel Hyperparameter Tuning. In Proceedings of the Machine Learning and Systems, Austin, TX, USA, 2–4 March 2020. [Google Scholar]
- Mochinski, M.A.; Biczkowski, M.; Chueiri, I.J.; Jamhour, E.; Zambenedetti, V.C.; Pellenz, M.E.; Enembreck, F. Developing an Intelligent Decision Support System for large-scale smart grid communication network planning. Knowl.-Based Syst. 2024, 283, 111159. [Google Scholar] [CrossRef]
- Szabo, B.; Babuska, I. Finite Element Analysis; Wiley: Hoboken, NJ, USA, 2021; p. 357. [Google Scholar]
- Kuang, Z.; Li, L.; Gao, J.; Zhao, L.; Liu, A. Partial Offloading Scheduling and Power Allocation for Mobile Edge Computing Systems. IEEE Internet Things J. 2019, 6, 6774–6785. [Google Scholar] [CrossRef]
- Zarifa, M.; Nazrin, Q. Analysis of Methods for Increasing the Efficiency of Information Transfer. In Proceedings of the Current Challenges, Trends and Transformations, Boston, MA, USA, 13–16 December 2022. [Google Scholar]
- Mangalampalli, S.; Karri, G.R.; Ratnamani, M.; Mohanty, S.N.; Jabr, B.A.; Ali, Y.A.; Ali, S.; Abdullaeva, B.S. Efficient deep reinforcement learning based task scheduler in multi cloud environment. Sci. Rep. 2024, 14, 21850. [Google Scholar] [CrossRef]
- Giambene, G. Queuing Theory and Telecommunications; Springer: Berlin, Germany, 2014; p. 513. [Google Scholar]
- Efrosinin, D.; Stepanova, N.; Sztrik, J. Algorithmic Analysis of Finite-Source Multi-Server Heterogeneous Queueing Systems. Mathematics 2021, 9, 2624. [Google Scholar] [CrossRef]
- Zou, Y.; Čepin, M. Loss of load probability for power systems based on renewable sources. Reliab. Eng. Syst. Saf. 2024, 247, 110136. [Google Scholar] [CrossRef]
- Chen, M.; Poor, H.V.; Saad, W.; Cui, S. Convergence Time Optimization for Federated Learning Over Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 2457–2471. [Google Scholar] [CrossRef]
- Feng, G. Analysis and Synthesis of Fuzzy Control Systems: A Model-Based Approach; CRC Press: Boca Raton, FL, USA, 2018; p. 281. [Google Scholar]
- Mattson, C.A.; Mullur, A.A.; Messac, A. Smart Pareto Filter: Obtaining a Minimal Representation of Multiobjective Design Space. Eng. Optim. 2004, 36, 721–740. [Google Scholar] [CrossRef]
- Ghosh, D.; Chakraborty, D. A Direction-Based Classical Method to Obtain Complete Pareto Set of Multi-Criteria Optimization Problems. OPSEARCH 2015, 52, 340–366. [Google Scholar] [CrossRef]
- Asadi, E.; Silva, M.d.; Antunes, C.; Dias, L.; Glicksman, L. Multi-Objective Optimization for Building Retrofit: A Model Using Genetic Algorithm and Artificial Neural Network and an Application. Energy Build. 2014, 81, 444–456. [Google Scholar] [CrossRef]
- Lindroth, P.; Patriksson, M.; Strömberg, A. Approximating the Pareto Optimal Set Using a Reduced Set of Objective Functions. Eur. J. Oper. Res. 2010, 207, 1519–1534. [Google Scholar] [CrossRef]
- Vikhar, P. Evolutionary Algorithms: A Critical Review and Its Future Prospects. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016. [Google Scholar]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-Archive Evolutionary Algorithm for Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2019, 23, 303–315. [Google Scholar] [CrossRef]
- Fleming, G.A. The New Method of Adaptive CPU Scheduling Using Fonseca and Fleming’s Genetic Algorithm. J. Theor. Appl. Inf. Technol. 2012, 37, 1–16. [Google Scholar]
- Abbass, H.A.; Sarker, R. The Pareto Differential Evolution Algorithm. Int. J. Artif. Intell. Tools 2002, 11, 531–552. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V. Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.; Blum, M.; Hutter, F. Efficient and Robust Automated Machine Learning. In Proceedings of the Advances in Neural Information Processing Systems, Red Hook, NY, USA, 7–12 December 2015. [Google Scholar]
- Bjarne, S. Programming: Principles and Practice Using C++; Williams: Moscow, Russia, 2016; p. 1328. [Google Scholar]
- Karaci, A. Performance Comparison of Managed C# and Delphi Prism in Visual Studio and Unmanaged Delphi 2009 and C++ Builder 2009 Languages. Int. J. Comput. Appl. 2011, 26, 9–15. [Google Scholar] [CrossRef]
- Jorgensen, P. Software Testing; Auerbach Publications: New York, NY, USA, 2013; p. 440. [Google Scholar]
- Arnott, D.; Pervan, G. A Critical Analysis of Decision Support Systems Research. Formul. Res. Methods Inf. Syst. 2015, 1, 127–168. [Google Scholar] [CrossRef]
- Gill, S.S.; Wu, H.; Patros, P.; Ottaviani, C.; Arora, P.; Pujol, V.C.; Haunschild, D.; Parlikad, A.K.; Cetinkaya, O.; Lutfiyya, H.; et al. Modern computing: Vision and challenges. Telemat. Inform. Rep. 2024, 13, 100116. [Google Scholar] [CrossRef]
- Fang, J.; Yang, Y. Chernoff type inequalities involving k-order width and their stability properties. Results Math. 2023, 78, 101. [Google Scholar] [CrossRef]
- Zhou, Y.; Zeng, C. On some sharp Chernoff type inequalities. Acta Math. Sci. 2025, 45, 540–552. [Google Scholar] [CrossRef]
- Liu, X.; Ying, L. Universal scaling of distributed queues under load balancing in the super-Halfin-Whitt regime. IEEE/ACM Trans. Netw. 2021, 30, 190–201. [Google Scholar] [CrossRef]
- Taghvaei, A.; Mehta, P.G. On the Lyapunov Foster criterion and Poincaré inequality for reversible Markov chains. IEEE Trans. Autom. Control 2021, 67, 2605–2609. [Google Scholar] [CrossRef]
- Kokkinos, K.; Karayannis, V.; Samaras, N.; Moustakas, K. Multi-scenario analysis on hydrogen production development using PESTEL and FCM models. J. Clean. Prod. 2023, 419, 138251. [Google Scholar] [CrossRef]
- Yu, X.; Zhu, L.; Wang, Y.; Filev, D.; Yao, X. Internal combustion engine calibration using optimization algorithms. Appl. Energy 2022, 305, 117894. [Google Scholar] [CrossRef]
- García-Zamora, D.; Labella, Á.; Ding, W.; Rodríguez, R.M.; Martínez, L. Large-scale group decision making: A systematic review and a critical analysis. IEEE/CAA J. Autom. Sin. 2022, 9, 949–966. [Google Scholar] [CrossRef]
- Truică, C.O.; Apostol, E.S.; Darmont, J.; Pedersen, T.B. The forgotten document-oriented database management systems: An overview and benchmark of native XML DODBMSes in comparison with JSON DODBMSes. Big Data Res. 2021, 25, 100205. [Google Scholar] [CrossRef]
- Sood, K.; Yu, S.; Nguyen, D.D.N.; Xiang, Y.; Feng, B.; Zhang, X. A tutorial on next generation heterogeneous IoT networks and node authentication. IEEE Internet Things Mag. 2022, 4, 120–126. [Google Scholar] [CrossRef]
- Ling, Z.; Jiang, X.; Tan, X.; He, H.; Zhu, S.; Yang, J. Joint Dynamic Data and Model Parallelism for Distributed Training of DNNs Over Heterogeneous Infrastructure. IEEE Trans. Parallel Distrib. Syst. 2024. [Google Scholar] [CrossRef]
- Poorzare, R.; Kanellopoulos, D.N.; Sharma, V.K.; Dalapati, P.; Waldhorst, O.P. Network Digital Twin Towards Networking, Telecommunications, and Traffic Engineering: A Survey. IEEE Access 2025, 13, 16489–16538. [Google Scholar] [CrossRef]
- Awaysheh, F.M.; Alazab, M.; Garg, S.; Niyato, D.; Verikoukis, C. Big data resource management & networks: Taxonomy, survey, and future directions. IEEE Commun. Surv. Tutor. 2021, 23, 2098–2130. [Google Scholar]
- Duer, S.; Woźniak, M.; Paś, J.; Zajkowski, K.; Bernatowicz, D.; Ostrowski, A.; Budniak, Z. Reliability testing of wind farm devices based on the mean time between failures (MTBF). Energies 2023, 16, 1659. [Google Scholar] [CrossRef]
- Bejarano, L.A.; Espitia, H.E.; Montenegro, C.E. Clustering analysis for the Pareto optimal front in multi-objective optimization. Computation 2022, 10, 37. [Google Scholar] [CrossRef]
- Montori, F.; Zyrianoff, I.; Gigli, L.; Calvio, A.; Venanzi, R.; Sindaco, S.; Sciullo, L.; Zonzini, F.; Zauli, M.; Testoni, N.; et al. An iot toolchain architecture for planning, running and managing a complete condition monitoring scenario. IEEE Access 2023, 11, 6837–6856. [Google Scholar] [CrossRef]
- Ulfert, A.S.; Antoni, C.H.; Ellwart, T. The role of agent autonomy in using decision support systems at work. Comput. Hum. Behav. 2022, 126, 106987. [Google Scholar] [CrossRef]
- Soori, M.; Jough, F.K.G.; Dastres, R.; Arezoo, B. AI-Based Decision Support Systems in Industry 4.0, A Review. J. Econ. Technol. in press. 2024. [Google Scholar] [CrossRef]
- Liu, G.S. Three m-failure group maintenance models for M/M/N unreliable queuing service systems. Comput. Ind. Eng. 2012, 62, 1011–1024. [Google Scholar] [CrossRef]
- Marinković, Z.; Stošić, B.P. Applications of artificial neural networks for calculation of the Erlang B formula and its inverses. Eng. Rep. 2023, 5, e12647. [Google Scholar] [CrossRef]
- Aras, A.K.; Chen, X.; Liu, Y. Many-server Gaussian limits for overloaded non-Markovian queues with customer abandonment. Queueing Syst. 2018, 89, 81–125. [Google Scholar] [CrossRef]
- Liao, H.; He, Y.; Wu, X.; Wu, Z.; Bausys, R. Reimagining multi-criterion decision making by data-driven methods based on machine learning: A literature review. Inf. Fusion 2023, 100, 101970. [Google Scholar] [CrossRef]
- Lin, L.; Cao, J.; Lam, J.; Rutkowski, L.; Dimirovski, G.M.; Zhu, S. A bisimulation-based foundation for scale reductions of continuous-time Markov chains. IEEE Trans. Autom. Control 2024, 69, 5743–5758. [Google Scholar] [CrossRef]
- Kabadurmus, O.; Smith, A.E. Evaluating reliability/survivability of capacitated wireless networks. IEEE Trans. Reliab. 2017, 67, 26–40. [Google Scholar] [CrossRef]
- Baktir, A.C.; Tunca, C.; Ozgovde, A.; Salur, G.; Ersoy, C. SDN-based multi-tier computing and communication architecture for pervasive healthcare. IEEE Access 2018, 6, 56765–56781. [Google Scholar] [CrossRef]
- Shiguihara, P.; Lopes, A.D.A.; Mauricio, D. Dynamic Bayesian network modeling, learning, and inference: A survey. IEEE Access 2021, 9, 117639–117648. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nedić, A.; Ozdaglar, A.; Johansson, M. Distributed subgradient methods for multi-agent optimization. IEEE Trans. Autom. Control 2009, 54, 148–160. [Google Scholar] [CrossRef]

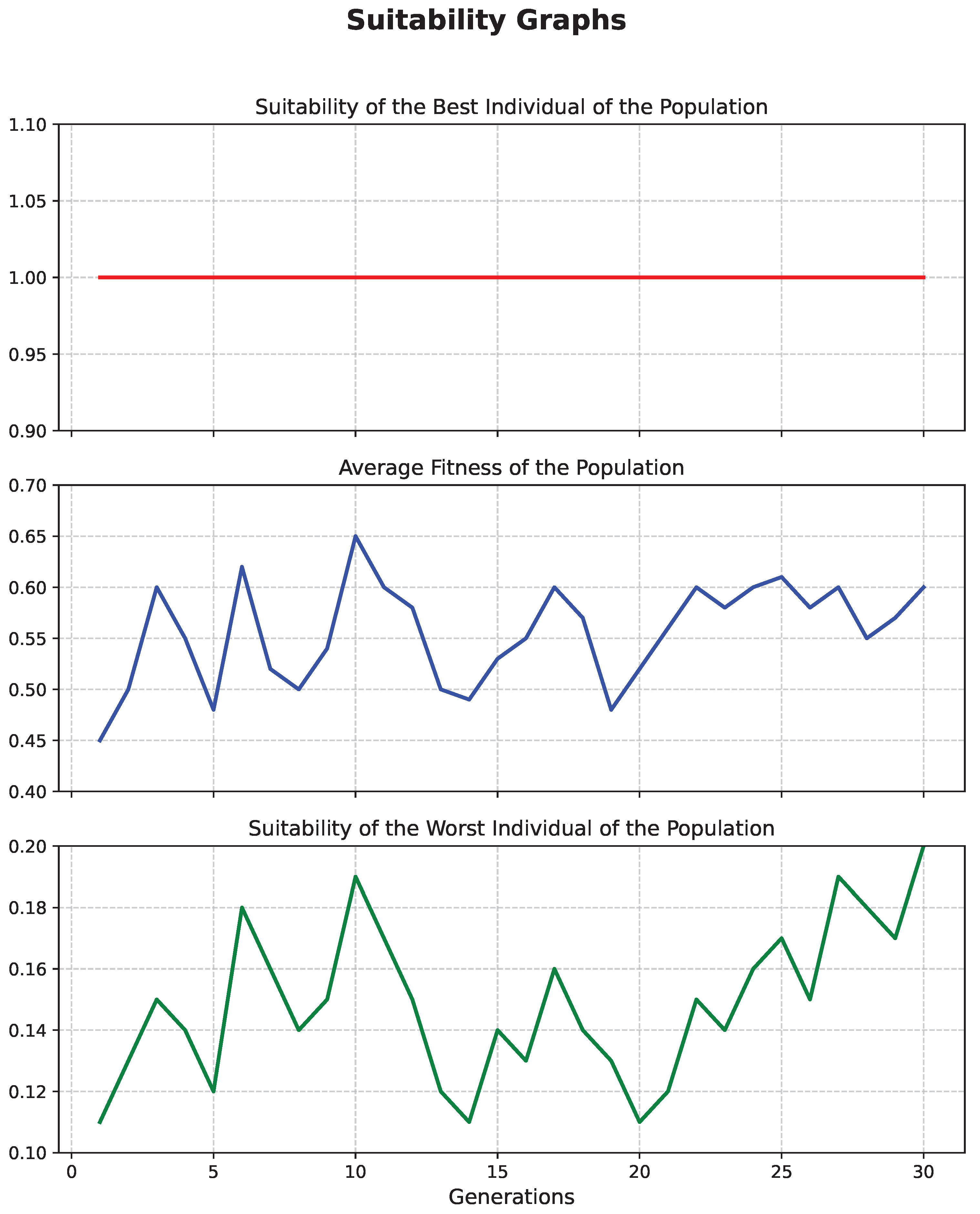
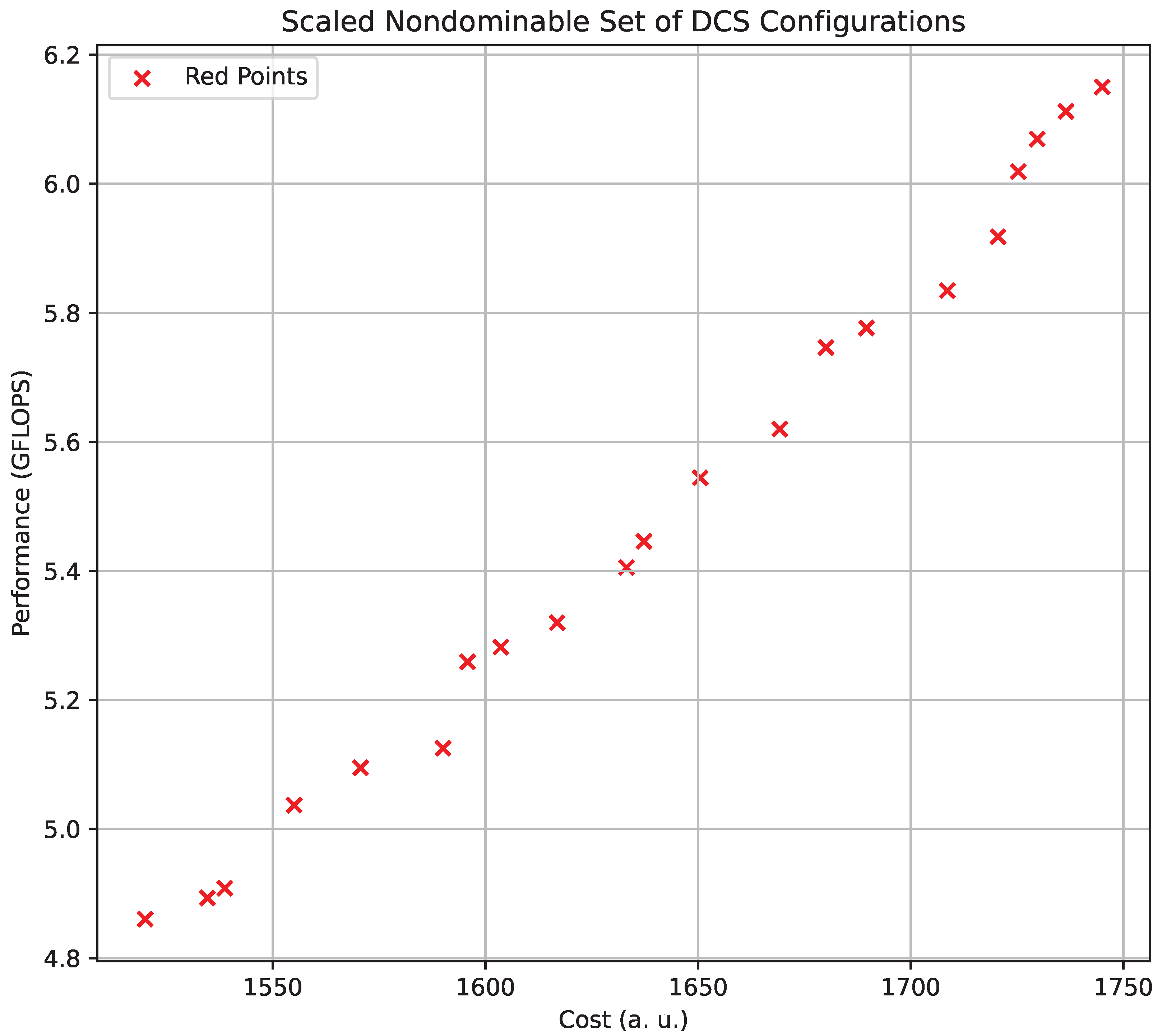
| Node Type | Number of Nodes | Performance (TFLOPS) | Data Link Speed (Gbit/s) |
|---|---|---|---|
| Client Node (Celeron G5905 ) | 15 | 3 | 8 |
| Client Node (Pentium Dual Core G4400) | 38 | 7.2 | 8 |
| Client Node (Intel Core i3-9100F) | 10 | 9.2 | 8 |
| Client Node (Intel Core i3-12100F) | 11 | 12 | 9 |
| Server Node (Xeon E-2176M) | 1 | 461 (per processor) | N/A |
| Architecture | (s) | (%) | (kUSD) |
|---|---|---|---|
| Homogeneous cluster | 3.6 | 98.5 | 270 |
| Heuristic heterogeneous configuration | 2.9 | 98.9 | 255 |
| FFGA-optimized configuration (this work) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tynchenko, V.V.; Malashin, I.; Kurashkin, S.O.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Multi-Criteria Genetic Algorithm for Optimizing Distributed Computing Systems in Neural Network Synthesis. Future Internet 2025, 17, 215. https://doi.org/10.3390/fi17050215
Tynchenko VV, Malashin I, Kurashkin SO, Tynchenko V, Gantimurov A, Nelyub V, Borodulin A. Multi-Criteria Genetic Algorithm for Optimizing Distributed Computing Systems in Neural Network Synthesis. Future Internet. 2025; 17(5):215. https://doi.org/10.3390/fi17050215
Chicago/Turabian StyleTynchenko, Valeriya V., Ivan Malashin, Sergei O. Kurashkin, Vadim Tynchenko, Andrei Gantimurov, Vladimir Nelyub, and Aleksei Borodulin. 2025. "Multi-Criteria Genetic Algorithm for Optimizing Distributed Computing Systems in Neural Network Synthesis" Future Internet 17, no. 5: 215. https://doi.org/10.3390/fi17050215
APA StyleTynchenko, V. V., Malashin, I., Kurashkin, S. O., Tynchenko, V., Gantimurov, A., Nelyub, V., & Borodulin, A. (2025). Multi-Criteria Genetic Algorithm for Optimizing Distributed Computing Systems in Neural Network Synthesis. Future Internet, 17(5), 215. https://doi.org/10.3390/fi17050215









