Multifractality and Its Sources in the Digital Currency Market
Abstract
1. Introduction
2. Materials and Methods
2.1. Data and Its Characteristics
2.2. Multifractal Formalism
2.3. Detrended Cross-Correlation Coefficient
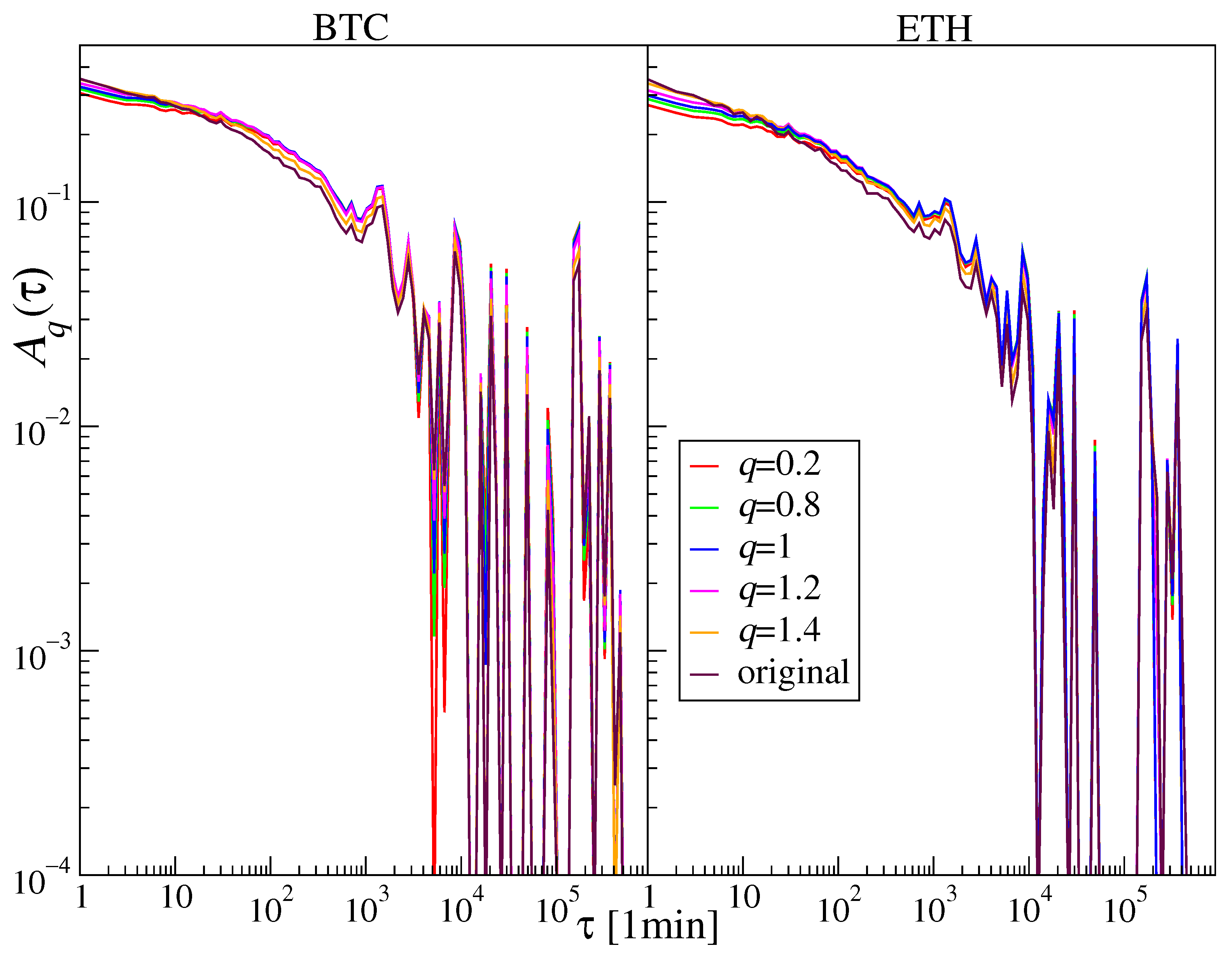
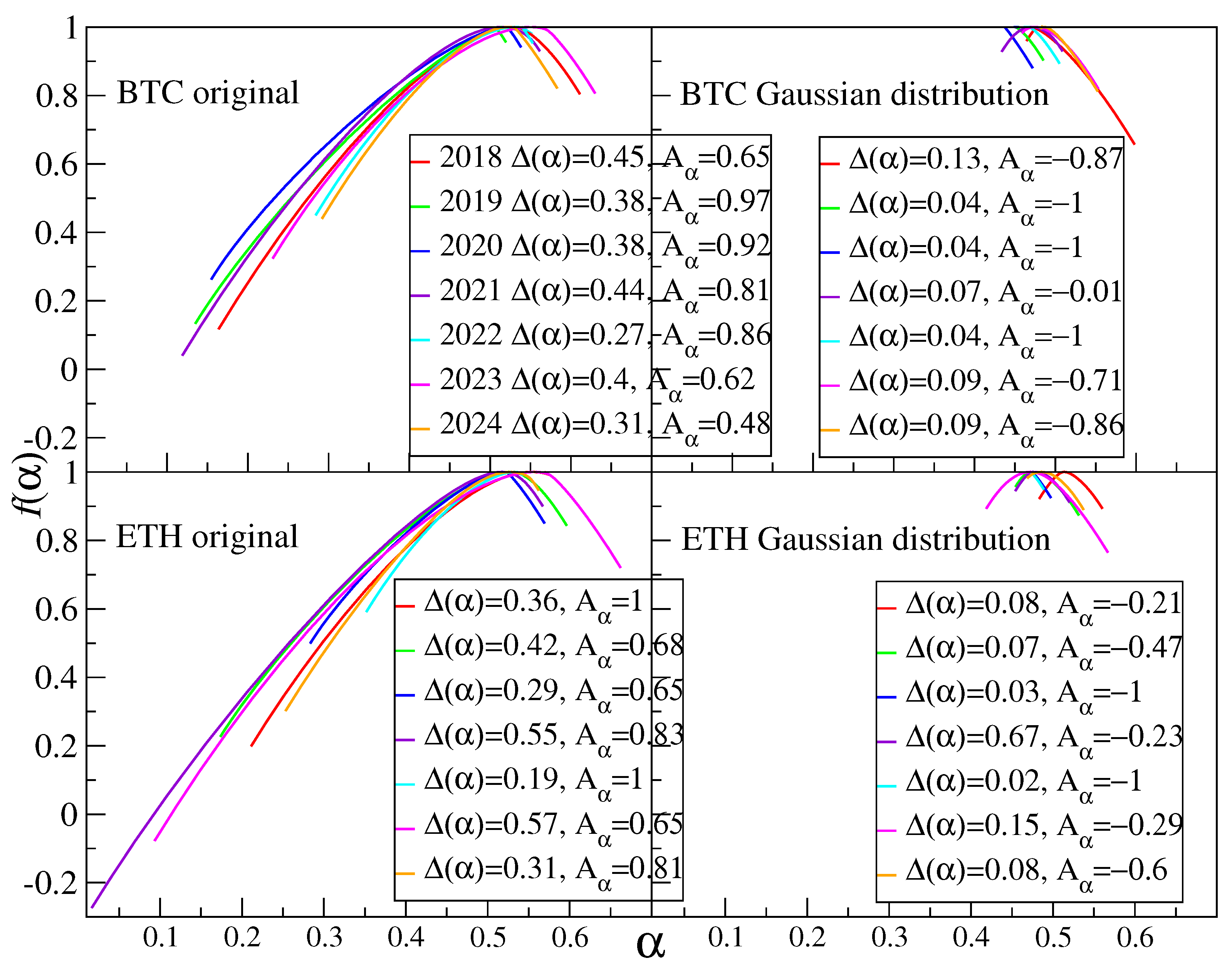
2.4. Decomposing Sources of Multifractality
3. Results
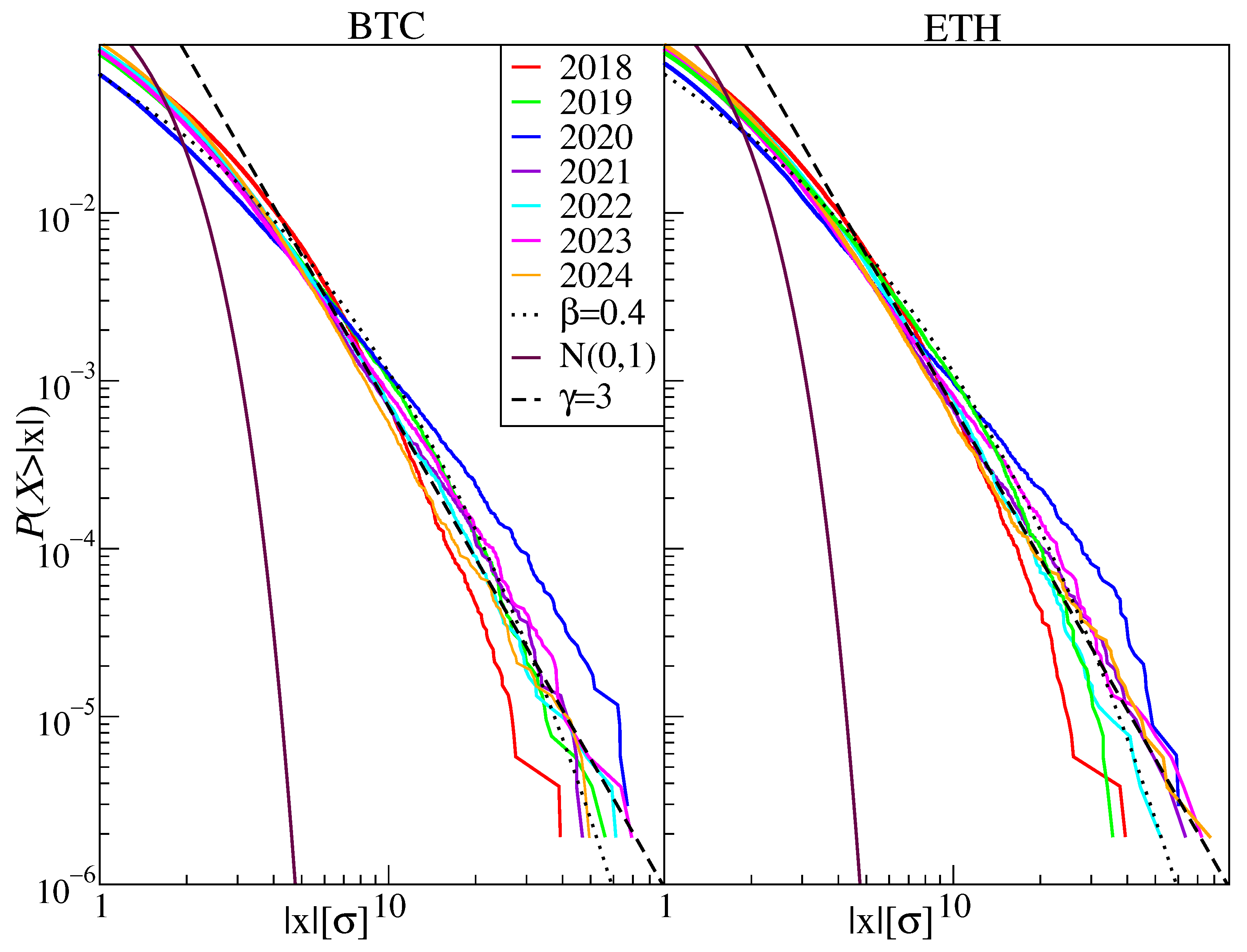
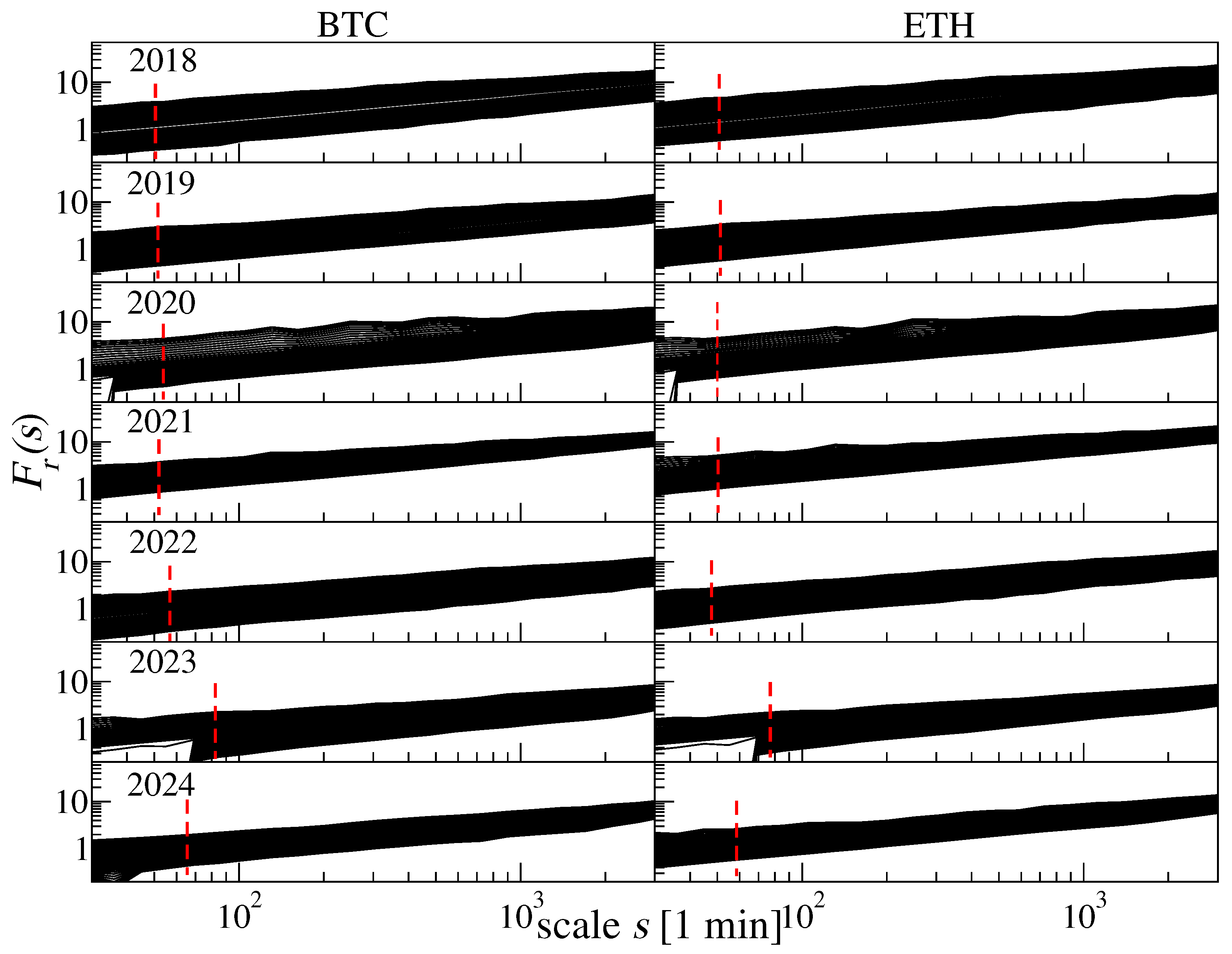
3.1. Multifractal Characteristics of BTC and ETH in the Years 2018–2024
3.2. Cross-Correlations Between BTC and ETH
3.3. Detrended Cross-Correlation
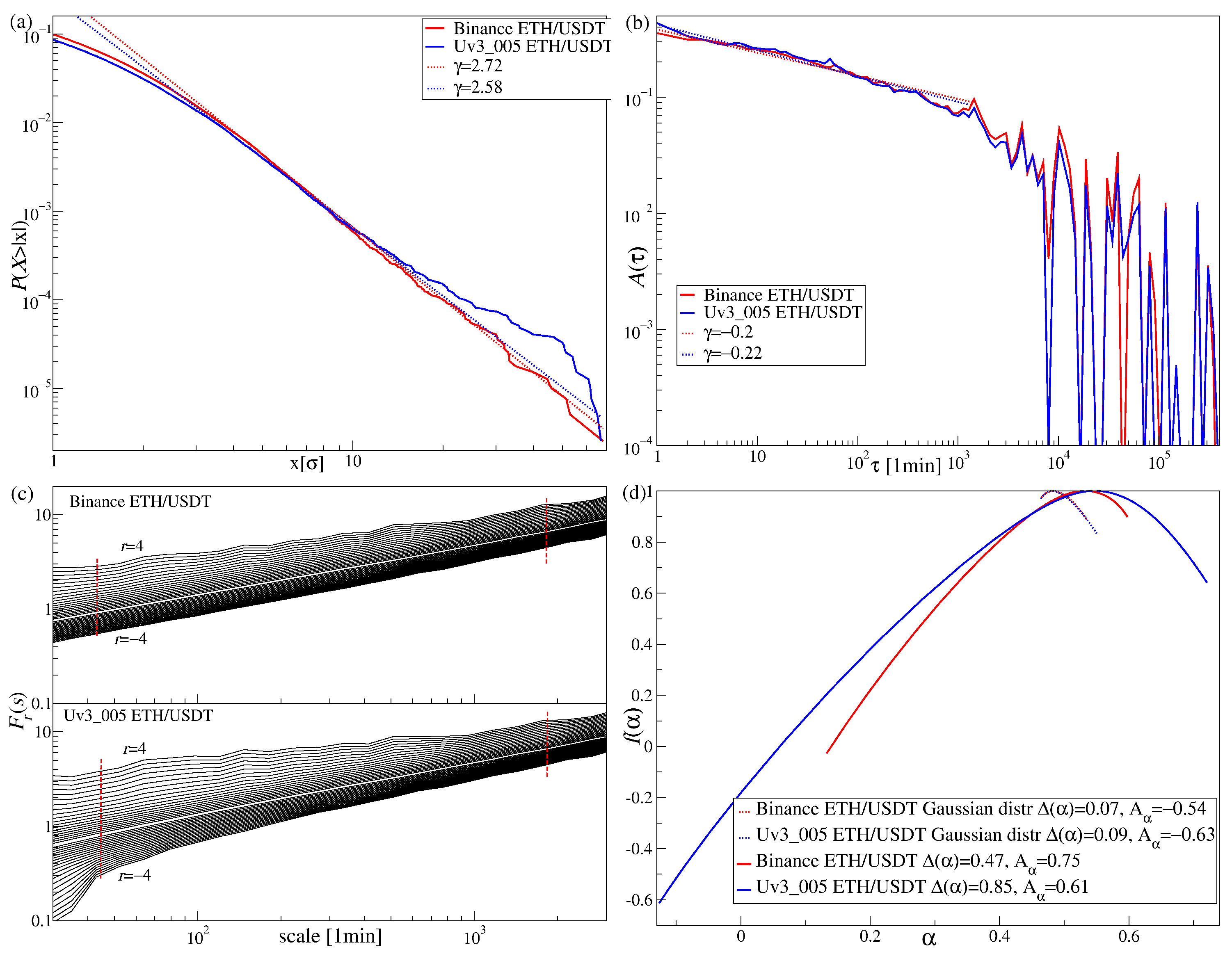
3.4. ETH from Decentralized Exchange
3.5. NFT Tokens
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: http://bitcoin.org/bitcoin.pdf (accessed on 1 July 2025).
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale characteristics of the emerging global cryptocurrency market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- Corbet, S.; Hou, Y.G.; Hu, Y.; Larkin, C.; Lucey, B.; Oxley, L. Cryptocurrency liquidity and volatility interrelationships during the COVID-19 pandemic. Financ. Res. Lett. 2022, 45, 102137. [Google Scholar] [CrossRef]
- Evrim Mandaci, P.; Cagli, E.C. Herding intensity and volatility in cryptocurrency markets during the COVID-19. Financ. Res. Lett. 2022, 46, 102382. [Google Scholar] [CrossRef]
- Nguyen, A.P.N.; Mai, T.T.; Bezbradica, M.; Crane, M. Volatility and returns connectedness in cryptocurrency markets: Insights from graph-based methods. Phys. A Stat. Mech. Its Appl. 2023, 632, 129349. [Google Scholar] [CrossRef]
- Drożdż, S.; Gębarowski, R.; Minati, L.; Oświęcimka, P.; Wątorek, M. Bitcoin market route to maturity? Evidence from return fluctuations, temporal correlations and multiscaling effects. Chaos 2018, 28, 071101. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Ludermir, T.B.; Stosic, T. Collective behavior of cryptocurrency price changes. Phys. A Stat. Mech. Its Appl. 2018, 507, 499–509. [Google Scholar] [CrossRef]
- James, N.; Menzies, M.; Chan, J. Changes to the extreme and erratic behaviour of cryptocurrencies during COVID-19. Phys. A Stat. Mech. Its Appl. 2021, 565, 125581. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Wątorek, M. What is mature and what is still emerging in the cryptocurrency market? Entropy 2023, 25, 772. [Google Scholar] [CrossRef]
- Takaishi, T. Statistical properties and multifractality of Bitcoin. Phys. A Stat. Mech. Its Appl. 2018, 506, 507–519. [Google Scholar] [CrossRef]
- Takaishi, T.; Adachi, T. Market efficiency, liquidity, and multifractality of Bitcoin: A dynamic study. Asia-Pac. Financ. Mark. 2020, 27, 145–154. [Google Scholar] [CrossRef]
- James, N. Dynamics, behaviours, and anomaly persistence in cryptocurrencies and equities surrounding COVID-19. Phys. A Stat. Mech. Its Appl. 2021, 570, 125831. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Collective correlations, dynamics, and behavioural inconsistencies of the cryptocurrency market over time. Nonlinear Dyn. 2022, 107, 4001–4017. [Google Scholar] [CrossRef]
- Wątorek, M.; Kwapień, J.; Drożdż, S. Multifractal cross-correlations of bitcoin and ether trading characteristics in the post-COVID-19 time. Future Internet 2022, 14, 215. [Google Scholar] [CrossRef]
- Brouty, X.; Garcin, M. Fractal properties, information theory, and market efficiency. Chaos Solitons Fractals 2024, 180, 114543. [Google Scholar] [CrossRef]
- Bui, H.Q.; Schinckus, C.; Al-Jaifi, H. Long-range correlations in cryptocurrency markets: A multi-scale DFA approach. Phys. A Stat. Mech. Its Appl. 2025, 661, 130417. [Google Scholar] [CrossRef]
- Kwapień, J.; Drożdż, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Manavi, S.A.; Jafari, G.; Rouhani, S.; Ausloos, M. Demythifying the belief in cryptocurrencies decentralized aspects. A study of cryptocurrencies time cross-correlations with common currencies, commodities and financial indices. Phys. A Stat. Mech. Its Appl. 2020, 556, 124759. [Google Scholar] [CrossRef]
- Spurr, A.; Ausloos, M. Challenging practical features of Bitcoin by the main altcoins. Qual. Quant. 2021, 55, 1541–1559. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Xie, W.J.; Zhou, W.X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraimant, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Farmer, J.D.; Gillemot, L.; Lillo, F.; Mike, S.; Sen, A. What really causes large price changes? Quant. Financ. 2004, 4, 383–397. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Ausloos, M.; Ivanova, K. Multifractal nature of stock exchange prices. Comput. Phys. Commun. 2002, 147, 582–585. [Google Scholar] [CrossRef][Green Version]
- Kutner, R.; Świtała, F. Remarks on the possible universal mechanism of the non-linear long-term autocorrelations in financial time-series. Phys. A Stat. Mech. Its Appl. 2004, 344, 244–251. [Google Scholar] [CrossRef]
- Cont, R. Volatility Clustering in Financial Markets: Empirical Facts and Agent-Based Models. In Long Memory in Economics; Teyssière, G., Kirman, A.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 289–309. [Google Scholar] [CrossRef]
- Oh, G.; Kim, S.; Eom, C. Long-term memory and volatility clustering in high-frequency price changes. Phys. A Stat. Mech. Its Appl. 2008, 387, 1247–1254. [Google Scholar] [CrossRef]
- Zhou, W.X. The components of empirical multifractality in financial returns. Europhys. Lett. 2009, 88, 28004. [Google Scholar] [CrossRef]
- Barunik, J.; Aste, T.; Di Matteo, T.; Liu, R. Understanding the source of multifractality in financial markets. Phys. A Stat. Mech. Its Appl. 2012, 391, 4234–4251. [Google Scholar] [CrossRef]
- Green, D.; Hanan, W.R.; Heffernan, S. The origins of multifractality in financial time series and the effect of extreme events. Eur. Phys. J. B 2014, 87, 129. [Google Scholar] [CrossRef]
- Morales, R.; Di Matteo, T.; Aste, T. Dependency structure and scaling properties of financial time series are related. Sci. Rep. 2014, 4, 4589. [Google Scholar] [CrossRef]
- Klamut, J.; Kutner, R.; Gubiec, T.; Struzik, Z.R. Multibranch multifractality and the phase transitions in time series of mean interevent times. Phys. Rev. E 2020, 101, 063303. [Google Scholar] [CrossRef]
- Kutner, R.; Ausloos, M.; Grech, D.; Matteo, T.D.; Schinckus, C.; Stanley, H.E. Econophysics and sociophysics: Their milestones & challenges. Phys. A Stat. Mech. Its Appl. 2019, 516, 240–253. [Google Scholar]
- Kwapień, J.; Blasiak, P.; Drożdż, S.; Oświęcimka, P. Genuine multifractality in time series is due to temporal correlations. Phys. Rev. E 2023, 107, 034139. [Google Scholar] [CrossRef]
- Kluszczyński, R.; Drożdż, S.; Kwapień, J.; Stanisz, T.; Wątorek, M. Disentangling sources of multifractality in time series. Mathematics 2025, 13, 205. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Oświęcimka, P.; Rak, R. Quantitative features of multifractal subtleties in time series. Europhys. Lett. 2009, 88, 60003. [Google Scholar] [CrossRef]
- Zhou, W.X. Finite-size effect and the components of multifractality in financial volatility. Chaos Solitons Fractals 2012, 45, 147–155. [Google Scholar] [CrossRef]
- Wątorek, M.; Kwapień, J.; Drożdż, S. Financial return distributions: Past, present, and COVID-19. Entropy 2021, 23, 884. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Makarov, I.; Schoar, A. Trading and arbitrage in cryptocurrency markets. J. Financ. Econ. 2020, 135, 293–319. [Google Scholar] [CrossRef]
- Cohen, G.; Qadan, M. The complexity of cryptocurrencies algorithmic trading. Mathematics 2022, 10, 2037. [Google Scholar] [CrossRef]
- Fang, F.; Ventre, C.; Basios, M.; Kanthan, L.; Martinez-Rego, D.; Wu, F.; Li, L. Cryptocurrency trading: A comprehensive survey. Financ. Innov. 2022, 8, 13. [Google Scholar] [CrossRef]
- Cohen, G. Intraday algorithmic trading strategies for cryptocurrencies. Rev. Quant. Financ. Account. 2023, 61, 395–409. [Google Scholar] [CrossRef]
- Wątorek, M.; Skupień, M.; Kwapień, J.; Drożdż, S. Decomposing cryptocurrency high-frequency price dynamics into recurring and noisy components. Chaos 2023, 33, 083146. [Google Scholar] [CrossRef]
- Gerlach, J.C.; Demos, G.; Sornette, D. Dissection of Bitcoin’s multiscale bubble history from January 2012 to February 2018. R. Soc. Open Sci. 2019, 6, 180643. [Google Scholar] [CrossRef]
- Huber, T.A.; Sornette, D. Boom, bust, and bitcoin: Bitcoin-bubbles as innovation accelerators. J. Econ. Issues 2022, 56, 113–136. [Google Scholar] [CrossRef]
- Bouri, E.; Gupta, R.; Vo, X.V. Jumps in Geopolitical Risk and the Cryptocurrency Market: The Singularity of Bitcoin. Def. Peace Econ. 2022, 33, 150–161. [Google Scholar] [CrossRef]
- Hong, M.Y.; Yoon, J.W. The impact of COVID-19 on cryptocurrency markets: A network analysis based on mutual information. PLoS ONE 2022, 17, e0259869. [Google Scholar] [CrossRef]
- Khalfaoui, R.; Gozgor, G.; Goodell, J.W. Impact of Russia-Ukraine war attention on cryptocurrency: Evidence from quantile dependence analysis. Financ. Res. Lett. 2023, 52, 103365. [Google Scholar] [CrossRef]
- Wątorek, M.; Kwapień, J.; Drożdż, S. Cryptocurrencies are becoming part of the world global financial market. Entropy 2023, 25, 377. [Google Scholar] [CrossRef]
- Fang, Y.; Tang, Q.; Wang, Y. Geopolitical Risk and Cryptocurrency Market Volatility. Emerg. Mark. Financ. Trade 2024, 60, 3254–3270. [Google Scholar] [CrossRef]
- Poongodi, M.; Nguyen, T.N.; Hamdi, M.; Cengiz, K. Global cryptocurrency trend prediction using social media. Inf. Process. Manag. 2021, 58, 102708. [Google Scholar] [CrossRef]
- Aharon, D.Y.; Demir, E.; Lau, C.K.M.; Zaremba, A. Twitter-Based uncertainty and cryptocurrency returns. Res. Int. Bus. Financ. 2022, 59, 101546. [Google Scholar] [CrossRef]
- Szydło, P.; Wątorek, M.; Kwapień, J.; Drożdż, S. Characteristics of price related fluctuations in non-fungible token (NFT) market. Chaos 2024, 34, 013108. [Google Scholar] [CrossRef]
- Wątorek, M.; Szydło, P.; Kwapień, J.; Drożdż, S. Correlations versus noise in the NFT market. Chaos 2024, 34, 073112. [Google Scholar] [CrossRef]
- Binance. Available online: https://www.binance.com/ (accessed on 1 July 2025).
- CoinMarketCap. Available online: https://coinmarketcap.com (accessed on 1 July 2025).
- Nguyen, A.P.N.; Mai, T.T.; Bezbradica, M.; Crane, M. The Cryptocurrency Market in Transition before and after COVID-19: An Opportunity for Investors? Entropy 2022, 24, 1317. [Google Scholar] [CrossRef]
- Ammy-Driss, A.; Garcin, M. Efficiency of the financial markets during the COVID-19 crisis: Time-varying parameters of fractional stable dynamics. Phys. A Stat. Mech. Its Appl. 2023, 609, 128335. [Google Scholar] [CrossRef]
- Kwapień, J.; Wątorek, M.; Bezbradica, M.; Crane, M.; Tan Mai, T.; Drożdż, S. Analysis of inter-transaction time fluctuations in the cryptocurrency market. Chaos 2022, 32, 083142. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Gümmer, F.; Ruf, F.; Speth, J. Are the contemporary financial fluctuations sooner converging to normal? Acta Phys. Pol. B 2002, 34, 4293–4306. [Google Scholar]
- Drożdż, S.; Forczek, M.; Kwapień, J.; Oświęcimka, P.; Rak, R. Stock market return distributions: From past to present. Phys. A Stat. Mech. Its Appl. 2007, 383, 59–64. [Google Scholar] [CrossRef]
- Clark, P.K. A subordinated stochastic process model with finite variance for speculative prices. Econom. J. Econom. Soc. 1973, 41, 135–155. [Google Scholar] [CrossRef]
- Oświęcimka, P.; Kwapień, J.; Drożdż, S. Wavelet versus detrended fluctuation analysis of multifractal structures. Phys. Rev. E 2006, 74, 016103. [Google Scholar] [CrossRef]
- Oświęcimka, P.; Drożdż, S.; Forczek, M.; Jadach, S.; Kwapień, J. Detrended cross-correlation analysis consistently extended to multifractality. Phys. Rev. E 2014, 89, 023305. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef]
- Zhou, W.X. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E 2008, 77, 066211. [Google Scholar] [CrossRef]
- Horvatic, D.; Stanley, H.E.; Podobnik, B. Detrended cross-correlation analysis for non-stationary time series with periodic trends. Europhys. Lett. 2011, 94, 18007. [Google Scholar] [CrossRef]
- Oświęcimka, P.; Drożdż, S.; Kwapień, J.; Górski, A. Effect of detrending on multifractal characteristics. Acta Phys. Pol. A 2013, 123, 597–603. [Google Scholar] [CrossRef]
- Ohashi, K.; Amaral, L.A.; Natelson, B.H.; Yamamoto, Y. Asymmetrical singularities in real-world signals. Phys. Rev. E 2003, 68, 065204. [Google Scholar] [CrossRef]
- Cao, G.; Cao, J.; Xu, L. Asymmetric multifractal scaling behavior in the Chinese stock market: Based on asymmetric MF-DFA. Phys. A Stat. Mech. Its Appl. 2013, 392, 797–807. [Google Scholar] [CrossRef]
- Drożdż, S.; Oświęcimka, P. Detecting and interpreting distortions in hierarchical organization of complex time series. Phys. Rev. E 2015, 91, 030902. [Google Scholar] [CrossRef]
- Gómez-Gómez, J.; Carmona-Cabezas, R.; Ariza-Villaverde, A.B.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Multifractal detrended fluctuation analysis of temperature in Spain (1960–2019). Phys. A Stat. Mech. Its Appl. 2021, 578, 126118. [Google Scholar] [CrossRef]
- Kwapień, J.; Oświęcimka, P.; Drożdż, S. Detrended fluctuation analysis made flexible to detect range of cross-correlated fluctuations. Phys. Rev. E 2015, 92, 052815. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C.; Steinberg, S. On a q-Central Limit Theorem Consistent with Nonextensive Statistical Mechanics. Milan J. Math. 2008, 76, 307–328. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-Mechanical Foundation of the Ubiquity of Lévy Distributions in Nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef]
- Nakao, H. Multi-scaling properties of truncated Levy flights. Phys. Lett. A 2000, 266, 282–289. [Google Scholar] [CrossRef]
- Wątorek, M.; Królczyk, M.; Kwapień, J.; Stanisz, T.; Drożdż, S. Approaching multifractal complexity in decentralized cryptocurrency trading. Fractal Fract. 2024, 8, 652. [Google Scholar] [CrossRef]
- Zhao, L.; Li, W.; Fenu, A.; Podobnik, B.; Wang, Y.; Stanley, H.E. The q-dependent detrended cross-correlation analysis of stock market. J. Stat. Mech. Theory Exp. 2018, 2018, 023402. [Google Scholar] [CrossRef]










| Year | [s] | Exponents | ACF Exponents | |||
|---|---|---|---|---|---|---|
| BTC | ETH | BTC | ETH | BTC | ETH | |
| 2018 | 0.361 | 0.604 | −0.10 | −0.13 | ||
| 2019 | 0.241 | 0.562 | , | , | −0.18 | −0.23 |
| 2020 | 0.101 | 0.257 | −0.16 | −0.18 | ||
| 2021 | 0.047 | 0.065 | −0.16 | −0.14 | ||
| 2022 | 0.026 | 0.096 | , | −0.16 | −0.15 | |
| 2023 | 0.034 | 0.145 | −0.23 | −0.25 | ||
| 2024 | 0.045 | 0.069 | −0.19 | −0.21 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drożdż, S.; Kluszczyński, R.; Kwapień, J.; Wątorek, M. Multifractality and Its Sources in the Digital Currency Market. Future Internet 2025, 17, 470. https://doi.org/10.3390/fi17100470
Drożdż S, Kluszczyński R, Kwapień J, Wątorek M. Multifractality and Its Sources in the Digital Currency Market. Future Internet. 2025; 17(10):470. https://doi.org/10.3390/fi17100470
Chicago/Turabian StyleDrożdż, Stanisław, Robert Kluszczyński, Jarosław Kwapień, and Marcin Wątorek. 2025. "Multifractality and Its Sources in the Digital Currency Market" Future Internet 17, no. 10: 470. https://doi.org/10.3390/fi17100470
APA StyleDrożdż, S., Kluszczyński, R., Kwapień, J., & Wątorek, M. (2025). Multifractality and Its Sources in the Digital Currency Market. Future Internet, 17(10), 470. https://doi.org/10.3390/fi17100470








