Healing Intelligence: A Bio-Inspired Metaheuristic Optimization Method Using Recovery Dynamics
Abstract
1. Introduction
- Injury phase: Rather than relying on static or simplistic modifications, BHO applies stochastic disturbances to selected dimensions of candidate solutions, emulating the initial, uncontrolled nature of biological injury. These disturbances may follow distributions that favor either gentler changes or rare, high-impact shifts, with their intensity dynamically adapted as the search progresses, encouraging broad exploration in the early stages and gradually reducing disruption near convergence.
- Healing phase: Subsequently, BHO selectively guides the modified dimensions toward the best-known solution in a process that mirrors the progressive restoration of biological tissues. This movement is neither mechanical nor fixed; the proportion and direction of adjustments are adapted to the search conditions, maintaining diversity while also enhancing the exploitation of high-quality solutions.
- Recombination phase: Optionally, this process is preceded by an information-exchange mechanism inspired by differential evolution (DE) [30,31,32], where components of the best solution are combined with differences from other members of the population. This allows the inheritance of strong traits while simultaneously introducing variations that keep the search active.
2. The BioHealing Optimization Algorithm
2.1. The Basic Body of the BioHealing Optimizer Pseudocode
- : coordinate j of individual i at iteration ;
- : bounds;
- : incumbent best;
- clamp(z, , ) = min (max(z, ), );
- : uniform random in [0,1].
| Algorithm 1 The basic body of the BioHealing Optimizer pseudocode |
|
- 1.
- Injury (Stochastic perturbation)Notations and definitions:
- Bounds and projection: lower and upper are vectors of per-dimension bounds, clamp (, ) projects a scalar to [, ];
- Wound intensity: is the injury intensity at iteration t, is its initial value.
- Stochastic step : At iteration , is a zero-mean scalar, sampled independently across i, j, and from either (i) a standard Gaussian (unit variance) or (ii) a Lévy/Mantegna generator with stability index and global-scale Lévy scale. An optional truncation may be applied to avoid extreme outliers.
With per-dimension wound probability (or adaptive ):where stochasticStep(), and the wound intensity can be scheduled, e.g.,Auxiliary (stochastic step definition):withand an optional global-scale Lévy scale.The injury mechanism relies on stochastic perturbations that are complementary in their search behavior. Gaussian steps exhibit light tails and finite variance, which favor fine-grained local exploration and controlled diffusion around the current region of interest. In contrast, Lévy-distributed steps (with stability index ) have heavy tails, producing occasional long jumps that help the algorithm escape local basins and probe distant regions of the search space. By enabling per-dimension perturbations, BHO can adjust the disruption intensity across coordinates, which is beneficial in non-separable and multimodal landscapes where sensitivity is uneven across variables. This dual-mode design (Gaussian vs. Lévy) therefore provides a principled mechanism to balance local refinement and global exploration within the same injury phase. - 2.
- Healing (guided move toward )Notations and definitions:
- Healing probability: is the per-dimension probability that a healing move is applied (if adaptive per coordinate, write ).
- Healing gain: is a scalar returned by healStep() at iteration iter; it controls the attraction strength toward the incumbent best. Unless stated otherwise, and is non-decreasing in (e.g., the simple rule = 0.15 + 0.35 , capped to stay below 1).
- Incumbent best: denotes the best solution available at iteration .
- Bounds and projection: lower and upper are vectors of per-dimension bounds; clamp (z, , ) projects a scalar to [, ].
- Order of updates: Healing takes as input the post-injury state and produces .
With per-dimension healing probability :,where , bounded in ) - 3.
- Recombination (DE/best/1/bin)Notations and definitions:
- Recombination probability: is the probability that differential evolution (DE) recombination is applied to candidate i. Otherwise, the candidate proceeds without recombination.
- Mutation strategy: The variant used is DE/best/1, meaning one difference vector is added to the current best solution. Specifically, two distinct indices , ≠i are sampled uniformly, and the donor vector is constructed as .
- Scaling factor: is the differential weight controlling the magnitude of the perturbation.
- Crossover mask: C is a binary mask with entries ∼Bernoulli(), where is the crossover probability. To ensure at least one coordinate crosses over, one randomly selected dimension is forced to have = 1.
- Offspring construction: The trial vector after recombination is , which combines donor and parent according to the mask and is then projected to the feasible range by clamp.
With probability the DE/best/1 with binomial crossover is applied: - 4.
- Greedy acceptanceNotations and definitions:
- Trial fitness: After injury, healing, or recombination, the candidate is evaluated to obtain . The previous fitness is .
- Greedy rule: The update is strictly elitist: if , the candidate is accepted and its fitness is updated; otherwise, the previous state is restored.
- Best solution update: If the accepted candidate also improves upon the current best value , then both and are updated.
- Rollback mechanism: If the trial vector fails to improve, the algorithm explicitly resets and to prevent quality degradation.
After the phases (in the algorithm’s prescribed order):
2.2. Integration of Adaptive Mechanisms into the BHO Core Loop
- 1.
- Scar Map: Momentum and BandageNotations and definitions:
- Per-dimension wound schedule: , clamped in [, ] and [, ].
- Momentum: [—1,1] = decayed running sign of recent accepted moves on dimension j.
- Improvement score: 0 = per-dimension score.
- Bandage counter: = freeze length for coordinate (i,j).
- Signals: [0,1] and {−1,+1}.
- Hyper-parameters: learning rate , momentum decay (0,1), bias coefficient k > 0, bandage length with bounds , , , .
After greedy acceptance ( < ), the scar map updates, per improved coordinate j, the wound probability and using learning rate and clamping to admissible ranges. The update strength grows with , so dimensions aligned with the incumbent best are reinforced. Momentum is refreshed aswhich biases future perturbations by . The score accumulates proportional improvement, supporting hot-dimension selection. Finally, the bandage sets , freezing recently improved coordinates.Scar map is invoked immediately after acceptance; in subsequent iterations, injury samples per-dimension parameters , (instead of a global ), applies bias from , and skips coordinates with 0. Healing remains unchanged and it graphically illustrate in Figure 1.The algorithm for Scar map is provided in Algorithm 2.Algorithm 2 Scar map: momentum and bandage - Input: Set D of improved coordinates, , forParams: , , , , , , ,State: , , ,01 For j∈D do02 = (0.5 + 0.5 )03 = (0.25 + 0.75 )04 = clamp( + , , )05 = clamp(, , ))06 = (1 — ) +07 = + improvement_signal()08 > 0 then09 =10 End if11 For each (i,j) do12 If > 0 then13 = − 114 Continue15 End if15 Apply injury with prob. , scale , and biasIf = sign()
Scar map updates per-dimension memory and momentum after successful acceptance and provides the scores that hot-dims will use to focus exploration.
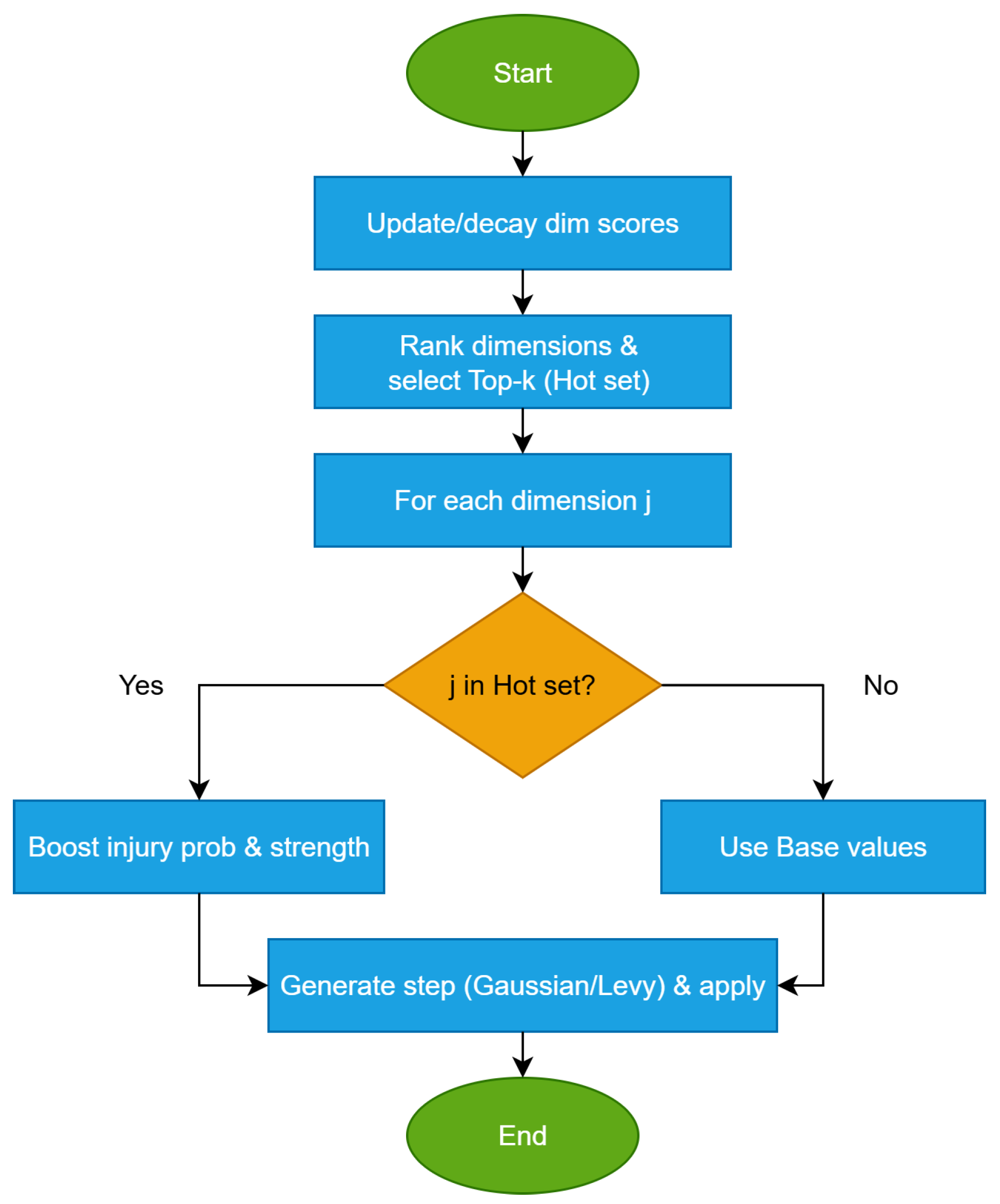
- 2.
- Hot-Dims Focus (Top-K and Boosts for Injury)Notations and definitions:
- Per-dimension score: 0 accumulates recent accepted improvements (same used by scar map).
- Decay: (0,1) applies a mild forgetting to down-weight stale gains.
- Top-K hot set: = (upright ) selects the K highest-scoring dimensions at iteration .
- Boost factors (used at injury time only): 1 for probability, 1 for scale.
- These do not modify the stored , ; they produce effective values for the current injury step:(Bounds , , , as in scar map.)
- Integration: Hot-dims runs once per iteration before injury: decay , select , then injury uses , in place of the base , . Scar-map updating of still happens after greedy acceptance. The hot dims algorithm is listed in Algorithm 3.
During injury (this iteration), use as the per-dimension injury probability and as the intensity scale in place of , ; feasibility remains enforced via clamp. (No persistent change to the stored scar-map state.) The Hot-dims procedure is graphically illustrated in Figure 2.Algorithm 3 Hot-dims focus: boosting probability and intensity on top-K dimensions - Params: , K, ,State: (scores), , from Scar Map01 For j= 1.. do02 = (1 — ) // mild forgetting03 End for04 =05 // Injury-time effective parameters06 For j= 1.. do07 If then08 = min(, )09 = min(), )10 Else11 =12 =12 End if13 End for
Once hot dimensions are identified, exploration intensity is dynamically escalated under stagnation through RAGE and hyper-RAGE.
- 3.
- RAGE and Hyper-RAGENotations and definitions:
- Trigger threshold: . A burst is armed when and no cooldown is active.
- Burst length: . During a burst, the counter is decremented each iteration.
- Hot-set magnifier: . While , the hot set size is enlarged to (otherwise K).
- Boost multipliers (RAGE): for probability and for scale; these are applied during a burst.
- Score shaping (hyper-RAGE): and per-dimension weights obtained from the scores (e.g., or rank-based).
- Cooldown: . After a burst ends (), a cooldown prevents immediate retriggering.
- Effective injury parameters: As in hot-dims, the current-iteration values are (possibly boosted for ). The stored schedules remain unchanged.
RAGE triggers immediately after greedy acceptance if and , opening a B-iteration window. Before injury, the hot set is computed with size (if in burst) or K (otherwise). The injury step then uses the effective parametersand , for .Hyper-RAGE makes boosts dimension-aware viaso that higher-scoring coordinates receive proportionally stronger yet bounded pressure. When the burst ends, cooldown starts, and healing remains unchanged. All boosts are non-persistent (state schedules are not overwritten). The rage procedure is given in Figure 3.The Explosive exploration under stagnation procedure is described in Algorithm 4.Algorithm 4 RAGE/hyper-RAGE: Explosive exploration under stagnation - Input current scores , base per-dimension schedules , hot-set size K.Parameters: trigger , burst length , magnifier , boosts , , shaping , cooldown .State: burst counter , cooldown .01 At acceptance (after )020304 End if05 //Before injury (each iteration):06 Hot-set size:070809101112 Hot set selection:.13 Effective bases (from hot-dims): compute for all j (temporary, non-persistent).14 //RAGE / hyper-RAGE boosts (for use in this injury):15 For ,…,16 If17 // RAGE: uniform boosts on hot dimensions18 ,1920 // Hyper-RAGE: score-shaped boosts (optional)21 choose from (e.g., )222324 Else252627 End if28 End For29 //Pass to injury: use for the current iteration’s stochastic perturbations, feasibility via clamp remains unchanged. (Stored are not overwritten.)30 //After injury (end of iteration):31 If32 ,33 If3435 End if35 Else36 If3738 End if39 End if
Outside burst windows, the injury sampling is governed by Lévy-wounds to allow rare long jumps when progress diminishes.
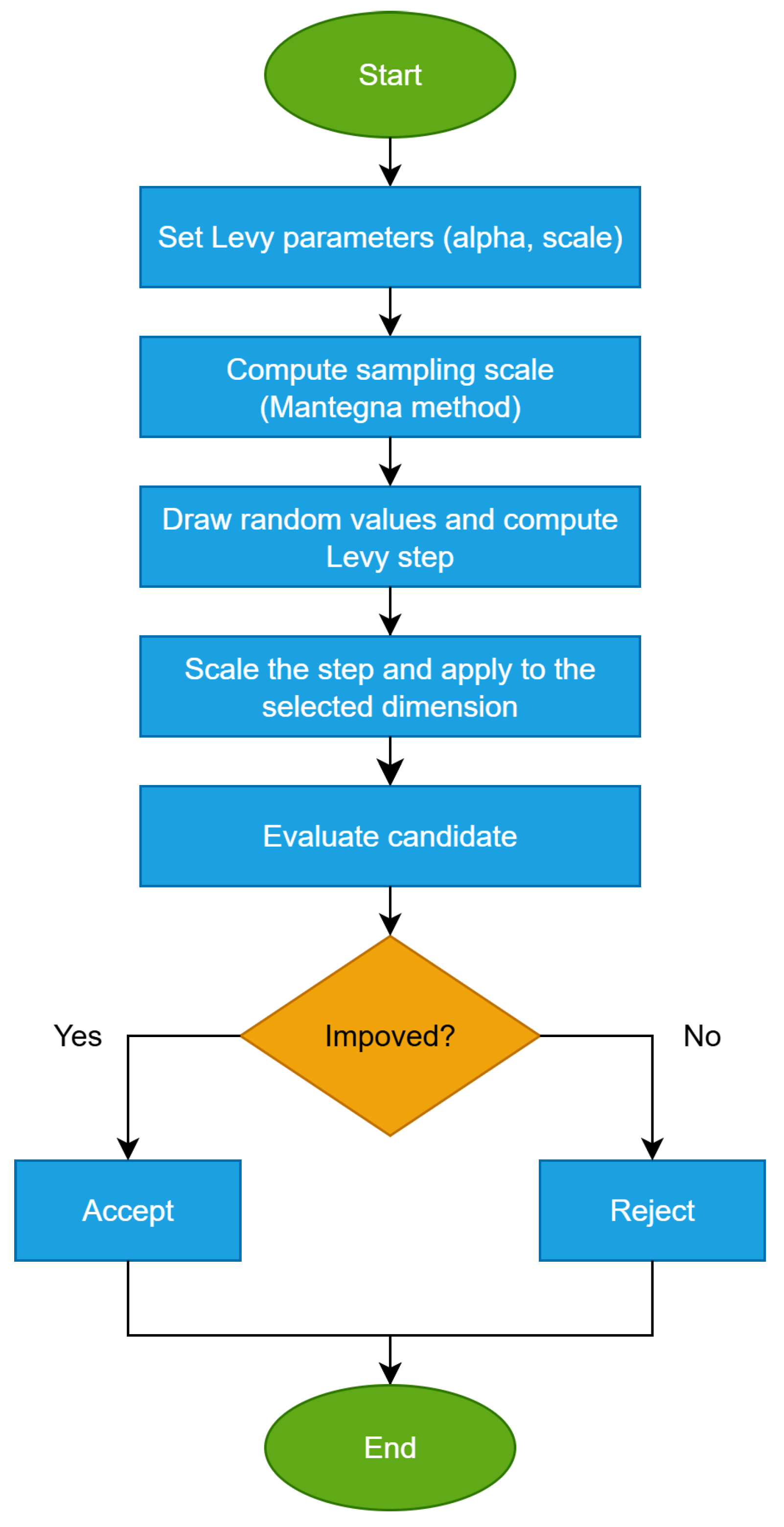
- 4.
- Lévy-Wounds (Mantegna)Notations and definitions:
- Stability index: .
- Global Lévy scale: (scalar).
- Per-dimension injury scheduling: use (probability) and (scale) from scar map/hot-dims; bandage/cooldowns apply as defined earlier.
- Stochastic step (Lévy/Mantegna) for iteration t and coordinate ,
withOptional truncation: to avoid extreme outliers.- Range scaling and projection: the raw move is scaled by and projected with to enforce feasibility.
Lévy-wounds replaces the Gaussian injury step with a heavy-tailed Mantegna draw, producing infrequent long jumps that enhance basin escape while retaining many small moves. For each dimension j of candidate i, with probability we apply the updateThe stability controls tail/heaviness (smaller ⇒ rarer but longer jumps), and sets the overall Lévy magnitude and can be tuned jointly with . If momentum is active, a mild directional bias (with small ) may be added to the step before clamping. Lévy-wounds integrates seamlessly with hot-dims and RAGE/hyper-RAGE: when a dimension j is hot, the effective injury parameters (or under bursts) are used in place of , while the Lévy draw remains unchanged. This procedure is given in Algorithm 5.Algorithm 5 Lévy-wounds (Mantegna): heavy-tailed jumps for rare long-range moves - Input: , optional .State: candidate , bounds .01 For do02 If bandage is active on Then03 Continue04 End if05 Draw06 If then07 Sample ,080910 If truncation enabled then1112 End if13 (optional bias)141516 End if17 End for
The flowchart of this method is given in Figure 4.Beyond step distribution, alpha-strike adds rare targeted large moves on a few coordinates to vault past barriers.
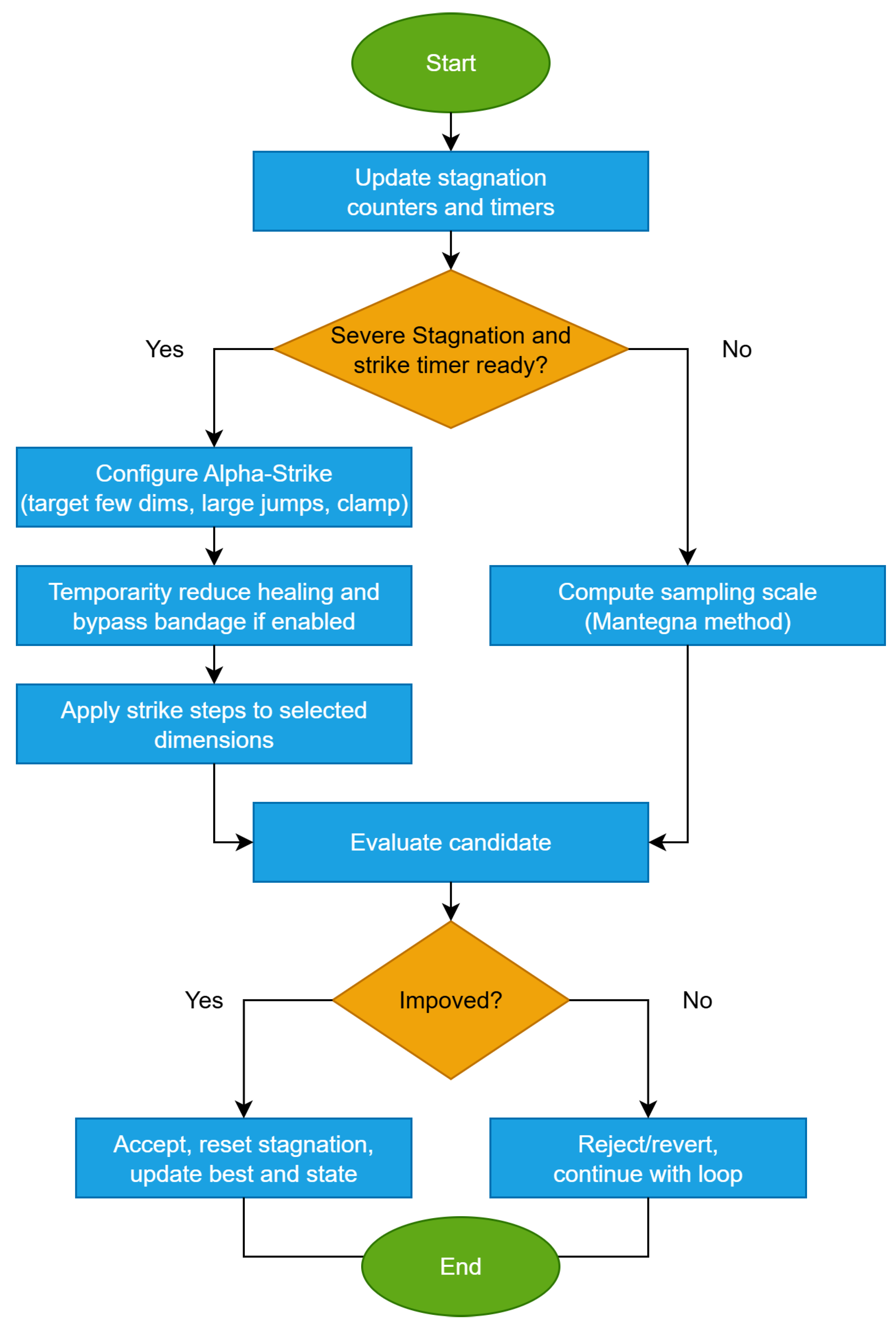
- 5.
- Alpha-StrikeNotations and definitions:
- Trigger condition: Alpha-strike activates when the algorithm stagnates for more than iterations (no improvement in ) or when the diversity indicator D falls below a threshold .
- Strike length: , the number of consecutive iterations in which strike mode remains active.
- Boost multipliers: (probability) and (scale), applied uniformly to hot dimensions during the strike.
- Hot set magnification: factor , enlarging the set selected from dimension scores.
- Reset option: fraction of the worst individuals may be re-initialized uniformly in to maximize disruption.
Mechanism (text). Alpha-strike is a deliberate, short burst of intensified perturbations designed to break strong stagnation. Once triggered, the algorithm enters a strike window of length . For all individuals and dimensions , the effective injury parameters are magnified:In addition, with probability , entire individuals are reinitialized within the feasible bounds. When the strike window expires, normal operation resumes. Healing is not modified, while scar map, momentum, and dimension scores continue to update, ensuring smooth integration with the other auxiliary mechanisms. The Alpha-strike procedure is given in Algorithm 6.Algorithm 6 Alpha-strike: targeted, rare, large jump on a few coordinates - Input:State: best fitness , stagnation counter , diversity indicator D, strike counter01 //At each iteration:02 If or then030405 End if06 If then07 Expand hot set:0809 Compute effective parameters for all j10 For each individual i do11 Draw12 If then13 Reinitialize14 Continue to next individual15 End if16 For each do171819 Apply injury using20 End for21 End for2223 Else24 Run normal injury / healing / recombination with parameters from scar map, hot-dims, RAGE/hyper-RAGE25 End if
Notes.- Alpha-strike is designed to be rare but disruptive, acting as a restart-like operator while preserving the algorithmic structure.
- Magnifiers should be chosen conservatively (e.g., boosts) to avoid instability.
- The diversity indicator D can be population variance, centroid spread, or any normalized measure.
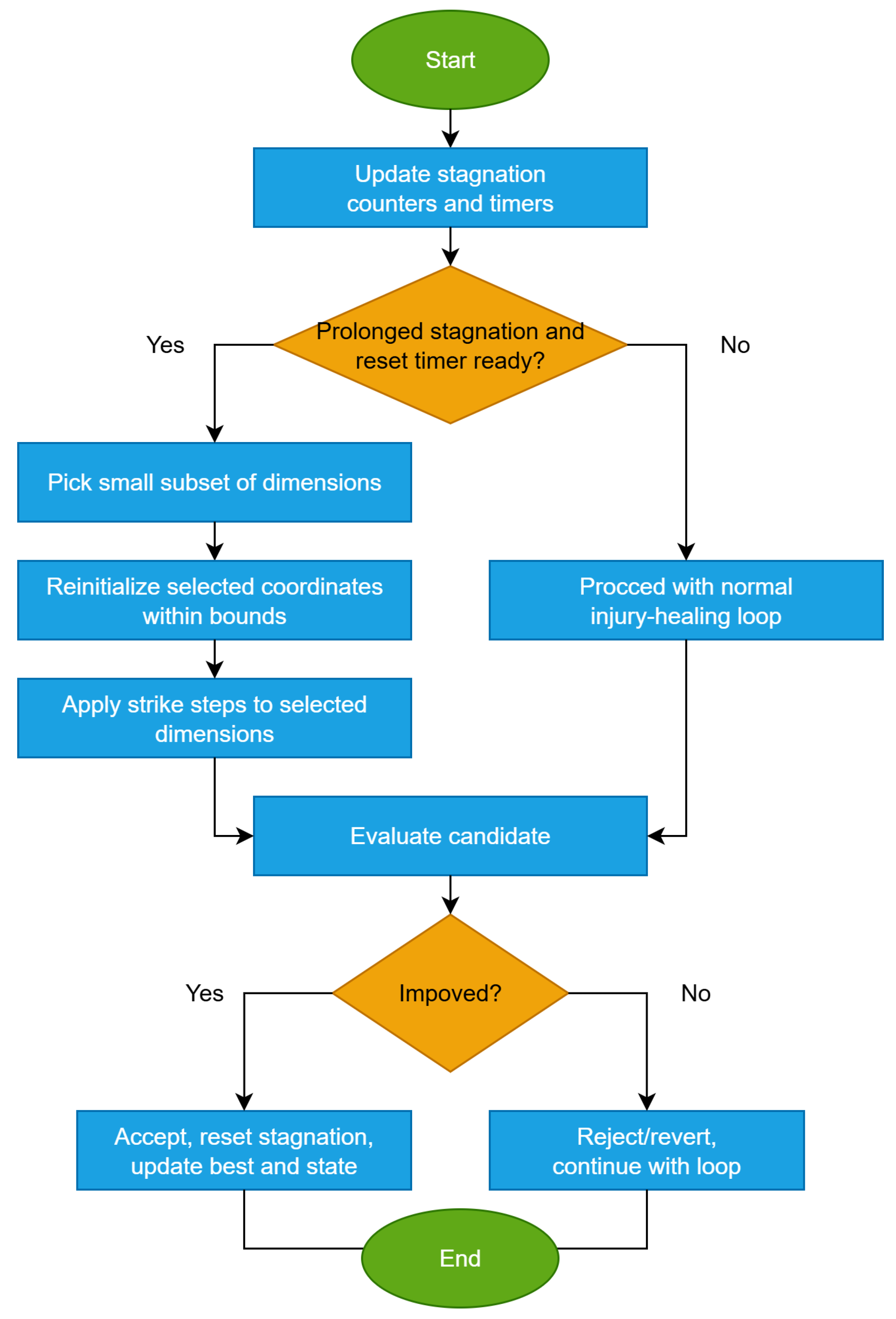
The flowchart of Alpha-strike is provided in Figure 5.If mild or targeted boosts do not revive progress, a small-scale restart around the incumbent best follows.
- 6.
- Catastrophic Micro-ResetNotations and definitions:
- Trigger condition: Activates when stagnation persists despite alpha-strike and Lévy-wounds, i.e., after consecutive iterations without improvement in .
- Reset fraction: , fraction of the worst individuals to be replaced.
- Reset policy: New candidates are sampled uniformly within , optionally blended with the elite centroid.
- Cooldown: prevents consecutive activations within a short window.
Catastrophic micro-reset is a last-resort disruption operator. Instead of modifying coordinates dimension by dimension, it directly replaces a portion of the population with fresh samples, injecting diversity. It is “micro” because only a small fraction of individuals are reset, rather than the entire population, thus preserving useful structure and elite solutions. Optionally, reset positions may be drawn from a mixture of uniform distribution and a Gaussian centered on the elite centroid, balancing exploration of new areas and exploitation near promising regions. After activation, a cooldown ensures micro-reset cannot be triggered again too soon. The steps of the algorithm are shown in Algorithm 7.Notes.- Catastrophic micro-reset should be rare and disruptive, serving as a population-level restart.
- The fraction is usually small (e.g., 5–15%) to avoid destroying global progress.
- The cooldown prevents repeated resets and stabilizes the dynamics. The flowchart for this procedure is given in Figure 6.
Algorithm 7 Catastrophic micro-reset: targeted mini-restart around the incumbent best - Input: (optionally: elite centroid , blend )State: best fitness , stagnation counter , cooldown counter , population with bounds01 At each iteration:02 If and then03 Identify worst set of size (largest objective values).04 For each do05 Sample06 If elite biasing enabled then0708 Else0910 End if11 End for121314 End if15 If then1617 End if18 Continue normal injury/healing/recombination.
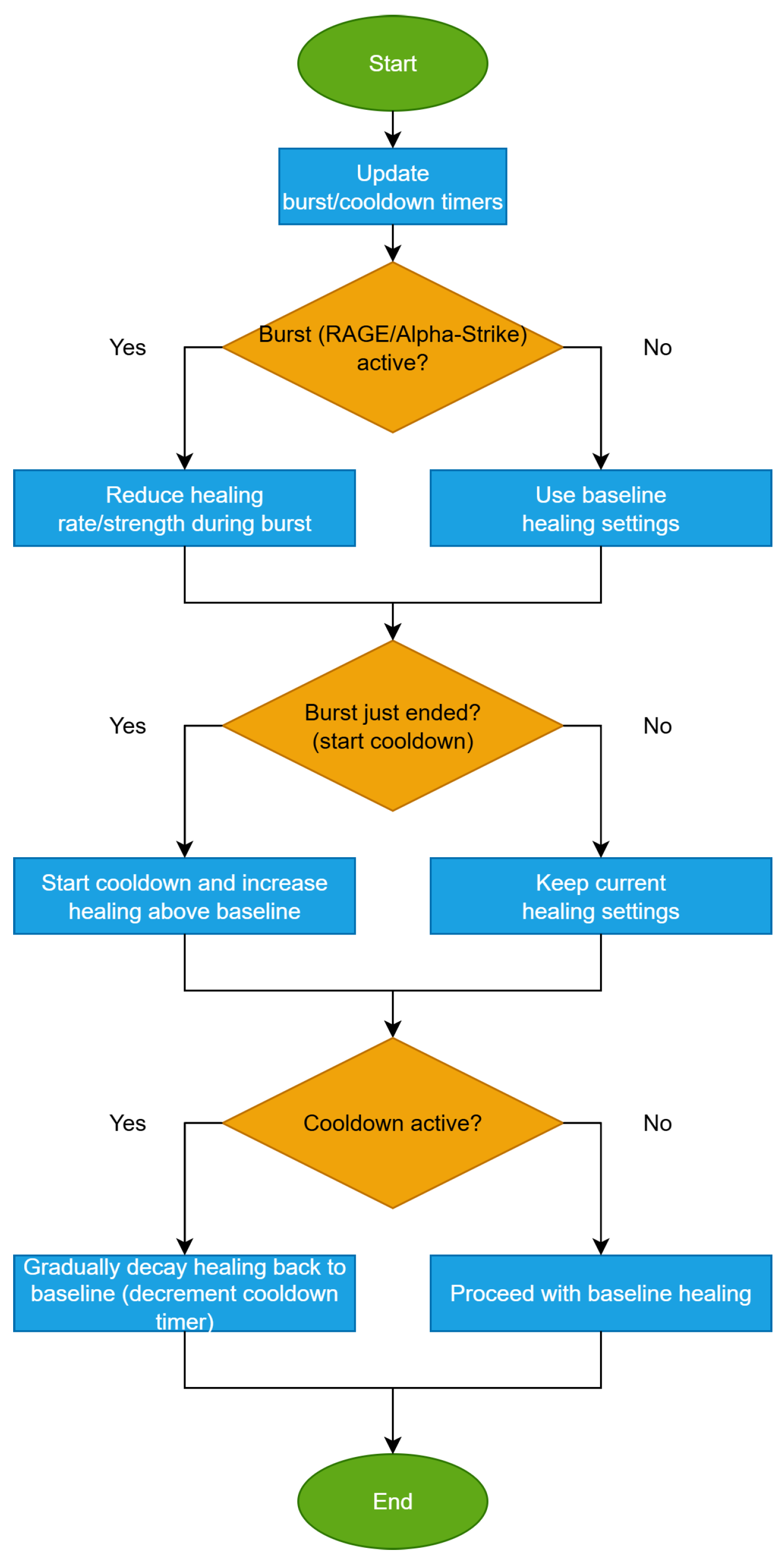
After a restart or a burst, a smooth return to stable exploitation is needed, which is controlled by healing adjustments with a short cooldown.
- 7.
- Healing Adjustments and CooldownNotations and definitions:
- Adaptive healing gain: , normally produced by healStep, is scaled dynamically based on recent outcomes; cap .
- Boost/decay factors: (boost on success), (decay on failure).
- Cooldown threshold: ; if a single healing move exceeds of the range, healing on that coordinate cools down.
- Cooldown length: ; per-dimension timer .
- Counters: consecutive successes, consecutive failures (per dimension j).
- Bounds/projection: vectors ; .
After each healing attempt on coordinate j, the algorithm checks whether the new state improves fitness. On success, the healing gain is strengthened and increments (reset ). On failure, the gain is reduced and increments (reset ). If the displacement magnitude exceeds a fraction of the variable’s range, a cooldown starts, and while , no healing is applied to that coordinate. This self-regulation complements scar map/bandage: bandage protects just-improved coordinates from injury, whereas cooldown throttles over-correction by healing. The steps of the algorithm are shown in Algorithm 8.Algorithm 8 Healing adjustments and cooldown: modulating healing during bursts with a smooth post-burst ramp - Input:State: gains , counters , cooldown timers , candidate , best , bounds01 For each dimension j (on healing step) do02 If then0304 Continue05 End if06 Propose update:07 //Evaluate fitness, let outcome be success if improved, else failure.08 If success then09101112 Else13 ;1415 End if16 IF then1718 End if19 End for
Notes.- Boosts/decays make healing stronger in promising directions and weaker in insensitive ones.
- Cooldown prevents oscillations and over-correction after large moves.
- Conservative tuning (e.g., , ) is often adequate; small (e.g., 2–5). The flowchart for this method is shown in Figure 7.
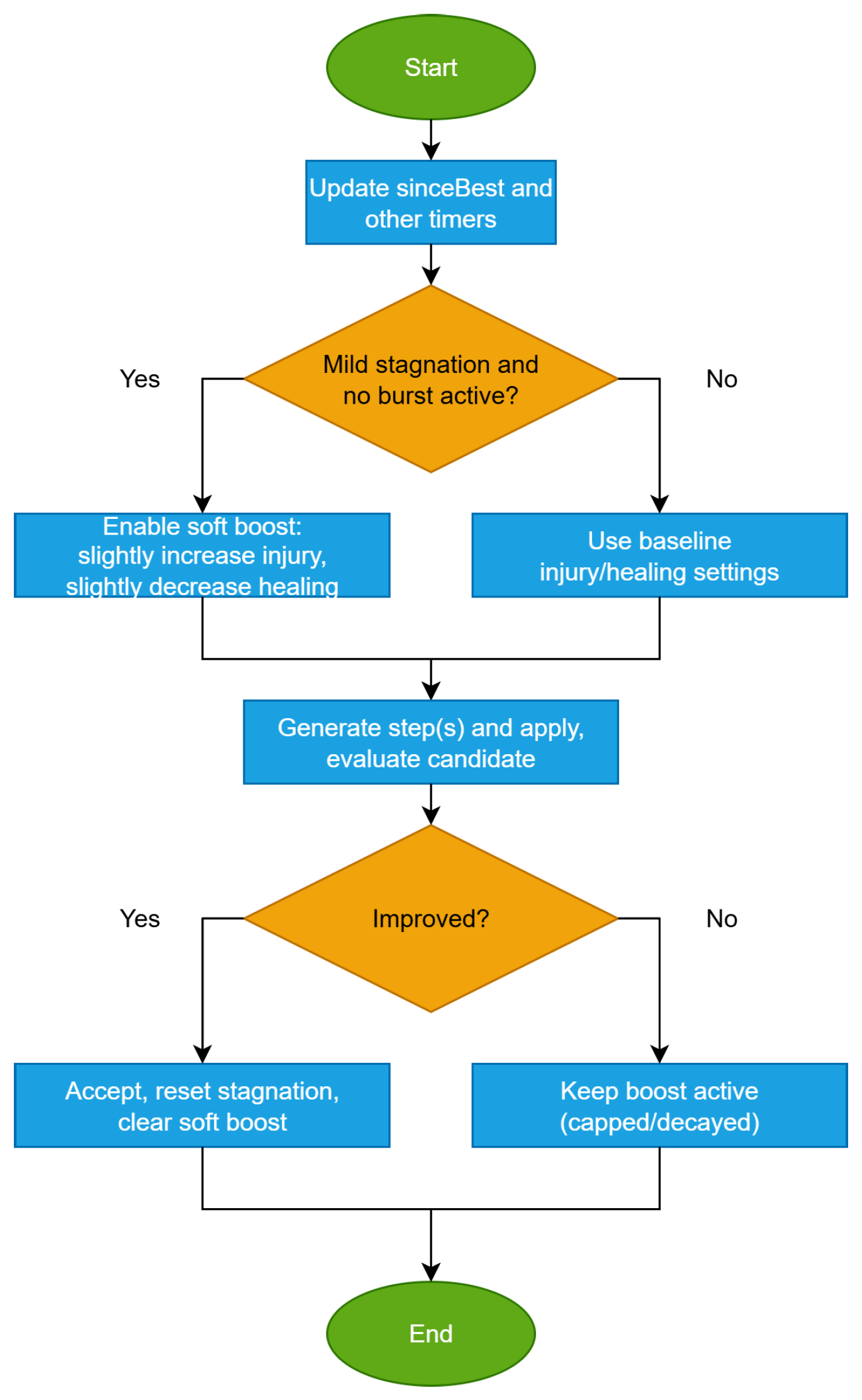
For early or mild stagnation, a gentle injury amplification is applied before more aggressive mechanisms are engaged.
- 8.
- Soft-Stagnation BoostNotations and definitions:
- Global restart threshold: , maximum stagnation length tolerated across all mechanisms.
- Restart fraction: , fraction of worst individuals replaced.
- Hybrid injection pool: , contains elite centroid, archived bests, or random samples.
- Blend parameter: , probability of using vs. uniform resampling.
- Diversity safeguard: must be re-established after restart; else increases temporarily.
Adaptive restarts and hybrid injection serve as a final safeguard against premature convergence. While scar map, hot-dims, RAGE/hyper-RAGE, alpha-strike, Lévy-wounds, healing and cooldown, and catastrophic micro-reset progressively increase disruption, there remains a chance that the population collapses to a narrow region. A global restart is triggered when no improvement in occurs for more than iterations.At restart, a fraction of the worst individuals is replaced. Each replacement is drawn using a hybrid scheme:- With probability , sample from (e.g., elite centroid, archived bests).
- With probability , sample uniformly from .
After injection, population diversity D is recomputed. If , is temporarily increased until diversity is restored. This mechanism thus preserves elites while re-introducing fresh search directions. The steps for this method are shown in Algorithm 9.Algorithm 9 Soft-stagnation boost: gentle injury amplification under early stagnation - Input:State: stagnation counter , population , injection pool , bounds01 At each iteration:02 If then03 Identify worst set of size .04 For each do05 Draw06 If then07 inject from08 Else09 010 End if11 End for1213 End if14 Recompute diversity D15 If then16 increase temporarily17 End if18 Continue normal injury/healing/recombination.
Notes.- Acts as a population-level reboot, but partial: elites are preserved.
- can evolve dynamically, e.g., storing historical elites.
- Parameters and should be tuned conservatively to avoid overly frequent resets. The flowchart for this method is shown in Figure 8.Figure 8. Soft-stagnation boost.
These mechanisms integrate without altering the backbone of Algorithm 1 and are triggered under simple stagnation or improvement conditions. Also, the flowchart for this technique is shown in Figure 9.
3. Experimental Setup and Benchmark Results
3.1. Test Functions
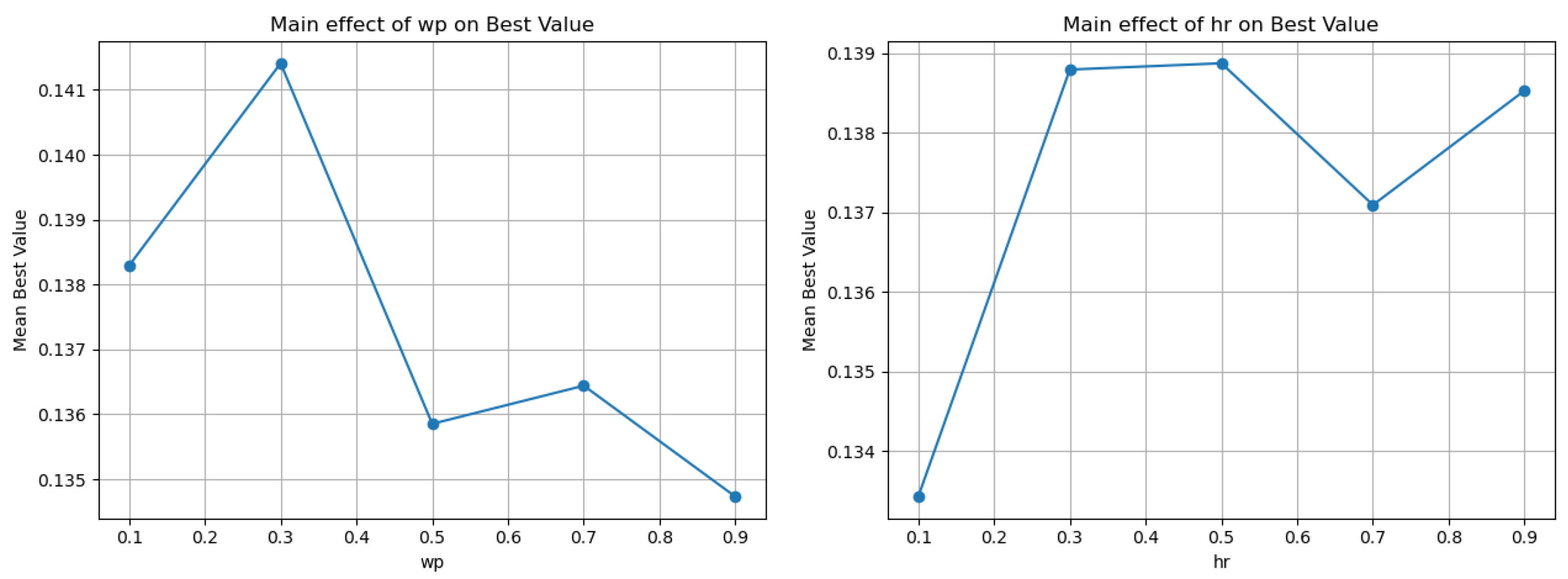
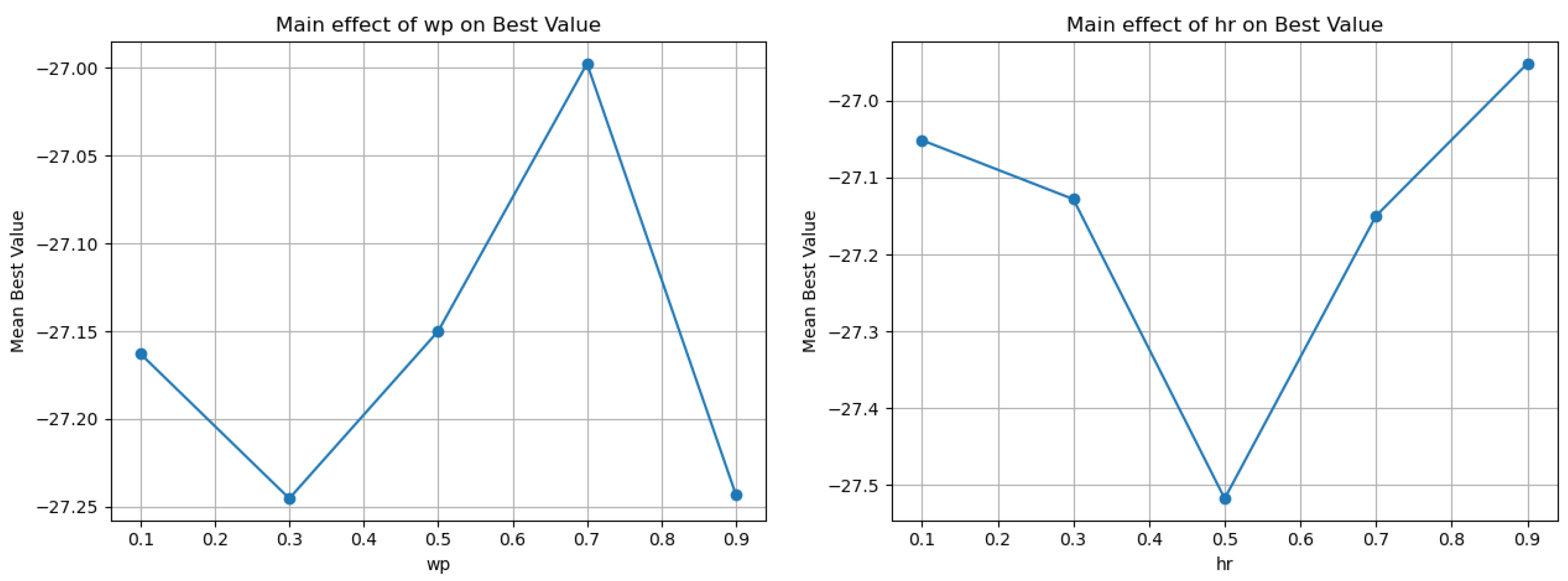
3.2. Parameter Sensitivity
3.3. Experimental Results
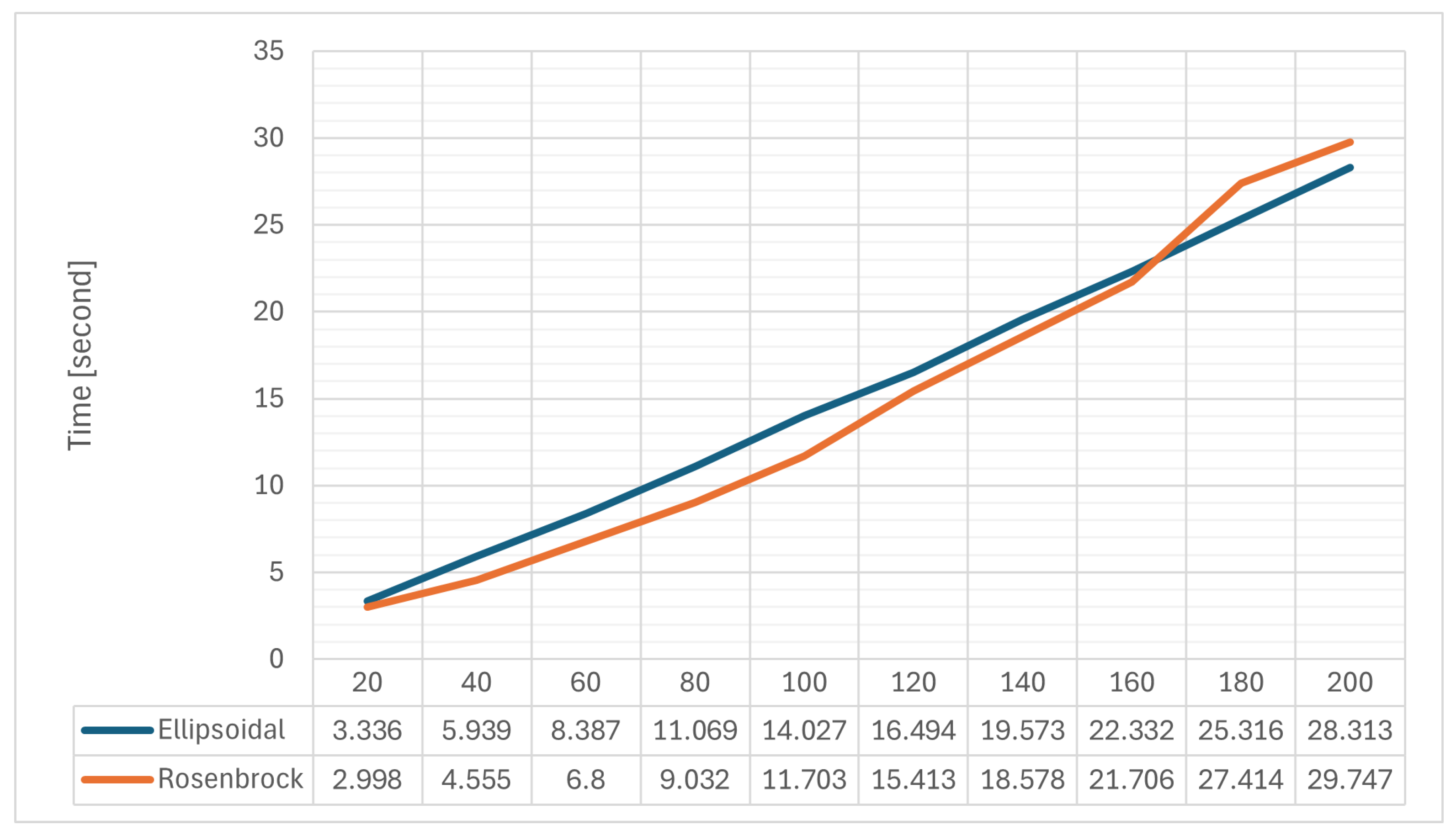
- Ellipsoidal: ;
- Rosenbrock: .
- EA4Eig [35], a cooperative evolutionary algorithm with an eigen-crossover operator. It was introduced at the IEEE Congress on Evolutionary Computation 2022 (CEC 2022) and evaluated on that event’s official single-objective benchmark suite. The method was primarily designed and tested within the CEC single-objective context.
- UDE3 (UDE-III) [36], a recent member of the Unified DE family for constrained problems, it was evaluated on the CEC 2024 constrained set, while its predecessor (UDE-II/IUDE) won first place at CEC 2018, giving UDE3 a clear lineage with proven competitive performance.
- mLSHADE_RL [37] is a multi-operator descendant of LSHADE-cnEpSin, and was one of the CEC 2017 winners for real-parameter optimization. This variant augments the base algorithm with restarts and local search, and it has been assessed on modern test suites.
- CLPSO [38], a classic PSO variant with comprehensive learning (2006) that has long served as a strong baseline in CEC benchmarks; it is not tied to a single award entry but is widely used in comparative studies.
- SaDE [39], the self-adaptive DE developed by Qin and Suganthan, was evaluated on the CEC 2005 test set and has since become a reference point for adaptive strategies.
- jDE [40], developed by Brest et al., introduced self-adaptation of F and CR and has been extensively evaluated, including special CEC 2009 sessions on dynamic/uncertain optimization. This work helped popularize self-adaptation in DE.
- CMA-ES [48] is the established covariance matrix adaptation evolution strategy for continuous domains. Beyond its vast literature, it is a staple baseline and frequent participant/reference in BBOB benchmarking at GECCO, effectively serving as a standard black-box comparison standard.
3.4. BHO-Assisted Neural Network Training
- The UCI database: https://archive.ics.uci.edu/ (accessed on 5 July 2025) [51].
- The Keel website: https://sci2s.ugr.es/keel/datasets.php (accessed on 5 July 2025) [52].
- The Statlib website: https://lib.stat.cmu.edu/datasets/index (accessed on 5 July 2025).
- APPENDICITIS, a medical dataset [53].
- ALCOHOL, a dataset related to alcohol consumption [54].
- AUSTRALIAN, a dataset derived from various bank transactions [55].
- BALANCE [56], a dataset derived from various psychological experiments.
- CIRCULAR, an artificial dataset.
- DERMATOLOGY, a medical dataset for dermatology problems [59].
- ECOLI, a dataset related to protein problems [60].
- GLASS, a dataset containing measurements from glass component analysis.
- HABERMAN, a medical dataset related to breast cancer.
- HAYES-ROTH [61].
- HEART, a dataset related to heart diseases [62].
- HEARTATTACK, a medical dataset for the detection of heart diseases.
- HOUSEVOTES, a dataset related to Congressional voting in the USA [63].
- LYMOGRAPHY [68].
- MAMMOGRAPHIC, a medical dataset used for the prediction of breast cancer [69].
- PIMA, a medical dataset for the detection of diabetes [72].
- PHONEME, a dataset that contains sound measurements.
- POPFAILURES, a dataset related to experiments regarding climate [73].
- REGIONS2, a medical dataset applied to liver problems [74].
- SAHEART, a medical dataset concerning heart diseases [75].
- SEGMENT [76].
- STATHEART, a medical dataset related to heart diseases.
- SPIRAL, an artificial dataset with two classes.
- STUDENT, a dataset related experiments in schools [77].
- TRANSFUSION, which is a medical dataset [78].
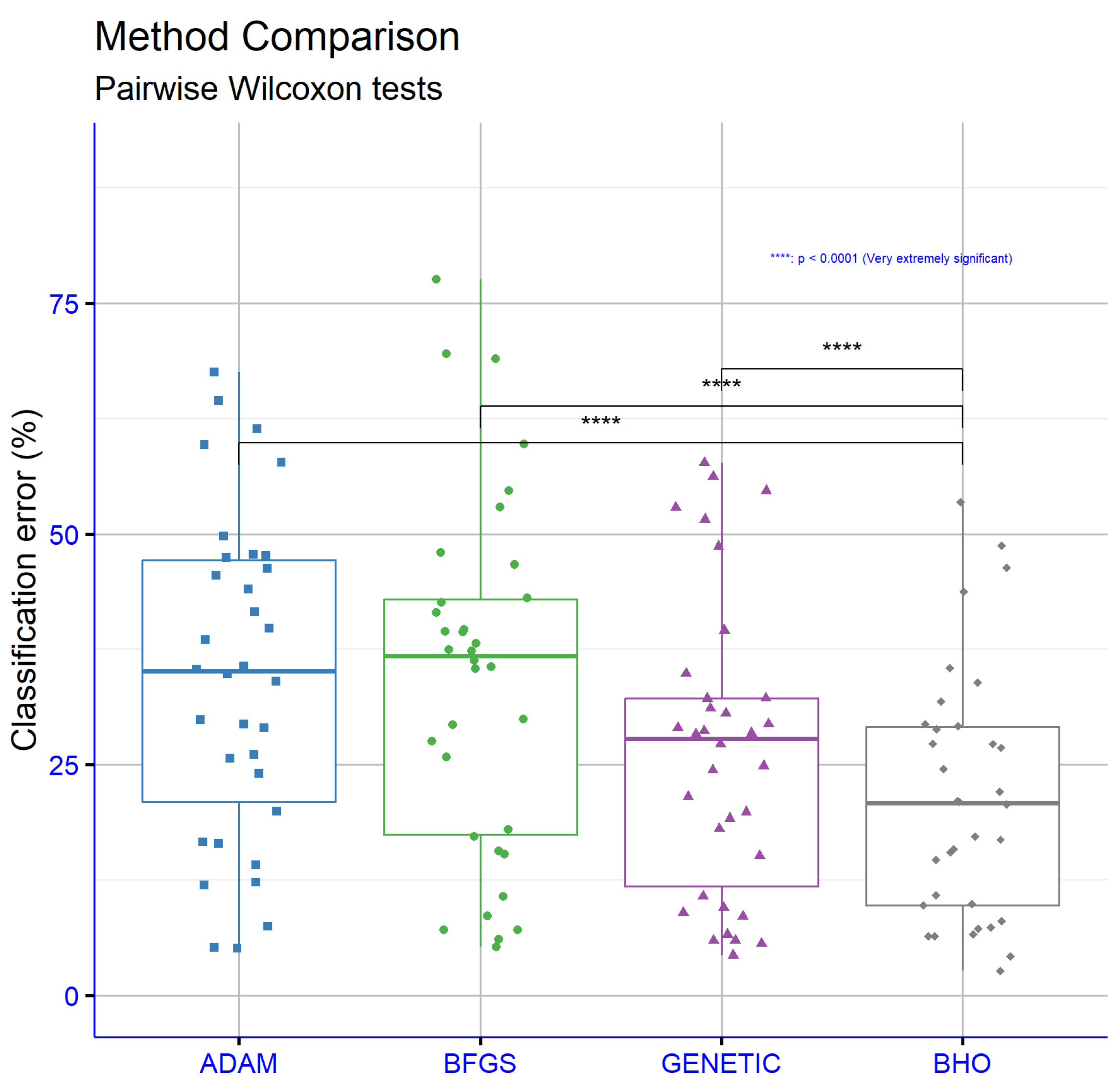
- ZOO, a dataset related to animal classification [85].Interpreting the entries as classification error rates, where lower is better, BHO attained the lowest average error at 21.52%, ahead of Genetic at 26.55%, BFGS at 34.34%, and Adam at 34.48%. This corresponded to a 5.03 percentage-point improvement over Genetic (≈19% relative reduction) and ≈ a 13 percentage-point improvement over Adam and BFGS (≈37% relative reduction). At the dataset level, BHO recorded the best error on a majority of datasets, including ALCOHOL 16.89%, AUSTRALIAN 29.20%, BALANCE 8.06%, CLEVELAND 46.36%, CIRCULAR 4.23%, DERMATOLOGY 9.89%, ECOLI 48.72%, HEART 20.96%, HEARTATTACK 21.06%, HOUSEVOTES 6.45%, LYMOGRAPHY 27.24%, PARKINSONS 14.72%, PIMA 29.40%, REGIONS2 26.83%, SAHEART 33.88%, SEGMENT 27.26%, SPIRAL 43.75%, STATHEART 20.71%, TRANSFUSION 24.56%, WDBC 6.43%, WINE 15.86%, ZO_NF_S 9.76%, ZONF_S 2.68%, and ZOO 7.27%, and it tied for best on MAMMOGRAPHIC at 17.24%. There were, however, datasets where other optimizers had an edge, notably Adam on APPENDICITIS and STUDENT, and Genetic on GLASS, IONOSPHERE, LIVERDISORDER, and Z_F_S, with BHO typically close behind in these cases. Overall, the pattern showed that BHO delivered consistently low error across heterogeneous benchmarks, while conceding a few instances where gradient-based or classical evolutionary baselines aligned better with the data geometry. Reporting dispersion measures or statistical tests alongside these point estimates would further substantiate the observed gains.
4. Conclusions
5. Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant Colony Optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 1472, pp. 1470–1477. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Karaboga, D. An idea based on honey bee swarm for numerical optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2005, 39, 459–471. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly Algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and applications. Future Gener. Comput. Syst. 2020, 97, 849–872. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2008. [Google Scholar]
- Krishnanand, K.N.; Ghose, D. Glowworm Swarm Optimization for simultaneous capture of multiple local optima of multimodal functions. Swarm Intell. 2009, 3, 87–124. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Optimization Algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Alyasseri, Z.A.A.; Awadallah, M.A.; Abu Doush, I. Coronavirus herd immunity optimizer (CHIO). Neural Comput. Appl. 2021, 33, 5011–5042. [Google Scholar] [CrossRef]
- Salhi, A.; Fraga, E.S. Nature-inspired optimisation approaches and the new plant propagation algorithm. In Proceedings of the International Conference on Numerical Analysis and Optimization (ICeMATH 2011), Halkidiki, Greece, 19–25 September 2011. [Google Scholar]
- Mehrabian, A.R.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Yang, X. Root growth optimizer: A metaheuristic algorithm inspired by root growth. IEEE Access 2020, 8, 109376–109389. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Sallam, K.M.; Chakraborty, S.; Elsayed, S.M. Gorilla troops optimizer for real-world engineering optimization problems. IEEE Access 2022, 10, 121396–121423. [Google Scholar]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Reptile search algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2021, 191, 116158. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the 1996 Biennial Conference of the North American Fuzzy Information Processing Society (NAFIPS), Berkeley, CA, USA, 19–22 June 1996; IEEE Press: New York, NY, USA, 1996; pp. 519–523. [Google Scholar]
- Charilogis, V.; Tsoulos, I.G.; Tzallas, A.; Karvounis, E. Modifications for the Differential Evolution Algorithm. Symmetry 2022, 14, 447. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G. A Parallel Implementation of the Differential Evolution Method. Analytics 2023, 2, 17–30. [Google Scholar] [CrossRef]
- Chawla, S.; Saini, J.S.; Kumar, M. Wound healing based optimization—Vision and framework. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 88–91. [Google Scholar]
- Dhivyaprabha, T.T.; Subashini, P.; Krishnaveni, M. Synergistic fibroblast optimization: A novel nature-inspired computing algorithm. Front. Inf. Technol. Electron. Eng. 2018, 19, 815–833. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovský, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P.; Malik, O.P. OOBO: A new metaheuristic algorithm for solving optimization problems. Biomimetics 2023, 8, 468. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Lang, Y.; Gao, Y. Dream Optimization Algorithm: A cognition-inspired metaheuristic and its applications to engineering problems. Comput. Methods Appl. Mech. Eng. 2025, 436, 117718. [Google Scholar] [CrossRef]
- Cao, Y.; Luan, J. A novel differential evolution algorithm with multi-population and elites regeneration. PLoS ONE 2024, 19, e0302207. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, Y.; Liu, Z. An improved differential evolution with adaptive population allocation and mutation selection. Expert Syst. Appl. 2024, 258, 125130. [Google Scholar] [CrossRef]
- Yang, Q.; Chu, S.C.; Pan, J.S.; Chou, J.H.; Watada, J. Dynamic multi-strategy integrated differential evolution algorithm based on reinforcement learning. Complex Intell. Syst. 2024, 10, 1845–1877. [Google Scholar] [CrossRef]
- Watanabe, Y.; Uchida, K.; Hamano, R.; Saito, S.; Nomura, M.; Shirakawa, S. (1+1)-CMA-ES with margin for discrete and mixed-integer problems. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO ’23, Lisbon, Portugal, 15–19 July 2023; pp. 882–890. [Google Scholar] [CrossRef]
- Uchida, K.; Hamano, R.; Nomura, M.; Saito, S.; Shirakawa, S. CMA-ES for discrete and mixed-variable optimization on sets of points. In Proceedings of the Parallel Problem Solving from Nature—PPSN XVIII, Hagenberg, Austria, 14–18 September 2024; pp. 236–251. [Google Scholar] [CrossRef]
- Siarry, P.; Berthiau, G.; Durdin, F.; Haussy, J. Enhanced simulated annealing for globally minimizing functions of many-continuous variables. ACM Trans. Math. Softw. (TOMS) 1997, 23, 209–228. [Google Scholar] [CrossRef]
- Koyuncu, H.; Ceylan, R. A PSO based approach: Scout particle swarm algorithm for continuous global optimization problems. J. Comput. Des. Eng. 2019, 6, 129–142. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Charilogis, V.; Kyrou, G.; Stavrou, V.N.; Tzallas, A. OPTIMUS: A Multidimensional Global Optimization Package. J. Open Source Softw. 2025, 10, 7584. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Suryadevara, S.; Yanamala, A.K.Y. A Comprehensive Overview of Artificial Neural Networks: Evolution, Architectures, and Applications. Rev. Intel. Artif. Med. 2021, 12, 51–76. [Google Scholar]
- Kelly, M.; Longjohn, R.; Nottingham, K. The UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu (accessed on 24 September 2025).
- Alcalá-Fdez, J.; Fernandez, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. -Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1991. [Google Scholar]
- Tzimourta, K.D.; Tsoulos, I.; Bilero, I.T.; Tzallas, A.T.; Tsipouras, M.G.; Giannakeas, N. Direct Assessment of Alcohol Consumption in Mental State Using Brain Computer Interfaces and Grammatical Evolution. Inventions 2018, 3, 51. [Google Scholar] [CrossRef]
- Quinlan, J.R. Simplifying Decision Trees. Int. J. -Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Horton, P.; Nakai, K. A Probabilistic Classification System for Predicting the Cellular Localization Sites of Proteins. In Proceedings of the International Conference on Intelligent Systems for Molecular Biology, St. Louis, MO, USA, 12–15 June 1996; Volume 4, pp. 109–115. [Google Scholar]
- Hayes-Roth, B.; Hayes-Roth, F. Concept learning and the recognition and classification of exemplars. J. Verbal Learn. Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef]
- Dy, J.G.; Brodley, C.E. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Input Feature Extraction for Multilayered Perceptrons Using Supervised Principal Component Analysis. Neural Process. Lett. 1999, 10, 243–252. [Google Scholar] [CrossRef]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Mcdermott, J.; Forsyth, R.S. Diagnosing a disorder in a classification benchmark. Pattern Recognit. Lett. 2016, 73, 41–43. [Google Scholar] [CrossRef]
- Cestnik, G.; Konenenko, I.; Bratko, I. Assistant-86: A Knowledge-Elicitation Tool for Sophisticated Users. In Progress in Machine Learning; Bratko, I., Lavrac, N., Eds.; Sigma Press: Wilmslow, UK, 1987; pp. 31–45. [Google Scholar]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Roberts, S.J.; Costello, D.A.E.; Moroz, I.M. Exploiting Nonlinear Recurrence and Fractal Scaling Properties for Voice Disorder Detection. BioMed Eng. OnLine 2007, 6, 23. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Spielman, J.; Ramig, L.O. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. Proc. Annu. Symp. Comput. Appl. Med. Care 1988, 9, 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Virtual, 1–5 November 2015; art. no. 7319047. pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression, JRSS-C. Appl. Stat. 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Cortez, P.; Silva, A.M.G. Using data mining to predict secondary school student performance. In Proceedings of the 5th Annual Future Business Technology Conference, EUROSIS-ETI, Porto, Portugal, 9–11 April 2008; pp. 5–12. [Google Scholar]
- Yeh, I.-C.; Yang, K.-J.; Ting, T.-M. Knowledge discovery on RFM model using Bernoulli sequence. Expert Syst. Appl. 2009, 36, 5866–5871. [Google Scholar] [CrossRef]
- Jeyasingh, S.; Veluchamy, M. Modified bat algorithm for feature selection with the Wisconsin diagnosis breast cancer (WDBC) dataset. Asian Pac. J. Cancer Prev. APJCP 2017, 18, 1257. [Google Scholar] [PubMed]
- Alshayeji, M.H.; Ellethy, H.; Gupta, R. Computer-aided detection of breast cancer on the Wisconsin dataset: An artificial neural networks approach. Biomed. Signal Process. Control 2022, 71, 103141. [Google Scholar] [CrossRef]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.C.; Rieke, P.D.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Automatic Seizure Detection Based on Time-Frequency Analysis and Artificial Neural Networks. Comput. Intell. Neurosci. 2007, 2007, 80510. [Google Scholar] [CrossRef]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]




| Group | Symbol/Name | Value | Description (Upright) |
|---|---|---|---|
| Core | 100 | Population size. | |
| 500 | Max iterations (also used in schedule). | ||
| 150,000 | Max function evaluations (stopping). | ||
| 0.14 | Initial injury intensity; decays with . | ||
| 0.38 | Per-dimension wounding probability. | ||
| 0.80 | Per-dimension healing probability. | ||
| 0.15 | Probability of DE (best/1,bin) move. | ||
| F | 0.70 | DE differential weight (scale factor). | |
| 0.50 | DE crossover probability. | ||
| enabled | yes | Enable scar map. | |
| 0.06 | Learning rate for updates. | ||
| 4 | Bandage freeze length (iters). | ||
| 0.05/0.98 | Bounds for per-dimension wound prob. | ||
| 0.50/3.00 | Bounds for per-dimension wound scale. | ||
| 0.25 | Momentum forgetting (decay). | ||
| 0.75 | Bias strength toward momentum direction. | ||
| Hot-Dims Focus | 0.05 | Decay rate for (dim scores). | |
| K | 6 | Number of top (hot) dimensions. | |
| 1.5 | Prob. boost on hot-dims (effective, non-persistent). | ||
| 1.6 | Scale boost on hot-dims (effective, non-persistent). | ||
| RAGE/hyper-RAGE | enabled | yes | Enable RAGE bursts. |
| 12 | No-improve threshold to arm RAGE (iters). | ||
| B | 10 | RAGE burst length (iters). | |
| 2.2 | Prob. multiplier during RAGE. | ||
| 2.8 | Scale multiplier during RAGE. | ||
| ignore bandage | yes | Ignore bandage during RAGE window. | |
| enabled | yes | Enable hyper-RAGE. | |
| 28 | Second stagnation threshold. | ||
| 12 | Hyper-RAGE burst length (iters). | ||
| 3.0 | Prob. multiplier during hyper-RAGE. | ||
| 3.5 | Scale multiplier during hyper-RAGE. | ||
| Lévy-Wounds (Mantegna) | enabled | yes | Enable Lévy steps. |
| 1.5 | Stability index (tail heaviness). | ||
| 0.6 | Global Lévy scale. | ||
| Alpha-Strike | 0.10 | Reinit probability per individual within strike. | |
| 0.90 | Strike step scaling modifier (implementation-specific). | ||
| Catastrophic Micro-Reset | enabled | yes | Enable micro-reset. |
| 40 | No-improve iters ⇒ reset. | ||
| 0.08 | Fraction of population to reset. | ||
| 0.25 | Std. around elite centroid for reset (if biased). | ||
| Healing Adjustments and Cooldown | 0.35 | Healing-rate reduction during bursts. | |
| 0.25 | Healing-rate increase post-burst. | ||
| 8 | Healing cooldown length (iters). | ||
| Adaptive Restarts and Hybrid Injection | 10 | Global stagnation threshold for restart. | |
| — | Replacement fraction at restart (set per experiment). | ||
| — | Probability of injection from (vs. uniform). | ||
| — | Minimum target diversity after restart. |
| Name | Value | Description |
|---|---|---|
| 100 | Population size for all methods | |
| 500 | Maximum number of iterations for all methods | |
| CLPSO | ||
| clProb | 0.3 | Comprehensive learning probability |
| cognitiveWeight | 1.49445 | Cognitive weight |
| inertiaWeight | 0.729 | Inertia weight |
| mutationRate | 0.01 | Mutation rate |
| socialWeight | 1.49445 | Social weight |
| CMA-ES | ||
| Population size | ||
| EA4Eig | ||
| archiveSize | 100 | Archive size for JADE-style mutation |
| eig_interval | 5 | Recompute eigenbasis every k iterations |
| maxCR | 1 | Upper bound for CR |
| maxF | 1 | Upper bound for F |
| minCR | 0 | Lower bound for CR |
| minF | 0.1 | Lower bound for F |
| pbest | 0.2 | p-best fraction (current-to-pbest/1) |
| tauCR | 0.1 | Self-adaptation prob. for CR |
| tauF | 0.1 | Self-adaptation prob. for F |
| mLSHADE_RL | ||
| archiveSize | 500 | Archive size |
| memorySize | 10 | Success-history memory size (H) |
| minPopulation | 4 | Minimum population size |
| pmax | 0.2 | Maximum p-best fraction |
| pmin | 0.05 | Minimum p-best fraction |
| SaDE | ||
| crSigma | 0.1 | Std for CR sampling |
| fGamma | 0.1 | Scale for Cauchy F sampling |
| initCR | 0.5 | Initial CR mean |
| initF | 0.7 | Initial F mean |
| learningPeriod | 25 | Iterations per adaptation window |
| UDE3 | ||
| minPopulation | 4 | Minimum population size. |
| memorySize | 10 | Success-history memory size (H). |
| archiveSize | 100 | Archive size. |
| pmin | 0.05 | Minimum p-best fraction. |
| pmax | 0.2 | Maximum p-best fraction. |
| Problem | Formula | Dim | Bounds |
|---|---|---|---|
| Parameter Estimation for Frequency-Modulated Sound Waves | 6 | ||
| Lennard–Jones Potential | 30 | ||
| Bifunctional Catalyst Blend Optimal Control | , , , , , | 1 | |
| Optimal Control of a Nonlinear Stirred- Tank Reactor | , | 1 | |
| Tersoff Potential for Model Si (B) | where , : cutoff function with : angle parameter | 30 | |
| Tersoff Potential for Model Si (C) | 30 | ||
| Spread Spectrum Radar Polly phase Code Design | , | 20 | |
| Transmission Network Expansion Planning | 7 | ||
| Electricity Transmission Pricing | 126 | ||
| Circular Antenna Array Design | 12 | ||
| Dynamic Economic Dispatch 1 | 120 | ||
| Dynamic Economic Dispatch 2 | 216 | ||
| Static Economic Load Dispatch (1, 2, 3, 4, 5) |
6 13 15 40 140 |
See Technical Report of CEC2011 |
| Problem | Modality | Separability | Conditioning |
|---|---|---|---|
| Parameter Estimation for Frequency-Modulated Sound Waves | Multimodal | Non-separable | Moderate |
| Lennard–Jones Potential |
Near-flat/ effectively | Non-separable | Ill-conditioned |
| Bifunctional- Catalyst Blend Optimal Control |
Near-flat / effectively unimodal | Non-separable |
Near-flat/ well-conditioned |
| Optimal Control of a Nonlinear Stirred- Tank Reactor |
Near-flat/ effectively unimodal | Non-separable |
Near-flat/ well-conditioned |
| Tersoff Potential for Model Si (B) | Multimodal | Non-separable | Ill-conditioned |
| Tersoff Potential for Model Si (C) | Multimodal | Non-separable | Ill-conditioned |
| Spread-Spectrum Radar Polly Phase- Code Design | Multimodal | Non-separable | Moderate |
| Transmission Network Expansion Planning |
Near-flat/ effectively unimodal | Non-separable | Near-flat |
| Electricity Transmission Pricing |
Structured/ likely multimodal | Non-separable | Moderate |
| Circular Antenna Array Design | Multimodal | Non-separable | Moderate |
| Dynamic Economic Dispatch 1 | Smooth (nearly quadratic) | Non-separable | |
| Dynamic Economic Dispatch 2 |
Structured/ possibly multimodal | Non-separable | Moderate |
| Static Economic Load Dispatch 1 |
Multimodal (valve-point effects) | Non-separable | Ill-conditioned |
| Static Economic Load Dispatch 2 |
Multimodal (valve-point effects) | Non-separable | Ill-conditioned |
| Static Economic Load Dispatch 3 |
Multimodal (valve-point effects) | Non-separable | Ill-conditioned |
| Static Economic Load Dispatch 4 |
Multimodal (valve-point effects) | Non-separable | Ill-conditioned |
| Static Economic Load Dispatch 5 |
Multimodal (valve-point effects) | Non-separable | Ill-conditioned |
| Parameter | Value | Mean | Min | Max | Iters | Main-Effect Range |
|---|---|---|---|---|---|---|
| 0.1 | 0.138292 | 0.274259 | 150 | 0.0066789 | ||
| 0.3 | 0.141141 | 0.274394 | 150 | |||
| 0.5 | 0.135853 | 0.234322 | 150 | |||
| 0.7 | 0.136441 | 0.272128 | 150 | |||
| 0.9 | 0.134732 | 0.21554 | 150 | |||
| 0.1 | 0.133427 | 0.221196 | 150 | 0.00544895 | ||
| 0.3 | 0.138797 | 0.274394 | 150 | |||
| 0.5 | 0.137095 | 0.274259 | 150 | |||
| 0.7 | 0.137095 | 0.235609 | 150 | |||
| 0.9 | 0.138533 | 0.23928 | 150 |
| Parameter | Value | Mean | Min | Max | Iters | Main-Effect Range |
|---|---|---|---|---|---|---|
| 0.1 | −27.1628 | −32.3234 | −19.509 | 150 | 0.247722 | |
| 0.3 | −27.2453 | −32.3291 | −20.1075 | 150 | ||
| 0.5 | −27.1499 | −33.3141 | −18.626 | 150 | ||
| 0.7 | −26.9975 | −33.0304 | −20.6726 | 150 | ||
| 0.9 | −27.243 | −33.216 | −19.6771 | 150 | ||
| 0.1 | −27.0514 | −33.0304 | −20.1075 | 150 | 0.565867 | |
| 0.3 | −27.1281 | −32.3291 | −18.626 | 150 | ||
| 0.5 | −27.5176 | −33.3141 | −21.4231 | 150 | ||
| 0.7 | −27.1498 | −33.216 | −19.509 | 150 | ||
| 0.9 | −26.9517 | −31.699 | −19.6771 | 150 |
| Parameter | Value | Mean | Min | Max | Iters | Main-Effect Range |
|---|---|---|---|---|---|---|
| 0.1 | −26.2187 | −27.4563 | −24.7514 | 150 | 0.20291 | |
| 0.3 | −26.2884 | −28.385 | −24.788 | 150 | ||
| 0.5 | −26.1057 | −27.5849 | −25.209 | 150 | ||
| 0.7 | −26.3086 | −28.1733 | −24.8844 | 150 | ||
| 0.9 | −26.2761 | −27.4406 | −25.5369 | 150 | ||
| 0.1 | −26.3295 | −28.385 | −24.7514 | 150 | 0.164339 | |
| 0.3 | −26.2855 | −28.1733 | −25.1714 | 150 | ||
| 0.5 | −26.1948 | −27.7785 | −24.788 | 150 | ||
| 0.7 | −26.2224 | −27.1772 | −25.2564 | 150 | ||
| 0.9 | −26.1652 | −27.5849 | −25.1464 | 150 |
| Function |
EA4Eig Best/Mean (2022) [35] |
UDE3 Best/Mean (2024) [36] |
mLSHADE_RL Best/Mean (2024) [37] |
CLPSO Best/Mean (2006) [38] |
SaDE Best/Mean (2009) [39] |
jDE Best/Mean (2006) [40] |
CMA-ES Best/Mean (2001) [48] |
BHO Best/Mean |
|---|---|---|---|---|---|---|---|---|
| Parameter Estimation for Frequency-Modulated Sound Waves | 0.153993305 | 0.03808755 | 0.116157535 | 0.1314837477 | 0.095829444 | 0.116157541 | 0.18160916 | |
| 0.213447296 | 0.115833815 | 0.205011062 | 0.2124981688 | 0.195600253 | 0.146008756 | 0.256863966 | 0.200220764 | |
| Lennard–Jones Potential | −18.48174236 | −21.41786661 | −28.41816707 | −13.43649135 | −21.93636189 | −29.98126575 | −28.42253189 | −32.07742417 |
| −16.3133561 | −17.33977959 | −22.49792055 | −10.25073403 | −17.95333019 | −27.49258505 | −25.78783328 | −24.33212306 | |
| Bifunctional- Catalyst Blend Optimal Control | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 |
| −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | −0.000286591 | |
| Optimal Control of a Nonlinear Stirred-Tank Reactor | 0.390376723 | 0.390376723 | 0.390376723 | 0.3903767228 | 0.390376723 | 0.390376723 | 0.3903767228 | 0.3903767228 |
| 0.390376723 | 0.390376723 | 0.390376723 | 0.3903767228 | 0.390376723 | 0.390376723 | 0.390376723 | 0.390376723 | |
| Tersoff Potential for Model Si (B) | −29.11960284 | −29.44152761 | −28.60814558 | −28.23544117 | −27.25703406 | −13.51157064 | −29.26244222 | −29.03183049 |
| −27.89597789 | −25.70627602 | −26.07976794 | −26.18834522 | −25.25867422 | −3.983690794 | −27.5889735 | −27.26630121 | |
| Tersoff Potential for Model Si (C) | −33.39767521 | −33.12997729 | −32.28575942 | −30.85200257 | −31.85343594 | −18.76214649 | −33.19699356 | −33.38947338 |
| −31.11610936 | −28.6603137 | −30.03594436 | −28.87349048 | −29.59692733 | −8.506037168 | −31.79270914 | −31.31864105 | |
| Spread-Spectrum Radar Polly Phase-Code Design | 0.517866993 | 1.048240196 | 0.033146096 | 1.085334991 | 0.572731322 | 1.525870558 | 0.01484822722 | 0.195096433 |
| 0.838752978 | 1.265152951 | 0.625788451 | 1.343956153 | 0.844014075 | 1.812042166 | 0.171988666 | 0.601190863 | |
| Transmission Network Expansion Planning | 250 | 250 | 250 | 250 | 250 | 250 | 250 | 250 |
| 250 | 250 | 250 | 250 | 250 | 250 | 250 | 250 | |
| Electricity Transmission Pricing | 13,773,680 | 13773582.53 | 13773567.36 | 13775010.1 | 13773468.68 | 13774627.84 | 13775841.77 | 13773334.9 |
| 13774198.28 | 13773582.53 | 13773852.63 | 13775395.07 | 13773930.93 | 14020953.78 | 13787550.18 | 13773632.45 | |
| Circular Antenna Array Design | 0.006809638 | 0.006809653 | 0.006809701 | 0.006933401045 | 0.00681287 | 0.006820072 | 0.007204797576 | 0.007101505 |
| 0.006809638 | 0.011722944 | 0.006823547 | 0.05181551798 | 0.008186204 | 0.017657998 | 0.008635655364 | 0.158523549 | |
| Dynamic Economic Dispatch 1 | 412736103.9 | 410197836.9 | 415275891.6 | 428607927.6 | 411226317.3 | 968042312.1 | 88285.6024 | 410074526.4 |
| 421199260.5 | 410628483.3 | 418526775.3 | 435250914.5 | 413699347.4 | 1034393036 | 102776.7103 | 410079513.3 | |
| Dynamic Economic Dispatch 2 | 346855.5418 | 357530.5408 | 392247.7213 | 33031590.31 | 519820.5596 | 340091475.3 | 502699.4187 | 347469.862 |
| 12332507.25 | 537163.4139 | 5966956.365 | 53906147.38 | 4090304.18 | 397471715.1 | 477720.1511 | 354734.7105 | |
| Static Economic Load Dispatch 1 | 6163.560978 | 6164.766919 | 6163.546883 | 6554.672173 | 6360.353305 | 6163.749006 | 6657.613028 | 6512.525519 |
| 6170.965013 | 6266.250251 | 6353.722019 | 7668.333603 | 6464.861828 | 6778.527028 | 415917.4625 | 6772.880257 | |
| Static Economic Load Dispatch 2 | 14.46160489 | 18725.64707 | 17905.85383 | 19030.36081 | 18455.37286 | 1161578.904 | 763001.2185 | 18754.99866 |
| 18779.92036 | 19660.49074 | 18661.20763 | 20699.00219 | 21829.10208 | 3671587.605 | 1425815.44 | 19232.05211 | |
| Static Economic Load Dispatch 3 | 470023233.3 | 470023232.3 | 470023232.6 | 470192288.3 | 470023232.7 | 471058115.8 | 470023232.3 | 470023233.2 |
| 470023234.5 | 470023232.3 | 470023234.7 | 470294703.2 | 470023232.7 | 471963142.3 | 470023232.3 | 470023278 | |
| Static Economic Load Dispatch 4 | 71193.07649 | 168334.7003 | 71067.8441 | 884980.5569 | 862196.432 | 6482592.714 | 476053.5197 | 71089.03508 |
| 71193.07649 | 348720.6677 | 406986.2181 | 1423887.358 | 1469886.142 | 17527314.24 | 2925852.935 | 100831.805 | |
| Static Economic Load Dispatch 5 | 8085796774 | 8070408727 | 8079118012 | 8105947615 | 8078489742 | 8453090778 | 8072077963 | 8072061692 |
| 8145304780 | 8071802922 | 8104455647 | 8110924071 | 8081680478 | 8459337082 | 8084017791 | 74458095 |
| Function | EA4Eig | UDE3 | mLSHADE_RL | CLPSO | SaDE | jDE | CMA-ES | BHO |
|---|---|---|---|---|---|---|---|---|
| (2022) [35] | (2024) [36] | (2024) [37] | (2006) [38] | (2009) [39] | (2006) [40] | (2001) [48] | ||
| Parameter Estimation for Frequency-Modulated Sound Waves | 7 | 2 | 4 | 6 | 3 | 5 | 8 | 1 |
| Lennard–Jones Potential | 7 | 6 | 4 | 8 | 5 | 2 | 3 | 1 |
| Bifunctional- Catalyst Blend Optimal Control | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Optimal Control of a Nonlinear Stirred- Tank Reactor | 4 | 4 | 4 | 1 | 4 | 4 | 1 | 1 |
| Tersoff Potential for Model Si (B) | 3 | 1 | 5 | 6 | 7 | 8 | 2 | 4 |
| Tersoff Potential for Model Si (C) | 1 | 4 | 5 | 7 | 6 | 8 | 3 | 2 |
| Spread-Spectrum Radar Polly Phase- Code Design | 4 | 6 | 2 | 7 | 5 | 8 | 1 | 3 |
| Transmission Network Expansion Planning | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Electricity Transmission Pricing | 5 | 4 | 3 | 7 | 2 | 6 | 8 | 1 |
| Circular Antenna Array Design | 1 | 2 | 3 | 6 | 4 | 5 | 8 | 7 |
| Dynamic Economic Dispatch 1 | 5 | 3 | 6 | 7 | 4 | 8 | 1 | 2 |
| Dynamic Economic Dispatch 2 | 1 | 3 | 4 | 7 | 6 | 8 | 5 | 2 |
| Static Economic Load Dispatch 1 | 2 | 4 | 1 | 7 | 5 | 3 | 8 | 6 |
| Static Economic Load Dispatch 2 | 1 | 4 | 2 | 6 | 3 | 8 | 7 | 5 |
| Static Economic Load Dispatch 3 | 1 | 1 | 4 | 7 | 5 | 8 | 1 | 6 |
| Static Economic Load Dispatch 4 | 3 | 4 | 1 | 7 | 6 | 8 | 5 | 2 |
| Static Economic Load Dispatch 5 | 6 | 1 | 5 | 7 | 4 | 8 | 3 | 2 |
| Total | 53 | 51 | 55 | 98 | 71 | 99 | 66 | 47 |
| Function | EA4Eig | UDE3 | mLSHADE_RL | CLPSO | SaDE | jDE | CMA-ES | BHO |
|---|---|---|---|---|---|---|---|---|
| (2022) [35] | (2024) [36] | (2024) [37] | (2006) [38] | (2009) [39] | (2006) [40] | (2001) [48] | ||
| Parameter Estimation for Frequency-Modulated Sound Waves | 7 | 1 | 5 | 6 | 3 | 2 | 8 | 4 |
| Lennard–Jones Potential | 7 | 6 | 4 | 8 | 5 | 1 | 2 | 3 |
| Bifunctional- Catalyst Blend Optimal Control | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Optimal Control of a Nonlinear Stirred- Tank Reactor | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 |
| Tersoff Potential for Model Si (B) | 1 | 6 | 5 | 4 | 7 | 8 | 2 | 3 |
| Tersoff Potential for Model Si (C) | 3 | 7 | 4 | 6 | 5 | 8 | 1 | 2 |
| Spread-Spectrum Radar Polly Phase- Code Design | 4 | 6 | 3 | 7 | 5 | 8 | 1 | 2 |
| Transmission Network Expansion Planning | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Electricity Transmission Pricing | 5 | 1 | 3 | 6 | 4 | 8 | 7 | 2 |
| Circular Antenna Array Design | 1 | 5 | 2 | 7 | 3 | 6 | 4 | 8 |
| Dynamic Economic Dispatch 1 | 6 | 3 | 5 | 7 | 4 | 8 | 1 | 2 |
| Dynamic Economic Dispatch 2 | 6 | 3 | 5 | 7 | 4 | 8 | 2 | 1 |
| Static Economic Load Dispatch 1 | 1 | 2 | 3 | 7 | 4 | 6 | 8 | 5 |
| Static Economic Load Dispatch 2 | 2 | 4 | 1 | 5 | 6 | 8 | 7 | 3 |
| Static Economic Load Dispatch 3 | 4 | 1 | 5 | 7 | 3 | 8 | 1 | 6 |
| Static Economic Load Dispatch 4 | 1 | 3 | 4 | 5 | 6 | 8 | 7 | 2 |
| Static Economic Load Dispatch 5 | 7 | 2 | 5 | 6 | 3 | 8 | 4 | 1 |
| Total | 59 | 54 | 58 | 91 | 66 | 99 | 59 | 48 |
| Algorithm | Best | Mean | Overall | Average | Rank |
|---|---|---|---|---|---|
| BHO | 47 | 48 | 95 | 2.794 | 1 |
| UDE3 (2024) [36] | 51 | 54 | 105 | 3.088 | 2 |
| EA4Eig (2022) [35] | 53 | 59 | 112 | 3.294 | 3 |
| mLSHADE_RL (2024) [37] | 55 | 58 | 113 | 3.323 | 4 |
| CMA-ES (2001) [48] | 66 | 59 | 125 | 3.676 | 5 |
| SaDE (2009) [39] | 71 | 66 | 137 | 4.029 | 6 |
| CLPSO (2006) [38] | 98 | 91 | 189 | 5.558 | 7 |
| jDE (2006) [40] | 99 | 99 | 198 | 5.823 | 8 |
| Dataset | Adam | BFGS | Genetic | BHO |
|---|---|---|---|---|
| APPENDICITIS | 16.50% | 18.00% | 24.40% | 22.07% |
| ALCOHOL | 57.78% | 41.50% | 39.57% | 16.89% |
| AUSTRALIAN | 35.65% | 38.13% | 32.21% | 29.20% |
| BALANCE | 12.27% | 8.64% | 8.97% | 8.06% |
| CLEVELAND | 67.55% | 77.55% | 51.60% | 46.36% |
| CIRCULAR | 19.95% | 6.08% | 5.99% | 4.23% |
| DERMATOLOGY | 26.14% | 52.92% | 30.58% | 9.89% |
| ECOLI | 64.43% | 69.52% | 54.67% | 48.72% |
| GLASS | 61.38% | 54.67% | 52.86% | 53.43% |
| HABERMAN | 29.00% | 29.34% | 28.66% | 28.82% |
| HAYES-ROTH | 59.70% | 37.33% | 56.18% | 35.49% |
| HEART | 38.53% | 39.44% | 28.34% | 20.96% |
| HEARTATTACK | 45.55% | 46.67% | 29.03% | 21.06% |
| HOUSEVOTES | 7.48% | 7.13% | 6.62% | 6.45% |
| IONOSPHERE | 16.64% | 15.29% | 15.14% | 15.54% |
| LIVERDISORDER | 41.53% | 42.59% | 31.11% | 31.87% |
| LYMOGRAPHY | 39.79% | 35.43% | 28.42% | 27.24% |
| MAMMOGRAPHIC | 46.25% | 17.24% | 19.88% | 17.24% |
| PARKINSONS | 24.06% | 27.58% | 18.05% | 14.72% |
| PIMA | 34.85% | 35.59% | 32.19% | 29.40% |
| POPFAILURES | 5.18% | 5.24% | 5.94% | 7.40% |
| REGIONS2 | 29.85% | 36.28% | 29.39% | 26.83% |
| SAHEART | 34.04% | 37.48% | 34.86% | 33.88% |
| SEGMENT | 49.75% | 68.97% | 57.72% | 27.26% |
| SPIRAL | 47.67% | 47.99% | 48.66% | 43.75% |
| STATHEART | 44.04% | 39.65% | 27.25% | 20.71% |
| STUDENT | 5.13% | 7.14% | 5.61% | 6.66% |
| TRANSFUSION | 25.68% | 25.84% | 24.87% | 24.56% |
| WDBC | 35.35% | 29.91% | 8.56% | 6.43% |
| WINE | 29.40% | 59.71% | 19.20% | 15.86% |
| Z_F_S | 47.81% | 39.37% | 10.73% | 10.88% |
| ZO_NF_S | 47.43% | 43.04% | 21.54% | 9.76% |
| ZONF_S | 11.99% | 15.62% | 4.36% | 2.68% |
| ZOO | 14.13% | 10.70% | 9.50% | 7.27% |
| AVERAGE | 34.48% | 34.34% | 26.55% | 21.52% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charilogis, V.; Tsoulos, I.G. Healing Intelligence: A Bio-Inspired Metaheuristic Optimization Method Using Recovery Dynamics. Future Internet 2025, 17, 441. https://doi.org/10.3390/fi17100441
Charilogis V, Tsoulos IG. Healing Intelligence: A Bio-Inspired Metaheuristic Optimization Method Using Recovery Dynamics. Future Internet. 2025; 17(10):441. https://doi.org/10.3390/fi17100441
Chicago/Turabian StyleCharilogis, Vasileios, and Ioannis G. Tsoulos. 2025. "Healing Intelligence: A Bio-Inspired Metaheuristic Optimization Method Using Recovery Dynamics" Future Internet 17, no. 10: 441. https://doi.org/10.3390/fi17100441
APA StyleCharilogis, V., & Tsoulos, I. G. (2025). Healing Intelligence: A Bio-Inspired Metaheuristic Optimization Method Using Recovery Dynamics. Future Internet, 17(10), 441. https://doi.org/10.3390/fi17100441