A Task Offloading and Resource Allocation Strategy Based on Multi-Agent Reinforcement Learning in Mobile Edge Computing
Abstract
1. Introduction
- (1)
- This paper constructs a cloud-edge collaborative computing model, and related task queue, delay, and energy consumption model, and gives joint optimization problem modeling for task offloading and resource allocation with multiple constraints.
- (2)
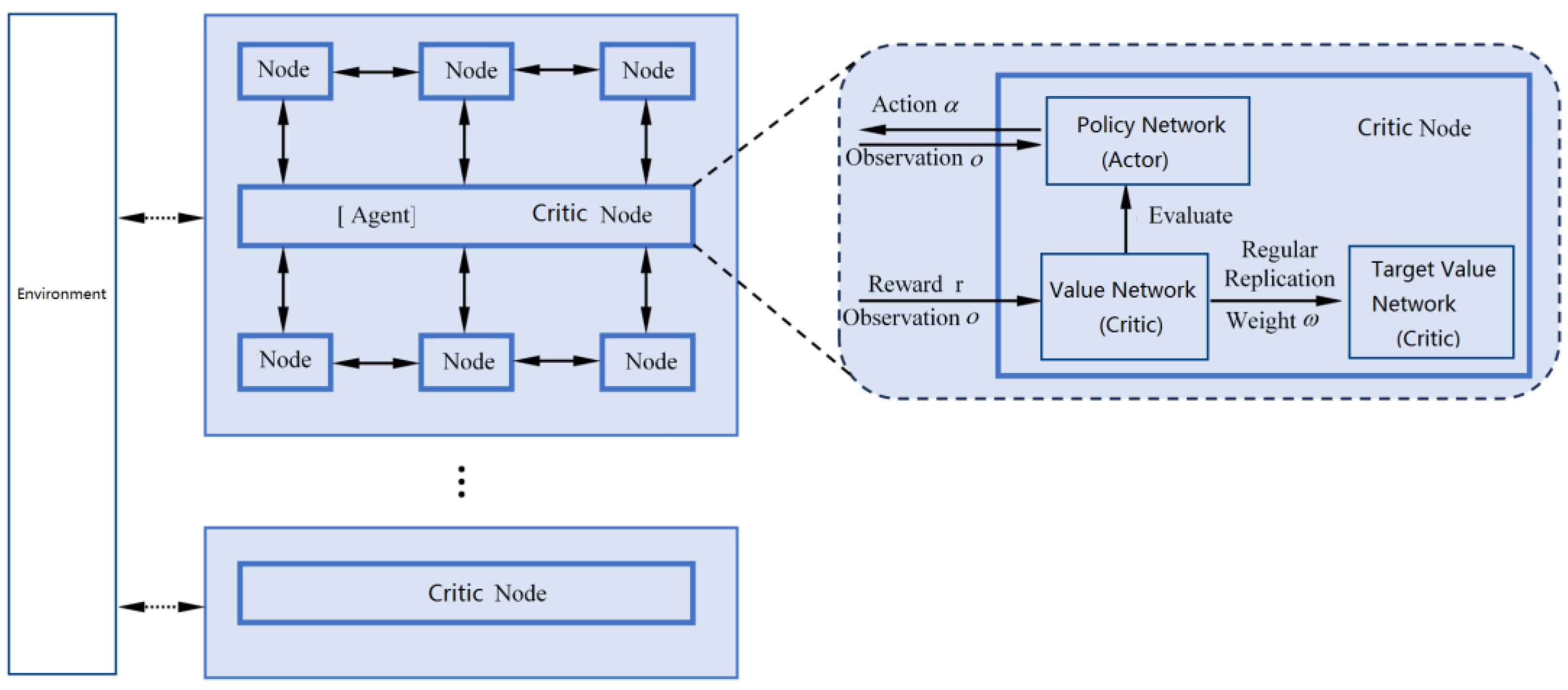
- In order to solve the joint optimization problem, this paper designs a decentralized task offloading and resource allocation scheme based on “task-oriented” multi-agent reinforcement learning. In this scheme, we present information synchronization protocol and offloading scheduling rules and use edge servers as agents to construct a multi-agent system based on the Actor–Critic framework.
- (3)
- An offloading decision algorithm TOMAC-PPO (Task-Oriented Multi-Agent Collaborative-Proximal Policy Optimization) is proposed. The algorithm applies the proximal policy optimization to the multi-agent system and combines the Transformer neural network model to realize the memory and prediction of network state information. Experimental results show that this algorithm has better convergence speed, and can effectively reduce the service cost, energy consumption, and task drop rate under high load and high failure rates.
2. Related Works
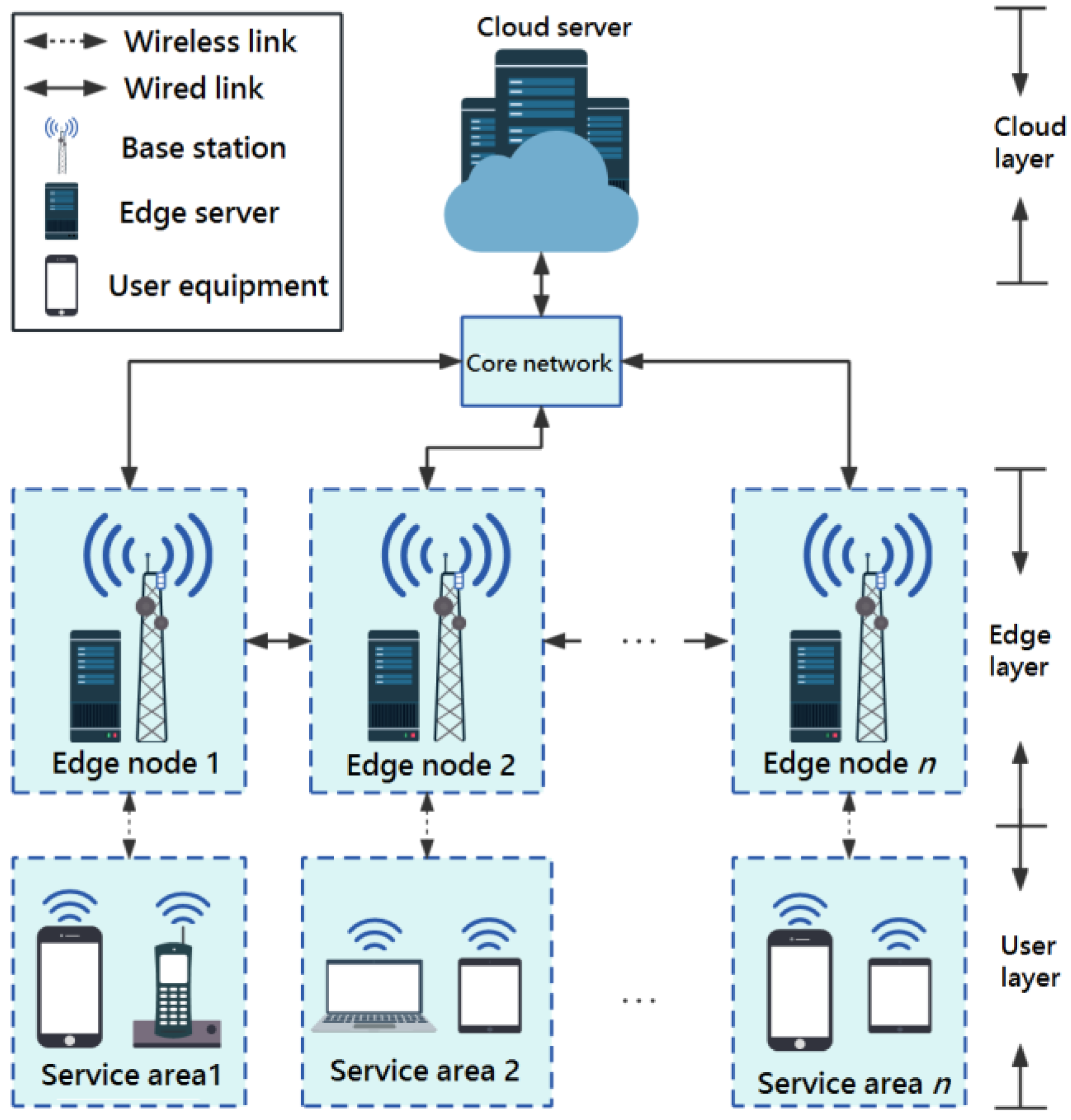
3. Preliminaries: Network Model and Problem Definition
3.1. Cloud-Edge Collaboration Model for MEC Network
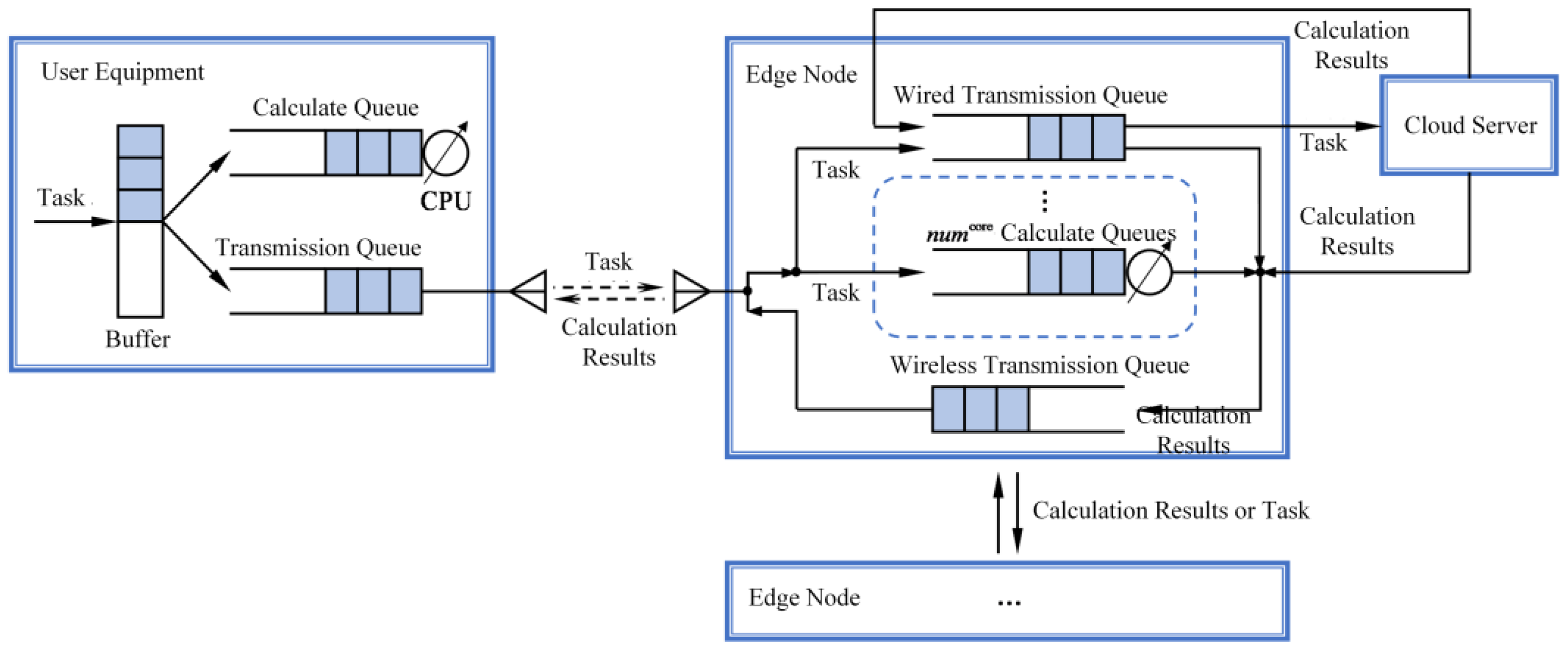
3.2. Task Queue Description
- If the average queue length is less than the minimum threshold , newly arrived tasks are pushed into the queue;
- If the average queue length is greater than the minimum threshold and less than the maximum threshold , randomly drop the newly arrived task according to probability;
- If the queue length has reached the maximum threshold , the newly arrived task is dropped .
3.3. Task Model
- (1)
- High-priority tasks have high requirements for delay, which are related to security and have hard indicators for task completion rate.
- (2)
- The key task is a computing task that requires extremely high security and can appropriately lower delay requirements but cannot be discarded.
- (3)
- Low-priority tasks are not related to security but are in scenarios that require energy savings, or tasks with excessive data volume and computation time.
- (4)
- Except for the above three types of computing tasks, all other computing tasks are routine tasks.
3.4. Network Communication and Observation Model
3.5. Network Delay and Energy Consumption Model
3.6. Offloading Decision and Resource Allocation Problem Modeling
4. A Joint Optimization Scheme for Task-Oriented Multi-Agent PPO Offloading Decision and Resource Allocation
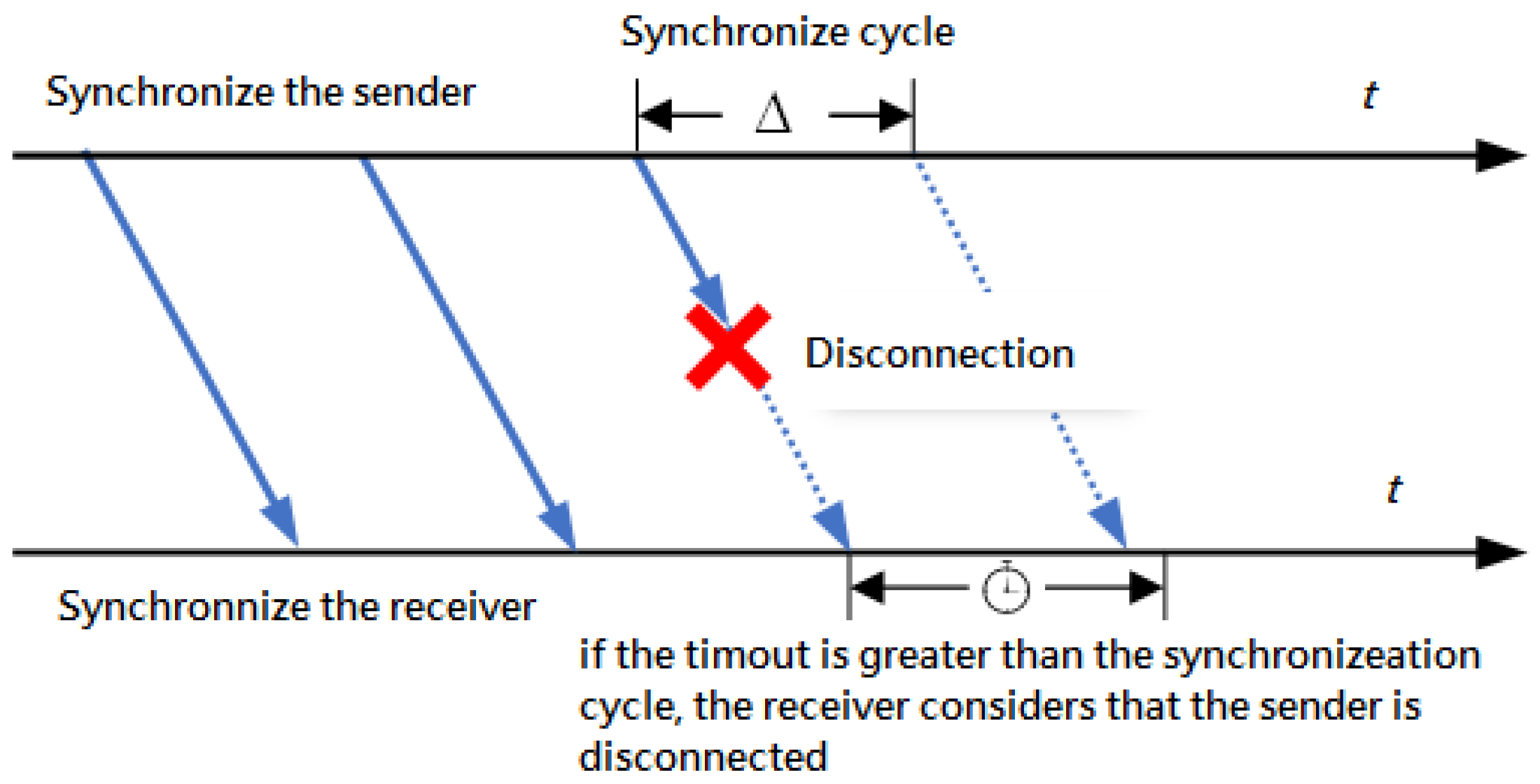
4.1. Network Information Synchronization Protocol
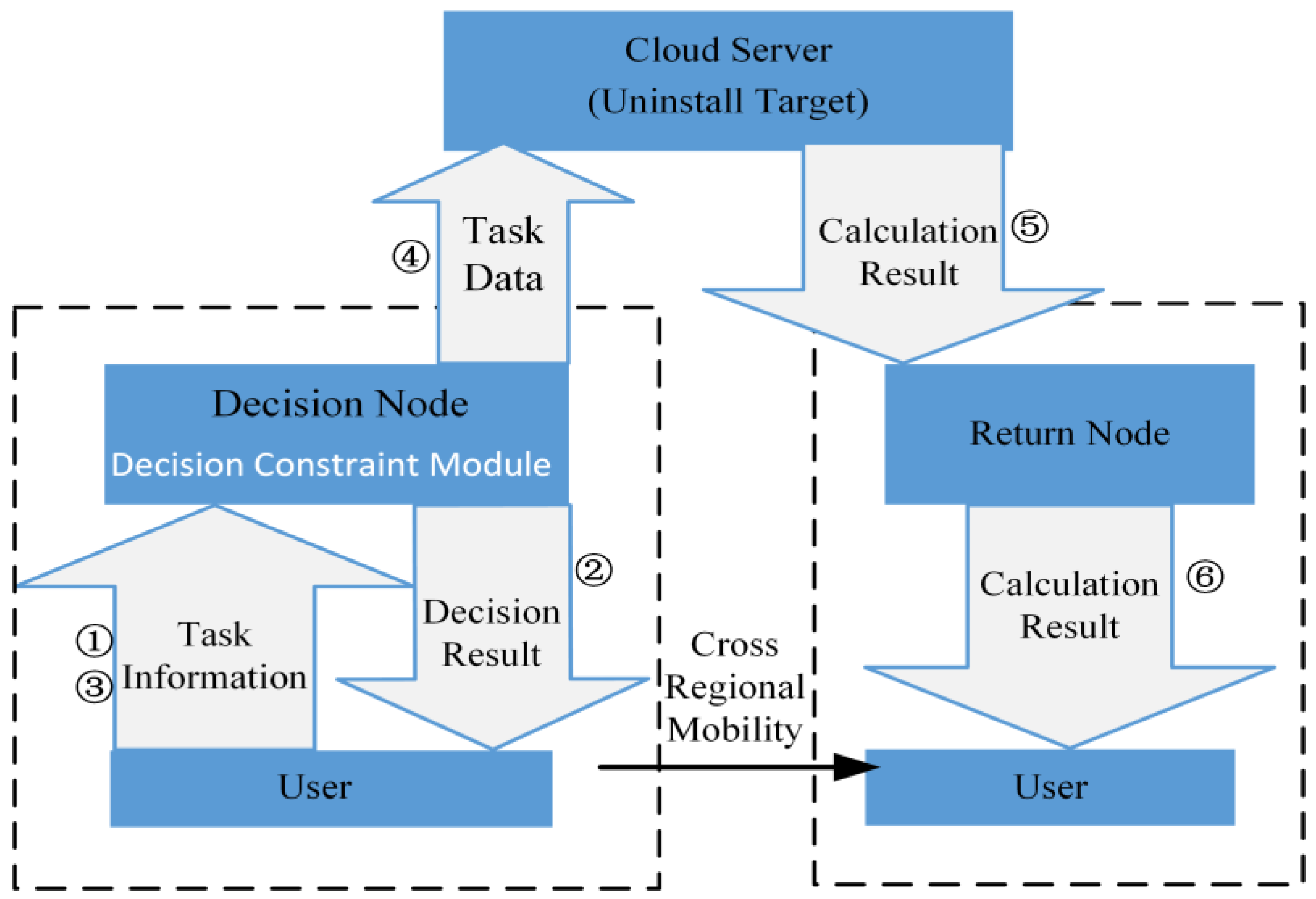
4.2. Distributed Offloading Scheduling Rules
- (1)
- If the user is within the service area, when they generate a task, they first report the summary information of the task to the nearest edge node they are connected to (referred to as the “decision node”).
- (2)
- The decision node makes an offloading decision based on this summary information and network conditions and sends it back to the user.
- (3)
- Users perform local calculations or offload tasks to decision nodes based on the received decision results.
- (4)
- After receiving task data, the node forwards the task to the offloading target node for calculation.
- (5)
- After the calculation is completed, offloading the target node will determine the node closest to the user as the “return node”, and then send the calculation result to the return node in the shortest path.
- (6)
- The final calculation result is sent back to the user by the return node.
4.3. Multi-Agent System Based on Actor–Critic Framework
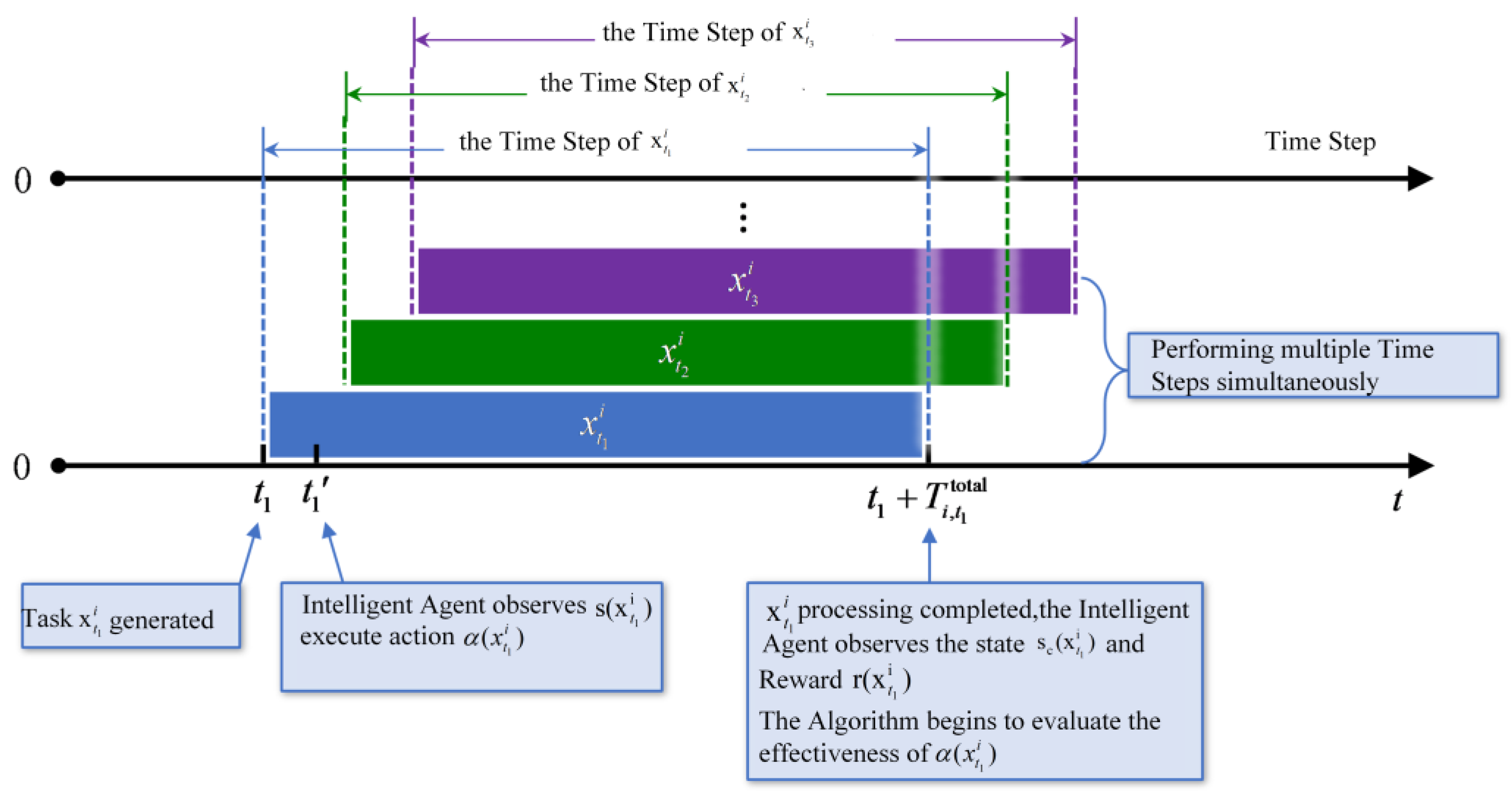
4.4. Task-Oriented Markov Decision-Making Process
- (1)
- Status
- (2)
- Action
- (3)
- Rewards
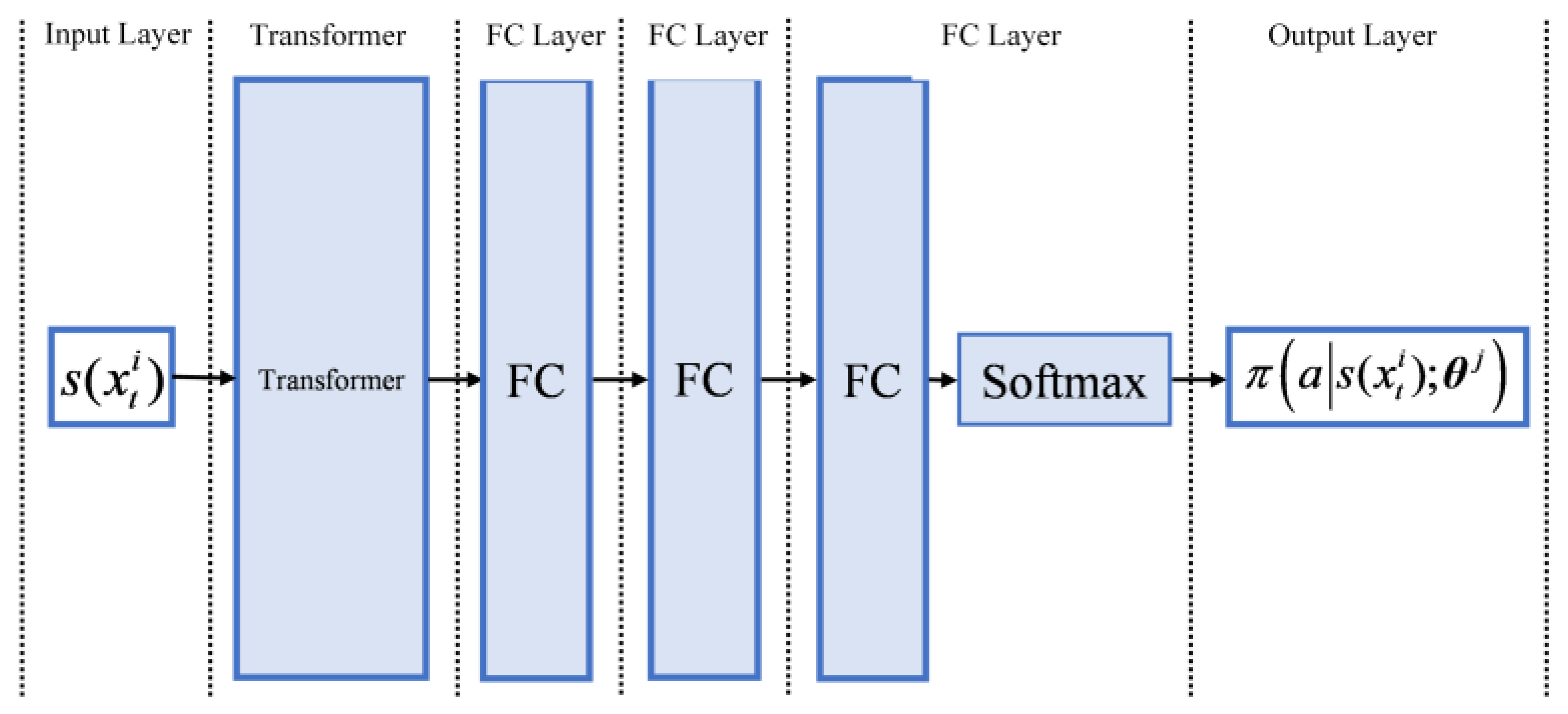
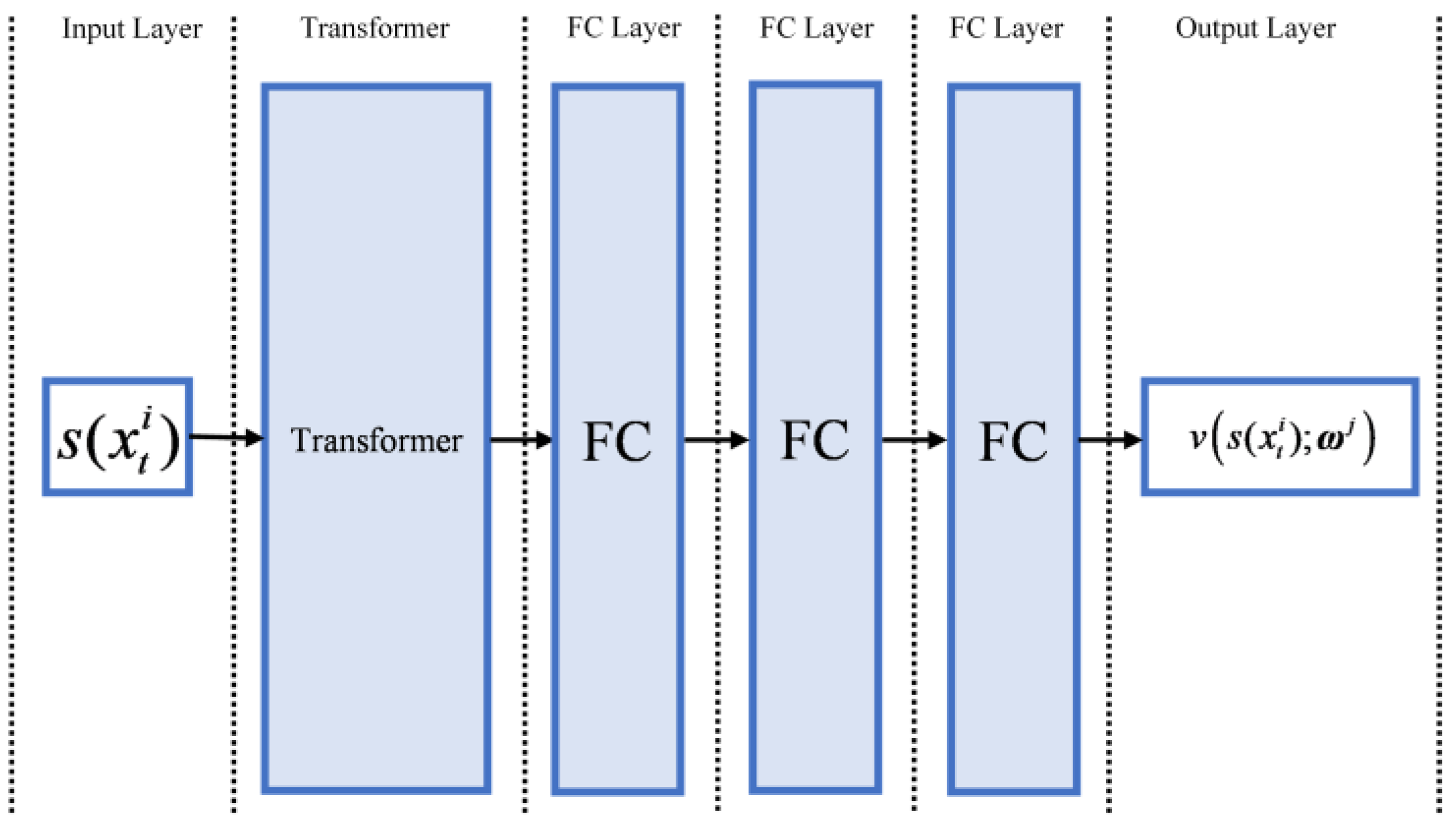
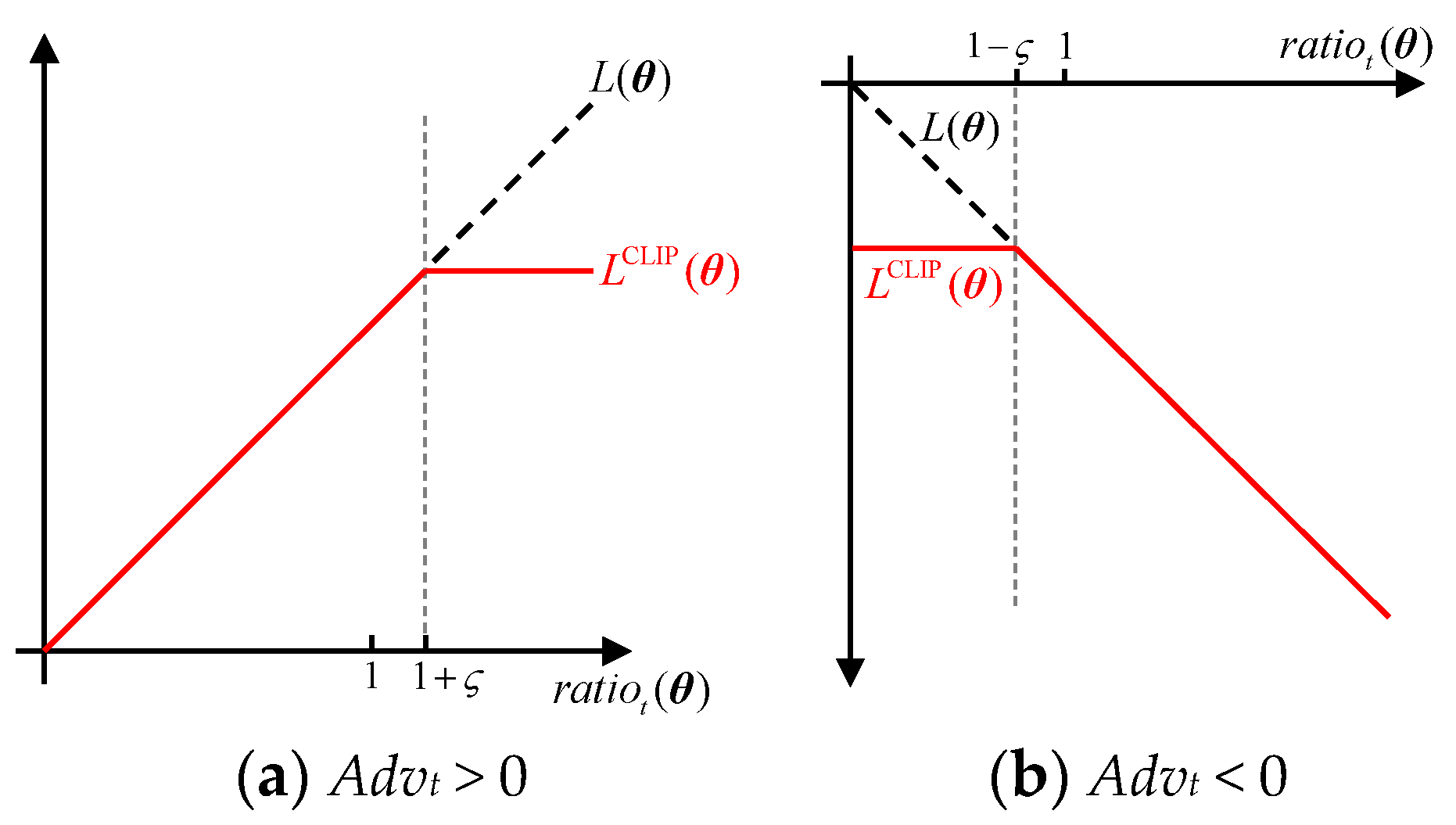
4.5. Neural Network Structure Used by TOMAC-PPO
4.6. TOMAC-PPO Algorithm Process
| Algorithm 1. Task-Oriented Multi-Agent Collaborative-Proximal Policy Optimization (TOMAC-PPO) |
| Input: Training rounds , pruning parameters , value network learning rate, strategy network learning rate , discount rate , target value network update ratio . Output: Optimal task offloading and resource allocation strategy . 1. Randomly initialize the parameter of each strategy network, as well as each value network parameter , and the target value network parameter ; 2. For do 3. For all agents , where do in parallel 4. According to the current strategy collect step trajectory 5. According to (19), calculate the approximate advantage ; 6. Update the policy network parameter of agent according to (20); 7. According to (22) and (23), the value network parameter and the target value network parameter of are updated. End for End for |
5. Experimental Results and Analysis
- (1)
- TOMAC-A2C (Task-Oriented Multi-Agent Cooperative Advantage Actor–Critic). A2C algorithm is one of the classic strategy learning algorithms in the RL field.
- (2)
- TO-A3C (Task-Oriented Asynchronous Advantage Actor–Critic). TO-A3C belongs to the parallel RL method and does not use multi-agent systems. The A3C algorithm improves its performance by establishing multiple independent single agent A2C training environments, enabling them to train in parallel [24].
- (3)
- CCP (Cloud Computing Priority). CCP adopts the principle of “deliver tasks to upper level processing as much as possible”, and prioritizes offloading all tasks to the cloud for processing.
- (4)
- LC (Local Computing). After the task is generated, skip the information reporting process and directly calculate locally by the user.
5.1. Experimental Environment and Parameter Settings
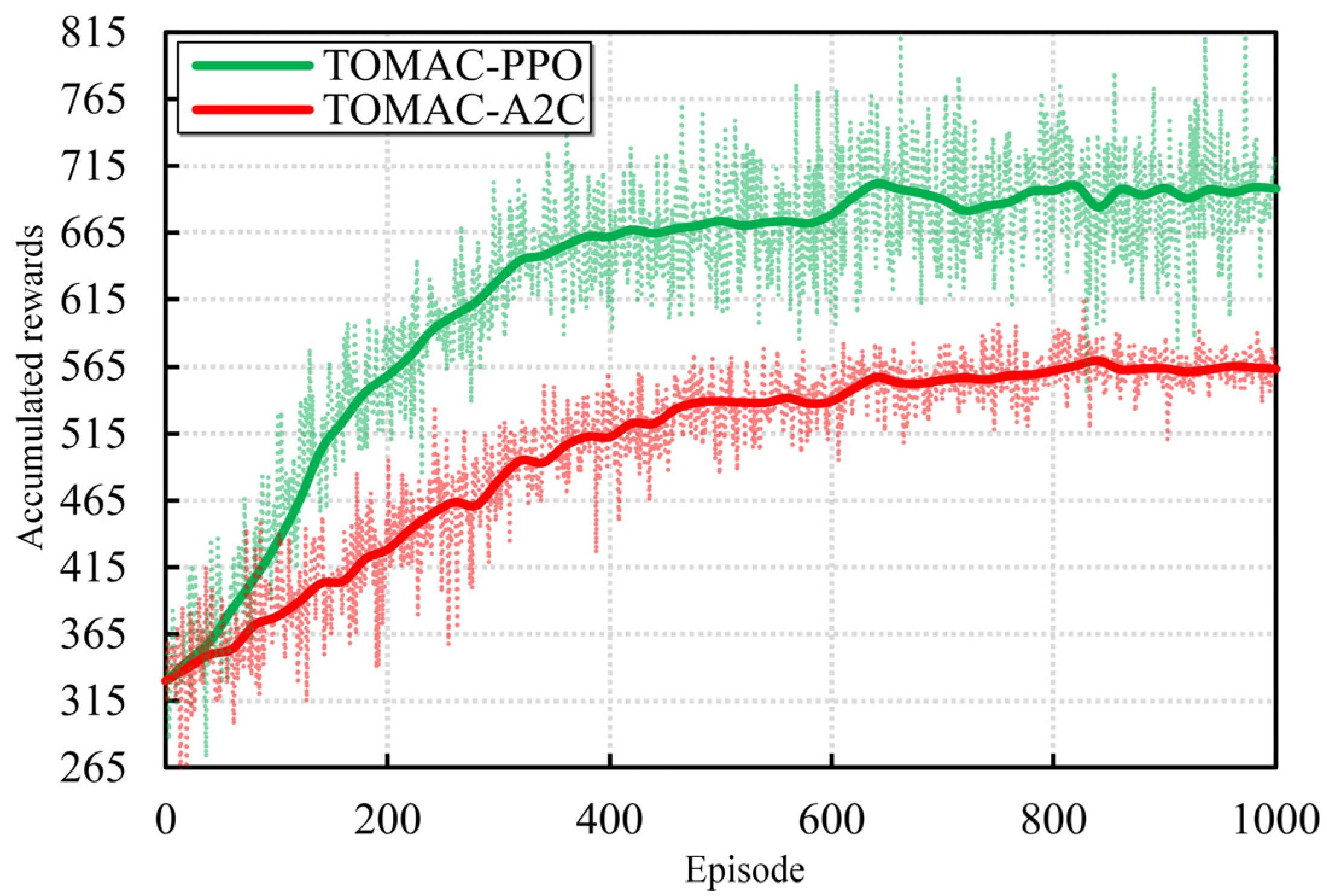
5.2. Convergence Analysis
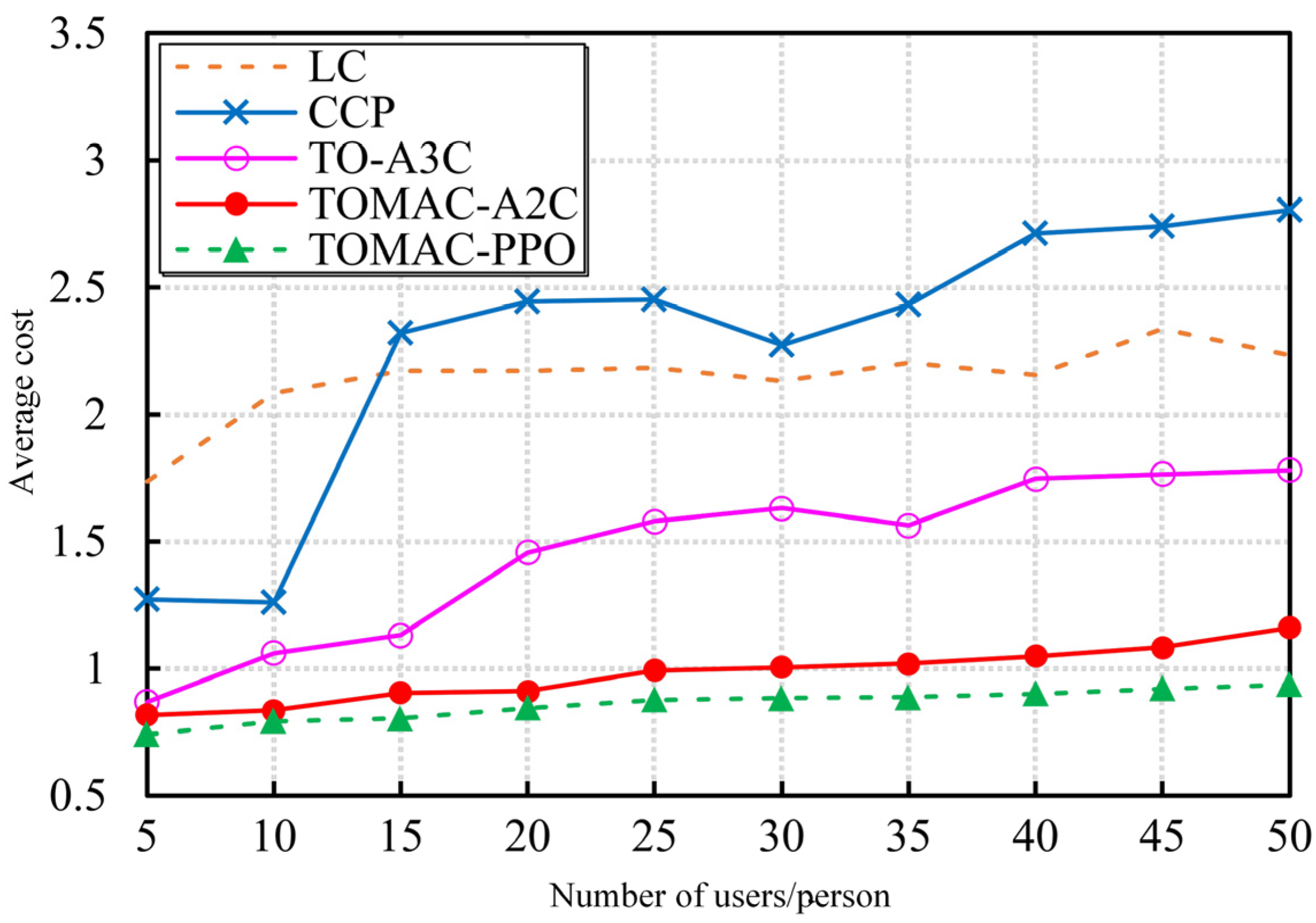
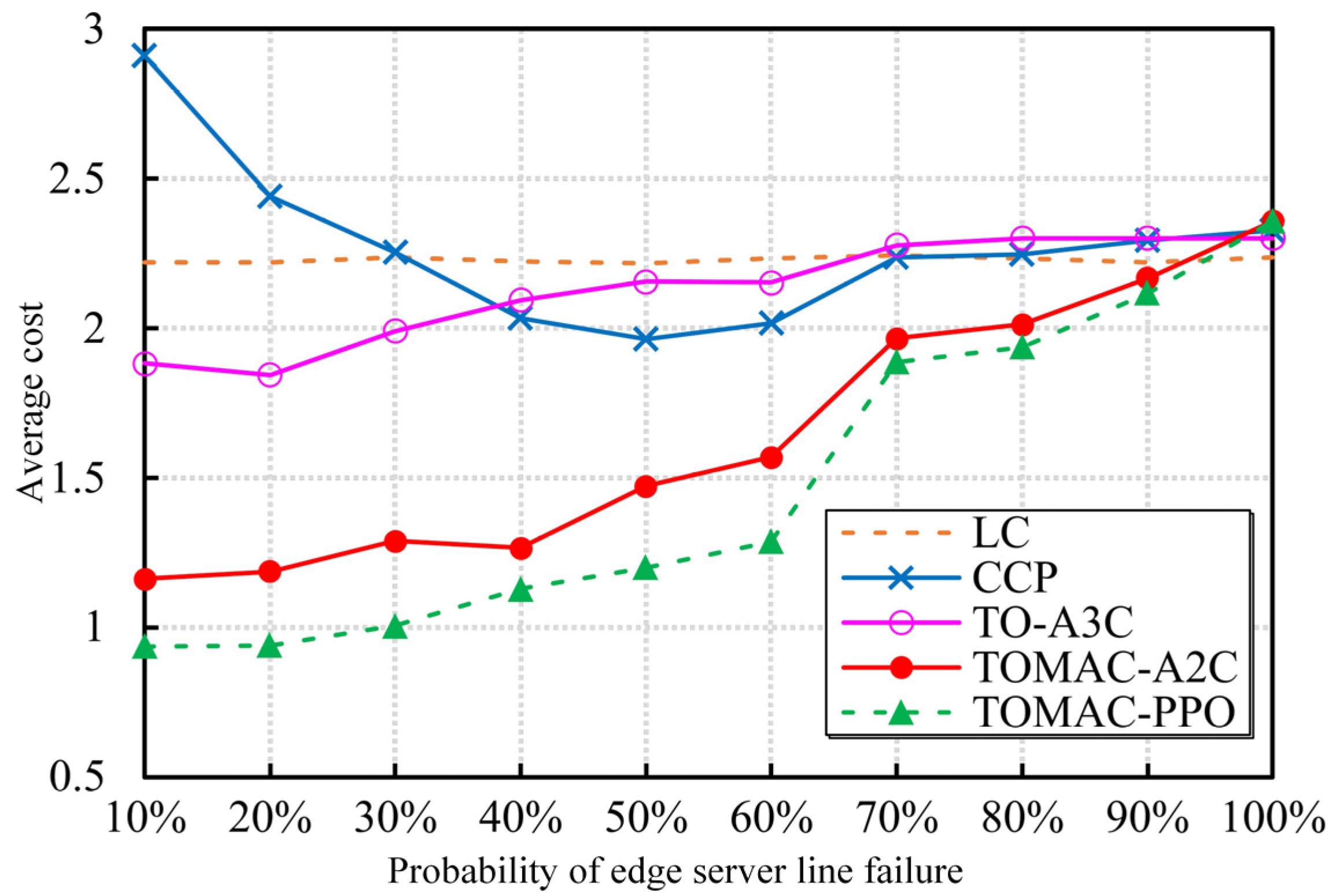
5.3. Optimization Performance Evaluation
5.4. Experiment Results Discussion
6. Conclusions and Further Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TOMAC-PPO | Task-Oriented Multi-Agent Collaborative-Proximal Policy Optimization |
| PPO | Proximal Policy Optimization |
| IoT | Internet of Thing |
| MEC | Mobile Edge Computing |
| RL | Reinforcement Learning |
| DRL | Deep Reinforcement Learning |
| UAVs | Unmanned Aerial Vehicles |
| DQN | Deep Q Network |
| MARL | Multi-Agent Reinforcement Learning |
| MADDPG | Multi-Agent Deep Determining Policy Gradient |
| FIFO | First In First Out |
| FC | Fully Connected |
| TOMAC-A2C | Task-Oriented Multi-Agent Cooperative Advantage Actor–Critic |
| CCP | Cloud Computing Priority |
| LC | Local Computing |
References
- IoT and Non-IoT Connections Worldwide 2010–2025. Available online: https://www.statista.com/statistics/1101442/iot-number-of-connected-devices-worldwide (accessed on 28 August 2024).
- IoT Is Not a Buzzword but Necessity. Available online: https://www.3i-infotech.com/iot-is-not-just-a-buzzword-but-has-practical-applications-even-in-industries/ (accessed on 28 August 2024).
- Zhang, Y.-L.; Liang, Y.-Z.; Yin, M.-J.; Quan, H.-Y.; Wang, T.; Jia, W.-J. Survey on the Methods of Computation Offloading in Molile Edge Computing. J. Comput. Sci. Technol. 2021, 44, 2406–2430. [Google Scholar]
- Duan, S.; Wang, D.; Ren, J.; Lyu, F.; Zhang, Y.; Wu, H.; Shen, X. Distributed artificial intelligence empowered by end-edge-cloud computing: A survey. IEEE Commun. Surv. Tutor. 2022, 25, 591–624. [Google Scholar] [CrossRef]
- Hua, H.; Li, Y.; Wang, T.; Dong, N.; Li, W.; Cao, J. Edge computing with artificial intelligence: A machine learning perspective. ACM Comput. Surv. 2023, 55, 1–35. [Google Scholar] [CrossRef]
- Kar, B.; Yahya, W.; Lin, Y.-D.; Ali, A. Offloading using traditional optimization and machine learning in federated cloud-edge-fog systems: A survey. IEEE Commun. Surv. Tutor. 2023, 25, 1199–1226. [Google Scholar] [CrossRef]
- Arjona-Medina, J.A.; Gillhofer, M.; Widrich, M.; Unterthiner, T.; Brandstetter, J.; Hochreiter, S. RUDDER: Return decomposition for delayed rewards. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 13544–13555. [Google Scholar]
- Zhang, X.-C.; Ren, T.-S.; Zhao, Y.; Rui, F. Joint Optimization Method of Energy Consumption and Time Delay for Mobile Edge Computing. J. Univ. Electron. Sci. Technol. China 2022, 51, 737–742. [Google Scholar]
- Wu, H.-Y.; Chen, Z.-W.; Shi, B.-W.; Deng, S.; Chen, S.; Xue, X.; Feng, Z. Decentralized Service Request Dispatching for Edge Computing Systems. Chin. J. Comput. 2023, 46, 987–1002. [Google Scholar]
- Ma, L.; Wang, X.; Wang, X.; Wang, L.; Shi, Y.; Huang, M. TCDA: Truthful combinatorial double auctions for mobile edge computing in industrial internet of things. IEEE Trans. Mob. Comput. 2021, 21, 4125–4138. [Google Scholar] [CrossRef]
- Cang, Y.; Chen, M.; Pan, Y.; Yang, Z.; Hu, Y.; Sun, H.; Chen, M. Joint user scheduling and computing resource allocation optimization in asynchronous mobile edge computing networks. IEEE Trans. Commun. 2024, 72, 3378–3392. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, G.; Nong, W.; Qiu, Y.; Huang, S. Task offloading in multiple-services mobile edge computing: A deep reinforcement learning algorithm. Comput. Commun. 2023, 202, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Wang, X.; Xia, Y.; Ni, S. Task offloading mechanism based on federated reinforcement learning in mobile edge computing. Digit. Commun. Netw. 2023, 9, 492–504. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H.; Dong, D. Path Planning for Cellular-Connected UAV: A DRL Solution with Quantum-Inspired Experience Replay. IEEE Trans. Wirel. Commun. 2022, 21, 7897–7912. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H. Radio Resource Management for Cellular-Connected UAV: A Learning Approach. IEEE Trans. Commun. 2023, 71, 2784–2800. [Google Scholar] [CrossRef]
- Kuang, Z.-F.; Chen, Q.-L.; Li, L.-F.; Deng, X.H.; Chen, Z.G. Multi-user edge computing task offloading scheduling and resource allocation based on deep reinforcement learning. Chin. J. Comput. 2022, 45, 812–824. (In Chinese) [Google Scholar]
- Tuli, S.; Ilager, S.; Ramamohanarao, K.; Buyya, R. Dynamic scheduling for stochastic edge-cloud computing environments using A3C learning and residual recurrent neural networks. IEEE Trans. Mob. Comput. 2020, 21, 940–954. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: New York, NY, USA, 2021; pp. 321–384. [Google Scholar]
- Zhang, P.; Tian, H.; Zhao, P.; He, S.; Tong, Y. Computation offloading strategy in multi-agent cooperation scenario based on reinforcement learning with value-decomposition. J. Commun. 2021, 42, 1–15. (In Chinese) [Google Scholar]
- Cao, Z.; Zhou, P.; Li, R.; Huang, S.; Wu, D. Multiagent deep reinforcement learning for joint multichannel access and task offloading of mobile-edge computing in industry 4.0. IEEE Internet Things J. 2020, 7, 6201–6213. [Google Scholar] [CrossRef]
- Wang, Y.; He, H.; Tan, X. Truly proximal policy optimization. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference (UAI), Tel Aviv, Israel, 23–25 July 2019; PMLR: New York, NY, USA, 2020; Volume 115, pp. 113–122. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; PMLR: New York, NY, USA, 2015; Volume 37, pp. 1889–1897. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York City, NY, USA, 19–24 June 2016; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1928–1937. [Google Scholar]

| Symbol | Meaning | Value |
|---|---|---|
| Number of edge nodes | 10 | |
| User device cache capacity | ||
| Edge node cache capacity | ||
| Base station bandwidth resources | ||
| Base station service radius | 100 m | |
| Base station transmission power | 200 W | |
| User device transmission power | 0.2 W | |
| User device energy efficiency coefficient | ||
| Gaussian noise power | ||
| The propagation rate of electromagnetic waves in the air | ||
| The propagation rate of electromagnetic waves in a circuit | ||
| The transmission rate of wired communication | ||
| Fault repair duration | ||
| Task input data volume | ||
| Task calculation result data volume | ||
| Task computing density | ||
| Number of CPU cores on edge servers | 14 | |
| Edge server CPU frequency | 2.4 GHz | |
| Cloud server CPU frequency | 10 GHz | |
| Core network forwarding delay | ||
| The distance between adjacent nodes | 150 m | |
| RED Dropped Task Probability | 1/50 | |
| Learning rate | ||
| Training epochs | 1000 | |
| Discount rate | 0.95 | |
| Target network update ratio | 0.01 | |
| Crop parameters | 0.2 | |
| Entropy weight | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Huang, R.; Bao, Z.; Wang, G. A Task Offloading and Resource Allocation Strategy Based on Multi-Agent Reinforcement Learning in Mobile Edge Computing. Future Internet 2024, 16, 333. https://doi.org/10.3390/fi16090333
Jiang G, Huang R, Bao Z, Wang G. A Task Offloading and Resource Allocation Strategy Based on Multi-Agent Reinforcement Learning in Mobile Edge Computing. Future Internet. 2024; 16(9):333. https://doi.org/10.3390/fi16090333
Chicago/Turabian StyleJiang, Guiwen, Rongxi Huang, Zhiming Bao, and Gaocai Wang. 2024. "A Task Offloading and Resource Allocation Strategy Based on Multi-Agent Reinforcement Learning in Mobile Edge Computing" Future Internet 16, no. 9: 333. https://doi.org/10.3390/fi16090333
APA StyleJiang, G., Huang, R., Bao, Z., & Wang, G. (2024). A Task Offloading and Resource Allocation Strategy Based on Multi-Agent Reinforcement Learning in Mobile Edge Computing. Future Internet, 16(9), 333. https://doi.org/10.3390/fi16090333






