1. Introduction
Digital twins are emerging as a pivotal technology in the landscape of Industry 4.0, offering dynamic and real-time simulation capabilities that extend across various sectors including manufacturing [
1,
2,
3,
4,
5], healthcare [
6], smart agriculture [
7] and scientific research. A digital twin is a real-time virtual model of a physical object or system that mirrors and analyzes its behavior for optimization and decision making [
5,
8]. Digital twins can be modeled using multiple approaches, each offering distinct advantages depending on the application. One method involves using formal verification techniques that offer theoretical guarantees on system performance by establishing a set of feasible working conditions through sensitivity analysis and uncertainty decomposition [
9,
10]. These analyses assess the robustness of system models by identifying conditions where the models are valid and stable. Any deviations from these established norms are leveraged for predictive monitoring, enhancing system reliability through proactive anomaly detection. However, these models require significant domain expertise and knowledge, which limits their application across heterogeneous environments. Additionally, their effectiveness is constrained by the accuracy of the initial assumptions and the feasibility of the working conditions derived from the analyses. Alternatively, data-driven approaches utilize real-world data to create virtual representations of physical systems [
5,
11]. These models require substantial amounts of data to train effectively. Once deployed as a digital twin, they continuously analyze incoming data to identify and report any deviations, anomalies, or faults in the physical system. Both approaches aim to optimize system performance and reliability, which makes them powerful tools for enabling preventive, predictive and reactive maintenance in varied application domains through real-time monitoring as well as informed decision making.
In the context of scientific manufacturing laboratories (commonly known as “
Cleanrooms”), which are strictly controlled environments for industries like semiconductor, pharmaceuticals, microelectronics and nanotechnology, data-driven digital twins play a vital role. These digital twins provide a high level of data monitoring and operational control to prevent contamination and ensure the integrity of sensitive manufacturing processes. For example, a cleanroom’s critical infrastructure components such as Fumehoods and high-end scientific equipment such as Electron Microscopes, Vacuum Pumps, and high-resolution Photolithography Units like the Karl Suss MJB3 Contact Mask Aligner [
12], all require continuous monitoring to maintain the laboratory’s operational standards. Digital twins facilitate this by enabling predictive, preventive and reactive maintenance within industrial laboratories as follows: (1) by continuously monitoring system conditions to predict potential failures before they occur, (2) through advanced analytics to anticipate equipment malfunctions and optimize maintenance schedules and (3) by generating real-time updates and alerts to control the physical environment.
Figure 1 shows each of the three critical components of cleanrooms that require real-time monitoring: (a) Fumehood (b) Vacuum Pump and (c) the Karl Suss Lithography Unit.
Existing deployments of cyber-physical systems (CPSs) in cleanrooms enhance laboratory functionality by deploying sensors, actuators and edge devices with the physical infrastructure and scientific equipment of the cleanroom labs. For example, Senselet++ [
13] uses cost-effective sensors to monitor airflow in Fumehoods and track calibration drifts caused by environmental changes to ensure it remains within safe limits [
13]. Similarly, the sensors within the Fumehood are used to monitor air leakage or chemical spillage causing changes in air pressure or hazardous vapor concentrations. Edge devices, which may be microcontrollers or microcomputers such as Raspberry Pis, facilitate the communication of sensor data to the cloud. These edge devices also host the complex data processing algorithms for real-time anomaly detection and identification. Actuators, then, provide real-time alerts to lab managers (in the form of alert messages and alarms), informing them of deviations so they can take immediate action to maintain the required cleanroom standards. Similarly, to monitor Vacuum Pump malfunctions, temperature and vibration sensors are deployed to detect any changes caused by overheating from nearby thermal furnaces. These sensors generate critical data that are required to be analyzed using various anomaly detection and fault classification models to extract meaningful insights from the data.
Despite the advancements in wireless communications and Internet of Things (IoT) technologies facilitating real-time data acquisition in cyber-physical systems, significant challenges persist in capturing and integrating this information. This is largely due to the complexities involved in transforming vast quantities of data into actionable insights. Since digital twins are the virtual representation of cyber-physical systems, they are enabled with real-time monitoring and analytics. Digital twins, serving as virtual representations of these CPSs, utilize data-driven models equipped with various machine learning and deep learning techniques. These models are trained on extensive historical data to provide robust anomaly detection and classification capabilities, ensuring continuous monitoring and analytics within these dynamic environments. However, despite their advanced monitoring capabilities, the effectiveness of these digital twins largely depends on the underlying anomaly detection models that are used for analysis. The static ML models used for data analysis and anomaly detection face several of the following limitations, which can hinder their effectiveness in such controlled IoT-driven smart laboratories:
Concept drift: Traditional ML models are typically trained on historical data representing specific, static conditions. These pre-trained models operate under the assumption that the training data accurately represent the relationships within all data from the target variables (anomaly or normal). This requires data stationarity throughout the model training, testing and deployment phases. However, this assumption is often not met in practical scenarios, particularly in CPS applications that involve streaming data analysis. In numerous industrial contexts, data gathered from manufacturing and operational processes inherently exhibit non-stationary characteristics [
1]. For example, over time, the physical components of Vacuum Pumps may wear down, subtly changing their operational efficiency and characteristics. This wear and tear can alter the vibration signatures, heat emissions, or other measurable parameters that were initially used to train the anomaly classification models. Similarly, changes in the operational parameters of the Pump, such as adjustments to speed, pressure settings, or duty cycles to accommodate different scientific experimental tasks in cleanrooms, can lead to concept drift. These operational changes can create new data patterns that the original model was not trained to recognize or handle. This can lead the model performance to deteriorate over time on new, unseen data of which its statistical characteristics have changed significantly from the training dataset. This shift can make the separation curve ambiguous for pre-trained models for correctly distinguishing the normal and anomalous data instance, affecting performance. This phenomenon, known as
concept drift, can render previously trained models outdated or irrelevant.
Figure 2 illustrates the challenge of concept drift in a data-driven digital twin model that has been trained on historical data distributions for anomaly classification. When the real-time data conforms to the identical and independently distributed (iid) model, the performance remains significantly high. However, as operational changes or sensor variations lead to drifts in data distribution (due to the existence of concept drift), the model’s performance drastically decreases. This highlights the critical need for adaptive learning mechanisms within digital twins to fit the current concepts of the new data streams.
Lack of continuous learning: Traditional ML models require manual retraining and fine-tuning to adapt to new data or changes within the environment, a process that is resource-intensive and impractical for real-time applications. These models typically do not support continuous learning, which is essential for adapting to unpredictable changes within the non-stationary streams of data from CPSs within cleanrooms.
Data quality and volume: The performance of these models heavily depends on the quality and volume of the data that they were trained on, often compromised by missing values or noise due to the complex equipment and multidimensional features involved.
To overcome these challenges, the integration of digital twins as adaptive anomaly identification systems represents a transformative solution. We propose,
TWIN-ADAPT, a continuous learning framework for digital twin-enabled real-time anomaly classification in IoT-driven smart manufacturing laboratories (cleanrooms). The digital twin framework of TWIN-ADAPT consists of a continual learning-based gradient boosting classifier, LightGBM, known for efficiently handling complex data structures in dynamic environments [
14]. These models are deployed on edge devices within the cyber-physical systems directly connected to the sensors. These sensors continuously produce real-time data streams that are fed into the adaptive anomaly classification model of the digital twin operating on the edge devices. The TWIN-ADAPT framework of the digital twin leverages a dual-window strategy combining an adaptive sliding window and a fixed size sliding window for concept drift detection, adaptation and data learning. The sizes of these windows are determined based on the arrival of the data streams. When new data arrive, both the adaptive and fixed windows slide forward, and the system evaluates the classification accuracy of data within the current window against the previous window. If a significant drop in accuracy is observed, surpassing a predefined threshold, it signals the presence of concept drift. This detection triggers an immediate retraining of the classifier using the most recent data captured in the adaptive window.
In addition, the framework also employs an optimization function using Particle Swarm Optimization (PSO) for choosing optimal hyperparameters for the drift adaptation algorithm as well as the anomaly classification model. The idea is based on the work by Yang and and Shami [
14] that was originally developed for high-dimensional (≈80 features) network traffic analysis, which we have adapted for the less complex, yet highly variable data dimensions (features) of cleanroom CPSs. Comparing with [
14], we also applied off-the-shelf popular drift adaptation techniques (see details in
Section 4.3) to compare their performance against that of TWIN-ADAPT’s continual learning framework. Other significant contributions of this work include the following:
Designing a more comprehensive dataset featuring diverse anomaly distributions to robustly train and evaluate the TWIN-ADAPT model under simulated drift conditions.
Leveraging the PSO enhanced continual learning models for real-time anomaly classification within a cleanroom’s CPSs, like Vacuum Pumps, Fumehoods and Lithography Units. Each CPS component’s monitoring model represents its digital twin that accurately reflects the current operational states and anomalies. When concept drift is detected—indicating changes in operational conditions or emerging anomaly patterns—the digital twin’s continual learning model dynamically adapts by retraining on new data samples captured through an adaptive sliding window. This ensures that the digital twin remains aligned with the dynamic and non-stationary data distributions, providing robust, up-to-date anomaly monitoring in the dynamic environment of cleanrooms.
It is also worth mentioning that TWIN-ADAPT is primarily deployed within a supervised setting, tailored for anomaly (binary) classification. This approach holds similarity to fault classification processes, where faults are identified through deviations from established normal behaviors—similar to detecting anomalies. The rest of this paper is organized as follows.
Section 2 provides a comprehensive background on the concept and importance of digital twins in Industry 4.0. In
Section 3, we discuss related works pertaining to the application of digital twins, concept drift detection, adaptation and continual learning strategies for scientific cleanroom laboratories.
Section 4 elaborates on this study’s methodology, including the dataset description, anomaly injection techniques, model selection and optimization for online drift adaptation. Next, we present a complete system overview in
Section 5 that explains the proposed TWIN-ADAPT algorithm and experimental setup. Experimental results are discussed in
Section 6 followed by the Discussion, Future Directions and Conclusion in
Section 7,
Section 8 and
Section 9, respectively.
4. Methodology
The end-to-end workflow for TWIN-ADAPT comprises dataset preparation to simulate different types of drift behavior, followed by the choice of different off-the-shelf models for online drift detection and adaption to compare their performances with that of our proposed TWIN-ADAPT’s continuous learning model. Model optimization is an integral part of TWIN-ADAPT’s continuous learning framework to select optimal values for different thresholds and window sizes.
4.1. Dataset Description
In the Senselet++ platform [
13], an IoT-driven end-to-end sensing platform was designed for the University of Illinois Urbana-Champaign’s (UIUC) scientific cleanroom laboratories (
Figure 5 shows a cleanroom semiconductor lab at UIUC). This IoT sensing platform consists of a CPS for the critical high-end components, including lab instruments and infrastructure, within the cleanroom laboratory. It monitors various physical factors such as temperature (in Celsius), humidity (in %), pressure (in Bar) and rate of airflow (in meters/second to measure quantity of air being moved) using low-cost sensors. Each cleanroom component is equipped with its own CPS, comprising a data acquisition system tailored to the specific requirements of the component. For more details on the data acquisition unit, please refer to our previous work on Senselet++ [
13]. Additionally, it is important to note that our current work is not focused on building the IoT system itself. Instead, our approach was designed to work with any existing IoT-driven CPS platform that exhibits the existence of concept drift, which poses considerable challenges in developing ML models, as their learning performance may progressively degrade due to data distribution changes. Subsequently, our aim is to demonstrate a framework for an advanced, online adaptive learning model that can detect and react to concept drift that occurs in IoT-driven CPS data streams. We narrow down the scope of the extensive CPS subsystems to the three most important components of cleanrooms: the Fumehood, Vacuum Pump, and Karl Suss Lithography Unit. The CPS connected to each of these cleanroom components collects time-series data from various sensors, as discussed below:
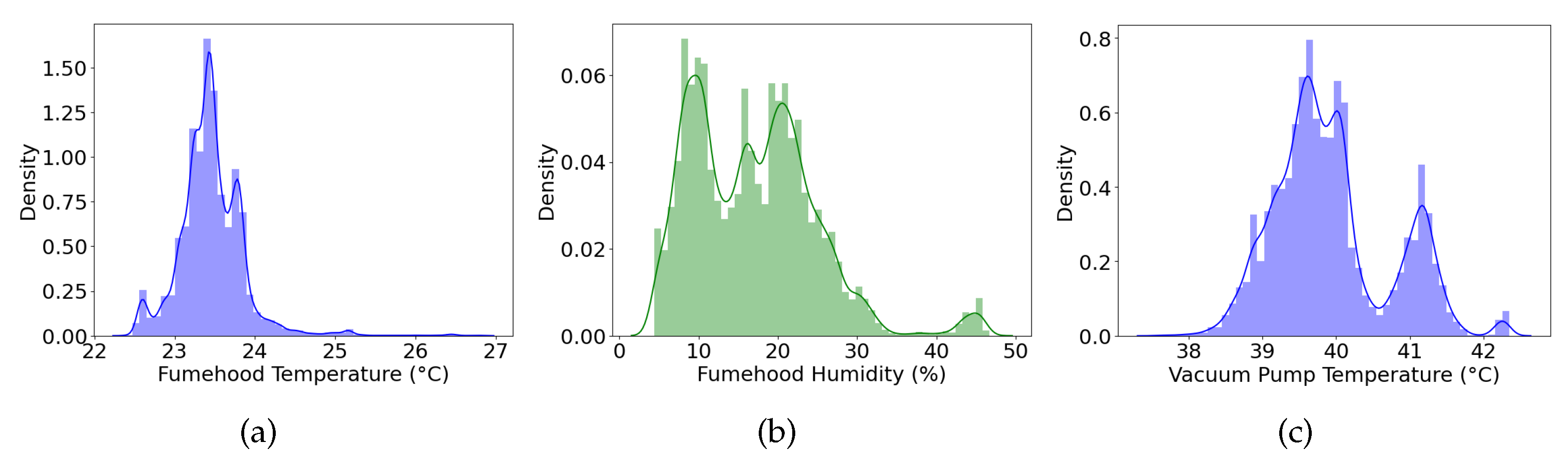
Fumehood: Data from temperature, humidity, and airflow are recorded, providing a comprehensive view of the environmental conditions within the Fumehood.
Vacuum Pump: Temperature sensor data (in Celsius) are aggregated to monitor the operational health and detect any thermal anomalies that may indicate malfunctions or efficiency issues.
Karl Suss Lithography Unit: Both temperature (in Celsius) and humidity sensor data (in %) are gathered to ensure that the system operates within optimal conditions for precise manufacturing processes.
These collected data form the basis for developing digital twins for each component’s CPS, enabling real-time drift detection and continuous adaptive learning for highly precise anomaly classification.
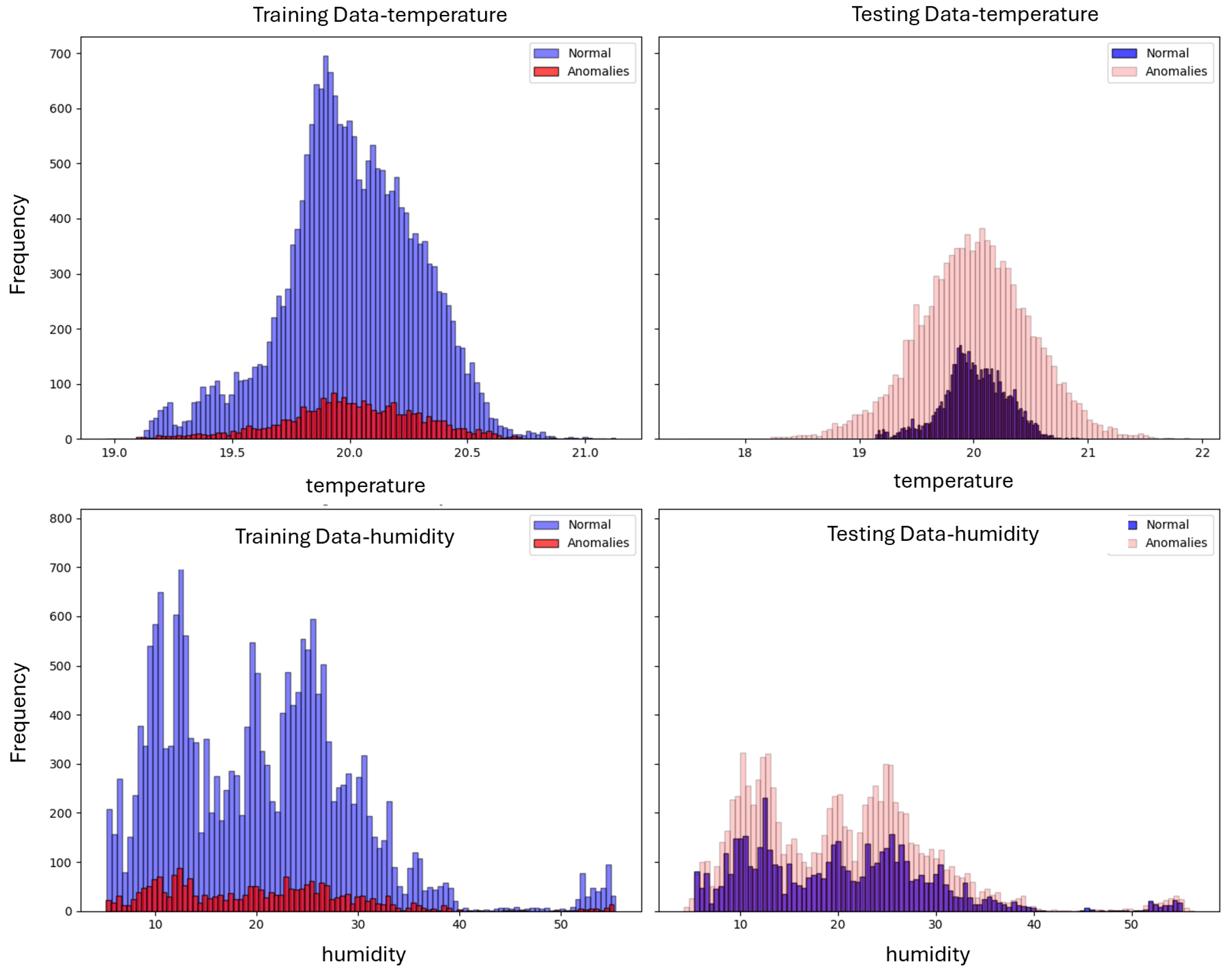
Figure 6a–c illustrate the distribution of data for the Fumehood’s temperature sensor and humidity sensor and the Vacuum Pump’s temperature data.
4.2. Dataset Preparation with Anomaly Injection
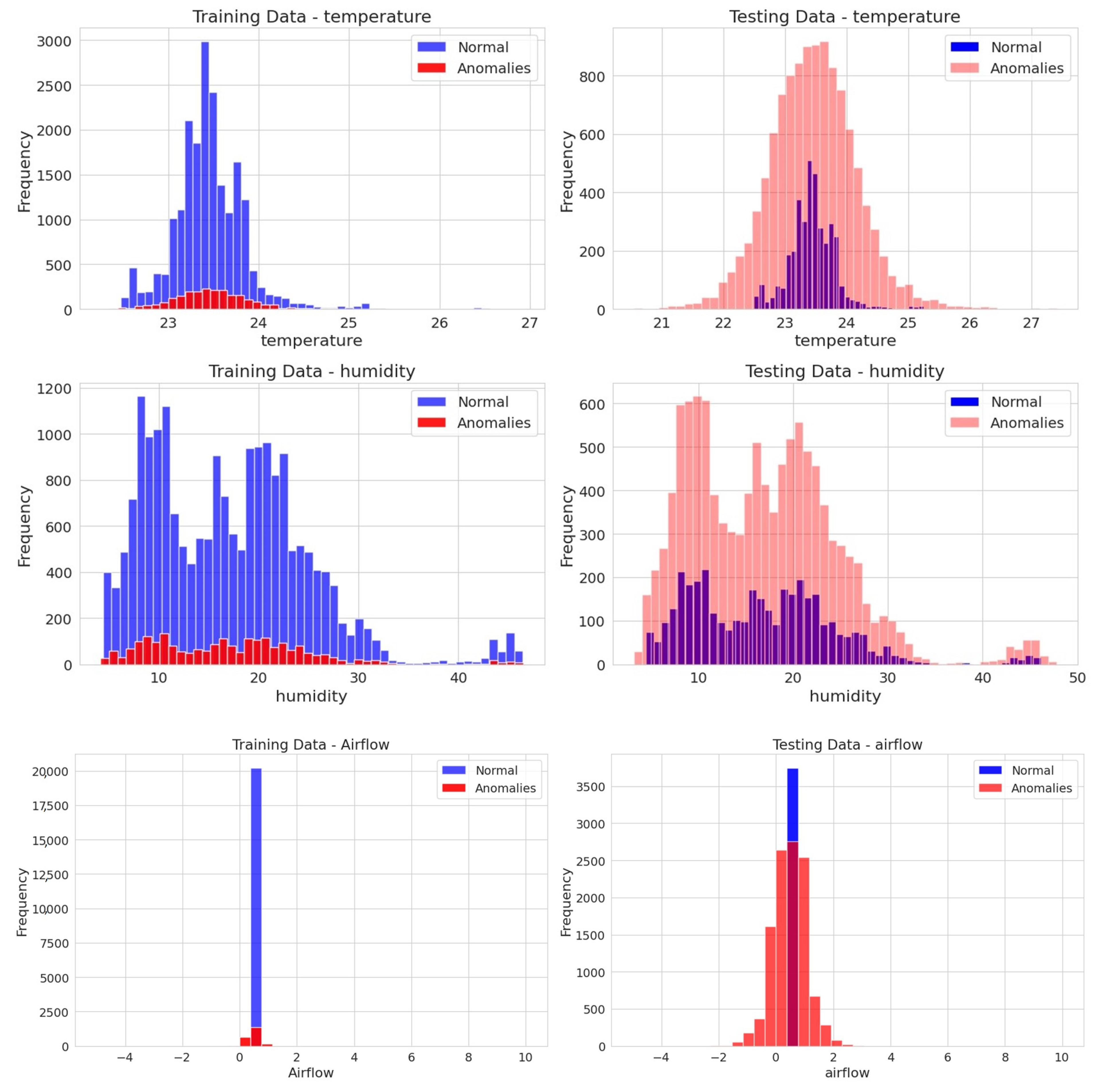
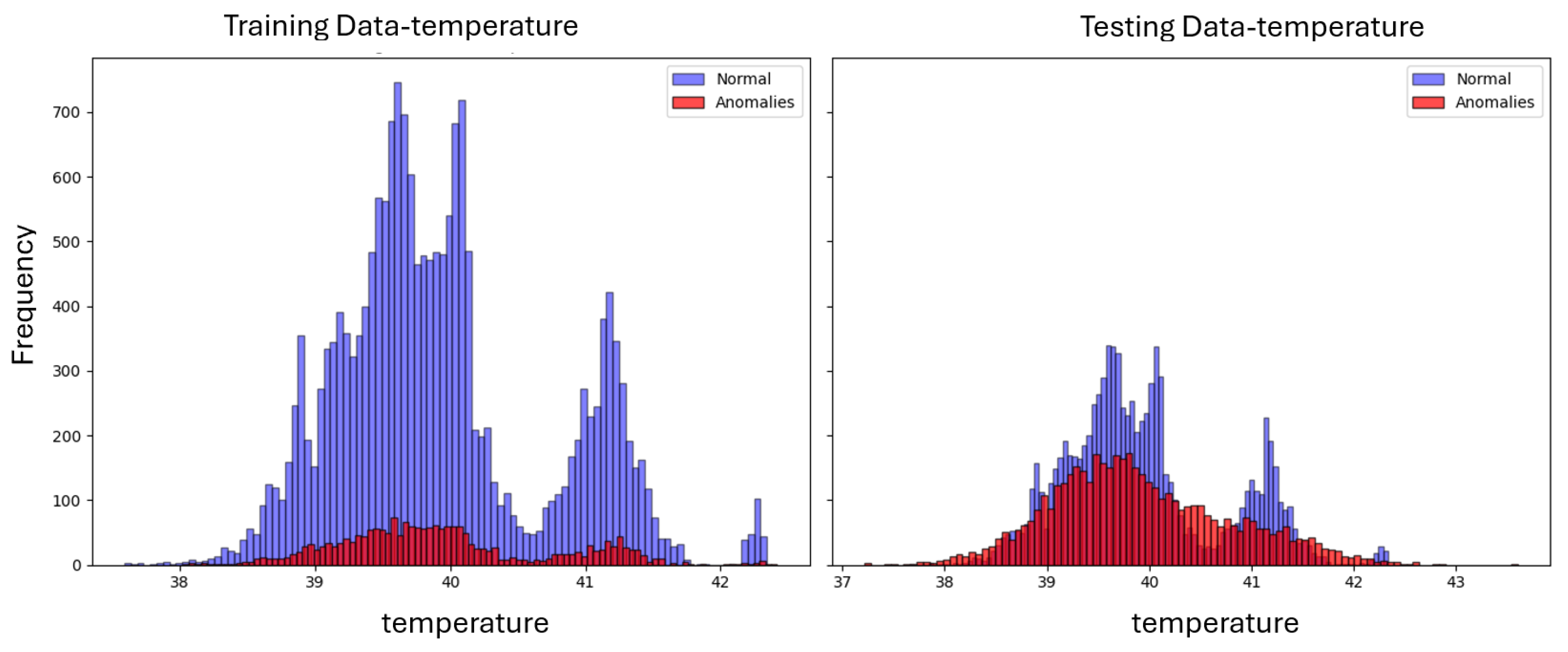
To simulate drift in the equipment’s CPS behavior, we inject synthetic noise into the sensor data values collected for each component of the cleanroom’s CPSs. Evaluating the performances of adaptive learning models requires distinct differences between training and testing data, which demonstrate changes in drift distributions. Consequently, we introduce one type of noise within the training data and a different noise distribution for the testing data. In the training dataset, Gaussian white noise is injected with a standard deviation () of 0.1 to emulate anomalous operational variations. For the testing dataset, a combination of Gaussian and Uniform distribution anomalies is introduced, each with a standard deviation () of 0.5. This mixed approach in the testing set is designed to challenge the classifiers’ ability to distinguish between normal operations and anomalies, where the latter follows a different distribution in the training and testing dataset.
Using a mixed-noise model (Gaussian and Uniform) in the testing data, we ensure a variety of anomaly profiles: some will be obvious due to the higher deviation of the Uniform distribution, while others will closely resemble the training dataset’s anomalies (Gaussian), albeit with a different standard deviation. This setup provides a comprehensive assessment of the classifier’s performance, evaluating its ability to detect anomalies across various thresholds. It tests the classifier’s robustness against clear anomalies and its precision in distinguishing between normal and anomalous conditions in a more ambiguous and realistic operational environment.
Figure 7 illustrates the probability density functions of the added noise distributions. For each type of distribution, the mean (expected) value of the noise is set to zero, and the standard deviation varies from 0.1 to 0.5 to simulate different noise levels.
Two hyperparameters control the extent of anomalies in both the training and testing sets: the noise ratio and the noise level. Specifically, these are defined as follows:
Noise Ratio: Determines the proportion of data points in the dataset that are affected by noise.
Noise Level: Determines the intensity of the noise injected into the data. A higher noise level means that the anomalies will deviate more significantly from the original data points. For example, if noise_level = 0.1, the anomalies will be relatively close to the original data, while noise_level = 0.5 will introduce larger deviations. This parameter is used directly as the standard deviation for the Gaussian and Uniform distributions of injected noise.
For instance, in the Vacuum Pump dataset, which primarily involves temperature readings (a single-feature dataset), even a slight increase in noise level significantly degrades the model performance, due to the model’s sensitivity to small deviations in a less complex feature space. Conversely, the Fumehood, equipped with multiple sensors for temperature, humidity and airflow, requires a more substantial injection of anomaly distribution to induce concept drift. This is because the presence of multiple features dilutes the impact of noise on a single sensor, necessitating stronger noise ratios and levels in the multiple-feature (multiple sensors) dataset in order to challenge the model’s performance during the test phase. Then,
Table 2 shows different values set for the noise level and noise ratio for each type of cyber-physical system’s training and testing dataset.
4.3. Model Selection for Online Drift Detection and Adaptation
In our work, we present TWIN-ADAPT, a continuous learning framework for online anomaly classification using digital twins. This framework incorporates advanced machine learning models, optimization and adaptive algorithms to maintain the precision and effectiveness of digital twins in classifying real-time anomalies. It is worth mentioning that each digital twin is a specialized model designed for anomaly classification specific to its respective CPS component of the cleanroom. For instance, the digital twin of the Fumehood classifies anomalies in multivariate data, including temperature, humidity and airflow, which are vital for maintaining stringent cleanroom standards. The digital twin for the Vacuum Pump focuses solely on the temperature data for anomaly classification to capture essential thermal dynamics of the Pump, while the digital twin for the Karl Suss Lithography Unit integrates both temperature and humidity data, crucial for accurate microfabrication process control.
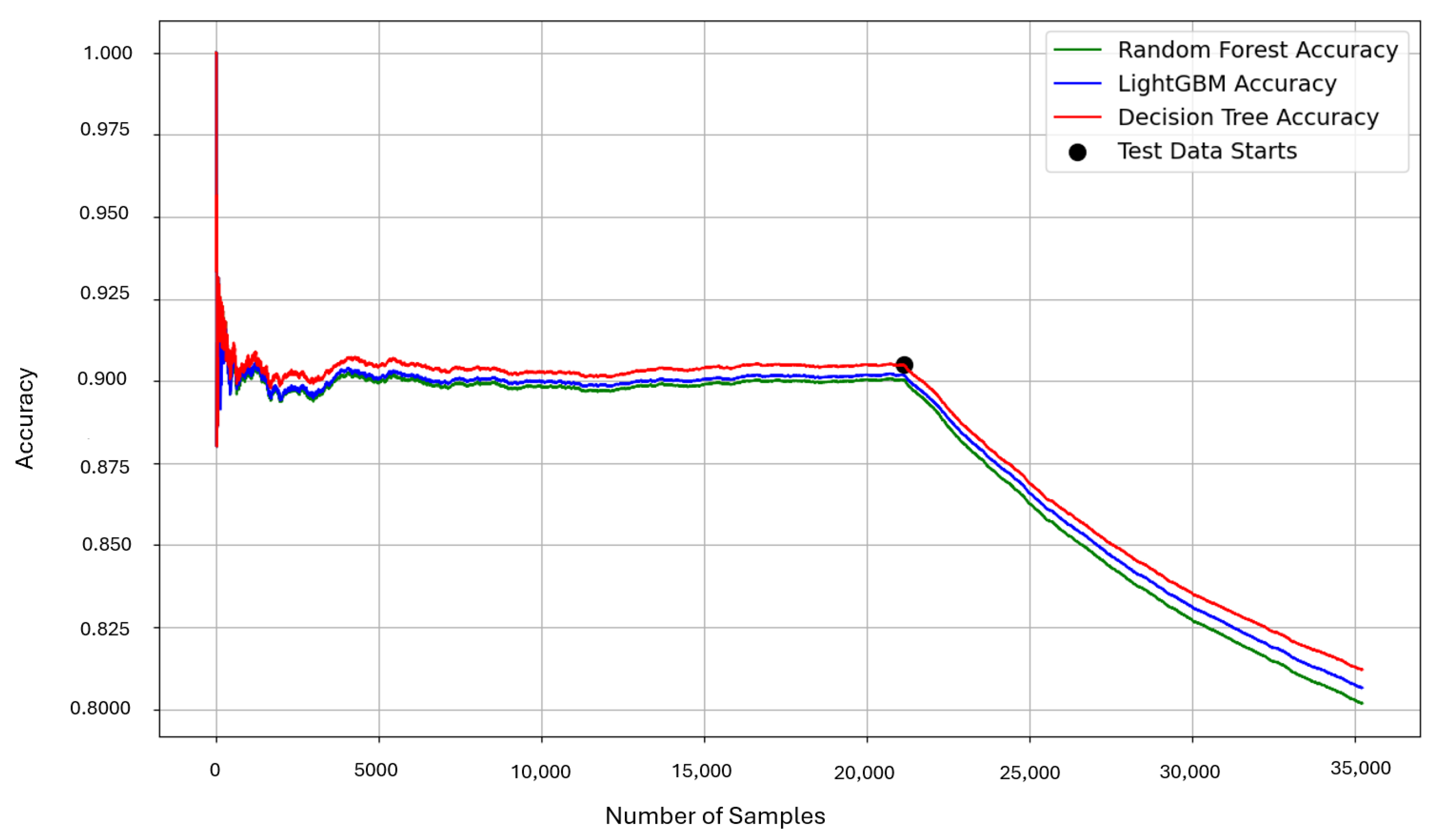
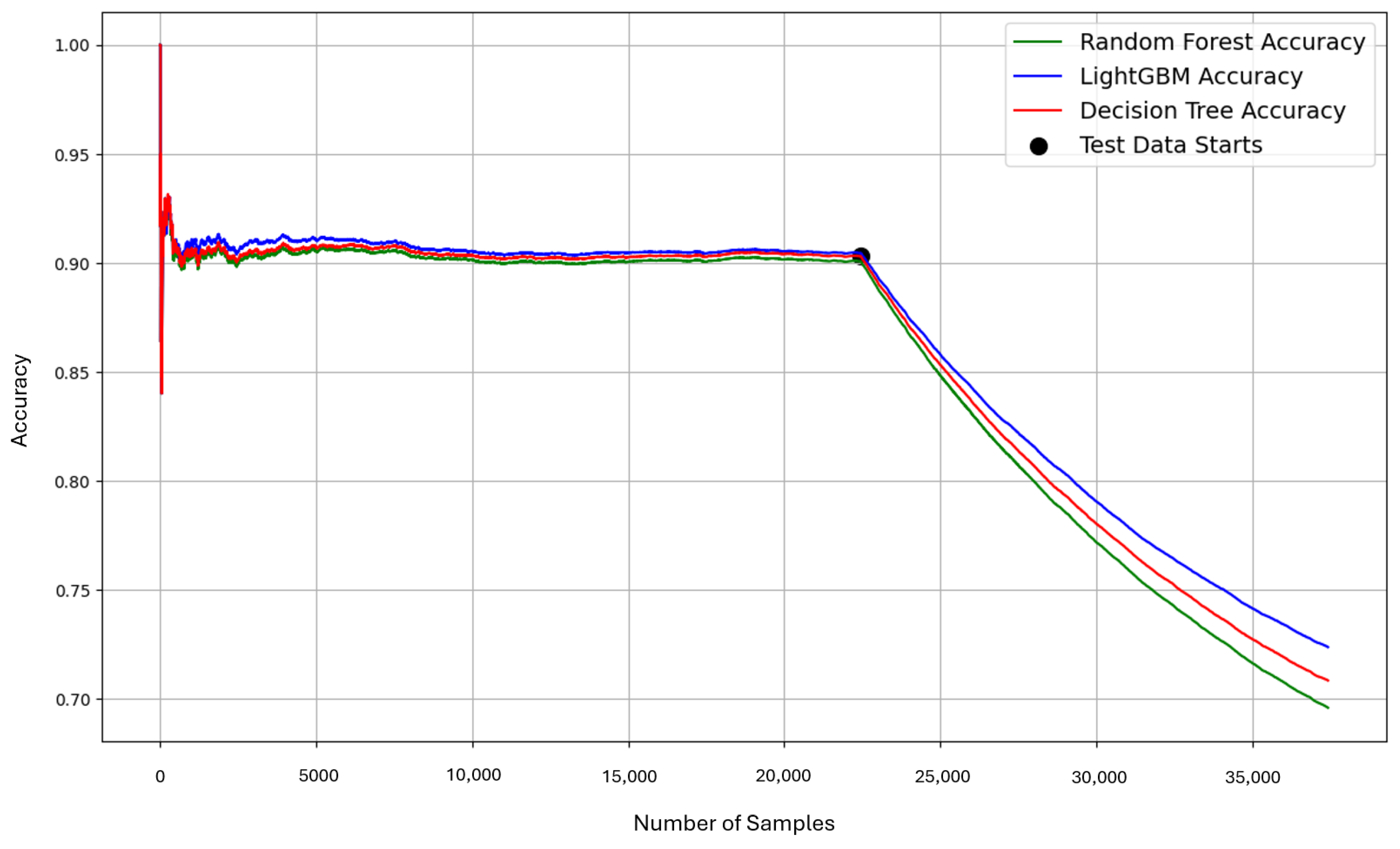
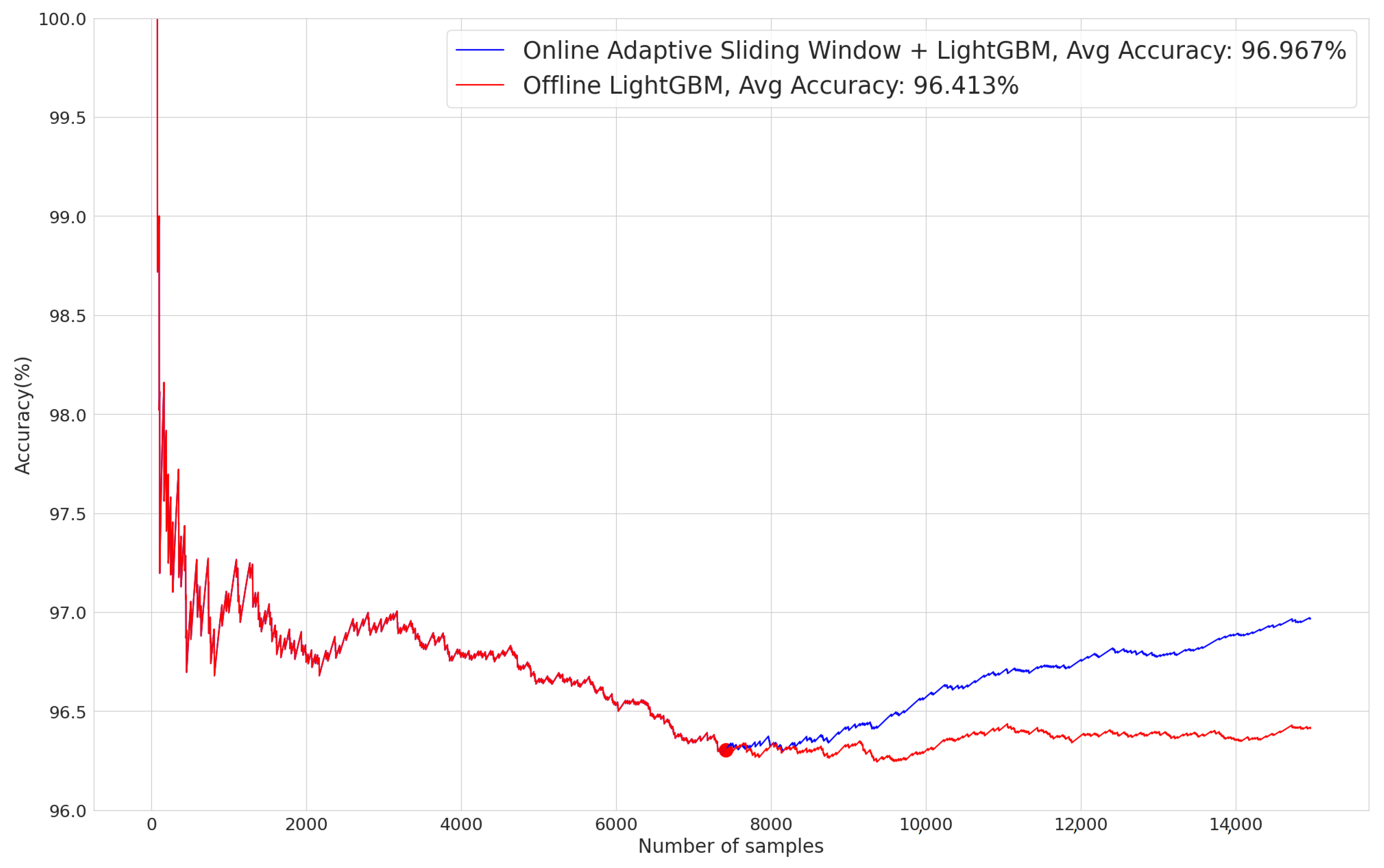
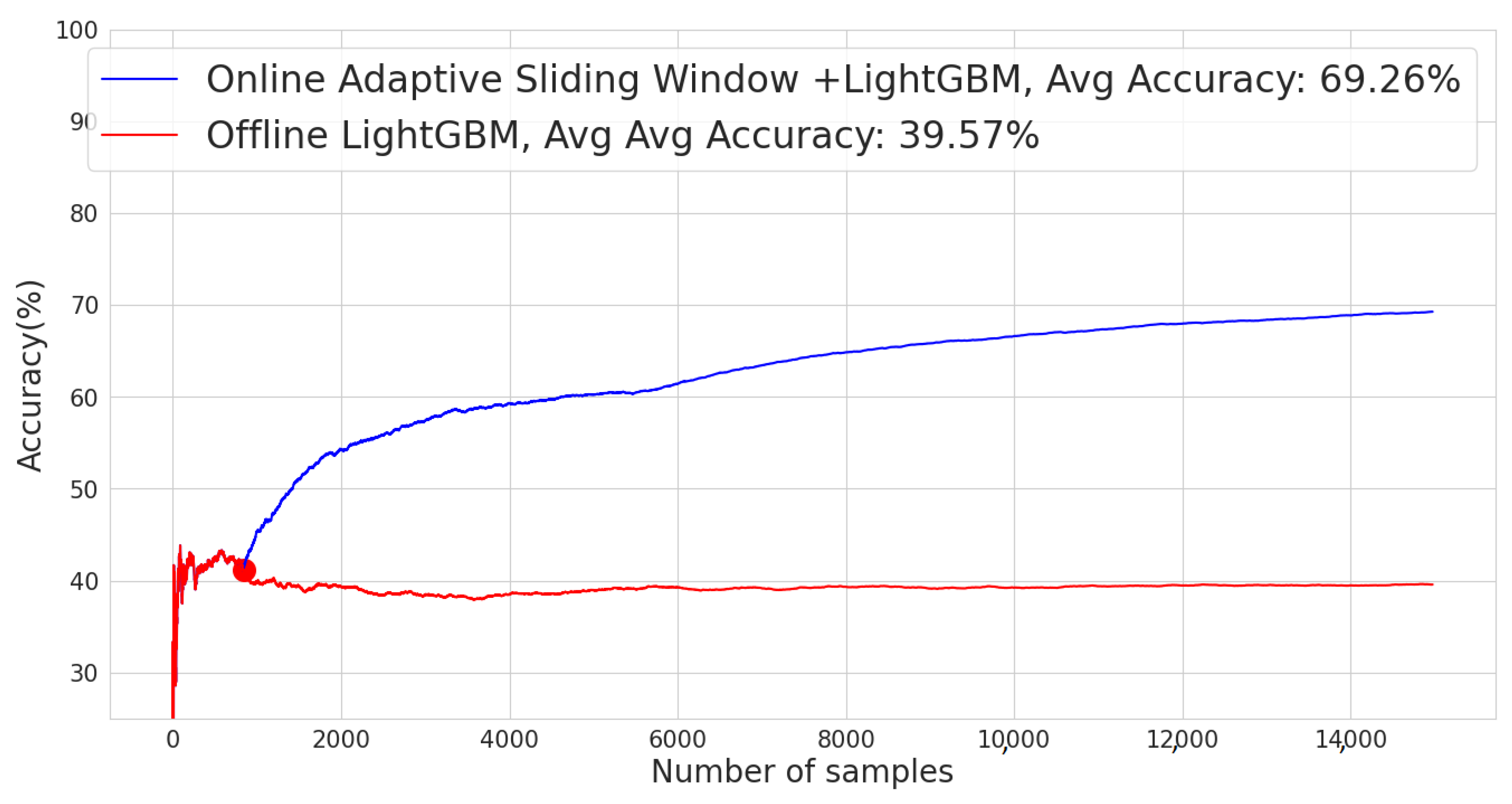
Specifically, the TWIN-ADAPT framework integrates the LightGBM model into the digital twin of each CPS component in order to enhance the system’s responsiveness and adaptability to dynamic environments. This robust machine learning model, an off-the-shelf gradient boosting decision tree (GBDT) system, is distinguished by its fast training speed, low memory requirements, superior accuracy and parallel processing capabilities. These attributes make LightGBM especially well suited for handling the vast and complex data streams inherent in cleanroom operations, where small fluctuations in equipment activity can significantly influence operational efficiency [
14,
48].
LightGBM’s unique capabilities stem from its innovative Gradient-based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB). GOSS enhances model training efficiency by focusing on data samples with large gradients that are more informative for creating predictive models, thereby reducing the computational burden without compromising model accuracy [
49]. Concurrently, EFB optimizes feature handling by bundling mutually exclusive features, significantly reducing the dimensionality of the data, which is crucial for processing the high-dimensional data typically found in cleanroom’s cyber-physical system sensors. These features of LightGBM are crucial for maintaining the digital twin’s accuracy and reliability over time, enabling it to effectively detect and adapt to concept drift within the data streams. In coupling LightGBM with a dual windowing strategy consisting of a sliding window and an adaptive window, the model is equipped to dynamically adjust its parameters in response to changing data distributions. The sliding window monitors the model’s performance on recent data, while the adaptive window accumulates new data to update the model when drift is detected. The algorithm operates by comparing the accuracy of the current observation window with that of the previous window. If the accuracy drops below a certain threshold, it indicates potential drift, prompting the system to adapt (see details for Algorithm 1 in
Section 5.1). This ensures that the digital twin continues to learn and evolve, maintaining a high anomaly classification accuracy even as new patterns emerge within the cleanroom’s cyber-physical systems’ operational data. Thus, compared to other online learning models, an optimized and adaptive LightGBM model within its digital twin framework offers an efficient and scalable solution for the continuous and real-time demands of cleanroom monitoring. This empowers the continuous learning model as an indispensable tool in the domain of the preventive and predictive maintenance of cyber-physical systems.
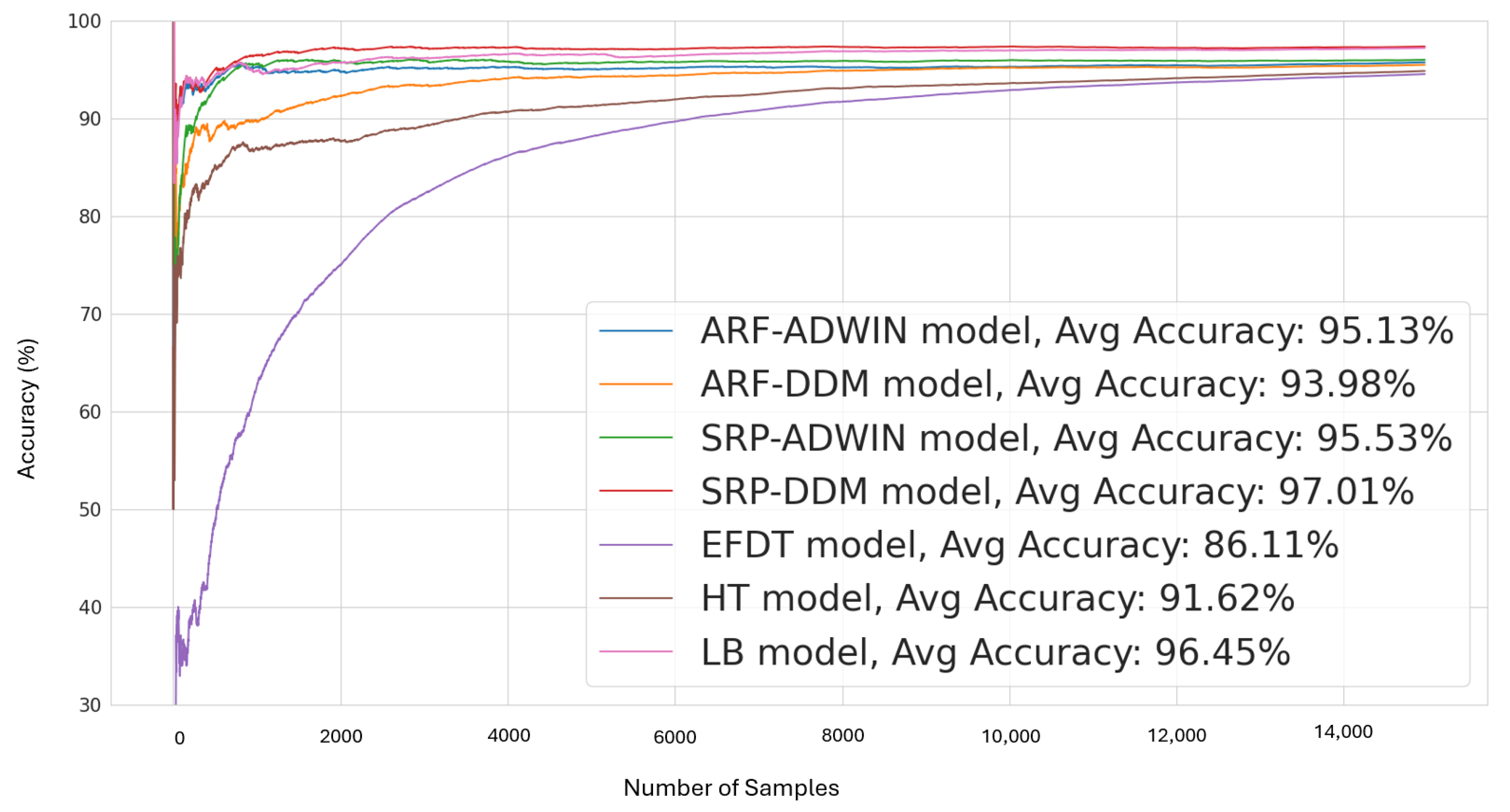
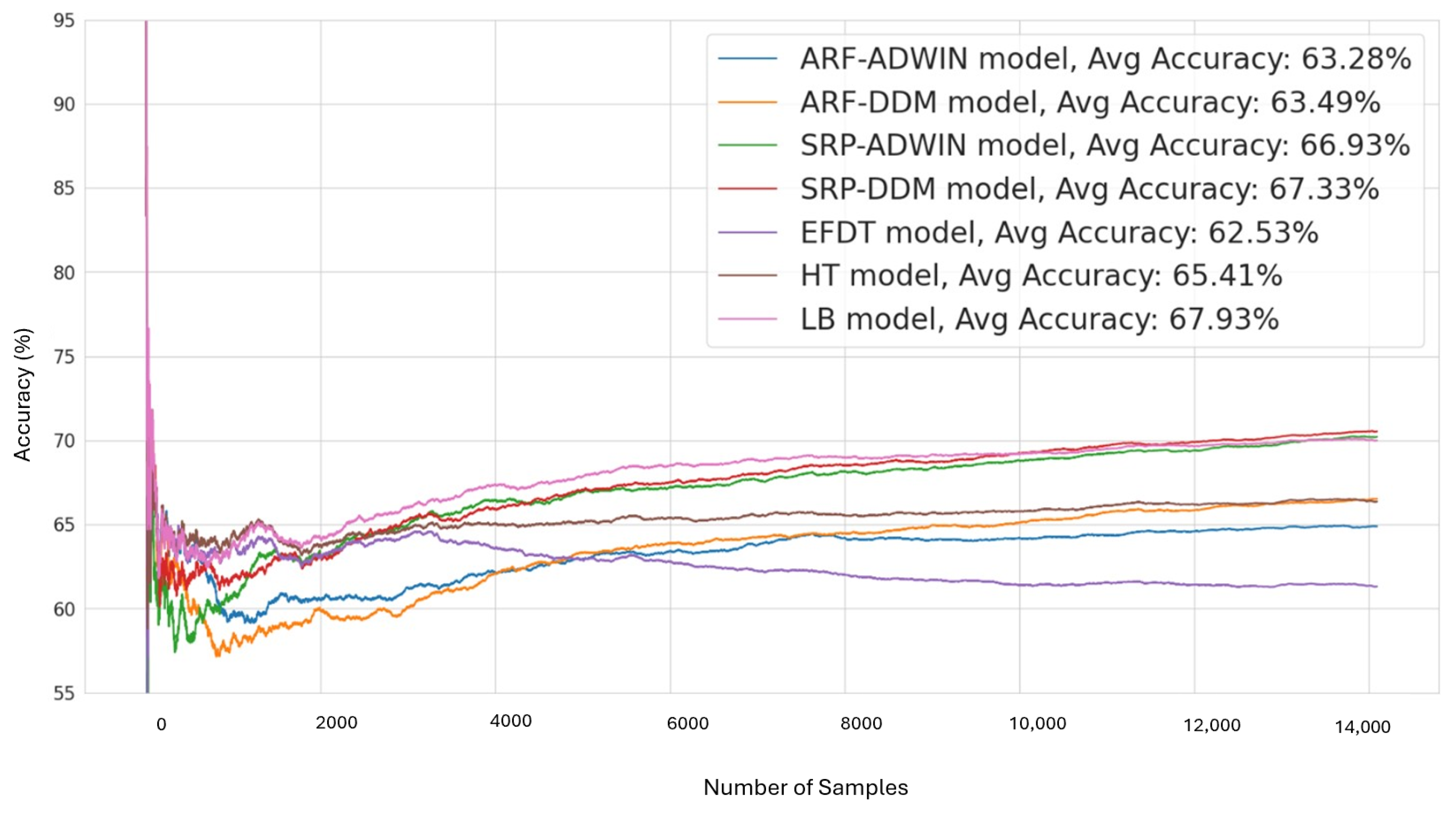
In addition to TWIN-ADAPT’s optimized and adaptive LightGBM model, we consider several existing online drift detection and learning models to serve as baselines for comparison. These online learning models include the following:
ARF-ADWIN: Adaptive Random Forest combined with ADWIN drift detection.
ARF-DDM: Adaptive Random Forest combined with DDM drift detection.
SRP-ADWIN: Streaming Random Patches model combined with ADWIN drift detection.
SRP-DDM: Streaming Random Patches model combined with DDM drift detection.
HTs: Hoeffding Trees that incrementally adapt to data streams using the Hoeffding bound to determine the necessary samples for node splitting.
EFDT: Extremely Fast Decision Trees quickly adapt to concept drifts by splitting nodes upon reaching confidence levels.
LB: Leverage Bagging uses bootstrap samples and the Poisson distribution to construct diverse online ensembles.
These models are selected for comparison due to their strong adaptability to concept drift and their robust data stream analysis capabilities. Both ARF and SRP are state-of-the-art drift adaptation methods that demonstrated superior performances in handling concept drift, as demonstrated in various experimental studies. Both methods are online ensemble models constructed with multiple HTs, which provide robust incremental learning capabilities. They do not require the tuning of data chunk sizes, which can lead to delays in drift detection and increased execution times in block-based ensembles. The choices of drift detection methods—ADWIN and DDM—are strategic: ADWIN excels at detecting gradual drifts, while DDM is more effective for sudden drifts. By combining these drift detection methods with ARF and SRP, we ensure that our base learners can handle both types of drifts efficiently. Additionally, three well-known individual drift adaptation models—EFDT, HT and LB provide a diverse range of mechanisms to adjust to changing data dynamics, making them ideal benchmarks for assessing their relative performances with our custom combination of online learning models and TWIN-ADAPT. Specifically, EFDT’s rapid adaptation through immediate node splitting offers a contrast to more gradual drift adjustments, while HT’s incremental learning approach and LB’s unique leveraging of bootstrap samples offers unique perspectives on managing data variability and drift. By comparing these established models with TWIN-ADAPT’s optimized and continuous learning-driven LightGBM model, we aim to demonstrate the effectiveness of our approach in classifying anomalies under varying conditions and drift scenarios in evolving data streams.
4.4. Model Optimization
To optimize the anomaly classifier model’s (LightGBM) hyperparameters, drift detection and adaptation thresholds and sliding window sizes in TWIN-ADAPT, we employ Particle Swarm Optimization (PSO). PSO, well known for its efficient global search capability and speed, is an ideal choice for this task due to its ability to operate without the need for gradient information, making it well suited for complex, non-linear optimization problems often found in real-world applications [
49,
50].
The integration of PSO in our system focuses on optimizing several critical hyperparameters of the LightGBM model, such as the number of tree leaves, maximum tree depth, minimum number of data samples in one leaf, learning rate and number of base learners. By adjusting these parameters, the model can be finely tuned to accurately model the data streams from various cleanroom CPS components, each represented by a dedicated digital twin. Our implementation uses PSO to iteratively explore the hyperparameter space. Each particle in the swarm represents a potential solution, i.e., a set of hyperparameters, and moves through the solution space by updating its velocity and position based on its own experience and that of its neighbors. This collective intelligence approach helps quickly converge to the best solution, which is the set of hyperparameters that result in the highest predictive accuracy for our LightGBM model. This approach not only improves the performance of the LightGBM classifier model in detecting and adapting to concept drift in the data streams of cleanroom’s CPS but also enhances the model’s efficiency by reducing computational overhead.
In addition to optimizing the LightGBM model parameters, PSO is also utilized to optimize the hyperparameters of TWIN-ADAPT’s adaptive and sliding window algorithm. This includes finding the optimal values for the thresholds used to determine drift and trigger adaptation by comparing the model accuracy across consecutive windows of samples in a data stream (refer to Algorithm 2 in
Section 5.1).
5. System Overview
The proposed TWIN-ADAPT system comprises an adaptive continuous learning-driven
digital twin specifically designed for anomaly classification on real-time streaming data from a cleanroom’s cyber-physical system components such as the Vacuum Pump, Fumehood and Photolithography Unit. Each component’s monitoring model (i.e., the anomaly classifier model or the learner) is represented by its digital twin, comprising both offline and online operational stages.
Figure 8 presents an overview of the TWIN-ADAPT framework.
During the offline stage, data from the CPS sensors of that component are aggregated to create a historical dataset, which is utilized to train an (offline) initial model using LightGBM. This model undergoes refinement through hyperparameter optimization using Particle Swarm Optimization (PSO), ensuring that it is finely tuned to the unique characteristics of each CPS component’s operational data. In the online stage, the digital twin model processes live data streams that are continuously generated by the cyber-physical system (sensors) of the cleanroom component. Initially, the LightGBM model trained during the offline phase is employed to monitor these data streams for anomalies. Upon the detection of concept drift in the streaming data—signifying operational changes or new anomaly patterns—by the optimized adaptive and sliding windowing method, the proposed continuous learning model collects new data samples through the adaptive window. These samples are reflective of the latest operational states of the CPS. The model is then retrained on these new data to accurately align with the latest patterns, ensuring that each component’s digital twin dynamically adapts to maintain effective anomaly classification and continuous operational monitoring in the non-stationary environment of cleanrooms.
5.1. TWIN-ADAPT: Continuous Learning for Digital Twin-Enabled Online Anomaly Classification
TWIN-ADAPT integrates two pivotal algorithms: Continuous Learning Model using Adaptive and Sliding Window (Algorithm 1) and Hyperparameter Optimization for Continuous Learning Model (Algorithm 2). The former dynamically adjusts to changing data from cleanroom equipment sensors, while the latter fine-tunes the model settings using Particle Swarm Optimization (PSO) for optimal performance. The continuous learning strategy for real-time, adaptive anomaly detection in TWIN-ADAPT assigns a dedicated digital twin to each critical CPS component of the cleanroom laboratory. This empowers precise preventive monitoring and analytics under heterogeneous data distribution settings. Similar to many sequential learning algorithms, TWIN-ADAPT’s adaptive and sliding window framework operates in two distinct phases: the offline learning phase and the online continuous learning phase. During the initial offline learning phase, a static classifier model (LightGBM) is trained on historical sensor data. In the subsequent online continuous learning phase, the pre-trained model’s performance is continuously monitored. The model’s performance metrics are compared against previous observations, and the model is updated using new concept data as they become available.
The continuous learning algorithm (
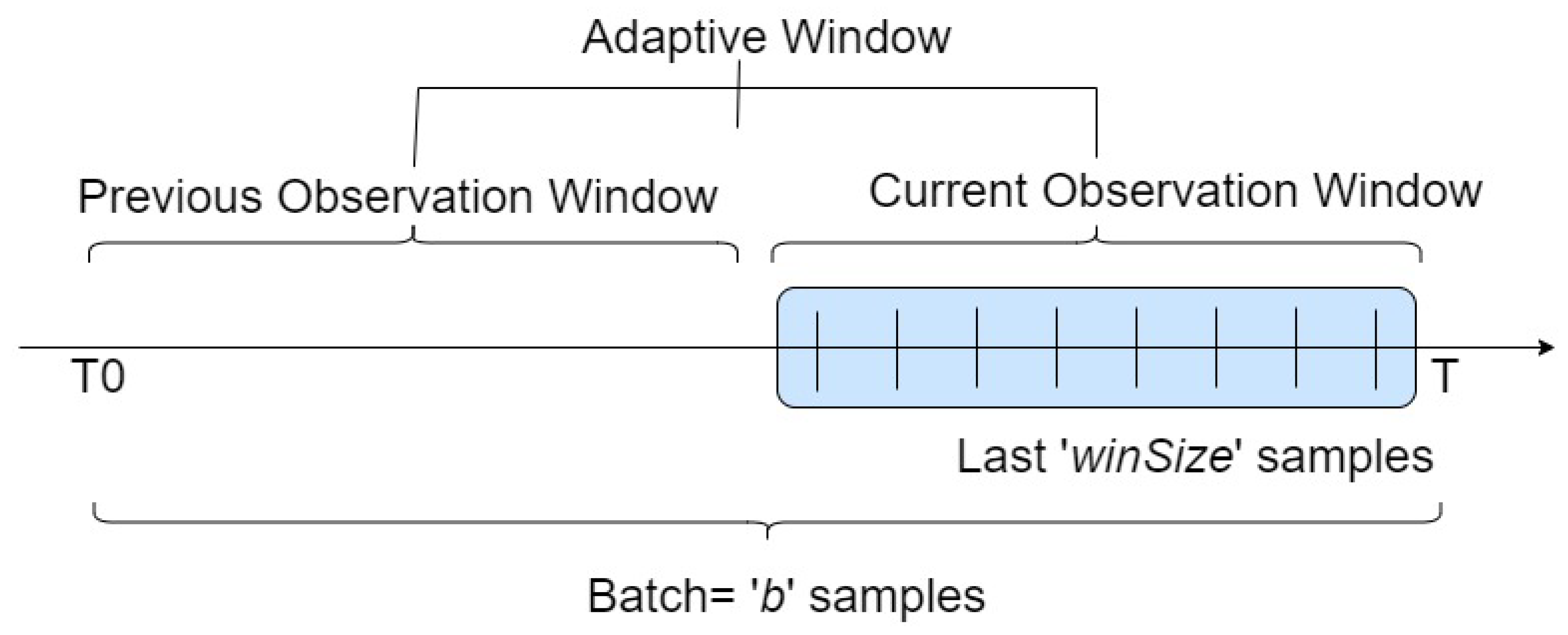
Algorithm 1) operates by monitoring the performance of a pre-trained model on incoming data and making adjustments as necessary to maintain the prediction accuracy. The algorithm utilizes a dual-window strategy that employs both adaptive and sliding windows. The sliding window is used for immediate change detection, while the adaptive window accumulates data necessary for retraining the models. The process begins by initializing an adaptive window
AdaptWin and setting the system
CurrentState to a normal state. As new data points arrive in a streaming batch of
b samples, the last few samples from the batch are collected into an observation window
ObsWin consisting of a fixed size
winSize such that
winSize is a subset of
b, specifically designed to capture the most recent data points within the batch. The accuracy of the current observation window
ObsWin is compared with the accuracy of the previous window
PrevAcc consisting of
b −
winSize samples to detect any significant drops in performance between the consecutive windows. In the normal state, if the accuracy drops below a defined threshold (
), it indicates a potential drift, and the system transitions to a warning state (lines: 5 to 11). In this warning state, new data samples are collected into the adaptive window
AdaptWin (this process is illustrated in
Figure 9). If the accuracy continues to drop further, confirming the drift (
), the model is updated using the samples in the adaptive window, and the system returns to the normal state after clearing the adaptive window (lines: 13 to 20). If the accuracy stabilizes before confirming the drift, indicating a false alarm, the adaptive window is cleared without updating the model, and the system returns to the normal state (lines: 21 to 24).
The rationale behind aggregating samples in the adaptive window is to identify abrupt changes in the data while being able to ignore spurious drifts. This approach ensures that only significant and persistent changes trigger model updates, reducing the overhead of adaptations to minor or transient data variations. The algorithm also includes a state for monitoring the model performance in the drift state (State 2) to check if further adaptation is required. If the model reaches State 2, it continues to collect new samples to compute the accuracy of the current observation window
CurrentAcc and compare it with the accuracy from the drift starting point (new concept accuracy,
NewConceptAcc). If this accuracy is below the warning level of the new concept, it indicates that the model is outdated and needs retraining with the new concept samples. The learner will be updated again on the samples in the adaptive window, and the system will transition to the normal state, emptying the adaptive window (lines: 35 to 41 of Algorithm 1). Similarly, the model will also continue collecting samples for updating if the size of the adaptive window has reached its maximum limit to ensure that the real-time constraints of memory and processing speed are met.
| Algorithm 1 Continuous Learning Model using Adaptive and Sliding Windows |
|
|
|
|
- 1:
function A daptModel()
|
- 2:
|
- 3:
| ▹ 0: Normal, 1: Warning, 2: Adaptation |
- 4:
for samples do
|
- 5:
last samples from batch b
|
- 6:
samples
|
- 7:
|
- 8:
|
- 9:
if and then
|
- 10:
|
- 11:
| ▹ Enter warning state |
- 12:
end if
|
- 13:
if then
|
- 14:
|
- 15:
if then
|
- 16:
▹ Accuracy of current observation window drops to drift level
|
- 17:
|
- 18:
▹ Record accuracy at drift starting point
|
- 19:
|
- 20:
▹ Update the model by retraining it on new concept samples
|
- 21:
else if or then
|
- 22:
▹ False alarm, accuracy increased back or max window size reached
|
- 23:
|
- 24:
|
- 25:
else
|
- 26:
|
- 27:
end if
|
- 28:
end if
|
- 29:
if then
| ▹ Within drift state |
- 30:
|
- 31:
if then
|
- 32:
▹ If sufficient new concept samples are collected
|
- 33:
|
- 34:
▹ Calculate accuracy on new concept window starting from index f
|
- 35:
if OR then
|
- 36:
▹ When new concept accuracy drops to the warning level or sufficient
|
- 37:
new concept samples are collected
|
- 38:
|
- 39:
▹ Retrain the classifier on all the newly collected samples
|
- 40:
| ▹ Empty new concept window |
- 41:
| ▹ Change to a normal state |
- 42:
else
|
- 43:
| ▹ Keep collecting new samples |
- 44:
end if
|
- 45:
end if
|
- 46:
end if
|
- 47:
end for
|
- 48:
return New Average Accuracy of
|
- 49:
end function
|
| Algorithm 2 Hyperparameter Optimization for Continuous Learning Model |
Input: : stream of sensor data, : space for Hyperparameter tuning, : maximum duration for optimization Output: : detected optimal hyperparameter values, : best accuracy achieved
- 1:
function HyperparameterOptimization() - 2:
- 3:
for to do - 4:
- 5:
- 6:
if then - 7:
- 8:
- 9:
end if - 10:
end for - 11:
return - 12:
end function
|
To ensure the model’s effectiveness, a hyperparameter optimization function is implemented. Subsequently, the Hyperparameter Optimization function in Algorithm 2 iteratively tunes the thresholds and window sizes within a specified time limit. Specifically, the digital twin model integrates Particle Swarm Optimization (PSO) within its Hyperparameter Tuning function. This allows for the fine-tuning of key model parameters like window sizes and sensitivity thresholds. In customizing hyper parameters such as windowSize, maxWindowSize and the detection thresholds ( and ), TWIN-ADAPT can tailor the model’s responsiveness by finding the optimal values of hyperparameters that can construct a highly accurate model. For each hyperparameter configuration space, the optimization function runs the continuous learning model function and evaluates the model’s accuracy (lines: 3 to 10 in Algorithm 2). The highest accuracy achieved and the corresponding optimal parameters are stored and returned at the end of the optimization process to generate an optimization anomaly classification model for the CPS. Specifically, the parameters for optimization include the following:
Drift detection threshold (): This threshold is used to compare the accuracy of the current observation window (with the most recent winSize samples) with the previous window (containing b − winSize samples from a batch of b samples). If the accuracy drops below times the previous accuracy, it indicates potential drift. Optimizing helps in accurately detecting when the data distribution changes.
Adaptation threshold (: Once drift is detected, this threshold determines whether the model should be adapted. If the accuracy of the current window of the most recent samples drops below times the previous accuracy, adaptation is triggered. Optimizing ensures that the model adapts appropriately to maintain performance. A small adaptation threshold can lead to frequent retraining, harming the overall prediction performance because it causes the model to react too sensitively to minor fluctuations, resulting in a high false alarm rate.
Window sizes (winSize and winSizeMax): The size of the observation window (winSize) and the maximum size of the adaptive window (winSizeMax) are crucial for the algorithm’s performance. The observation window size affects how quickly changes in data distribution are detected, while the adaptive window size determines how much historical data are considered for retraining the model. A larger adaptive window size implies a greater capacity for the model to retain past information, while a smaller size facilitates quicker adaptation to recent changes. The winSizeMax value sets the sensitivity to the forgetting rule, dictating when the adaptive window should be emptied, effectively resetting the model’s memory.
This strategic use of adaptive and sliding windows coupled with hyperparameter optimization makes TWIN-ADAPT an advanced system capable of maintaining the high standards required in smart laboratory operations. This approach allows the model to dynamically adapt to changes in data patterns, maintaining high prediction accuracy even in the presence of concept drift. By continuously monitoring performance and adjusting the model as needed, the algorithm ensures robust and reliable analytics for dynamic distributions in cleanroom environments.
5.2. Experimental Setup
In the experimental setup, we use the
River Python module to implement and evaluate various tree-based models and algorithms on evolving data streams. Python has been widely adopted in scientific development in recent years due to its versatility, extensive support for libraries in machine learning and active community support. Therefore, it is used in this study. RiverML provides a robust framework for continuous learning and concept drift detection, which are essential for handling real-time data streams. Three CPS datasets are considered for the anomaly injection and adaptive online classification models: Fumehood data, Vacuum Pump data and Lithography data. The data for each CPS component consists of time-series data collected over a period of one month from different sensors attached to each CPS, as discussed in
Section 4.1. Each dataset is split into 70% for training and 30% for testing. The raw data collected from the CPS sensors are considered normal, and to simulate drifts with anomalies, we inject different distributions of anomalies into the training and testing data as discussed in
Section 4.2. The datasets are treated as binary datasets with two labels: “normal” for the unaltered data and “abnormal” for the samples where noise was injected in either the training or testing set.
To evaluate the performance of the proposed TWIN-ADAPT’s adaptive anomaly classification framework, we use hold-out validation. The model is trained on the training set and then evaluated on the test set. Given that the datasets are unbalanced, we utilize four different metrics to assess the model’s performance: accuracy, precision, recall and F1 score. These metrics provide a comprehensive evaluation of the model’s ability to distinguish between normal and abnormal states, reflecting its effectiveness in identifying CPS anomalies and attacks in real time.