SUDC: Synchronous Update with the Division and Combination of SRv6 Policy

Abstract

With the expansion of network scale, new network services are emerging. Segment Routing over IPv6 (SRv6) can meet the diverse needs of more new services due to its excellent scalability and programmability. In the intelligent 6-Generation (6G) scenario, frequent SRv6 Traffic Engineering (TE) policy updates will result in the serious problem of unsynchronized updates across routers. Existing solutions suffer from issues such as long update cycles or large data overhead. To optimize the policy-update process, this paper proposes a scheme called Synchronous Update with the Division and Combination of SRv6 Policy (SUDC). Based on the characteristics of the SRv6 TE policy, SUDC divides the policies and introduces Bit Index Explicit Replication IPv6 Encapsulation (BIERv6) to multicast the policy blocks derived from policy dividing. The contribution of this paper is to propose the policy-dividing and combination mechanism and the policy-dividing algorithm. The simulation results demonstrate that compared with the existing schemes, the update overhead and update cycle of SUDC are reduced by 46.71% and 46.6%, respectively. The problem of unsynchronized updates across routers has been further improved.

1. Introduction

In the face of an increasingly heterogeneous and dynamic network, 6G introduces the concept of intelligent network management and control [1,2,3]. The concept refers to applying artificial intelligence technology to 6G network management. Intelligent network management and control can deal with complex decision problems and obtain accurate results in a dynamic network environment. It makes real-time network management decisions by analyzing large amounts of network data and then updates network management policies. Therefore, 6G intelligent network management and control leads to frequent policy updates.

There are some examples of intelligent network management and control. For example, the core networks of some operators have intelligent systems. The system relies on artificial intelligence technology to dynamically sense the current network status, such as node failures and other topology changes, therefore automatically calculating new paths for the flows passing through the fault point [4,5]. In this way, network services can be performed normally, and the user experience will not be affected.

In 6G networks, SRv6 [6] TE Policy is utilized as a technical tool to assist in realizing the intelligent control of the network. SRv6 TE [7] Policy provides functionalities such as path selection, path switching, and backup protection during the traffic-forwarding process. These functionalities are realized by distributing SRv6 policies derived from one routing calculation by the controller to SRv6 nodes. With the increasing number of connected devices and applications in the network [8], traffic patterns and network topology may change. And then the policies need to be adjusted and optimized according to real-time network conditions and traffic demands [9,10,11,12]. As a result, the SRv6 policies will be updated more frequently in an intelligent 6G network.

An SRv6 policy update involves numerous new policy entries and affects several routers in the network at the same time [13]. However, due to various factors, the activation time of each new policy entry on the corresponding target router may vary [14,15]. Therefore, from the initial policy push to the completion of policy updates across routers, partially legacy policies and partially new policies take effect simultaneously. The coexistence of legacy and new policies increases the risk of network congestion, thus introducing instability to the network [16,17].

The reasons for this phenomenon include but are not limited to the following two points:

1.

Numerous policy entries in one single update: SRv6 TE policy updates will be more frequent in the intelligent 6G scenario. Consequently, each centralized computation yields numerous strategies, resulting in a substantial number of new policy entries waiting for distribution. There is a noticeable delay between distributing the first and last policy. The more policy entries per update, the longer the delay. Accordingly, the problem of unsynchronized policy updates across routers will be more serious.

2.

The serial distribution of policies: Numerous new policy entries are obtained through one centralized computation. These new policies are queued within the controller and are waiting to be distributed to the corresponding target routers. All these new policies are not distributed at the same time. Instead, they are distributed one after another in a unicast manner to their corresponding target routers. Consequently, the distribution time of each new policy varies. Due to the time lag between the distribution of each new policy, the policy updates across routers are unsynchronized.

The key to improving the problem of unsynchronized policy updates across routers is to improve the efficiency of policy distribution and shorten the time lag between the activation of each new policy. An SRv6 policy entry is represented in the form of a Segment Identifier (SID) list [18]. In other words, it is a sequence formed by multiple SIDs. Based on this fact, this paper proposes a scheme called SUDC. It can reduce the time lag between the activation time of each new policy and improve the problem of unsynchronized updates among routers, thus mitigating the risk of network failure due to instability. In brief, the primary contributions of our work are presented as follows:

1.

We propose an SRv6 TE policy-dividing and combination mechanism to improve the efficiency of policy distribution.

2.

Furthermore, we design a policy-dividing algorithm that can rationally divide new policy entries to be distributed.

3.

We conduct simulation tests and compare our approach with ordered update and two-phase update. The results show that our approach is more effective in improving the problem of unsynchronized policy updates across routers.

The paper is organized as follows. In Section 2, we discuss the existing schemes for synchronized policy updates. In Section 3, the policy-dividing and combination mechanism is described in detail. Section 4 depicts the policy-dividing algorithm. The simulation results are presented in Section 5. Section 6 is the conclusion.

2. Related Works

The schemes proposed in the existing literature in this area can be categorized into three main types: ordered update, incremental update, and buffered update.

2.1. Ordered Update

Francois and Bonaventure [19] have proposed an ordered update scheme to protect the network from transient loops by ordering routing table updates, which ensures packet-level consistency in the network.

Clad et al. [20] generated an optimized sequence for updating the weights of links. The incremental modification of link weights protects the network from transient loops when routers update their flow tables.

Jin et al. [16] utilized a system for consistent network updates called Dionysus. Dionysus first generates a global dependency graph describing the effective ordering, and then schedules updates based on the dependency graph.

Wang et al. [17] improves on the work of Jin et al. [16]. They divided the global dependencies into local dependencies between key nodes to speed up the update, but it can lead to congestion in some cases.

Wu et al. [21] proposed a four-phase ordered update scheme, which includes dividing traffic pairs, generating dependency graphs, generating non-deadlock rounds, and resolving deadlocks. This scheme ensures that black holes, loops, congestion, and deadlocks will not occur during the four phases of the update process.

It can be seen from the above schemes that the ordered update schemes divide the entire update process into multiple phases. At the start of each phase, we need to wait for the completion of the previous phase. Therefore, the ordered update has a long update cycle. In addition, the ordered update requires additional storage space to store the legacy rules.

2.2. Incremental Update

Reitblatt et al. [22] proposed a two-phase update approach, where phase 1 updates the internal switches and phase 2 updates the ingress switches. The ingress switches append version tags to incoming packets to determine whether the legacy rules or the new rules subsequently process the packets. When all packets with old version tags are processed, the legacy rules are deleted.

Canini et al. [23] proposed an elegant policy composition abstraction based on a transactional interface with all-or-nothing semantics: all new policies are either installed all or none. There, conflicts between concurrent policy updates are avoided, and consistency on the data plane is maintained.

To reduce storage overhead, Maity et al. [24] proposed a consistent update approach with rule redundancy reduction, named CURE. CURE prioritizes switches according to their usage pattern and schedules updates based on priority. It maintains packet-level consistency through a multi-level queue-based approach.

The above incremental update schemes update the network in multiple rounds. A portion of the flow rules or a subset of the switches is updated in each round. The update cycle for incremental updates has been shortened compared to ordered updates, but it is still relatively long. Moreover, the incremental update requires the controller to be involved throughout the process and extra flow-table space to accommodate the legacy rules.

2.3. Buffered Update

McGeer et al. [14] described a new protocol called OpenFlow Safe Update Protocol for the update of OpenFlow networks. The protocol redirects routing affected packets to the control plane by installing intermediate rule sets on all switches before switches are updated. Until all switches have completed the update, these packets complete buffering at the control plane and are processed according to the new rules. Hence, this solution is called a buffered update.

The update cycle of buffered updates is greatly shortened. But buffered update aggravates the controller load, resulting in its weak scalability. Furthermore, installing intermediate rule sets on all switches occupies additional flow-table space.

In general, existing schemes are difficult to achieve in terms of both the update cycle and data overhead. Data overhead includes storage overhead and transmission overhead. Ordered and incremental updates have long update cycles and require extra space to store legacy rules. Buffered update has short update cycles but impose a significant burden on the control plane, which results in huge additional storage overhead. Buffered update requires intermediate rule sets to be installed on all switches, which also results in storage overhead. Ordered, incremental, and buffered updates all have large transmission overhead due to the serial distribution of policies. However, both aspects of short update cycles and data overhead are highly valued by intelligent 6G networks. The scheme proposed in this paper balances both the update cycle and data overhead and improves both two aspects.

3. Policy-Dividing and Combination Mechanism in SUDC

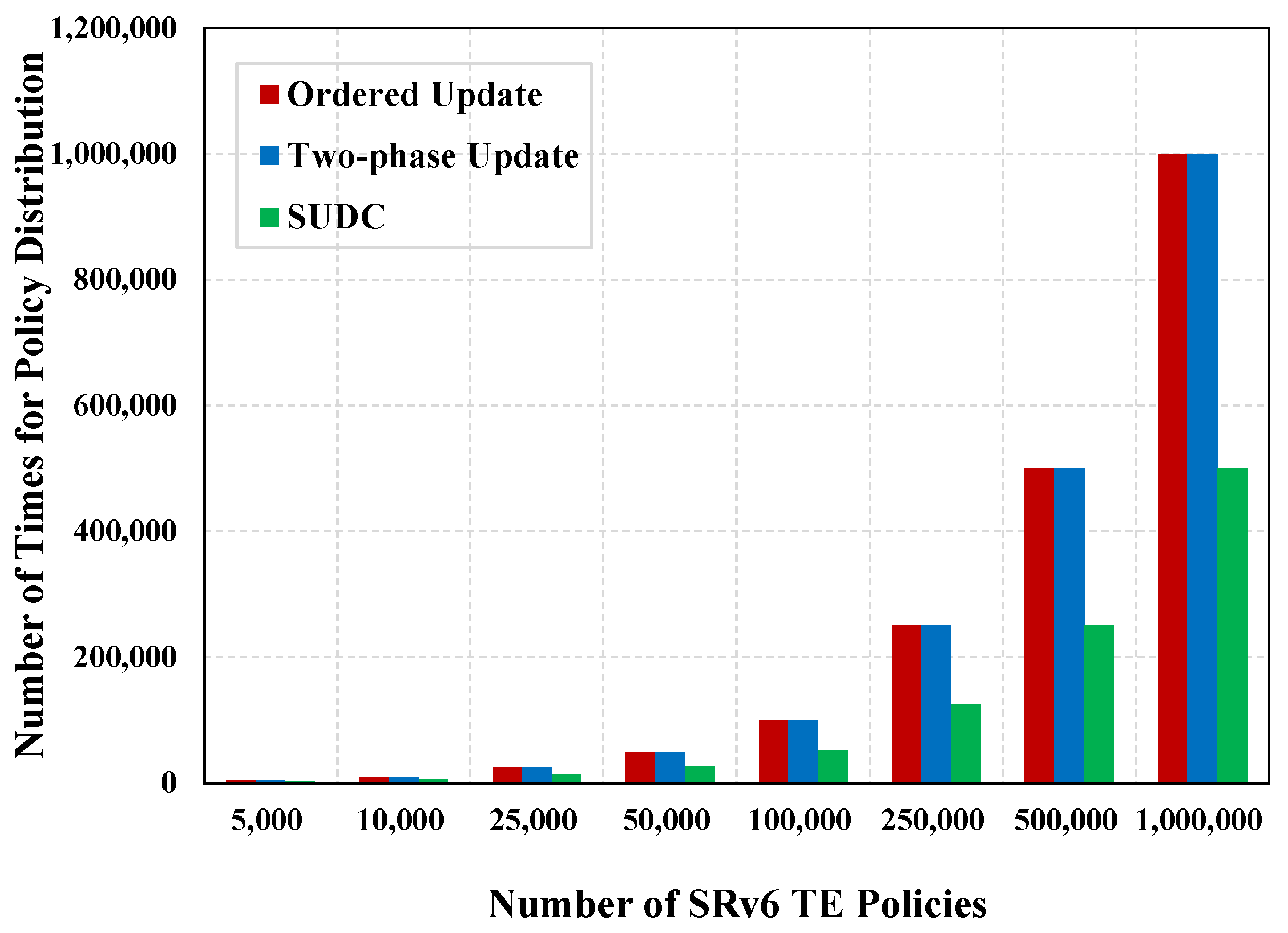
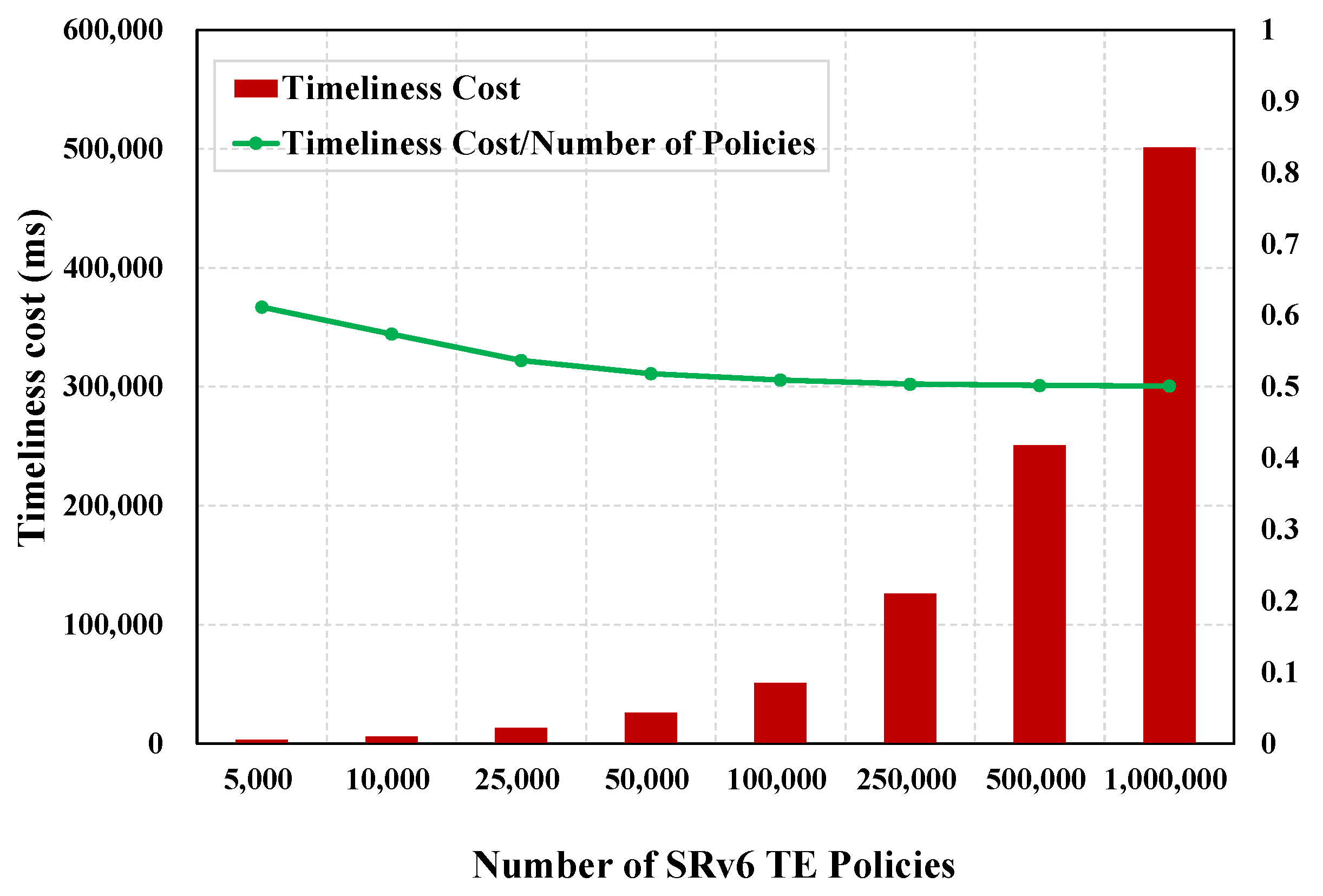
In this section, we describe the policy-dividing and combination mechanism, which aims to improve the efficiency of policy distribution, therefore improving the problem of unsynchronized policy updates across routers and maintaining network consistency. SR technology is key to two points. The first point is to segment the forwarding path, and each segment is identified by SID. The second point is to sort and combine SIDs at the start node to form a SID list and determine the forwarding path of data packets. Data packets can then be transmitted through the network along a forwarding path that has been planned in advance. In SRv6, SID is a 128-bit value in the form of an IPv6 address. Considering that an SRv6 policy entry is a sequence formed by multiple SIDs, we propose to divide each SRv6 policy into several SID blocks and transmit these blocks in multicast form with the aim of improving policy distribution efficiency.

Based on the above ideas, the mechanism contains three functional modules: SRv6 policy dividing, SRv6 policy pushing, and SRv6 policy combination. First, the policy-dividing function module is responsible for dividing the policy entries into multiple policy distribution SID blocks. Then, the policy-pushing function module is responsible for distributing these SID blocks in a multicast manner to the corresponding target nodes of the policy to which the SID blocks belong. Finally, the SRv6 policy combination function module is responsible for combining the SID blocks to generate complete SRv6 policies. Figure 1 shows the architecture of SUDC.

We will describe the three functional modules in detail and use a specific example throughout the entire process to make SUDC easier to understand. Figure 2 shows an example of SUDC.

3.1. SRv6 Policy Dividing

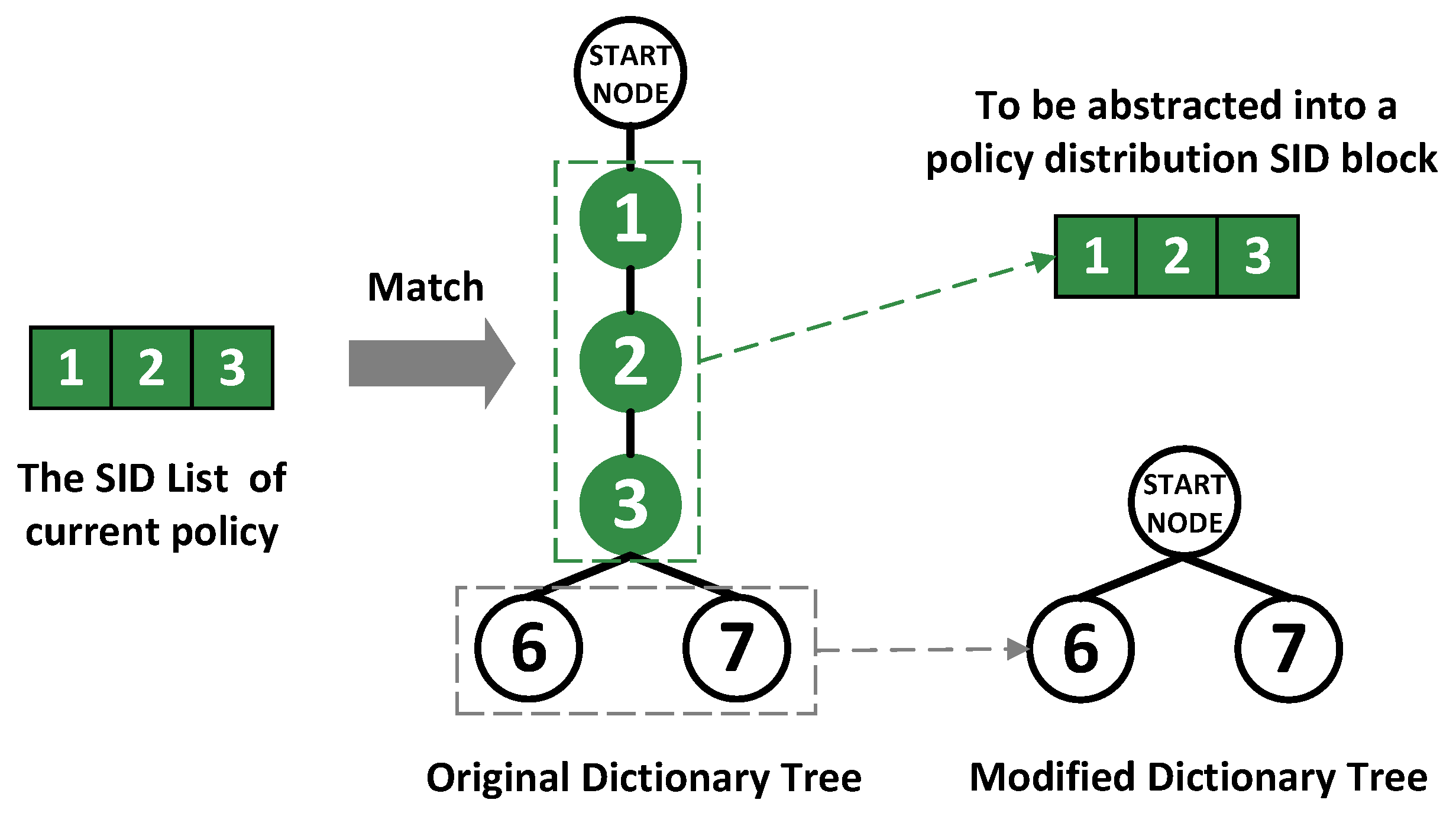
In the SRv6 policy-dividing module, the SID lists of policy entries to be distributed are divided into multiple parts, some of which are common to multiple policies and some of which are unique to a single policy. Each part is wrapped into a policy distribution SID block in order to facilitate policy pushing. This function is performed at the control plane.

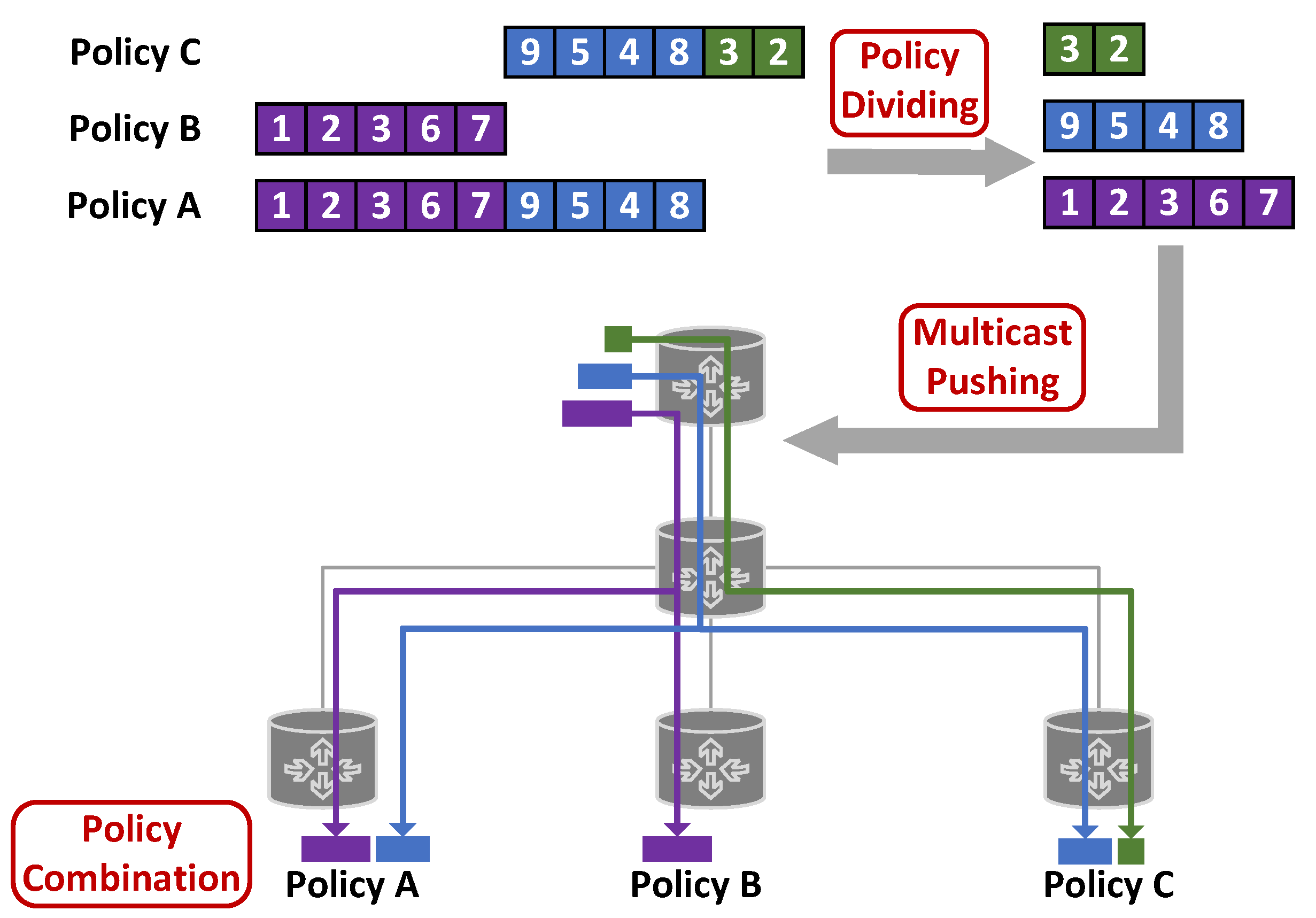
The process of distributing all policy entries derived from one routing calculation by the controller is called one policy distribution. During one policy distribution, this function module first analyzes all SRv6 policy entries to be distributed. Each SRv6 policy entry includes two parts: the policy target and the SID list. The policy target indicates the target router to which the SRv6 policy needs to be published, and the SID list indicates the path rule of the policy entry. For the sake of simplicity of representation and ease of understanding, SIDs in this paper are denoted by the label of routers. For example, each number in the SID List of Policy A below represents a SID. For different SRv6 policy entries, SID blocks with consecutive SIDs of the same order are abstracted to form policy distribution SID blocks. The remaining SID blocks are also wrapped into policy distribution SID blocks, respectively. The policy distribution SID block is the target structure formed after dividing the SID list of these SRv6 policy entries. It is also the minimum unit for policy distribution in SUDC. The minimum unit needs some numbers to mark it in order to facilitate policy pushing and policy combination. Therefore, we stipulate that each policy distribution SID block must contain the distribution serial number, sequence number, and SID list. The distribution serial number indicates the number assigned to the current policy distribution. The sequence number identifies the order of the SID blocks. The SID list indicates the SID sequence of the policy distribution block.

A practical example of SRv6 policy dividing is given:

Suppose there are three SRv6 policy entries to be distributed, and the distribution serial number is 101.

Policy A: The policy target is router a, and the SID list is 1->2->3->6->7->9->5->4->8.

Policy B: The policy target is router b, and the SID list is 1->2->3->6->7.

Policy C: The policy target is router c, and the SID list is 9->5->4->8->3->2.

The SID block of Policy A and Policy B with consecutive SIDs in the same order is 1->2->3->6->7. Therefore, the first policy distribution SID block is shown in the first row of

Table 1. The policy distribution SID blocks of the example.

Distribution	Sequence	SID	Belonging
Serial Number	Number	List	SRv6 Policy
101	1	1->2->3->6->7	A, B
101	2	9->5->4->8	A, C
101	3	3->2	C

.

After abstracting the policy distribution SID block 1->2->3->6->7, the entire SID list of Policy B has been distributed. However, the remaining SID sequence of Policy A, 9->5->4->8, has not yet been distributed. Therefore, we will continue to plan for the remaining part of Policy A.

Policy C and the remaining part of Policy A have consecutive SID sequences in the same order, which are 9->5->4->8. Therefore, the second policy distribution SID block is shown in the second row of Table 1.

After abstracting the policy distribution SID block 9->5->4->8, the entire SID list of Policy A has been distributed. However, the remaining SID sequence of Policy C, 3->2, has not yet been distributed. Therefore, we will continue to plan for the remaining part of Policy C.

For Policy C, the unique SID sequence is 3->2. Therefore, the third policy distribution SID block is individually planned for Policy C, as shown in the third row of Table 1.

After the SRv6 policy-dividing function is performed, the SRv6 policy entries derived from one routing calculation by the controller are decomposed into multiple policy distribution SID blocks.

3.2. SRv6 Policy Pushing

The SRv6 policy-pushing module distributes the SID blocks derived from the SRv6 policy-dividing module to the target routers. This function is carried out on the control plane. SRv6 policy-pushing module consists of four steps: push initiation, BitString mapping, BIERv6 multicast push, and push completion.

SRv6 policy pushing relies on BIERv6 [25], which enables the network to specify the set of destination nodes at the multicast source endpoint. In BIERv6, BitString is set at the source endpoint to specify the destination node set for multicast. Subsequent nodes replicate and forward the multicast packet based solely on the BitString. Therefore, BIERv6 avoids the resource and time overhead required to build and maintain multicast trees in the traditional multicast approach.

3.2.1. Push Initiation

Push initiation involves multicasting the policy push initiation signal to all target nodes involved in this policy distribution through BIERv6 technology. The BitString of the push initiation signal is encoded in such a way that all the bits corresponding to the nodes that need to perform the policy update are set to 1. The specific type of signal is not specified in this scheme, which can be a specific multicast Internet Protocol (IP) address or a specific User Datagram Protocol (UDP) port.

3.2.2. BitString Mapping

BitString mapping involves determining the BitString encoding for each policy distribution SID block in ascending order of sequence number. First, identify the SRv6 policies to which the policy distribution SID block belongs and determine all target nodes to which this policy distribution SID block needs to be multicast. Then, the BitString encoding of the policy distribution SID block is set in such a way that the corresponding bits of all target nodes are set to 1, and the remaining bits are set to 0. After BitString mapping is completed, each policy distribution SID block has its own BitString encoding that indicates the target node set.

3.2.3. BIERv6 Multicast Push

BIERv6 multicast push aims to distribute all policy distribution SID blocks via multicast in ascending order of sequence number. Multicast push adopts BIERv6 or a BIERv6-derived technology, such as Multicast Source Routing over IPv6 Best Effort (MSR6 BE). The BitString encoding required for BIERv6 multicast push is determined by the step BitString mapping.

3.2.4. Push Completion

After completing the push of all policy distribution SID blocks, the control plane pushes a push completion signal via multicast to all policy target nodes involved in this policy distribution. The BitString of the push completion signal is encoded in such a way that all the bits corresponding to the nodes that need to perform the policy update are set to 1. The specific type of signal, which can be a specific multicast IP address or a specific UDP port, is not specified in this scheme. As soon as the policy target nodes receive the push completion signal, they execute the SRv6 policy combination function.

3.3. SRv6 Policy Combination

The SRv6 policy combination module aims to combine policy distribution SID blocks to generate complete SRv6 policies. This function is executed at the data plane, and the policy target SRv6 nodes execute this function. Each relevant SRv6 node combines the received policy distribution SID blocks in ascending order of sequence number to generate a complete SRv6 policy. The destination Internet Protocol version 6 (IPv6) address matched by the combination-complete policy is the last address of the SID list. Then, the node writes the combination-complete SRv6 policy to the SRv6 node pipeline.

We continue to illustrate the process of the SRv6 policy combination using the example given in the SRv6 policy-dividing module.

After SRv6 policy pushing, node a receives two policy distribution SID blocks, which are shown in the first and second lines of

Table 2. Policy distribution SID blocks received by node a.

Distribution	Sequence	SID	Belonging	Target
Serial Number	Number	List	SRv6 Policy	Router
101	1	1->2->3->6->7	A, B	a, b
101	2	9->5->4->8	A, C	a, c
101	3	3->2	C	c

. Node a combines the received SID blocks in ascending order of sequence number to generate the complete SRv6 policy, 1->2->3->6->7->9->5->4->8. The destination IPv6 address matched by the combination-complete policy is the IPv6 address of node 9. Then, node a writes this policy to its SRv6 pipeline.

After SRv6 policy pushing, node b receives one policy distribution SID block, which is shown in the first line of Table 2. Node b receives one policy distribution SID block, so the complete SRv6 policy is 1->2->3->6->7. The destination IPv6 address matched by the combination-complete policy is the IPv6 address of node 7. Then, node b writes this policy to its SRv6 pipeline.

After SRv6 policy pushing, node c receives two policy distribution SID blocks, which are shown in the second and third lines of Table 2. Node c combines the received SID blocks in ascending order of sequence number to generate the complete SRv6 policy, 9->5->4->8->3->2. The destination IPv6 address matched by the combination-complete policy is the IPv6 address of node 2. Then, node c writes this policy to its SRv6 pipeline.

4. Policy-Dividing Algorithm in SUDC

In this section, we design a policy-dividing algorithm to implement the policy-dividing module of the mechanism in Section 3. This algorithm enables numerous SRv6 policies to be divided into as many identical SID blocks as possible by prefix matching while guaranteeing a low time complexity. This algorithm can reduce the number of times for policy distribution.

4.1. Algorithm Overview

The core idea of this algorithm is to divide the SID lists by identifying the longest common prefix of different SID lists. The longest common prefix refers to the longest common SID block starting from the first SID. In the example given in Section 3, SID block 1->2->3->6->7 is the longest common prefix of policy A’s SID list and policy B’s SID list. The policies perform prefix matching sequentially in descending order of SID list length. When the complete SID list of a shorter policy is the prefix of the SID list of a longer policy, it becomes possible to obtain two entirely identical SID sequences and the suffix sequence of the longer SID list by partitioning the longer SID list. As shown in Figure 3, the identical sequence is abstracted to be wrapped into a policy distribution SID block, which will be distributed to target nodes set in a multicast manner. The suffix sequence of the longer SID list can go for prefix matching with the SID list of other policies.

In this algorithm, if a SID list is the prefix of k SID lists at the same time, then this SID list is abstracted and wrapped into a policy distribution SID block. This policy distribution SID block will be multicast to k+1 target nodes. And the remaining k suffix sequences continue to wait to be matched. In the worst case, none of the k suffix sequences can be matched. Then, all these suffix sequences will be distributed to corresponding target nodes in unicast form. The total number of times for policy distribution is k + 1. This algorithm ensures that the number of times for policy distribution in SUDC is always less than or equal to that in the conventional unicast-based sequential distribution method.

4.2. Algorithm Procedure

The algorithm implements policy dividing based on prefix matching, and we leverage two data structures, a priority queue, and a dictionary tree, to reduce the time complexity.

4.2.1. Priority Queue for Policy to Be Divided

The priority queues are utilized to control the order in which SRv6 policies undergo prefix matching. After analysis, it has been determined that the order in which SRv6 policies perform prefix matching significantly impacts the matching success rate. Therefore, the policies need to perform prefix matching sequentially in descending order of SID list length so as to ensure optimal matching success rate. The priority queue is characterized by elements being dequeued in descending order of priority. So, it serves as an essential tool for efficient prefix matching. This algorithm states that the longer the SID list length of the policy is, the higher the priority is.

4.2.2. Dictionary Tree

The dictionary tree is utilized to store SRv6 policies that are waiting to be abstracted from the longest common prefixes to construct policy distribution SID blocks. The dictionary tree will merge the common prefixes of SID lists of different policies. For example, the current dictionary tree has two SID lists of different policies, 1->2->3->6 and 1->2->3->7, and their common prefix 1->2->3 are merged. The left part of Figure 4 shows how the dictionary tree stores and merges SID lists with the same prefixes. The current policy with SID list 1->2->3 successfully matches with two policies in the dictionary tree. The common prefix will be deleted from the dictionary tree and abstracted into the policy distribution SID block. The whole process is shown in the Figure 4.

Suppose a single prefix matching is performed on a policy set of size N and average policy length M. When not using the dictionary tree, the current matching policy needs to be compared with n policies one by one, with the time complexity of O(N*M). The dictionary tree can merge the same prefixes of different SID lists, so the time complexity of a single prefix matching is O(M) when using the dictionary tree. The dictionary tree drastically reduces the time for each prefix matching. In addition, the dictionary tree can also effectively save storage space.

With the above two data structures, the time complexity of prefix matching is approximately O(width*height), where width represents the average number of child nodes for each branching node, and height signifies the height of the tree. This time complexity will be much lower than the time complexity of the naive prefix-matching algorithm.

We define a series of functions in the algorithm to operate on the dictionary tree. STARTWITHPREFIX(Argus) function is to check whether the dictionary tree contains branches prefixed with the SID list of the incoming policy and return TRUE or FALSE. INSERT(Argus) function is to insert the incoming policy into the dictionary tree. The DELETEWITHPREFIX(Argus) function deletes all the branches in the dictionary tree prefixed with the SID list of the incoming policy and returns the suffix policies of these branches. GETALLLIST() function is to obtain all the policies stored in the dictionary tree.

Algorithm 1 depicts the detailed procedure of SRv6 policy dividing. Collection S holds all the SRv6 policies to be distributed. Policies are divided to form multiple policy distribution SID blocks. These policy distribution SID blocks are stored in collection R. Priority queue P is used to control the order in which SRv6 policies perform prefix matching. The longer the SID list length of the policy, the higher the priority. The dictionary tree T is utilized to store the set of SRv6 policies waiting to be matched.

All the policies in the policy set S are added to the priority queue P (line4 –line6). Process each policy dequeued in descending order of priority in turn until all policies have been processed (line7–line21). The current policy dequeued from P is p (line8). If no branch prefixed with the SID list of p exists in the current dictionary tree T, then policy p is inserted into T (line9–line10). Otherwise, it indicates that there exists one or more policies whose SID lists are prefixed by the SID list of p. Then the SID lists of these matched policies can be divided, and the longest common prefix that is also the SID list of p can be abstracted into a policy distribution SID block r (line12). The target nodes of r should contain the target node of strategy p and the target nodes of all the matched policies (line13, line18). The SID list of r is the SID list of Policy p (line14). All the matched policies are then removed from the dictionary tree (line15). The suffix policies of these matched policies have not yet been distributed to the corresponding policy target nodes. Therefore, these suffix policies should be re-enqueued into the priority queue P and await further prefix matching (line16–line19).

After all the policies in P have completed prefix matching, there may exist some policies in T that cannot match up with other policies (line22). These remaining policies should each independently form policy distribution SID blocks (line23–line24). The target node of each policy distribution SID block is the target node of the respective policy, and the SID list of each policy distribution SID block is the SID list of the respective policy (Algorithm 1).

Algorithm 1 Policy-Dividing Algorithm

Input:  S                        ▹ Set of SRv6 policies Output:  R               ▹ Set of policy distribution SID blocks 1: $P\leftarrow \varnothing$;                       ▹ Empty priority queue 2: $T\leftarrow \varnothing$;                      ▹ Empty dictionary tree 3: $R\leftarrow \varnothing$; 4: for $s\in S$ do 5:     $P\leftarrow P\bigcup \left\{s\right\}$; 6: end for 7:  while $P\ne \varnothing$ do 8:     $p\leftarrow P.POP\left(\right)$;             ▹ Each policy exits from P in turn 9:     if not T.STARTWITHPREFIX(p) then 10:         $T.INSERT\left(p\right)$; 11:     else 12:         r;                  ▹ A policy distribution SID block 13:         $r.target\leftarrow r.target\bigcup p.target$; 14:         $r.sidlist\leftarrow p.sidlist$; 15:         $F\leftarrow T.DELELTEWITHPREFIX\left(p\right)$;  ▹ Set of suffix policies obtained by deleting p from policies prefixed with p in T 16:         for $f\in F$ do 17:            $P.PUSH\left(f\right)$; 18:            $r.target\leftarrow r.target\bigcup f.target$; 19:         end for 20:     end if 21: end while 22: $U\leftarrow T.GETALLLIST\left(\right)$;          ▹ The set of remaining policies in T 23: for $u\in U$ do 24:     $R\leftarrow R\bigcup \left\{u\right\}$; 25: end for 26: return R

4.3. Analysis of Time Complexity

We also analyze the time complexity of the policy-dividing algorithm. The number of policies in set S is denoted as N, and the average length of policies is denoted as M. The time complexities of the STARTWITHPREFIX(Argus) function, INSERT(Argus) function, and DELELTEWITHPREFIX(Argus) function are all O(M). The time complexity of the GETALLLIST() function is O(N*M). Since the maximum size of set F is close to N, the time complexity of the step of re-entering the suffix policies into priority queue P (line16–19) is O (N). According to the detailed process of the policy-dividing algorithm, it is clear that the time complexity of the loop from line 7 to line 21 is O (N*M) or O(N*(M+N)). Therefore, the time complexity of the whole algorithm is O(N*(M+N)).

5. Performance Evaluation

In this section, we evaluate the performance of SUDC based on the following metrics. And we also measure the timeliness cost that certain nodes have to pay.

1.

Number of times for policy distribution: This metric is used to evaluate the data overhead of SUDC during policy updates.

2.

Coexisting time of new and legacy policies: This metric is used to evaluate the effectiveness of SUDC in improving the problem of unsynchronized updates across routers.

3.

Propagation time of policies in the network: This metric is used to evaluate the policy-update cycle of SUDC.

5.1. Simulation Setup

In this section, we develop a simulator in Python language and implement our scheme to evaluate the performance of SUDC. The version of Python Interpreter is Python 3.9. To evaluate its performance, we generate a random topology containing 100 nodes, which is stored as an adjacency matrix. On the basis of this topology, we hypothesize the transmission delay of each link and a comprehensive metric for resource overhead during packet transmission within each link segment.

The comprehensive metric for various resource overheads on any link ranges from 5 to 50, including 5 and 50. The transmission delay of any link ranges from 5 ms to 15 ms, including 5 ms and 15 ms. We assume a time interval of 1 ms between consecutive policy transmissions from the controller. Twenty nodes with the lowest degree in the topology are selected as entry switches. There are eight distinct test sets, each containing 5000/10,000/25,000/50,000/100,000/250,000/500,000/1,000,000 SRv6 TE policies, respectively.

Subsequently, we employ the Shortest Path First (SPF) algorithm to compute the least comprehensive resource overhead paths between any two nodes, simulating the SRv6 TE policy set derived from the controller calculation. These simulated SRv6 policies are stored, and eight test sets of different sizes are randomly drawn from all these simulated SRv6 policies. We utilize the SPF algorithm to calculate the minimum transmission delay paths from the controller to the other nodes, therefore simulating the packet propagation trajectory when policies are unicastably distributed by the controller to each node individually. We utilize the Prime algorithm to build a transmission delay minimizing the spanning tree, including all nodes, and, therefore, simulating the packet propagation trajectory when the SID blocks are distributed by the controller to the nodes in a multicast manner. We select some of the switches within the topology as ingress switches in order to evaluate the performance of the two-phase update scheme.

Finally, simulations are conducted on the three metrics of ordered update, two-stage update, and SUDC. To test the performance of SUDC, the policy splitting algorithm is executed on each test set to obtain multiple policy distribution SID blocks before simulation.

5.2. Result and Analysis

5.2.1. Number of Times for Policy Distribution

The number of times for policy distribution is the number of times the controller distributes the numerous policies derived from a single computation to the corresponding target nodes.

Table 3. Number of times for policy distribution.

Number of Policies	SUDC	Ordered Update	Two-Phase Update	Reduction Ratio
5000	3075	5000	5000	38.50%
10,000	5757	10,000	10,000	42.43%
25,000	13,438	25,000	25,000	46.25%
50,000	25,934	50,000	50,000	48.13%
100,000	50,965	100,000	100,000	49.04%
250,000	125,968	250,000	250,000	49.61%
500,000	250,963	500,000	500,000	49.81%
1,000,000	500,963	1,000,000	1,000,000	49.90%

and Figure 5 depicts the number of times for policy distribution of ordered update, two-phase update, and SUDC.

From Figure 5 and Table 3, it can be seen that the number of times for policy distribution of ordered update and two-phase update is equal to the number of policy entries contained in the test set. This is due to the fact that policies are distributed to the target nodes one by one in these two schemes. SUDC needs to distribute all the SID blocks obtained by the policy-dividing algorithm, so the number of times for policy distribution of SUDC is the number of policy distribution SID blocks.

The distribution policy times in SUDC are 46.71% less than those in ordered update and two-phase update. Furthermore, as the test set size increases, the reduction in the number of times for policy distribution of SUDC becomes increasingly pronounced.

5.2.2. Coexisting Time of New and Legacy Policies

In the network, some packets execute the new SRv6 TE policy while others execute the legacy SRv6 TE policy simultaneously. The time during which this state persists is referred to as the new policy and legacy policy coexisting time.

For ordered updates, each SRv6 policy is distributed to the destination router along the path with the smallest transmission delay. The coexisting time of new and legacy policies for ordered updates is the time lag between the moment when the first policy is received and the moment when the last policy is received.

For a two-phase update, each SRv6 policy whose target node is an internal switch is distributed sequentially along the path with the smallest transmission delay, and then each SRv6 policy whose target node is an ingress switch is distributed sequentially along the path with the smallest transmission delay. Before updating ingress switches, all packets are processed according to legacy policies. Starting from updating ingress switches, new policies process packets with new version tags, and packets with old version tags are processed by legacy rules. Therefore, the coexisting time of new and legacy policies for two-phase updates is the time lag between the moment when the first policy, whose target node is an ingress switch, is received and the moment when the last policy, whose target node is an ingress switch, is received.

For SUDC, each policy distribution SID block is multicast to the set of target routers along the transmission delay minimizing spanning tree. In addition, this metric of SUDC is the time lag between the moment when the first multicast SID block first arrives at one router in its set of target routers and the moment when the last multicast SID block finally arrives at one router in its set of target routers.

Table 4. Coexisting time of new and legacy policies.

Number of Policies	SUDC	Ordered Update	Reduction Ratio	Two-Phase Update	Reduction Ratio
5000	0.131 s	5.018 s	97.39%	0.949 s	86.20%
10,000	0.131 s	9.99 s	98.69%	1.961 s	93.32%
25,000	0.131 s	24.982 s	99.48%	4.905 s	97.33%
50,000	0.131 s	50.01 s	99.74%	10.005 s	98.69%
100,000	0.131 s	99.989 s	99.87%	19.952 s	99.34%
250,000	0.131 s	249.999 s	99.95%	49.878 s	99.74%
500,000	0.131 s	500.022 s	99.97%	99.894 s	99.87%
1,000,000	0.131 s	1000.01 s	99.99%	200.113 s	99.93%

and Figure 6 show the coexisting time of new and legacy policies for an ordered update, two-phase update, and SUDC. The average coexisting time in SUDC is 99.38% and 96.80% less than that in ordered updates and two-phase updates, respectively.

As shown in Figure 6, the coexisting time of new and legacy policies for SUDC is not affected by the size of the test set. The coexisting time of new and legacy policies for SUDC is the time lag between the time when the push-stop signal finally reaches a node and the time when it first reaches a node. As a result, this metric does not become larger as the size of the test set increases.

The results indicate that the coexisting time in SUDC is independent of the quantity size of policies. The data implies that SUDC can effectively improve the problem of unsynchronized updates across routers and reduce the risk of network instability.

5.2.3. Propagation Time of Policies in the Network

The period from when the controller initiates new policy distribution until all policies are received by their corresponding target nodes is referred to as the propagation time of policies.

For ordered updates, each SRv6 policy is distributed to the destination router along the path with the smallest transmission delay. The propagation time for ordered updates is the time lag between the moment when the first policy is distributed and the moment when the last policy is received.

For a two-phase update, each SRv6 policy whose target node is an internal switch is distributed sequentially along the path with the smallest transmission delay, and then each SRv6 policy whose target node is an ingress switch is distributed sequentially along the path with the smallest transmission delay. The propagation time for a two-phase update is the time lag between the moment when the first policy is distributed to one internal switch in phase 1 and the moment when the last policy is received by one ingress switch.

For SUDC, each policy distribution SID block is multicast to the set of target routers along the transmission delay minimizing spanning tree. In addition, this metric of SUDC is the time lag between the moment when the first multicast SID block is multicast to its set of target routers and the moment when the last multicast SID block finally arrives at one router in its set of target routers.

Table 5. Propagation time of policies in the network.

Number of Policies	SUDC	Ordered Update	Reduction Ratio	Two-Phase Update	Reduction Ratio
5000	3.124 s	5.035 s	37.95%	5.035 s	37.95%
10,000	5.806 s	10.007 s	41.98%	10.049 s	42.22%
25,000	13.487 s	25.025 s	46.11%	25.045 s	46.15%
50,000	25.983 s	50.045 s	48.08%	50.037 s	48.07%
100,000	51.014 s	100.03 s	49.00%	100.035 s	49.00%
250,000	126.017 s	250.037 s	49.60%	250.035 s	49.60%
500,000	251.012 s	500.06 s	49.80%	500.06 s	49.80%
1,000,000	501.012 s	1000.031 s	49.91%	1000.045 s	49.91%

and Figure 7 demonstrate the propagation time for an ordered update, two-phase update, and SUDC. In both ordered updates and two-phase updates, the controller distributes policies to the target routers one by one. Therefore, this metric is nearly the same for both schemes. Compared with ordered updates and two-phase updates, SUDC can improve the policy transmission speed in the network and shorten the propagation time by 46.6% on average.

As observed from Table 5 and Figure 7, it is evident that with the increase in the size of the test set, SUDC exhibits an increasingly improved reduction in the propagation time of policies in the network.

5.2.4. Timeliness Cost of SUDC

We define the timeliness cost of SUDC as the time that the router receiving the first policy distribution SID block must wait. In SUDC, some nodes need to wait for some time before updating their flow tables, even though these nodes have received all the policy distribution SID blocks that they should have received. That is the timeliness cost that certain nodes need to pay under the SUDC scheme. Under the definition of timeliness cost, the time that all routers need to wait is usually less than or equal to this metric.

Table 6. Timeliness cost of SUDC.

Number of Policies	Timeliness Cost of SUDC
5000	3.058 s
10,000	5.740 s
25,000	13.421 s
50,000	25.917 s
100,000	50.948 s
250,000	125.951 s
500,000	250.946 s
1,000,000	500.946 s

and Figure 8 present the variation of timeliness cost for different test set sizes. It can be observed that the growth of timeliness cost slows down as the test set size grows.

6. Conclusions

For the problem of unsynchronized updates across routers resulting from frequent SRv6 TE policy updates in the intelligent 6G scenario, this paper proposes a scheme called SUDC. We propose the policy-dividing and combination mechanism and design the policy-dividing algorithm based on this mechanism. Mathematical simulation results prove that SUDC can significantly reduce update overhead and shorten the policy-update cycle. The unsynchronization of policy updates across routers has also been greatly improved. In the future, we will continue to optimize SUDC based on existing research results in order to achieve better synchronization effects among routers during SRv6 TE policy updates.

7. Patents

The work in Section 3 has produced a patent, the patent application publication number is CN115766580A, and the legal status of the patent is initiative for examination as to substance.